5 Манипуляционная часть реляционной модели данных реляционная алгебра

5. Манипуляционная часть реляционной модели данных: реляционная алгебра

5. 1. Введение Основа – спецификационные операторы, базирующиеся на теории множеств. Языки запросов: • алгебраические языки (реляционная алгебра) – как получить требуемый результат • языки исчисления предикатов (реляционное исчисление) – что должно быть получено – с переменными-кортежами – с переменными на доменах

5. 2. Общая характеристика РА Средства для записи и интерпретации выражений: операнд 1 операция операнд 2 результат 1. Свойство замкнутости: R 1 опц R 2 опц R 3 … 2. Отношение = интенсионал (схема отношения) + экстенсионал (реализация отношения)

5. 3. Вычисление выражения Правила наследования имен атрибутов: Даны R 1(A 1, A 2, …) и R 2(B 1, B 2, …). R = R 1 опц R 2 R(C 1, C 2, …), где Ci – атрибут, совпадающий с Aj, или Bk

5. 4. Операции реляционной алгебры • Теоретико-множественные объединение, вычитание, пересечение, прямое (декартово) произведение • Специальные выбор (селекция), проекция, соединение, деление • Переименования

5. 5. Операция переименования Изменяет только схему отношения, сохраняя реализацию Пример: переименовать атрибут C в SC До переименования После переименования S A B SC S A B C a b c d b e

5. 6. Теоретико-множественные операции • • Объединение Вычитание Пересечение Прямое (декартово) произведение

5. 7. Объединение множеств Даны два множества S 1 и S 2 Объединение множеств: S = S 1 S 2 = { si | si S 1 и/или si S 2 }

5. 7. Объединение множеств D 1 = {1, 3, 5, 7, 9}, D 2 = {‘a’, ‘b’, ‘c’}, D 3 = {2, 4, 6, 8} – домены Объединение D 1 и D 2: S = D 1 D 2 = {1, 3, 5, 7, 9, ‘a’, ‘b’, ‘c’} – множество, но не домен Объединение D 1 и D 3: D = D 1 D 3 = {1, 3, 5, 7, 9, 2, 4, 6, 8} – домен

5. 7. Объединение множеств Отношения – R 1(A 1: D 1, A 2: D 1), r 1 = {<1, 3>, <1, 1>} R 2(A 1: D 1, A 2: D 2), r 2 = {<1, 'a'>, <2, 'b'>} R 3(A 1: D 1, A 2: D 3), r 3 = {<1, 2>, <7, 2>} Объединение r = r 1 r 2 = {<1, 3>, <1, 1>, <1, 'a'>, <2, 'b'>} – не отношение Объединение r = r 1 r 3 = {<1, 3>, <1, 1>, <1, 2>, <7, 2>} – отношение

5. 8. Совместимость по объединению Простые домены считаются совместимыми по объединению, если они состоят из элементов одного типа. Два отношения считаются совместимыми по объединению, если: • оба отношения имеют одно и то же множество атрибутов, • одноименные атрибуты двух отношений определены на совместимых по объединению доменах.

5. 9. Объединение отношений Объединение (Union) двух отношений r 1(R 1) и r 2(R 2), совместимых по объединению: s = r 1 r 2 • схема отношения – совпадает с R 1 или R 2, • реализация отношения – множество кортежей, принадлежащих реализации r 1 и/или r 2

5. 9. Объединение отношений Даны r 1(R 1), r 2(R 2), r 1 = {t 1 i}, r 2 = {t 2 i}, R 1 R, R 2 R s = r 1 r 2 = s(R), s = {ti | ti r 1 и/или ti r 2} r 1 A B C r 2 A B C a a b e c c a d e c c c d b a d d d b c b a c b d b b

5. 10. Свойства операции объединения • коммутативна r 1 r 2 r 1 • ассоциативна r 1 (r 2 r 3) (r 1 r 2) r 3 r 1 r 2 r 3

5. 11. Вычитание отношений Вычитание (Except) двух отношений r 1(R 1) и r 2(R 2), совместимых по объединению: s = r 1 – r 2 • схема отношения – совпадает с R 1 или R 2 • реализация отношения – множество кортежей из r 1, за исключением тех, которые имеются в r 2

5. 11. Вычитание отношений Даны r 1(R 1), r 2(R 2), r 1 = {t 1 i}, r 2 = {t 2 i}, R 1 R, R 2 R s = r 1 – r 2 = s(R), s = {ti | ti r 1 и ti r 2} r 1 A B C r 2 A B C r A B C a a b e c c a d e c c c a d b b c a d b d

5. 12. Свойства операции вычитания • не коммутативна r 1 – r 2 – r 1 • не ассоциативна r 1 – r 2 – r 3 (r 1 – r 2) – r 3 r 1 – (r 2 – r 3)

5. 13. Пересечение отношений Пересечение (Intersect) двух отношений r 1(R 1) и r 2(R 2), совместимых по объединению: s = r 1 r 2 • схема отношения – совпадает с R 1 или R 2 • реализация отношения – множество кортежей, содержащихся и в r 1, и в r 2

5. 13. Пересечение отношений Даны r 1(R 1), r 2(R 2), r 1 = {t 1 i}, r 2 = {t 2 i}, R 1 R, R 2 R s = r 1 r 2 = s(R), s = {ti | ti r 1 и ti r 2} r 1 A B C r 2 A B C r A B C a a b e c c a d e c c c a e c d b a d b d

5. 14. Свойства операции пересечения • коммутативна r 1 r 2 r 1 • ассоциативна r 1 (r 2 r 3) (r 1 r 2) r 3 r 1 r 2 r 3 Эквивалентность: r 1 r 2 = r 1 – (r 1 – r 2)

5. 15. Декартово произведение двух отношений r 1(R 1) и r 2(R 2), R 1 и R 2 не имеют одноименных атрибутов: s = r 1 r 2 • схема отношения – сцепление схем R 1 и R 2 • реализация отношения – сцепление каждого кортежа из r 1 с каждым кортежем из r 2

5. 15. Декартово произведение Даны r 1(R 1), R 1(A 1, A 2, …, Am), r 2(R 2), R 2(B 1, B 2, …, Bn), r 1 = {t 1 i}, r 2 = {t 2 i}, R 1 R 2 = 0 s = r 1 r 2 = s(R), R(A 1, A 2, …, Am, B 1, B 2, …, Bn), s = {ui vj | ui r 1, vj r 2} r 1 A B a c r 2 X Y Z b a d b x c s A B X Y Z x a b a d x a c a b x a c d b a b c d b c b a d x c b x a c c b c d b

5. 16. Свойства декартова произведения • коммутативна r 1 r 2 r 1 • ассоциативна r 1 (r 2 r 3) = (r 1 r 2) r 3 = r 1 r 2 r 3 В теории множеств данная операция и не коммутативна, и не ассоциативна

517. Специальные операции • Проекция • Выбор (или селекция) • Соединение • Деление Наряду с отношениями, в операциях используются и отдельные атрибуты

5. 18. Проекция отношения r(R), R = {Ai}, на список имен атрибутов L из R s = L(r) • схема отношения – определяется списком L, • реализация отношения – множество кортежей, полученных из кортежей отношения r путем вычеркивания элементов, соответствующих атрибутам R – L, и исключением дубликатов

5. 18. Проекция Дано r(R), R(A 1, A 2, …, Am), r = {<t 1 : A 1, t 2 : A 2…, tm : Am >} s(L) = L(r), L(B 1, B 2, …, Bk), Bi R, s = {<u 1 : B 1, u 2 : B 2, …, uk : Bk> | таких, что ui = tj, если Bi Aj} r A a a d B b b b C c x a D d c c S = AB(r) A a d B b b

5. 19. Свойства проекции • Если Y R и X R, то Y( X(r)) X( Y(r)) X Y(r) • Если Y X R, то Y( X(r)) Y(r)

5. 20. Выбор из отношения r(R) по условию F: s = F(r) • схема отношения – совпадает со схемой R • реализация отношения – множество кортежей из r, удовлетворяющих условию F

5. 20. Выбор Условие (предикат) F: • операнды – атрибуты отношения и/или константы; • операции – операции отношения (=, и т. д. ) и логические операции ( , , ).

5. 20. Выбор Дано r(R), r = {ti} s(R) = F(r), s = {ui | ui R и F(ui) – истинно} r A a a c B b d b C c c d A = ‘a’ C = ‘c’(r) A a a B b d C c c

5. 21. Свойства операции выбора • коммутативна F 1( F 2(r)) = F 2( F 1(r)) = F 1 F 2 (r) • дистрибутивна относительно операций = ( , , –): F (r s) = F (r) F (s)

5. 22. Соединение • Естественное соединение • Соединение по условию

5. 23. Естественное соединение Естественным соединением (Inner Join) отношений r 1(R 1), R 1 = XY, и r 2(R 2), R 2 = YZ, где Y – общее подмножество атрибутов из R 1 и R 2, определенных на одних и тех же доменах, называется отношение s(R) = r 1 r 2, для которого: • схема отношения R = R 1 R 2 = XYZ, • реализация отношения есть множество кортежей {t}, для которых XY(t) r 1 и YZ(t) r 2

5. 23. Естественное соединение Даны r 1(R 1), R 1 = XY, и r 2(R 2), R 2 = YZ. s(R) = r 1 r 2, R = R 1 R 2 = XYZ, s = {t | таких, что XY(t) r 1 и YZ(t) r 2} r 1 A a d b B b b b C c c f r 2 B b b a ? ? ? C c c d D d e b c a d a b f s = r 1 r 2 A a a d d c B C D b c d b c e b c d b a c e d b

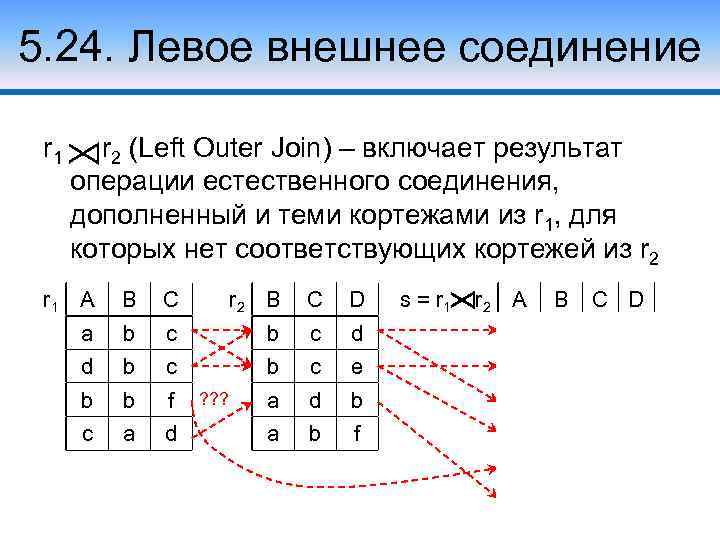
5. 24. Левое внешнее соединение r 1 r 2 (Left Outer Join) – включает результат операции естественного соединения, дополненный и теми кортежами из r 1, для которых нет соответствующих кортежей из r 2 r 1 A B C r 2 B C D a b c d b c b b b f c a d ? ? ? s = r 1 r 2 A B C D d a b c d c e a b c e a d b c d a b f d b c e b b f – c a d b

5. 25. Правое внешнее соединение r 1 r 2 (Right Outer Join) – включает результат операции естественного соединения, дополненный и теми кортежами из r 2, для которых нет соответствующих кортежей из r 1 A a d b B b b b C c c f r 2 B b b a C c c d D d e b c a d a b f s = r 1 r 2 A a a d d c – B C D b c d b c e b c d b a a c e d b b f

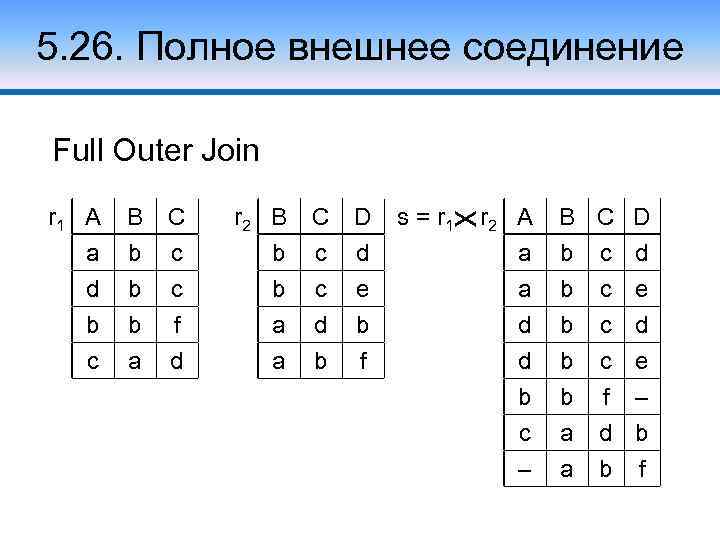
5. 26. Полное внешнее соединение Full Outer Join r 1 A a d b B b b b C c c f r 2 B b b a C c c d D d e b c a d a b f s = r 1 r 2 A a a d d b c – B C D b c d b c e b c d b b a a c e f – d b b f

5. 27. Соединение по условию Даны два отношения r 1(R 1) и r 2(R 2), для которых R 1 R 2 = . Атрибут A R 1 сравним по условию с атрибутом B R 2. Соединением отношений r 1(R 1) и r 2(R 2) по условию называется отношение s(R) = r 1 A B r 2, для которого: • схема отношения R = R 1 R 2 = R 1 R 2, • реализация отношения есть множество кортежей, полученных сцеплением кортежей из r 1 и r 2, удовлетворяющих условию A B

5. 27. Соединение по условию Даны r 1(R 1) и r 2(R 2), R 1 R 2 = . s(R) = r 1 A B r 2, R = R 1 R 2, s = {uv | таких, что u r 1, v r 2 и для u и v выполняется условие } r 1 A B C 1 2 4 7 r 2 X Y 3 3 1 5 6 6 2 8 9 r = r 1 r B <X 2 A B C X Y 1 2 3 3 1 1 2 3 6 2 4 5 6 6 2

5. 28. Деление Даны два отношения r 1(R 1) и r 2(R 2), для которых R 2 R 1 и R 2 не пусто. Частным от деления отношения r 1 на отношение r 2 называется отношение s(R) = r 1 r 2, для которого: • схема отношения R = R 1 – R 2, • реализация отношения есть множество кортежей t таких, что для всех ui r 2 существует vj r 1 такой, что vj(R 1 – R 2) = t и vj(R 2) = ui

5. 28. Деление Даны r 1(R 1), r 2(R 2), R 2 R 1, R 2 0. s(R) = r 1 r 2, R = R 1 – R 2, s = {tj | u r 2 (tju r 1)} Другими словами, s r 2 r 1 Выражение реляционной алгебры, эквивалентное операции деления: r 1 r 2 = R 1 -R 2(r 1) – R 1 -R 2(( R 1 -R 2(r 1) r 2) – r 1)

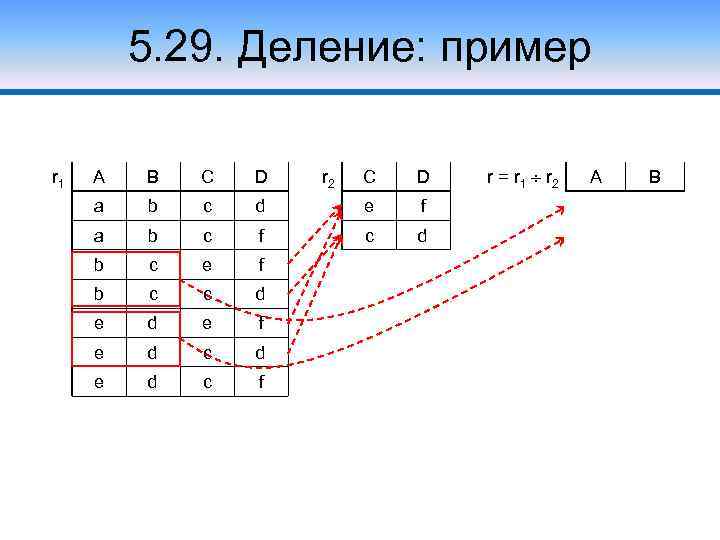
5. 29. Деление: пример r 1 A B C D a b c a b b r 2 C D d e c f c c e f b c c d e f e d c d e d c f r = r 1 r 2 A B f b c d e d

5. 30. Примеры запросов Схема базы данных: S(Sid, SN, SC) – ПОСТАВЩИК ( Номер поставщика, Имя, Город) P(Pid, PN, PC) – ДЕТАЛЬ ( Номер детали, Название, Цена) SP(Sid (FK 1), Pid (FK 2), QTY) – ПОСТАВКА ( Номер поставщика, Номер детали, Количество)

5. 30. Примеры запросов • Получить имена поставщиков, поставляющих деталь с номером P 1. SN( Pid =’ P 1’(S SP)) • Получить имена поставщиков, не поставляющих деталь с номером P 1. SN(S) – SN( Pid = ‘P 1’(S SP))

5. 30. Примеры запросов • Получить имена поставщиков, поставляющих только деталь с номером P 1 SN( Pid =’P 1’(S SP)) – SN( Pid ’ P 1’(S SP)) • Получить имена поставщиков, поставляющих все детали SN(( Sid, Pid(SP) Pid(P)) S)