5 Дифракция волн Принцип Гюйгенса Френеля

5. Дифракция волн. Принцип Гюйгенса – Френеля

Дифракция – явление огибания волнами препятствий и проникновения колебаний в область геометрической тени.

Дифракция от края преграды.

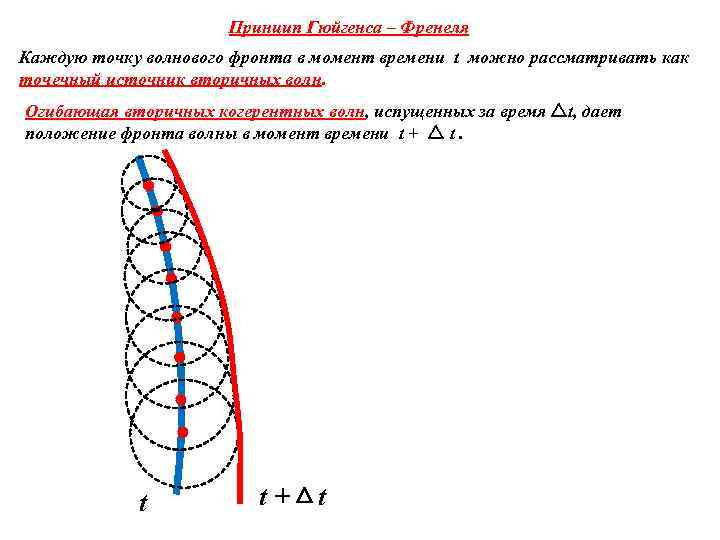Принцип Гюйгенса – Френеля Каждую точку волнового фронта в момент времени t можно рассматривать как точечный источник вторичных волн. Огибающая вторичных когерентных волн, испущенных за время t, дает положение фронта волны в момент времени t + t. t t+ t

Каждый элемент волновой поверхности площадью d. S служит источником вторичной сферической волны, от которой в некоторую точку Р приходят колебания. Результирующее колебание в точке Р – суперпозиция колебаний, приходящих от всех d. S волновой поверхности S. Р - коэффициент, убывающий при увеличении

6. Метод зон Френеля. Дифракция Френеля на круглом отверстии и диске.

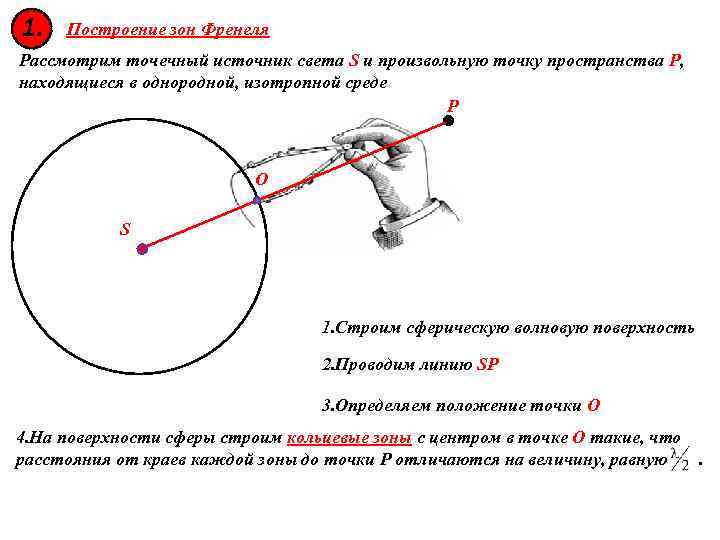1. Построение зон Френеля Рассмотрим точечный источник света S и произвольную точку пространства P, находящиеся в однородной, изотропной среде P O S 1. Строим сферическую волновую поверхность 2. Проводим линию SP 3. Определяем положение точки О 4. На поверхности сферы строим кольцевые зоны с центром в точке О такие, что расстояния от краев каждой зоны до точки Р отличаются на величину, равную.

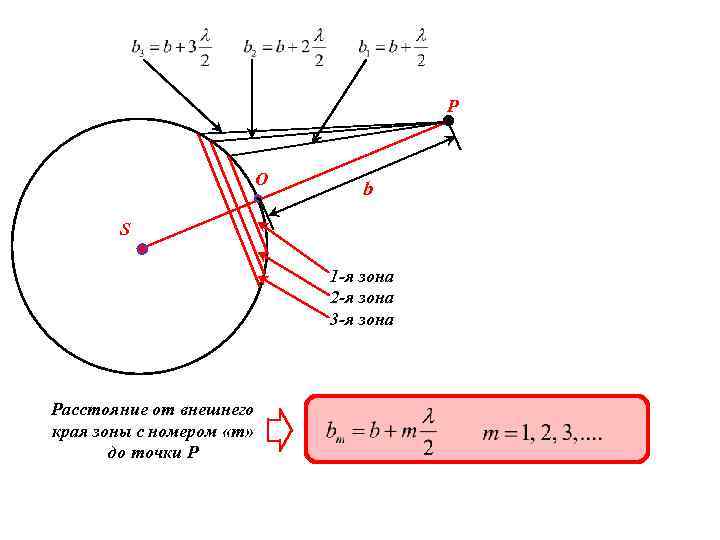P O b S 1 -я зона 2 -я зона 3 -я зона Расстояние от внешнего края зоны с номером «m» до точки Р

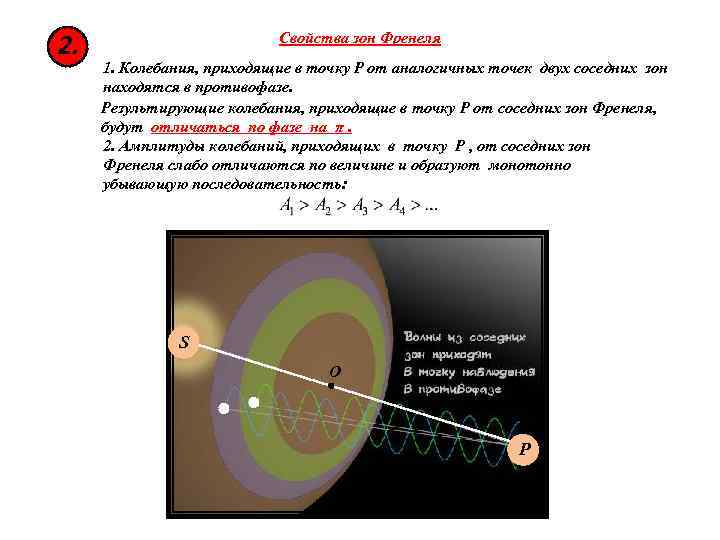2. Свойства зон Френеля 1. Колебания, приходящие в точку Р от аналогичных точек двух соседних зон находятся в противофазе. Результирующие колебания, приходящие в точку Р от соседних зон Френеля, будут отличаться по фазе на π. 2. Амплитуды колебаний, приходящих в точку Р , от соседних зон Френеля слабо отличаются по величине и образуют монотонно убывающую последовательность: S O P

3. Дифракция Френеля на круглом отверстии. Амплитуда результирующего колебания в точке Р может быть представлена в виде N - число зон Френеля в круглом отверстии для точки P (в центре экрана) Если N чётное, то в точке P будет темно Если N нечётное, то в точке P будет светло

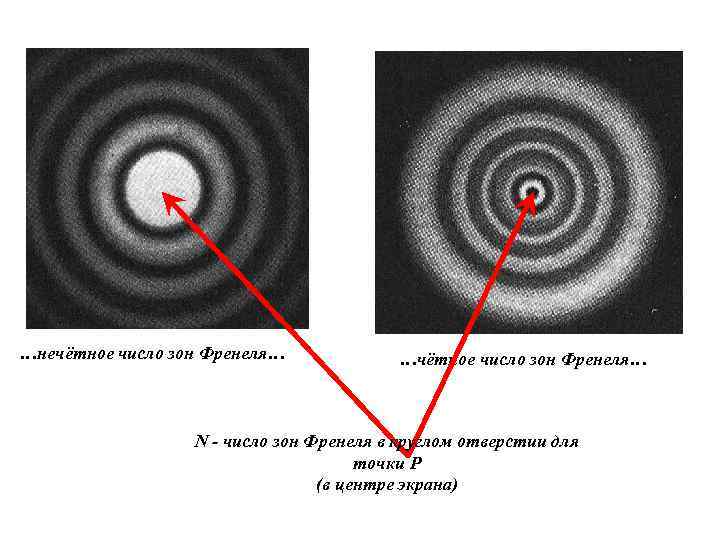…нечётное число зон Френеля… …чётное число зон Френеля… N - число зон Френеля в круглом отверстии для точки P (в центре экрана)

Что будет в точке P, когда ?

4. Дифракция Френеля на круглом диске. Пусть диск закрывает «т» зон Френеля. Тогда амплитуда в точке Р будет равна В точке Р всегда светло!!!

7. Дифракция Фраунгофера от одной щели.

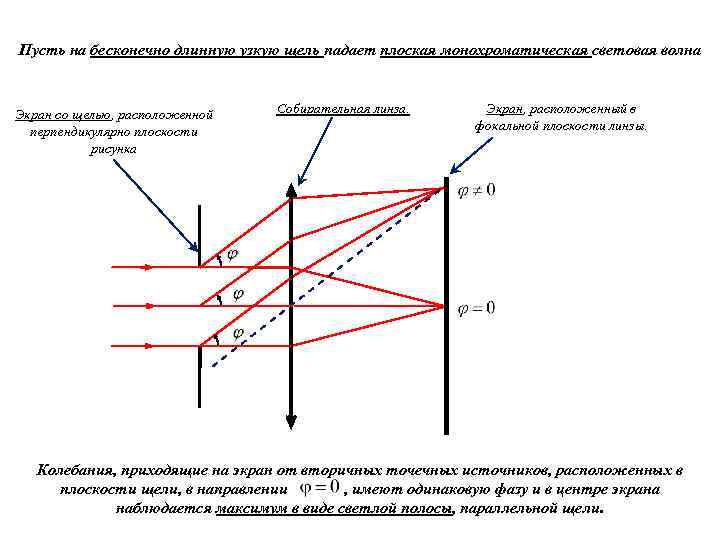Пусть на бесконечно длинную узкую щель падает плоская монохроматическая световая волна Экран со щелью, расположенной перпендикулярно плоскости рисунка Собирательная линза. Экран, расположенный в фокальной плоскости линзы. Колебания, приходящие на экран от вторичных точечных источников, расположенных в плоскости щели, в направлении , имеют одинаковую фазу и в центре экрана наблюдается максимум в виде светлой полосы, параллельной щели.

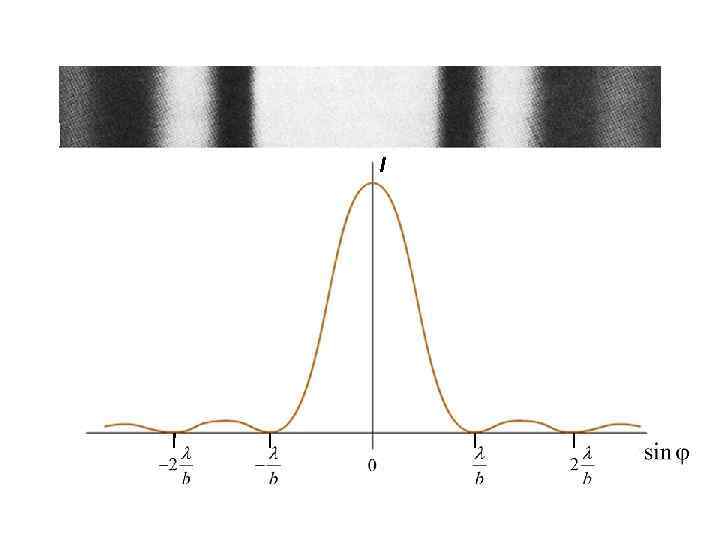
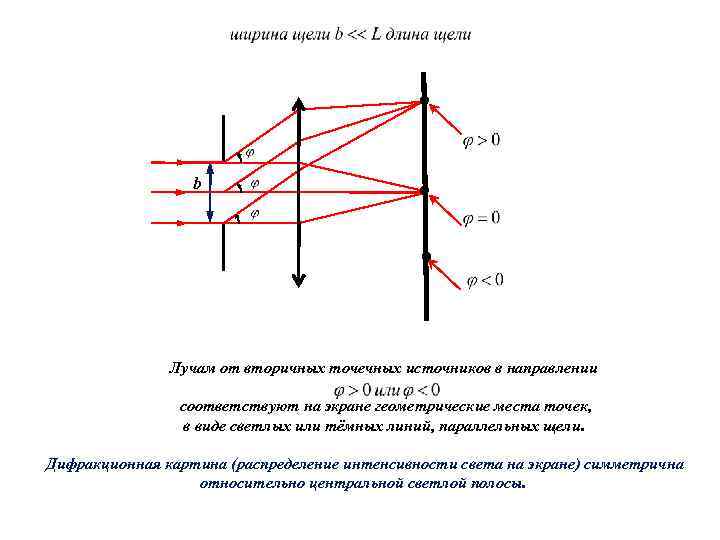b Лучам от вторичных точечных источников в направлении соответствуют на экране геометрические места точек, в виде светлых или тёмных линий, параллельных щели. Дифракционная картина (распределение интенсивности света на экране) симметрична относительно центральной светлой полосы.

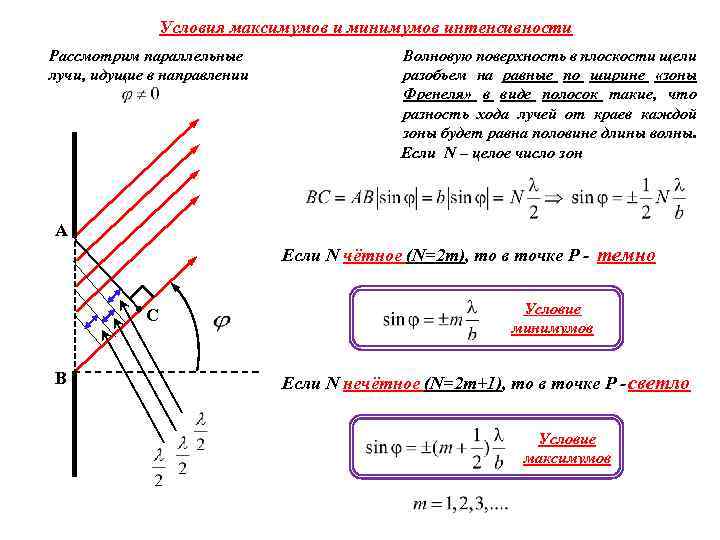Условия максимумов и минимумов интенсивности Рассмотрим параллельные лучи, идущие в направлении Волновую поверхность в плоскости щели разобьем на равные по ширине «зоны Френеля» в виде полосок такие, что разность хода лучей от краев каждой зоны будет равна половине длины волны. Если N – целое число зон А Если N чётное (N=2 m), то в точке P - темно С В Условие минимумов Если N нечётное (N=2 m+1), то в точке P - светло Условие максимумов

I

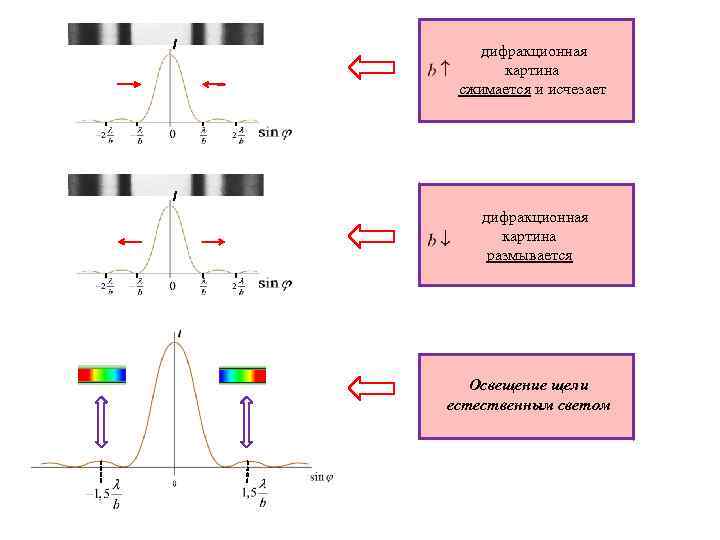I дифракционная картина сжимается и исчезает I дифракционная картина размывается Освещение щели естественным светом