 5. AVL – деревья
5. AVL – деревья
 5. 1. AVL – деревья Бинарное дерево является сбалансированным, если для любого узла дерева высоты его левого и правого поддеревьев отличаются не более чем на 1 Высота дерева – максимальная длина пути от корня дерева до подчиненных листьев этого дерева Представление листьев – как в красночерном дереве 2
5. 1. AVL – деревья Бинарное дерево является сбалансированным, если для любого узла дерева высоты его левого и правого поддеревьев отличаются не более чем на 1 Высота дерева – максимальная длина пути от корня дерева до подчиненных листьев этого дерева Представление листьев – как в красночерном дереве 2
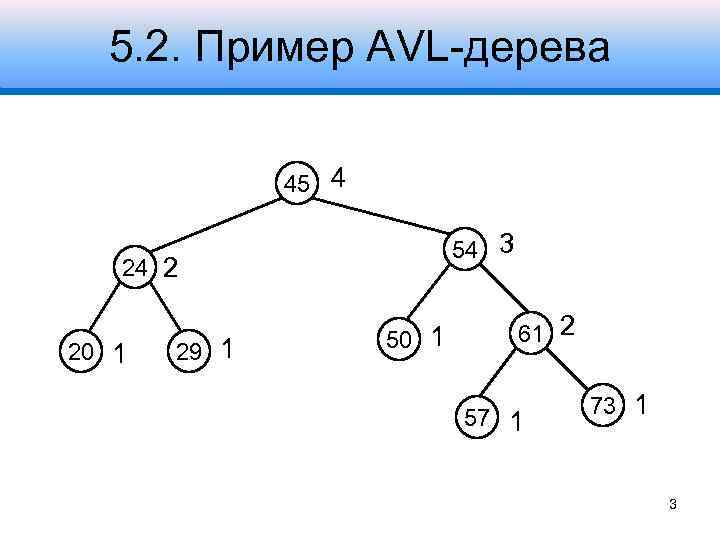 5. 2. Пример AVL-дерева 45 4 54 3 24 2 20 1 29 1 50 1 61 2 57 1 73 1 3
5. 2. Пример AVL-дерева 45 4 54 3 24 2 20 1 29 1 50 1 61 2 57 1 73 1 3
 5. 3. Высота AVL-дерева Г. М. Адельсон-Вельский, Е. М. Ландис (1962 г. ) Высота сбалансированного дерева с n внутренними узлами log 2(n + 1) h 1, 404 log 2(n + 2) – 0, 328 4
5. 3. Высота AVL-дерева Г. М. Адельсон-Вельский, Е. М. Ландис (1962 г. ) Высота сбалансированного дерева с n внутренними узлами log 2(n + 1) h 1, 404 log 2(n + 2) – 0, 328 4
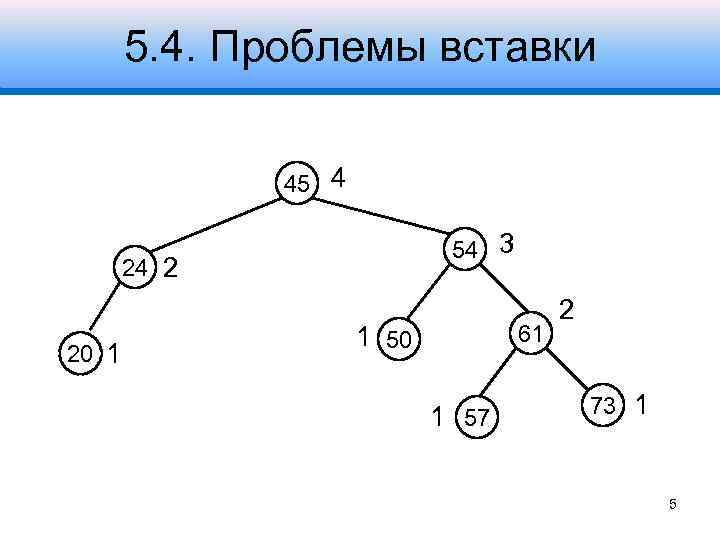 5. 4. Проблемы вставки 45 4 54 3 24 2 20 1 61 1 50 1 57 2 73 1 5
5. 4. Проблемы вставки 45 4 54 3 24 2 20 1 61 1 50 1 57 2 73 1 5
 5. 5. Узлы AVL-дерева 1. С дополнительным полем сбалансированности в узле: -1, левое поддерево выше на 1 balance = 0, высота поддеревьев одинаковая +1, правое поддерево выше на 1 struct Node { int balance; int key; struct Node *left, *right, *parent; }; 6
5. 5. Узлы AVL-дерева 1. С дополнительным полем сбалансированности в узле: -1, левое поддерево выше на 1 balance = 0, высота поддеревьев одинаковая +1, правое поддерево выше на 1 struct Node { int balance; int key; struct Node *left, *right, *parent; }; 6
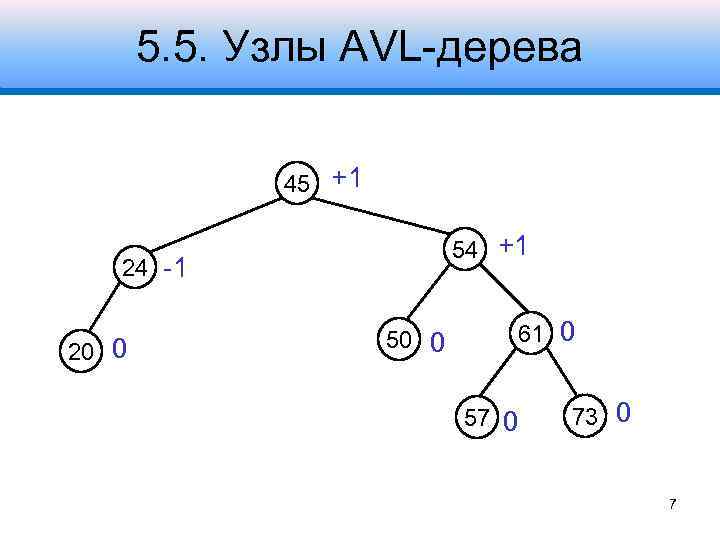 5. 5. Узлы AVL-дерева 45 +1 54 +1 24 -1 20 0 50 0 61 0 57 0 73 0 7
5. 5. Узлы AVL-дерева 45 +1 54 +1 24 -1 20 0 50 0 61 0 57 0 73 0 7
 5. 5. Узлы AVL-дерева 2. С дополнительными полями высоты левого и правого поддеревьев в узле: struct Node { int hleft; – высота левого поддерева int hright; – высота правого поддерева int key; struct Node *left, *right, *parent; }; 8
5. 5. Узлы AVL-дерева 2. С дополнительными полями высоты левого и правого поддеревьев в узле: struct Node { int hleft; – высота левого поддерева int hright; – высота правого поддерева int key; struct Node *left, *right, *parent; }; 8
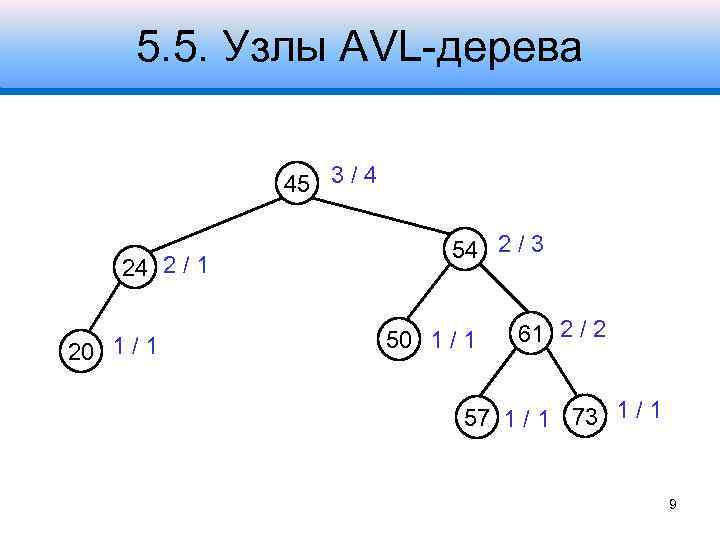 5. 5. Узлы AVL-дерева 45 3 / 4 24 2 / 1 20 1 / 1 54 2 / 3 50 1 / 1 61 2 / 2 57 1 / 1 73 1 / 1 9
5. 5. Узлы AVL-дерева 45 3 / 4 24 2 / 1 20 1 / 1 54 2 / 3 50 1 / 1 61 2 / 2 57 1 / 1 73 1 / 1 9
 5. 6. Вставка в AVL-дерево • Вставить новый элемент как в двоичное дерево поиска • Скорректировать свойство сбалансированности узлов дерева • При необходимости скорректировать само AVL-дерево 10
5. 6. Вставка в AVL-дерево • Вставить новый элемент как в двоичное дерево поиска • Скорректировать свойство сбалансированности узлов дерева • При необходимости скорректировать само AVL-дерево 10
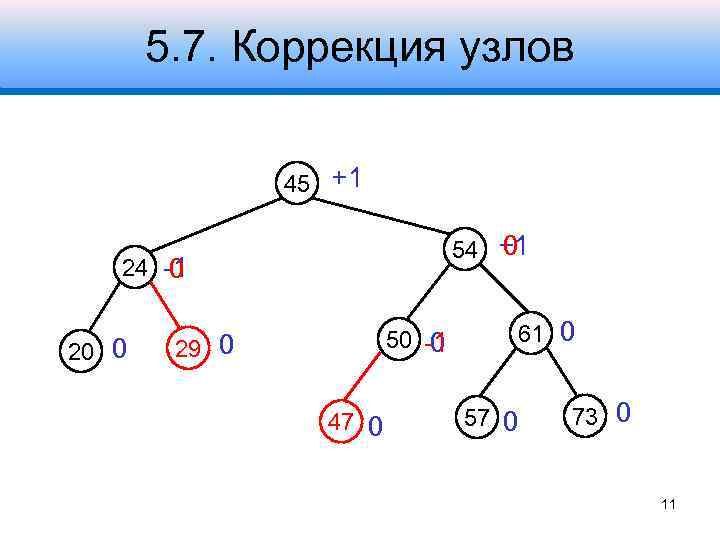 5. 7. Коррекция узлов 45 +1 0 54 +1 24 -1 0 20 0 50 -1 0 29 0 47 0 61 0 57 0 73 0 11
5. 7. Коррекция узлов 45 +1 0 54 +1 24 -1 0 20 0 50 -1 0 29 0 47 0 61 0 57 0 73 0 11
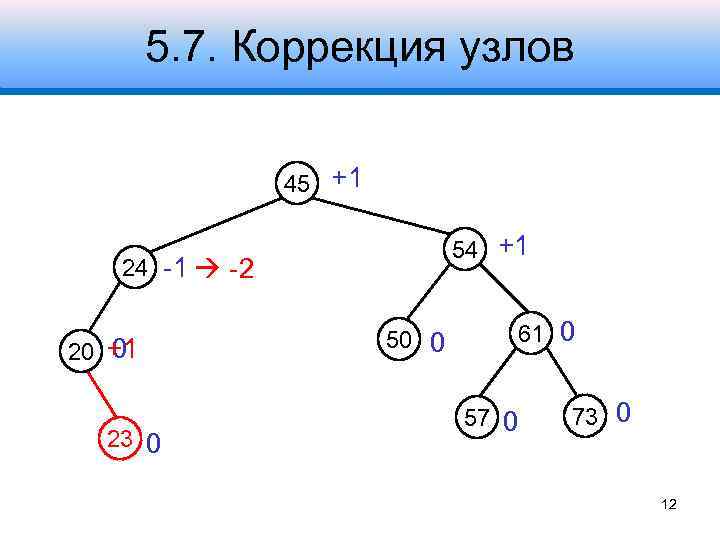 5. 7. Коррекция узлов 45 +1 54 +1 24 -1 -2 0 20 +1 23 0 50 0 61 0 57 0 73 0 12
5. 7. Коррекция узлов 45 +1 54 +1 24 -1 -2 0 20 +1 23 0 50 0 61 0 57 0 73 0 12
 5. 7. Коррекция узлов x – новый узел дерева q=x p = q->parent – родительский узел while p ≠ EList и p->balance = 0 { if q в левом поддереве p p->balance = -1 else p->balance = +1 q=p p = q->parent } 13
5. 7. Коррекция узлов x – новый узел дерева q=x p = q->parent – родительский узел while p ≠ EList и p->balance = 0 { if q в левом поддереве p p->balance = -1 else p->balance = +1 q=p p = q->parent } 13
 5. 7. Коррекция узлов p – узел дерева, у которого p->balance ≠ 0, или EList if p = EList успех if x в левом поддереве p и p->balance = +1 или x в правом поддереве p и p->balance = -1 { p->balance = 0 успех } 14
5. 7. Коррекция узлов p – узел дерева, у которого p->balance ≠ 0, или EList if p = EList успех if x в левом поддереве p и p->balance = +1 или x в правом поддереве p и p->balance = -1 { p->balance = 0 успех } 14
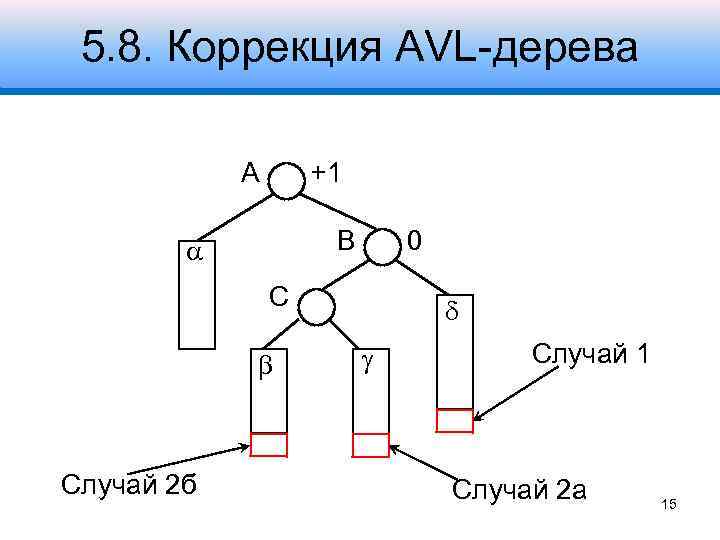 5. 8. Коррекция AVL-дерева A +1 B 0 С Случай 2 б Случай 1 Случай 2 а 15
5. 8. Коррекция AVL-дерева A +1 B 0 С Случай 2 б Случай 1 Случай 2 а 15
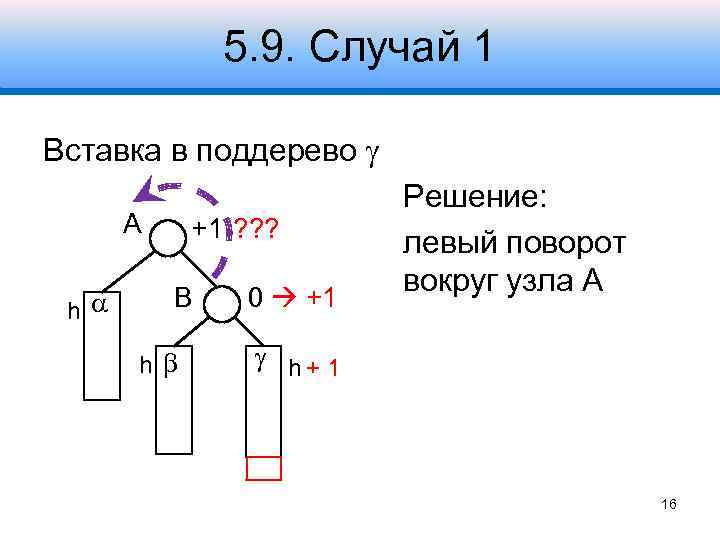 5. 9. Случай 1 Вставка в поддерево A h +1 ? ? ? B h 0 +1 Решение: левый поворот вокруг узла A h+ 1 16
5. 9. Случай 1 Вставка в поддерево A h +1 ? ? ? B h 0 +1 Решение: левый поворот вокруг узла A h+ 1 16
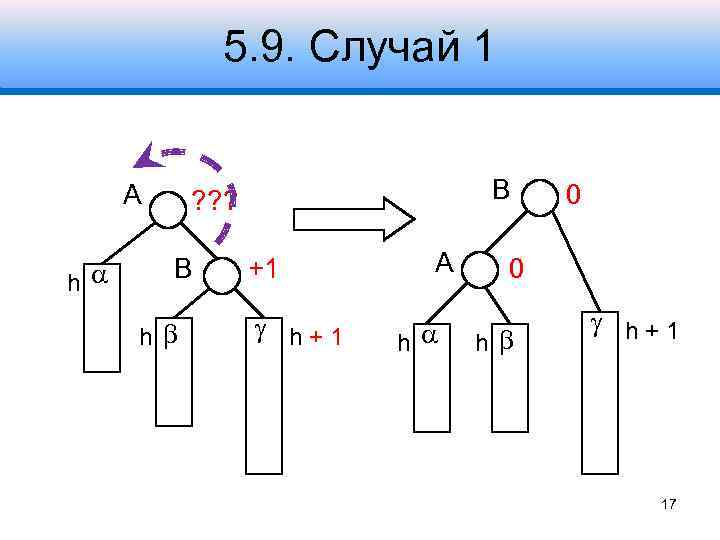 5. 9. Случай 1 A h B ? ? ? B h +1 h+1 A h 0 0 h h+1 17
5. 9. Случай 1 A h B ? ? ? B h +1 h+1 A h 0 0 h h+1 17
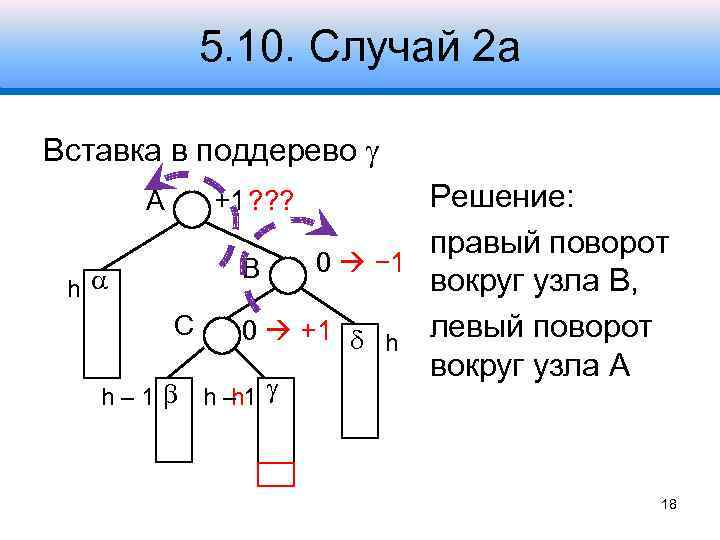 5. 10. Случай 2 а Вставка в поддерево A Решение: правый поворот 0 − 1 B вокруг узла B, 0 +1 h левый поворот вокруг узла A +1 ? ? ? h С h– 1 h 18
5. 10. Случай 2 а Вставка в поддерево A Решение: правый поворот 0 − 1 B вокруг узла B, 0 +1 h левый поворот вокруг узла A +1 ? ? ? h С h– 1 h 18
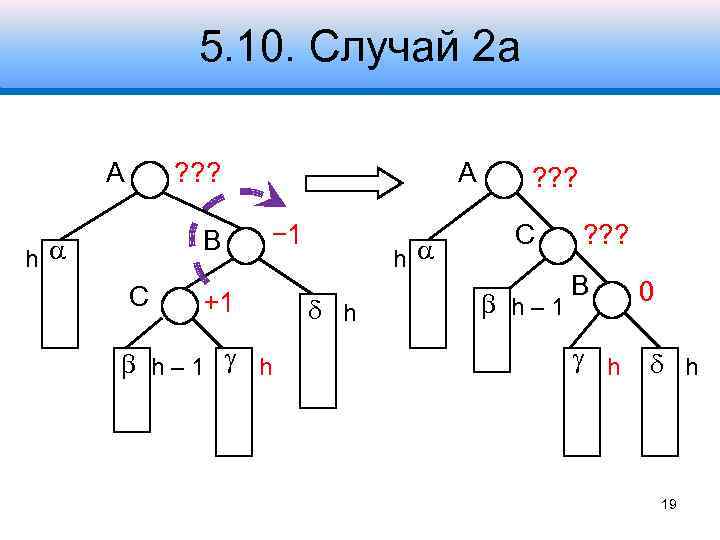 5. 10. Случай 2 а A ? ? ? B h С A − 1 +1 h– 1 h h h ? ? ? С h– 1 ? ? ? B h 0 h 19
5. 10. Случай 2 а A ? ? ? B h С A − 1 +1 h– 1 h h h ? ? ? С h– 1 ? ? ? B h 0 h 19
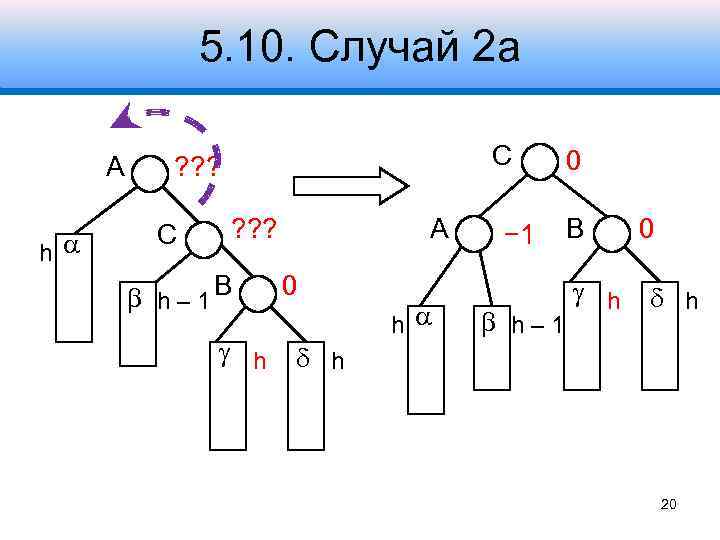 5. 10. Случай 2 а A h С ? ? ? h – 1 B h A 0 h − 1 h– 1 0 B h 0 h h 20
5. 10. Случай 2 а A h С ? ? ? h – 1 B h A 0 h − 1 h– 1 0 B h 0 h h 20
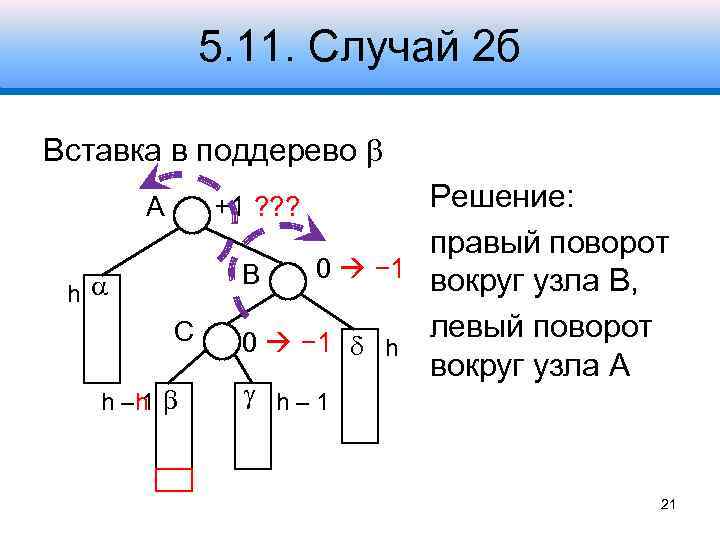 5. 11. Случай 2 б Вставка в поддерево A Решение: правый поворот 0 − 1 вокруг узла B, B левый поворот 0 − 1 h вокруг узла A +1 ? ? ? h С h –h 1 h– 1 21
5. 11. Случай 2 б Вставка в поддерево A Решение: правый поворот 0 − 1 вокруг узла B, B левый поворот 0 − 1 h вокруг узла A +1 ? ? ? h С h –h 1 h– 1 21
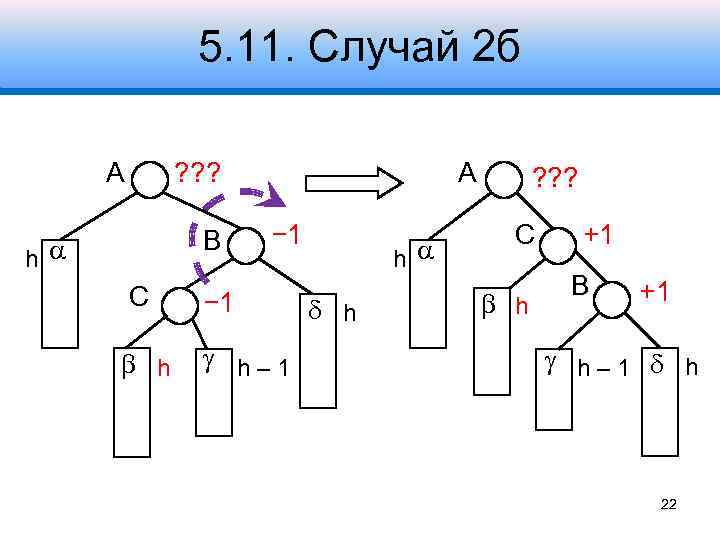 5. 11. Случай 2 б A ? ? ? B h A − 1 С − 1 h h– 1 h h ? ? ? С h +1 B +1 h– 1 h 22
5. 11. Случай 2 б A ? ? ? B h A − 1 С − 1 h h– 1 h h ? ? ? С h +1 B +1 h– 1 h 22
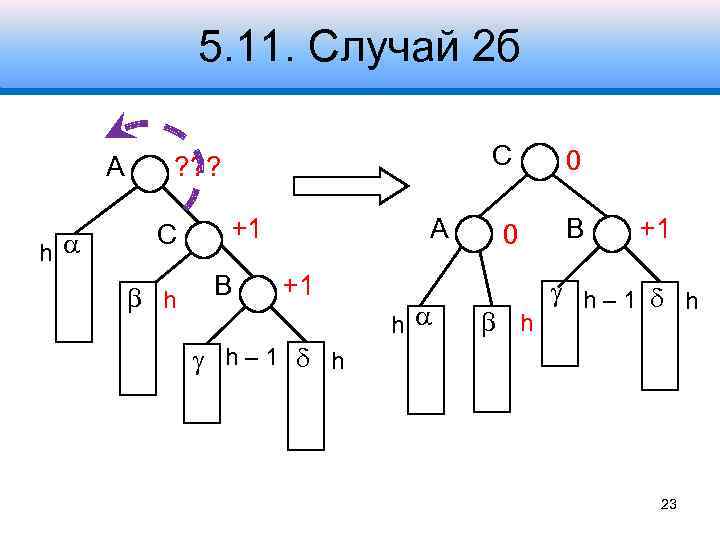 5. 11. Случай 2 б A h С ? ? ? С h +1 B A +1 h 0 0 B h +1 h– 1 h 23
5. 11. Случай 2 б A h С ? ? ? С h +1 B A +1 h 0 0 B h +1 h– 1 h 23
 5. 12. Удаление из AVL-дерева • • • Удалить элемент так же, как в двоичном дереве поиска (с учетом внешних листьев – EList) Скорректировать свойство сбалансированности узлов дерева При необходимости скорректировать само AVL-дерево 24
5. 12. Удаление из AVL-дерева • • • Удалить элемент так же, как в двоичном дереве поиска (с учетом внешних листьев – EList) Скорректировать свойство сбалансированности узлов дерева При необходимости скорректировать само AVL-дерево 24
 5. 13. Узел AVL-дерева struct Node { int key; int hleft; – высота левого поддерева int hright; – высота правого поддерева struct Node *left, *right, *parent; }; 25
5. 13. Узел AVL-дерева struct Node { int key; int hleft; – высота левого поддерева int hright; – высота правого поддерева struct Node *left, *right, *parent; }; 25
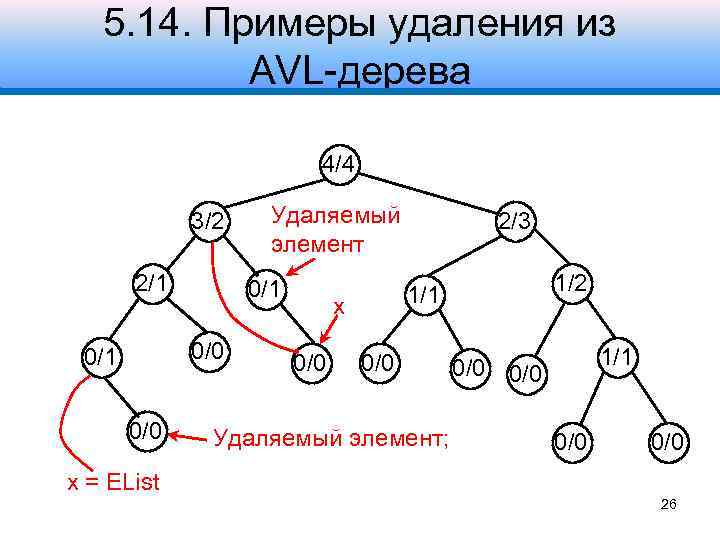 5. 14. Примеры удаления из AVL-дерева 4/4 3/2 2/1 0/0 0/1 0/0 Удаляемый элемент 1/2 1/1 x 0/0 2/3 0/0 Удаляемый элемент; 1/1 0/0 0/0 x = EList 26
5. 14. Примеры удаления из AVL-дерева 4/4 3/2 2/1 0/0 0/1 0/0 Удаляемый элемент 1/2 1/1 x 0/0 2/3 0/0 Удаляемый элемент; 1/1 0/0 0/0 x = EList 26
 5. 15. Алгоритм удаления Удалить узел из бинарного дерева поиска x – дочерний узел удаленного элемента p = x->parent while p ≠ EList { коррекция узла дерева p: if x в левом поддереве p p->hleft = p->hleft – 1 else p->hright = p->hright – 1 27
5. 15. Алгоритм удаления Удалить узел из бинарного дерева поиска x – дочерний узел удаленного элемента p = x->parent while p ≠ EList { коррекция узла дерева p: if x в левом поддереве p p->hleft = p->hleft – 1 else p->hright = p->hright – 1 27
 5. 15. Алгоритм удаления dh = | p->hleft – p->hright | if dh > 1{ коррекция дерева успех } else if dh = 1 успех 28
5. 15. Алгоритм удаления dh = | p->hleft – p->hright | if dh > 1{ коррекция дерева успех } else if dh = 1 успех 28
 5. 15. Алгоритм удаления else { x=p p = x->parent } } -- цикл while p – узел AVL-дерева, для которого нарушены требования сбалансированности 29
5. 15. Алгоритм удаления else { x=p p = x->parent } } -- цикл while p – узел AVL-дерева, для которого нарушены требования сбалансированности 29
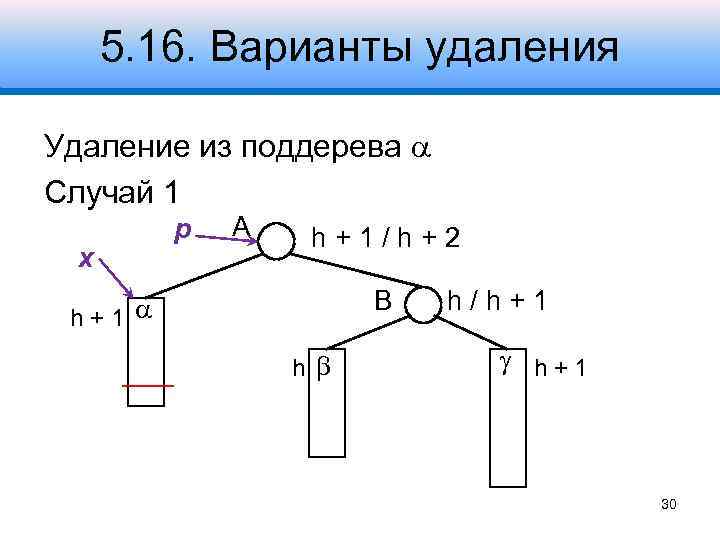 5. 16. Варианты удаления Удаление из поддерева Случай 1 x p A h+1/h+2 B h+1 h h/h+1 30
5. 16. Варианты удаления Удаление из поддерева Случай 1 x p A h+1/h+2 B h+1 h h/h+1 30
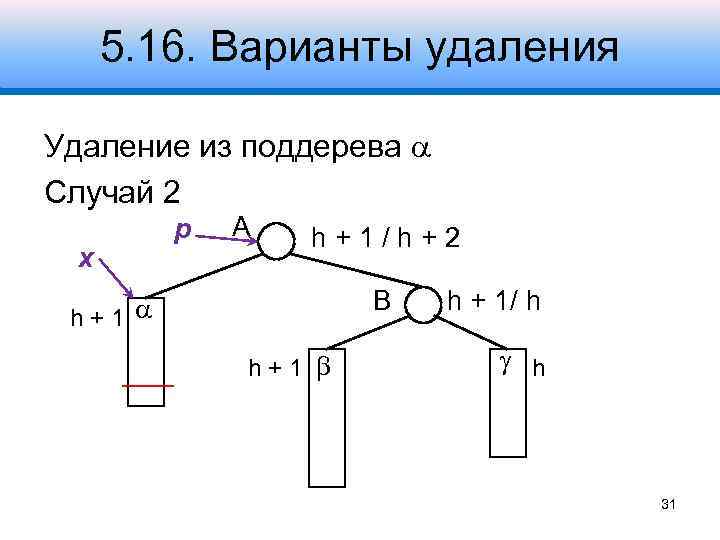 5. 16. Варианты удаления Удаление из поддерева Случай 2 x p A h+1/h+2 B h+1 h + 1/ h h 31
5. 16. Варианты удаления Удаление из поддерева Случай 2 x p A h+1/h+2 B h+1 h + 1/ h h 31
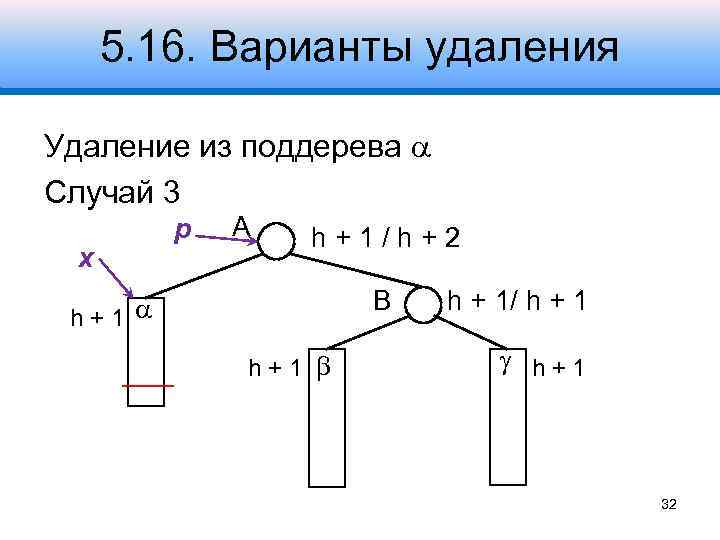 5. 16. Варианты удаления Удаление из поддерева Случай 3 x p A h+1/h+2 B h+1 h + 1/ h + 1 h+1 32
5. 16. Варианты удаления Удаление из поддерева Случай 3 x p A h+1/h+2 B h+1 h + 1/ h + 1 h+1 32
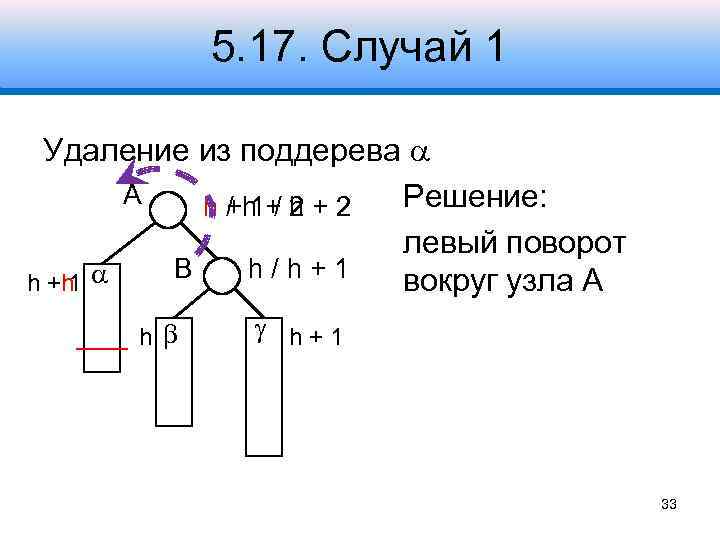 5. 17. Случай 1 Удаление из поддерева A Решение: h +h + 2 / 1/2 левый поворот B h/h+1 вокруг узла A h +h 1 h h+1 33
5. 17. Случай 1 Удаление из поддерева A Решение: h +h + 2 / 1/2 левый поворот B h/h+1 вокруг узла A h +h 1 h h+1 33
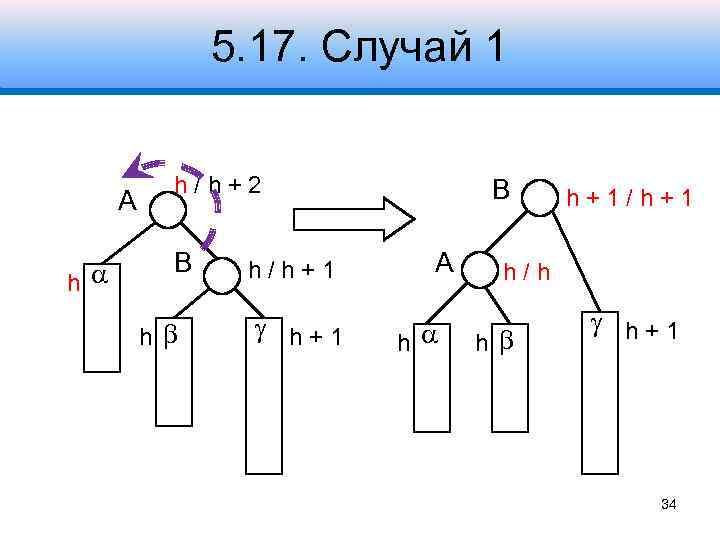 5. 17. Случай 1 A h h/h+2 B h h/h+1 B A h h+1/h+1 h/h h h+1 34
5. 17. Случай 1 A h h/h+2 B h h/h+1 B A h h+1/h+1 h/h h h+1 34
 5. 17. Случай 1 Высота поддерева уменьшилась !!! Необходимо продолжить коррекцию узлов дерева, переустановив значение x 35
5. 17. Случай 1 Высота поддерева уменьшилась !!! Необходимо продолжить коррекцию узлов дерева, переустановив значение x 35
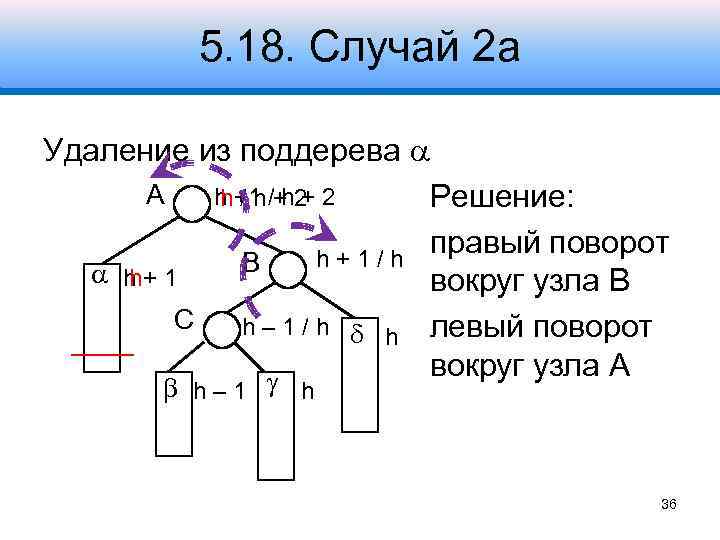 5. 18. Случай 2 а Удаление из поддерева A h +1 /+ 2 2 h/h h+ Решение: правый поворот h+1/h B h+1 h вокруг узла B С h – 1 / h h левый поворот вокруг узла A h– 1 h 36
5. 18. Случай 2 а Удаление из поддерева A h +1 /+ 2 2 h/h h+ Решение: правый поворот h+1/h B h+1 h вокруг узла B С h – 1 / h h левый поворот вокруг узла A h– 1 h 36
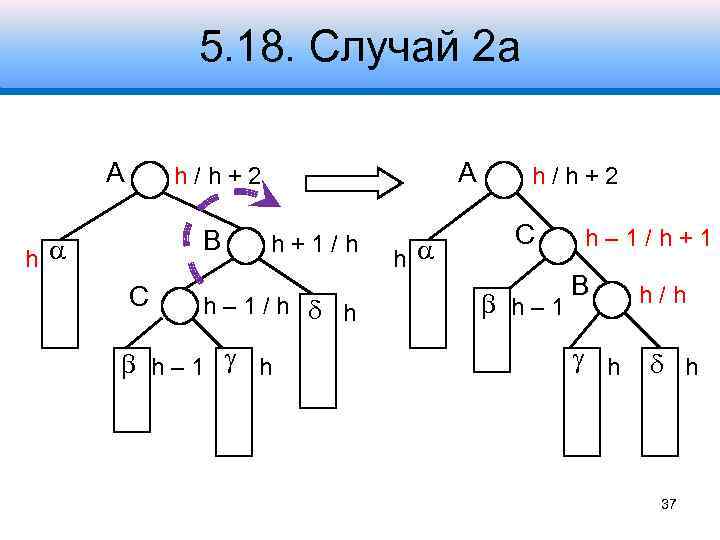 5. 18. Случай 2 а A A h/h+2 B h С h+1/h h– 1/h h h– 1 h h h/h+2 С h– 1/h+1 B h h/h h 37
5. 18. Случай 2 а A A h/h+2 B h С h+1/h h– 1/h h h– 1 h h h/h+2 С h– 1/h+1 B h h/h h 37
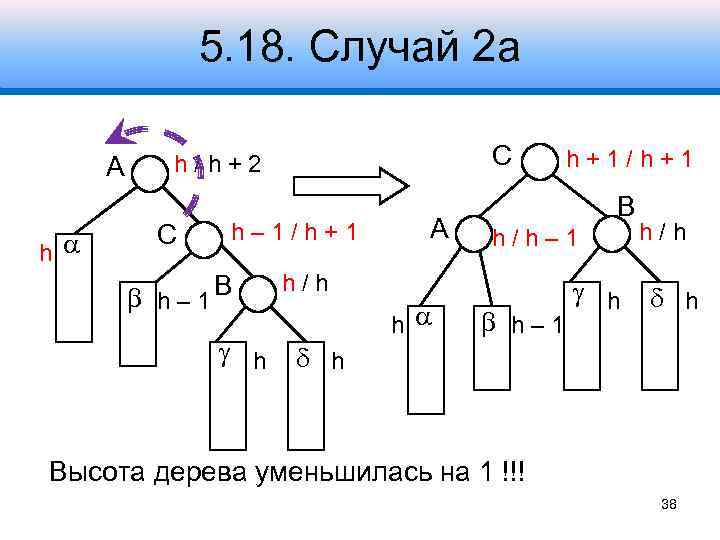 5. 18. Случай 2 а A h С h/h+2 С h– 1/h+1 h – 1 B h A B h/h– 1 h/h h h+1/h+1 h– 1 h h/h h h Высота дерева уменьшилась на 1 !!! 38
5. 18. Случай 2 а A h С h/h+2 С h– 1/h+1 h – 1 B h A B h/h– 1 h/h h h+1/h+1 h– 1 h h/h h h Высота дерева уменьшилась на 1 !!! 38
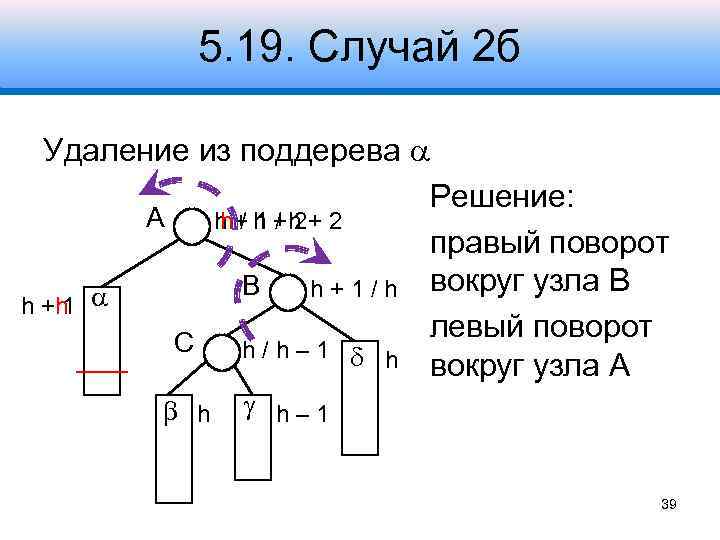 5. 19. Случай 2 б Удаление из поддерева Решение: A h +h + 2 h/1/ 2 правый поворот B h + 1 / h вокруг узла B h +h 1 левый поворот С h/h– 1 h вокруг узла A h h– 1 39
5. 19. Случай 2 б Удаление из поддерева Решение: A h +h + 2 h/1/ 2 правый поворот B h + 1 / h вокруг узла B h +h 1 левый поворот С h/h– 1 h вокруг узла A h h– 1 39
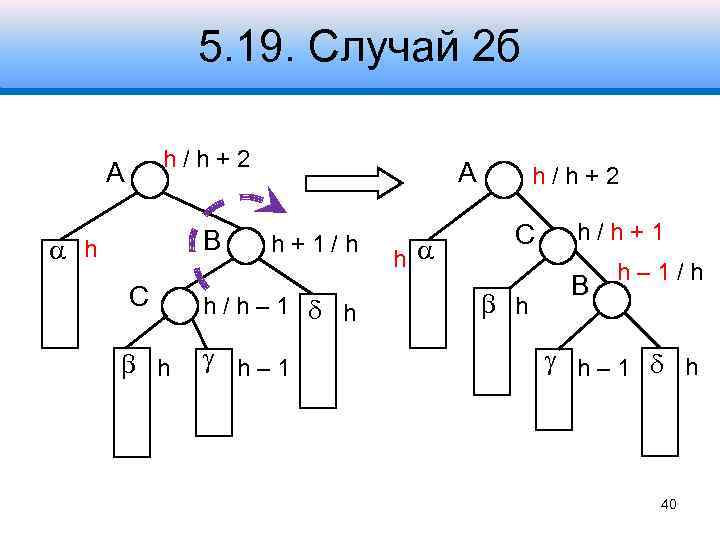 5. 19. Случай 2 б h/h+2 A B h С h A h+1/h h/h– 1 h h– 1 h h/h+2 С h h/h+1 B h– 1/h h– 1 h 40
5. 19. Случай 2 б h/h+2 A B h С h A h+1/h h/h– 1 h h– 1 h h/h+2 С h h/h+1 B h– 1/h h– 1 h 40
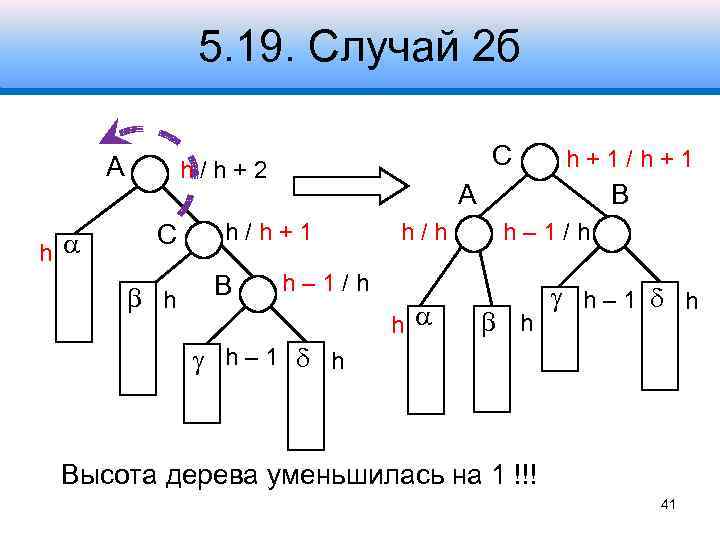 5. 19. Случай 2 б A h С h/h+2 С h A h/h+1 B h+1/h+1 h/h B h– 1/h h h h– 1 h Высота дерева уменьшилась на 1 !!! 41
5. 19. Случай 2 б A h С h/h+2 С h A h/h+1 B h+1/h+1 h/h B h– 1/h h h h– 1 h Высота дерева уменьшилась на 1 !!! 41
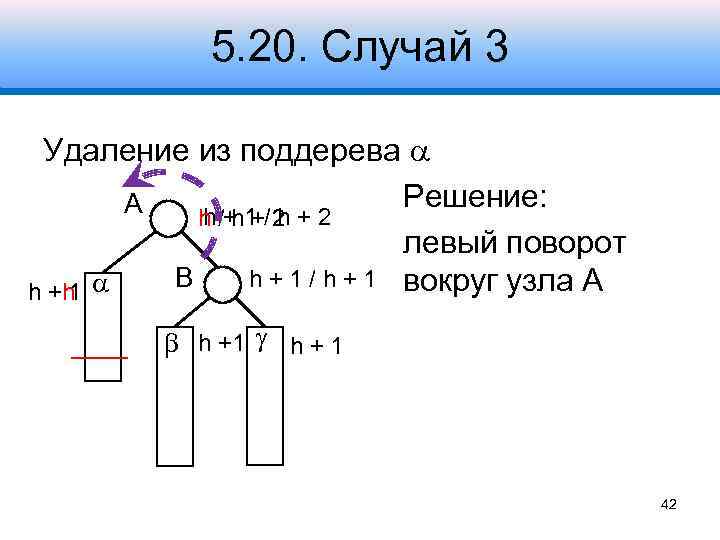 5. 20. Случай 3 Удаление из поддерева Решение: A h h+ h h /+ 1 / 2 + 2 левый поворот B h + 1 / h + 1 вокруг узла A h +h 1 h + 1 42
5. 20. Случай 3 Удаление из поддерева Решение: A h h+ h h /+ 1 / 2 + 2 левый поворот B h + 1 / h + 1 вокруг узла A h +h 1 h + 1 42
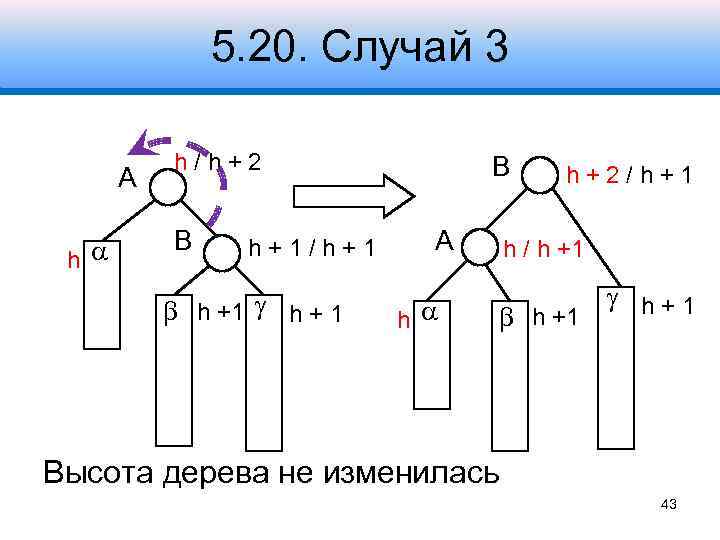 5. 20. Случай 3 Случай 1 A h h/h+2 B h+1/h+1 h + 1 B A h h+2/h+1 h / h +1 h+1 Высота дерева не изменилась 43
5. 20. Случай 3 Случай 1 A h h/h+2 B h+1/h+1 h + 1 B A h h+2/h+1 h / h +1 h+1 Высота дерева не изменилась 43


