5 5 Кинетическая энергия твёрдого тела вращающегося вокруг

5. 5 Кинетическая энергия твёрдого тела, вращающегося вокруг неподвижной оси Кинетическая энергия механической системы – величина аддитивная, равная сумме кинетических энергий входящих в неё частей. Следовательно, кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех материальных точек, на которые это тело можно разбить:

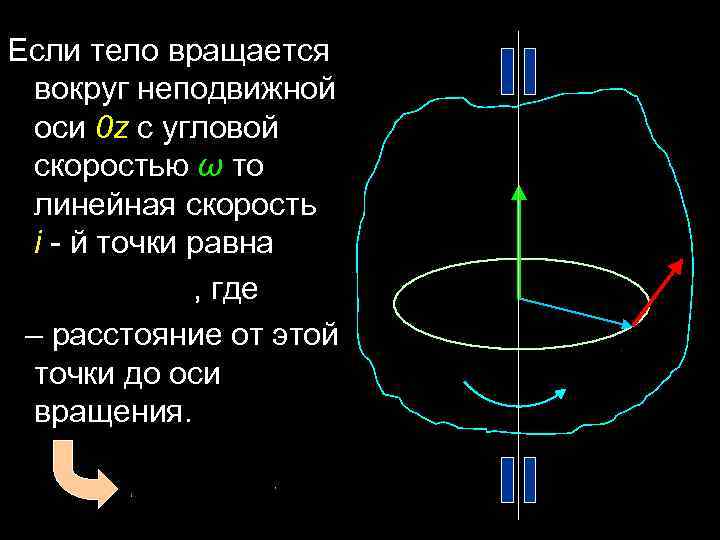Если тело вращается вокруг неподвижной оси 0 z c угловой скоростью ω то линейная скорость i - й точки равна , где – расстояние от этой точки до оси вращения.

Кинетическая энергия всего твёрдого тела где – момент инерции тела относительно оси вращения.

В общем случае движение твёрдого тела можно представить в виде суммы двух движений – поступательного со скоростью, равной скорости центра инерции тела, и вращения с угловой скоростью ω вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела имеет вид:

где – момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции. В общем случае положение мгновенной оси вращения по отношению к системе координат, связанной с телом, в процессе вращения изменяется. Следовательно, момент инерции при этом зависит от времени.

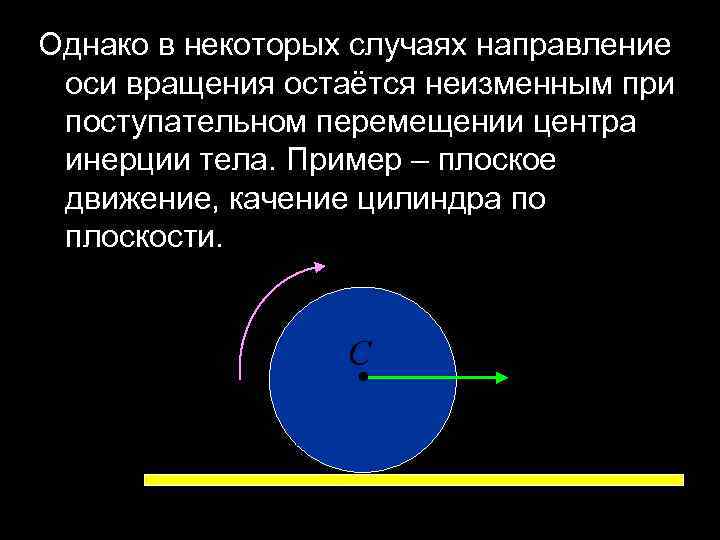Однако в некоторых случаях направление оси вращения остаётся неизменным при поступательном перемещении центра инерции тела. Пример – плоское движение, качение цилиндра по плоскости.

В этом случае момент инерции тела не зависит от времени и кинетическую энергию можно представить в виде суммы двух частей, относящихся порознь к поступательному и вращательному движениям: где = const.

Опыт Скатывание сплошного и полого цилиндров одинаковой массы и радиуса с наклонной плоскости.

5. 6 Работа внешних сил при вращении тела вокруг неподвижной оси Для изменения состояния вращающегося тела внешние силы должны совершить работу. Эта работа затрачивается только на изменение кинетической энергии тела, так как потенциальная энергия при этом не меняется:

– изменение кинетической энергии тела за малый промежуток времени dt равно элементарной работе, совершённой за время dt внешними силами, приложенными к телу. Внешними – потому, что тело не деформируется и внутренние силы работы не совершают.

Выражение (5. 19) для кинетической энергии вращающегося тела представим в виде Тогда

Здесь – проекция результирующего момента внешних сил на направление вектора угловой скорости тела, а – угол поворота тела за рассматриваемый малый промежуток времени dt. Итак,

Работа – величина алгебраическая: если и ω имеют одинаковые знаки, то A>0 , если же их знаки противоположны, то A<0. Другими словами если

Работа внешних сил при повороте твёрдого тела на конечный угол φ Если , то Работа внешних сил при вращении твёрдого тела вокруг неподвижной оси определяется действием момента этих сил относительно данной оси.

Если силы таковы, что их момент , то работы они не производят. Так, не совершает никакой работы сила тяготения при движении Земли вокруг Солнца, так как её момент относительно центра Солнца всё время равен нулю.

5. 7 Закон сохранения момента импульса Вернёмся к уравнению движения механической системы относительно неподвижной точки (5. 11). Оно выражает тот факт, что скорость изменения момента импульса системы относительно неподвижной точки равна результирующему моменту относительно той же точки всех внешних сил, действующих на систему.

Итак, момент импульса системы может изменяться только под действием суммарного момента всех внешних сил. Для замкнутой системы результирующий вектор внешних сил тождественно равен нулю, следовательно, и момент всех внешних сил тоже равен нулю. Поэтому для замкнутой системы выполняется соотношение

в инерциальной системе отсчёта момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.

При этом моменты импульса отдельных частей или частиц замкнутой системы могут изменяться со временем. Однако эти изменения всегда происходят так, что приращение момента импульса одной части системы равно убыли момента импульса другой её части относительно одной и той же точки системы отсчёта:

Из основного закона динамики для тела, вращающегося вокруг неподвижной оси, следует закон сохранения момента импульса тела относительно оси вращения: если , то Если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется в процессе движения.

Согласно формуле (5. 14), момент импульса тела, вращающегося вокруг неподвижной оси, равен произведению момента инерции относительно данной оси и угловой скорости: Следовательно, закон сохранения момента импульса для тела, вращающегося вокруг неподвижной оси, можно переписать в виде:

Этот закон обобщается на любую незамкнутую систему тел: если результирующий момент всех внешних сил, приложенных к системе, относительно какой-либо неподвижной оси тождественно равен нулю, то момент импульса системы относительно той же оси не изменяется с течением времени.

Если в такой системе осуществляется какое-либо перераспределение массы, то согласно закону сохранения момента импульса должно выполняться равенство где , – исходное и конечное значения угловой скорости, , – исходное и конечное значения момента инерции относительно оси вращения.

Таким образом, изменение момента инерции системы влечёт за собой соответствующее изменение угловой скорости. При этом кинетический энергии вращающейся системы до и после изменения момента инерции не равны между собой: – изменение энергии происходит за счёт работы внутренних сил. Подобно тому, как кинетическая энергия орудия и снаряда до и после выстрела неодинакова, в то время как импульс данной системы сохраняется.

Уравнение (5. 14) мы получили в предположении, что ось вращения тела закреплена и неподвижна. В общем случае не совпадает по направлению с вектором и связь между этими векторами носит тензорный характер. Поэтому вследствие ЗСМИ, если твёрдое тело привести во вращение и предоставить самому себе, то направление оси вращения в пространстве, вообще говоря, будет меняться.

Для того, чтобы произвольная ось вращения тела сохраняла своё направление неизменным, к ней необходимо приложить определённые силы. Однако у любого тела существуют такие оси, при вращении вокруг которых они будут сохранять своё направление в пространстве без внешнего воздействия. Ось вращения, направление которой в пространстве остаётся неизменным без воздействия на неё каких-либо сил извне, называется свободной осью тела.

Можно показать, что для любого твёрдого тела существуют три взаимно перпендикулярные и проходящие через центр инерции тела оси, которые могут служить свободными осями. Их называют главными осями инерции тела. У симметричных тел главные оси совпадают с осями симметрии. При вращении тела вокруг любой из его главных осей инерции вектор момента импульса совпадает по направлению с вектором угловой скорости где J – момент инерции тела относительно данной главной оси инерции.

Моменты инерции относительно главных осей называются главными моментами инерции тела. Если тело свободно вращается при отсутствии каких-либо внешних воздействий, то устойчивым оказывается только вращение вокруг главных осей. При отклонении вращения от устойчивой оси под действием возникающих при этом сил тело возвращается к вращению вокруг соответствующей главной оси.

В справедливости ЗСМИ можно убедиться на опыте с уравновешенным гироскопом, имеющим три степени свободы. Гироскоп – это быстро вращающееся твёрдое тело, ось вращения которого может изменять своё направление в пространстве. Гироскоп имеет три степени свободы, если он может совершать любой поворот вокруг некоторой неподвижной точки, называемой центром подвеса.

Если центр подвеса гироскопа совпадает с его центром тяжести, то результирующий момент сил тяжести всех частей гироскопа относительно центра подвеса равен нулю. Такой гироскоп называется уравновешенным. Все три оси вращения обойм пересекаются в центре подвеса, совпадающем с центром тяжести гироскопа.

На опыте с таким гироскопом легко убедиться в том, что при любых поворотах стойки ось вращения гироскопа сохраняет неизменное направление в пространстве (относительно лабораторной системы координат).

Объясняется это так. Момент относительно точки подвеса всех внешних сил, прикладываемых к гироскопу через стойку при её поворотах равен только моменту сил трения (момент сил тяжести равен нулю, так как гироскоп уравновешен).

Обычно момент сил трения очень мал, так что за малый промежуток времени, в течение которого производится поворот стойки, момент импульса гироскопа относительно центра подвеса практически не изменяется. Так как гироскоп симметричен и вращается вокруг своей оси симметрии, то его момент импульса направлен вдоль оси вращения.

Поскольку вектор момента импульса сохраняется неизменным по модулю и направлению, то сохраняет своё положение и ось гироскопа. Поэтому при всевозможных поворотах стойки ориентация оси вращения гироскопа должна оставаться неизменной.