39f12ca7607e0e24516fb53b92491b0e.ppt
- Количество слайдов: 20

5 -3 Solving Proportions Warm Up Problem of the Day Lesson Presentation Course 2

5 -3 Solving Proportions Warm Up Determine whether the ratios are proportional. 1. 5 , 15 8 24 2. 12, 16 15 25 15, 20 3. 10 16 4. 14, 42 18 54 Course 2 yes no no yes

5 -3 Solving Proportions Problem of the Day If A = 1, B = 2, C = 3, D = 4, and so on, all the way to Z = 26, then what is A+B+C+D+. . . +Z=? (Hint: A + Z = B + Y. ) 351 Course 2

5 -3 Solving Proportions Learn to solve proportions by using cross products. Course 2

5 -3 Solving Proportions Here Insert Lesson Title Vocabulary cross product Course 2

5 -3 Solving Proportions For two ratios, the product of the numerator in one ratio and the denominator in the other is a cross product. If the cross products of the ratios are equal, then the ratios form a proportion. 2 = 6 5 15 Course 2 5 · 6 = 30 2 · 15 = 30

5 -3 Solving Proportions CROSS PRODUCT RULE In the proportion a = c , the cross products, b d a · d and b · c are equal. You can use the cross product rule to solve proportions with variables. Course 2

5 -3 Solving Proportions Additional Example 1: Solving Proportions Using Cross Products Use cross products to solve the proportion. 9 = m 15 5 15 · m = 9 · 5 15 m = 45 15 15 m=3 Course 2 The cross products are equal. Multiply. Divide each side by 15 to isolate the variable.

5 -3 Solving Proportions. Here Insert Lesson Title Check It Out: Example 1 Use cross products to solve the proportion. 6 = m 7 14 7 · m = 6 · 14 The cross products are equal. 7 m = 84 Multiply. 7 m = 84 7 7 m = 12 Divide each side by 7 to isolate the variable. Course 2

5 -3 Solving Proportions When setting up a proportion to solve a problem, use a variable to represent the number you want to find. In proportions that include different units of measurement, either the units in the numerators must be the same and the units in the denominators must be the same or the units within each ratio must be the same. 16 mi = 8 mi 4 hr x hr Course 2 16 mi = 4 hr 8 mi x hr

5 -3 Solving Proportions Additional Example 2: Problem Solving Application If 3 volumes of Jennifer’s encyclopedia takes up 4 inches of space on her shelf, how much space will she need for all 26 volumes? 1 Understand the Problem Rewrite the question as a statement. • Find the space needed for 26 volumes of the encyclopedia. List the important information: • 3 volumes of the encyclopedia take up 4 inches of space. Course 2

5 -3 Solving Proportions Additional Example 2 Continued 2 Make a Plan Set up a proportion using the given information. Let x represent the inches of space needed. 3 volumes = 26 volumes 4 inches x Course 2 volumes inches

5 -3 Solving Proportions Additional Example 2 Continued 3 Solve 3 = 26 Write the proportion. 4 x 3 · x = 4 · 26 The cross products are equal. 3 x = 104 Multiply. Divide each side by 3 to isolate 3 x = 104 the variable. 3 3 x = 34 2 3 She needs 34 2 inches for all 26 volumes. 3 Course 2
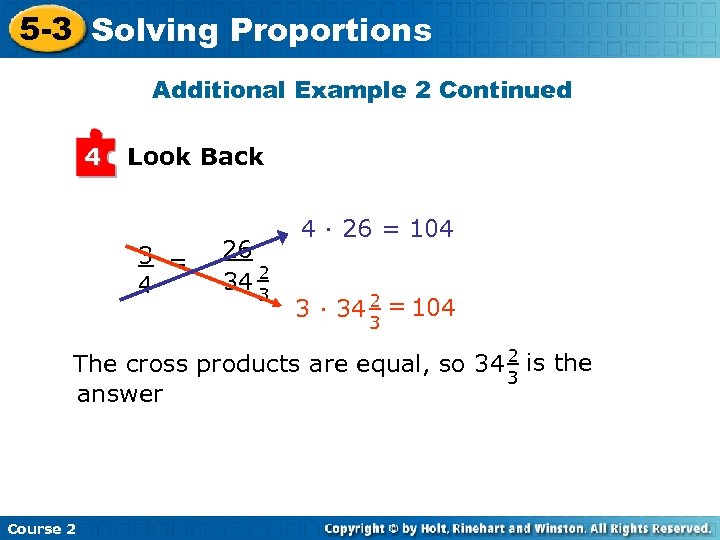
5 -3 Solving Proportions Additional Example 2 Continued 4 Look Back 3 = 4 26 34 2 3 4 · 26 = 104 3 · 34 2 = 104 3 The cross products are equal, so 34 2 is the 3 answer Course 2

5 -3 Solving Proportions 1 Check It Out: Example 2 John filled his new radiator with 6 pints of coolant, which is the 10 inch mark. How many pints of coolant would be needed to fill the radiator to the 25 inch level? Understand the Problem Rewrite the question as a statement. • Find the number of pints of coolant required to raise the level to the 25 inch level. List the important information: • 6 pints is the 10 inch mark. Course 2

5 -3 Solving Proportions Check It Out: Example 2 Continued 2 Make a Plan Set up a proportion using the given information. Let p represent the pints of coolant. 6 pints 10 inches Course 2 = p 25 inches pints inches

5 -3 Solving Proportions Check It Out: Example 2 Continued 3 Solve 6 = p Write the proportion. 10 25 10 · p = 6 · 25 The cross products are equal. 10 p = 150 Multiply. 10 p = 150 10 10 p = 15 Divide each side by 10 to isolate the variable. 15 pints of coolant will fill the radiator to the 25 inch level. Course 2
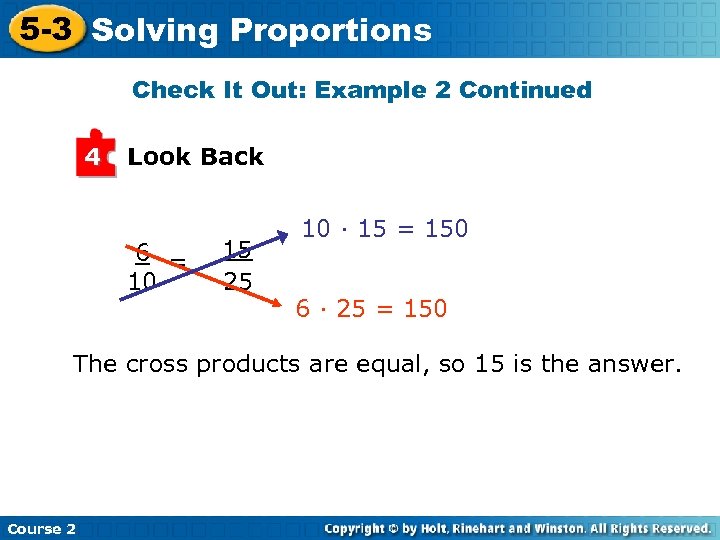
5 -3 Solving Proportions Check It Out: Example 2 Continued 4 Look Back 6 = 10 15 25 10 · 15 = 150 6 · 25 = 150 The cross products are equal, so 15 is the answer. Course 2

5 -3 Solving Proportions Here Insert Lesson Title Lesson Quiz: Part I Use cross products to solve the proportion. 1. 25 = 45 t 20 2. x = 19 9 57 3. 2 = r 3 36 4. n = 28 10 8 Course 2 t = 36 x=3 r = 24 n = 35

5 -3 Solving Proportions Here Insert Lesson Title Lesson Quiz: Part II 5. Carmen bought 3 pounds of bananas for $1. 08. June paid $ 1. 80 for her purchase of bananas. If they paid the same price per pound, how many pounds did June buy? 5 pounds Course 2
39f12ca7607e0e24516fb53b92491b0e.ppt