5 -2 Ratios Rates and Unit Rates Warm

5 -2 Ratios, Rates, and Unit Rates Warm Up Problem of the Day Lesson Presentation Course 3 3

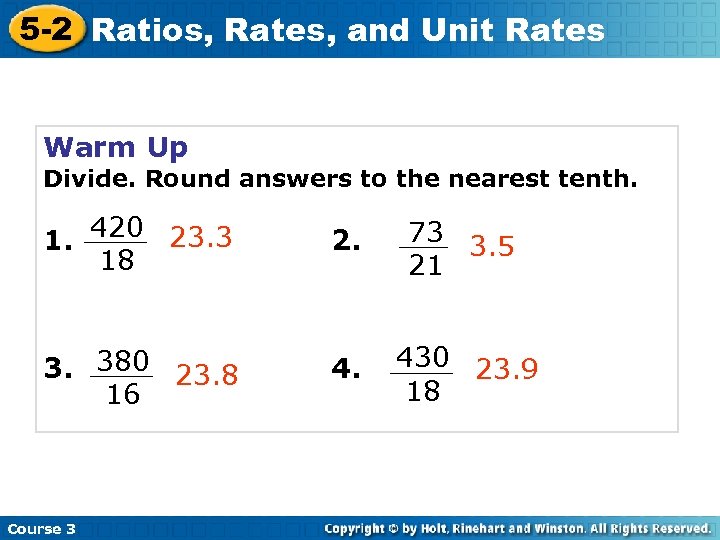5 -2 Ratios, Rates, and Unit Rates Warm Up Divide. Round answers to the nearest tenth. 1. 420 23. 3 18 2. 73 3. 5 21 3. 380 23. 8 16 4. 430 23. 9 18 Course 3

5 -2 Ratios, Rates, and Unit Rates Problem of the Day There are 3 bags of flour for every 2 bags of sugar in a freight truck. A bag of flour weighs 60 pounds, and a bag of sugar weighs 80 pounds. Which part of the truck’s cargo is heavier, the flour or the sugar? flour Course 3

5 -2 Ratios, Rates, and Unit Rates Learn to work with rates and ratios. Course 3

5 -2 Ratios, Rates, and Unit Rates Vocabulary rate unit price Course 3

5 -2 Ratios, Rates, and Unit Rates A rate is a comparison of two quantities that have different units. Ratio: 90 3 Rate: 90 miles 3 hours Course 3 Read as “ 90 miles per 3 hours. ”

5 -2 Ratios, Rates, and Unit Rates Unit rates are rates in which the second quantity is 1. The ratio 90 can be simplified by dividing: 3 90 = 30 3 1 unit rate: 30 miles, or 30 mi/h 1 hour Course 3

5 -2 Ratios, Rates, and Unit Rates Additional Example 1: Finding Unit Rates Geoff can type 30 words in half a minute. How many words can he type in 1 minute? 30 words 1 2 minute Write a rate. 30 words • 2 = 60 words 1 1 minute 2 minute • 2 Multiply to find words per minute. Geoff can type 60 words in one minute. Course 3

5 -2 Ratios, Rates, and Unit Rates Check It Out: Example 1 Penelope can type 90 words in 2 minutes. How many words can she type in 1 minute? 90 words 2 minutes Write a rate. 90 words ÷ 2 = 45 words 2 minutes ÷ 2 1 minute Divide to find words per minute. Penelope can type 45 words in one minute. Course 3

5 -2 Ratios, Rates, and Unit Rates Additional Example 2 A: Chemistry Application Five cubic meters of copper has a mass of 44, 800 kilograms. What is the density of copper? 44, 800 kg 5 m 3 Write a rate. 44, 800 kg ÷ 5 5 m 3 ÷ 5 Divide to find kilograms per 1 m 3. 8, 960 kg 1 m 3 Copper has a density of 8, 960 kg/m 3. Course 3

5 -2 Ratios, Rates, and Unit Rates Additional Example 2 B: Chemistry Application A piece of gold with a volume of 0. 5 cubic meters weighs 9650 kilograms. What is the density of gold? 9650 kg 0. 5 m 3 Write a rate. 9650 kg • 2 0. 5 m 3 • 2 Multiply to find kilograms per 1 m 3. 19, 300 kg 1 m 3 Gold has a density of 19, 300 kg/m 3. Course 3

5 -2 Ratios, Rates, and Unit Rates Check It Out: Example 2 A Four cubic meters of precious metal has a mass of 18, 128 kilograms. What is the density of the precious metal? 18, 128 kg 4 m 3 Write a rate. 18, 128 kg ÷ 4 4 m 3 ÷ 4 Divide to find kilograms per 1 m 3. 4, 532 kg 1 m 3 Precious metal has a density of 4, 532 kg/m 3. Course 3

5 -2 Ratios, Rates, and Unit Rates Check It Out: Example 2 B A piece of gem stone with a volume of 0. 25 cubic meters weighs 3540 kilograms. What is the density of the gem stone? 3540 kg 0. 25 m 3 Write a rate. 3540 kg • 4 0. 25 m 3 • 4 Multiply to find kilograms per 1 m 3. 14, 160 kg 1 m 3 The gem stone has a density of 14, 160 kg/m 3. Course 3

5 -2 Ratios, Rates, and Unit Rates Additional Example 3 A: Estimating Unit Rates Estimate each unit rate. 468 students to 91 computers Choose a number 468 students 455 students close to 468 that is 91 computers divisible by 91. 5 students 1 computer Divide to find students per computer. 468 students to 91 computers is approximately 5 students per computer. Course 3

5 -2 Ratios, Rates, and Unit Rates Additional Example 3 B: Estimating Unit Rates Estimate each unit rate. 313 feet in 8 seconds 312 feet 8 seconds Choose a number close to 313 that is divisible by 8. 313 feet 8 seconds 39 feet 1 second Divide to find feet per second. 313 feet to 8 seconds is approximately 39 feet per second. Course 3

5 -2 Ratios, Rates, and Unit Rates Check It Out: Example 3 A Estimate each unit rate. 583 soccer players to 85 soccer balls. Choose a number 583 players 595 players close to 583 that is 85 soccer balls divisible by 85. 7 players 1 soccer ball Divide to find players per soccer ball. 583 soccer players to 85 soccer balls is approximately 7 players per soccer ball. Course 3

5 -2 Ratios, Rates, and Unit Rates Check It Out: Example 3 B Estimate each unit rate. 271 yards in 3 hours 276 yards 3 hours Choose a number close to 271 that is divisible by 3. 271 yards 3 hours 92 yards 1 hour Divide to find yards per hour. 271 yards to 3 hours is approximately 92 yards per hour. Course 3

5 -2 Ratios, Rates, and Unit Rates Unit price is a unit rate used to compare price per item. Course 3

5 -2 Ratios, Rates, and Unit Rates Additional Example 4 A: Finding Unit Prices to Compare Costs Pens can be purchased in a 5 -pack for $1. 95 or a 15 -pack for $6. 20. Which is the better buy? price for package = $1. 95 $0. 39 Divide the price by the number of pens 5 of pens. price for package = $6. 20 $0. 41 number of pens 15 The better buy is the 5 -pack for $1. 95. Course 3

5 -2 Ratios, Rates, and Unit Rates Additional Example 4 B: Finding Unit Prices to Compare Costs Jamie can buy a 15 -oz jar of peanut butter for $2. 19 or a 20 -oz jar for $2. 78. Which is the better buy? price for jar = $2. 19 $0. 15 number of ounces 15 Divide the price by the number of ounces. price for jar = $2. 78 $0. 14 number of ounces 20 The better buy is the 20 -oz jar for $2. 78. Course 3

5 -2 Ratios, Rates, and Unit Rates Check It Out: Example 4 A Golf balls can be purchased in a 3 -pack for $4. 95 or a 12 -pack for $18. 95. Which is the better buy? price for package = $4. 95 $1. 65 Divide the price by the number of balls 3 of balls. price for package = $18. 95 $1. 58 number of balls 12 The better buy is the 12 -pack for $18. 95. Course 3

5 -2 Ratios, Rates, and Unit Rates Check It Out: Example 4 B John can buy a 24 oz bottle of ketchup for $2. 19 or a 36 oz bottle for $3. 79. Which is the better buy? price for bottle = $2. 19 $0. 09 number of ounces 24 Divide the price by the number of ounces. price for bottles = $3. 79 $0. 11 number of ounces 36 The better buy is the 24 -oz jar for $2. 19. Course 3

5 -2 Ratios, Rates, and Unit Rates Lesson Quiz Part 1 1. A penny has a mass of 2. 5 g and a volume of approximately 0. 360 cm 3. What is the approximate density of a penny? ≈ 6. 94 g/cm 3 2. Meka can make 6 bracelets per half hour. How many bracelets can she make in 1 hour? 12 Estimate the unit rate. 3. $2. 22 for 6 stamps $0. 37 per stamp 4. 8 heartbeats in 6 seconds 1. 3 beats/s Course 3

5 -2 Ratios, Rates, and Unit Rates Lesson Quiz: Part 2 Determine the better buy. 5. A half dozen carnations for $4. 75 or a dozen for $9. 24 a dozen 6. 4 pens for $5. 16 or a ten-pack for $12. 90. They cost the same. Course 3