5 2 Queues 2004 Goodrich Tamassia Queues

Скачать презентацию 5 2 Queues 2004 Goodrich Tamassia Queues

43d2820a1688f1e8bf0dae8b1b7e69cd.ppt

Количество слайдов: 24

Definition: a Queue is a collection of objects that are inserted and removed according to the first-in-first-out (FIFI – LILO) principle. That is, elements can be inserted at any time, but only the element that has been in the queue the longest (first inserted) can be removed at any time. Usually, elements enter a queue at the Rear, and are accessed or removed from the Front. © 2004 Goodrich, Tamassia Queues 2

The Queue ADT (§ 5. 2. 1) The Queue ADT stores a sequence of arbitrary objects. Insertions and deletions follow the first-in first-out scheme. Insertions are restricted to the end of the sequence (Rear). Accesses and removals are restricted to the first element of the sequence (Front). © 2004 Goodrich, Tamassia Queues 3

The queue abstract data type (ADT) supports the following methods (operations): Main queue operations: n n enqueue(e): inserts an element e at the end of the queue dequeue(): removes and returns the element at the front of the queue Auxiliary queue operations: n n n front(): returns the element at the front without removing it size(): returns an integer value that indicates the number of elements stored in the queue is. Empty(): returns a Boolean value that indicates whether the queue is empty Exceptions: n Attempting the execution of dequeue or front on an empty queue throws an Empty. Queue. Exception © 2004 Goodrich, Tamassia Queues 4

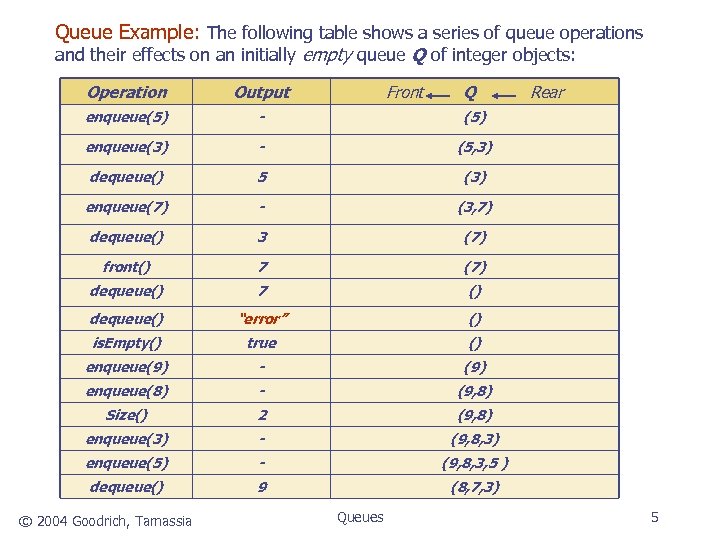Queue Example: The following table shows a series of queue operations and their effects on an initially empty queue Q of integer objects: Operation Output enqueue(5) - (5) enqueue(3) - (5, 3) dequeue() 5 (3) enqueue(7) - (3, 7) dequeue() 3 (7) front() 7 (7) dequeue() 7 () dequeue() “error” () is. Empty() true () enqueue(9) - (9) enqueue(8) - (9, 8) Size() 2 (9, 8) enqueue(3) - (9, 8, 3) enqueue(5) - (9, 8, 3, 5 ) dequeue() 9 (8, 7, 3) © 2004 Goodrich, Tamassia Front Queues Q Rear 5

Applications of Queues Direct applications n n n Waiting lists, theaters, reservation centers, … etc Access to shared resources (e. g. , printer) Multiprogramming Indirect applications n n Auxiliary data structure for algorithms Component of other data structures © 2004 Goodrich, Tamassia Queues 6

Queue Interface in Java public interface Queue { Java interface public int size(); corresponding to public boolean is. Empty(); our Queue ADT public Object front() Requires the throws definition of class Empty. Queue. Exception; Empty. Queue. Exc public void enqueue(Object eption o); No corresponding public Object dequeue() built-in Java class throws © 2004 Goodrich, Tamassia Empty. Queue. Exception; Queues 7

5. 2. 2 Array-Based Queue Implementation a- Simple Array Implementation Using an array Q, of fixed size N, to store queue elements. If we let Front is Q[0], and let queue grow from left to right, as in case of Stack, it’s not efficient solution. It requires moving all queue-elements forward onearray cell, each time we perform dequeue operation. Such an implementation requires O(n) time to perform dequeue-method, where n is the current elements in queue. © 2004 Goodrich, Tamassia Queues 8

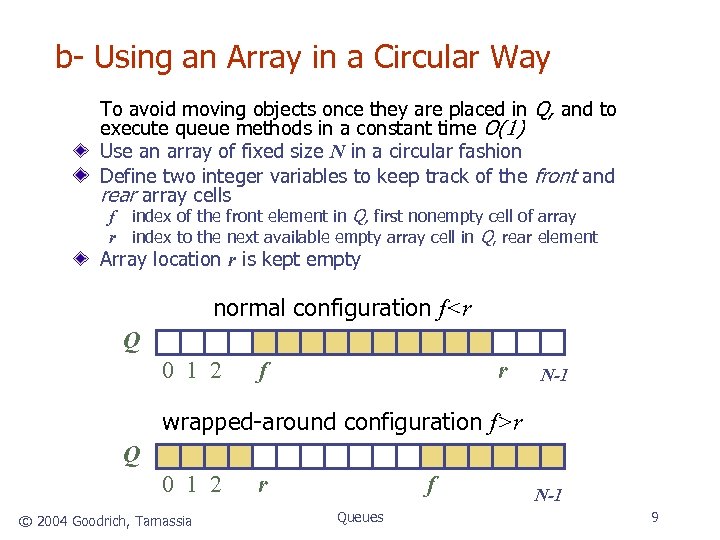b- Using an Array in a Circular Way To avoid moving objects once they are placed in Q, and to execute queue methods in a constant time O(1) Use an array of fixed size N in a circular fashion Define two integer variables to keep track of the front and rear array cells f index of the front element in Q, first nonempty cell of array r index to the next available empty array cell in Q, rear element Array location r is kept empty normal configuration fr Q 0 1 2 © 2004 Goodrich, Tamassia r f Queues N-1 9

Queue Operations Algorithm size() return (N f + r) mod N Initially, we assign Algorithm is. Empty() f = r =0, which indicates return (f = r) that the queue is empty. We use the modulo operator % (remainder of Algorithm Front() division) if is. Empty() then throw Empty. Queue. Exception else return Q[f] Q 0 1 2 f 0 1 2 r r N-1 Q © 2004 Goodrich, Tamassia f Queues N-1 10

Queue Operations (cont. ) Algorithm enqueue(o) Operation enqueue if size() = N 1 then throws an exception if throw Full. Queue. Exception the array is full else This exception is { Q[r] o implementationr (r + 1) mod N } dependent Q 0 1 2 f 0 1 2 r r N-1 Q © 2004 Goodrich, Tamassia f Queues N-1 11

Queue Operations (cont. ) Operation dequeue throws an exception if the queue is empty This exception is specified in the queue ADT Algorithm dequeue() if is. Empty() then throw Empty. Queue. Exception else {o Q[f] f (f + 1) mod N return o } Q 0 1 2 f 0 1 2 r r N-1 Q © 2004 Goodrich, Tamassia f Queues N-1 12

Queue Operations (cont. ) Method and Time Size O(1) is. Empty O(1) Front O(1) Enqueue O(1) Dequeue O(1) Disadvantage of the array-based queue implementation: fixed capacity value. © 2004 Goodrich, Tamassia 13

5. 2. 3 Implementing Queue with Linked Lists we choose the front of the queue to be at the head of the list the rear of the queue to be at the tail of the list. we remove from the head and insert at the tail. © 2004 Goodrich, Tamassia Queues 14

5. 2. 3 Implementing Queue with Linked Lists Each method of the singly linked list implementation of the queue ADT runs in O(1) time. We avoid the need to specify a maximum size for the queue but this benefit comes at the expense of increasing the amount of space used per element. We must take care with special cases n n where the queue is empty before an enqueue where the queue becomes empty after a dequeue. © 2004 Goodrich, Tamassia Queues 16

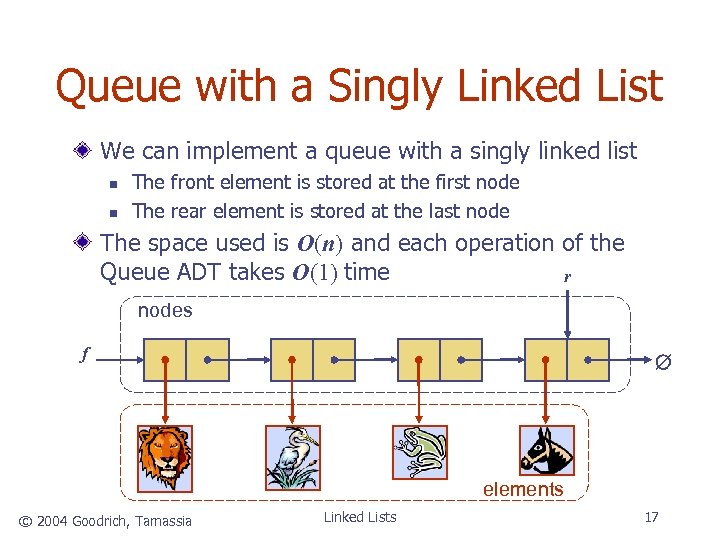Queue with a Singly Linked List We can implement a queue with a singly linked list n n The front element is stored at the first node The rear element is stored at the last node The space used is O(n) and each operation of the Queue ADT takes O(1) time r nodes f elements © 2004 Goodrich, Tamassia Linked Lists 17

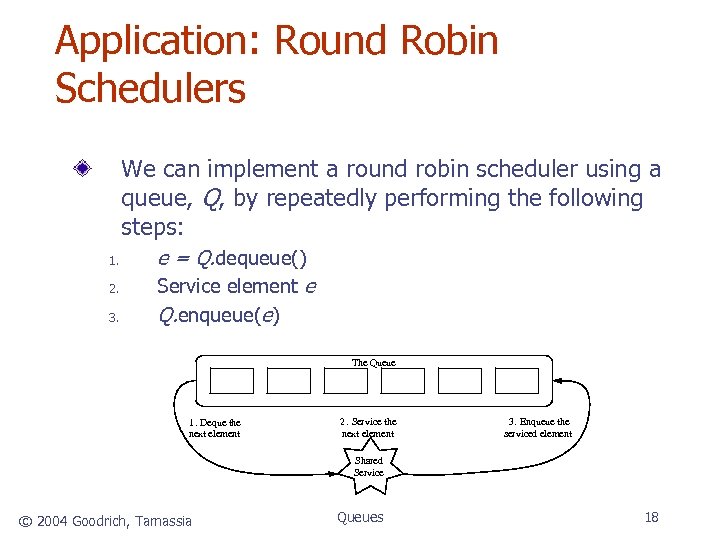Application: Round Robin Schedulers We can implement a round robin scheduler using a queue, Q, by repeatedly performing the following steps: 1. 2. 3. e = Q. dequeue() Service element e Q. enqueue(e) The Queue 1. Deque the next element 2. Service the next element 3. Enqueue the serviced element Shared Service © 2004 Goodrich, Tamassia Queues 18

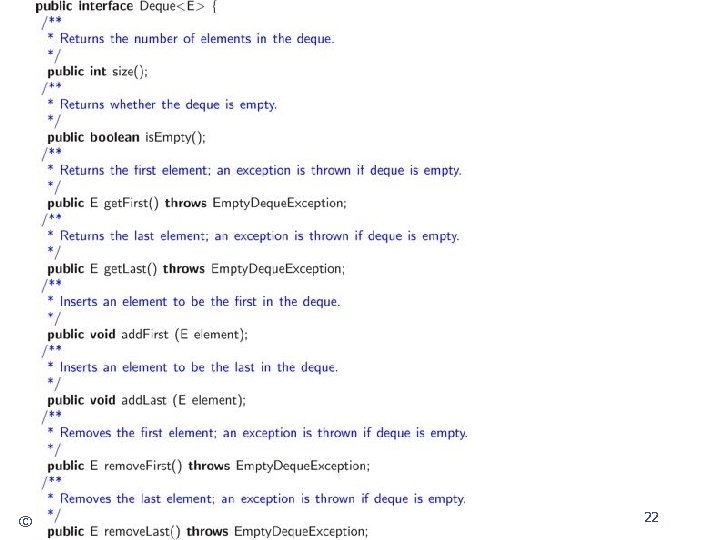
Double-Ended Queues (deque)( "D. Q. ") Supports insertion and deletion at both the front and the rear of the queue. The Deque Abstract Data Type add. First(e): Insert a new element e at the beginning of the deque. add. Last(e): Insert a new element e at the end of the deque. remove. First(): Remove and return the first element of the deque; an error occurs if the deque is empty. remove. Last(): Remove and return the last element of the deque; an error occurs if the deque is empty. get. First(): Return the first element of the deque; an error occurs if the deque is empty. get. Last(): Return the last element of the deque; an error occurs if the deque is empty. size(): Return the number of elements of the deque. is. Empty(): Determine if the deque is empty. © 2004 Goodrich, Tamassia Queues 19

Double-Ended Queues (cont. ) Operation Output D add. First(3) - (3) add. First(5) - (5, 3) remove. First() 5 (3) add. Last(7) - (3, 7) remove. First() 3 (7) remove. Last() 7 () remove. First() "error" () is. Empty() true () © 2004 Goodrich, Tamassia Queues 20

Implementing a Deque Doubly linked list: Since the deque requires insertion and removal at both ends of a list, using a singly linked list to implement a deque would be inefficient. Method Time size, is. Empty O(1) get. First, get. Last O(1) add First, add. Last O(1) remove. First, remove. Last O(1) © 2004 Goodrich, Tamassia Queues 21