e61379bf95bd9233ef94e6402c645e53.ppt
- Количество слайдов: 90
 5. 1 Systems of Linear Equations 5. 1 5. 3 5. 5 5. 6 5. 7 Linear Systems ▪ Substitution Method ▪ Elimination Method ▪ Special Systems ▪ Applying Systems of Equations ▪ Solving Linear Systems with Three Unknowns (Variables) ▪ Using Systems of Equations to Model Data Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -1
5. 1 Systems of Linear Equations 5. 1 5. 3 5. 5 5. 6 5. 7 Linear Systems ▪ Substitution Method ▪ Elimination Method ▪ Special Systems ▪ Applying Systems of Equations ▪ Solving Linear Systems with Three Unknowns (Variables) ▪ Using Systems of Equations to Model Data Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -1
 5. 1 Example (page 495) 1 Solving a System by Substitution Solve the system by substitution method. x = 1 + 2 y Substitute 1 + 2 y for x in L 1: 4 x – 3(2) = 14 4 x – 6 = 14 4 x = 20 x = 5 Solution: (5, 2) Check the solution Eq 1: 4(5) – 3(2) = 20 – 6 = 14 Eq 2: (5) – 2(2) = 5 – 4 = 1 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -2
5. 1 Example (page 495) 1 Solving a System by Substitution Solve the system by substitution method. x = 1 + 2 y Substitute 1 + 2 y for x in L 1: 4 x – 3(2) = 14 4 x – 6 = 14 4 x = 20 x = 5 Solution: (5, 2) Check the solution Eq 1: 4(5) – 3(2) = 20 – 6 = 14 Eq 2: (5) – 2(2) = 5 – 4 = 1 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -2
 5. 1 Example (page 496) 2 Solving a System by Elimination Solve the system algebraically. 2 x + 3 y = -1 (2) 2(4) + 3 y = -1 8 + 3 y = -1 3 y 3 x – 2 y = 18 (3) = -9 y = -3 4 x + 6 y = -2 Solution: (4, -3) 9 x – 6 y = 54 13 x = 52 x = 4 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Check the solution: 2(4) + 3(-3) = 8 – 9 = -1 3(4) – 2(-3) = 12 + 6 = 18 5 -3
5. 1 Example (page 496) 2 Solving a System by Elimination Solve the system algebraically. 2 x + 3 y = -1 (2) 2(4) + 3 y = -1 8 + 3 y = -1 3 y 3 x – 2 y = 18 (3) = -9 y = -3 4 x + 6 y = -2 Solution: (4, -3) 9 x – 6 y = 54 13 x = 52 x = 4 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Check the solution: 2(4) + 3(-3) = 8 – 9 = -1 3(4) – 2(-3) = 12 + 6 = 18 5 -3
 5. 1 Example (page 496) 3 Solving an Inconsistent System Solve the system. (2) The graphs of the equations are parallel and never intersect. 14 x + 6 y = – 10 – 14 x – 6 y = – 10 0 = – 20 The system is inconsistent. Solution set: ø Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -4
5. 1 Example (page 496) 3 Solving an Inconsistent System Solve the system. (2) The graphs of the equations are parallel and never intersect. 14 x + 6 y = – 10 – 14 x – 6 y = – 10 0 = – 20 The system is inconsistent. Solution set: ø Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -4
 5. 1 Example 4 Solving a System with Infinitely Many Solutions (page 497) Solve the system. The graphs of the two equations coincide. (3) 3 x – y = 8 Solve for x 3 x = y + 8 0 = 0 Always true Infinite Solutions x = 1/3 y + 8/3 The solution set with an arbitrary y is {(1/3 y + 8/3, y)}. Find the solution with arbitrary y Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -5
5. 1 Example 4 Solving a System with Infinitely Many Solutions (page 497) Solve the system. The graphs of the two equations coincide. (3) 3 x – y = 8 Solve for x 3 x = y + 8 0 = 0 Always true Infinite Solutions x = 1/3 y + 8/3 The solution set with an arbitrary y is {(1/3 y + 8/3, y)}. Find the solution with arbitrary y Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -5
 5. 1 Example 5 Using a Linear System to Solve an Application (page 498) In the 2006 Winter Olympics in Torino, Italy, the two countries winning the most medals were Germany and the United States. The total number of medals won by these two countries was 54, with Germany winning 4 more medals than the United States. How many medals were won by each country? (Source: www. infoplease. com) Let U = the # of medals won by the U. S. Let G = the # of medals won by Germany. Then, we have the system: U + G = 54 G – U = 4 U + G = 54 -U + G = 4 The U. S. won 25 medals and Germany won 29 medals. 2 G = 58 G = 29 U = 25 5 -6
5. 1 Example 5 Using a Linear System to Solve an Application (page 498) In the 2006 Winter Olympics in Torino, Italy, the two countries winning the most medals were Germany and the United States. The total number of medals won by these two countries was 54, with Germany winning 4 more medals than the United States. How many medals were won by each country? (Source: www. infoplease. com) Let U = the # of medals won by the U. S. Let G = the # of medals won by Germany. Then, we have the system: U + G = 54 G – U = 4 U + G = 54 -U + G = 4 The U. S. won 25 medals and Germany won 29 medals. 2 G = 58 G = 29 U = 25 5 -6
 5. 1 Ex 6 Solving a System of Three Equations with Three Variables (pg 500) Solve the system (-2) 3 x + 4 y – 2 z = 14 2 x + y + 2 z = -9 2 x + 2 y – 2 z = 18 Planning to eliminate z Add lines 1 & 2 and 2 & 3 5 x + 5 y = 5 3 y = 9 y = 3 3(-2) + 4(3) – 2 z = 14 5 x + 5(3) = 5 -6 + 12 – 2 z = 14 5 x + 15 = 5 5 x = -10 6 – 2 z = 14 – 2 z = 8 x = -2 z = -4 Solution: (-2, 3, -4) 5 -7
5. 1 Ex 6 Solving a System of Three Equations with Three Variables (pg 500) Solve the system (-2) 3 x + 4 y – 2 z = 14 2 x + y + 2 z = -9 2 x + 2 y – 2 z = 18 Planning to eliminate z Add lines 1 & 2 and 2 & 3 5 x + 5 y = 5 3 y = 9 y = 3 3(-2) + 4(3) – 2 z = 14 5 x + 5(3) = 5 -6 + 12 – 2 z = 14 5 x + 15 = 5 5 x = -10 6 – 2 z = 14 – 2 z = 8 x = -2 z = -4 Solution: (-2, 3, -4) 5 -7
 5. 1 Example 6 Solving a System of Three Equations with Three Variables (cont. ) Verify that (– 2, 3, – 4) satisfies all three equations in the original system. Solution set: {(– 2, 3, – 4)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -8
5. 1 Example 6 Solving a System of Three Equations with Three Variables (cont. ) Verify that (– 2, 3, – 4) satisfies all three equations in the original system. Solution set: {(– 2, 3, – 4)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -8
 5. 1 Example 8 Find equation of the parabola (page 502) Find the equation of the parabola that passes through the points (– 5, 7), (– 1, – 2), and (3, 5). y = ax 2 + bx + c x 2 a + xb + c = y y = 0. 5 x 2 + 0. 75 x – 1. 75 (– 5, 7) 25 a – 5 b + c = 7 (– 1, – 2) 1 a – b + c = – 2 –a + b – c = 2 (3, 5) 9 a + 3 b + c = 5 24 a – 4 b = 9 8 a + 4 b = 7 32 a = 16 a = ½ 24(½) – 4 b = 9 (½) – (¾) + c = -2 12 – 4 b = 9 – 4 b = -3 -¼ + c = -2 b = ¾ c = -7/4 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -9
5. 1 Example 8 Find equation of the parabola (page 502) Find the equation of the parabola that passes through the points (– 5, 7), (– 1, – 2), and (3, 5). y = ax 2 + bx + c x 2 a + xb + c = y y = 0. 5 x 2 + 0. 75 x – 1. 75 (– 5, 7) 25 a – 5 b + c = 7 (– 1, – 2) 1 a – b + c = – 2 –a + b – c = 2 (3, 5) 9 a + 3 b + c = 5 24 a – 4 b = 9 8 a + 4 b = 7 32 a = 16 a = ½ 24(½) – 4 b = 9 (½) – (¾) + c = -2 12 – 4 b = 9 – 4 b = -3 -¼ + c = -2 b = ¾ c = -7/4 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -9
 5. 1 add on: If infinite solutions, arbitrary z Solve. 4 x – 3 y + z = 0 (4) 16 x – 12 y + 4 z = 0 x + y = 0 x + y = 0 -16 x + 12 y – 4 z = 0 Infinite solutions so go back to original equations Plan to eliminate z Add L 1 & L 2 solve for x by eliminating y 4 x – 3 y + z = 0 3 x + 3 y = 0 7 x + z = 0 Add L 1 & L 2 solve for y by eliminating x 4 x – 3 y + z = 0 -4 x – 4 y = 0 x = -1/7 z Copyright © 2008 Pearson Addison-Wesley. All rights reserved. – 7 y + z = 0 y = 1/7 z Answer: – 1/7 z ( , , z) 5 -10
5. 1 add on: If infinite solutions, arbitrary z Solve. 4 x – 3 y + z = 0 (4) 16 x – 12 y + 4 z = 0 x + y = 0 x + y = 0 -16 x + 12 y – 4 z = 0 Infinite solutions so go back to original equations Plan to eliminate z Add L 1 & L 2 solve for x by eliminating y 4 x – 3 y + z = 0 3 x + 3 y = 0 7 x + z = 0 Add L 1 & L 2 solve for y by eliminating x 4 x – 3 y + z = 0 -4 x – 4 y = 0 x = -1/7 z Copyright © 2008 Pearson Addison-Wesley. All rights reserved. – 7 y + z = 0 y = 1/7 z Answer: – 1/7 z ( , , z) 5 -10
 5. 1 Summary Systems of Linear Substitution Method Equations Elimination Method Special Systems: no solution and infinite solution Applying Systems of Equations Solving Systems with Three Unknowns (Variables) Using Systems of Equations to Model Data Solve with an arbitrary X ( X , ______, _____ ) solve for Z solve for Y eliminate Z Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Solve with an arbitrary Z ( ______, Z ) solve for X solve for Y eliminate X 5 -11
5. 1 Summary Systems of Linear Substitution Method Equations Elimination Method Special Systems: no solution and infinite solution Applying Systems of Equations Solving Systems with Three Unknowns (Variables) Using Systems of Equations to Model Data Solve with an arbitrary X ( X , ______, _____ ) solve for Z solve for Y eliminate Z Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Solve with an arbitrary Z ( ______, Z ) solve for X solve for Y eliminate X 5 -11
 5. 3 Determinant Solution of Linear Systems Determinants ▪ Cofactors ▪ Evaluating n × n Determinants ▪ Cramer’s Rule Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -12
5. 3 Determinant Solution of Linear Systems Determinants ▪ Cofactors ▪ Evaluating n × n Determinants ▪ Cramer’s Rule Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -12
 5. 3 Example (page 523) 1 Evaluating a 2 × 2 Determinant minus You are being asked to find the determinant of matrix B Det = -20 – (– 16) = = -20 + 16 = -4 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -13
5. 3 Example (page 523) 1 Evaluating a 2 × 2 Determinant minus You are being asked to find the determinant of matrix B Det = -20 – (– 16) = = -20 + 16 = -4 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -13
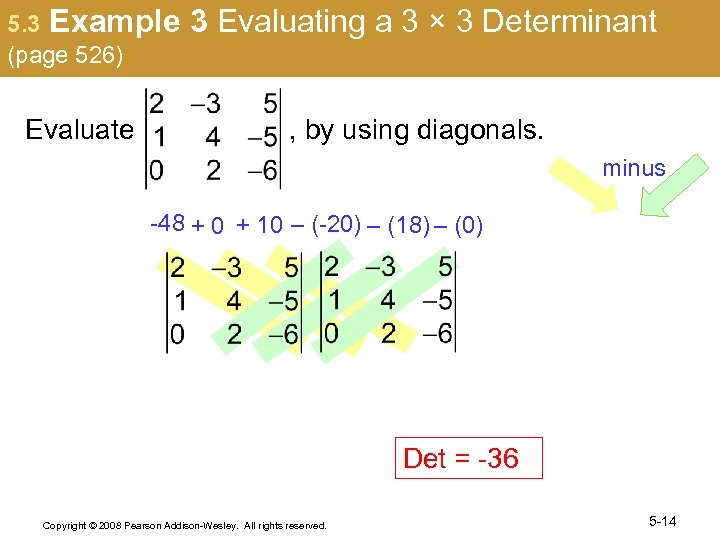 5. 3 Example (page 526) 3 Evaluating a 3 × 3 Determinant Evaluate , by using diagonals. minus -48 + 0 + 10 – (-20) – (18) – (0) Det = -36 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -14
5. 3 Example (page 526) 3 Evaluating a 3 × 3 Determinant Evaluate , by using diagonals. minus -48 + 0 + 10 – (-20) – (18) – (0) Det = -36 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -14
 5. 3 Example (page 526) 3 Evaluating a 3 × 3 Determinant Evaluate , by using expansion by minors. Start with row 1: keep it, change it, keep it Det = 2 + 3 + 5 = 2(-24 – -10) + 3(-6 – 0) + 5(2 – 0) = 2(-14) + 3(-6) + 5(2) = -28 – 18 + 10 = -36 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -15
5. 3 Example (page 526) 3 Evaluating a 3 × 3 Determinant Evaluate , by using expansion by minors. Start with row 1: keep it, change it, keep it Det = 2 + 3 + 5 = 2(-24 – -10) + 3(-6 – 0) + 5(2 – 0) = 2(-14) + 3(-6) + 5(2) = -28 – 18 + 10 = -36 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -15
 5. 3 Ex 4 Applying Cramer’s Rule to a 2 × 2 System (page 528) Use Cramer’s rule to solve the system. By Cramer’s rule, Find D first, since if D = 0, Cramer’s rule does not apply. If D ≠ 0, find Dx and Dy. D = -8 – 3 Dx = -4 – 15 Dy = 20 – 2 = -11 = -19 = 18 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -16
5. 3 Ex 4 Applying Cramer’s Rule to a 2 × 2 System (page 528) Use Cramer’s rule to solve the system. By Cramer’s rule, Find D first, since if D = 0, Cramer’s rule does not apply. If D ≠ 0, find Dx and Dy. D = -8 – 3 Dx = -4 – 15 Dy = 20 – 2 = -11 = -19 = 18 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -16
 5. 3 Example 5 Applying Cramer’s Rule to a 3 × 3 System (page 529) Use Cramer’s rule to solve the system. Rewrite each equation in the form ax + by + cz = k. By Cramer’s rule, Find D first, since if D = 0, Cramer’s rule does not apply. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -17
5. 3 Example 5 Applying Cramer’s Rule to a 3 × 3 System (page 529) Use Cramer’s rule to solve the system. Rewrite each equation in the form ax + by + cz = k. By Cramer’s rule, Find D first, since if D = 0, Cramer’s rule does not apply. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -17
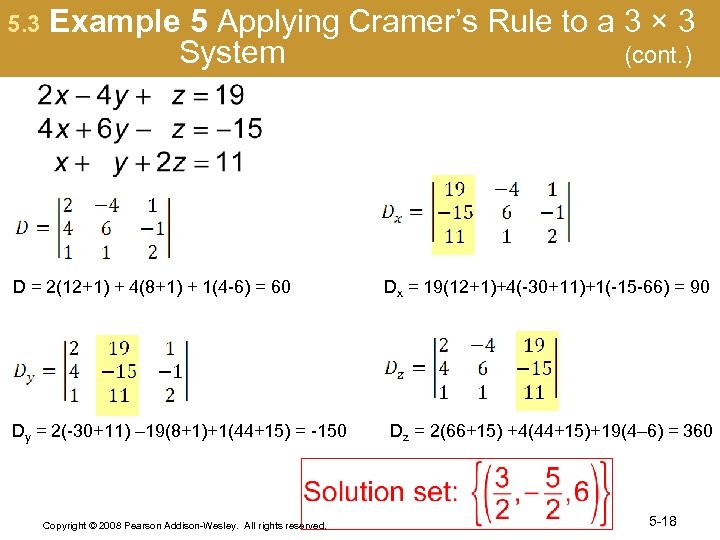 5. 3 Example 5 Applying Cramer’s Rule to a 3 × 3 System (cont. ) D = 2(12+1) + 4(8+1) + 1(4 -6) = 60 Dy = 2(-30+11) – 19(8+1)+1(44+15) = -150 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Dx = 19(12+1)+4(-30+11)+1(-15 -66) = 90 Dz = 2(66+15) +4(44+15)+19(4– 6) = 360 5 -18
5. 3 Example 5 Applying Cramer’s Rule to a 3 × 3 System (cont. ) D = 2(12+1) + 4(8+1) + 1(4 -6) = 60 Dy = 2(-30+11) – 19(8+1)+1(44+15) = -150 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Dx = 19(12+1)+4(-30+11)+1(-15 -66) = 90 Dz = 2(66+15) +4(44+15)+19(4– 6) = 360 5 -18
 5. 3 Example 6 Showing That Cramer’s Rule Does Not Apply (page 530) Show that Cramer’s rule does not apply to the system. We need to show that D = 0. = 1(12 – 12) + 3(36 – 36) + 2(-9 + 9) = 0 Thus, Cramer’s rule does not apply to the system. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -19
5. 3 Example 6 Showing That Cramer’s Rule Does Not Apply (page 530) Show that Cramer’s rule does not apply to the system. We need to show that D = 0. = 1(12 – 12) + 3(36 – 36) + 2(-9 + 9) = 0 Thus, Cramer’s rule does not apply to the system. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -19
 Additional – Area of a Triangle Find the area of a triangle with the given vertices: (-2, 3), (4, 5), and (-10, -3) = 10 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -20
Additional – Area of a Triangle Find the area of a triangle with the given vertices: (-2, 3), (4, 5), and (-10, -3) = 10 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -20
 5. 3 Summary Determinant Solution of Linear Systems Determinants Evaluating n × n Determinants Cramer’s Rule Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -21
5. 3 Summary Determinant Solution of Linear Systems Determinants Evaluating n × n Determinants Cramer’s Rule Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -21
 5. 5 Nonlinear Systems of Equations Solving Nonlinear Systems with Real Solutions ▪ Solving Nonlinear Systems with Nonreal Complex Solutions ▪ Applying Nonlinear Systems Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -22
5. 5 Nonlinear Systems of Equations Solving Nonlinear Systems with Real Solutions ▪ Solving Nonlinear Systems with Nonreal Complex Solutions ▪ Applying Nonlinear Systems Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -22
 5. 5 Example Substitution 1 Solving a Nonlinear System by (page 543) Solve the system. Substitute x = -2 in line 2 (-2) – y = -4 -y = -2 Add lines 1 & 2 y = 2 x 2 + x – 2 = 0 Substitute x =1 in line 2 (x + 2)(x – 1) = 0 (1) – y = -4 -y = -5 x = -2 x = 1 y = 5 Solution set: {(– 2, 2), (1, 5)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -23
5. 5 Example Substitution 1 Solving a Nonlinear System by (page 543) Solve the system. Substitute x = -2 in line 2 (-2) – y = -4 -y = -2 Add lines 1 & 2 y = 2 x 2 + x – 2 = 0 Substitute x =1 in line 2 (x + 2)(x – 1) = 0 (1) – y = -4 -y = -5 x = -2 x = 1 y = 5 Solution set: {(– 2, 2), (1, 5)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -23
 5. 5 Example Elimination 2 Solving a Nonlinear System by (page 544) Solve the system. Substitute x = 0 in line (1), then solve for y. (0)2 + y 2 = 9 Multiply line 1 by (– 4) y 2 = 9 y = ± 3 – 4 x 2 – 4 y 2 = – 36 9 x 2 + 4 y 2 = 36 5 x 2 = 0 Solution set: {(0, – 3), (0, 3)} x 2 = 0 x = 0 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -24
5. 5 Example Elimination 2 Solving a Nonlinear System by (page 544) Solve the system. Substitute x = 0 in line (1), then solve for y. (0)2 + y 2 = 9 Multiply line 1 by (– 4) y 2 = 9 y = ± 3 – 4 x 2 – 4 y 2 = – 36 9 x 2 + 4 y 2 = 36 5 x 2 = 0 Solution set: {(0, – 3), (0, 3)} x 2 = 0 x = 0 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -24
 5. 5 Example 3 Solving a Nonlinear System with Nonreal Complex Numbers in its Solutions (page 547) Solve the system. Substitute x = 2 i which means Substitute x 2 = -4 into L 1 -4 + y 2 = 6 Mult L 1 by (-2) y 2 = 10 -2 x 2 – 2 y 2 = -12 y = ±√ 10 3 x 2 + 2 y 2 = 8 x 2 = – 4 Substitute x = -2 i which means Substitute x 2 = -4 into L 1 -4 + y 2 = 6 x = ± √-4 y 2 = 10 x = ± 2 i y = ±√ 10 Solution set:
5. 5 Example 3 Solving a Nonlinear System with Nonreal Complex Numbers in its Solutions (page 547) Solve the system. Substitute x = 2 i which means Substitute x 2 = -4 into L 1 -4 + y 2 = 6 Mult L 1 by (-2) y 2 = 10 -2 x 2 – 2 y 2 = -12 y = ±√ 10 3 x 2 + 2 y 2 = 8 x 2 = – 4 Substitute x = -2 i which means Substitute x 2 = -4 into L 1 -4 + y 2 = 6 x = ± √-4 y 2 = 10 x = ± 2 i y = ±√ 10 Solution set:
 5. 5 Example 4 Using a Nonlinear System to Find the Dimensions of a Box (page 547) The length of the hypotenuse of a right triangle is 41 cm. One of the legs is 31 cm longer than the other. Find the lengths of the two legs of the triangle. X 2 + (X + 31)2 = 412 X 41 X 2 + 62 X + 961 = 1681 2 X 2 + 62 X – 720 = 0 X+31 X 2 + 31 X – 360 = 0 (X + 40) (X – 9) = 0 X = -40 or X = 9 The lengths of the legs are 9 cm and 40 cm. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -26
5. 5 Example 4 Using a Nonlinear System to Find the Dimensions of a Box (page 547) The length of the hypotenuse of a right triangle is 41 cm. One of the legs is 31 cm longer than the other. Find the lengths of the two legs of the triangle. X 2 + (X + 31)2 = 412 X 41 X 2 + 62 X + 961 = 1681 2 X 2 + 62 X – 720 = 0 X+31 X 2 + 31 X – 360 = 0 (X + 40) (X – 9) = 0 X = -40 or X = 9 The lengths of the legs are 9 cm and 40 cm. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -26
 Additional Problem Solve the system of equations: From the 1 st line y = -x + 21 sub this into the 2 nd equation x + y = 21 xy = 80 x(-x + 21) = 80 -x 2 + 21 x = 80 0 = x 2 – 21 x + 80 0 = (x – 5) (x – 16) Solution: x = 5 or x = 16 (5, 16), (16, 5) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -27
Additional Problem Solve the system of equations: From the 1 st line y = -x + 21 sub this into the 2 nd equation x + y = 21 xy = 80 x(-x + 21) = 80 -x 2 + 21 x = 80 0 = x 2 – 21 x + 80 0 = (x – 5) (x – 16) Solution: x = 5 or x = 16 (5, 16), (16, 5) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -27
 Additional Problem Solve the system of equations: Since solving for x or y in the 1 st equation would lead to a really ugly equation with the square root of a binomial we will solve for y in the 2 nd equation y = 6/x Sub y = 6/ x into 1 st equation x 2 + (6/x)2 = 13 x 2 + y 2 = 13 xy = 6 x 2 = 4 or x 2 = 9 x = ± 2 or x = ± 3 When x = 2, y = 3 When x = -2, y = -3 When x = 3, y = 2 When x = -3, y = -2 Answers: {(2, 3), (-2, -3), (3, 2), (-3, -2)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -28
Additional Problem Solve the system of equations: Since solving for x or y in the 1 st equation would lead to a really ugly equation with the square root of a binomial we will solve for y in the 2 nd equation y = 6/x Sub y = 6/ x into 1 st equation x 2 + (6/x)2 = 13 x 2 + y 2 = 13 xy = 6 x 2 = 4 or x 2 = 9 x = ± 2 or x = ± 3 When x = 2, y = 3 When x = -2, y = -3 When x = 3, y = 2 When x = -3, y = -2 Answers: {(2, 3), (-2, -3), (3, 2), (-3, -2)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -28
 Add on to notes Solve: –x 2 + xy + 2 y 2 = 26 x 2 – xy + y 2 = 13 3 y 2 = 39 y 2 = 13 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -29
Add on to notes Solve: –x 2 + xy + 2 y 2 = 26 x 2 – xy + y 2 = 13 3 y 2 = 39 y 2 = 13 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -29
 5. 5 add on Find two numbers whose ratio is 9 to 2 and whose product is 162. Let 9 x and 2 x represent the numbers 18 x 2 = 162 x 2 = 9 x = ± 3 Solutions: 27 and 6 or – 27 and – 6 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -30
5. 5 add on Find two numbers whose ratio is 9 to 2 and whose product is 162. Let 9 x and 2 x represent the numbers 18 x 2 = 162 x 2 = 9 x = ± 3 Solutions: 27 and 6 or – 27 and – 6 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -30
 5. 5 add on A box with an open top has a square base and four sides of equal height. The volume of the box is 360 ft 3. If the surface area is 276 ft 2, find the dimensions of the box. V = 360 A = 276 x 2 y = 360 x 2 + 4 xy = 276 y = 360/x 2 + 4 x(360/x 2) = 276 x 2 + 1440/x = 276 y x x x 3 + 1440 = 276 x x 3 – 276 x + 1440 = 0 Continued on next slide Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -31
5. 5 add on A box with an open top has a square base and four sides of equal height. The volume of the box is 360 ft 3. If the surface area is 276 ft 2, find the dimensions of the box. V = 360 A = 276 x 2 y = 360 x 2 + 4 xy = 276 y = 360/x 2 + 4 x(360/x 2) = 276 x 2 + 1440/x = 276 y x x x 3 + 1440 = 276 x x 3 – 276 x + 1440 = 0 Continued on next slide Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -31
 Cont from previous slide V = 360 A = 276 x 2 y = 360 x 2 + 4 xy = 276 y x x x 3 – 276 x + 1440 = 0 Use synthetic division to find a zero 6 1 0 -276 1440 6 36 1 6 -240 -1440 0 Then use Quad Formula with a = 1, b = 6, and c = -240 Keep the positive answer Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Disc = 996 x = (-6 ± √(996))/2 x ≈12. 780 Solutions: x = 6 ft and y = 10 ft x = 12. 780 ft and y = 2. 204 ft 5 -32
Cont from previous slide V = 360 A = 276 x 2 y = 360 x 2 + 4 xy = 276 y x x x 3 – 276 x + 1440 = 0 Use synthetic division to find a zero 6 1 0 -276 1440 6 36 1 6 -240 -1440 0 Then use Quad Formula with a = 1, b = 6, and c = -240 Keep the positive answer Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Disc = 996 x = (-6 ± √(996))/2 x ≈12. 780 Solutions: x = 6 ft and y = 10 ft x = 12. 780 ft and y = 2. 204 ft 5 -32
 5. 5 Summary Nonlinear Systems of Equations Solving Nonlinear Systems with Real Solutions Solving Nonlinear Systems with Nonreal Complex Solutions Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -33
5. 5 Summary Nonlinear Systems of Equations Solving Nonlinear Systems with Real Solutions Solving Nonlinear Systems with Nonreal Complex Solutions Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -33
 5. 6 Systems of Inequalities and Linear Programming Solving Linear Inequalities ▪ Solving Systems of Inequalities ▪ Linear Programming Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -34
5. 6 Systems of Inequalities and Linear Programming Solving Linear Inequalities ▪ Solving Systems of Inequalities ▪ Linear Programming Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -34
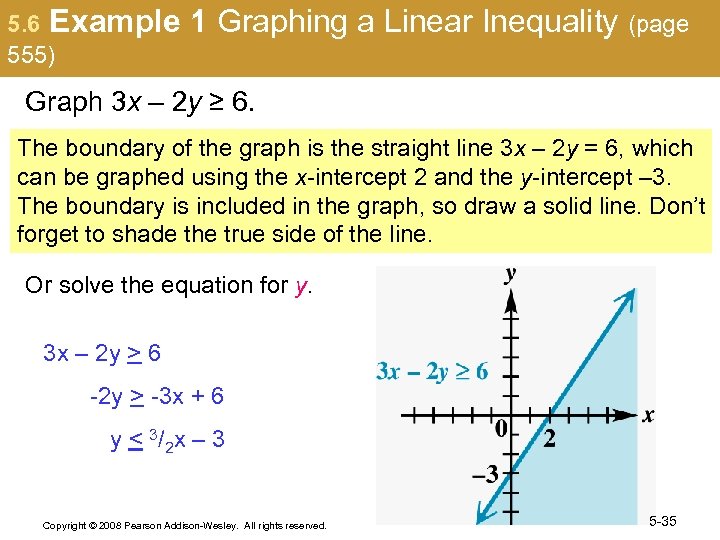 5. 6 Example 555) 1 Graphing a Linear Inequality (page Graph 3 x – 2 y ≥ 6. The boundary of the graph is the straight line 3 x – 2 y = 6, which can be graphed using the x-intercept 2 and the y-intercept – 3. The boundary is included in the graph, so draw a solid line. Don’t forget to shade the true side of the line. Or solve the equation for y. 3 x – 2 y > 6 -2 y > -3 x + 6 y < 3/2 x – 3 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -35
5. 6 Example 555) 1 Graphing a Linear Inequality (page Graph 3 x – 2 y ≥ 6. The boundary of the graph is the straight line 3 x – 2 y = 6, which can be graphed using the x-intercept 2 and the y-intercept – 3. The boundary is included in the graph, so draw a solid line. Don’t forget to shade the true side of the line. Or solve the equation for y. 3 x – 2 y > 6 -2 y > -3 x + 6 y < 3/2 x – 3 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -35
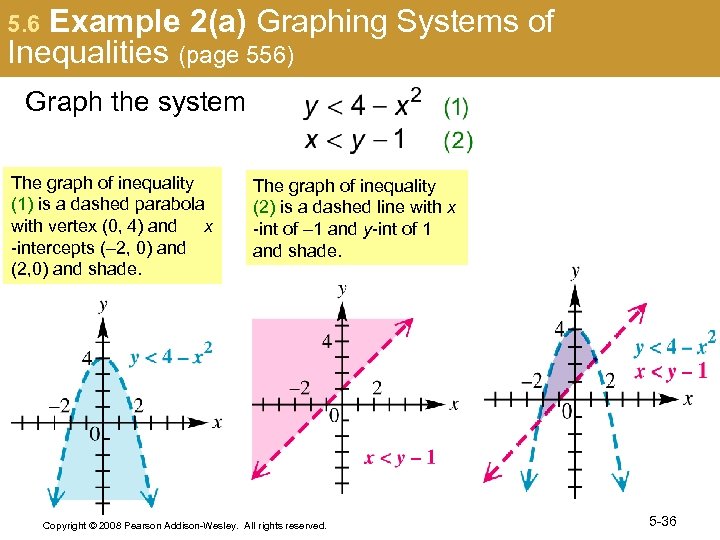 5. 6 Example 2(a) Graphing Systems of Inequalities (page 556) Graph the system The graph of inequality (1) is a dashed parabola with vertex (0, 4) and x -intercepts (– 2, 0) and (2, 0) and shade. The graph of inequality (2) is a dashed line with x -int of – 1 and y-int of 1 and shade. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -36
5. 6 Example 2(a) Graphing Systems of Inequalities (page 556) Graph the system The graph of inequality (1) is a dashed parabola with vertex (0, 4) and x -intercepts (– 2, 0) and (2, 0) and shade. The graph of inequality (2) is a dashed line with x -int of – 1 and y-int of 1 and shade. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -36
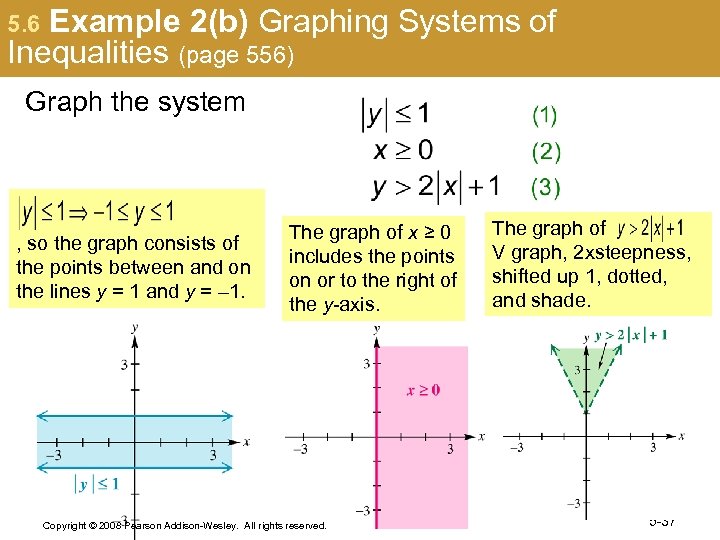 5. 6 Example 2(b) Graphing Systems of Inequalities (page 556) Graph the system , so the graph consists of the points between and on the lines y = 1 and y = – 1. The graph of x ≥ 0 includes the points on or to the right of the y-axis. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. The graph of V graph, 2 xsteepness, shifted up 1, dotted, and shade. 5 -37
5. 6 Example 2(b) Graphing Systems of Inequalities (page 556) Graph the system , so the graph consists of the points between and on the lines y = 1 and y = – 1. The graph of x ≥ 0 includes the points on or to the right of the y-axis. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. The graph of V graph, 2 xsteepness, shifted up 1, dotted, and shade. 5 -37
 5. 6 Example 2(b) Graphing Systems of Inequalities (page 556) Since there are no points in common, the solution set is ø. x > 0 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -38
5. 6 Example 2(b) Graphing Systems of Inequalities (page 556) Since there are no points in common, the solution set is ø. x > 0 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -38
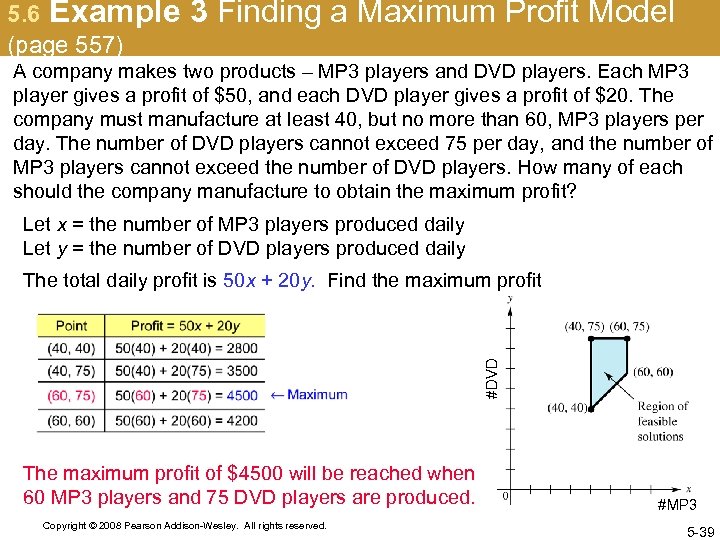 5. 6 Example (page 557) 3 Finding a Maximum Profit Model A company makes two products – MP 3 players and DVD players. Each MP 3 player gives a profit of $50, and each DVD player gives a profit of $20. The company must manufacture at least 40, but no more than 60, MP 3 players per day. The number of DVD players cannot exceed 75 per day, and the number of MP 3 players cannot exceed the number of DVD players. How many of each should the company manufacture to obtain the maximum profit? Let x = the number of MP 3 players produced daily Let y = the number of DVD players produced daily #DVD The total daily profit is 50 x + 20 y. Find the maximum profit The maximum profit of $4500 will be reached when 60 MP 3 players and 75 DVD players are produced. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. #MP 3 5 -39
5. 6 Example (page 557) 3 Finding a Maximum Profit Model A company makes two products – MP 3 players and DVD players. Each MP 3 player gives a profit of $50, and each DVD player gives a profit of $20. The company must manufacture at least 40, but no more than 60, MP 3 players per day. The number of DVD players cannot exceed 75 per day, and the number of MP 3 players cannot exceed the number of DVD players. How many of each should the company manufacture to obtain the maximum profit? Let x = the number of MP 3 players produced daily Let y = the number of DVD players produced daily #DVD The total daily profit is 50 x + 20 y. Find the maximum profit The maximum profit of $4500 will be reached when 60 MP 3 players and 75 DVD players are produced. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. #MP 3 5 -39
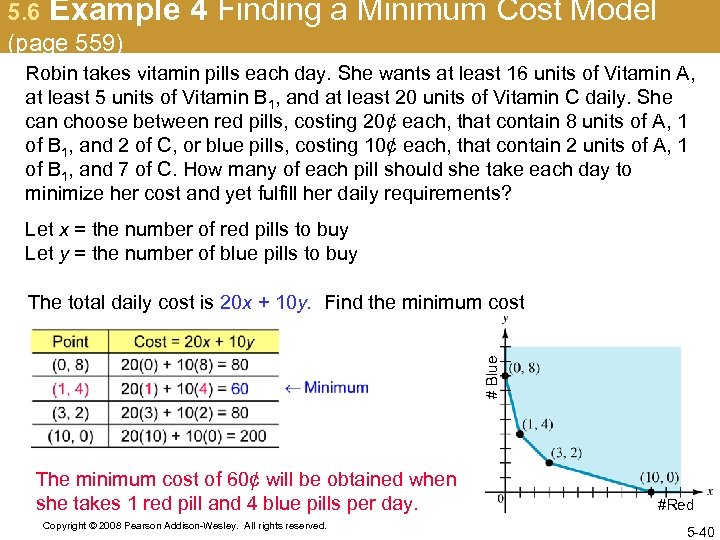 5. 6 Example (page 559) 4 Finding a Minimum Cost Model Robin takes vitamin pills each day. She wants at least 16 units of Vitamin A, at least 5 units of Vitamin B 1, and at least 20 units of Vitamin C daily. She can choose between red pills, costing 20¢ each, that contain 8 units of A, 1 of B 1, and 2 of C, or blue pills, costing 10¢ each, that contain 2 units of A, 1 of B 1, and 7 of C. How many of each pill should she take each day to minimize her cost and yet fulfill her daily requirements? Let x = the number of red pills to buy Let y = the number of blue pills to buy # Blue The total daily cost is 20 x + 10 y. Find the minimum cost The minimum cost of 60¢ will be obtained when she takes 1 red pill and 4 blue pills per day. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. #Red 5 -40
5. 6 Example (page 559) 4 Finding a Minimum Cost Model Robin takes vitamin pills each day. She wants at least 16 units of Vitamin A, at least 5 units of Vitamin B 1, and at least 20 units of Vitamin C daily. She can choose between red pills, costing 20¢ each, that contain 8 units of A, 1 of B 1, and 2 of C, or blue pills, costing 10¢ each, that contain 2 units of A, 1 of B 1, and 7 of C. How many of each pill should she take each day to minimize her cost and yet fulfill her daily requirements? Let x = the number of red pills to buy Let y = the number of blue pills to buy # Blue The total daily cost is 20 x + 10 y. Find the minimum cost The minimum cost of 60¢ will be obtained when she takes 1 red pill and 4 blue pills per day. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. #Red 5 -40
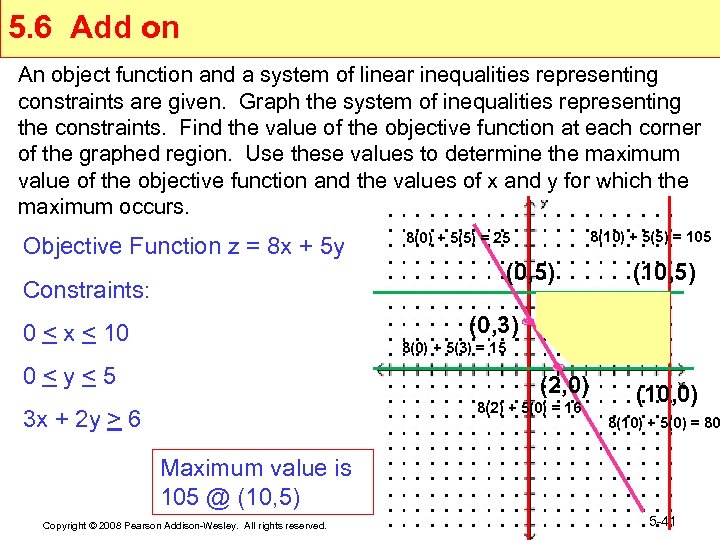 5. 6 Add on An object function and a system of linear inequalities representing constraints are given. Graph the system of inequalities representing the constraints. Find the value of the objective function at each corner of the graphed region. Use these values to determine the maximum value of the objective function and the values of x and y for which the maximum occurs. Objective Function z = 8 x + 5 y Constraints: 8(10) + 5(5) = 105 8(0) + 5(5) = 25 (0, 5) (10, 5) (0, 3) 0 < x < 10 8(0) + 5(3) = 15 0 < y < 5 (2, 0) 8(2) + 5(0) = 16 3 x + 2 y > 6 (10, 0) 8(10) + 5(0) = 80 Maximum value is 105 @ (10, 5) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -41
5. 6 Add on An object function and a system of linear inequalities representing constraints are given. Graph the system of inequalities representing the constraints. Find the value of the objective function at each corner of the graphed region. Use these values to determine the maximum value of the objective function and the values of x and y for which the maximum occurs. Objective Function z = 8 x + 5 y Constraints: 8(10) + 5(5) = 105 8(0) + 5(5) = 25 (0, 5) (10, 5) (0, 3) 0 < x < 10 8(0) + 5(3) = 15 0 < y < 5 (2, 0) 8(2) + 5(0) = 16 3 x + 2 y > 6 (10, 0) 8(10) + 5(0) = 80 Maximum value is 105 @ (10, 5) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -41
 5. 6 add on Cabinet X costs $100, requires 10 sq ft of floor space, and holds 30 cu ft of files. Cabinet Y costs $140, requires 4 sq ft of floor space, and holds 12 cu ft. To get maximum storage, how many of each should be purchased with a budget limit of $1400 and floor space of 90 sq ft? X > 0, and Y > 0 Want Max Storage=30 X + 12 Y (0, 22. 5) Purchase 7 of Cabinet X and 5 of Cabinet Y (0, 10) Money: 100 X + 140 Y < 1400 Floor Space: 10 X + 4 Y < 90 Find the pt. of intersection of green and purple eq If there are two values that are maxima, the office manager will purchase at least one of each cabinet Copyright © 2008 Pearson Addison-Wesley. All rights reserved. (7, 5) (9, 0) (14, 0) Value @ (0, 10) = 120 Value @ (7, 5) = 270 Value @ (9, 0) = 270 5 -42
5. 6 add on Cabinet X costs $100, requires 10 sq ft of floor space, and holds 30 cu ft of files. Cabinet Y costs $140, requires 4 sq ft of floor space, and holds 12 cu ft. To get maximum storage, how many of each should be purchased with a budget limit of $1400 and floor space of 90 sq ft? X > 0, and Y > 0 Want Max Storage=30 X + 12 Y (0, 22. 5) Purchase 7 of Cabinet X and 5 of Cabinet Y (0, 10) Money: 100 X + 140 Y < 1400 Floor Space: 10 X + 4 Y < 90 Find the pt. of intersection of green and purple eq If there are two values that are maxima, the office manager will purchase at least one of each cabinet Copyright © 2008 Pearson Addison-Wesley. All rights reserved. (7, 5) (9, 0) (14, 0) Value @ (0, 10) = 120 Value @ (7, 5) = 270 Value @ (9, 0) = 270 5 -42
 5. 6 Summary Systems of Inequalities and Linear Programming Solving Linear Inequalities Solving Systems of Inequalities Linear Programming Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -43
5. 6 Summary Systems of Inequalities and Linear Programming Solving Linear Inequalities Solving Systems of Inequalities Linear Programming Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -43
 5. 7 Properties of Matrices Basic Definitions ▪ Adding Matrices ▪ Special Matrices ▪ Subtracting Matrices ▪ Multiplying Matrices ▪ Applying Matrix Algebra Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -44
5. 7 Properties of Matrices Basic Definitions ▪ Adding Matrices ▪ Special Matrices ▪ Subtracting Matrices ▪ Multiplying Matrices ▪ Applying Matrix Algebra Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -44
 5. 7 Example 1 Finding Values to Make Two Matrices Equal (page 565) Find the values of the variables for which each statement is true, if possible. a + 3 = 0 (a) b – 4 = 5 -5 = c a = – 3, b = 9, c = – 5, and d = 0. (b) 5 = d + 5 Not possible, since the matrices do not have the same dimensions Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -45
5. 7 Example 1 Finding Values to Make Two Matrices Equal (page 565) Find the values of the variables for which each statement is true, if possible. a + 3 = 0 (a) b – 4 = 5 -5 = c a = – 3, b = 9, c = – 5, and d = 0. (b) 5 = d + 5 Not possible, since the matrices do not have the same dimensions Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -45
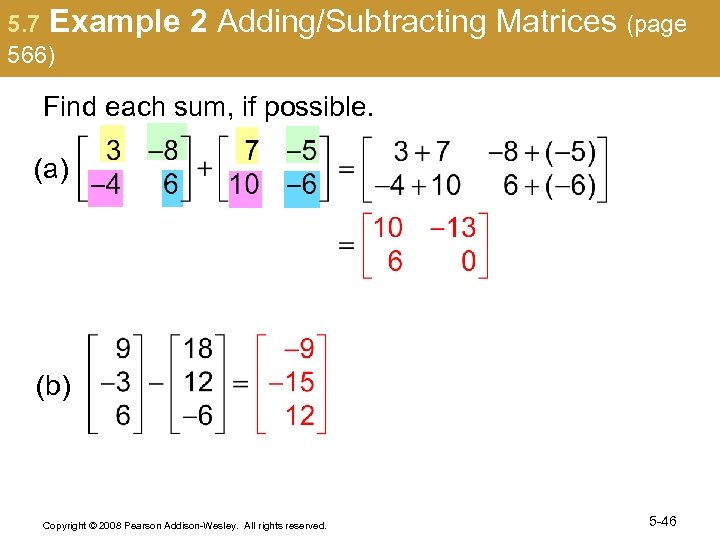 5. 7 Example 566) 2 Adding/Subtracting Matrices (page Find each sum, if possible. (a) (b) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -46
5. 7 Example 566) 2 Adding/Subtracting Matrices (page Find each sum, if possible. (a) (b) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -46
 5. 7 Example 3 Subtracting Matrices (cont. ) (c) A – B if and A and B cannot be subtracted because A is a 2 × 3 matrix, while B is a 2 × 2 matrix. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -47
5. 7 Example 3 Subtracting Matrices (cont. ) (c) A – B if and A and B cannot be subtracted because A is a 2 × 3 matrix, while B is a 2 × 2 matrix. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -47
 Add on to notes Solve for each variable x + 3 + 2 x = 9 3 x = 6 x = 2 y – 2 + 5 = 10 y = 7 5 + z = 4 z = – 1 2 w – 4 + 4 = – 12 2 w = – 12 w = – 6 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -48
Add on to notes Solve for each variable x + 3 + 2 x = 9 3 x = 6 x = 2 y – 2 + 5 = 10 y = 7 5 + z = 4 z = – 1 2 w – 4 + 4 = – 12 2 w = – 12 w = – 6 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -48
 5. 7 Example (page 568) 4 Multiplying Matrices by Scalars Find each product. (a) (b) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -49
5. 7 Example (page 568) 4 Multiplying Matrices by Scalars Find each product. (a) (b) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -49
 5. 7 Example 5 Deciding Whether Two Matrices Can Be Multiplied (page 570) Suppose C is a 2 × 5 matrix and D is a 4 × 2 matrix. (a, b) Can the product CD be calculated? If so, what size is it? No, CD cannot be calculated. (c, d) Can the product DC be calculated? If so, what size is it? Yes, DC can be calculated. The result is a 4 × 5 matrix. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -50
5. 7 Example 5 Deciding Whether Two Matrices Can Be Multiplied (page 570) Suppose C is a 2 × 5 matrix and D is a 4 × 2 matrix. (a, b) Can the product CD be calculated? If so, what size is it? No, CD cannot be calculated. (c, d) Can the product DC be calculated? If so, what size is it? Yes, DC can be calculated. The result is a 4 × 5 matrix. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -50
 5. 7 Example 6 Multiplying Matrices (page 571) Find each product, if possible. (a) AB (b) BA AB cannot be calculated. Matrix B Matrix A 2 x 2 2 x 3 BA can be calculated and would yield a 2 x 3 matrix Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -51
5. 7 Example 6 Multiplying Matrices (page 571) Find each product, if possible. (a) AB (b) BA AB cannot be calculated. Matrix B Matrix A 2 x 2 2 x 3 BA can be calculated and would yield a 2 x 3 matrix Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -51
 5. 7 Example 7 Multiplying Square Matrices (page 571) Find each product. (a) CD (b) DC Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -52
5. 7 Example 7 Multiplying Square Matrices (page 571) Find each product. (a) CD (b) DC Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -52
 5. 7 Summary Properties of Matrices Basic Definitions Adding Matrices Special Matrices Subtracting Matrices Multiplying Matrices Applying Matrix Algebra Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -53
5. 7 Summary Properties of Matrices Basic Definitions Adding Matrices Special Matrices Subtracting Matrices Multiplying Matrices Applying Matrix Algebra Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -53
 5. 2 Matrix Solution of Linear Systems The Gauss-Jordan Method ▪ Special Systems Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -54
5. 2 Matrix Solution of Linear Systems The Gauss-Jordan Method ▪ Special Systems Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -54
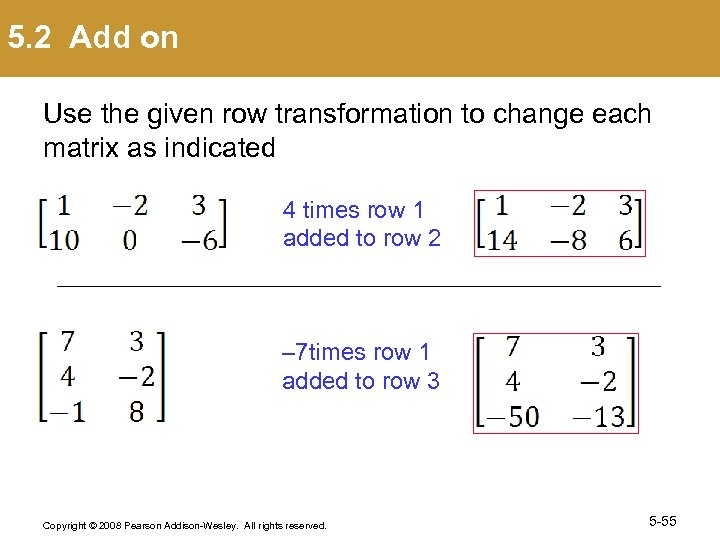 5. 2 Add on Use the given row transformation to change each matrix as indicated 4 times row 1 added to row 2 – 7 times row 1 added to row 3 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -55
5. 2 Add on Use the given row transformation to change each matrix as indicated 4 times row 1 added to row 2 – 7 times row 1 added to row 3 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -55
 5. 2 add on Write the augmented matrix for the system and give its dimensions. Do NOT solve. 3 x + 5 y = – 13 2 x 3 2 x + 3 y = – 9 Write the system of equations associated with the augmented matrix. Do NOT solve. 3 x + 2 y + z = 1 2 y + 4 z = 22 –x – 2 y + 3 y = 15 +3 z Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -56
5. 2 add on Write the augmented matrix for the system and give its dimensions. Do NOT solve. 3 x + 5 y = – 13 2 x 3 2 x + 3 y = – 9 Write the system of equations associated with the augmented matrix. Do NOT solve. 3 x + 2 y + z = 1 2 y + 4 z = 22 –x – 2 y + 3 y = 15 +3 z Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -56
 5. 2 Example (page 512) 1 Using the Gauss-Jordan Method Solve the system. The system has the augmented matrix Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -57
5. 2 Example (page 512) 1 Using the Gauss-Jordan Method Solve the system. The system has the augmented matrix Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -57
 5. 2 Example (page 512) 1 Using the Gauss-Jordan Method 3 -2 1 st goal: element 2, 1 = 0 R 2 + R 1 + R 2 3 rd goal: 1’s in the main diagonal R 1 ∕-102 and R 2 ∕ 153 -17 9 2 nd goal: element 1, 2 = 0 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Solution: (-4, 5) 5 -58
5. 2 Example (page 512) 1 Using the Gauss-Jordan Method 3 -2 1 st goal: element 2, 1 = 0 R 2 + R 1 + R 2 3 rd goal: 1’s in the main diagonal R 1 ∕-102 and R 2 ∕ 153 -17 9 2 nd goal: element 1, 2 = 0 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Solution: (-4, 5) 5 -58
 5. 2 Example (page 514) 2 Using the Gauss-Jordan Method We will use elimination instead of Gauss-Jordan Method Solve the system. x + y – 4 z = 10 8 x – 12 y + 4 z = 28 12 x – 4 y – 4 z = 48 (4) Add L 1+L 2 : L 2+L 3 9 x – 11(-1) = 38 (3) + (-1) – 4 z = 10 9 x + 11 = 38 2 – 4 z = 10 – 180 x + 220 y = – 760 9 x = 27 – 4 z = 8 180 x – 144 y = 684 x = 3 z = – 2 9 x – 11 y = 38 20 x – 16 y = 76 76 y = – 76 y = – 1 (-20) (9) Solution set: {(3, – 1, – 2)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -59
5. 2 Example (page 514) 2 Using the Gauss-Jordan Method We will use elimination instead of Gauss-Jordan Method Solve the system. x + y – 4 z = 10 8 x – 12 y + 4 z = 28 12 x – 4 y – 4 z = 48 (4) Add L 1+L 2 : L 2+L 3 9 x – 11(-1) = 38 (3) + (-1) – 4 z = 10 9 x + 11 = 38 2 – 4 z = 10 – 180 x + 220 y = – 760 9 x = 27 – 4 z = 8 180 x – 144 y = 684 x = 3 z = – 2 9 x – 11 y = 38 20 x – 16 y = 76 76 y = – 76 y = – 1 (-20) (9) Solution set: {(3, – 1, – 2)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -59
 5. 2 Example (page 515) 3 Solving an Inconsistent System We will use elimination instead of Gauss-Jordan Method Use the Gauss-Jordan method to solve the system. (3) 6 x – 9 y = 21 – 6 x + 9 y = 0 0 = 21 Never true Solution set: ø Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -60
5. 2 Example (page 515) 3 Solving an Inconsistent System We will use elimination instead of Gauss-Jordan Method Use the Gauss-Jordan method to solve the system. (3) 6 x – 9 y = 21 – 6 x + 9 y = 0 0 = 21 Never true Solution set: ø Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -60
 5. 2 Ex 4 Solving a System with Infinitely Many We will use elimination instead of Gauss-Jordan Method Solutions (page 516) Use the Gauss-Jordan method to solve the system. Write the solution set with z arbitrary. Eliminate y (-2) -4 x – 2 y – 2 z = -10 3 x + 2 y – z = -8 -x – 3 z = -18 -x = 3 z – 18 x = -3 z + 18 Eliminate x (-3) -6 x – 3 y – 3 z = -15 (2) 6 x + 4 y – 2 z = -16 y – 5 z = -31 Solution set: {(– 3 z + 18, 5 z – 31, z)} y = 5 z – 31 5 -61 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.
5. 2 Ex 4 Solving a System with Infinitely Many We will use elimination instead of Gauss-Jordan Method Solutions (page 516) Use the Gauss-Jordan method to solve the system. Write the solution set with z arbitrary. Eliminate y (-2) -4 x – 2 y – 2 z = -10 3 x + 2 y – z = -8 -x – 3 z = -18 -x = 3 z – 18 x = -3 z + 18 Eliminate x (-3) -6 x – 3 y – 3 z = -15 (2) 6 x + 4 y – 2 z = -16 y – 5 z = -31 Solution set: {(– 3 z + 18, 5 z – 31, z)} y = 5 z – 31 5 -61 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.
 5. 2 additional example Write the system of linear equations represented by the augmented matrix. Use x, y, z, and if necessary, w for the variables. Then find the solution. x + y + 3 z = 6 y + 7 z = 5 y + 7(9) = 5 z = 9 y + 63 = 5 y = -58 x + (-58) + 3(9) = 6 Solution set: {(37, – 58, 9)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. x – 58 + 27 = 6 x = 37 5 -62
5. 2 additional example Write the system of linear equations represented by the augmented matrix. Use x, y, z, and if necessary, w for the variables. Then find the solution. x + y + 3 z = 6 y + 7 z = 5 y + 7(9) = 5 z = 9 y + 63 = 5 y = -58 x + (-58) + 3(9) = 6 Solution set: {(37, – 58, 9)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. x – 58 + 27 = 6 x = 37 5 -62
 5. 2 add on A chemist has two prepared acid solutions, one of which is 2% acid by volume, the other 7% acid. How many cubic centimeters of each should the chemist mix together to obtain 40 cm 3 of a 3. 2% acid solution? X + Y = 40 2%X + 7%Y = 3. 2%(40) X + Y = 40 2 X + 7 Y = 128 (100) Then solve by either substitution or elimination Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -63
5. 2 add on A chemist has two prepared acid solutions, one of which is 2% acid by volume, the other 7% acid. How many cubic centimeters of each should the chemist mix together to obtain 40 cm 3 of a 3. 2% acid solution? X + Y = 40 2%X + 7%Y = 3. 2%(40) X + Y = 40 2 X + 7 Y = 128 (100) Then solve by either substitution or elimination Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -63
 5. 2 add on In a special diet for a hospital patient, the total amount per meal of food groups A, B, and C must equal 400 g. The diet should include one-third as much of group A as of group B. The sum of the amounts of group A and group C should equal twice the amount of group B. How many grams of each food group should be included? A + B + C = 400 3 A = B 3 A – B = 0 A + C = 2 B A – 2 B + C = 0 Then solve by either substitution or elimination Copyright © 2008 Pearson Addison-Wesley. All rights reserved. A B 5 -64
5. 2 add on In a special diet for a hospital patient, the total amount per meal of food groups A, B, and C must equal 400 g. The diet should include one-third as much of group A as of group B. The sum of the amounts of group A and group C should equal twice the amount of group B. How many grams of each food group should be included? A + B + C = 400 3 A = B 3 A – B = 0 A + C = 2 B A – 2 B + C = 0 Then solve by either substitution or elimination Copyright © 2008 Pearson Addison-Wesley. All rights reserved. A B 5 -64
 5. 2 Summary Matrix Solution of Linear Systems The Gauss-Jordan Method Special Systems Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -65
5. 2 Summary Matrix Solution of Linear Systems The Gauss-Jordan Method Special Systems Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -65
 5. 8 Matrix Inverses Identity Matrices ▪ Multiplicative Inverses ▪ Solving Systems Using Inverse Matrices Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -66
5. 8 Matrix Inverses Identity Matrices ▪ Multiplicative Inverses ▪ Solving Systems Using Inverse Matrices Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -66
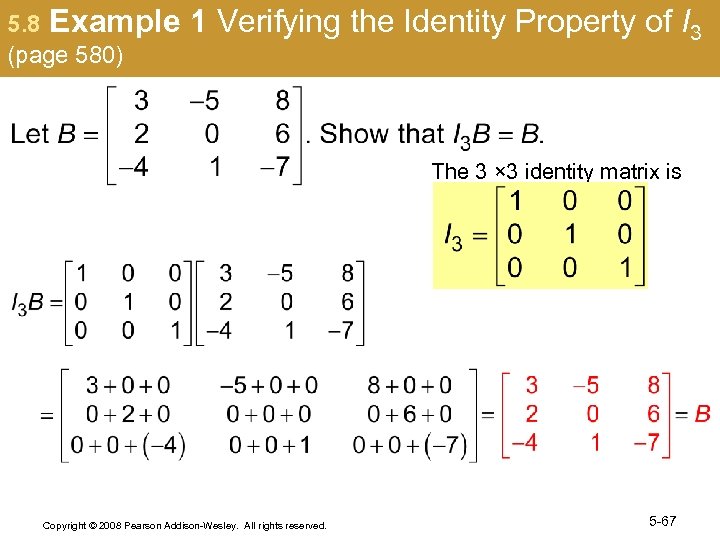 5. 8 Example (page 580) 1 Verifying the Identity Property of I 3 The 3 × 3 identity matrix is Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -67
5. 8 Example (page 580) 1 Verifying the Identity Property of I 3 The 3 × 3 identity matrix is Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -67
 5. 8 Example 2 Finding the Inverse of a 2 x 2 Matrix (page 583) Find A-1 Det [A] = 3(5) – (2)(-1) = 17 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -68
5. 8 Example 2 Finding the Inverse of a 2 x 2 Matrix (page 583) Find A-1 Det [A] = 3(5) – (2)(-1) = 17 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -68
 5. 8 Example 2 Finding the Inverse of a 3 × 3 Matrix (page 583) 1 in first row, first column Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -69
5. 8 Example 2 Finding the Inverse of a 3 × 3 Matrix (page 583) 1 in first row, first column Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -69
 5. 8 Example 2 Finding the Inverse of a 3 × 3 Matrix (page 583) 0 in second row, first column 0 in third row, second column 1 in second row, second column; 1 in third row, third column Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -70
5. 8 Example 2 Finding the Inverse of a 3 × 3 Matrix (page 583) 0 in second row, first column 0 in third row, second column 1 in second row, second column; 1 in third row, third column Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -70
 5. 8 Example 2 Finding the Inverse of a 3 × 3 Matrix (page 583) 0 in second row, third column 0 in first row, second column Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -71
5. 8 Example 2 Finding the Inverse of a 3 × 3 Matrix (page 583) 0 in second row, third column 0 in first row, second column Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -71
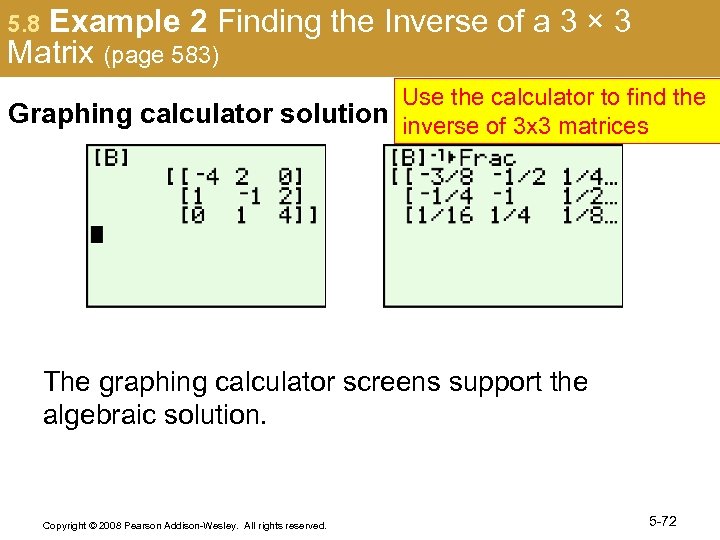 5. 8 Example 2 Finding the Inverse of a 3 × 3 Matrix (page 583) Use the calculator to find the Graphing calculator solution inverse of 3 x 3 matrices The graphing calculator screens support the algebraic solution. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -72
5. 8 Example 2 Finding the Inverse of a 3 × 3 Matrix (page 583) Use the calculator to find the Graphing calculator solution inverse of 3 x 3 matrices The graphing calculator screens support the algebraic solution. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -72
 5. 8 Example 4(a) Solving Systems of Equations Using Matrix Inverses (page 585) Use the inverse of the coefficient matrix to solve the system. Write the system in matrix form. Solution set: {(– 3, 7)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -73
5. 8 Example 4(a) Solving Systems of Equations Using Matrix Inverses (page 585) Use the inverse of the coefficient matrix to solve the system. Write the system in matrix form. Solution set: {(– 3, 7)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -73
 5. 8 Example 4(b) Solving Systems of Equations Using Matrix Inverses (page 585) Use the inverse of the coefficient matrix to solve the system. Write the system in matrix form. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. For these questions you will use elimination method as shown in previous sections … 5 -74
5. 8 Example 4(b) Solving Systems of Equations Using Matrix Inverses (page 585) Use the inverse of the coefficient matrix to solve the system. Write the system in matrix form. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. For these questions you will use elimination method as shown in previous sections … 5 -74
 5. 8 Summary Matrix Inverses Identity Matrices Multiplicative Inverses Solving Systems Using Inverse Matrices Use the calculator to find the inverse of a 3 x 3 matrix Use elimination method to solve a system of equations with 3 variables instead of using the inverse matrix method Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -75
5. 8 Summary Matrix Inverses Identity Matrices Multiplicative Inverses Solving Systems Using Inverse Matrices Use the calculator to find the inverse of a 3 x 3 matrix Use elimination method to solve a system of equations with 3 variables instead of using the inverse matrix method Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -75
 View Example: 5. 1 B #9, 10 Solve the system of equations 6 5 30 30 30 42 x – 6 + 5 y + 50 = 1890 42 x + 5 y = 1846 5 20 -4 20 20 5 x + 5 – 4 x + 4 y = 80 x + 4 y = 75 Original problem Now solve: 42 x + 5 y = 1846 x + 4 y = 75 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Answer: (43, 8) 5 -76
View Example: 5. 1 B #9, 10 Solve the system of equations 6 5 30 30 30 42 x – 6 + 5 y + 50 = 1890 42 x + 5 y = 1846 5 20 -4 20 20 5 x + 5 – 4 x + 4 y = 80 x + 4 y = 75 Original problem Now solve: 42 x + 5 y = 1846 x + 4 y = 75 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. Answer: (43, 8) 5 -76
 5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (page 572) A contractor builds three kinds of houses, models A, B, and C, with a choice of two styles, colonial or ranch. Matrix M shows the number of each kind of house the contractor is planning to build for a new 150 -home subdivision. The amounts for each of the main materials used depend on the style of the house. These amounts are shown in matrix Q, while matrix R gives the cost in dollars for each kind of material. Concrete is measured here in cubic yards, lumber in 1000 board feet, brick in 1000 s, and shingles in 100 square feet. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -77
5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (page 572) A contractor builds three kinds of houses, models A, B, and C, with a choice of two styles, colonial or ranch. Matrix M shows the number of each kind of house the contractor is planning to build for a new 150 -home subdivision. The amounts for each of the main materials used depend on the style of the house. These amounts are shown in matrix Q, while matrix R gives the cost in dollars for each kind of material. Concrete is measured here in cubic yards, lumber in 1000 board feet, brick in 1000 s, and shingles in 100 square feet. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -77
 5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (cont. ) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -78
5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (cont. ) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -78
 5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (cont. ) (a) What is the total cost of materials for all houses of each model? To calculate the total cost of material for all houses of each model, first find MQ, which will show the total amount of each material needed for all houses of each model. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -79
5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (cont. ) (a) What is the total cost of materials for all houses of each model? To calculate the total cost of material for all houses of each model, first find MQ, which will show the total amount of each material needed for all houses of each model. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -79
 5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (cont. ) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -80
5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (cont. ) Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -80
 5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (cont. ) Multiplying MQ and the cost matrix R gives the total cost of material for each model. The cost of materials for model A is $79, 000. For model B, the cost is $69, 900. For model C, the cost is $124, 600. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -81
5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (cont. ) Multiplying MQ and the cost matrix R gives the total cost of material for each model. The cost of materials for model A is $79, 000. For model B, the cost is $69, 900. For model C, the cost is $124, 600. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -81
 5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (cont. ) (b) How much of each of the four kinds of material must be ordered? To find how much of each kind of material to order, total each column of matrix MQ. Write this as a row matrix, 5500 units of concrete, 200 units of lumber, 2000 units of brick and 300 units of shingles must be ordered. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -82
5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (cont. ) (b) How much of each of the four kinds of material must be ordered? To find how much of each kind of material to order, total each column of matrix MQ. Write this as a row matrix, 5500 units of concrete, 200 units of lumber, 2000 units of brick and 300 units of shingles must be ordered. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -82
 5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (cont. ) (c) What is the total cost of the materials? To find the total cost of the materials, find TR. The total cost of the materials is $273, 500. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -83
5. 7 Example 8 Using Matrix Multiplication to Model Plans for a Subdivision (cont. ) (c) What is the total cost of the materials? To find the total cost of the materials, find TR. The total cost of the materials is $273, 500. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -83
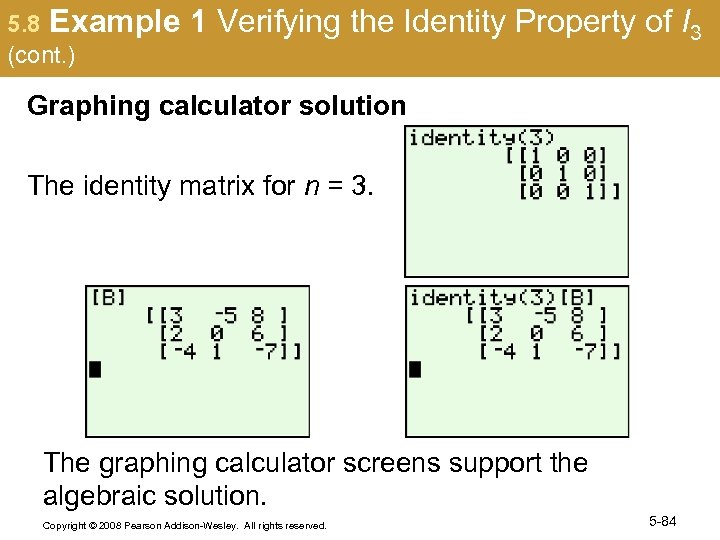 5. 8 Example (cont. ) 1 Verifying the Identity Property of I 3 Graphing calculator solution The identity matrix for n = 3. The graphing calculator screens support the algebraic solution. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -84
5. 8 Example (cont. ) 1 Verifying the Identity Property of I 3 Graphing calculator solution The identity matrix for n = 3. The graphing calculator screens support the algebraic solution. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -84
 5. 8 Example 3 Identifying a Matrix With No Inverse (page 584) Write the augmented matrix : Since there is no way to convert the third element in the third row to a 1, does not exist. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -85
5. 8 Example 3 Identifying a Matrix With No Inverse (page 584) Write the augmented matrix : Since there is no way to convert the third element in the third row to a 1, does not exist. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -85
 5. 8 Example 4(b) Solving Systems of Equations Using Matrix Inverses (cont. ) Find : Write the augmented matrix. 1 in first row, first column 0 in second row, first column Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -86
5. 8 Example 4(b) Solving Systems of Equations Using Matrix Inverses (cont. ) Find : Write the augmented matrix. 1 in first row, first column 0 in second row, first column Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -86
 5. 8 Example 4(b) Solving Systems of Equations Using Matrix Inverses (cont. ) 0 in second row, third column 1 in second row, second column 0 in first row, second column; 0 in third row, second column Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -87
5. 8 Example 4(b) Solving Systems of Equations Using Matrix Inverses (cont. ) 0 in second row, third column 1 in second row, second column 0 in first row, second column; 0 in third row, second column Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -87
 5. 8 Example 4(b) Solving Systems of Equations Using Matrix Inverses (cont. ) 1 in third row, third column Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -88
5. 8 Example 4(b) Solving Systems of Equations Using Matrix Inverses (cont. ) 1 in third row, third column Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -88
 5. 8 Example 4(b) Solving Systems of Equations Using Matrix Inverses (cont. ) Now find : Solution set: {(– 3, 0, 5)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -89
5. 8 Example 4(b) Solving Systems of Equations Using Matrix Inverses (cont. ) Now find : Solution set: {(– 3, 0, 5)} Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -89
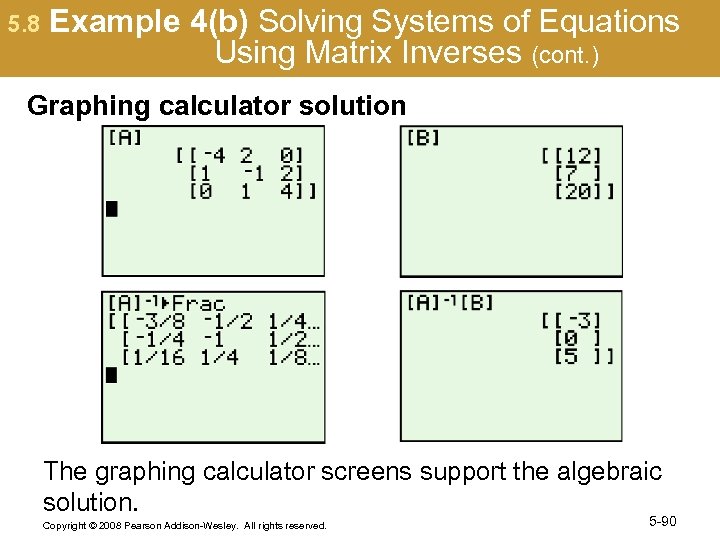 5. 8 Example 4(b) Solving Systems of Equations Using Matrix Inverses (cont. ) Graphing calculator solution The graphing calculator screens support the algebraic solution. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -90
5. 8 Example 4(b) Solving Systems of Equations Using Matrix Inverses (cont. ) Graphing calculator solution The graphing calculator screens support the algebraic solution. Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 5 -90


