5 02 14 1 Верно ли что

5. 02. 14

1. Верно ли, что две прямые, параллельные одной плоскости, перпендикулярны (две прямые, перпендикулярные к одной плоскости, параллельны). 2. Может ли прямая, перпендикулярная к плоскости, скрещиваться с прямой, лежащей в этой плоскости (прямая, перпендикулярная к плоскости, быть параллельна прямой, лежащей в этой плоскости)? 3. Верно ли, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум прямым этой плоскости (она перпендикулярна к двум прямым, параллельным этой плоскости)? 4. Могут ли две скрещивающиеся прямые быть перпендикулярными к одной плоскости (две пересекающиеся прямые быть перпендикулярными к одной плоскости)?

5. Верно ли, что любая из трех взаимно перпендикулярных прямых перпендикулярна к плоскости двух других прямых (две прямые в пространстве, перпендикулярные к третьей прямой, параллельны)? 6. Могут ли пересекаться две плоскости, перпендикулярные к одной прямой ( прямая а и плоскость, перпендикулярные к одной прямой с)? 7. Верно ли, что длина перпендикуляра меньше длины наклонной, проведенной из той же точки (длина перпендикуляра меньше длины проекции наклонной, проведенной из той же точки)?

I уровень. (на « 3» ) Дано: , АС ┴ ВС, SA = SB = SC =10 см; СМ =5 см – медиана. Найти: SM (расстояние от точки S до плоскости (АВС)). II уровень ( на « 4» ) Дано: ABCD – прямоугольник; АК ┴ (АВС), KD= 6 см, КВ = = 7 см, КС = 9 см. Найти: расстояние от точки К до (АВС). III уровень. ( на « 5» ) Дано: АВ = 17 см, АС = 15 см, ВС = 8 см, АМ ┴ (АВС), <А – меньший, АМ = 20 см. Найти: МЕ.

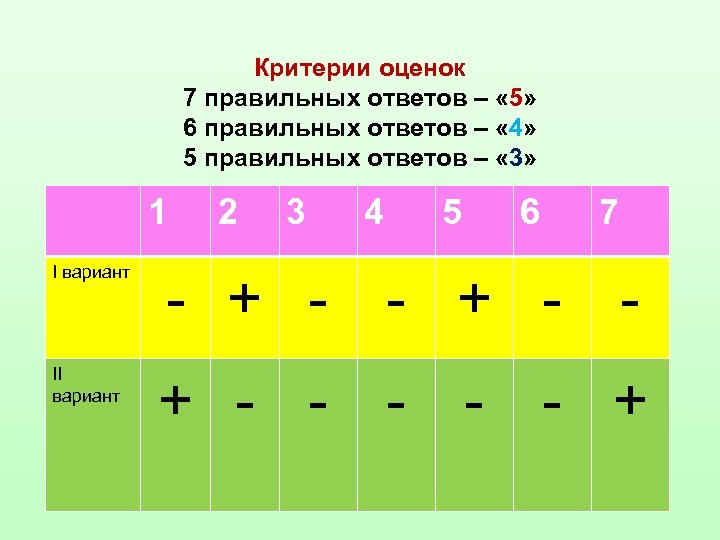Критерии оценок 7 правильных ответов – « 5» 6 правильных ответов – « 4» 5 правильных ответов – « 3» 1 2 3 4 5 6 7 I вариант - + - - II вариант + - - - +

5. 02. 14

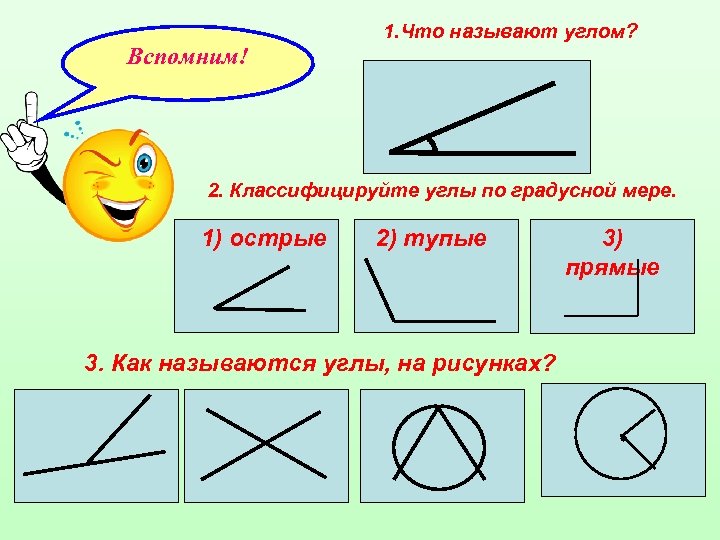1. Что называют углом? Вспомним! 2. Классифицируйте углы по градусной мере. 1) острые 2) тупые 3. Как называются углы, на рисунках? 3) прямые

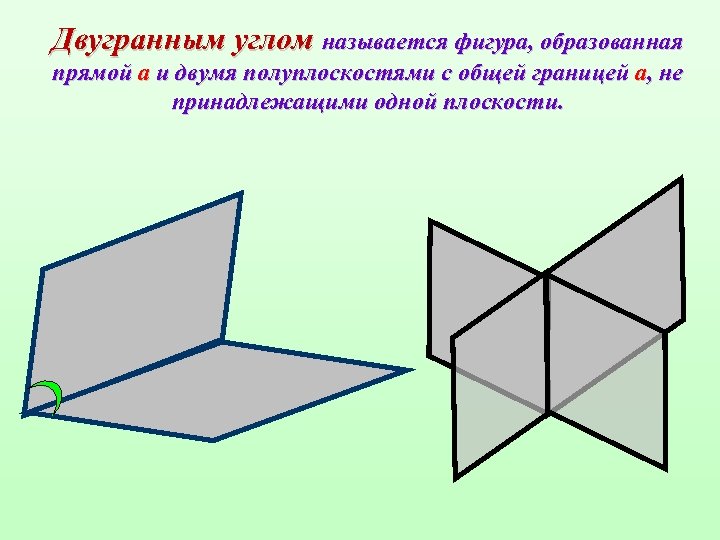Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости.

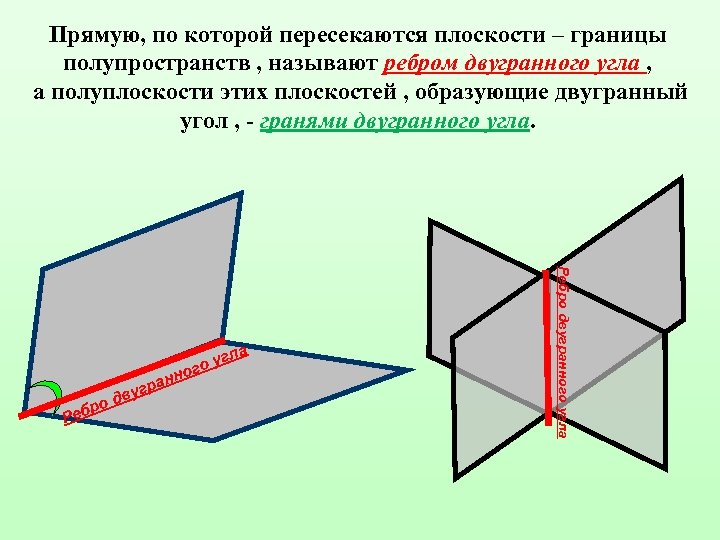Прямую, по которой пересекаются плоскости – границы полупространств , называют ребром двугранного угла , а полуплоскости этих плоскостей , образующие двугранный угол , - гранями двугранного угла. ро Реб нн гра дву Ребро двугранного угла у ого

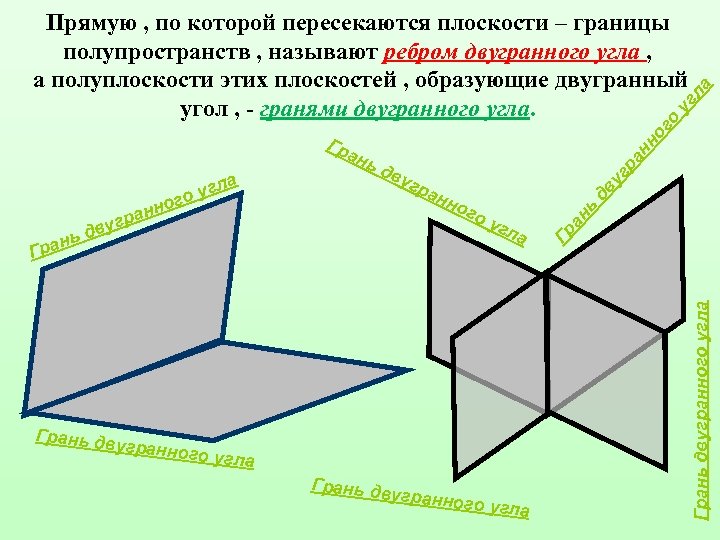Грань дв ан но го дв у гр угл а угранног о угла Грань дв угранног о угла ь г дву ву Грань двугранного угла нь Гра н ран ого а угл ьд ан ан Гр Гр гр ан но го уг ла Прямую , по которой пересекаются плоскости – границы полупространств , называют ребром двугранного угла , а полуплоскости этих плоскостей , образующие двугранный угол , - гранями двугранного угла.

В обыденной жизни, форму двугранного угла имеют

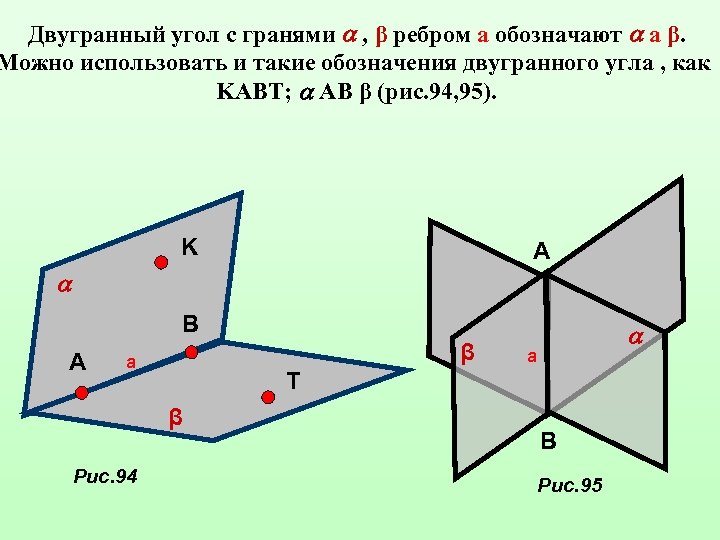Двугранный угол с гранями , β ребром а обозначают а β. Можно использовать и такие обозначения двугранного угла , как KABT; AB β (рис. 94, 95). K A B A β a a T β Рис. 94 B Рис. 95

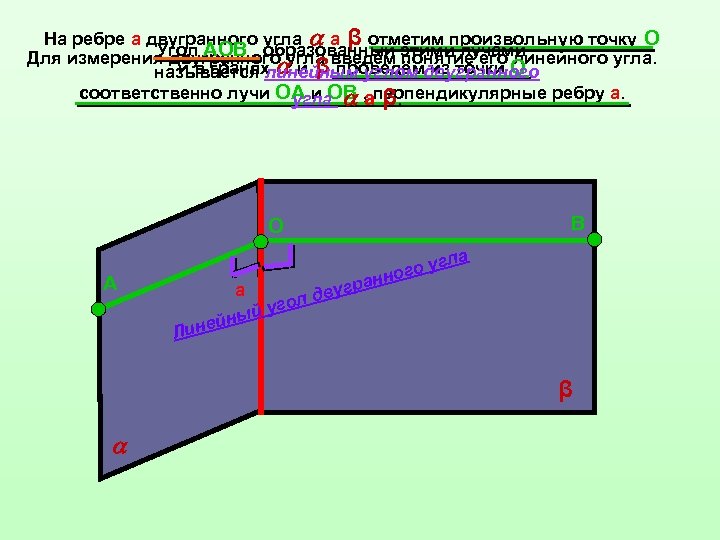На ребре а двугранного угла а β отметим произвольную точку O Угол АОВ , образованный понятие его линейного угла. Для измерения двугранного угла введём этими лучами , и в гранях и β проведём из точки O называется линейным углом двугранного соответственно лучи ОА и ОВ , аперпендикулярные ребру а. угла β. В О ла о уг г анно А Лин р а двуг ол й уг ейны β

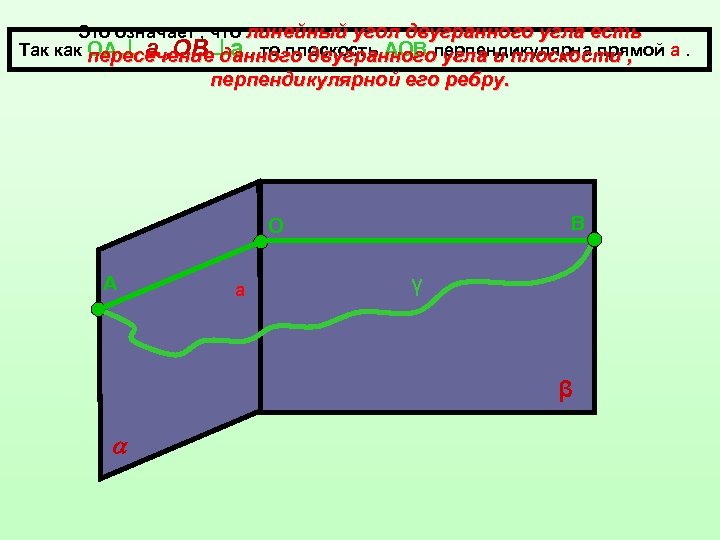Это означает , что линейный угол двугранного угла есть Так как пересечение а , то плоскость АОВ перпендикулярна прямой а. ОА а , ОВ данного двугранного угла и плоскости , перпендикулярной его ребру. В О А а γ β

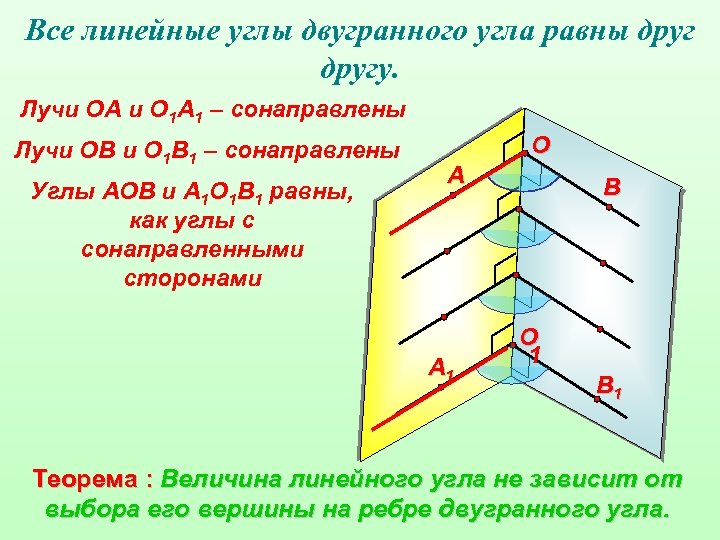Все линейные углы двугранного угла равны другу. Лучи ОА и О 1 А 1 – сонаправлены Лучи ОВ и О 1 В 1 – сонаправлены Углы АОВ и А 1 О 1 В 1 равны, как углы с сонаправленными сторонами O А А 1 В O 1 В 1 Теорема : Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла.

Определение : Величиной двугранного угла называется величина его линейного угла. Величина двугранного угла (измеренная в градусах ) принадлежит промежутку (0°; 180°).

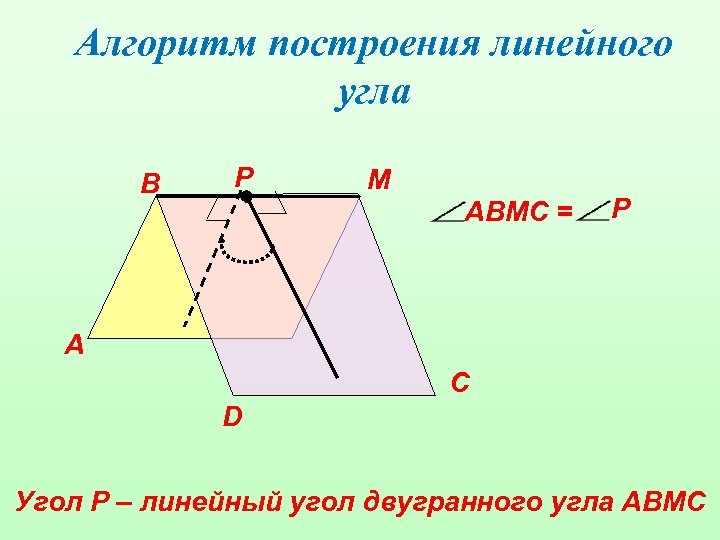Алгоритм построения линейного угла В Р М АВМС = Р А С D Угол Р – линейный угол двугранного угла АВМС

Способ построения линейного угла. 1. Найти ( увидеть) ребро и грани двугранного угла 2. В гранях найти прямые перпендикулярные ребру 3. (при необходимости) заменить выбранные прямые параллельными им лучами с общим началом на ребре двугранного угла При изображении сохраняется параллельность и отношение длин параллельных отрезков

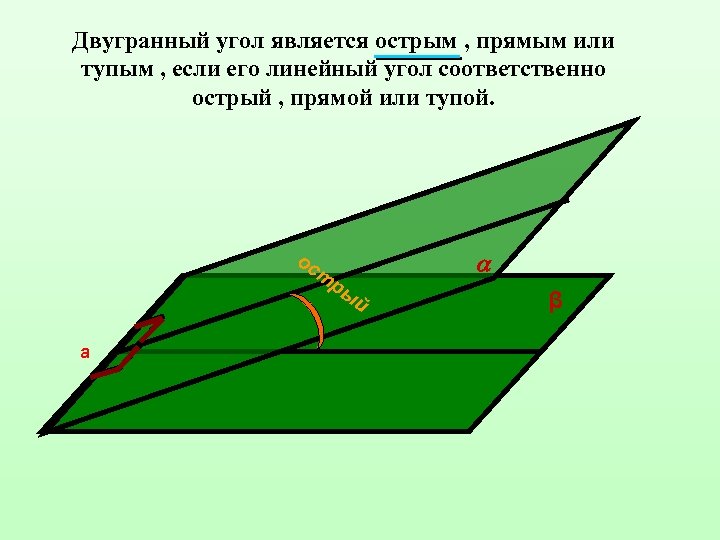Двугранный угол является острым , прямым или тупым , если его линейный угол соответственно острый , прямой или тупой. ос т а ры й β

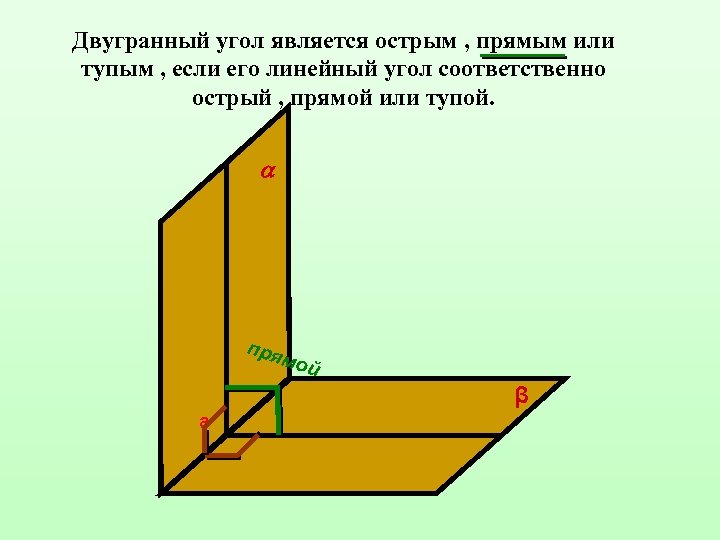Двугранный угол является острым , прямым или тупым , если его линейный угол соответственно острый , прямой или тупой. пря м ой β а

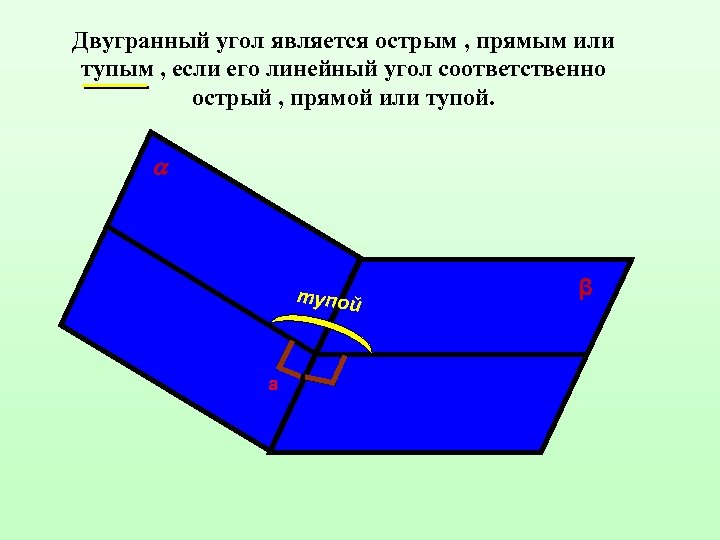Двугранный угол является острым , прямым или тупым , если его линейный угол соответственно острый , прямой или тупой а β

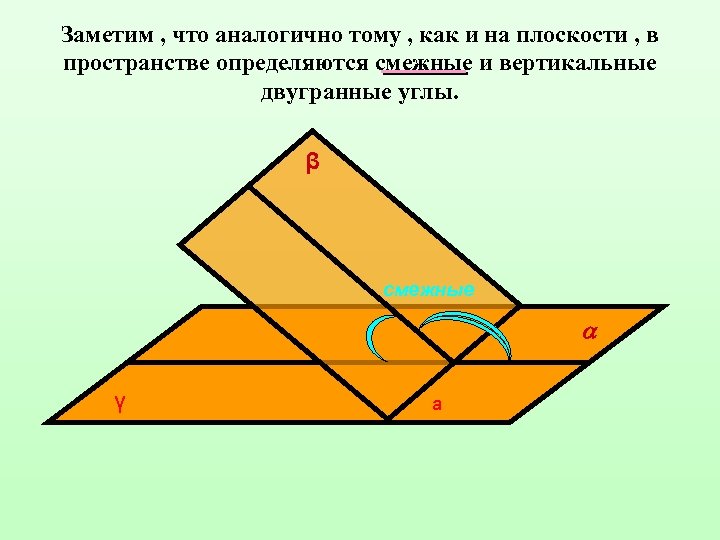Заметим , что аналогично тому , как и на плоскости , в пространстве определяются смежные и вертикальные двугранные углы. β смежные γ а

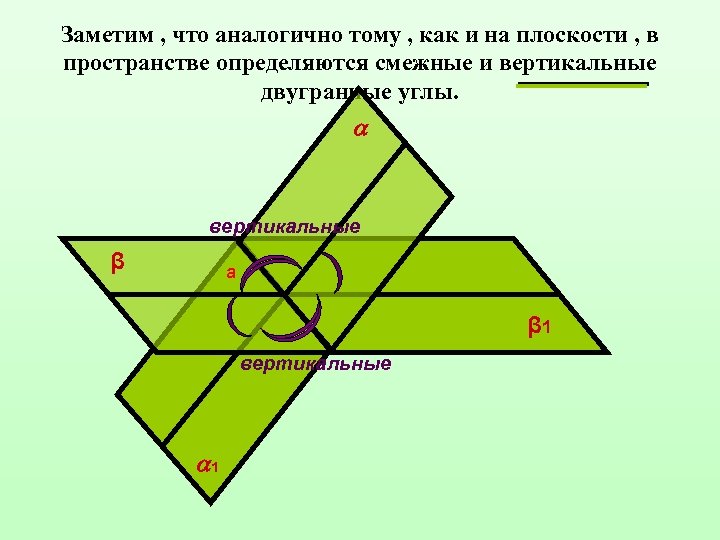Заметим , что аналогично тому , как и на плоскости , в пространстве определяются смежные и вертикальные двугранные углы. вертикальные β а β 1 вертикальные 1

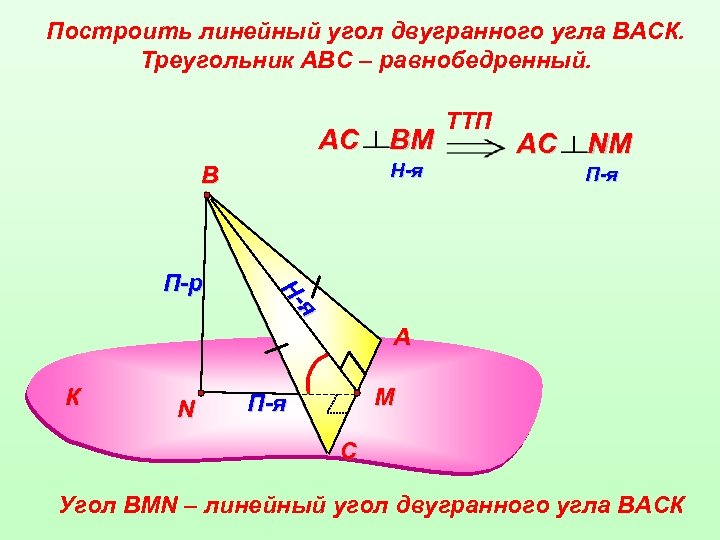Построить линейный угол двугранного угла ВАСК. Треугольник АВС – равнобедренный. АС H-я В АС NМ П-я я я Н-Н П-р ВМ TTП А К N M П-я С Угол ВMN – линейный угол двугранного угла ВАСК

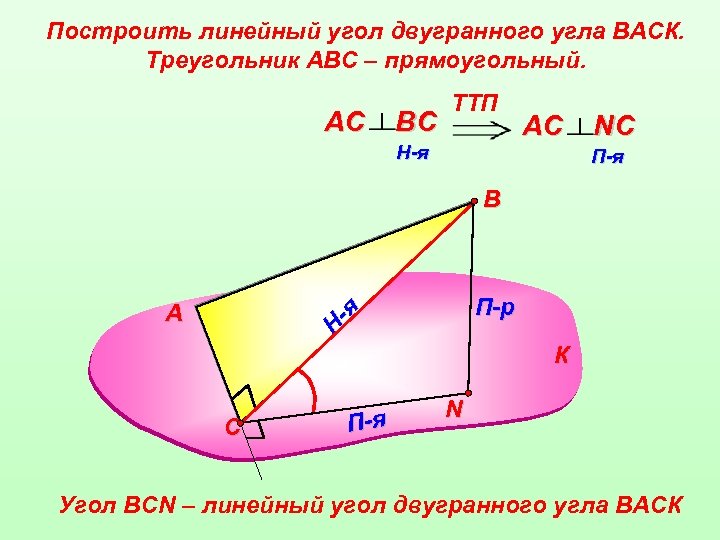Построить линейный угол двугранного угла ВАСК. Треугольник АВС – прямоугольный. АС ВС TTП H-я АС NС П-я В П-р Н -я А К С П-я N Угол ВСN – линейный угол двугранного угла ВАСК

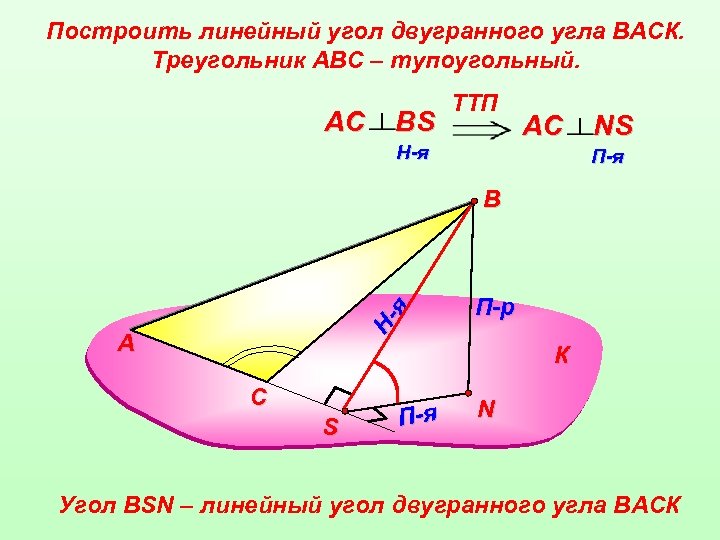Построить линейный угол двугранного угла ВАСК. Треугольник АВС – тупоугольный. АС ВS TTП H-я АС NS П-я Ня В А П-р К С S П-я N Угол ВSN – линейный угол двугранного угла ВАСК

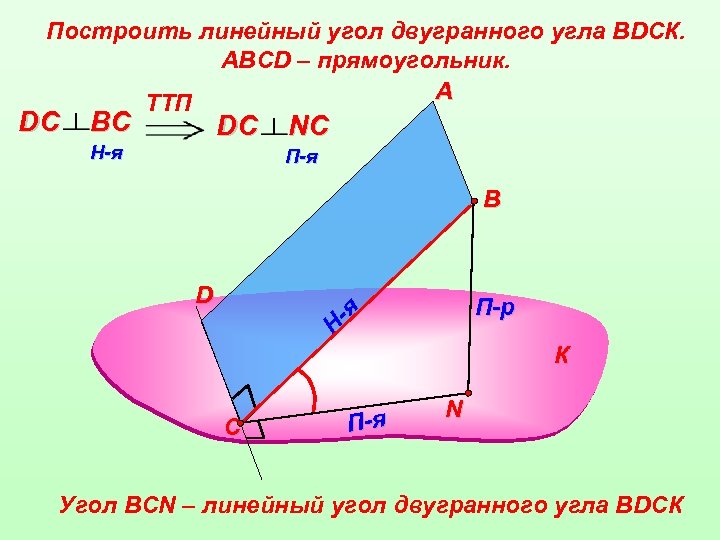Построить линейный угол двугранного угла ВDСК. АВСD – прямоугольник. А TTП DС BС DС H-я NС П-я В П-р Н -я D К С П-я N Угол ВСN – линейный угол двугранного угла ВDСК

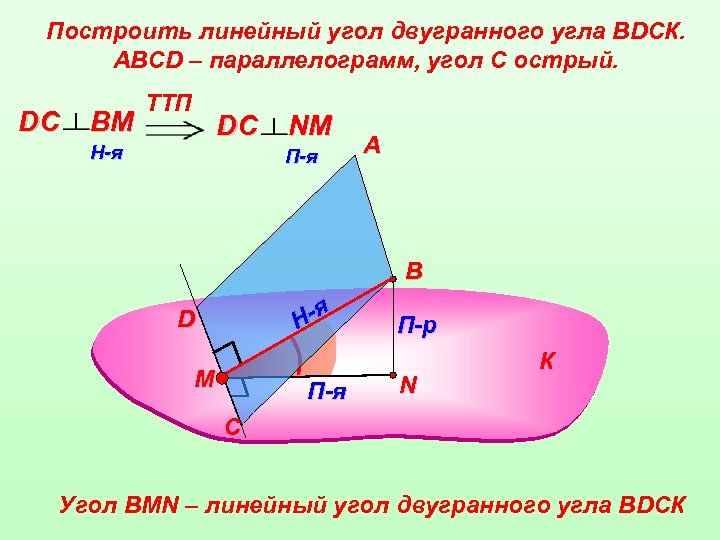Построить линейный угол двугранного угла ВDСК. АВСD – параллелограмм, угол С острый. DС ВM TTП DС H-я NM П-я А В я Н- D M П-я П-р N К С Угол ВMN – линейный угол двугранного угла ВDСК

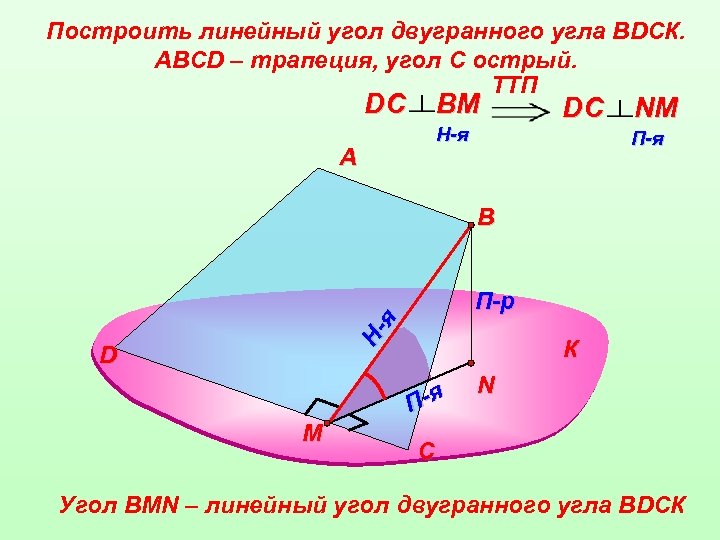Построить линейный угол двугранного угла ВDСК. АВСD – трапеция, угол С острый. TTП DС ВM H-я А DС NM П-я В Ня П-р D К П-я M N С Угол ВMN – линейный угол двугранного угла ВDСК

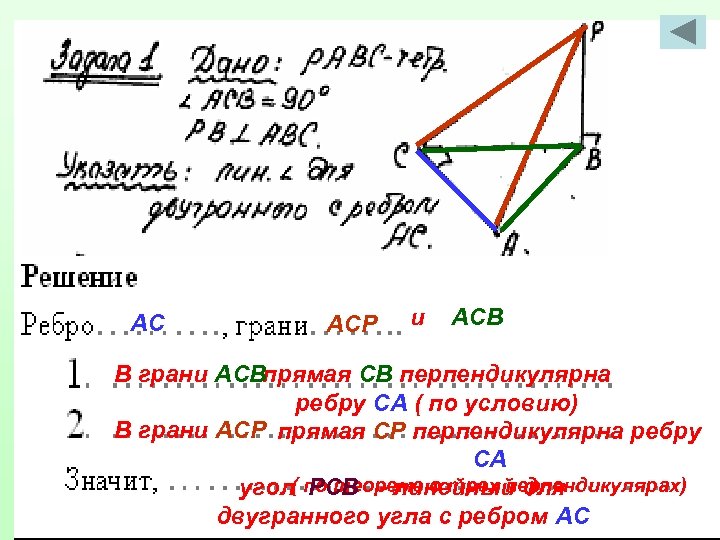АС АСР и АСВ В грани АСВпрямая СВ перпендикулярна ребру СА ( по условию) В грани АСР прямая СР перпендикулярна ребру СА угол( по теореме о трех перпендикулярах) РСВ - линейный для двугранного угла с ребром АС

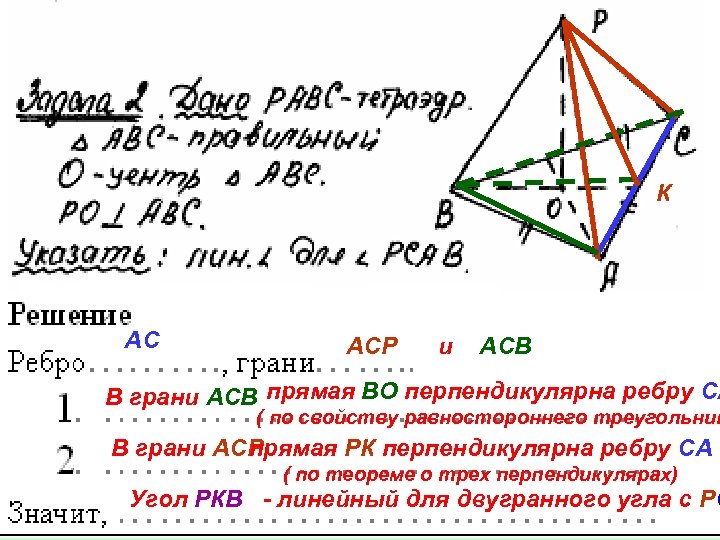К АС АСР и АСВ В грани АСВ прямая ВО перпендикулярна ребру СА ( по свойству равностороннего треугольник В грани АСРрямая РК перпендикулярна ребру СА п ( по теореме о трех перпендикулярах) Угол РКВ - линейный для двугранного угла с РС

№ 167. В тетраэдре DАВС все ребра равны, точка М – середина ребра АС. Докажите, что угол DМВ – линейный угол двугранного угла ВАСD. D А В M С

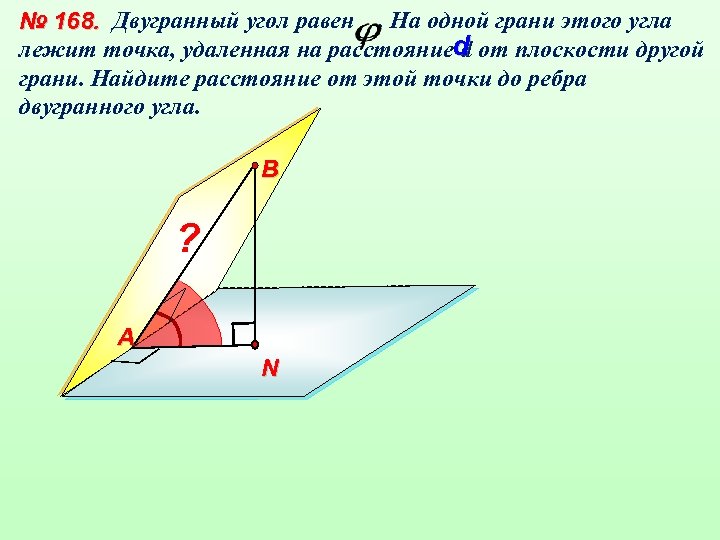№ 168. Двугранный угол равен. На одной грани этого угла лежит точка, удаленная на расстояниеd от плоскости другой d грани. Найдите расстояние от этой точки до ребра двугранного угла. В ? А N

ПОДУМАЙ! 1. В кубе A…D 1 найдите угол между плоскостями ABC и CDD 1. ПРАВИЛЬНО! Ответ:

ПОДУМАЙ! 2. В кубе A…D 1 найдите угол между плоскостями ABC и CDA 1. Ответ: ПРАВИЛЬНО!

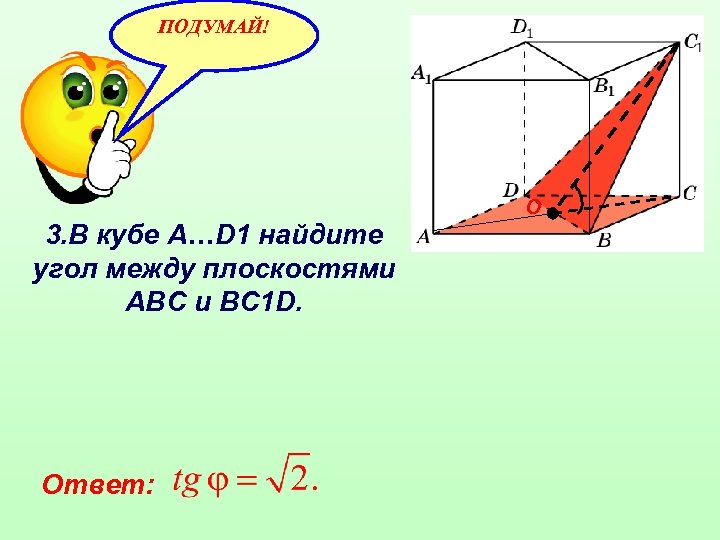ПОДУМАЙ! О 3. В кубе A…D 1 найдите угол между плоскостями ABC и BC 1 D. Ответ:

Определение : Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов , образованных при их пересечении. Угол между параллельными или совпадающими плоскостями полагается равным нулю.

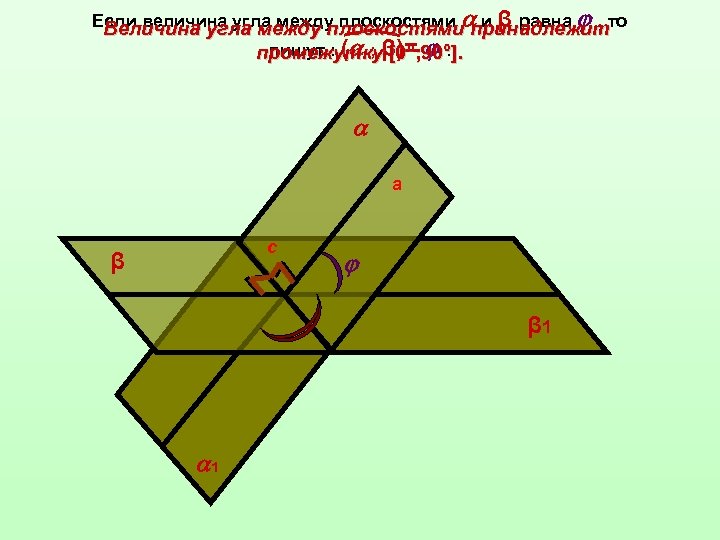Если величина угла между плоскостями и β равна , то Величина угла между плоскостями принадлежит пишут : ( ; [0°; 90° промежуткуβ)= . ]. а с β β 1 1