4 Зубчатые механизмы 4. 1

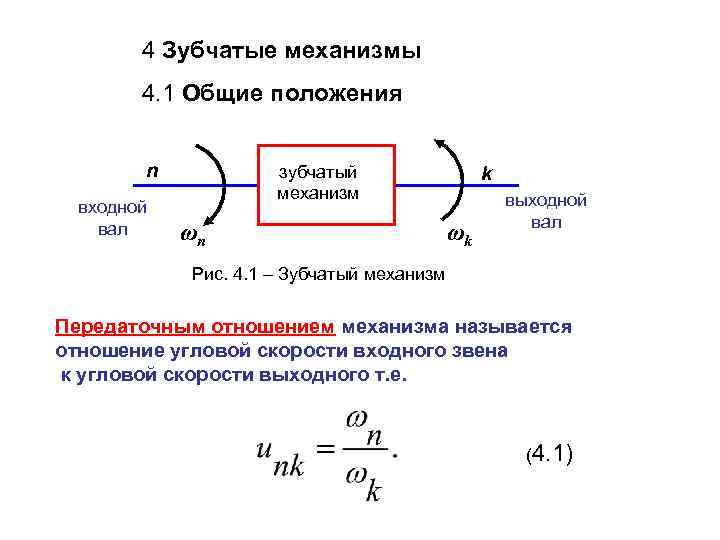
4 Зубчатые механизмы 4. 1 Общие положения n зубчатый k механизм выходной входной вал ωn ωk Рис. 4. 1 – Зубчатый механизм Передаточным отношением механизма называется отношение угловой скорости входного звена к угловой скорости выходного т. е. (4. 1)
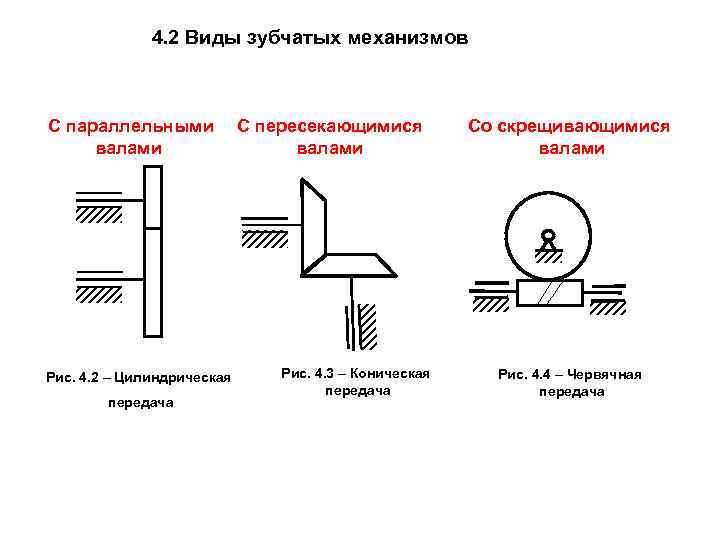
4. 2 Виды зубчатых механизмов С параллельными С пересекающимися Со скрещивающимися валами валами Рис. 4. 2 – Цилиндрическая Рис. 4. 3 – Коническая Рис. 4. 4 – Червячная передача
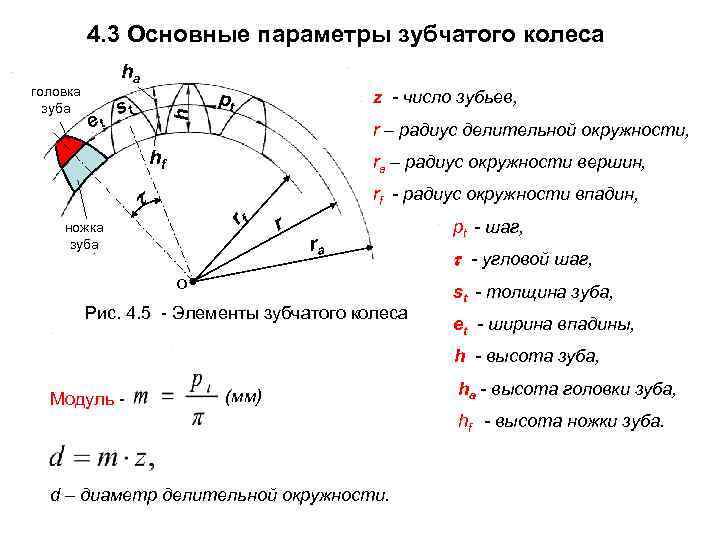
4. 3 Основные параметры зубчатого колеса ha головка pt z - число зубьев, зуба st h et r – радиус делительной окружности, hf ra – радиус окружности вершин, rf - радиус окружности впадин, ножка rf r pt - шаг, зуба ra - угловой шаг, o st - толщина зуба, Рис. 4. 5 - Элементы зубчатого колеса et - ширина впадины, h - высота зуба, (мм) ha - высота головки зуба, Модуль - hf - высота ножки зуба. d – диаметр делительной окружности.
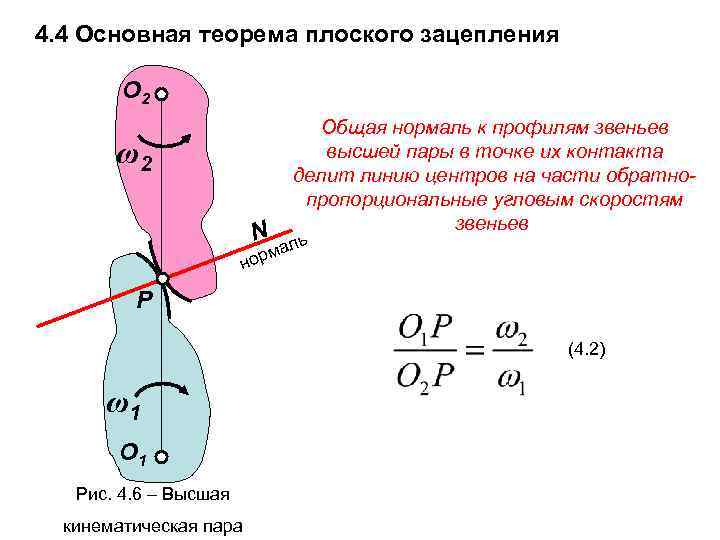
4. 4 Основная теорема плоского зацепления О 2 Общая нормаль к профилям звеньев ω2 высшей пары в точке их контакта делит линию центров на части обратно- пропорциональные угловым скоростям звеньев N ль но рма Р (4. 2) ω1 О 1 Рис. 4. 6 – Высшая кинематическая пара
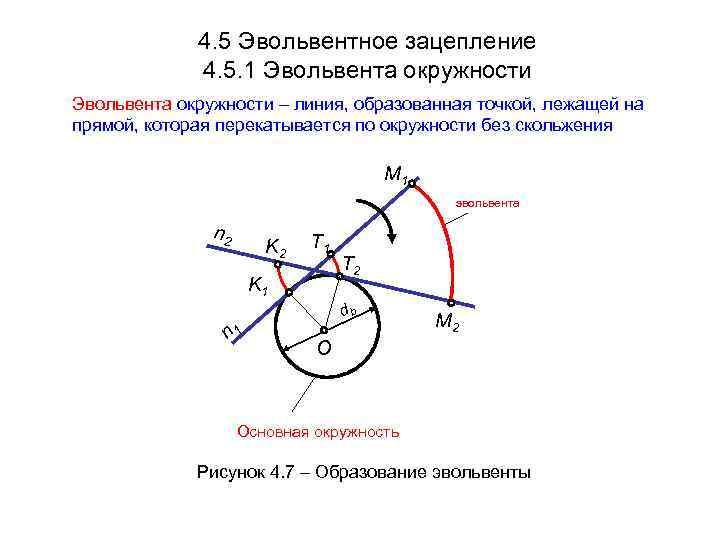
4. 5 Эвольвентное зацепление 4. 5. 1 Эвольвента окружности – линия, образованная точкой, лежащей на прямой, которая перекатывается по окружности без скольжения M 1 эвольвента n 2 T 1 K 2 T 2 K 1 db M 2 1 n O Основная окружность Рисунок 4. 7 – Образование эвольвенты
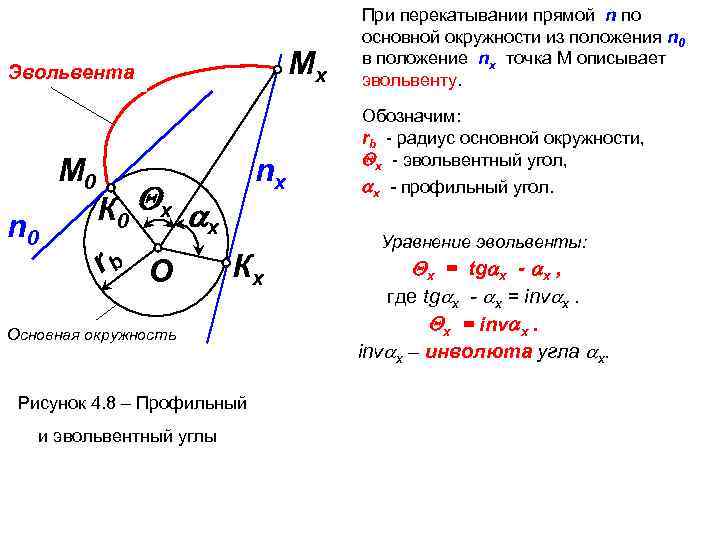
При перекатывании прямой n по основной окружности из положения n 0 Эвольвента Мх в положение nх точка М описывает эвольвенту. Обозначим: rb - радиус основной окружности, х - эвольвентный угол, М 0 nх х - профильный угол. К 0 х х n 0 Уравнение эвольвенты: rb О Кх х = tg х - х , где tg х - х = inv х. Основная окружность х = inv х. inv х – инволюта угла х. Рисунок 4. 8 – Профильный и эвольвентный углы
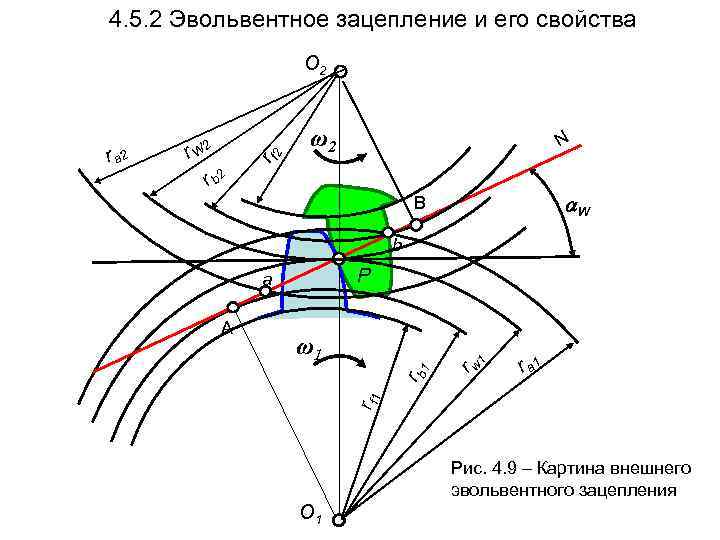
4. 5. 2 Эвольвентное зацепление и его свойства О 2 ω2 N r a 2 r W 2 rf 2 2 rb B W b a Р A ω1 r a 1 rw 1 rb rf 1 Рис. 4. 9 – Картина внешнего эвольвентного зацепления О 1

Обозначим: N – нормаль к профилям зубьев, W – угол зацепления, АВ – линия зацепления, ab – активная линия зацепления, r. W 1 и r. W 2 - радиусы начальных окружностей колёс 1 и 2, rb 1 и rb 2 - радиусы основных окружностей колёс 1 и 2, ra 1 и ra 2 - радиусы окружностей вершин колёс 1 и 2, rf 1 и rf 2 - радиусы окружностей впадин колёс 1 и 2, ω1 и ω2 - угловые скорости колёс 1 и 2,

Свойства эвольвентного зацепления: 1 – Обеспечивает постоянство передаточного отношения при работе передачи, т. е. 2 – Точка контакта зубьев перемещается по линии зацепления АВ на участке ab, который называется активной линией зацепления, 3 – Величина и постоянство передаточного отношения эвольвентной передачи не нарушатся при некотором небольшом изменении межосевого расстояния О 1 О 2 , 4 – Изготовление эвольвентных колёс и инструмента для их нарезания является наиболее простым, что имеет важное практическое значение.

4. 6 Методы нарезания зубчатых колёс 1 – Метод копирования, 2 – Метод обкатки. 4. 6. 1 Метод копирования 1 – Фреза 2 - Заготовка Рис. 4. 10 - Нарезание колеса методом копирования
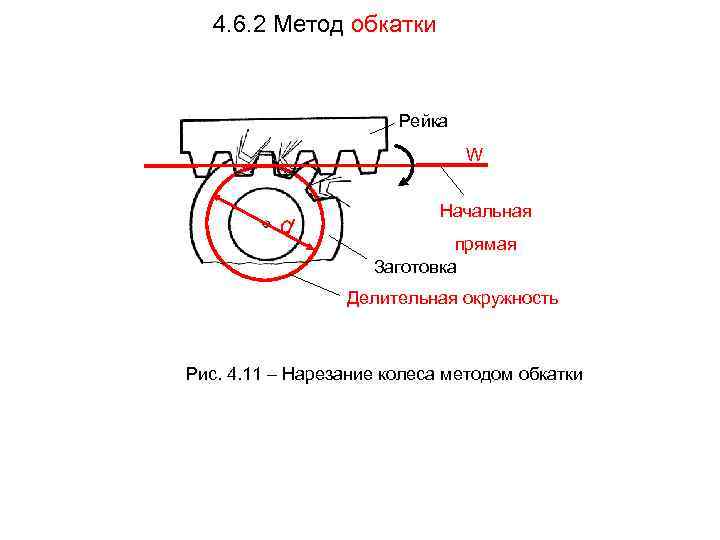
4. 6. 2 Метод обкатки Рейка W Начальная d прямая Заготовка Делительная окружность Рис. 4. 11 – Нарезание колеса методом обкатки
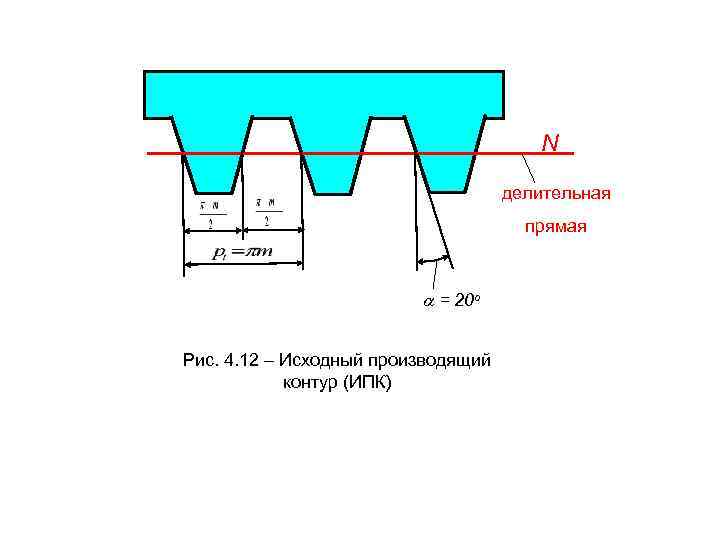
N делительная прямая = 20 o Рис. 4. 12 – Исходный производящий контур (ИПК)
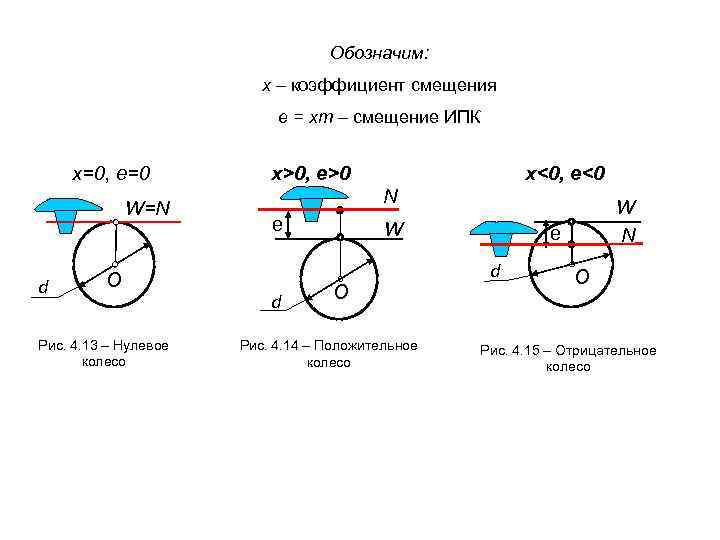
Обозначим: х – коэффициент смещения е = xm – смещение ИПК х=0, e=0 x>0, e>0 x<0, e<0 N W=N W е W е N d О d О Рис. 4. 13 – Нулевое Рис. 4. 14 – Положительное Рис. 4. 15 – Отрицательное колесо колесо
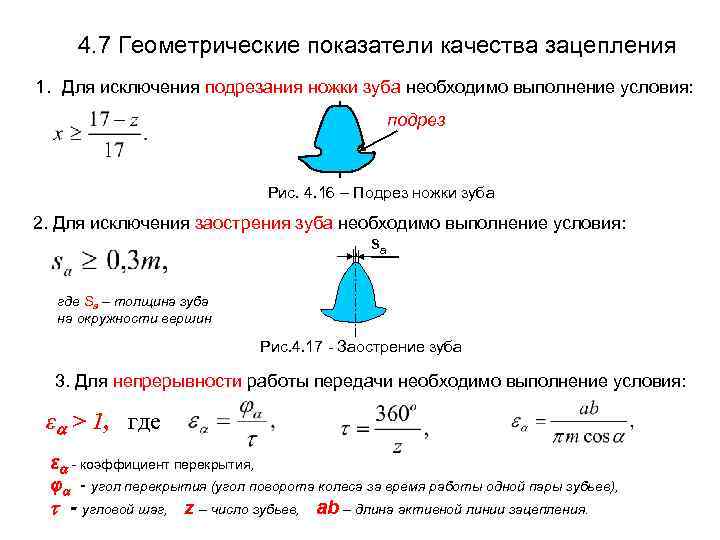
4. 7 Геометрические показатели качества зацепления 1. Для исключения подрезания ножки зуба необходимо выполнение условия: подрез Рис. 4. 16 – Подрез ножки зуба 2. Для исключения заострения зуба необходимо выполнение условия: sa где Sа – толщина зуба на окружности вершин Рис. 4. 17 - Заострение зуба 3. Для непрерывности работы передачи необходимо выполнение условия: ε > 1, где ε - коэффициент перекрытия, φ - угол перекрытия (угол поворота колеса за время работы одной пары зубьев), - угловой шаг, z – число зубьев, ab – длина активной линии зацепления.
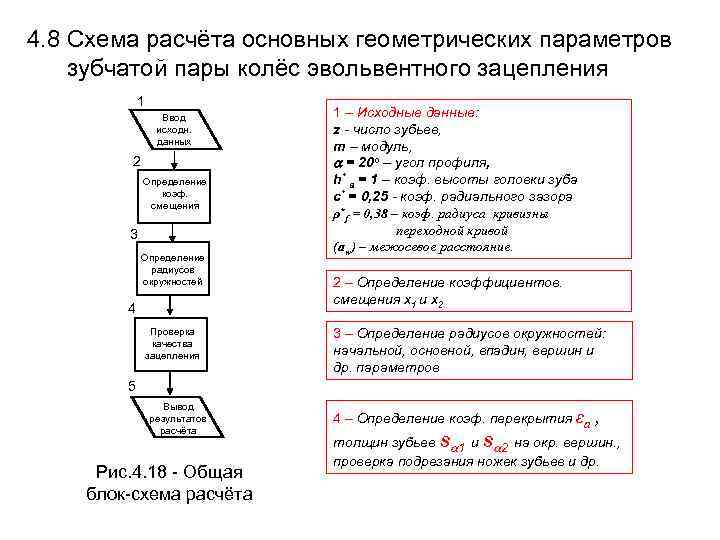
4. 8 Схема расчёта основных геометрических параметров зубчатой пары колёс эвольвентного зацепления 1 Ввод 1 – Исходные данные: исходн. z - число зубьев, данных m – модуль, 2 = 20 о – угол профиля, Определение h* a = 1 – коэф. высоты головки зуба коэф. c* = 0, 25 - коэф. радиального зазора смещения ρ*f = 0, 38 – коэф. радиуса кривизны 3 переходной кривой (аw) – межосевое расстояние. Определение радиусов окружностей 2 – Определение коэффициентов. смещения х1 и х2 4 Проверка 3 – Определение радиусов окружностей: качества зацепления начальной, основной, впадин, вершин и др. параметров 5 Вывод результатов 4 – Определение коэф. перекрытия εа , расчёта толщин зубьев s 1 и s 2 на окр. вершин. , проверка подрезания ножек зубьев и др. Рис. 4. 18 - Общая блок-схема расчёта

Зубы

4. 9 Кинематика многозвенных зубчатых механизмов 4. 9. 1 Зубчатые механизмы с неподвижными осями колёс Основная характеристика – передаточное отношение т. е. отношение угловой скорости входного звена к угловой скорости выходного звена. n зубчатый k механизм входной выходной вал ωn ωk вал Рис. 4. 19 – Зубчатый механизм 1 Скорость точки К 1 : V 1 = r 1 ω1 , r 1 = m z 1 /2 Скорость точки К 2 : V 2 = r 2 ω2 , r 2 = m z 2 /2 ω1 r 1 ω1 = V 1 / r 1 , ω2 = V 2 / r 2 , ¯ V 1 = V 2 , К 1 V 1 u 12 = ω1 / ω2 , К 2 ¯ 2 V u 12 = - z 2 / z 1 , (4. 3) ω2 r 2 Передаточное отношение пары зубчатых колёс 2 равно обратному отношению чисел зубьев колёс. Если направления угловых скоростей колёс одинаковы, то передаточное отношение – Рис. 4. 20 – Зубчатая пара положительно, если нет, то – отрицательно.
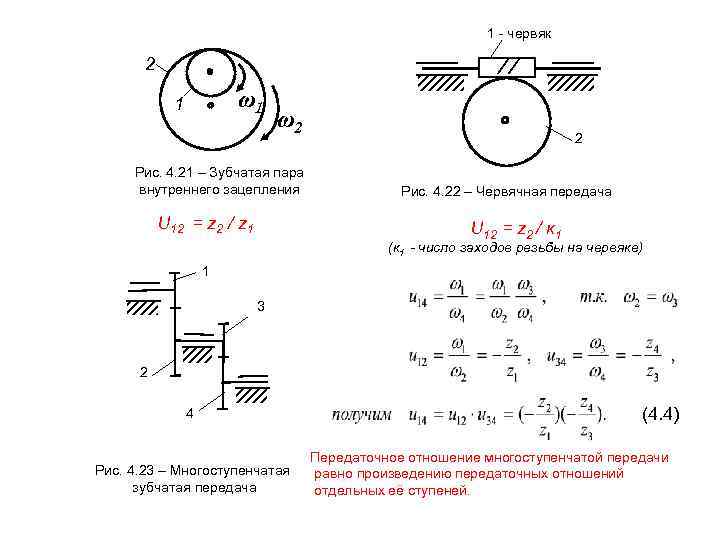
1 - червяк 2 1 ω1 ω2 2 Рис. 4. 21 – Зубчатая пара внутреннего зацепления Рис. 4. 22 – Червячная передача U 12 = z 2 / z 1 U 12 = z 2 / к 1 (к 1 - число заходов резьбы на червяке) 1 3 2 4 (4. 4) Передаточное отношение многоступенчатой передачи Рис. 4. 23 – Многоступенчатая равно произведению передаточных отношений зубчатая передача отдельных её ступеней.

2 (паразитное колесо) 3 1 Рис. 4. 24 – Зубчатая передача с паразитным колесом Число зубьев паразитного колеса не влияет на общее передаточное отношение передачи

4. 9. 2 Дифференциальные зубчатые механизмы Дифференциальный механизм – зубчато-рычажный механизм 2 3 с двумя и более степенями свободы 1 и 4 – центральные колёса ( с неподвижными осями), 4 2 и 3 – сателлиты (колёса с подвижными осями), 1 Н – водило (рычаг, несущий подшипники сателлитов). Н Число степеней свободы дифференциального механизма : W = 3·n – 2·p 1 – p 2 = 3· 4 – 2 = 2, где n = 4 - число подвижных звеньев, p 1 = 4 - число одноподвижных кинематических пар (1 -0, 4 -0, Н-0, 23 -Н), p 2 = 2 - число двухподвижных кинематических пар (1 -2, 3 -4). Рис. 4. 25 – Дифференциальныё зубчатый механизм Зависимость между угловыми скоростями звеньев дифференциального зубчатого механизма 2 3 определяется формулой Виллиса (англ. 1841 г. ) (4. 5) ωn – угловая скорость звена n, 4 ωk – угловая скорость звена k, 1 ωH – угловая скорость водила Н, Н - передаточное отношение обращённого механизма (с неподвижным водилом). Рис. 4. 26 – Обращённый механизм (ωН = 0)

4. 9. 3 Планетарные передачи Планетарной называется передача, полученная из дифференциального механизма, путём остановки одного из центральных колёс Передаточное отношение планетарной передачи определяется из формулы Виллиса (4. 5). Примем ωк = 0. (4. 6) 2 3 4 1 4 1 Н Рис. 4. 27 – Планетарная передача (ω4 = 0) Рис. 4. 28 – Планетарная передача (ω1 = 0)

4. 9. 4 Синтез планетарных передач Синтез планетарной передачи заключается в подборе чисел зубьев колёс передачи для воспроизведения заданного передаточного отношения После выбора схемы передачи числа зубьев колёс необходимо подбирать так, чтобы выполнялись следующие условия: 1. Условие обеспечения заданного передаточного отношения, 2. Условие соосности входного и выходного валов (центральные колёса и водило должны иметь общую геометрическую ось вращения), 3. Условие соседства (соседние сателлиты не должны задевать зубьями друга), 4. Условие сборки (при равных углах между сателлитами их зубья должны находиться в зацеплениях с зубьями центральных колёс, не налагаясь на них, 5. Условие отсутствия интерференции в зацеплениях.
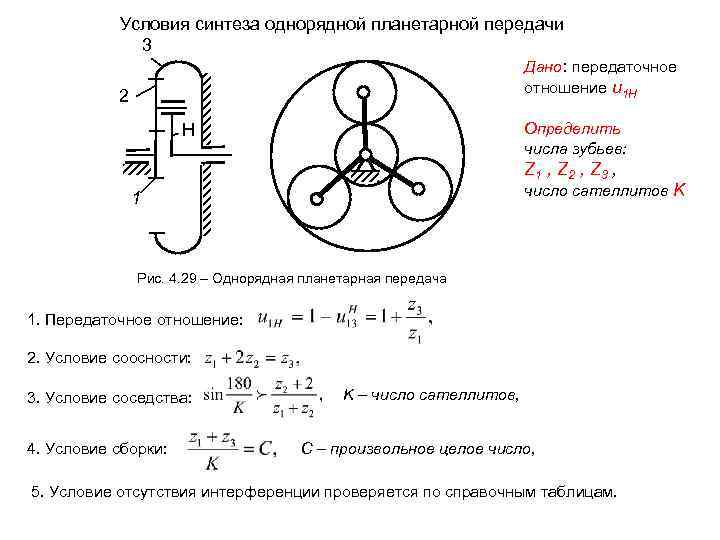
Условия синтеза однорядной планетарной передачи 3 Дано: передаточное отношение u 1 H 2 Н Определить числа зубьев: Z 1 , Z 2 , Z 3 , 1 число сателлитов K Рис. 4. 29 – Однорядная планетарная передача 1. Передаточное отношение: 2. Условие соосности: 3. Условие соседства: K – число сателлитов, 4. Условие сборки: C – произвольное целое число, 5. Условие отсутствия интерференции проверяется по справочным таблицам.
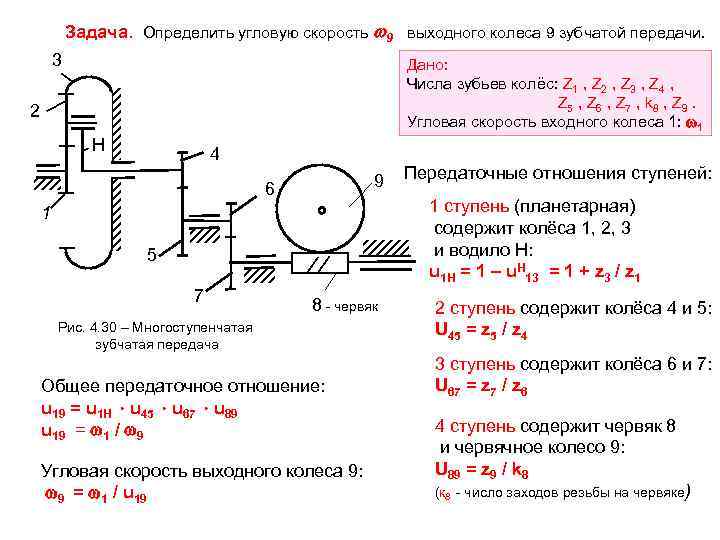
Задача. Определить угловую скорость 9 выходного колеса 9 зубчатой передачи. 3 Дано: Числа зубьев колёс: Z 1 , Z 2 , Z 3 , Z 4 , Z 5 , Z 6 , Z 7 , k 8 , Z 9. 2 Угловая скорость входного колеса 1: 1 Н 4 9 Передаточные отношения ступеней: 6 1 1 ступень (планетарная) содержит колёса 1, 2, 3 5 и водило Н: u 1 H = 1 – u. H 13 = 1 + z 3 / z 1 7 8 - червяк 2 ступень содержит колёса 4 и 5: Рис. 4. 30 – Многоступенчатая U 45 = z 5 / z 4 зубчатая передача 3 ступень содержит колёса 6 и 7: Общее передаточное отношение: U 67 = z 7 / z 6 u 19 = u 1 H u 45 u 67 u 89 u 19 = 1 / 9 4 ступень содержит червяк 8 и червячное колесо 9: Угловая скорость выходного колеса 9: U 89 = z 9 / k 8 9 = 1 / u 19 (к 8 - число заходов резьбы на червяке)

