все лекции.pptx
- Количество слайдов: 184
 4 Тепловое излучение 4. 1 Природа и свойства теплового излучения Тепловое излучение представляет собой электромагнитные волны, испускаемые нагретыми телами за счет энергии теплового движения атомов и молекул. Тепловое излучение характеризуется непрерывным спектром и зависит от температуры тела. При высоких температурах ( Т > 1000 К 0 ) тела в основном излучают короткие (видимые и ультрафиолетовые) волны, при низких температурах – длинные (инфракрасные - ИК).
4 Тепловое излучение 4. 1 Природа и свойства теплового излучения Тепловое излучение представляет собой электромагнитные волны, испускаемые нагретыми телами за счет энергии теплового движения атомов и молекул. Тепловое излучение характеризуется непрерывным спектром и зависит от температуры тела. При высоких температурах ( Т > 1000 К 0 ) тела в основном излучают короткие (видимые и ультрафиолетовые) волны, при низких температурах – длинные (инфракрасные - ИК).
 Тепловое излучение является единственным видом излучения, которое может находиться в равновесии с излучающими телами. В равновесном состоянии тело в единицу времени поглощает столько же энергии, сколько излучает, поэтому температура равновесного теплового излучения равна температуре находящихся с ним в равновесии тел.
Тепловое излучение является единственным видом излучения, которое может находиться в равновесии с излучающими телами. В равновесном состоянии тело в единицу времени поглощает столько же энергии, сколько излучает, поэтому температура равновесного теплового излучения равна температуре находящихся с ним в равновесии тел.
 4. 2 Характеристики теплового излучения Интенсивность теплового излучения описывается потоком излучения Ф, который равен количеству энергии, излучаемому телом в единицу времени. Размерность потока совпадает с размерностью мощности и измеряется в ваттах (Вт). Поток излучения, испускаемый с единицы поверхности тела по всем направлениям в пределах телесного угла 2π (то есть в одну сторону), называется энергетической светимостью R, которая измеряется в единицах Вт/м 2.
4. 2 Характеристики теплового излучения Интенсивность теплового излучения описывается потоком излучения Ф, который равен количеству энергии, излучаемому телом в единицу времени. Размерность потока совпадает с размерностью мощности и измеряется в ваттах (Вт). Поток излучения, испускаемый с единицы поверхности тела по всем направлениям в пределах телесного угла 2π (то есть в одну сторону), называется энергетической светимостью R, которая измеряется в единицах Вт/м 2.
 Тепловое излучение состоит из волн с различными длинами. В узком интервале длин волн от λ до λ +dλ энергетическая светимость пропорциональна ширине этого интервала: d. R = rλ dλ (4. 1) Коэффициент пропорциональности rλ называется спектральной плотностью энергетической светимости. Она равна мощности излучения с единицы поверхности тела в единичном интервале длин волн
Тепловое излучение состоит из волн с различными длинами. В узком интервале длин волн от λ до λ +dλ энергетическая светимость пропорциональна ширине этого интервала: d. R = rλ dλ (4. 1) Коэффициент пропорциональности rλ называется спектральной плотностью энергетической светимости. Она равна мощности излучения с единицы поверхности тела в единичном интервале длин волн
 Cпектральная плотность энергетической светимости измеряется в единицах Вт/м 3. Зависимость rλ от длины волны называется спектром излучения тела. Используют также спектральную плотность энергетической светимости как функцию от частоты rv rv = d. R/dv = (d. R /dλ)(d λ/d v) = rλс/v 2 = rλλ 2/c Знак минус в производной опущен. Если спектр излучения известен, то можно найти энергетическую светимость тела: (4. 3)
Cпектральная плотность энергетической светимости измеряется в единицах Вт/м 3. Зависимость rλ от длины волны называется спектром излучения тела. Используют также спектральную плотность энергетической светимости как функцию от частоты rv rv = d. R/dv = (d. R /dλ)(d λ/d v) = rλс/v 2 = rλλ 2/c Знак минус в производной опущен. Если спектр излучения известен, то можно найти энергетическую светимость тела: (4. 3)
 Способность тела поглощать излучение характеризуется коэффициентом поглощения , равным отношению потока излучения, поглощенного телом, к потоку излучения, упавшего на него: = Фпогл/Фпад (4. 4) Коэффициент поглощения величина безразмерная. Для потоков монохроматического излучения с заданной длиной волны Ф(λ), можно определить монохроматический коэффициент поглощения: λ = Фпогл(λ)/ Фпад (λ) (4. 5)
Способность тела поглощать излучение характеризуется коэффициентом поглощения , равным отношению потока излучения, поглощенного телом, к потоку излучения, упавшего на него: = Фпогл/Фпад (4. 4) Коэффициент поглощения величина безразмерная. Для потоков монохроматического излучения с заданной длиной волны Ф(λ), можно определить монохроматический коэффициент поглощения: λ = Фпогл(λ)/ Фпад (λ) (4. 5)
 Коэффициенты поглощения и λ принимают значения от 0 до 1 в зависимости от природы тела. Модельное тело, которое при любой температуре полностью поглощает падающее на него излучение c любой длиной волны, называется абсолютно черным телом. Коэффициент поглощения абсолютно черного тела при любых длинах волн и температурах равен единице λАчт = 1 Абсолютно черное тело поглощает все падающее на него излучение. Излучение абсолютно черного тела зависит только от его температуры.
Коэффициенты поглощения и λ принимают значения от 0 до 1 в зависимости от природы тела. Модельное тело, которое при любой температуре полностью поглощает падающее на него излучение c любой длиной волны, называется абсолютно черным телом. Коэффициент поглощения абсолютно черного тела при любых длинах волн и температурах равен единице λАчт = 1 Абсолютно черное тело поглощает все падающее на него излучение. Излучение абсолютно черного тела зависит только от его температуры.
 4. 3 Закон Кирхгофа Тепловое излучение является равновесным процессом, поэтому оно должно подчиняться законам термодинамики. Из условий равновесия вытекает связь между величинами λ и rλ. Для ее нахождения рассмотрим замкнутую полость, внутри которой находятся различные тела. Пусть температура полости поддерживается постоянной термостатом, а тела обмениваются энергией между собой и с полостью только путем испускания и поглощения электромагнитного излучения.
4. 3 Закон Кирхгофа Тепловое излучение является равновесным процессом, поэтому оно должно подчиняться законам термодинамики. Из условий равновесия вытекает связь между величинами λ и rλ. Для ее нахождения рассмотрим замкнутую полость, внутри которой находятся различные тела. Пусть температура полости поддерживается постоянной термостатом, а тела обмениваются энергией между собой и с полостью только путем испускания и поглощения электромагнитного излучения.
 Через некоторое время система придет в состояние термодинамического равновесия и все тела примут температуру оболочки. Это значит, что каждое тело независимо от своей формы и состава излучает и поглощает одинаковую энергию при любой длине волны. Отсюда следует, что отношение спектральной плотности энергетической светимости к монохроматическому коэффициенту поглощения одинаково для любых тел и является универсальной функцией длины волны и температуры (закон Кирхгофа) : rλ/ λ = f(λ, T) (4. 6)
Через некоторое время система придет в состояние термодинамического равновесия и все тела примут температуру оболочки. Это значит, что каждое тело независимо от своей формы и состава излучает и поглощает одинаковую энергию при любой длине волны. Отсюда следует, что отношение спектральной плотности энергетической светимости к монохроматическому коэффициенту поглощения одинаково для любых тел и является универсальной функцией длины волны и температуры (закон Кирхгофа) : rλ/ λ = f(λ, T) (4. 6)
 Закон Кирхгофа справедлив для всех тел, в том числе и для абсолютно черного тела, для которого λАчт = 1. Поэтому функция Кирхгофа f(λ, T) равна спектральной плотности энергетической светимости абсолютно черного тела: f (λ, T) = rλ Ачт (4. 7) Из формул (4. 6) и (4. 7) получаем : rλ= λ rλ Ачт (4. 8)
Закон Кирхгофа справедлив для всех тел, в том числе и для абсолютно черного тела, для которого λАчт = 1. Поэтому функция Кирхгофа f(λ, T) равна спектральной плотности энергетической светимости абсолютно черного тела: f (λ, T) = rλ Ачт (4. 7) Из формул (4. 6) и (4. 7) получаем : rλ= λ rλ Ачт (4. 8)

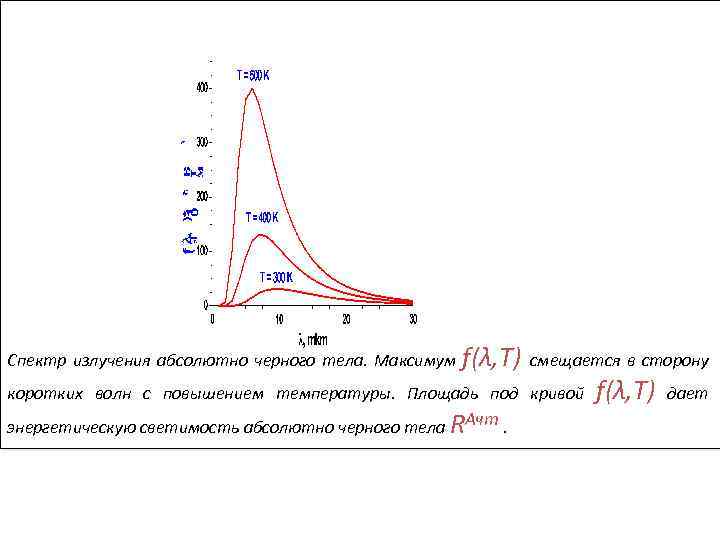 Спектр излучения абсолютно черного тела. Максимум f(λ, T) смещается в сторону коротких волн с повышением температуры. Площадь под кривой энергетическую светимость абсолютно черного тела RАчт. f(λ, T) дает
Спектр излучения абсолютно черного тела. Максимум f(λ, T) смещается в сторону коротких волн с повышением температуры. Площадь под кривой энергетическую светимость абсолютно черного тела RАчт. f(λ, T) дает
 4. 4 Классическая формула излучения В 1900 -1905 г. Релей и Джинс на основе классической теории получили функцию Кирхгофа f(λ, T). Они рассматривали АЧТ как полость, состоящую из гармонических осцилляторов, имеющих среднюю энергию <ε>кл = k. T Число осцилляторов, приходящихся на единичный интервал длин волн и единицу объема излучающей, замкнутой полости равно 4 /λ 4. Осцилляторы испускают электромагнитные волны с двумя взаимно перпендикулярными направлениями поляризации, поэтому плотность энергии излучения надо удвоить и она будет равна <ε>кл 8 /λ 4.
4. 4 Классическая формула излучения В 1900 -1905 г. Релей и Джинс на основе классической теории получили функцию Кирхгофа f(λ, T). Они рассматривали АЧТ как полость, состоящую из гармонических осцилляторов, имеющих среднюю энергию <ε>кл = k. T Число осцилляторов, приходящихся на единичный интервал длин волн и единицу объема излучающей, замкнутой полости равно 4 /λ 4. Осцилляторы испускают электромагнитные волны с двумя взаимно перпендикулярными направлениями поляризации, поэтому плотность энергии излучения надо удвоить и она будет равна <ε>кл 8 /λ 4.
 Если умножить эту величину на скорость света, то получим поток излучения, распространяющийся в направлении, перпендикулярном к поверхности полости <ε>кл 8 с/λ 4 В действительности, излучение идет под разными углами во всех направлениях в пределах телесного угла 2π. Усреднение по направлениям уменьшает поток излучения в 4 раза и он становится равным <ε>кл 2 с/λ 4 Полученная величина и является спектральной плотностью энергетической светимости АЧТ, а поэтому и функцией Кирхгофа формула Релея-Джинса fкл(λ, T)= 2πсk. T/λ 4 (4. 9)
Если умножить эту величину на скорость света, то получим поток излучения, распространяющийся в направлении, перпендикулярном к поверхности полости <ε>кл 8 с/λ 4 В действительности, излучение идет под разными углами во всех направлениях в пределах телесного угла 2π. Усреднение по направлениям уменьшает поток излучения в 4 раза и он становится равным <ε>кл 2 с/λ 4 Полученная величина и является спектральной плотностью энергетической светимости АЧТ, а поэтому и функцией Кирхгофа формула Релея-Джинса fкл(λ, T)= 2πсk. T/λ 4 (4. 9)
 Из формулы Релея-Джинса (4. 9) следует, что для очень коротких волн АЧТ должно излучать неограниченную энергию, вся излучаемая им энергия тоже будет бесконечной. Однако, это противоречит эксперименту – ультрафиолетовая катастрофа.
Из формулы Релея-Джинса (4. 9) следует, что для очень коротких волн АЧТ должно излучать неограниченную энергию, вся излучаемая им энергия тоже будет бесконечной. Однако, это противоречит эксперименту – ультрафиолетовая катастрофа.
 4. 5 Квантовая теория излучения Анализируя накопленные результаты по излучению АЧТ, Планк в 1900 г. пришел к выводу, что для объяснения экспериментальной кривой f(λ, T) необходимо считать, что электромагнитное излучение испускается и поглощается не непрерывно, а дискретными порциями (квантами или фотонами). Минимальная энергия одного кванта равна ε = hv Энергии других порций излучения εn кратны этой величине: εn = nhv, (n = 0, 1, 2, …) -34
4. 5 Квантовая теория излучения Анализируя накопленные результаты по излучению АЧТ, Планк в 1900 г. пришел к выводу, что для объяснения экспериментальной кривой f(λ, T) необходимо считать, что электромагнитное излучение испускается и поглощается не непрерывно, а дискретными порциями (квантами или фотонами). Минимальная энергия одного кванта равна ε = hv Энергии других порций излучения εn кратны этой величине: εn = nhv, (n = 0, 1, 2, …) -34
 Состояния осцилляторов с разными энергиями реализуются с разными вероятностями. В равновесном состоянии вероятности осцилляторов подчиняются распределению Больцмана: Поэтому среднее значение энергии одного колебания равно: Суммируя геометрическую прогрессию, получаем : (4. 10)
Состояния осцилляторов с разными энергиями реализуются с разными вероятностями. В равновесном состоянии вероятности осцилляторов подчиняются распределению Больцмана: Поэтому среднее значение энергии одного колебания равно: Суммируя геометрическую прогрессию, получаем : (4. 10)
 В пределе h 0 средняя энергия квантового осциллятора (4. 10) переходит в среднюю энергию классического осциллятора <ε>кл = k. T. Умножая (4. 10) на прежнее число осцилляторов 2πс/λ 4 и выражая частоту v через длину волны, получаем функцию Кирхгофа в виде формула Планка (4. 11) В пределе длинных волн эта формула переходит в формулу Релея-Джинса.
В пределе h 0 средняя энергия квантового осциллятора (4. 10) переходит в среднюю энергию классического осциллятора <ε>кл = k. T. Умножая (4. 10) на прежнее число осцилляторов 2πс/λ 4 и выражая частоту v через длину волны, получаем функцию Кирхгофа в виде формула Планка (4. 11) В пределе длинных волн эта формула переходит в формулу Релея-Джинса.
 4. 6 Законы излучения абсолютно черного тела Из формулы Планка следуют законы, которые были установлены в экспериментальных исследованиях. Найдем максимум функции Кирхгофа f( , T). Из условия экстремума функции получается трансцендентное уравнение решением которого является xmax 4. 965
4. 6 Законы излучения абсолютно черного тела Из формулы Планка следуют законы, которые были установлены в экспериментальных исследованиях. Найдем максимум функции Кирхгофа f( , T). Из условия экстремума функции получается трансцендентное уравнение решением которого является xmax 4. 965
 Отсюда находим связь между температурой и длиной волны, соответствующей максимуму спектральной плотности закон смещения Вина max = b/T (4. 12) - постоянная Вина. Из (4. 12) следует, что максимум излучения АЧТ с ростом температуры сдвигается в сторону коротких волн. Поэтому при нагревании тел их цвет меняется от темно-красного до голубого.
Отсюда находим связь между температурой и длиной волны, соответствующей максимуму спектральной плотности закон смещения Вина max = b/T (4. 12) - постоянная Вина. Из (4. 12) следует, что максимум излучения АЧТ с ростом температуры сдвигается в сторону коротких волн. Поэтому при нагревании тел их цвет меняется от темно-красного до голубого.

 Таким образом, энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его
Таким образом, энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его
 5. Фотоэффектом называется испускание электронов веществом под действием света. Явление было открыто в 1887 г. Герцем. В 1888 1889 гг. Столетов установил, что : 1) испускаемые под действием света заряды имеют отрицательный знак 2) наибольшее действие оказывают ультрафиолетовые лучи 3) величина испущенного телом заряда пропорциональна поглощенной им световой энергии
5. Фотоэффектом называется испускание электронов веществом под действием света. Явление было открыто в 1887 г. Герцем. В 1888 1889 гг. Столетов установил, что : 1) испускаемые под действием света заряды имеют отрицательный знак 2) наибольшее действие оказывают ультрафиолетовые лучи 3) величина испущенного телом заряда пропорциональна поглощенной им световой энергии
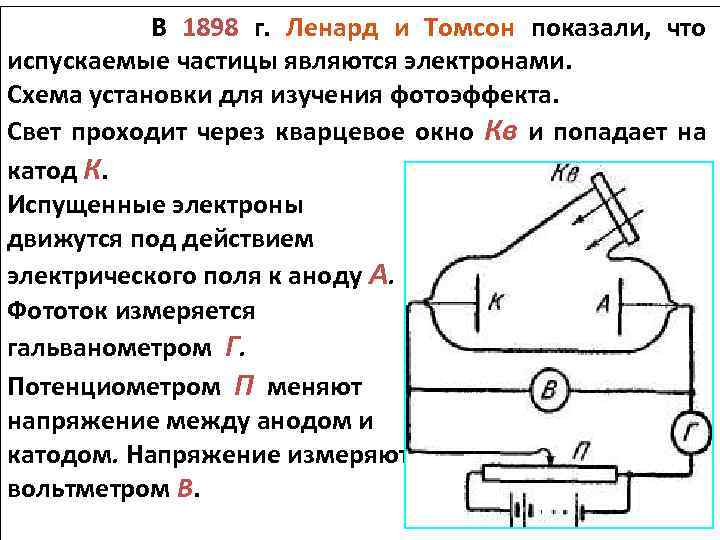 В 1898 г. Ленард и Томсон показали, что испускаемые частицы являются электронами. Схема установки для изучения фотоэффекта. Свет проходит через кварцевое окно Кв и попадает на катод К. Испущенные электроны движутся под действием электрического поля к аноду А. Фототок измеряется гальванометром Г. Потенциометром П меняют напряжение между анодом и катодом. Напряжение измеряют вольтметром В.
В 1898 г. Ленард и Томсон показали, что испускаемые частицы являются электронами. Схема установки для изучения фотоэффекта. Свет проходит через кварцевое окно Кв и попадает на катод К. Испущенные электроны движутся под действием электрического поля к аноду А. Фототок измеряется гальванометром Г. Потенциометром П меняют напряжение между анодом и катодом. Напряжение измеряют вольтметром В.
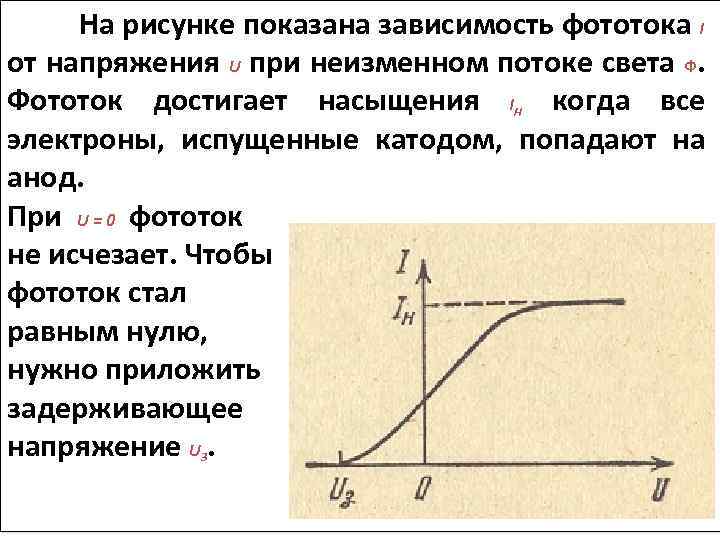 На рисунке показана зависимость фототока I от напряжения U при неизменном потоке света Ф. Фототок достигает насыщения I когда все электроны, испущенные катодом, попадают на анод. При U = 0 фототок не исчезает. Чтобы фототок стал равным нулю, нужно приложить задерживающее напряжение U. Н 3
На рисунке показана зависимость фототока I от напряжения U при неизменном потоке света Ф. Фототок достигает насыщения I когда все электроны, испущенные катодом, попадают на анод. При U = 0 фототок не исчезает. Чтобы фототок стал равным нулю, нужно приложить задерживающее напряжение U. Н 3
 При напряжении U ни один электрон, даже обладающий максимальной скоростью max , не может преодолеть задерживающее поле и достигнуть анод. Поэтому можно написать 3 (5. 1) где т - масса электрона. Таким образом, измерив задерживающее напряжение U , можно определить максимальное значение скорости фото электронов max. 3
При напряжении U ни один электрон, даже обладающий максимальной скоростью max , не может преодолеть задерживающее поле и достигнуть анод. Поэтому можно написать 3 (5. 1) где т - масса электрона. Таким образом, измерив задерживающее напряжение U , можно определить максимальное значение скорости фото электронов max. 3
 Экспериментально были установлены основные законы фотоэффекта: 1) Фототок насыщения пропорционален падающему световому потоку 2) Для каждого металла существует максимальная длина волны λкр (красная граница фотоэффекта), при которой еще происходит вырывание электронов. Если же длина волны больше λкр, то испускание фотоэлектронов отсутствует даже при большой интенсивности света. 3) Максимальная кинетическая энергия Тmax фотоэлектронов линейно зависит от частоты облучающего света и не зависит от интенсивности света. 4) Фотоэффект возникает почти мгновенно после освещения (< 10 9 c). Кроме 1 закона волновая теория света объяснить остальные законы не смогла.
Экспериментально были установлены основные законы фотоэффекта: 1) Фототок насыщения пропорционален падающему световому потоку 2) Для каждого металла существует максимальная длина волны λкр (красная граница фотоэффекта), при которой еще происходит вырывание электронов. Если же длина волны больше λкр, то испускание фотоэлектронов отсутствует даже при большой интенсивности света. 3) Максимальная кинетическая энергия Тmax фотоэлектронов линейно зависит от частоты облучающего света и не зависит от интенсивности света. 4) Фотоэффект возникает почти мгновенно после освещения (< 10 9 c). Кроме 1 закона волновая теория света объяснить остальные законы не смогла.
 В 1905 г. Эйнштейн объяснил законы фотоэффекта предположив, что свет представляет собой совокупность квантов фотонов, энергии которых равны ε = h При поглощении фотона его энергия мгновенно и целиком передается одному электрону, которая частично затрачивается на освобождение электрона из металла, а остальная часть переходит в кинетическую энергию электрона. Из закона сохранения энергии h =А+ Тmax где А – работа выхода металла – минимальная энергия, необходимая для освобождения электрона из металла.
В 1905 г. Эйнштейн объяснил законы фотоэффекта предположив, что свет представляет собой совокупность квантов фотонов, энергии которых равны ε = h При поглощении фотона его энергия мгновенно и целиком передается одному электрону, которая частично затрачивается на освобождение электрона из металла, а остальная часть переходит в кинетическую энергию электрона. Из закона сохранения энергии h =А+ Тmax где А – работа выхода металла – минимальная энергия, необходимая для освобождения электрона из металла.
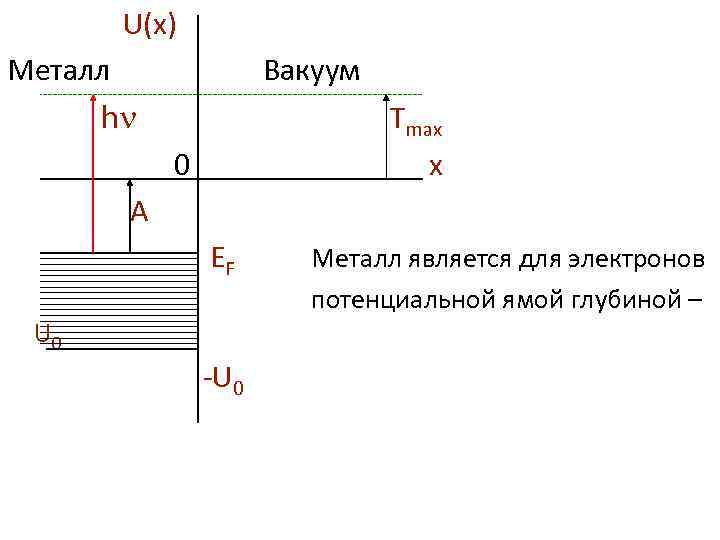 U(x) Металл Вакуум h Тmax 0 x A EF Металл является для электронов потенциальной ямой глубиной – U 0 -U 0
U(x) Металл Вакуум h Тmax 0 x A EF Металл является для электронов потенциальной ямой глубиной – U 0 -U 0
 Из формулы Эйнштейна вытекают все законы фотоэффекта. Если ε = h < A, то электроны не могут выйти из металла. Минимальная частота света, при которой фотоэффект возможен кр = A/h Отсюда максимальная длина волны (красная граница фотоэффекта) λкр = hс/A
Из формулы Эйнштейна вытекают все законы фотоэффекта. Если ε = h < A, то электроны не могут выйти из металла. Минимальная частота света, при которой фотоэффект возможен кр = A/h Отсюда максимальная длина волны (красная граница фотоэффекта) λкр = hс/A
 Пример. Для цезия А = 1. 8 э. В. Найдем длину волны света, выбивающего из металла электроны с максимальной кинетической энергией 2 э. В. Из Тmax = h – A находим частоту Тогда
Пример. Для цезия А = 1. 8 э. В. Найдем длину волны света, выбивающего из металла электроны с максимальной кинетической энергией 2 э. В. Из Тmax = h – A находим частоту Тогда
 Эффект Комптона Фотон с энергией Е = h обладает импульсом р = Е/с = h /c = h/λ При фотоэффекте импульс фотона передается всему образцу и испущенному электрону. Приобретенный образцом импульс слишком мал и не поддается измерению. Но при столкновении фотона со свободным электроном величину передаваемого импульса можно измерить. Этот процесс – рассеяние фотона на свободном электроне – называется эффектом Комптона.
Эффект Комптона Фотон с энергией Е = h обладает импульсом р = Е/с = h /c = h/λ При фотоэффекте импульс фотона передается всему образцу и испущенному электрону. Приобретенный образцом импульс слишком мал и не поддается измерению. Но при столкновении фотона со свободным электроном величину передаваемого импульса можно измерить. Этот процесс – рассеяние фотона на свободном электроне – называется эффектом Комптона.
 Исследуя рассеяние рентгеновского излучения на парафине, Комптон в 1923 г. обнаружил, что в рассеянном излучении присутствуют волны с длиной волны большей длины волны падающего излучения
Исследуя рассеяние рентгеновского излучения на парафине, Комптон в 1923 г. обнаружил, что в рассеянном излучении присутствуют волны с длиной волны большей длины волны падающего излучения
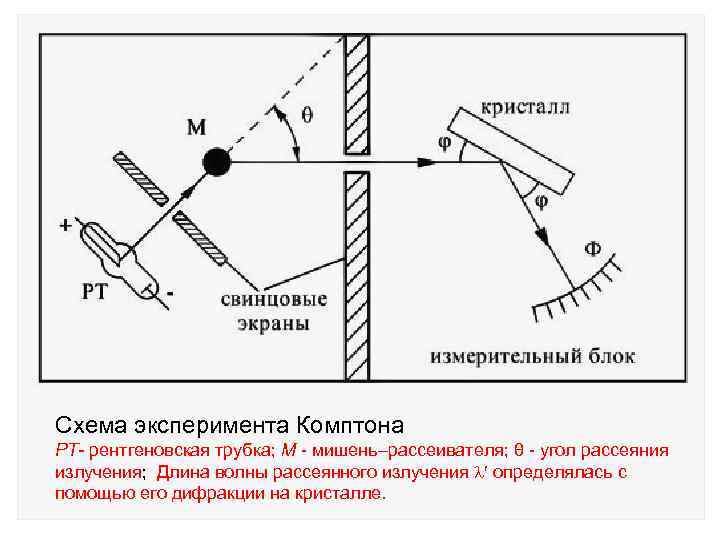 Схема эксперимента Комптона РТ- рентгеновская трубка; М - мишень рассеивателя; θ - угол рассеяния излучения; Длина волны рассеянного излучения определялась с помощью его дифракции на кристалле.
Схема эксперимента Комптона РТ- рентгеновская трубка; М - мишень рассеивателя; θ - угол рассеяния излучения; Длина волны рассеянного излучения определялась с помощью его дифракции на кристалле.
 Комптон установил, что разность длин волн рассеянного и падающего излучения не зависит от материала рассеивателя, а определяется только величиной угла рассеяния θ: = - = с (1 – cos ) формула Комптона Значение постоянной с = 2, 426 10 12 м Комптон определил экспериментально.
Комптон установил, что разность длин волн рассеянного и падающего излучения не зависит от материала рассеивателя, а определяется только величиной угла рассеяния θ: = - = с (1 – cos ) формула Комптона Значение постоянной с = 2, 426 10 12 м Комптон определил экспериментально.
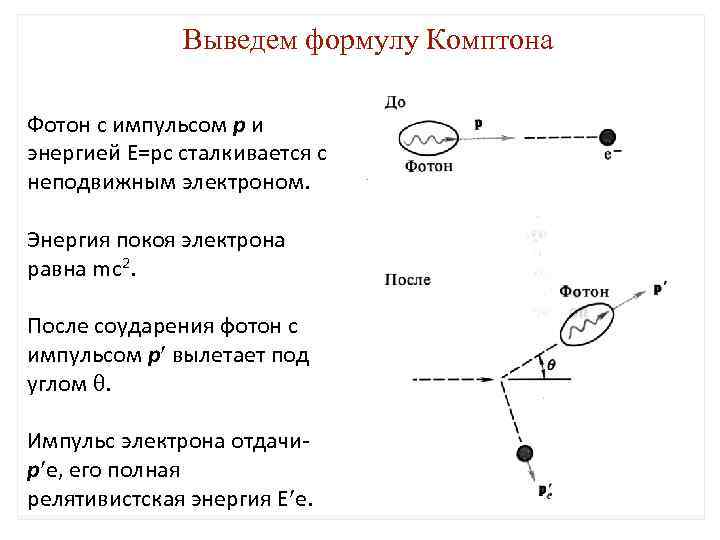 Выведем формулу Комптона Фотон с импульсом р и энергией Е=рс сталкивается с неподвижным электроном. Энергия покоя электрона равна mc 2. После соударения фотон с импульсом р вылетает под углом . Импульс электрона отдачи- р e, его полная релятивистская энергия Е e.
Выведем формулу Комптона Фотон с импульсом р и энергией Е=рс сталкивается с неподвижным электроном. Энергия покоя электрона равна mc 2. После соударения фотон с импульсом р вылетает под углом . Импульс электрона отдачи- р e, его полная релятивистская энергия Е e.
 Запишем законы сохранения энергии и импульса. Закон сохранения энергии: Закон сохранения импульса
Запишем законы сохранения энергии и импульса. Закон сохранения энергии: Закон сохранения импульса
 Откуда находим Воспользовавшись тем, что р = h/ , получаем или где c= волны. = 0, 024 Å – комптоновская длина
Откуда находим Воспользовавшись тем, что р = h/ , получаем или где c= волны. = 0, 024 Å – комптоновская длина
 6 . Модель атома Резерфорда В 1911 г. Резерфорд изучал рассеяние α – частиц (ядер атомов гелия, состав 2 р+2 n, заряд +2|е|) тонкими металлическими пленками (~1 мкм). α –частицы возникают при радиоактивном распаде ядер тяжелых атомов (радий, …). Их скорость при вылете из ядер составляет ~ 107 м/c. Резерфорд обнаружил, что основная часть α – частиц проходят через пленки без изменения направления своего движения. Лишь 3% из них испытывают небольшие отклонения. Но некоторые из них (1 частица из 20000)
6 . Модель атома Резерфорда В 1911 г. Резерфорд изучал рассеяние α – частиц (ядер атомов гелия, состав 2 р+2 n, заряд +2|е|) тонкими металлическими пленками (~1 мкм). α –частицы возникают при радиоактивном распаде ядер тяжелых атомов (радий, …). Их скорость при вылете из ядер составляет ~ 107 м/c. Резерфорд обнаружил, что основная часть α – частиц проходят через пленки без изменения направления своего движения. Лишь 3% из них испытывают небольшие отклонения. Но некоторые из них (1 частица из 20000)
 Атом в целом нейтрален. Z электронов подобно планетам вращаются вокруг ядер по круговым орбитам с радиусами r ~ 10 10 м (размер атома). Из второго закона Ньютона следует (6. 1) Однако одного этого уравнения недостаточно для определения радиуса орбиты r и скорости υ. Кроме того, двигаясь в электрическом поле ядра по круговой орбите с ускорением, электрон должен терять свою кинетическую энергию на излучение электромагнитных волн. Если принять, что орбитальная скорость электрона составляет ~ 106 м/c, то через ~ 10 11 с вся энергия электрона уйдет в излучение и он упадет на ядро. Таким образом классическая теория приводит к неустойчивости атома.
Атом в целом нейтрален. Z электронов подобно планетам вращаются вокруг ядер по круговым орбитам с радиусами r ~ 10 10 м (размер атома). Из второго закона Ньютона следует (6. 1) Однако одного этого уравнения недостаточно для определения радиуса орбиты r и скорости υ. Кроме того, двигаясь в электрическом поле ядра по круговой орбите с ускорением, электрон должен терять свою кинетическую энергию на излучение электромагнитных волн. Если принять, что орбитальная скорость электрона составляет ~ 106 м/c, то через ~ 10 11 с вся энергия электрона уйдет в излучение и он упадет на ядро. Таким образом классическая теория приводит к неустойчивости атома.
 7. Линейчатые спектры атомов В конце 19 века исследовались спектры излучения нагретых газов. Было найдено, что каждому атому присущ свой линейчатый спектр, подчиняющийся определенным закономерностям. Наиболее простой вид эти закономерности имеют для атома водорода. В 1885 г. Бальмер установил, что длины излучаемых электромагнитных волн в видимой области спектра подчиняются формуле
7. Линейчатые спектры атомов В конце 19 века исследовались спектры излучения нагретых газов. Было найдено, что каждому атому присущ свой линейчатый спектр, подчиняющийся определенным закономерностям. Наиболее простой вид эти закономерности имеют для атома водорода. В 1885 г. Бальмер установил, что длины излучаемых электромагнитных волн в видимой области спектра подчиняются формуле
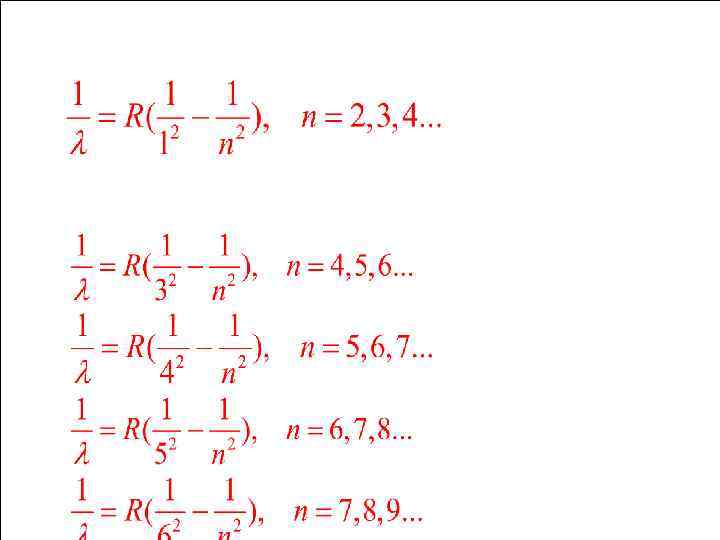
 Все серии описываются обобщенной формулой Бальмера (7. 1) m – номер серии, n – номер линии в серии. Линия, соответствующая n = ∞, называется границей серии. За границей серии спектр становится непрерывным. По классической теории спектр излучения атомов должен быть везде непрерывным.
Все серии описываются обобщенной формулой Бальмера (7. 1) m – номер серии, n – номер линии в серии. Линия, соответствующая n = ∞, называется границей серии. За границей серии спектр становится непрерывным. По классической теории спектр излучения атомов должен быть везде непрерывным.
 8. Теория Бора
8. Теория Бора
 2) При переходе атома из стационарного состояния с большей энергией En в стационарное состояние с меньшей энергией Em происходит излучение кванта света (фотона) с энергией hν = En Em При поглощении фотона атом с низшего уровня Em переходит в состояние с более высокой энергией En. En излучение hν поглощение hν Em
2) При переходе атома из стационарного состояния с большей энергией En в стационарное состояние с меньшей энергией Em происходит излучение кванта света (фотона) с энергией hν = En Em При поглощении фотона атом с низшего уровня Em переходит в состояние с более высокой энергией En. En излучение hν поглощение hν Em
 Условие квантования импульса (8. 1) вместе с уравнением Ньютона (6. 1) позволяют определить радиус стационарных орбит и энергии стационарных состояний. (8. 2) Состояния с n > 1 являются возбужденными.
Условие квантования импульса (8. 1) вместе с уравнением Ньютона (6. 1) позволяют определить радиус стационарных орбит и энергии стационарных состояний. (8. 2) Состояния с n > 1 являются возбужденными.
 Из второго постулата Бора получаем обобщенную формулу Бальмера Таким образом, номер серии m – это номер стационарного состояния с низшей энергией. Номер линии в серии связан с номером n стационарного состояния с большей энергией.
Из второго постулата Бора получаем обобщенную формулу Бальмера Таким образом, номер серии m – это номер стационарного состояния с низшей энергией. Номер линии в серии связан с номером n стационарного состояния с большей энергией.
 Несмотря на успехи, теория Бора имеет существенные недостатки: 1) Квантование момента импульса не объясняется, а постулируется. Смысл этого постулата не ясен. 2) Интенсивность спектральных линий не объясняется. 3) Не учитывается поляризация излучаемого света. 4) Применение к другим атомам (кроме атома водорода) оказалось не удачным. Никакие усовершенствования теории Бора к успеху не привели.
Несмотря на успехи, теория Бора имеет существенные недостатки: 1) Квантование момента импульса не объясняется, а постулируется. Смысл этого постулата не ясен. 2) Интенсивность спектральных линий не объясняется. 3) Не учитывается поляризация излучаемого света. 4) Применение к другим атомам (кроме атома водорода) оказалось не удачным. Никакие усовершенствования теории Бора к успеху не привели.
 9. Гипотеза де Бройля. Корпускулярно-волновой дуализм В 1923 г. Луи де Бройль предположил, что не только для фотонов, но и вообще для всех частиц, справедливы соотношения и E = h С каждой свободной частицей связана волна – волна де-Бройля (подобная плоской электромагнитной волне) (9. 1
9. Гипотеза де Бройля. Корпускулярно-волновой дуализм В 1923 г. Луи де Бройль предположил, что не только для фотонов, но и вообще для всех частиц, справедливы соотношения и E = h С каждой свободной частицей связана волна – волна де-Бройля (подобная плоской электромагнитной волне) (9. 1
 Стационарные состояния атомов получаются из условия, чтобы на длине круговой боровской орбиты укладывалось целое число длин волн де. Бройля (стоячая волна)
Стационарные состояния атомов получаются из условия, чтобы на длине круговой боровской орбиты укладывалось целое число длин волн де. Бройля (стоячая волна)
 Таким образом, согласно де Бройлю материя должна обладать корпускулярно-волновым дуализмом. Поэтому пучок любых частиц должен создавать на двойной щели интерференционную картину, характерную для опыта Юнга с двумя щелями. Три года спустя эксперименты подтвердили гипотезу де Бройля в опытах по дифракции электронов на кристаллах.
Таким образом, согласно де Бройлю материя должна обладать корпускулярно-волновым дуализмом. Поэтому пучок любых частиц должен создавать на двойной щели интерференционную картину, характерную для опыта Юнга с двумя щелями. Три года спустя эксперименты подтвердили гипотезу де Бройля в опытах по дифракции электронов на кристаллах.
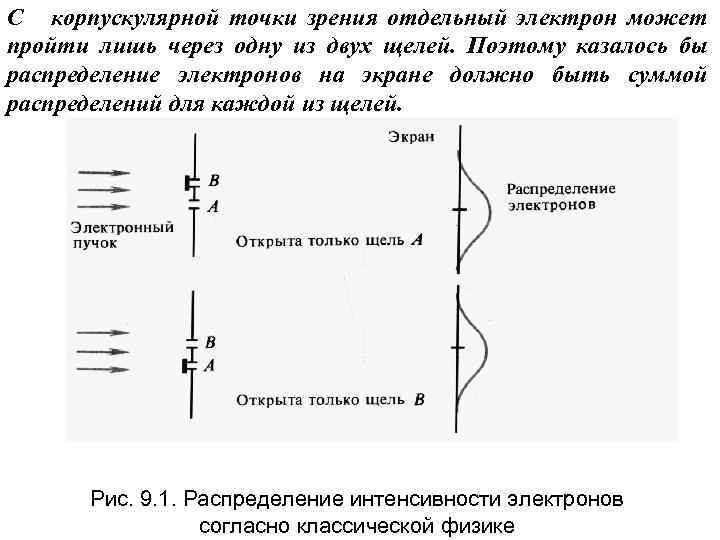 С корпускулярной точки зрения отдельный электрон может пройти лишь через одну из двух щелей. Поэтому казалось бы распределение электронов на экране должно быть суммой распределений для каждой из щелей. Рис. 9. 1. Распределение интенсивности электронов согласно классической физике
С корпускулярной точки зрения отдельный электрон может пройти лишь через одну из двух щелей. Поэтому казалось бы распределение электронов на экране должно быть суммой распределений для каждой из щелей. Рис. 9. 1. Распределение интенсивности электронов согласно классической физике
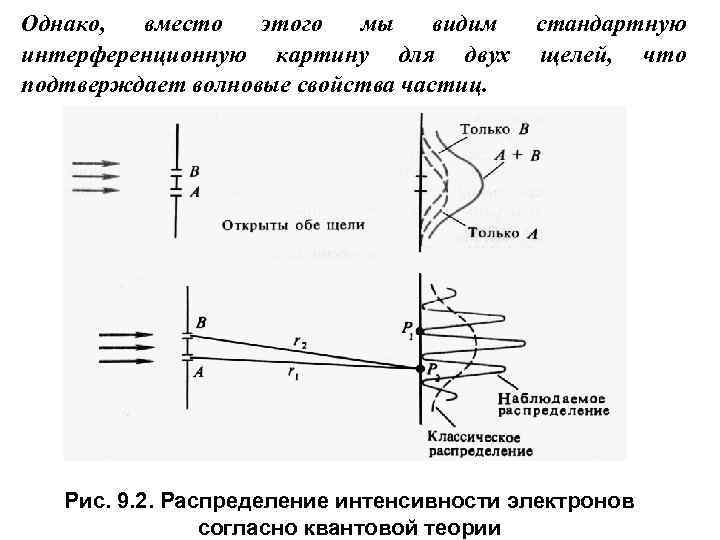 Однако, вместо этого мы видим интерференционную картину для двух подтверждает волновые свойства частиц. стандартную щелей, что Рис. 9. 2. Распределение интенсивности электронов согласно квантовой теории
Однако, вместо этого мы видим интерференционную картину для двух подтверждает волновые свойства частиц. стандартную щелей, что Рис. 9. 2. Распределение интенсивности электронов согласно квантовой теории
 Пусть в точке Р 1 на рис. 9. 2 находится счетчик Гейгера, регистрирующий электроны, когда открыта любая из щелей А или В. Когда открыты обе щели одновременно, счетчик перестает регистрировать электроны в точке Р 1. Это значит, что точка Р 1 попадает в интерференционный минимум (r 2 – r 1 = /2). Если же счетчик находится в точке Р 2, то в ней он зарегистрирует больше электронов, чем при простом суммировании интенсивностей от отдельных щелей. Значит в точке Р 2 имеется интерференционный
Пусть в точке Р 1 на рис. 9. 2 находится счетчик Гейгера, регистрирующий электроны, когда открыта любая из щелей А или В. Когда открыты обе щели одновременно, счетчик перестает регистрировать электроны в точке Р 1. Это значит, что точка Р 1 попадает в интерференционный минимум (r 2 – r 1 = /2). Если же счетчик находится в точке Р 2, то в ней он зарегистрирует больше электронов, чем при простом суммировании интенсивностей от отдельных щелей. Значит в точке Р 2 имеется интерференционный
 10. Волновая функция В квантовой механике поведение частицы описывается волновой функцией (х, у, z, t). В частном случае свободной частицы волновая функция есть волна де-Бройля (9. 1). Вероятность обнаружения частицы в некоторый момент времени t в любой точке (х, у, z) пропорциональна | (х, у, z, t)|2.
10. Волновая функция В квантовой механике поведение частицы описывается волновой функцией (х, у, z, t). В частном случае свободной частицы волновая функция есть волна де-Бройля (9. 1). Вероятность обнаружения частицы в некоторый момент времени t в любой точке (х, у, z) пропорциональна | (х, у, z, t)|2.
 Если событие может произойти несколькими взаимно исключающими способами (например, прохождение частицы через одну из щелей А или В), то амплитуда вероятности этого события равна сумме амплитуд вероятностей каждого из способов: = 1 + 2 (принцип суперпозиции).
Если событие может произойти несколькими взаимно исключающими способами (например, прохождение частицы через одну из щелей А или В), то амплитуда вероятности этого события равна сумме амплитуд вероятностей каждого из способов: = 1 + 2 (принцип суперпозиции).
 В случае (рис. 9. 2) волновая функция 1 описывает волну, проходящую через щель А, а волновая функция 2 – через щель В. На экране обе волновые функции перекрываются и дают интерференционную картину от двух щелей. При этом n -й интерференционный максимум определяется выражением sin n = n /d
В случае (рис. 9. 2) волновая функция 1 описывает волну, проходящую через щель А, а волновая функция 2 – через щель В. На экране обе волновые функции перекрываются и дают интерференционную картину от двух щелей. При этом n -й интерференционный максимум определяется выражением sin n = n /d
 Вероятность обнаружения частицы в некоторый момент времени t в элементарном объеме d. V, окружающем точку Р, равна: Вероятностный смысл волновой функции накладывает ограничения на ее свойства.
Вероятность обнаружения частицы в некоторый момент времени t в элементарном объеме d. V, окружающем точку Р, равна: Вероятностный смысл волновой функции накладывает ограничения на ее свойства.
 Они включают в себя: 1. Условие конечности волновой функции. Волновая функция не может принимать бесконечных значений.
Они включают в себя: 1. Условие конечности волновой функции. Волновая функция не может принимать бесконечных значений.
 2. Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно.
2. Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно.
 3. Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть и первые частные производные волновой функции d /dx, d /dy, d /dz.
3. Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть и первые частные производные волновой функции d /dx, d /dy, d /dz.
 4. Условие нормировки волновой функции Это значит, что пребывание частицы где- либо в пространстве есть достоверное событие и его вероятность должна быть равна единице.
4. Условие нормировки волновой функции Это значит, что пребывание частицы где- либо в пространстве есть достоверное событие и его вероятность должна быть равна единице.
 11. Уравнение Шредингера Для описания поведения микро частиц уравнения классической физики (уравнения Ньютона) не пригодны. В квантовой механике состояние движущейся в силовом поле частицы полностью описывается волновой функцией (х), которая находится из решения дифференциального уравнения, сформулированного Шредингером в 1926 г.
11. Уравнение Шредингера Для описания поведения микро частиц уравнения классической физики (уравнения Ньютона) не пригодны. В квантовой механике состояние движущейся в силовом поле частицы полностью описывается волновой функцией (х), которая находится из решения дифференциального уравнения, сформулированного Шредингером в 1926 г.
 Временное уравнение Шредингера для частицы с массой m 0 в потенциальном поле U(x, y, z, t) имеет вид: ( 10. 1) где - мнимая единица - оператор Гамильтона (гамильтониан) – оператор полной энергии (набла) оператор Лапласа, который в декартовой системе координат имеет вид
Временное уравнение Шредингера для частицы с массой m 0 в потенциальном поле U(x, y, z, t) имеет вид: ( 10. 1) где - мнимая единица - оператор Гамильтона (гамильтониан) – оператор полной энергии (набла) оператор Лапласа, который в декартовой системе координат имеет вид
 Уравнение Шредингера решается с учетом начальных и граничных условий, накладываемых на волновую функцию. Начальное условие задаёт значение волновой функции в начальный момент времени t = 0. Граничные условия задаются на границах областей, где потенциальная функция U терпит разрывы первого или второго рода.
Уравнение Шредингера решается с учетом начальных и граничных условий, накладываемых на волновую функцию. Начальное условие задаёт значение волновой функции в начальный момент времени t = 0. Граничные условия задаются на границах областей, где потенциальная функция U терпит разрывы первого или второго рода.
 В качестве примера вычислим волновую функцию свободной частицы, с кинетической энергий E = p 2/2 m Пусть частица движется в отсутствие силовых полей (U = 0, F = 0) в направлении оси x.
В качестве примера вычислим волновую функцию свободной частицы, с кинетической энергий E = p 2/2 m Пусть частица движется в отсутствие силовых полей (U = 0, F = 0) в направлении оси x.
 Уравнение Шредингера для этого случая записывается в виде: Его решением является волновая функция: - плоская волна де Бройля. Вероятность обнаружения частицы | |2 = A 2, не зависит от t и х. То есть свободная частица в любой точке х и в любой момент времени обнаруживается с равной
Уравнение Шредингера для этого случая записывается в виде: Его решением является волновая функция: - плоская волна де Бройля. Вероятность обнаружения частицы | |2 = A 2, не зависит от t и х. То есть свободная частица в любой точке х и в любой момент времени обнаруживается с равной
 В квантовой механике существует класс задач, в которых потенциальное поле U(x, y, z) не зависит от времени - это стационарное поле В стационарных полях квантовая система находится в состояниях с определенным значением энергии E. Эти состояния называются стационарными состояниями.
В квантовой механике существует класс задач, в которых потенциальное поле U(x, y, z) не зависит от времени - это стационарное поле В стационарных полях квантовая система находится в состояниях с определенным значением энергии E. Эти состояния называются стационарными состояниями.
 Если потенциальная функция U(x, y, z) не зависит от времени, то волновую функцию (x, y, z, t) можно представить в виде произведения двух функций: (x, y, z, t) = (x, y, z) (t), (x, y, z) зависит только от координат; (t) зависит только от времени.
Если потенциальная функция U(x, y, z) не зависит от времени, то волновую функцию (x, y, z, t) можно представить в виде произведения двух функций: (x, y, z, t) = (x, y, z) (t), (x, y, z) зависит только от координат; (t) зависит только от времени.
 Подставляя (x, y, z) (t) в уравнение Шредингера и разделив обе части уравнения на (x, y, z) (t), получаем В этом уравнении левая часть зависит только от времени, а правая только от координат.
Подставляя (x, y, z) (t) в уравнение Шредингера и разделив обе части уравнения на (x, y, z) (t), получаем В этом уравнении левая часть зависит только от времени, а правая только от координат.
 Данное равенство возможно лишь в случае, если левая и правая части уравнения равны одной и той же постоянной величине. Обозначим её буквой Е, получаем два уравнения:
Данное равенство возможно лишь в случае, если левая и правая части уравнения равны одной и той же постоянной величине. Обозначим её буквой Е, получаем два уравнения:
 Константа Е представляет полную энергию квантовомеханической системы. Перепишем 1 - ое уравнение с учетом вида оператора Ĥ Полученное уравнение называется уравнением Шредингера для стационарных состояний (стационарное уравнение Шредингера).
Константа Е представляет полную энергию квантовомеханической системы. Перепишем 1 - ое уравнение с учетом вида оператора Ĥ Полученное уравнение называется уравнением Шредингера для стационарных состояний (стационарное уравнение Шредингера).
 12. Соотношение неопределенностей Гейнзенберга Соотношение или принцип неопределенностей Гейзенберга утверждает: Невозможно одновременно точно определить значения координаты и импульса частицы: где х и рх – неопределённости значений координаты х и компоненты импульса рх на ту же самую ось.
12. Соотношение неопределенностей Гейнзенберга Соотношение или принцип неопределенностей Гейзенберга утверждает: Невозможно одновременно точно определить значения координаты и импульса частицы: где х и рх – неопределённости значений координаты х и компоненты импульса рх на ту же самую ось.
 Двойственная природа микрочастиц накладывает ограничения на точность определения физических величин. Эти ограничения никак не связаны с точностью измерений, достижимой в конкретном эксперименте, а имеют принципиальное значение. Соотношение неопределенностей – фундаментальное соотношение квантовой механики. Оно устанавливает предел точности одновременного определения переменных, характеризующих квантовую систему.
Двойственная природа микрочастиц накладывает ограничения на точность определения физических величин. Эти ограничения никак не связаны с точностью измерений, достижимой в конкретном эксперименте, а имеют принципиальное значение. Соотношение неопределенностей – фундаментальное соотношение квантовой механики. Оно устанавливает предел точности одновременного определения переменных, характеризующих квантовую систему.
 13. Частица в потенциальном ящике. Рассмотрим частицу в одномерном ящике с абсолютно отражающими стенками, расстояние между которыми равно L. Потенциальная энергия частицы вне и внутри потенциального ящика имеет следующее значения: U=0 (0< x < L ) Задача о U=∞ движении частицы Lв > одномерном (x =0, <0, x= , L ) ящике с бесконечно высокими стенками сводится к решению уравнения Шредингера:
13. Частица в потенциальном ящике. Рассмотрим частицу в одномерном ящике с абсолютно отражающими стенками, расстояние между которыми равно L. Потенциальная энергия частицы вне и внутри потенциального ящика имеет следующее значения: U=0 (0< x < L ) Задача о U=∞ движении частицы Lв > одномерном (x =0, <0, x= , L ) ящике с бесконечно высокими стенками сводится к решению уравнения Шредингера:
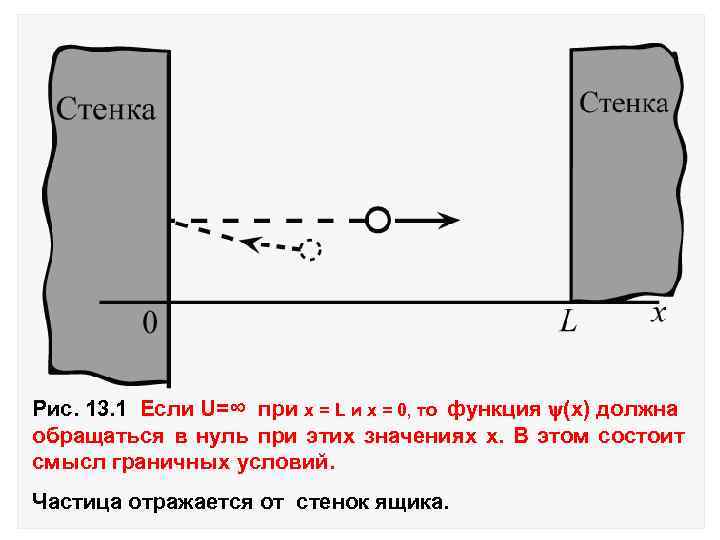 Рис. 13. 1 Если U=∞ при х = L и х = 0, то функция (x) должна обращаться в нуль при этих значениях х. В этом состоит смысл граничных условий. Частица отражается от стенок ящика.
Рис. 13. 1 Если U=∞ при х = L и х = 0, то функция (x) должна обращаться в нуль при этих значениях х. В этом состоит смысл граничных условий. Частица отражается от стенок ящика.
 Решением этого уравнения при U= 0 является функция где Функция должна обращаться в нуль на границах при х = L, х = 0. Подставляя в (х) вместо х величину L, получаем Это справедливо при k. L = n , где n – целое число. Разрешены только дискретные значения волнового числа kn:
Решением этого уравнения при U= 0 является функция где Функция должна обращаться в нуль на границах при х = L, х = 0. Подставляя в (х) вместо х величину L, получаем Это справедливо при k. L = n , где n – целое число. Разрешены только дискретные значения волнового числа kn:
 Это значит, что в ящике укладывается целое число полуволн, что совпадает с условием возникновения стоячей волны на струне: L = n( /2) На рис. 13. 2 изображены волновые функции n(х) = A sin(n /L)x для n = 1, 2, 3, 4. Значения импульса: или Значения кинетической энергии
Это значит, что в ящике укладывается целое число полуволн, что совпадает с условием возникновения стоячей волны на струне: L = n( /2) На рис. 13. 2 изображены волновые функции n(х) = A sin(n /L)x для n = 1, 2, 3, 4. Значения импульса: или Значения кинетической энергии
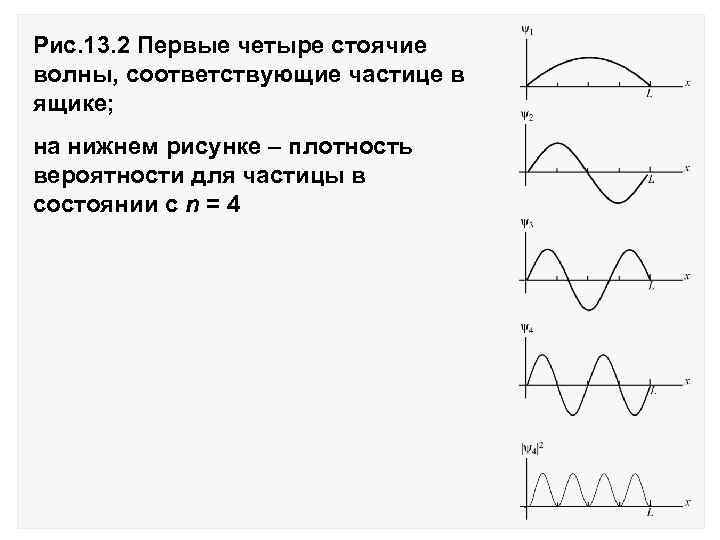 Рис. 13. 2 Первые четыре стоячие волны, соответствующие частице в ящике; на нижнем рисунке – плотность вероятности для частицы в состоянии с n = 4
Рис. 13. 2 Первые четыре стоячие волны, соответствующие частице в ящике; на нижнем рисунке – плотность вероятности для частицы в состоянии с n = 4
 Значения En называются собственными значениями гамильтониана. Соответствующие им волновые функции – собственными функциями.
Значения En называются собственными значениями гамильтониана. Соответствующие им волновые функции – собственными функциями.
 Наинизшая возможная энергия (энергия основного состояния) отвечает n = 1, соответствующая ей волновая функция имеет вид половины синусоиды. В квантовой механике частица в ящике не может иметь энергию меньше Е 1 ( в ящике не должна быть нулевой функцией), в классической же физике частица может иметь нулевую энергию.
Наинизшая возможная энергия (энергия основного состояния) отвечает n = 1, соответствующая ей волновая функция имеет вид половины синусоиды. В квантовой механике частица в ящике не может иметь энергию меньше Е 1 ( в ящике не должна быть нулевой функцией), в классической же физике частица может иметь нулевую энергию.
 14. Атом водорода Задача о движении электрона в атоме водорода сводится к задаче о движении электрона в сферически симметричном кулоновском потенциале. Уравнение Шредингера удобнее решать в сферических координатах, которые связаны с декартовыми соотношениями: х = r sin cos y = r sin z = r cos
14. Атом водорода Задача о движении электрона в атоме водорода сводится к задаче о движении электрона в сферически симметричном кулоновском потенциале. Уравнение Шредингера удобнее решать в сферических координатах, которые связаны с декартовыми соотношениями: х = r sin cos y = r sin z = r cos
 Уравнение Шредингера в сферической системе координат: где U = –k 0 e 2/r – кулоновский потенциал. Для основного состояния атома водорода решением уравнения является экспоненциальная функция = e r/a, где , , .
Уравнение Шредингера в сферической системе координат: где U = –k 0 e 2/r – кулоновский потенциал. Для основного состояния атома водорода решением уравнения является экспоненциальная функция = e r/a, где , , .
 Подставляя в Е выражение для а, находим: Подстановка численных значений m, k 0, e и ħ дает E = 21, 8 10 19 Дж = 13, 6 э. В. Эта энергия есть минимальное количество энергии, необходимое для удаления электрона из атома водорода. Она называется энергией потенциалом ионизации. связи или
Подставляя в Е выражение для а, находим: Подстановка численных значений m, k 0, e и ħ дает E = 21, 8 10 19 Дж = 13, 6 э. В. Эта энергия есть минимальное количество энергии, необходимое для удаления электрона из атома водорода. Она называется энергией потенциалом ионизации. связи или
 При r = а амплитуда волны уменьшается в е раз по сравнению с максимальным значением (e r/а = 1/e). Данное значение r выбирается в качестве Используя выражение для а, находим радиуса атома водорода. = 5, 3 10 11 м (радиус атома водорода).
При r = а амплитуда волны уменьшается в е раз по сравнению с максимальным значением (e r/а = 1/e). Данное значение r выбирается в качестве Используя выражение для а, находим радиуса атома водорода. = 5, 3 10 11 м (радиус атома водорода).
 Функция = e r/а представляет собой стоячую волну основного состояния, которая соответствует нижнему уровню энергии Е 1. Волновые функции для следующих энергетических уровней имеют вид двух и Графики этих функций приведены на рис. 14. 1.
Функция = e r/а представляет собой стоячую волну основного состояния, которая соответствует нижнему уровню энергии Е 1. Волновые функции для следующих энергетических уровней имеют вид двух и Графики этих функций приведены на рис. 14. 1.
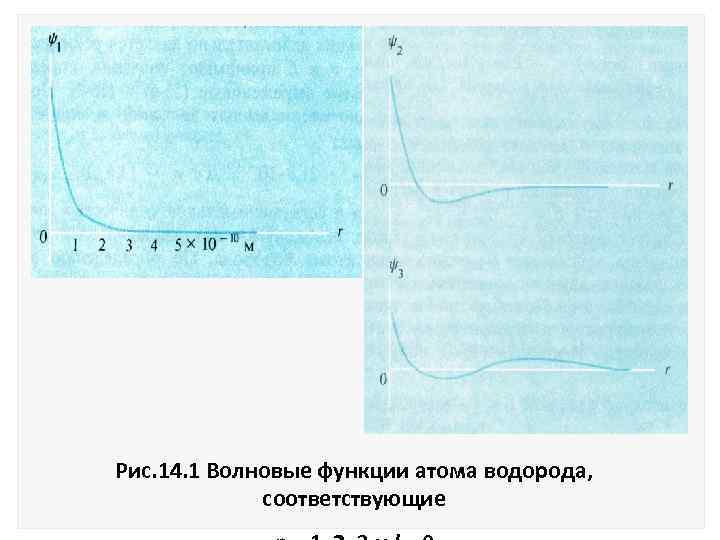 Рис. 14. 1 Волновые функции атома водорода, соответствующие
Рис. 14. 1 Волновые функции атома водорода, соответствующие
 Энергетические уровни атома водорода: где n целое положительное число. Величина n называется главным квантовым числом. Для полного описания трехмерной стоячей волны необходимы еще два квантовых числа, которые характеризуют момент импульса частицы.
Энергетические уровни атома водорода: где n целое положительное число. Величина n называется главным квантовым числом. Для полного описания трехмерной стоячей волны необходимы еще два квантовых числа, которые характеризуют момент импульса частицы.
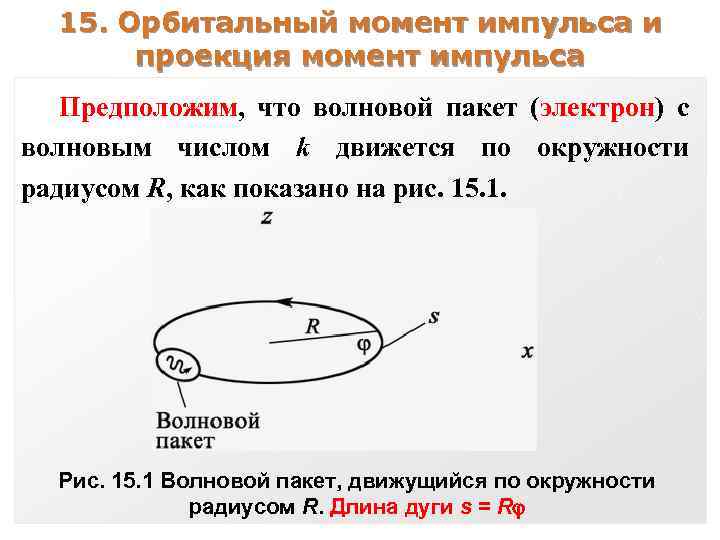 15. Орбитальный момент импульса и проекция момент импульса Предположим, что волновой пакет (электрон) с волновым числом k движется по окружности радиусом R, как показано на рис. 15. 1. Рис. 15. 1 Волновой пакет, движущийся по окружности радиусом R. Длина дуги s = R
15. Орбитальный момент импульса и проекция момент импульса Предположим, что волновой пакет (электрон) с волновым числом k движется по окружности радиусом R, как показано на рис. 15. 1. Рис. 15. 1 Волновой пакет, движущийся по окружности радиусом R. Длина дуги s = R
 Такой пакет имеет момент импульса относительно оси z, равный Lz = Rp = R(ħk). Волновую функцию пакета на дуге s = R можно записать в виде ~ ei(ks t) = ei(k. R t). Поскольку ( = 0) и ( = 2 ) измеряются в одной и той же точке пространства, их значения совпадают, т. е. eik. R(0) = eik. R(2 ) Это соотношение выполняется, если k. R = ml , где ml – целое число.
Такой пакет имеет момент импульса относительно оси z, равный Lz = Rp = R(ħk). Волновую функцию пакета на дуге s = R можно записать в виде ~ ei(ks t) = ei(k. R t). Поскольку ( = 0) и ( = 2 ) измеряются в одной и той же точке пространства, их значения совпадают, т. е. eik. R(0) = eik. R(2 ) Это соотношение выполняется, если k. R = ml , где ml – целое число.
 Умножив обе части этого равенства на ħ, имеем ħk. R = ml ħ или Lz = m. L ħ Момент импульса квантуется и составляет целое кратное ħ. Lz принимает значения: 0, ± ħ, ± 2 ħ, ± 3 ħ и т. д.
Умножив обе части этого равенства на ħ, имеем ħk. R = ml ħ или Lz = m. L ħ Момент импульса квантуется и составляет целое кратное ħ. Lz принимает значения: 0, ± ħ, ± 2 ħ, ± 3 ħ и т. д.
 В общем виде волновая функция для частицы, движущейся в сферически симметричном потенциале (например, в кулоновском) записывается в следующем общим виде: где
В общем виде волновая функция для частицы, движущейся в сферически симметричном потенциале (например, в кулоновском) записывается в следующем общим виде: где
 Индексы: n- главное квантовое число, l – орбитальное квантовое число, ml – магнитное квантовое число Кулоновский потенциал обладает свойством: все собственные функции с одним и тем же квантовым числом n имеют единственное собственное значение энергии. l принимает значения: 0, 1, … n – 1, ml пробегает от l до + l.
Индексы: n- главное квантовое число, l – орбитальное квантовое число, ml – магнитное квантовое число Кулоновский потенциал обладает свойством: все собственные функции с одним и тем же квантовым числом n имеют единственное собственное значение энергии. l принимает значения: 0, 1, … n – 1, ml пробегает от l до + l.
 Возможные комбинации n, l и ml для случая n = 2 n l ml 2 2 0 1 1 1 0 1 Кинетическая энергия вращательного движения твердого тела К = L 2/2 I, где I момент инерции. L – момент импульса. Согласно квантовой теории:
Возможные комбинации n, l и ml для случая n = 2 n l ml 2 2 0 1 1 1 0 1 Кинетическая энергия вращательного движения твердого тела К = L 2/2 I, где I момент инерции. L – момент импульса. Согласно квантовой теории:
 Сопоставляя два последних выражений, находим: L= Величина определяет квадрат величины момента импульса, ħl представляет собой максимальное значение проекции момента импульса на выбранное направление.
Сопоставляя два последних выражений, находим: L= Величина определяет квадрат величины момента импульса, ħl представляет собой максимальное значение проекции момента импульса на выбранное направление.
 13. Частица в потенциальном ящике. Рассмотрим частицу в одномерном ящике с абсолютно отражающими стенками, расстояние между которыми равно L. Потенциальная энергия частицы вне и внутри потенциального ящика имеет следующее значения: U=0 (0< x < L ) Задача о U=∞ движении частицы Lв > одномерном (x =0, <0, x= , L ) ящике с бесконечно высокими стенками сводится к решению уравнения Шредингера:
13. Частица в потенциальном ящике. Рассмотрим частицу в одномерном ящике с абсолютно отражающими стенками, расстояние между которыми равно L. Потенциальная энергия частицы вне и внутри потенциального ящика имеет следующее значения: U=0 (0< x < L ) Задача о U=∞ движении частицы Lв > одномерном (x =0, <0, x= , L ) ящике с бесконечно высокими стенками сводится к решению уравнения Шредингера:
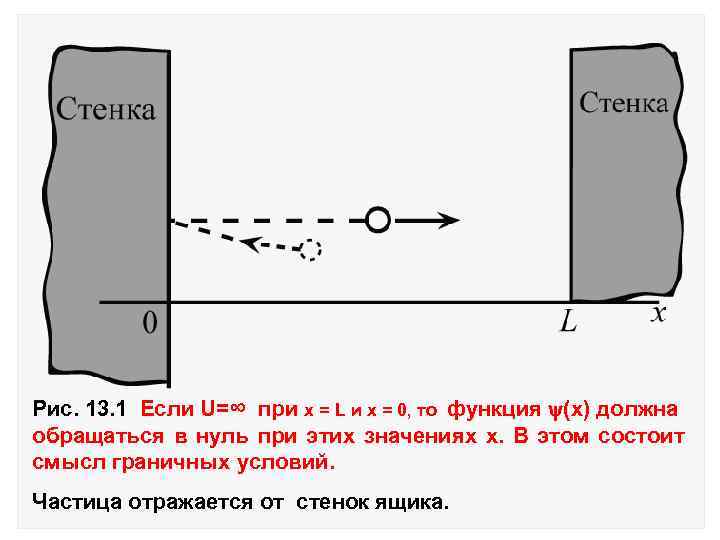 Рис. 13. 1 Если U=∞ при х = L и х = 0, то функция (x) должна обращаться в нуль при этих значениях х. В этом состоит смысл граничных условий. Частица отражается от стенок ящика.
Рис. 13. 1 Если U=∞ при х = L и х = 0, то функция (x) должна обращаться в нуль при этих значениях х. В этом состоит смысл граничных условий. Частица отражается от стенок ящика.
 Решением этого уравнения при U= 0 является функция где Функция должна обращаться в нуль на границах при х = L, х = 0. Подставляя в (х) вместо х величину L, получаем Это справедливо при k. L = n , где n – целое число. Разрешены только дискретные значения волнового числа kn:
Решением этого уравнения при U= 0 является функция где Функция должна обращаться в нуль на границах при х = L, х = 0. Подставляя в (х) вместо х величину L, получаем Это справедливо при k. L = n , где n – целое число. Разрешены только дискретные значения волнового числа kn:
 Это значит, что в ящике укладывается целое число полуволн, что совпадает с условием возникновения стоячей волны на струне: L = n( /2) На рис. 13. 2 изображены волновые функции n(х) = A sin(n x/L) для n = 1, 2, 3, 4. Значения импульса: или Значения кинетической энергии
Это значит, что в ящике укладывается целое число полуволн, что совпадает с условием возникновения стоячей волны на струне: L = n( /2) На рис. 13. 2 изображены волновые функции n(х) = A sin(n x/L) для n = 1, 2, 3, 4. Значения импульса: или Значения кинетической энергии
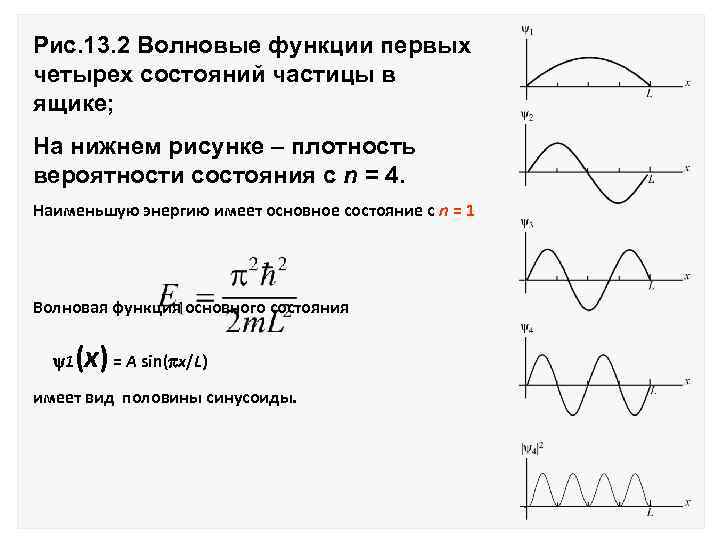 Рис. 13. 2 Волновые функции первых четырех состояний частицы в ящике; На нижнем рисунке – плотность вероятности состояния с n = 4. Наименьшую энергию имеет основное состояние с n = 1 Волновая функция основного состояния 1 (х) = A sin( x/L) имеет вид половины синусоиды.
Рис. 13. 2 Волновые функции первых четырех состояний частицы в ящике; На нижнем рисунке – плотность вероятности состояния с n = 4. Наименьшую энергию имеет основное состояние с n = 1 Волновая функция основного состояния 1 (х) = A sin( x/L) имеет вид половины синусоиды.
 Значения En называются собственными значениями гамильтониана Ĥ. Соответствующие им волновые функции n(х) называются собственными функциями гамильтониана Ĥ.
Значения En называются собственными значениями гамильтониана Ĥ. Соответствующие им волновые функции n(х) называются собственными функциями гамильтониана Ĥ.
 В квантовой механике частица в ящике не может иметь энергию меньше энергии основного состояния Е 1 ( в ящике не должна быть нулевой функцией), в классической же физике частица может иметь нулевую энергию.
В квантовой механике частица в ящике не может иметь энергию меньше энергии основного состояния Е 1 ( в ящике не должна быть нулевой функцией), в классической же физике частица может иметь нулевую энергию.
 14. Атом водорода Задача о движении электрона в атоме водорода сводится к задаче о движении электрона в сферически симметричном кулоновском потенциале. Уравнение Шредингера удобнее решать в сферических координатах (r, θ, φ), которые связаны с декартовыми координатами (x, y, z) соотношениями: х = r sin cos y = r sin
14. Атом водорода Задача о движении электрона в атоме водорода сводится к задаче о движении электрона в сферически симметричном кулоновском потенциале. Уравнение Шредингера удобнее решать в сферических координатах (r, θ, φ), которые связаны с декартовыми координатами (x, y, z) соотношениями: х = r sin cos y = r sin
 Уравнение Шредингера в сферической системе координат имеет вид: где U = –k 0 e 2/r – кулоновский потенциал, k 0 =1/(4πε 0). Для основного состояния атома водорода решением уравнения является волновая функция = А 1 e r/a Энергия основного состояния атома водорода равна
Уравнение Шредингера в сферической системе координат имеет вид: где U = –k 0 e 2/r – кулоновский потенциал, k 0 =1/(4πε 0). Для основного состояния атома водорода решением уравнения является волновая функция = А 1 e r/a Энергия основного состояния атома водорода равна
 Подставляя в Е выражение для а, находим: Подстановка значений m, k 0, e и ħ дает E = 21, 8 10 19 Дж = 13, 6 э. В = - 1 Ry. Эта энергия есть минимальное количество энергии, необходимое для удаления электрона из атома водорода. Она называется энергией потенциалом ионизации. связи или
Подставляя в Е выражение для а, находим: Подстановка значений m, k 0, e и ħ дает E = 21, 8 10 19 Дж = 13, 6 э. В = - 1 Ry. Эта энергия есть минимальное количество энергии, необходимое для удаления электрона из атома водорода. Она называется энергией потенциалом ионизации. связи или
 При r = а амплитуда волны уменьшается в е раз по сравнению с максимальным значением (e r/а = 1/e). Данное значение r выбирается в качестве Используя выражение для а, находим радиуса атома водорода. = 5, 3 10 11 м = 0. 52917 Å (радиус атома водорода).
При r = а амплитуда волны уменьшается в е раз по сравнению с максимальным значением (e r/а = 1/e). Данное значение r выбирается в качестве Используя выражение для а, находим радиуса атома водорода. = 5, 3 10 11 м = 0. 52917 Å (радиус атома водорода).
 Функция = e r/а представляет собой стоячую волну основного состояния, которая соответствует нижнему уровню энергии Е 1. Волновые функции для следующих энергетических уровней имеют вид двух и Графики этих функций приведены на рис. 14. 1.
Функция = e r/а представляет собой стоячую волну основного состояния, которая соответствует нижнему уровню энергии Е 1. Волновые функции для следующих энергетических уровней имеют вид двух и Графики этих функций приведены на рис. 14. 1.
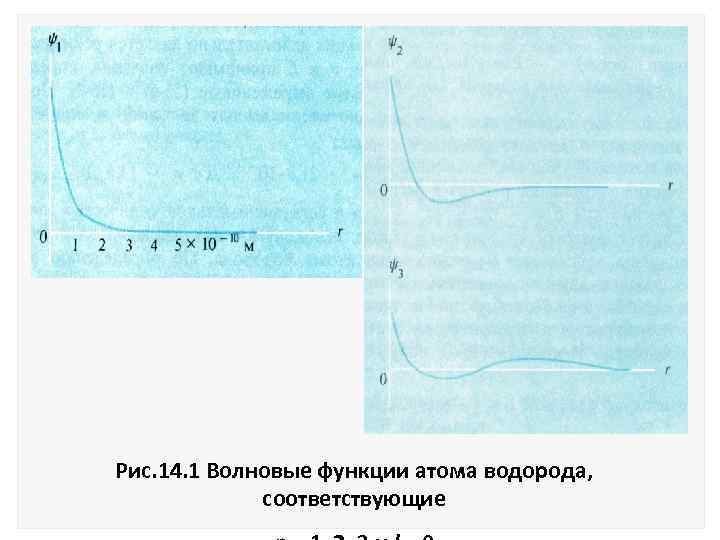 Рис. 14. 1 Волновые функции атома водорода, соответствующие
Рис. 14. 1 Волновые функции атома водорода, соответствующие
 Все возможные энергетические уровни атома водорода равны : (14. 1) где n целое положительное число (n=1, 2, 3, …). Число n называется главным квантовым числом. Для полного описания трехмерной стоячей волны необходимы еще два квантовых числа, которые характеризуют момент импульса частицы.
Все возможные энергетические уровни атома водорода равны : (14. 1) где n целое положительное число (n=1, 2, 3, …). Число n называется главным квантовым числом. Для полного описания трехмерной стоячей волны необходимы еще два квантовых числа, которые характеризуют момент импульса частицы.
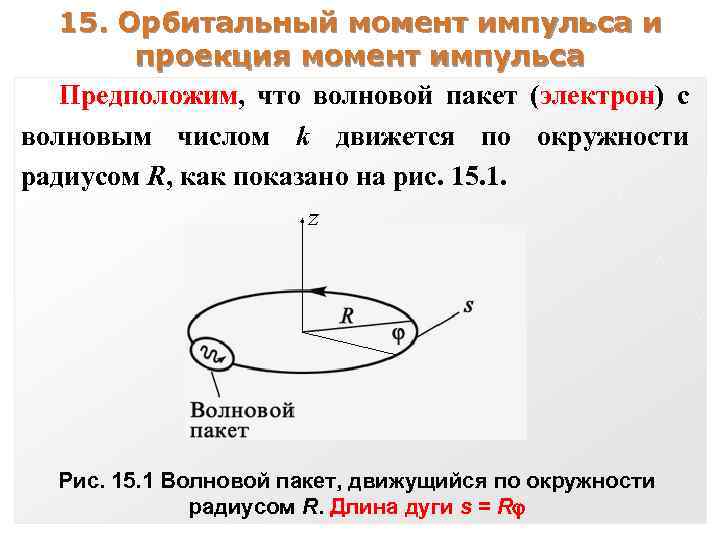 15. Орбитальный момент импульса и проекция момент импульса Предположим, что волновой пакет (электрон) с волновым числом k движется по окружности радиусом R, как показано на рис. 15. 1. z Рис. 15. 1 Волновой пакет, движущийся по окружности радиусом R. Длина дуги s = R
15. Орбитальный момент импульса и проекция момент импульса Предположим, что волновой пакет (электрон) с волновым числом k движется по окружности радиусом R, как показано на рис. 15. 1. z Рис. 15. 1 Волновой пакет, движущийся по окружности радиусом R. Длина дуги s = R
 Такой пакет имеет момент импульса относительно оси z, равный Lz = Rp = R(ħk). Волновую функцию пакета на дуге s = R можно записать в виде ~ ei(ks t) = ei(k. R t). Поскольку функции ( = 0) и ( = 2 ) отвечают одной и той же точке пространства, то их значения должны совпадать, т. е. eik. R(0) = 1= eik. R(2 ) Это равенство выполняется в общем случае, если k. R = m , где m – целое число.
Такой пакет имеет момент импульса относительно оси z, равный Lz = Rp = R(ħk). Волновую функцию пакета на дуге s = R можно записать в виде ~ ei(ks t) = ei(k. R t). Поскольку функции ( = 0) и ( = 2 ) отвечают одной и той же точке пространства, то их значения должны совпадать, т. е. eik. R(0) = 1= eik. R(2 ) Это равенство выполняется в общем случае, если k. R = m , где m – целое число.
 Умножив обе части этого равенства на ħ, имеем ħk. R = m ħ или Lz = m ħ Таким образом момент импульса атома водорода квантуется и составляет целое кратное ħ. Lz принимает значения: 0, ± ħ, ± 2 ħ, ± 3 ħ и т. д.
Умножив обе части этого равенства на ħ, имеем ħk. R = m ħ или Lz = m ħ Таким образом момент импульса атома водорода квантуется и составляет целое кратное ħ. Lz принимает значения: 0, ± ħ, ± 2 ħ, ± 3 ħ и т. д.
 В общем случае волновые функции частицы, движущейся в сферически симметричном кулоновском потенциале, записываются как : где - радиальные функции - шаровые функции, - присоединенные полиномы Лежандра
В общем случае волновые функции частицы, движущейся в сферически симметричном кулоновском потенциале, записываются как : где - радиальные функции - шаровые функции, - присоединенные полиномы Лежандра
 Индексы: n - главное квантовое число, l – орбитальное квантовое число, m – магнитное квантовое число Кулоновский потенциал обладает свойством: все собственные функции с одним и тем же квантовым числом n имеют одинаковое собственное значение энергии. l принимает значения: 0, 1, … n – 1, m пробегает значения от l до + l.
Индексы: n - главное квантовое число, l – орбитальное квантовое число, m – магнитное квантовое число Кулоновский потенциал обладает свойством: все собственные функции с одним и тем же квантовым числом n имеют одинаковое собственное значение энергии. l принимает значения: 0, 1, … n – 1, m пробегает значения от l до + l.
 Возможные комбинации n, l и m для случая n = 2 n 2 2 l m 0 0 1 1 1 0 1 1 Известно, что кинетическая энергия вращательного движения твердого тела равна К = L 2/2 I, где I момент инерции, L – момент импульса. Согласно квантовой теории:
Возможные комбинации n, l и m для случая n = 2 n 2 2 l m 0 0 1 1 1 0 1 1 Известно, что кинетическая энергия вращательного движения твердого тела равна К = L 2/2 I, где I момент инерции, L – момент импульса. Согласно квантовой теории:
 Сравнивая два последних выражения, находим: L= Величина определяет квадрат величины момента импульса, Lz = lħ представляет собой максимальное значение проекции момента импульса на выбранное направление (ось z).
Сравнивая два последних выражения, находим: L= Величина определяет квадрат величины момента импульса, Lz = lħ представляет собой максимальное значение проекции момента импульса на выбранное направление (ось z).
 16. Излучение фотонов Спонтанное излучение Согласно квантовой механике, электрон, находящийся на энергетическом уровне выше основного, может испустить фотон и перейти на более низкий энергетический уровень. Такой процесс называется спонтанным излучением. Типичное время, необходимое для процесса испускания фотона, составляет порядка 10 8 с.
16. Излучение фотонов Спонтанное излучение Согласно квантовой механике, электрон, находящийся на энергетическом уровне выше основного, может испустить фотон и перейти на более низкий энергетический уровень. Такой процесс называется спонтанным излучением. Типичное время, необходимое для процесса испускания фотона, составляет порядка 10 8 с.
 Если фотон испускается в результате перехода между уровнями с энергиями Еn' и Еn, то его энергия: h = Еn' – Еn Частота фотона = (Еn' – Еn)/h Если атом имеет, например, четыре различных энергетических уровня, как показано на рис. 16. 1, то возможны шесть различных переходов с более высоких уровней на более низкие.
Если фотон испускается в результате перехода между уровнями с энергиями Еn' и Еn, то его энергия: h = Еn' – Еn Частота фотона = (Еn' – Еn)/h Если атом имеет, например, четыре различных энергетических уровня, как показано на рис. 16. 1, то возможны шесть различных переходов с более высоких уровней на более низкие.
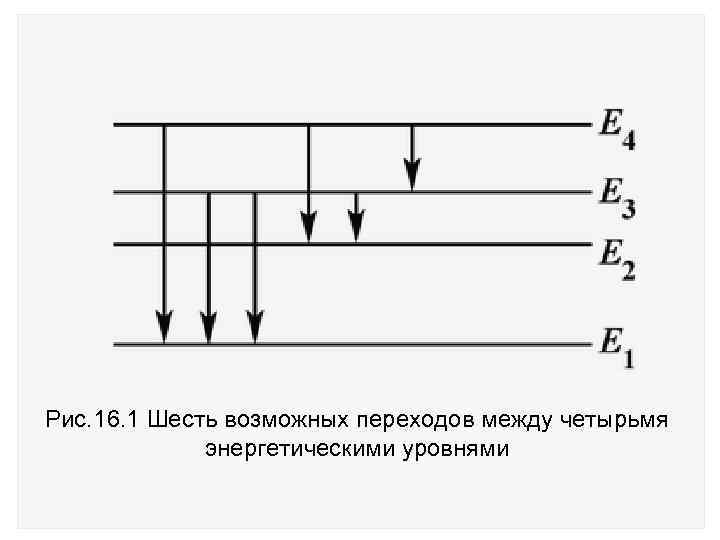 Рис. 16. 1 Шесть возможных переходов между четырьмя энергетическими уровнями
Рис. 16. 1 Шесть возможных переходов между четырьмя энергетическими уровнями
 Фотоны представляют собой элементарные частицы со спином 1 и моментом импульса L = ħ. При испускании фотона орбитальное квантовое число атома l изменяется на единицу.
Фотоны представляют собой элементарные частицы со спином 1 и моментом импульса L = ħ. При испускании фотона орбитальное квантовое число атома l изменяется на единицу.
 16. 1 Спектр излучения атома водорода Пусть энергия более высокого возбужденного уровня равна а энергия более низкого уровня равна
16. 1 Спектр излучения атома водорода Пусть энергия более высокого возбужденного уровня равна а энергия более низкого уровня равна
 Частоты, отвечающие различным спектральным линиям, равны Серия спектральных линий при переходах с верхних возбуждённых состояний на нижнее основное состояние (n = 1) дает серию Лаймана. Все линии серии расположены в ультрафиолетовой области спектра излучения. При переходе на n = 2 возникает другая серия линий, называемая серией Бальмера (видимый свет) (рис. 16. 2 а, б).
Частоты, отвечающие различным спектральным линиям, равны Серия спектральных линий при переходах с верхних возбуждённых состояний на нижнее основное состояние (n = 1) дает серию Лаймана. Все линии серии расположены в ультрафиолетовой области спектра излучения. При переходе на n = 2 возникает другая серия линий, называемая серией Бальмера (видимый свет) (рис. 16. 2 а, б).
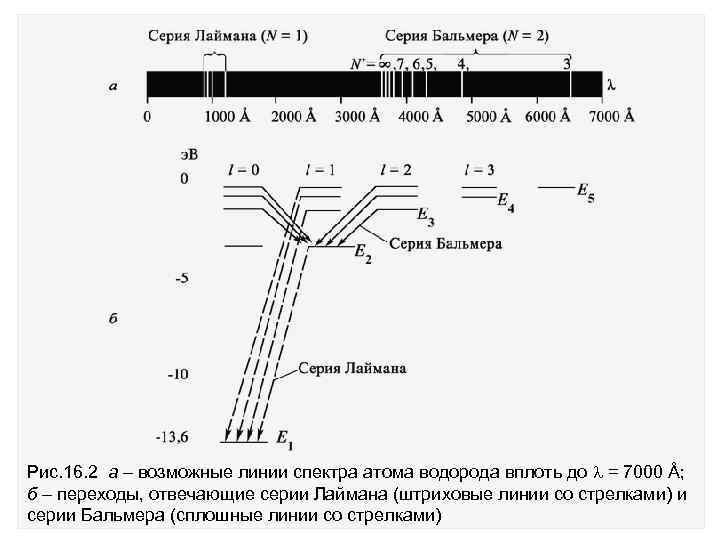 Рис. 16. 2 а возможные линии спектра атома водорода вплоть до = 7000 Å; б переходы, отвечающие серии Лаймана (штриховые линии со стрелками) и серии Бальмера (сплошные линии со стрелками)
Рис. 16. 2 а возможные линии спектра атома водорода вплоть до = 7000 Å; б переходы, отвечающие серии Лаймана (штриховые линии со стрелками) и серии Бальмера (сплошные линии со стрелками)
 16. 2 Вынужденное излучение Обозначим через N 1 - число атомов находящихся в основном состоянии с энергией Е 1, а через N 2 число возбужденных атомов с энергией Е 2, N = N 1 + N 2 общее число атомов. Величины N 1 и N 2 называют заселенностью соответствующих энергетических уровней.
16. 2 Вынужденное излучение Обозначим через N 1 - число атомов находящихся в основном состоянии с энергией Е 1, а через N 2 число возбужденных атомов с энергией Е 2, N = N 1 + N 2 общее число атомов. Величины N 1 и N 2 называют заселенностью соответствующих энергетических уровней.
 В состоянии термодинамического равновесия формула Больцмана дает соотношение между числами N 1 и N 2 при заданной температуре T Из него следует, что при любой температуре для равновесной системы N 1 N 2.
В состоянии термодинамического равновесия формула Больцмана дает соотношение между числами N 1 и N 2 при заданной температуре T Из него следует, что при любой температуре для равновесной системы N 1 N 2.
 Как отмечалось ранее, атом в возбужденном состоянии находится в течение очень малого промежутка времени и самопроизвольно переходит в основное состояние, испустив квант излучения ħ. Самопроизвольное излучение возбужденного атома называется спонтанным излучением.
Как отмечалось ранее, атом в возбужденном состоянии находится в течение очень малого промежутка времени и самопроизвольно переходит в основное состояние, испустив квант излучения ħ. Самопроизвольное излучение возбужденного атома называется спонтанным излучением.
 Спонтанное излучение атомов не коррелированно, неполяризованно и некогерентно. Такое излучение испускают обычные источники света лампы накаливания, люминесцентные лампы, нагретые тела, Солнце и др.
Спонтанное излучение атомов не коррелированно, неполяризованно и некогерентно. Такое излучение испускают обычные источники света лампы накаливания, люминесцентные лампы, нагретые тела, Солнце и др.
 Эйнштейн показал, что существует еще один процесс вынужденного или стимулированного излучения. Оно стимулируется излучением, падающим извне на возбужденный атом. С вероятностью В 12 оно вынуждает атом излучать. Скорость процесса вынужденного излучения равна Z 21 = B 21 N 2 U , T. , где U , T – плотность энергии излучения. Происходящий процесс изображен на рис. 16. 3.
Эйнштейн показал, что существует еще один процесс вынужденного или стимулированного излучения. Оно стимулируется излучением, падающим извне на возбужденный атом. С вероятностью В 12 оно вынуждает атом излучать. Скорость процесса вынужденного излучения равна Z 21 = B 21 N 2 U , T. , где U , T – плотность энергии излучения. Происходящий процесс изображен на рис. 16. 3.
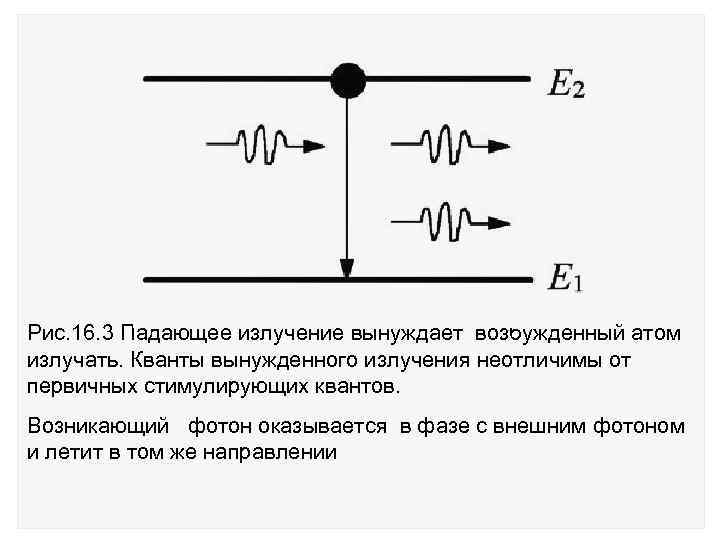 Рис. 16. 3 Падающее излучение вынуждает возбужденный атом излучать. Кванты вынужденного излучения неотличимы от первичных стимулирующих квантов. Возникающий фотон оказывается в фазе с внешним фотоном и летит в том же направлении
Рис. 16. 3 Падающее излучение вынуждает возбужденный атом излучать. Кванты вынужденного излучения неотличимы от первичных стимулирующих квантов. Возникающий фотон оказывается в фазе с внешним фотоном и летит в том же направлении
 Отметим свойства вынужденного излучения отличающие его от спонтанного излучения: 1. Вынужденное излучение распространяется в том же направлении, что и вызвавшее его излучение. 2. Фаза волны вынужденного излучения точно совпадает с фазой падающей волны. 3. Вынужденное излучение линейно поляризовано в той же плоскости поляризации, что и падающее излучение. 4. Кванты вынужденного излучения неотличимы от первичных квантов.
Отметим свойства вынужденного излучения отличающие его от спонтанного излучения: 1. Вынужденное излучение распространяется в том же направлении, что и вызвавшее его излучение. 2. Фаза волны вынужденного излучения точно совпадает с фазой падающей волны. 3. Вынужденное излучение линейно поляризовано в той же плоскости поляризации, что и падающее излучение. 4. Кванты вынужденного излучения неотличимы от первичных квантов.
 Среды с инверсной заселенностью уровней По мере распространения излучения в веществе его энергия уменьшается, а интенсивность убывает по экспоненциальному закону (закон Бугера): I(z) = I 0 exp( z). где I 0, I(z) интенсивность излучения на входе и на выходе слоя вещества; - коэффициент поглощения вещества. Для поглощающих излучение сред коэффициент положителен.
Среды с инверсной заселенностью уровней По мере распространения излучения в веществе его энергия уменьшается, а интенсивность убывает по экспоненциальному закону (закон Бугера): I(z) = I 0 exp( z). где I 0, I(z) интенсивность излучения на входе и на выходе слоя вещества; - коэффициент поглощения вещества. Для поглощающих излучение сред коэффициент положителен.
 Существуют среды, при распространении в которых излучение усиливается, а не ослабляется (среды с отрицательным коэффициентом поглощения) рис. 16. 4. Впервые эта идея была высказана Фабрикантом в 1939 г. Такая активная среда должна иметь N 2>N 1 инверсную заселенность энергетических уровней.
Существуют среды, при распространении в которых излучение усиливается, а не ослабляется (среды с отрицательным коэффициентом поглощения) рис. 16. 4. Впервые эта идея была высказана Фабрикантом в 1939 г. Такая активная среда должна иметь N 2>N 1 инверсную заселенность энергетических уровней.
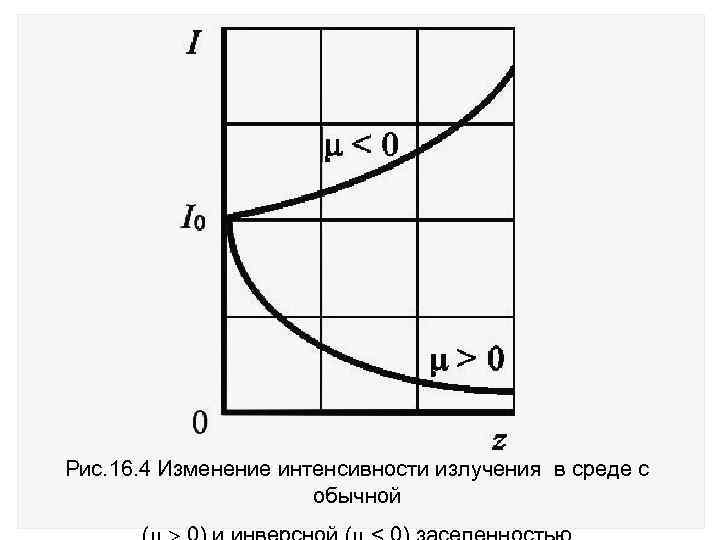 Рис. 16. 4 Изменение интенсивности излучения в среде с обычной
Рис. 16. 4 Изменение интенсивности излучения в среде с обычной
 Механизм усиления вынужденного излучения при распространении его в активной среде состоит в следующем. Если атом находится в возбужденном состоянии, то под действием падающего излучения он может вынужденно испустить еще один квант излучения, увеличивая энергию излучения в веществе на ħ.
Механизм усиления вынужденного излучения при распространении его в активной среде состоит в следующем. Если атом находится в возбужденном состоянии, то под действием падающего излучения он может вынужденно испустить еще один квант излучения, увеличивая энергию излучения в веществе на ħ.
 В равновесном состоянии вещества число атомов в основном состоянии N 1 всегда больше числа атомов N 2 в возбужденном состоянии. Для создания активной среды с инверсной заселенностью уровней необходимы особые условия, обеспечивающие генерацию возбужденных атомов.
В равновесном состоянии вещества число атомов в основном состоянии N 1 всегда больше числа атомов N 2 в возбужденном состоянии. Для создания активной среды с инверсной заселенностью уровней необходимы особые условия, обеспечивающие генерацию возбужденных атомов.
 16. 3 Лазер Квантовые усилители и генераторы. Идея усиления и генерации вынужденного излучения активной средой была реализована в 1955 г. Басовым и Прохоровым в СССР и в США Таунсом, Вебером. В 1960 г. был создан оптический квантовый генератор - лазер (Light Amplification by Stimulated Emission of Radiation усиление света с помощью вынужденного излучения).
16. 3 Лазер Квантовые усилители и генераторы. Идея усиления и генерации вынужденного излучения активной средой была реализована в 1955 г. Басовым и Прохоровым в СССР и в США Таунсом, Вебером. В 1960 г. был создан оптический квантовый генератор - лазер (Light Amplification by Stimulated Emission of Radiation усиление света с помощью вынужденного излучения).
 Первый твердотельный лазер был создан на основе монокристалла рубина (корунд Al 2 O 3 с примесями ионов хрома Cr 3+). Для создания инверсии заселенностей уровней использовалась трехуровневая схема. Энергетический спектр атомов содержит три уровня с энергиями Е 1, Е 2 и Е 3 (рис. 16. 5).
Первый твердотельный лазер был создан на основе монокристалла рубина (корунд Al 2 O 3 с примесями ионов хрома Cr 3+). Для создания инверсии заселенностей уровней использовалась трехуровневая схема. Энергетический спектр атомов содержит три уровня с энергиями Е 1, Е 2 и Е 3 (рис. 16. 5).
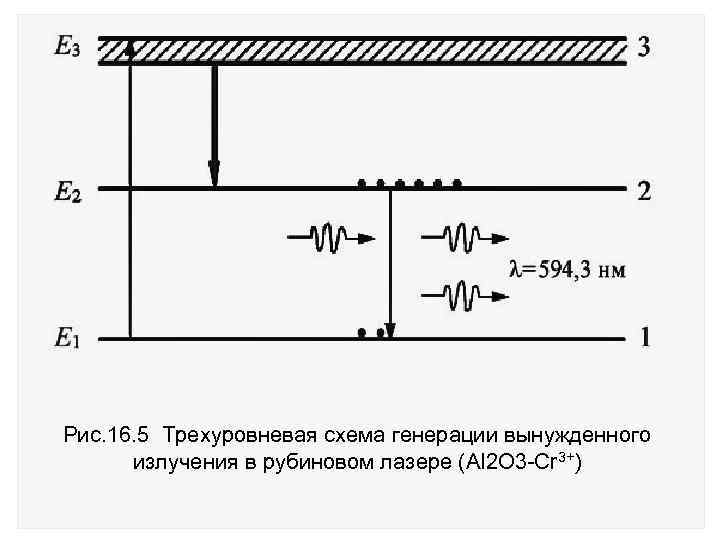 Рис. 16. 5 Трехуровневая схема генерации вынужденного излучения в рубиновом лазере (Al 2 O 3 -Cr 3+)
Рис. 16. 5 Трехуровневая схема генерации вынужденного излучения в рубиновом лазере (Al 2 O 3 -Cr 3+)
 Главная особенность трехуровневой системы состоит в том, что средний уровень 2 метастабильный, но время жизни атома в нем (~ 10 3 с) в сотни тысяч раз превышает время жизни в обычном возбужденном состоянии (~ 10 8 с). Это позволяет накапливать возбужденные атомы на втором уровне с энергией Е 2.
Главная особенность трехуровневой системы состоит в том, что средний уровень 2 метастабильный, но время жизни атома в нем (~ 10 3 с) в сотни тысяч раз превышает время жизни в обычном возбужденном состоянии (~ 10 8 с). Это позволяет накапливать возбужденные атомы на втором уровне с энергией Е 2.
 Процесс перевода атомов в возбужденное состояние называют накачкой. В рубиновом лазере используется импульсная оптическая накачка. Кристалл рубина Р освещают ксеноновой лампой Л, работающей в импульсном режиме, длительность вспышки ~ 10 3 с (рис. 16. 6).
Процесс перевода атомов в возбужденное состояние называют накачкой. В рубиновом лазере используется импульсная оптическая накачка. Кристалл рубина Р освещают ксеноновой лампой Л, работающей в импульсном режиме, длительность вспышки ~ 10 3 с (рис. 16. 6).
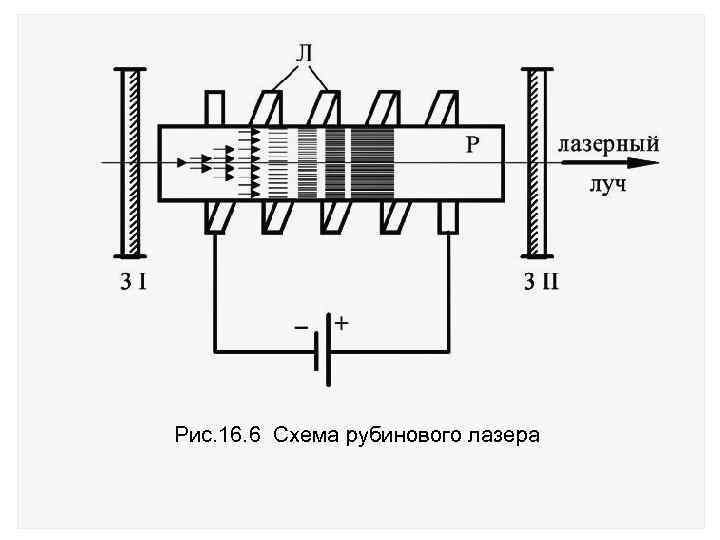 Рис. 16. 6 Схема рубинового лазера
Рис. 16. 6 Схема рубинового лазера
 Поглощая это излучение, атомы хрома переходят в возбужденное состояние с энергией Е 3, время жизни которых < 10 7 с. За это время атомы хрома переходят на более низкий метастабильный энергетический уровень с Е 2. Переход 3 2 является безызлучательным (без испускания фотона), избыток энергии передается от атома хрома к кристаллической решетке рубина.
Поглощая это излучение, атомы хрома переходят в возбужденное состояние с энергией Е 3, время жизни которых < 10 7 с. За это время атомы хрома переходят на более низкий метастабильный энергетический уровень с Е 2. Переход 3 2 является безызлучательным (без испускания фотона), избыток энергии передается от атома хрома к кристаллической решетке рубина.
 Метастабильность уровня 2 обеспечивает инверсную заселенность уровней 1 и 2. Рубиновый стержень превращается в активную среду, способную усиливать вынужденное излучение с λ = 594, 3 нм (переход 2 1). Если в результате спонтанного перехода рождается фотон с такой длиной волны, то он индуцирует новые фотоны, точно копирующие первоначальный.
Метастабильность уровня 2 обеспечивает инверсную заселенность уровней 1 и 2. Рубиновый стержень превращается в активную среду, способную усиливать вынужденное излучение с λ = 594, 3 нм (переход 2 1). Если в результате спонтанного перехода рождается фотон с такой длиной волны, то он индуцирует новые фотоны, точно копирующие первоначальный.
 Рождение вынужденных фотонов носит лавинообразный характер. Чтобы оптический усилитель превратить в оптический генератор когерентного лазерного излучения, необходимо обеспечить положительную обратную связь. Для этого усиленный пучок излучения надо снова направить в активную среду.
Рождение вынужденных фотонов носит лавинообразный характер. Чтобы оптический усилитель превратить в оптический генератор когерентного лазерного излучения, необходимо обеспечить положительную обратную связь. Для этого усиленный пучок излучения надо снова направить в активную среду.
 Обратную связь обеспечивает оптический резонатор, состоящий из двух параллельных плоских зеркал (ЗI и ЗII на рис. 16. 6), расположенных вблизи торцов рубинового стержня. Одно из зеркал делается полупрозрачным. После многократного отражения от зеркал и усиления лазерный пучок становится интенсивным и выходит через полупрозрачное зеркало. Затем следует новая вспышка лампы накачки и процесс повторяется.
Обратную связь обеспечивает оптический резонатор, состоящий из двух параллельных плоских зеркал (ЗI и ЗII на рис. 16. 6), расположенных вблизи торцов рубинового стержня. Одно из зеркал делается полупрозрачным. После многократного отражения от зеркал и усиления лазерный пучок становится интенсивным и выходит через полупрозрачное зеркало. Затем следует новая вспышка лампы накачки и процесс повторяется.
 Основные выводы Уравнение Шредингера в трех измерениях записывается следующим образом: В случае, когда (x, у, z) зависит только от r, это уравнение принимает вид
Основные выводы Уравнение Шредингера в трех измерениях записывается следующим образом: В случае, когда (x, у, z) зависит только от r, это уравнение принимает вид
 В случае атома водорода U = k 0(e 2/r). При этом решением, соответствующим состоянию с низшей энергией E 1 = k 0(me 4/2 ħ 2) = 13, 6 э. В, является функция 1 = ехр(–r/а), где а = ħ /(k 0 me 2) радиус. Собственные значения энергии En = ( 13, 6/n 2) э. В. Соответствующие им решения могут зависеть от углов и .
В случае атома водорода U = k 0(e 2/r). При этом решением, соответствующим состоянию с низшей энергией E 1 = k 0(me 4/2 ħ 2) = 13, 6 э. В, является функция 1 = ехр(–r/а), где а = ħ /(k 0 me 2) радиус. Собственные значения энергии En = ( 13, 6/n 2) э. В. Соответствующие им решения могут зависеть от углов и .
 Зависимость волновой функции от угла имеет вид exp(im ), где Lz = mħ проекция момента импульса на ось z. Зависимость от угла характеризуется значением квантового числа l, причем L = l ħ максимальное значение величины Lz; иными словами, m может быть любым целым числом в пределах от l до + l. Квантовое число l может принимать целочисленные значения от 0 до n 1. При n > n возможен спонтанный переход с уровня Еn' на уровень Еn, сопровождающийся испусканием фотона.
Зависимость волновой функции от угла имеет вид exp(im ), где Lz = mħ проекция момента импульса на ось z. Зависимость от угла характеризуется значением квантового числа l, причем L = l ħ максимальное значение величины Lz; иными словами, m может быть любым целым числом в пределах от l до + l. Квантовое число l может принимать целочисленные значения от 0 до n 1. При n > n возможен спонтанный переход с уровня Еn' на уровень Еn, сопровождающийся испусканием фотона.
 Энергия фотона h = Еn' – Еn. Если фотон с такой частотой сталкивается с атомом в состоянии Еn, то фотон может поглотиться, а атом при этом перейдет из начального состояния Еn в состояние Еn'. Если газообразный водород нагрет и часть атомов находится в возбужденных состояниях с более высокой энергией, то энергии фотонов в спектре излучения запишутся в виде
Энергия фотона h = Еn' – Еn. Если фотон с такой частотой сталкивается с атомом в состоянии Еn, то фотон может поглотиться, а атом при этом перейдет из начального состояния Еn в состояние Еn'. Если газообразный водород нагрет и часть атомов находится в возбужденных состояниях с более высокой энергией, то энергии фотонов в спектре излучения запишутся в виде
 17. Плотность потока вероятности. Уравнение непрерывности. Получим уравнение, которому удовлетворяет плотность вероятности
17. Плотность потока вероятности. Уравнение непрерывности. Получим уравнение, которому удовлетворяет плотность вероятности
 Подставляя, получаем - плотность потока вероятности Уравнение непрерывности Оно является аналогом уравнений непрерывности тока и и жидкости.
Подставляя, получаем - плотность потока вероятности Уравнение непрерывности Оно является аналогом уравнений непрерывности тока и и жидкости.
 Возьмем интеграл по некоторому объему Применим теорему Остроградского-Гаусса
Возьмем интеграл по некоторому объему Применим теорему Остроградского-Гаусса
 Таким образом, изменение вероятности обнаружения частицы в объеме V за 1 сек равно потоку плотности вероятности через поверхность S, ограничивающую объем V.
Таким образом, изменение вероятности обнаружения частицы в объеме V за 1 сек равно потоку плотности вероятности через поверхность S, ограничивающую объем V.
 18. Туннелирование частиц через потенциальный барьер Потенциальным барьером называется область пространства, в которой классическая частица с малой энергией не может находиться. Рассмотрим одномерный случай с потенциалом в виде прямоугольного барьера с шириной L и высотой U 0. Потенциальная энергия частицы U(x) вне и внутри потенциального барьера имеет значения: U=U 0 (0
18. Туннелирование частиц через потенциальный барьер Потенциальным барьером называется область пространства, в которой классическая частица с малой энергией не может находиться. Рассмотрим одномерный случай с потенциалом в виде прямоугольного барьера с шириной L и высотой U 0. Потенциальная энергия частицы U(x) вне и внутри потенциального барьера имеет значения: U=U 0 (0
 Задача заключается в определении вероятности прохождения частиц с энергией Е < U 0, налетающих из области 1, через барьер 2 в область 3. Обозначим эту вероятность как Р(Е). Она равна отношению плотностей потоков вероятности прошедших и налетающих частиц Плотность потока вероятности в одномерном случае равны
Задача заключается в определении вероятности прохождения частиц с энергией Е < U 0, налетающих из области 1, через барьер 2 в область 3. Обозначим эту вероятность как Р(Е). Она равна отношению плотностей потоков вероятности прошедших и налетающих частиц Плотность потока вероятности в одномерном случае равны
 Волновые функции, отвечающие налетающим и прошедшим частицам, определим из решения стационарного уравнения Шредингера
Волновые функции, отвечающие налетающим и прошедшим частицам, определим из решения стационарного уравнения Шредингера
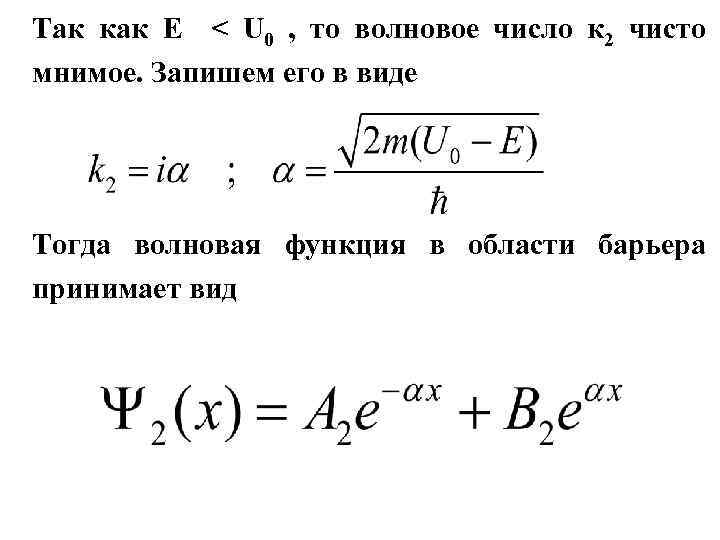 Так как Е < U 0 , то волновое число к 2 чисто мнимое. Запишем его в виде Тогда волновая функция в области барьера принимает вид
Так как Е < U 0 , то волновое число к 2 чисто мнимое. Запишем его в виде Тогда волновая функция в области барьера принимает вид
 Падающим и прошедшим частицам отвечают первые слагаемые в волновых функциях в области 1 и в области 3 соответственно Тогда плотности потоков вероятности будут равны
Падающим и прошедшим частицам отвечают первые слагаемые в волновых функциях в области 1 и в области 3 соответственно Тогда плотности потоков вероятности будут равны
 В результате вероятность прохождения (коэффициент прохождения) равна Отношение коэффициентов определим из граничных условий. Во первых, так как справа частицы на барьер не налетают, то В 3 =0. Потребуем непрерывность волновых функций и их производных на двух границах барьера.
В результате вероятность прохождения (коэффициент прохождения) равна Отношение коэффициентов определим из граничных условий. Во первых, так как справа частицы на барьер не налетают, то В 3 =0. Потребуем непрерывность волновых функций и их производных на двух границах барьера.
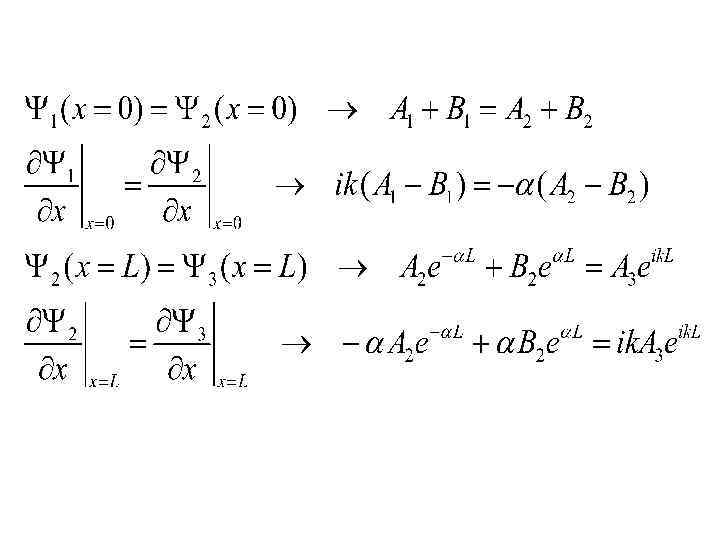
 Их совместное решение дает Так как α > 0, то для достаточно толстых барьеров
Их совместное решение дает Так как α > 0, то для достаточно толстых барьеров
 Это позволяет пренебречь в условиях сшивания слагаемыми с коэффициентом В 2. Исключая коэффициенты В 1 и А 2, получаем В результате коэффициент прохождения равен
Это позволяет пренебречь в условиях сшивания слагаемыми с коэффициентом В 2. Исключая коэффициенты В 1 и А 2, получаем В результате коэффициент прохождения равен
 Р 0 ≈1. Коэффициент прохождения Р(Е) зависит от толщины и высоты барьера, массы и энергии частицы. Туннелирование частиц через барьер – чисто квантовое явление, связанное с волновыми свойствами частиц. В макроскопических явлениях туннельный эффект не играет существенной роли. Пример : Пусть частицей является электрон с U 0 -E ≈ 10 э. В. Если L=1 см, то Р(Е) ≈ exp(-108) ≈0. Если L=1 Å, то Р(Е) ≈exp(-1).
Р 0 ≈1. Коэффициент прохождения Р(Е) зависит от толщины и высоты барьера, массы и энергии частицы. Туннелирование частиц через барьер – чисто квантовое явление, связанное с волновыми свойствами частиц. В макроскопических явлениях туннельный эффект не играет существенной роли. Пример : Пусть частицей является электрон с U 0 -E ≈ 10 э. В. Если L=1 см, то Р(Е) ≈ exp(-108) ≈0. Если L=1 Å, то Р(Е) ≈exp(-1).
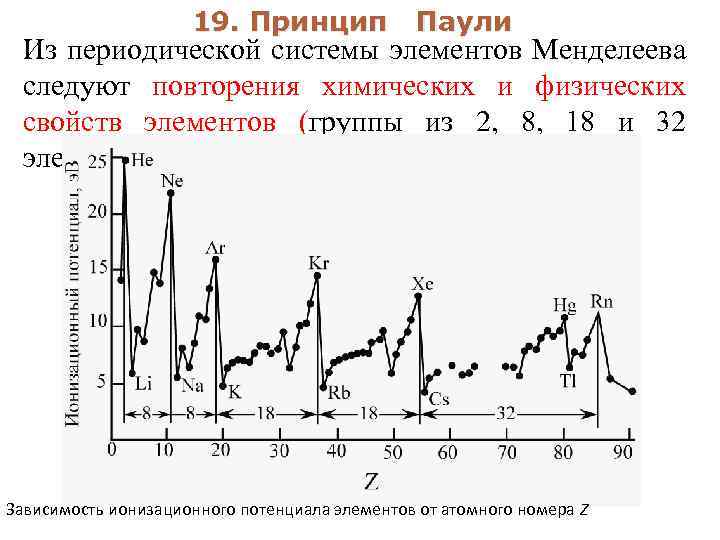 19. Принцип Паули Из периодической системы элементов Менделеева следуют повторения химических и физических свойств элементов (группы из 2, 8, 18 и 32 элементов). Зависимость ионизационного потенциала элементов от атомного номера Z
19. Принцип Паули Из периодической системы элементов Менделеева следуют повторения химических и физических свойств элементов (группы из 2, 8, 18 и 32 элементов). Зависимость ионизационного потенциала элементов от атомного номера Z
 Спин электрона. В 1925 г. Уленбек и Гаудсмит предположили, что у электрона имеется собственный момент импульса (спин), равный Sz=msħ, где ms=± 1/2 – магнитное спиновое число. Это похоже на то, как если бы электрон представлял собой сферу, вращающуюся вокруг собственной оси с постоянным моментом ħ /2. Собственный момент (спин) невозможно ни уменьшить, ни увеличить. Он одинаков у всех элементарных частиц данного
Спин электрона. В 1925 г. Уленбек и Гаудсмит предположили, что у электрона имеется собственный момент импульса (спин), равный Sz=msħ, где ms=± 1/2 – магнитное спиновое число. Это похоже на то, как если бы электрон представлял собой сферу, вращающуюся вокруг собственной оси с постоянным моментом ħ /2. Собственный момент (спин) невозможно ни уменьшить, ни увеличить. Он одинаков у всех элементарных частиц данного
 В 1925 г. Паули предложил правило, которое автоматически объясняло наличие групп из 2, 8, 18 и 32 элементов. Паули постулировал: в атоме не может быть двух электронов, имеющих одинаковые значения четырёх квантовых чисел: главного n, орбитального l , магнитного m и спинового ms.
В 1925 г. Паули предложил правило, которое автоматически объясняло наличие групп из 2, 8, 18 и 32 элементов. Паули постулировал: в атоме не может быть двух электронов, имеющих одинаковые значения четырёх квантовых чисел: главного n, орбитального l , магнитного m и спинового ms.
 Согласно Паули число электронов в состоянии n равно Z = 2 n 2, а число электронов в состоянии l равно Z = 2(2 l +1). Следовательно, в состоянии с n = 1 могут находиться два электрона, в состоянию с n = 2, 8 электронов, с n = 3, 18 электронов и т. д. Мы видим, что числа 2, 8 и 18 являются прямым следствием принципа запрета Паули.
Согласно Паули число электронов в состоянии n равно Z = 2 n 2, а число электронов в состоянии l равно Z = 2(2 l +1). Следовательно, в состоянии с n = 1 могут находиться два электрона, в состоянию с n = 2, 8 электронов, с n = 3, 18 электронов и т. д. Мы видим, что числа 2, 8 и 18 являются прямым следствием принципа запрета Паули.
 20. Периодическая система элементов Уравнение Шредингера и принцип Паули позволяют «рассчитать» свойства всех элементов, не обращаясь к результатам химических опытов. К настоящему времени рассчитаны электронные плотности и энергии связи более тяжелых, чем водород, атомов. Стало возможным вычислять скорости химических реакций и изучать структуру молекулярной связи. Рассмотрим электронные оболочки атомов.
20. Периодическая система элементов Уравнение Шредингера и принцип Паули позволяют «рассчитать» свойства всех элементов, не обращаясь к результатам химических опытов. К настоящему времени рассчитаны электронные плотности и энергии связи более тяжелых, чем водород, атомов. Стало возможным вычислять скорости химических реакций и изучать структуру молекулярной связи. Рассмотрим электронные оболочки атомов.
 Z = 1 (ВОДОРОД) Единственный электрон находится в состоянии 1 s (s- состояние l =0; p - l = 1; d - l = 2) с n = 1, l =0, ms=± ½. Энергия электрона равна – 13, 6 э. В. Эта минимальная энергия, необходимая для ионизации атома, называется ионизационным потенциалом.
Z = 1 (ВОДОРОД) Единственный электрон находится в состоянии 1 s (s- состояние l =0; p - l = 1; d - l = 2) с n = 1, l =0, ms=± ½. Энергия электрона равна – 13, 6 э. В. Эта минимальная энергия, необходимая для ионизации атома, называется ионизационным потенциалом.
 Z = 2 (ГЕЛИЙ). В атоме гелия имеются два электрона. Второй электрон находится в состоянии 1 s с n = 1, l = 0, m=0, но спин его ориентирован противоположно спину первого электрона. Два электрона Не образуют заполненную оболочку с n = 1, завершающую 1 -ый периодической системы Менделеева. У гелия значение ионизационного потенциала равно 24, 6 В. Это самый большой из ионизационных потенциалов всех элементов.
Z = 2 (ГЕЛИЙ). В атоме гелия имеются два электрона. Второй электрон находится в состоянии 1 s с n = 1, l = 0, m=0, но спин его ориентирован противоположно спину первого электрона. Два электрона Не образуют заполненную оболочку с n = 1, завершающую 1 -ый периодической системы Менделеева. У гелия значение ионизационного потенциала равно 24, 6 В. Это самый большой из ионизационных потенциалов всех элементов.
 Из-за значительного ионизационного потенциала и отсутствия на оболочке с n = 1 места для третьего электрона, гелий химически крайне инертен. Химические силы не в состоянии обеспечить энергию в 24, 6 э. В, чтобы мог образоваться положительный ион Не+. Гелий не образует молекул ни с одним из элементов. Его и другие атомы с заполненными оболочками называют благородными (или инертными) газами.
Из-за значительного ионизационного потенциала и отсутствия на оболочке с n = 1 места для третьего электрона, гелий химически крайне инертен. Химические силы не в состоянии обеспечить энергию в 24, 6 э. В, чтобы мог образоваться положительный ион Не+. Гелий не образует молекул ни с одним из элементов. Его и другие атомы с заполненными оболочками называют благородными (или инертными) газами.
 Z = 3 (ЛИТИЙ) Литием начинается 2 -ой периодической системы Менделеева. Литий содержит 3 электрона. Согласно принципу Паули 3 -ий электрон не может находиться в заполненной оболочке с n = 1, поэтому он занимает наинизшее энергетическое состояние в оболочке с n = 2, l =0, m=0. Ионизационный потенциал лития равен 5, 4 э. В. В соединениях литий всегда обнаруживает валентность +1 (т. е. теряет один электрон) и никогда не обнаруживает валентность +2 (т. е. не теряет два электрона).
Z = 3 (ЛИТИЙ) Литием начинается 2 -ой периодической системы Менделеева. Литий содержит 3 электрона. Согласно принципу Паули 3 -ий электрон не может находиться в заполненной оболочке с n = 1, поэтому он занимает наинизшее энергетическое состояние в оболочке с n = 2, l =0, m=0. Ионизационный потенциал лития равен 5, 4 э. В. В соединениях литий всегда обнаруживает валентность +1 (т. е. теряет один электрон) и никогда не обнаруживает валентность +2 (т. е. не теряет два электрона).
 Периодическая система элементов
Периодическая система элементов
 Z = 4 (БЕРИЛЛИЙ) Согласно принципу Паули, в состоянии с n = 2 и l = 0 могут находиться два электрона. Ионизационный потенциал бериллия равен 9, 32 э. В.
Z = 4 (БЕРИЛЛИЙ) Согласно принципу Паули, в состоянии с n = 2 и l = 0 могут находиться два электрона. Ионизационный потенциал бериллия равен 9, 32 э. В.
 Z = 5 (БОР), Z = 6 (УГЛЕРОД), Z = 7 (АЗОТ), Z = 8 (КИСЛОРОД), Z = 9 (ФТОР) И Z = 10 (НЕОН) Эти атомы образуются при заполнении состояний с орбитальным числом l = 1 в оболочке с nразличных Поскольку значению l = 1 отвечают три = 2. значения m, то на подоболочке (n = 2, l = 1) могут разместиться 6 электронов. В состоянии с n = 2 в атомах бора, углерода и азота находятся соответственно три, четыре и пять электронов, что отвечает валентностям +3, +4 и +5.
Z = 5 (БОР), Z = 6 (УГЛЕРОД), Z = 7 (АЗОТ), Z = 8 (КИСЛОРОД), Z = 9 (ФТОР) И Z = 10 (НЕОН) Эти атомы образуются при заполнении состояний с орбитальным числом l = 1 в оболочке с nразличных Поскольку значению l = 1 отвечают три = 2. значения m, то на подоболочке (n = 2, l = 1) могут разместиться 6 электронов. В состоянии с n = 2 в атомах бора, углерода и азота находятся соответственно три, четыре и пять электронов, что отвечает валентностям +3, +4 и +5.
 НЕОН. У неона все состояния с n = 2 заняты, оболочка полностью заполнена. Неон, как и гелий, является химически инертным. Если продолжить описание следующих элементов, то мы обнаружим, что их свойства очень сходны со свойствами уже перечисленных ранее элементов.
НЕОН. У неона все состояния с n = 2 заняты, оболочка полностью заполнена. Неон, как и гелий, является химически инертным. Если продолжить описание следующих элементов, то мы обнаружим, что их свойства очень сходны со свойствами уже перечисленных ранее элементов.
 ОТ Z = 11 (НАТРИЙ) ДО Z = 18 (АРГОН) Согласно принципу Паули, одиннадцатый электрон натрия занимает состояние с n = 3, занимая низшее состояние 3 s. Теория предсказывает, что всякий раз, когда внешний электрон попадает на оболочку с большим квантовым числом n, размер атома значительно увеличивается. Такое резкое увеличение размеров наблюдается для Z = 3, 11, 19. . . ,
ОТ Z = 11 (НАТРИЙ) ДО Z = 18 (АРГОН) Согласно принципу Паули, одиннадцатый электрон натрия занимает состояние с n = 3, занимая низшее состояние 3 s. Теория предсказывает, что всякий раз, когда внешний электрон попадает на оболочку с большим квантовым числом n, размер атома значительно увеличивается. Такое резкое увеличение размеров наблюдается для Z = 3, 11, 19. . . ,
 Энергетические уровни электронов. Состояния с одинаковыми главными квантовыми числами соединены штриховыми линиями. Состояния образуют группы периодичности с числом электронов 2, 8, 8, 18, 32
Энергетические уровни электронов. Состояния с одинаковыми главными квантовыми числами соединены штриховыми линиями. Состояния образуют группы периодичности с числом электронов 2, 8, 8, 18, 32
 В восьми элементах от натрия до аргона – заполняются состояния с n = 3, l = 0 и n = 3, l = 1. Заполнение происходит аналогично предшествующим восьми элементам. Поэтому химические свойства этих элементов оказываются весьма похожими на свойства соответствующих элементов предыдущей восьмерки. В этом и заключается объяснение «периодической системы» химических элементов.
В восьми элементах от натрия до аргона – заполняются состояния с n = 3, l = 0 и n = 3, l = 1. Заполнение происходит аналогично предшествующим восьми элементам. Поэтому химические свойства этих элементов оказываются весьма похожими на свойства соответствующих элементов предыдущей восьмерки. В этом и заключается объяснение «периодической системы» химических элементов.
 ОТ Z = 19 (КАЛИЙ) И ДАЛЕЕ Можно было бы предположить, что внешний электрон следующего элемента окажется в состоянии с n = 3 и l = 2. Однако, для состояний с n = 4, l = 0 величина эффективного заряда ядра Zэфф, заметно больше, чем в случае состояний с n = 3, l = 2, поскольку волновая функция с l = 0 локализована в области r = 0, где эффективный заряд максимален. Для электронного состояния с n = 4, l = 0 имеем Zэфф = 2, 26 и энергию связи 13, 6 Z 2 эфф/42 = 4, 34 э. В, в то время как для волны с n = 3, l = 2 величина Zэфф несколько меньше 1, 7, чему соответствует энергия связи меньше 4, 34 э. В.
ОТ Z = 19 (КАЛИЙ) И ДАЛЕЕ Можно было бы предположить, что внешний электрон следующего элемента окажется в состоянии с n = 3 и l = 2. Однако, для состояний с n = 4, l = 0 величина эффективного заряда ядра Zэфф, заметно больше, чем в случае состояний с n = 3, l = 2, поскольку волновая функция с l = 0 локализована в области r = 0, где эффективный заряд максимален. Для электронного состояния с n = 4, l = 0 имеем Zэфф = 2, 26 и энергию связи 13, 6 Z 2 эфф/42 = 4, 34 э. В, в то время как для волны с n = 3, l = 2 величина Zэфф несколько меньше 1, 7, чему соответствует энергия связи меньше 4, 34 э. В.
 Если бы девятнадцатый электрон оказался в состоянии с n = 3, l = 2, то очень скоро он перешел бы в состояние с n = 4, l = 0, которому отвечает меньшая энергия. При переходе к Z = 21 (скандий) состояние с n = 4, l = 0 оказывается заполненным, так что при размещении двадцать первого электрона возникнет конкуренция между состояниями n = 3, l = 2 и n = 4, l = 1. Более низким оказывается состояние с n = 3, поэтому в скандии начинают заполняться десять состояний с l = 2 оболочки n = 3. Затем заполняются следующие шесть состояний с n = 4, l = 1. Таким образом, всего имеется 2 + 10 + 6 = 18 состояний с близкими энергиями.
Если бы девятнадцатый электрон оказался в состоянии с n = 3, l = 2, то очень скоро он перешел бы в состояние с n = 4, l = 0, которому отвечает меньшая энергия. При переходе к Z = 21 (скандий) состояние с n = 4, l = 0 оказывается заполненным, так что при размещении двадцать первого электрона возникнет конкуренция между состояниями n = 3, l = 2 и n = 4, l = 1. Более низким оказывается состояние с n = 3, поэтому в скандии начинают заполняться десять состояний с l = 2 оболочки n = 3. Затем заполняются следующие шесть состояний с n = 4, l = 1. Таким образом, всего имеется 2 + 10 + 6 = 18 состояний с близкими энергиями.
 На рисунке приведены 18 состояний, отвечающие изменению Z от 19 до 36. При любом заданном значении n энергия уровней скачкообразно увеличивается с ростом l. После чисел электронов 2, 10, 18, 36, 54 и 86 имеются особенно большие скачки энергии. У элементов с атомными номерами Z = 2, 10, 18, 36, 54 и 86 оболочки заполнены, так что внешние электроны связаны особенно прочно. Этими элементами являются благородные газы Не, Ne, Ar, Kr, Xe и Rn.
На рисунке приведены 18 состояний, отвечающие изменению Z от 19 до 36. При любом заданном значении n энергия уровней скачкообразно увеличивается с ростом l. После чисел электронов 2, 10, 18, 36, 54 и 86 имеются особенно большие скачки энергии. У элементов с атомными номерами Z = 2, 10, 18, 36, 54 и 86 оболочки заполнены, так что внешние электроны связаны особенно прочно. Этими элементами являются благородные газы Не, Ne, Ar, Kr, Xe и Rn.
 Можно указать значения квантовых чисел и энергий уровней для каждого электрона любого из элементов. В таблице приведены электронные конфигурации атомов. Соответствующая периодическая система элементов приведена в следующей таблице. Элементы в одной группе (колонке) обладают одними и теми же валентностями и аналогичными химическими свойствами.
Можно указать значения квантовых чисел и энергий уровней для каждого электрона любого из элементов. В таблице приведены электронные конфигурации атомов. Соответствующая периодическая система элементов приведена в следующей таблице. Элементы в одной группе (колонке) обладают одними и теми же валентностями и аналогичными химическими свойствами.
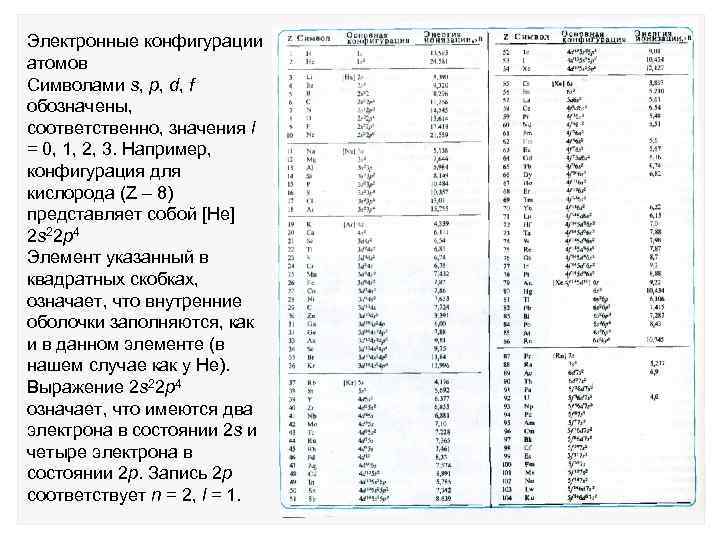 Электронные конфигурации атомов Символами s, р, d, f обозначены, соответственно, значения l = 0, 1, 2, 3. Например, конфигурация для кислорода (Z – 8) представляет собой [Не] 2 s 22 p 4 Элемент указанный в квадратных скобках, означает, что внутренние оболочки заполняются, как и в данном элементе (в нашем случае как у Не). Выражение 2 s 22 p 4 означает, что имеются два электрона в состоянии 2 s и четыре электрона в состоянии 2 р. Запись 2 р соответствует n = 2, l = 1.
Электронные конфигурации атомов Символами s, р, d, f обозначены, соответственно, значения l = 0, 1, 2, 3. Например, конфигурация для кислорода (Z – 8) представляет собой [Не] 2 s 22 p 4 Элемент указанный в квадратных скобках, означает, что внутренние оболочки заполняются, как и в данном элементе (в нашем случае как у Не). Выражение 2 s 22 p 4 означает, что имеются два электрона в состоянии 2 s и четыре электрона в состоянии 2 р. Запись 2 р соответствует n = 2, l = 1.


