4_Солнечная система Законы движения планет.ppt
- Количество слайдов: 60
 4. Солнечная система Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
4. Солнечная система Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
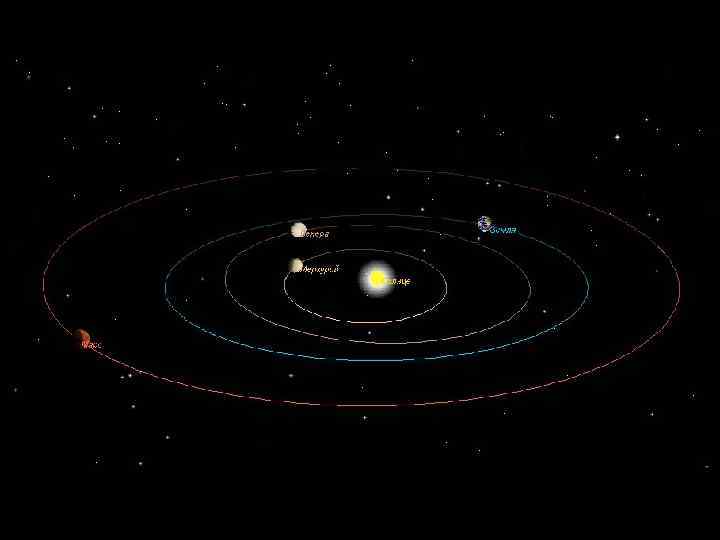
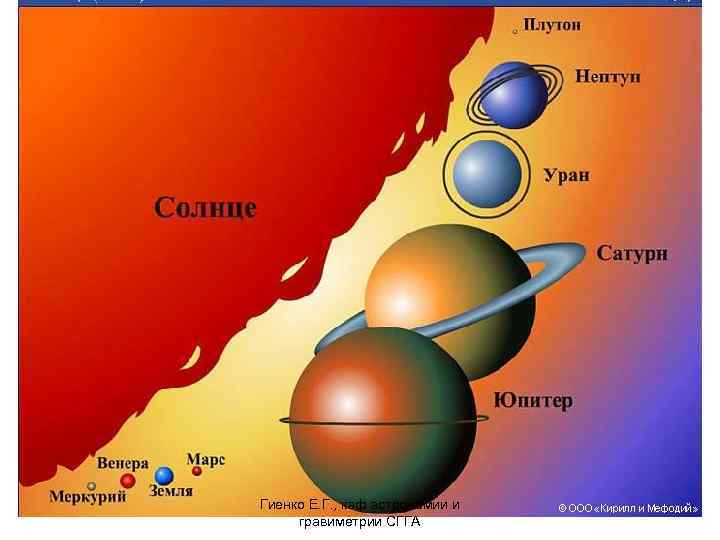
 Солнечная система: Солнце – звезда, 99, 8% массы всей системы 8 больших планет + спутники Карликовые планеты (Плутоиды - Плутон и др. аналоги) Малые тела С. С. : астероиды, кометы, метеорные тела Газ, пыль Элементарные частицы Электромагнитное излучение Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Солнечная система: Солнце – звезда, 99, 8% массы всей системы 8 больших планет + спутники Карликовые планеты (Плутоиды - Плутон и др. аналоги) Малые тела С. С. : астероиды, кометы, метеорные тела Газ, пыль Элементарные частицы Электромагнитное излучение Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 4. 1 Представления о Солнечной системе Геоцентрическая картина мира Неподвижная Земля – в центре мира. Мир таков, каким мы его видим Клавдий Птолемей, II век н. э. , Александрия Деференты и эпициклы Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
4. 1 Представления о Солнечной системе Геоцентрическая картина мира Неподвижная Земля – в центре мира. Мир таков, каким мы его видим Клавдий Птолемей, II век н. э. , Александрия Деференты и эпициклы Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Гелиоцентрическая картина мира Николай Коперник (1473 – 1543), Польша. Остановил Солнце, сдвинул Землю. Гелиоцентрическая картина мира. 1. В центре мира – Солнце. 2. Шарообразная Земля вращается вокруг оси. 3. Земля и др. планеты вращаются вокруг Солнца по равномерным круговым орбитам. Галилео Галилей (1564 - 1642), Италия Описал первые телескопические наблюдения: Пятна на Солнце и его вращение, Горы на Луне, Фазы Венеры, 4 спутника Юпитера Джордано Бруно, (1548 – 1600), философ, Италия Современные представления о картине мира: Множество звездных систем и обитаемых миров. Сожжен 17 февраля 1600 года на Площади Цветов (Campo de Fiori) в Риме астрономии и Гиенко Е. Г. , каф гравиметрии СГГА
Гелиоцентрическая картина мира Николай Коперник (1473 – 1543), Польша. Остановил Солнце, сдвинул Землю. Гелиоцентрическая картина мира. 1. В центре мира – Солнце. 2. Шарообразная Земля вращается вокруг оси. 3. Земля и др. планеты вращаются вокруг Солнца по равномерным круговым орбитам. Галилео Галилей (1564 - 1642), Италия Описал первые телескопические наблюдения: Пятна на Солнце и его вращение, Горы на Луне, Фазы Венеры, 4 спутника Юпитера Джордано Бруно, (1548 – 1600), философ, Италия Современные представления о картине мира: Множество звездных систем и обитаемых миров. Сожжен 17 февраля 1600 года на Площади Цветов (Campo de Fiori) в Риме астрономии и Гиенко Е. Г. , каф гравиметрии СГГА
 4. 2 Видимое движение планет Планеты: нижние (внутренние) – внутри орбиты Земли (Меркурий, Венера) верхние (внешние) – за орбитой Земли (остальные) Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
4. 2 Видимое движение планет Планеты: нижние (внутренние) – внутри орбиты Земли (Меркурий, Венера) верхние (внешние) – за орбитой Земли (остальные) Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Видимое движение планет – рядом с эклиптикой (по зодиакальным созвездиям) Прямое движение: с запада на восток Попятное движение: с востока на запад Конфигурации – характерное расположение планет относительно Солнца и Земли Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Видимое движение планет – рядом с эклиптикой (по зодиакальным созвездиям) Прямое движение: с запада на восток Попятное движение: с востока на запад Конфигурации – характерное расположение планет относительно Солнца и Земли Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
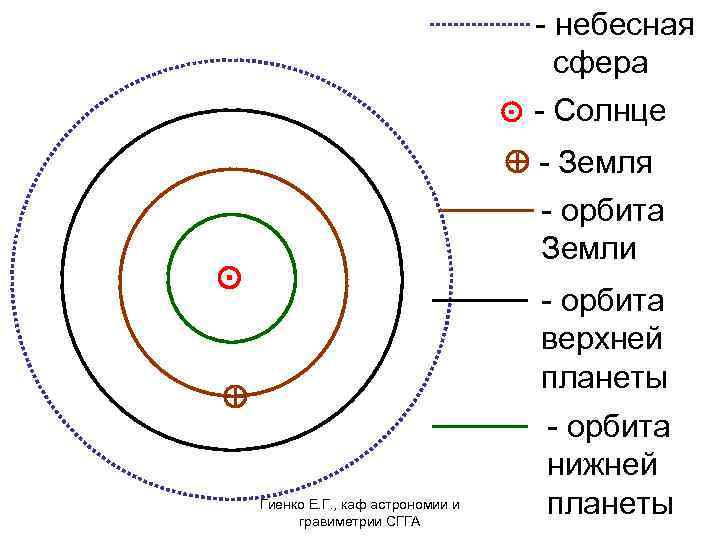 - небесная сфера ⊙ - Солнце - Земля - орбита Земли ⊙ - орбита верхней планеты Гиенко Е. Г. , каф астрономии и гравиметрии СГГА - орбита нижней планеты
- небесная сфера ⊙ - Солнце - Земля - орбита Земли ⊙ - орбита верхней планеты Гиенко Е. Г. , каф астрономии и гравиметрии СГГА - орбита нижней планеты
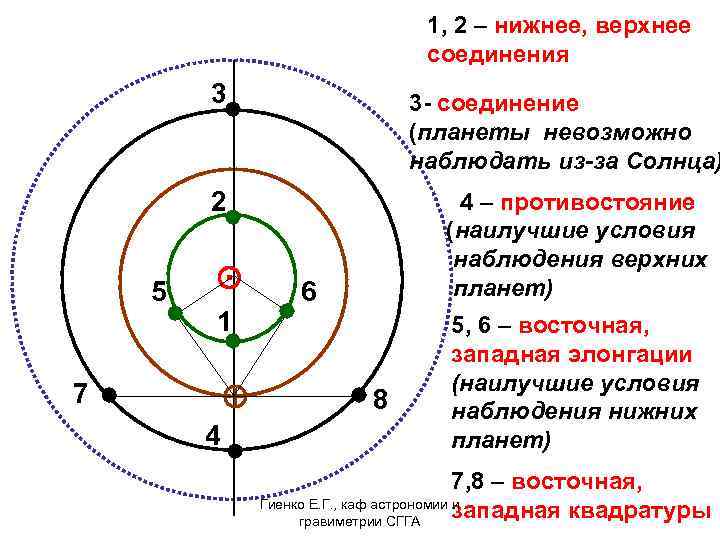 1, 2 – нижнее, верхнее соединения 3 3 - соединение (планеты невозможно наблюдать из-за Солнца) 2 5 ⊙ 1 7 4 4 – противостояние (наилучшие условия наблюдения верхних планет) 6 8 5, 6 – восточная, западная элонгации (наилучшие условия наблюдения нижних планет) 7, 8 – восточная, Гиенко Е. Г. , каф астрономии и западная квадратуры гравиметрии СГГА
1, 2 – нижнее, верхнее соединения 3 3 - соединение (планеты невозможно наблюдать из-за Солнца) 2 5 ⊙ 1 7 4 4 – противостояние (наилучшие условия наблюдения верхних планет) 6 8 5, 6 – восточная, западная элонгации (наилучшие условия наблюдения нижних планет) 7, 8 – восточная, Гиенко Е. Г. , каф астрономии и западная квадратуры гравиметрии СГГА
 Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Фотографии Марса, сделанные в г. Эншед (Голландия) в 2007 -2008 гг. Гиенко Е. Г. , каф астрономии и Увеличение одинаковое гравиметрии СГГА
Фотографии Марса, сделанные в г. Эншед (Голландия) в 2007 -2008 гг. Гиенко Е. Г. , каф астрономии и Увеличение одинаковое гравиметрии СГГА
 Прохождение Венеры по диску Солнца 8 июня 2004 г Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Прохождение Венеры по диску Солнца 8 июня 2004 г Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Прохождения Венеры: 1761: 6 июня (спустя 122 года) 1769: 3 -4 июня 1874: 8 -9 декабря (спустя 105 лет) 1882: 6 декабря 2004: 8 июня (спустя 122 года) 2012: 5 -6 июня 2117: 11 декабря (спустя 105 лет) 2125 : 8 декабря Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Прохождения Венеры: 1761: 6 июня (спустя 122 года) 1769: 3 -4 июня 1874: 8 -9 декабря (спустя 105 лет) 1882: 6 декабря 2004: 8 июня (спустя 122 года) 2012: 5 -6 июня 2117: 11 декабря (спустя 105 лет) 2125 : 8 декабря Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
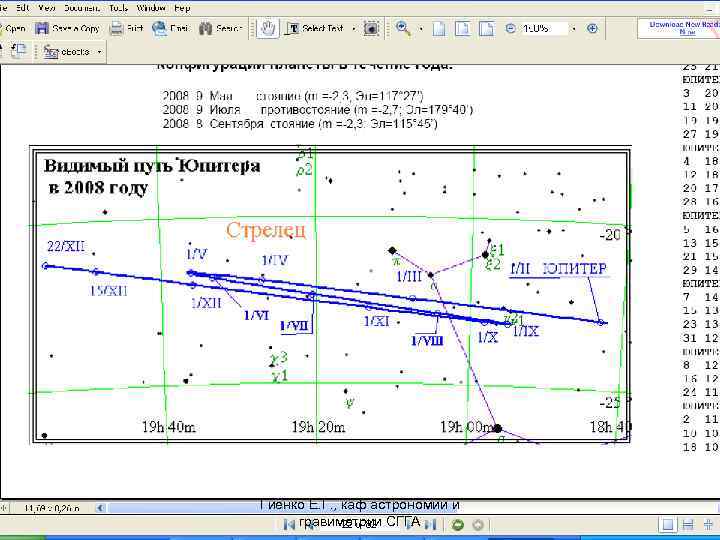
 Планеты в 2012 году: У Меркурия за весь год будет 4 утренних и 3 вечерних видимости. Для Венеры 2012 год - самый благоприятный за истекшие 8 лет (27 марта - вечерняя, а 15 августа утренняя элонгация). Марс 3 марта вступит в противостояние с Солнцем с видимым диаметром, достигающим 14 угловых секунд. Наилучшая видимость Юпитера относится ко второй половине года с противостоянием 3 декабря. Сатурн, наоборот, лучше всего виден в первом полугодии с противостоянием 15 апреля. Уран и Нептун являются осенними планетами, т. к. вступают в противостояние с Солнцем соответственно 29 сентября и 24 августа. Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Планеты в 2012 году: У Меркурия за весь год будет 4 утренних и 3 вечерних видимости. Для Венеры 2012 год - самый благоприятный за истекшие 8 лет (27 марта - вечерняя, а 15 августа утренняя элонгация). Марс 3 марта вступит в противостояние с Солнцем с видимым диаметром, достигающим 14 угловых секунд. Наилучшая видимость Юпитера относится ко второй половине года с противостоянием 3 декабря. Сатурн, наоборот, лучше всего виден в первом полугодии с противостоянием 15 апреля. Уран и Нептун являются осенними планетами, т. к. вступают в противостояние с Солнцем соответственно 29 сентября и 24 августа. Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
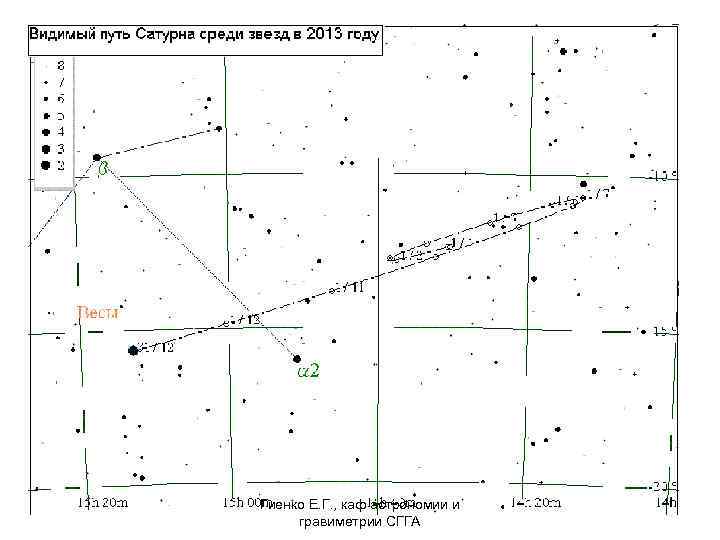
 • Планеты в 2013 году: • Не столь благоприятна, как в 2012. • У Меркурия за весь год будет 4 утренних и 3 вечерних видимости. • Для Венеры наиболее благоприятное время для наблюдений ноябрь и декабрь (1 ноября вечерняя элонгация). • Марс весь год находится вдали от Земли с видимым диаметром около 4 угловых секунд и пройдет соединение с Солнцем 18 апреля. • Наилучшая видимость Юпитера относится ко второй половине года с противостоянием 5 января 2014 года. • Сатурн лучше всего виден в первом полугодии с противостоянием 28 апреля. • Уран и Нептун являются осенними планетами, т. к. вступают в противостояние с Солнцем соответственно 3 октября и 27 августа. Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
• Планеты в 2013 году: • Не столь благоприятна, как в 2012. • У Меркурия за весь год будет 4 утренних и 3 вечерних видимости. • Для Венеры наиболее благоприятное время для наблюдений ноябрь и декабрь (1 ноября вечерняя элонгация). • Марс весь год находится вдали от Земли с видимым диаметром около 4 угловых секунд и пройдет соединение с Солнцем 18 апреля. • Наилучшая видимость Юпитера относится ко второй половине года с противостоянием 5 января 2014 года. • Сатурн лучше всего виден в первом полугодии с противостоянием 28 апреля. • Уран и Нептун являются осенними планетами, т. к. вступают в противостояние с Солнцем соответственно 3 октября и 27 августа. Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Синодический период S – промежуток времени между двумя одинаковыми конфигурациями Звездный период обращения T – время оборота планеты вокруг Солнца относительно звезд Для Земли T = 1 год Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Синодический период S – промежуток времени между двумя одинаковыми конфигурациями Звездный период обращения T – время оборота планеты вокруг Солнца относительно звезд Для Земли T = 1 год Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
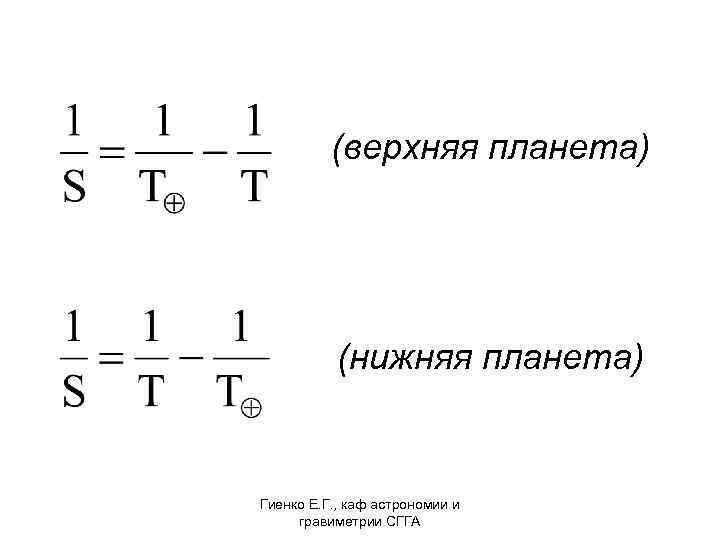 (верхняя планета) (нижняя планета) Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
(верхняя планета) (нижняя планета) Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 • Можно ли увидеть Венеру утром на Западе? • Можно ли увидеть Марс вечером на востоке? • Юпитер в противостоянии. Он виден: а) всю ночь б) по утро в) вечером г) не виден • Назовите верхние и нижние планеты • Что такое синодический период? • Что такое конфигурация? • В каких конфигурациях лучше всего наблюдать Венеру и Меркурий? • В какой конфигурации лучше всего наблюдать Марс? Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
• Можно ли увидеть Венеру утром на Западе? • Можно ли увидеть Марс вечером на востоке? • Юпитер в противостоянии. Он виден: а) всю ночь б) по утро в) вечером г) не виден • Назовите верхние и нижние планеты • Что такое синодический период? • Что такое конфигурация? • В каких конфигурациях лучше всего наблюдать Венеру и Меркурий? • В какой конфигурации лучше всего наблюдать Марс? Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 4. 3 Законы движения планет Тихо Браге (1546 – 1601), Дания 20 -летние наблюдения Марса Передал своему ученику И. Кеплеру Иоганн Кеплер (1571 – 1630), Германия На основании наблюдений Т. Браге вывел эмпирически (опытным путем) 3 закона движения планет Исаак Ньютон (1643 – 1727), Англия Закон Всемирного тяготения. На основании закона получил теоретически законы движения планет. Начало небесной механики. Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
4. 3 Законы движения планет Тихо Браге (1546 – 1601), Дания 20 -летние наблюдения Марса Передал своему ученику И. Кеплеру Иоганн Кеплер (1571 – 1630), Германия На основании наблюдений Т. Браге вывел эмпирически (опытным путем) 3 закона движения планет Исаак Ньютон (1643 – 1727), Англия Закон Всемирного тяготения. На основании закона получил теоретически законы движения планет. Начало небесной механики. Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
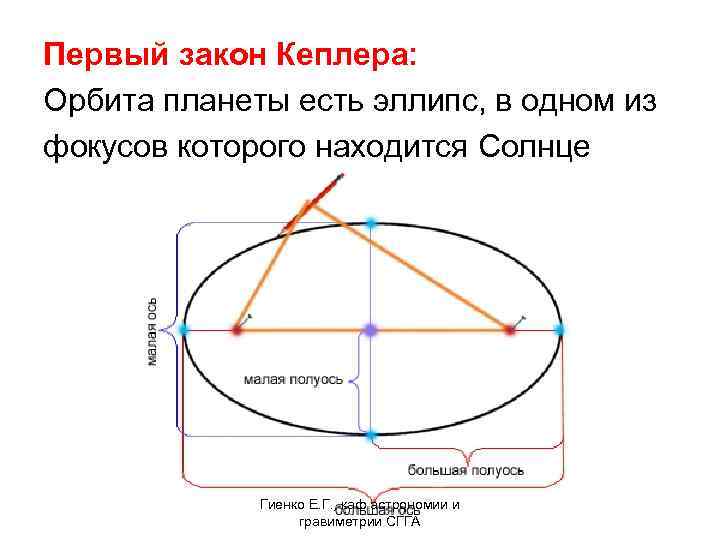 Первый закон Кеплера: Орбита планеты есть эллипс, в одном из фокусов которого находится Солнце Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Первый закон Кеплера: Орбита планеты есть эллипс, в одном из фокусов которого находится Солнце Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
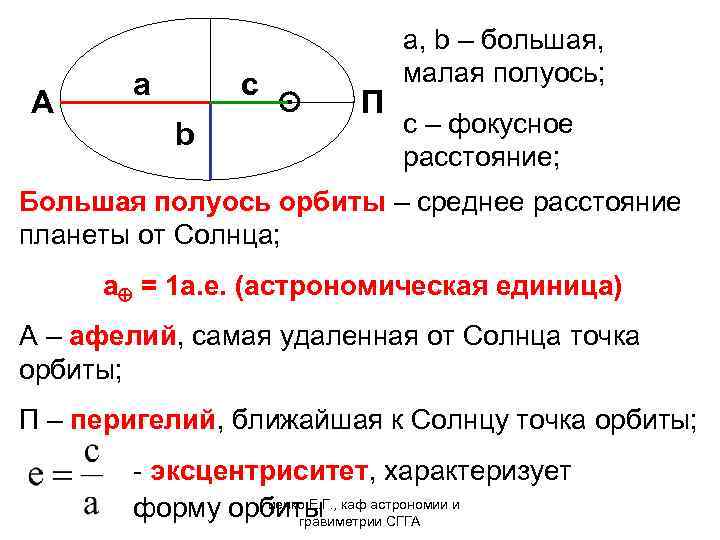 A а c b ⊙ П a, b – большая, малая полуось; с – фокусное расстояние; Большая полуось орбиты – среднее расстояние планеты от Солнца; a = 1 а. е. (астрономическая единица) A – афелий, самая удаленная от Солнца точка орбиты; П – перигелий, ближайшая к Солнцу точка орбиты; - эксцентриситет, характеризует Гиенко Е. Г. , форму орбиты каф астрономии и гравиметрии СГГА
A а c b ⊙ П a, b – большая, малая полуось; с – фокусное расстояние; Большая полуось орбиты – среднее расстояние планеты от Солнца; a = 1 а. е. (астрономическая единица) A – афелий, самая удаленная от Солнца точка орбиты; П – перигелий, ближайшая к Солнцу точка орбиты; - эксцентриситет, характеризует Гиенко Е. Г. , форму орбиты каф астрономии и гравиметрии СГГА
 Первый закон в формулировке Ньютона: Движение тела под действием тяготения может происходить по кривой конического сечения: окружность (e =0) эллипс (0
Первый закон в формулировке Ньютона: Движение тела под действием тяготения может происходить по кривой конического сечения: окружность (e =0) эллипс (0
 Второй закон Кеплера-Ньютона: Радиус-вектор планеты за равные промежутки времени описывает равные площади (секториальная скорость планеты постоянна), S – площадь сектора, t - время Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Второй закон Кеплера-Ньютона: Радиус-вектор планеты за равные промежутки времени описывает равные площади (секториальная скорость планеты постоянна), S – площадь сектора, t - время Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 ⊛ A SА S А= S П ⊛ ⊙ SП П при Dt. A = Dt. П Вывод из второго закона: скорость движения планеты вокруг Солнца не постоянна, максимальная – в перигелии, минимальная – в афелии Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
⊛ A SА S А= S П ⊛ ⊙ SП П при Dt. A = Dt. П Вывод из второго закона: скорость движения планеты вокруг Солнца не постоянна, максимальная – в перигелии, минимальная – в афелии Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Третий закон Кеплера: Квадраты звездных периодов обращения планет пропорциональны кубам больших полуосей их орбит Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Третий закон Кеплера: Квадраты звездных периодов обращения планет пропорциональны кубам больших полуосей их орбит Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Уточнение Ньютоном третьего закона Кеплера: Закон Всемирного тяготения: cила F взаимного притяжения планеты и Солнца: где G = 6, 67⋅10 -11 Н⋅м 2/кг 2 – постоянная тяготения, а – большая полуось орбиты (среднее расстояние) Ускорение w планеты, направленное к Солнцу: Ускорение w 0 Солнца, направленное к планете: Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Уточнение Ньютоном третьего закона Кеплера: Закон Всемирного тяготения: cила F взаимного притяжения планеты и Солнца: где G = 6, 67⋅10 -11 Н⋅м 2/кг 2 – постоянная тяготения, а – большая полуось орбиты (среднее расстояние) Ускорение w планеты, направленное к Солнцу: Ускорение w 0 Солнца, направленное к планете: Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Суммарное ускорение: - уравновешивается центробежным ускорением планеты относительно Солнца где , T – звездный период обращения Приравняем ускорения W=Wц: Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Суммарное ускорение: - уравновешивается центробежным ускорением планеты относительно Солнца где , T – звездный период обращения Приравняем ускорения W=Wц: Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Перенесем постоянные в правую часть и окончательно получим 3 закон Кеплера-Ньютона: Отношение квадрата периода обращения к кубу среднего расстояния, умноженное на сумму масс центрального тела и его спутника, есть величина постоянная Система двух тел: Солнце-планета, планета-спутник, звезда – звезда … Для двух систем: Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Перенесем постоянные в правую часть и окончательно получим 3 закон Кеплера-Ньютона: Отношение квадрата периода обращения к кубу среднего расстояния, умноженное на сумму масс центрального тела и его спутника, есть величина постоянная Система двух тел: Солнце-планета, планета-спутник, звезда – звезда … Для двух систем: Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 • На основании чьих наблюдений были выведены эмпирически законы движения планет? • На основании какого закона были получены теоретически законы движения планет? • Вид орбиты небесного тела, движущегося под действием силы тяжести: • Основной вывод из второго закона Кеплера: • Чему равны большая полуось орбиты Земли и ее звездный период обращения? • Какой закон позволяет определять массы небесных тел? • Как определяют массы планет, не имеющих Гиенко Е. Г. , каф астрономии и спутники? гравиметрии СГГА
• На основании чьих наблюдений были выведены эмпирически законы движения планет? • На основании какого закона были получены теоретически законы движения планет? • Вид орбиты небесного тела, движущегося под действием силы тяжести: • Основной вывод из второго закона Кеплера: • Чему равны большая полуось орбиты Земли и ее звездный период обращения? • Какой закон позволяет определять массы небесных тел? • Как определяют массы планет, не имеющих Гиенко Е. Г. , каф астрономии и спутники? гравиметрии СГГА
 Третий закон Кеплера-Ньютона позволяет сравнивать массу планеты, имеющей спутник, с массой Солнца, либо массы планет, имеющих спутники, между собой. Закон справедлив и для двойных звезд – для любых систем “центральное тело - спутник” Массы планет, не имеющих спутники, определяются по вызываемым ими возмущениям в движении других планет или искусственных спутников. Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Третий закон Кеплера-Ньютона позволяет сравнивать массу планеты, имеющей спутник, с массой Солнца, либо массы планет, имеющих спутники, между собой. Закон справедлив и для двойных звезд – для любых систем “центральное тело - спутник” Массы планет, не имеющих спутники, определяются по вызываемым ими возмущениям в движении других планет или искусственных спутников. Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
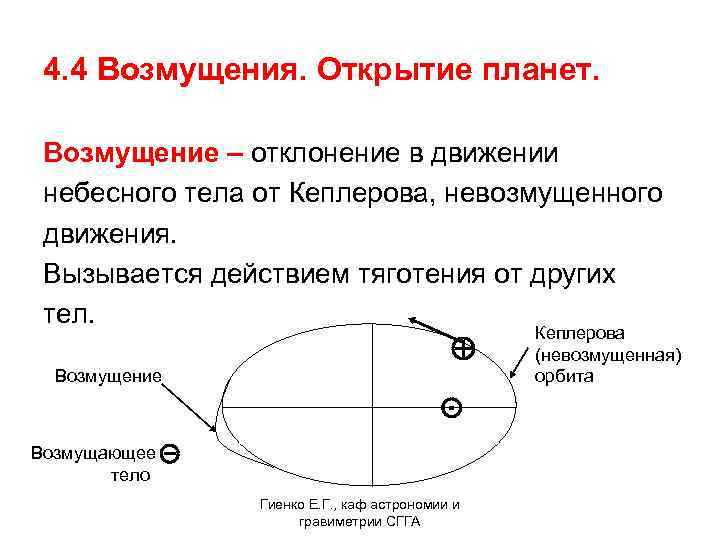 4. 4 Возмущения. Открытие планет. Возмущение – отклонение в движении небесного тела от Кеплерова, невозмущенного движения. Вызывается действием тяготения от других тел. Возмущение Возмущающее тело ⊝ ⊙ Гиенко Е. Г. , каф астрономии и гравиметрии СГГА Кеплерова (невозмущенная) орбита
4. 4 Возмущения. Открытие планет. Возмущение – отклонение в движении небесного тела от Кеплерова, невозмущенного движения. Вызывается действием тяготения от других тел. Возмущение Возмущающее тело ⊝ ⊙ Гиенко Е. Г. , каф астрономии и гравиметрии СГГА Кеплерова (невозмущенная) орбита
 Открытие Урана, 1781 г Уильям Гершель (1738 – 1822), Англия Открытие планеты Уран в телескоп 40 – футовый телескоп Гершеля Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Открытие Урана, 1781 г Уильям Гершель (1738 – 1822), Англия Открытие планеты Уран в телескоп 40 – футовый телескоп Гершеля Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Открытие Нептуна, 1846 г – торжество небесной механики Урбан Жозеф Леверрье (1811 -1877), Франция Точно рассчитал положение неизвестной ранее планеты на основании данных о движении Урана. Используя эти расчеты, немец Иоганн Галле (1812 – 1910) обнаружил Нептун всего лишь за полчаса наблюдений. Джон Кауч Адамс (1819 -1892), Англия Независимо занимался проблемой возмущения Урана новой планетой, но его неточные и непостоянные предсказания не позволили астрономам Кембриджа добиться успеха за шесть недель поисков. Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Открытие Нептуна, 1846 г – торжество небесной механики Урбан Жозеф Леверрье (1811 -1877), Франция Точно рассчитал положение неизвестной ранее планеты на основании данных о движении Урана. Используя эти расчеты, немец Иоганн Галле (1812 – 1910) обнаружил Нептун всего лишь за полчаса наблюдений. Джон Кауч Адамс (1819 -1892), Англия Независимо занимался проблемой возмущения Урана новой планетой, но его неточные и непостоянные предсказания не позволили астрономам Кембриджа добиться успеха за шесть недель поисков. Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Открытие Плутона, 1930 г Персиваль Ловелл (1855 – 1916), США 1915 г : Вычислил орбиту 9 -й планеты по возмущениям в движении Урана и Нептуна. 1930 г. , Клайд Томбо, США – открыл Плутон 1978 г. – открыт спутник Плутона – Харон PL - Persival Lovell Один из методов поиска планетных систем у других звезд – по возмущениям в их движении Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Открытие Плутона, 1930 г Персиваль Ловелл (1855 – 1916), США 1915 г : Вычислил орбиту 9 -й планеты по возмущениям в движении Урана и Нептуна. 1930 г. , Клайд Томбо, США – открыл Плутон 1978 г. – открыт спутник Плутона – Харон PL - Persival Lovell Один из методов поиска планетных систем у других звезд – по возмущениям в их движении Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 • Орбиты каких планеты, не видимых невооруженным глазом, были рассчитаны по возмущениям? • Какая планета, не видимая невооруженным глазом, была открыта в телескоп? • Какие ученые рассчитали орбиту Нептуна? Плутона? • Почему Плутон не был обнаружен в 1915 г, в год расчета его орбиты? Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
• Орбиты каких планеты, не видимых невооруженным глазом, были рассчитаны по возмущениям? • Какая планета, не видимая невооруженным глазом, была открыта в телескоп? • Какие ученые рассчитали орбиту Нептуна? Плутона? • Почему Плутон не был обнаружен в 1915 г, в год расчета его орбиты? Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 2005, май, Телескоп им. Хаббла: обнаружение двух спутников Плутона. 2006, август: резолюция МАС: исключение Плутона из списка больших планет. Новый класс объектов Солнечной системы: карликовые планеты 2008, июнь: Плутон и несколько др. карликовых планет - Плутоиды Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
2005, май, Телескоп им. Хаббла: обнаружение двух спутников Плутона. 2006, август: резолюция МАС: исключение Плутона из списка больших планет. Новый класс объектов Солнечной системы: карликовые планеты 2008, июнь: Плутон и несколько др. карликовых планет - Плутоиды Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Обнаружение транснептуновых объектов: Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Обнаружение транснептуновых объектов: Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
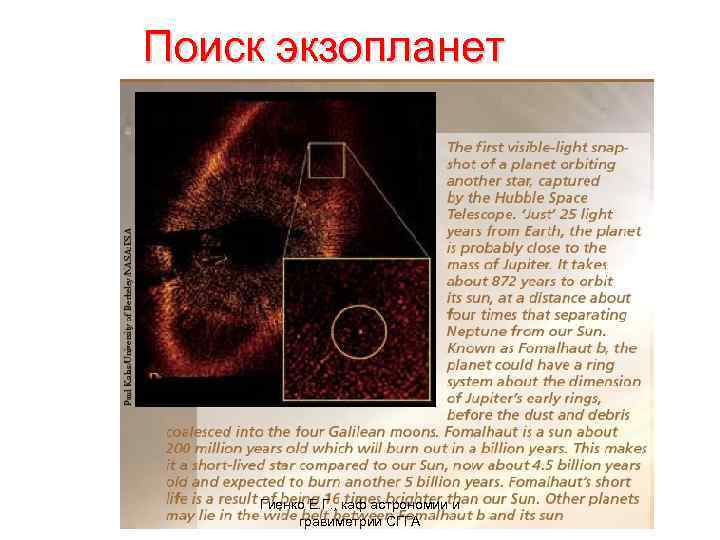 Поиск экзопланет На настоящий момент: более 300 экзопланет, обращающихся около других звезд. Методы обнаружения: -фотометрический (транзитный); - астрометрический; - спектральный; -прямой (наблюдение света, отраженного планетой) Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Поиск экзопланет На настоящий момент: более 300 экзопланет, обращающихся около других звезд. Методы обнаружения: -фотометрический (транзитный); - астрометрический; - спектральный; -прямой (наблюдение света, отраженного планетой) Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Поиск экзопланет На настоящий момент: Более 700 экзопланет, обращающихся около других звезд. Методы обнаружения: -фотометрический (транзитный); - астрометрический; - спектральный; -прямой (наблюдение света, отраженного планетой) Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Поиск экзопланет На настоящий момент: Более 700 экзопланет, обращающихся около других звезд. Методы обнаружения: -фотометрический (транзитный); - астрометрический; - спектральный; -прямой (наблюдение света, отраженного планетой) Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
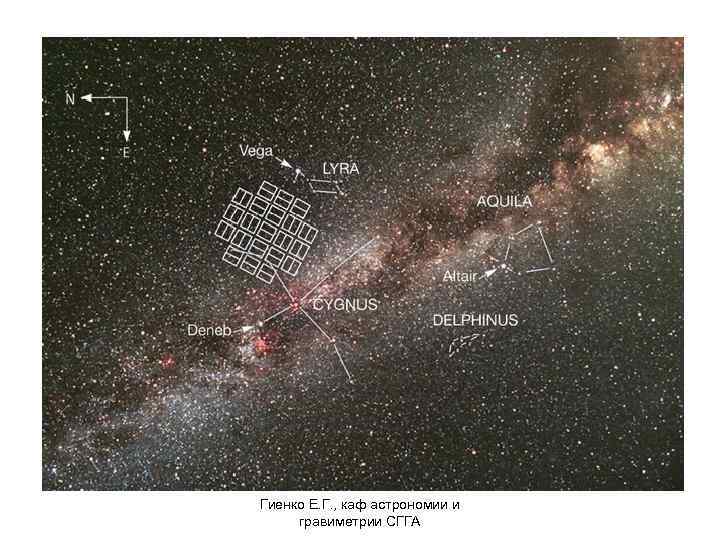
 Космический телескоп “Кеплер” (NASA). Задача – поиск похожих на Землю планет, орбиты которых находятся в обитаемых зонах около других звезд. Запуск телескопа “Кеплер” 06. 03. 09 с мыса Канаверал, Флорида Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Космический телескоп “Кеплер” (NASA). Задача – поиск похожих на Землю планет, орбиты которых находятся в обитаемых зонах около других звезд. Запуск телескопа “Кеплер” 06. 03. 09 с мыса Канаверал, Флорида Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
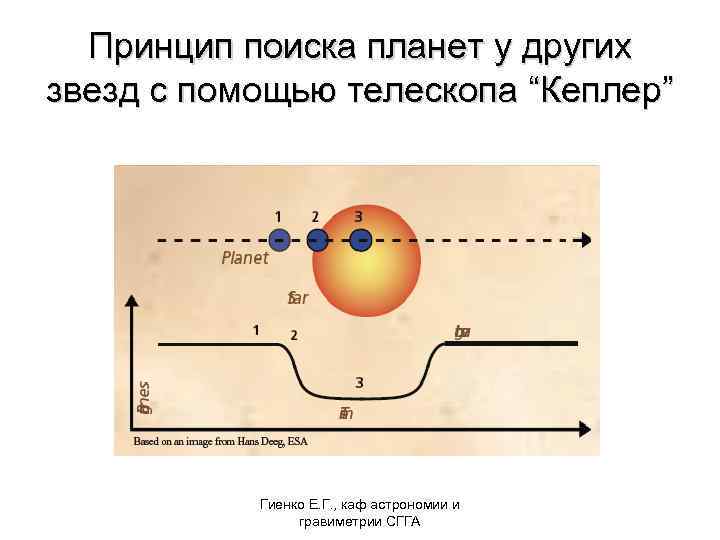 Принцип поиска планет у других звезд с помощью телескопа “Кеплер” Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Принцип поиска планет у других звезд с помощью телескопа “Кеплер” Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
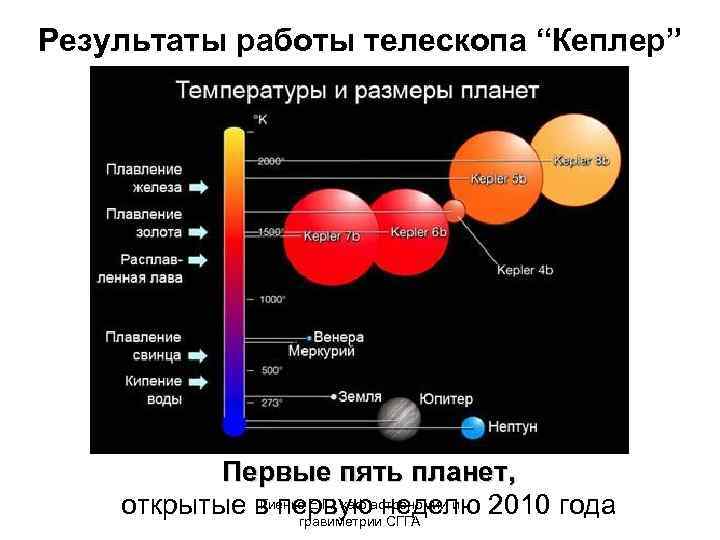 Результаты работы телескопа “Кеплер” Первые пять планет, Гиенко Е. Г. , каф неделю открытые в первуюастрономии и 2010 года гравиметрии СГГА
Результаты работы телескопа “Кеплер” Первые пять планет, Гиенко Е. Г. , каф неделю открытые в первуюастрономии и 2010 года гравиметрии СГГА
 К 1 сентября 2010 г. “Кеплер” обнаружил около 700 экзопланет Два газовых гиганта, вращающиеся вокруг звезды Kepler-9. Масса их лишь. Гиенко Е. Г. , каф астрономиимассе Сатурна немногим уступает и гравиметрии СГГА
К 1 сентября 2010 г. “Кеплер” обнаружил около 700 экзопланет Два газовых гиганта, вращающиеся вокруг звезды Kepler-9. Масса их лишь. Гиенко Е. Г. , каф астрономиимассе Сатурна немногим уступает и гравиметрии СГГА
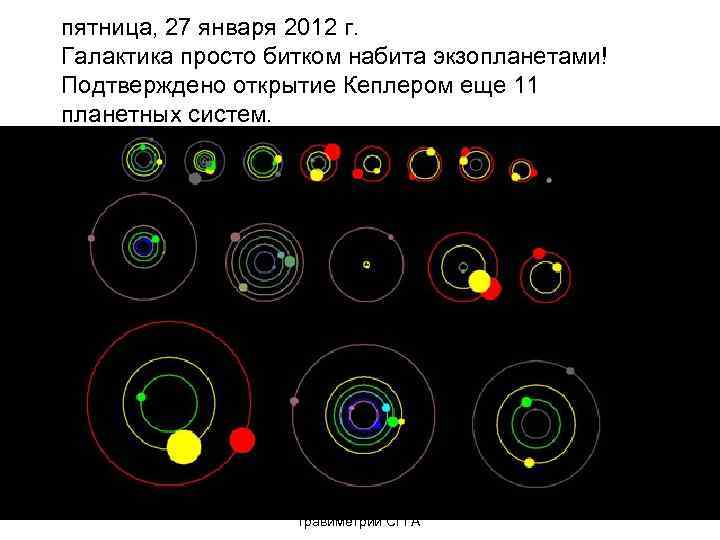 пятница, 27 января 2012 г. Галактика просто битком набита экзопланетами! Подтверждено открытие Кеплером еще 11 планетных систем. Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
пятница, 27 января 2012 г. Галактика просто битком набита экзопланетами! Подтверждено открытие Кеплером еще 11 планетных систем. Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Автоматические межпланетные станции (АМС) • Меркурий: Мессенджер • Венера: Венера-Экспресс • Марс: несколько искусственных спутников и марсоходы Спирит и Оппротьюнити • Юпитер: Галилео • Сатурн: Кассини • Уран, Нептун, Плутон: Вояджер-1, Вояджер-2, Новые астрономии и Гиенко Е. Г. , каф горизонты гравиметрии СГГА
Автоматические межпланетные станции (АМС) • Меркурий: Мессенджер • Венера: Венера-Экспресс • Марс: несколько искусственных спутников и марсоходы Спирит и Оппротьюнити • Юпитер: Галилео • Сатурн: Кассини • Уран, Нептун, Плутон: Вояджер-1, Вояджер-2, Новые астрономии и Гиенко Е. Г. , каф горизонты гравиметрии СГГА
 4. 5 Методы определения расстояний до тел солнечной системы и их размеров Определение расстояний 1. Геометрический метод Коперника Расстояния до нижних планет: измерение угла ⊙ D элонгации a D = 1 a. e. ⋅ sin a Планета в 900⊛ элонгации 1 a. e. a Расстояния до верхних планет - по размерам петель, описываемых планетами на звездном небе Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
4. 5 Методы определения расстояний до тел солнечной системы и их размеров Определение расстояний 1. Геометрический метод Коперника Расстояния до нижних планет: измерение угла ⊙ D элонгации a D = 1 a. e. ⋅ sin a Планета в 900⊛ элонгации 1 a. e. a Расстояния до верхних планет - по размерам петель, описываемых планетами на звездном небе Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 2. Применение третьего закона Кеплера. Примечание: методы 1, 2 дают расстояния в относительных единицах – астрономических (а. е. ) А чему равна астрономическая единица? 3. Метод параллакса Определение расстояний до недоступных объектов путем измерения линейного базиса и углов C D A Ба с зи B Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
2. Применение третьего закона Кеплера. Примечание: методы 1, 2 дают расстояния в относительных единицах – астрономических (а. е. ) А чему равна астрономическая единица? 3. Метод параллакса Определение расстояний до недоступных объектов путем измерения линейного базиса и углов C D A Ба с зи B Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 4. Определение астрономической единицы. Параллакс Солнца Суточный параллакс Солнца P⊙ (планеты, Луны) – угол, ⊙ P⊙ под которым с Солнца R . (планеты, Луны) наблюдается = 1 а. е D радиус Земли. Может быть измерен. D = R /sin P⊙ , P⊙ - мал, P⊙≈ 8. 8 " sin P⊙ ≈ P⊙ (рад. ) = P⊙“/206265“, D = 206265“⋅R /P⊙“ 5. Радио- и свето- локация D = C⋅(Tприема – Tотправления)/2 1961 – 1963 гг – первая радиолокация Венеры и Меркурия Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
4. Определение астрономической единицы. Параллакс Солнца Суточный параллакс Солнца P⊙ (планеты, Луны) – угол, ⊙ P⊙ под которым с Солнца R . (планеты, Луны) наблюдается = 1 а. е D радиус Земли. Может быть измерен. D = R /sin P⊙ , P⊙ - мал, P⊙≈ 8. 8 " sin P⊙ ≈ P⊙ (рад. ) = P⊙“/206265“, D = 206265“⋅R /P⊙“ 5. Радио- и свето- локация D = C⋅(Tприема – Tотправления)/2 1961 – 1963 гг – первая радиолокация Венеры и Меркурия Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 • Методы определения расстояний до небесных тел: • Какой метод самый точный? • Что такое суточный параллакс? Чему равен суточный параллакс звезд? • Как была определена астрономическая единица? • В каких единицах измерения дает расстояние метод Коперника? Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
• Методы определения расстояний до небесных тел: • Какой метод самый точный? • Что такое суточный параллакс? Чему равен суточный параллакс звезд? • Как была определена астрономическая единица? • В каких единицах измерения дает расстояние метод Коперника? Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
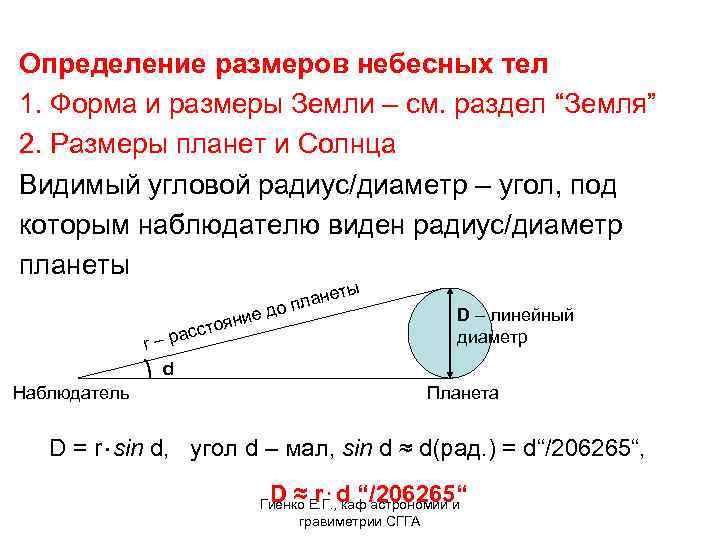 Определение размеров небесных тел 1. Форма и размеры Земли – см. раздел “Земля” 2. Размеры планет и Солнца Видимый угловой радиус/диаметр – угол, под которым наблюдателю виден радиус/диаметр планеты расс ед ояни т r– d Наблюдатель о ы ет план D – линейный диаметр Планета D = r⋅sin d, угол d – мал, sin d ≈ d(рад. ) = d“/206265“, D ≈ r⋅d “/206265“ Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Определение размеров небесных тел 1. Форма и размеры Земли – см. раздел “Земля” 2. Размеры планет и Солнца Видимый угловой радиус/диаметр – угол, под которым наблюдателю виден радиус/диаметр планеты расс ед ояни т r– d Наблюдатель о ы ет план D – линейный диаметр Планета D = r⋅sin d, угол d – мал, sin d ≈ d(рад. ) = d“/206265“, D ≈ r⋅d “/206265“ Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 Запуск космических аппаратов. Космические скорости Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
Запуск космических аппаратов. Космические скорости Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
 • http: //www. astronet. ru/db/msg/1170734 Гиенко Е. Г. , каф астрономии и гравиметрии СГГА
• http: //www. astronet. ru/db/msg/1170734 Гиенко Е. Г. , каф астрономии и гравиметрии СГГА


