4 Soil Composition Prepared From The Coduto s Text

4) Soil Composition Prepared From The Coduto’s Text Book by Instr. Nurullah AKBULUT. in engineering practice difficulties with soils are almost exclusively do not to the soils themselves but to the water contained in their voids. On a planet without any water there would be NO need for soil mechanics. Karl Terzaghi, 1939

Once the soil and rock samples have been brought to the laboratory, we need to conduct appropriate tests to develop data for our analyses. Some of these tests measure familiar engineering properties, such as shear strength, while others focus on the sample's composition and structure. The composition of soil and rock is quite different from that of other civil engineering materials, such as steel, concrete, or wood. These differences include: ü Soil and rock are natural materials, not manufactured products ü Soil is a particulate material that consists of individual particles ü Soil can contain all three phases of matter (solid, liquid, and gas) simultaneously, and these three phases can be present in varying proportions. Rock also can contain all three phases, although the liquid and gas phases may be confined to the fissures.

The most Important Properties of Soils • • • Elastoplastic material Particulate structure Heterogenity Non-Isotropi Three phases of matter This chapter discusses the methods we use to assess the composition of soils and the parameters we use to describe this composition

SOIL AS A PARTICULATE MATERIAL

Most civil engineering materials consist of a continuous mass held together with molecular bonds, and the mechanical properties of such materials depend on their chemical makeup and on the nature of these bonds. For example, the shear strength of steel depends on the strength of the molecular bonds, and shear failure requires breaking them. In contrast, soil is a particulate material that consists of individual particles assembled together as shown in Figure 4. 1. Its engineering properties depend largely on the interaction between these particles, and only secondarily on their internal properties. This is especially true in gravels, sands, and silts. For example, when soils fail in shear, they do so because the particles begin to roll and slide past each other, not because the particles break internally. Breakage of individual particles is typically minimal. Thus, the shear strength depends on factors such as the coefficient of friction between the particles, the tightness of packing, and so on, rather than the chemical bonds inside the particles. Clays also have a particulate structure, but the nature of the particles is quite different, as discussed later in this chapter. In clays, there is much more interaction between the particles and the pore water, so their behavior is more complex than that of other soils.

THE THREE PHASES • Soil also is different from most civil engineering materials in that it can simultaneously contain solid, liquid, and gas phases. • The liquid and gas phases are contained in the voids or pores between the solid particles. • The three phases often interact, and these interactions have important effects on the soil's behavior.

The Mineral Skeleton-Three Phase Solid Particles Volume Voids

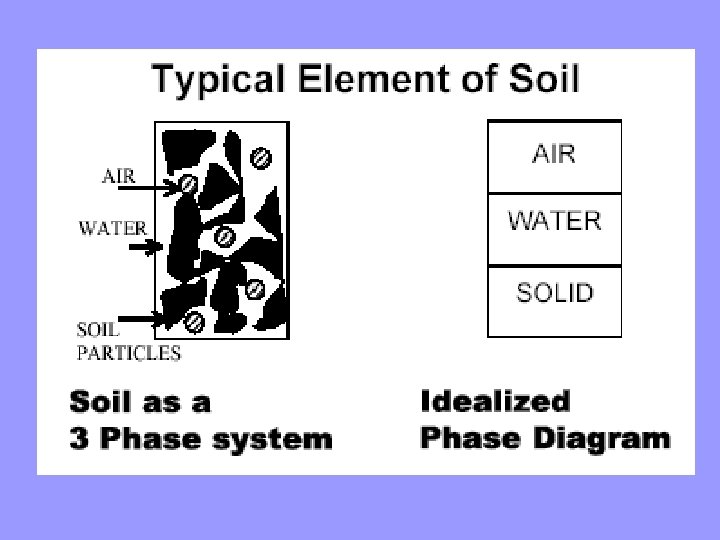
• The solid phase: is always present in soil, and usually consists of particles derived from rocks. It also can include organic material. • The liquid phase: is usually present, and most often consists of water. However, it also can include other materials, such as: gasoline, leachate, seawater, petroleum seeps. • The gas phase: If the liquid phase does not completely fill the voids, then the remaining space is occupied by the gas phase. It is usually air, but can include other gasses, such as: methane, carbon diokside, hydrogen sulfide, e. t. c.

Clearly, components other than water and air are very important. However, they generally represent only a small portion of the soil weight and volume. Therefore, for purposes of this chapter, we will simply refer to the liquid and gas phases as "pore water" or “water” and "pore air“ or “air”.

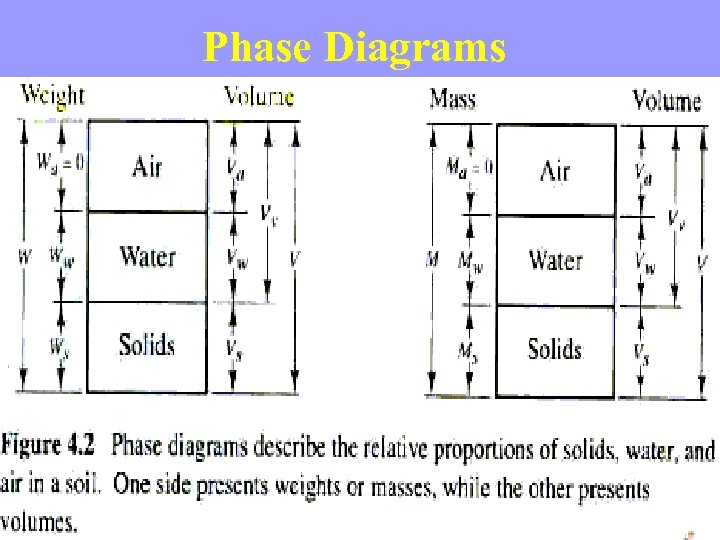
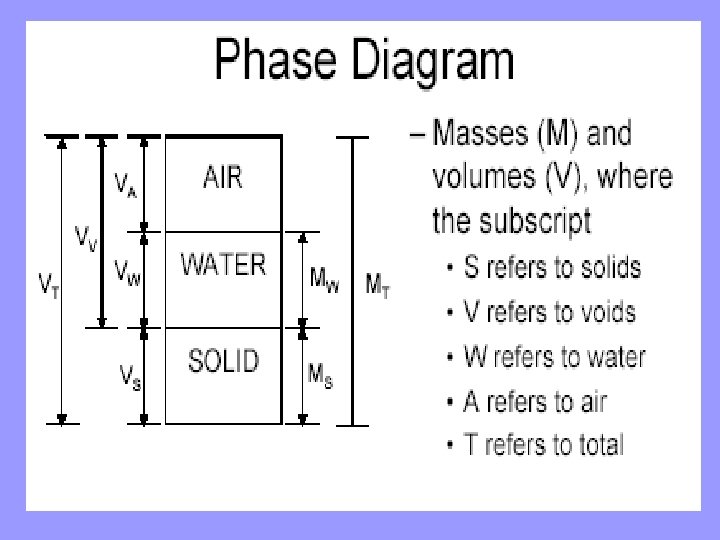
WEIGHT-VOLUME RELATIONSHIPS It is helpful to identify the relative proportions of solids, water, and air in a soil, because these proportions have a significant effect on its behavior. Therefore, geotechnical engineers have developed quantitative methods of assessing these components.

Phase Diagrams

Three Phase System Va Air Vw Water Wa=0 Vv V Ww W Vs Volume Solid Ws Weight, or Mass

Definitions of Weight-Volume Parameters Moisture Content or Water Content A small w indicates a dry soil, while a large w indicates a wet one. Values in the field are usually between 3 and 70%. But values greater than 100% are sometimes found in soft soils below the groundwater table, which simply means such soils have more water than solids.

Degree of Saturation ü This is similar to moisture content in that both are equal to zero when there is no water. However, S has a maximum value of 100%, which occurs when all of the voids are filled with water. We use the term saturated to describe this condition. ü Soils below the groundwater table are generally saturated. ü Values of S above the groundwater table are usually between 5 and 100%, although values approaching zero can be found in very arid areas. ü Capillary effects can draw water upward from the groundwater table, often producing soils with S =100% well above the groundwater table. Therefore, do not use saturation computations to determine the location of the groundwater table. Instead, use observation wells.

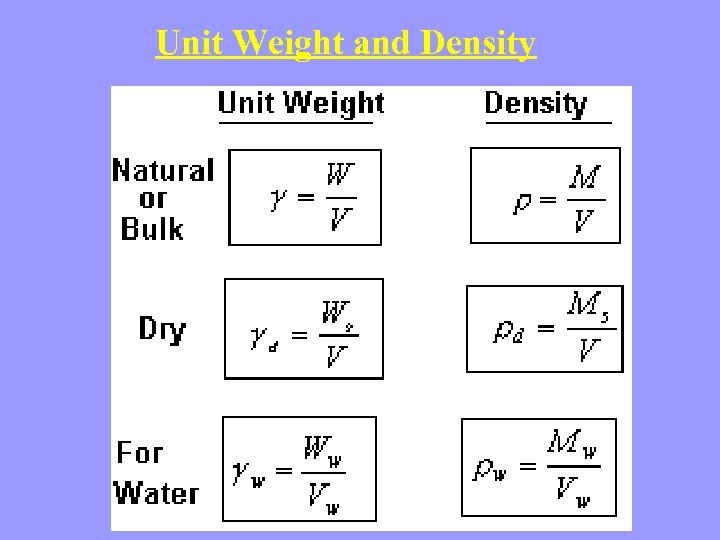Unit Weight and Density

In all calculations, w = 9. 81 k. N/ m 3= 62. 4 Ib/ft 3, w= 1000 kg/m 3 for fresh water.

ü The unit weight of undisturbed soil samples can easily be determined in the laboratory by measuring their physical dimensions and weighing them. This method produces reliable assessments of for many soils. ü However, it is affected by sample disturbance, especially in sandy and gravelly soils. ü Sometimes unit weight measurements are made on supposedly "undisturbed" samples that in reality have significant disturbance. ü Such measurements are very misleading, so it is best to not even attempt unit weight measurements on poor quality samples ü For most geotechnical computations, unit weight is more useful than density because we use it to compute stresses due to the weight of the soil.

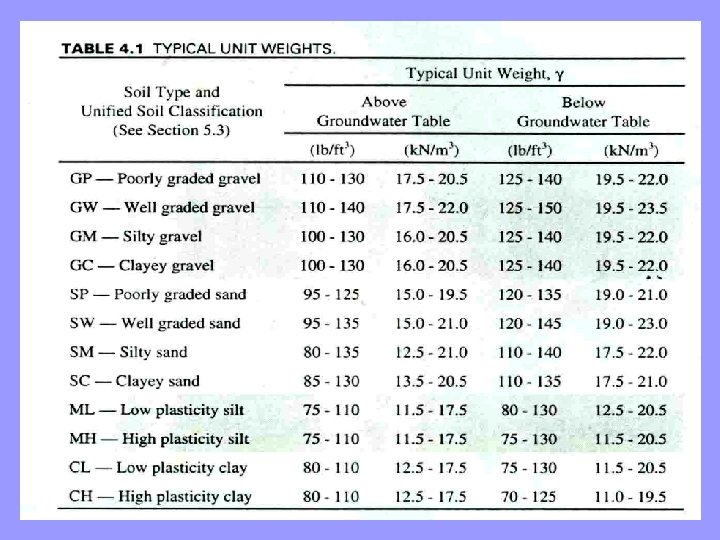
Specific Gravity of Solids ü The specific gravity of any material is the ratio of its density to that of water. In the case of soils, we compute it for the solid phase only, and express the results as the specific-gravity of solids; ü This is quite different from the specific gravity of the entire soil mass, which would include solid, water, and air. Therefore, do not make the common mistake of computing Gs as / w. ü Nearly all real soils have 2. 60

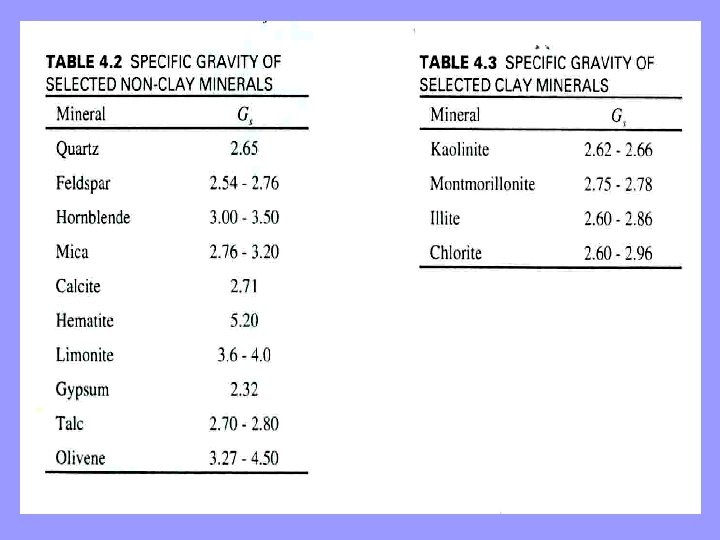
For most practical problems, it is sufficient to estimate , from the following list: • Clean, light colored sand of quartz and feldspar 2. 65 • Dark colored sand 2. 72 • Sand-silt-clay mixtures 2. 72 • Clay 2. 65 Nevertheless, some unusual soils have olivene values well outside these limits. For example, the olivene sands in Hawaii have Gs values as high as 4. 50, while organic soils have low Gs values, sometimes less than 2. 0.

Void Ratio ü The relative volumes of voids and solids may be expressed as the void ratio ü Densely packed soils have a low void ratio. ü Typical values in the field range from 0. 1 to 2. 5.

Porosity ü It is a similar parameter and related with e ü It typically is between 9 and 70% ü Sometimes geotechnical engineers divide the porosity into two parts: the water porosity, nw, and the air porosity, na:

Relative Density ü It is a special weight-volume parameter used in sandy and gravelly soils. ü The values of emax and emin represent the soil in very dense and very loose conditions, respectively. Thus, loose soils have low values of Dr while dense soils have high values. ü In theory, the lowest possible value of Dr is 0% and the highest possible value Dr is 100%. ü Thus, Dr is often more useful than e because we can easily compare the field value to the lowest and highest possible values.

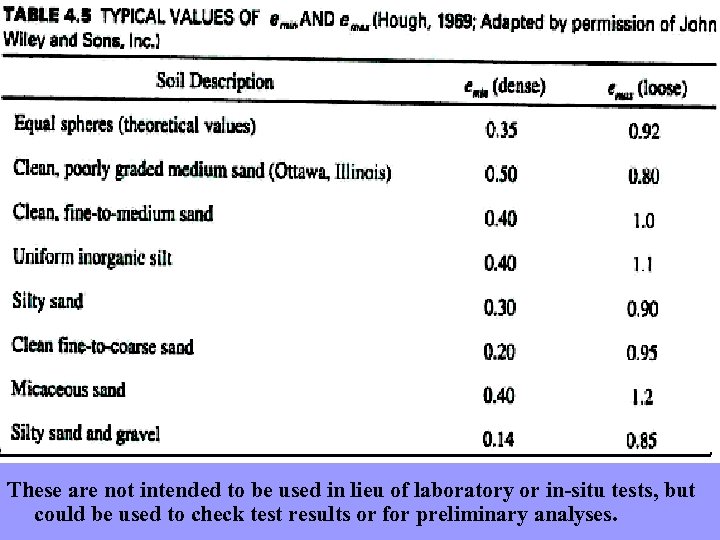These are not intended to be used in lieu of laboratory or in-situ tests, but could be used to check test results or for preliminary analyses.

Derived Equations with Weight Volume Relationships by Phase Diagrams

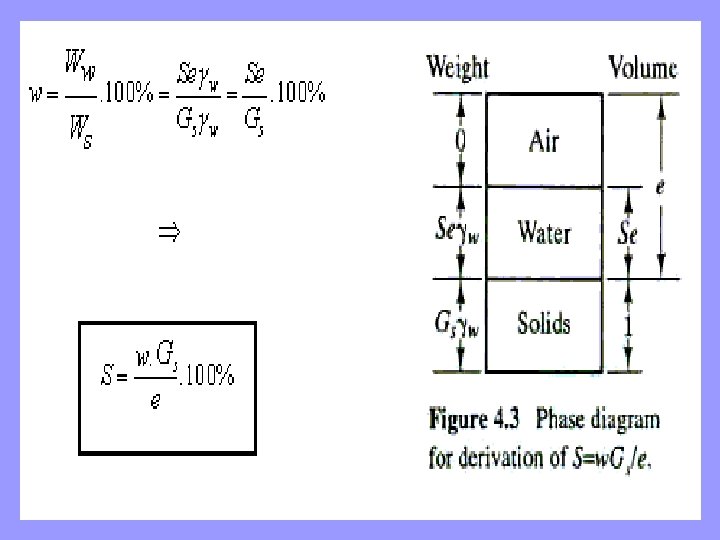
üFor all of these equations, parameters normally expressed as a percentage must be inserted in decimal form. üFor example, a degree of saturation of 45% in Equation would be expressed as 0. 45 not 45

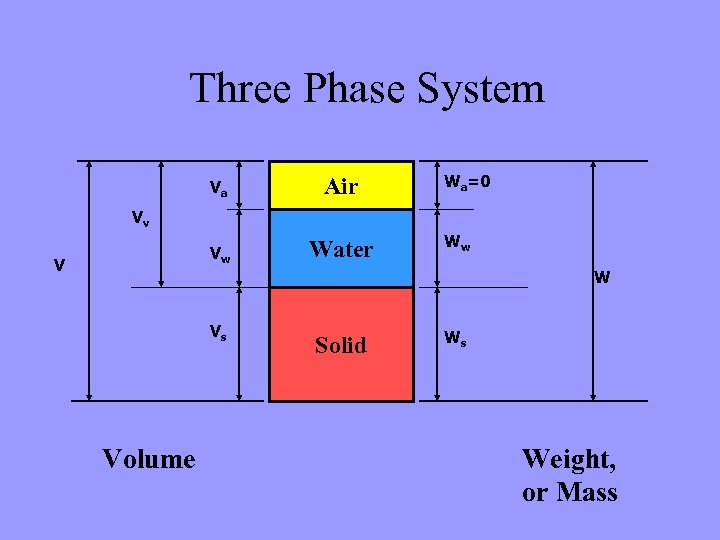
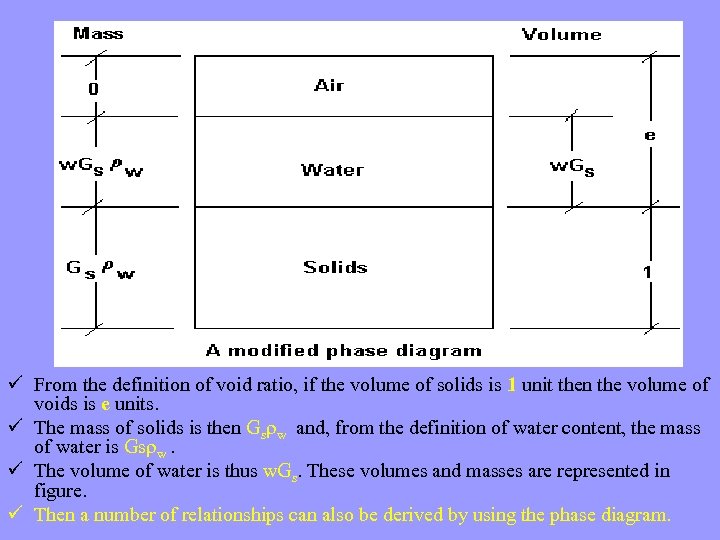ü From the definition of void ratio, if the volume of solids is 1 unit then the volume of voids is e units. ü The mass of solids is then Gs w and, from the definition of water content, the mass of water is Gs w. ü The volume of water is thus w. Gs. These volumes and masses are represented in figure. ü Then a number of relationships can also be derived by using the phase diagram.

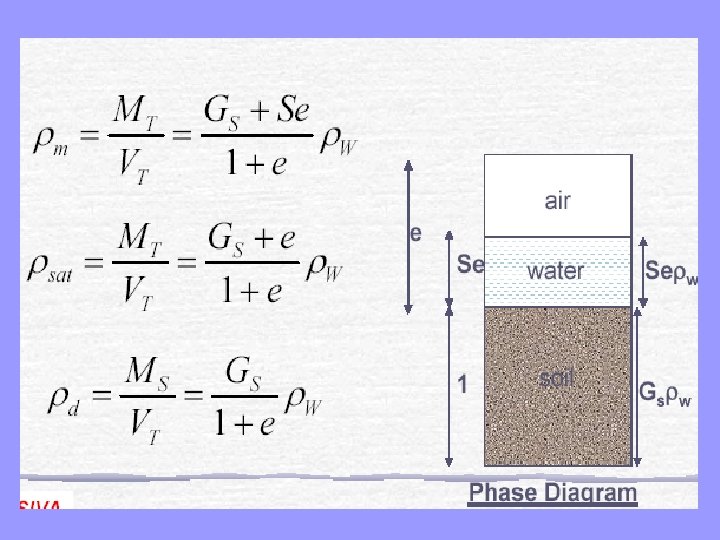
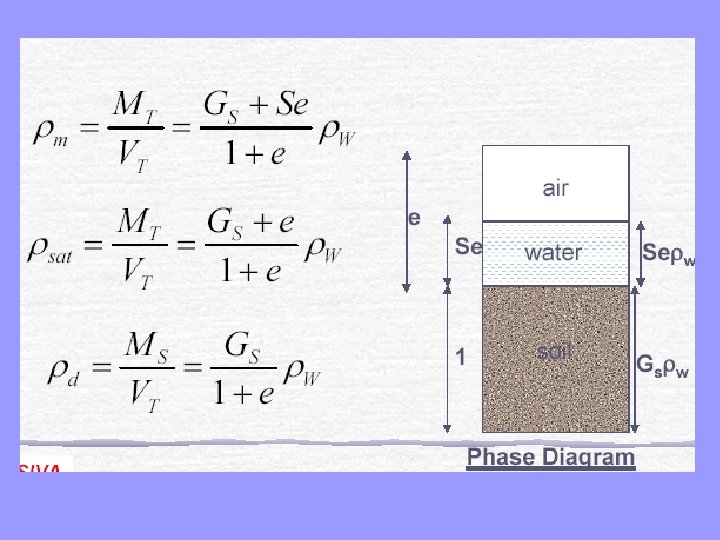
Solving Weight-Volume Problems We often encounter problems where one or more of the weight-volume parameters is known and others need to be determined. For example, some parameters, such as moisture content, can be measured in the laboratory, while others, such as void ratio, cannot. Therefore, we need to have a means of computing them. Often we can perform these computations using the derived equations presented last. However, if this method does not work, we go back to fundamentals and solve the problem using a phase diagram as follows: 1. Draw a phase diagram and annotate all of the dimensions presented in the problem statement. Remember to set Wa = 0. If the soil is saturated, we also can set Va = 0. 2. Sometimes no weights or volumes are given in the problem statement, or the only dimensions given are equal to zero (i. e. , no air or no water). If this is the case, then the given data is applicable to the entire soil strata, regardless of the sample size. However, the phase diagram analysis method requires that a certain quantity of soil be specified, and will not work unless we do so. Therefore, we must assume a quantity. Any one dimension may be assumed (but only one!). Usually we assume V= 1 m 3 or V= 1 ft 3. 3. Using basic equations and obvious addition and subtraction from the phase diagram (i. e. , Va= V - Vs - Vw), determine all of the remaining dimensions. 4. Compute the required parameters using basic equations from these dimensions in phase diagram

Example 1 A 27. 50 Ib soil sample has a volume of 0. 220 ft 3, a moisture content of 10. 2%, and a specific gravity of solids of 2. 65. Compute the unit weight, dry unit weight, degree of saturation, void ratio, and porosity.

Solution using fundamental and derived equations

Solution using a phase diagram • Although the fundamental and derived equations were sufficient to solve this problem, and would be the easiest method, we also will illustrate a solution using a phase diagram. • IN EXAMINATIONS and QUIZES, YOU MUST SOLVE RELEVANT PROBLEMS BY USING ONLY THIS METHOD

Step 1: Draw and annotate a phase diagram Step 2: Assume dimension Not applicable to this problem, because weights and volumes have been given

Step 3: Determine dimensions in phase diagram.

Step 4: Compute parameters.

Example 2 A certain soil has the following properties: Gs= 2. 71 n= 41. 9% w = 21. 3% Find the degree of saturation, S and the unit weight, by using phase relations?

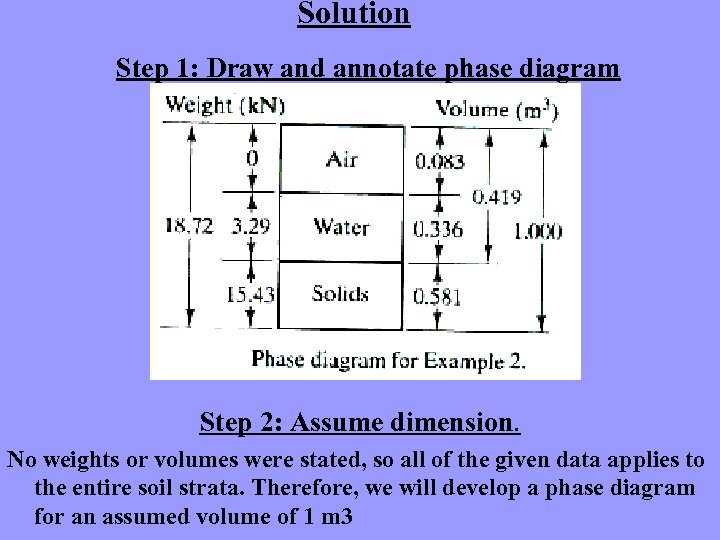Solution Step 1: Draw and annotate phase diagram Step 2: Assume dimension. No weights or volumes were stated, so all of the given data applies to the entire soil strata. Therefore, we will develop a phase diagram for an assumed volume of 1 m 3

Step 3: Determine dimensions in phase diagram.

Step 4: Compute parameters.

Example 3 The standard method of measuring the specific gravity of solids (ASTM D 854) uses a calibrated glass flask known as a pycnometer, as shown in Figure 4. 6. The pycnometer is first filled with water and set on a balance to find its mass. Then, it is refilled with a known mass of dry soil plus water so the total volume is the same as before. Again, its mass is determined. From this data, we can compute Gs Using this technique on a certain soil sample, we have obtained the following data: • • • Mass of soil = 81. 8 g Moisture content of soil = 11. 2% Mass of pycnometer+water = 327. 12 g Mass of pycnometer+soil+water = 373. 18 g Volume of pycnometer = 250. 00 ml Compute Gs for this soil.

Solution:

PARTICLE SIZE AND SHAPE • The individual solid particles in a soil can have different sizes and shapes. • These characteristics also have a significant effect on its engineering behavior. • Therefore, geotechnical engineers often assess particle size and shape.

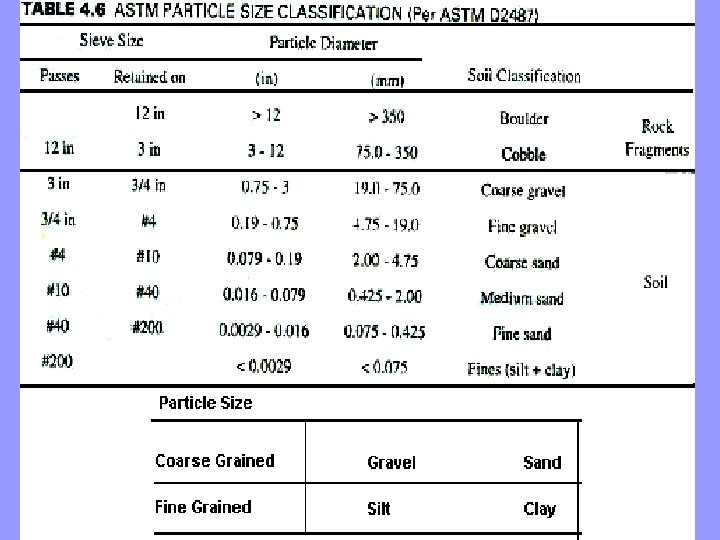
Particle Size Classification • Several systems have been developed to classify soil particles based on their size. • We will now examine only one: the ASTM system. • According to ASTM, particles larger than 3 in (75 mm) in diameter are known as rock fragments. Smaller particles are defined as soil, and are classified according their ability to pass through certain size sieves. • A sieve is a carefully manufactured mesh of wires with a specified opening size, as shown in Figure 4. 8.

Photographs of samples from each category Natural deposits often include a mixture of both rock fragments and soil.

Laboratory Tests Although the distribution of particle sizes can often he estimated by eye, two laboratory tests are commonly used to provide more precise assessments: 1) sieve analysis 2) hydrometer analysis.

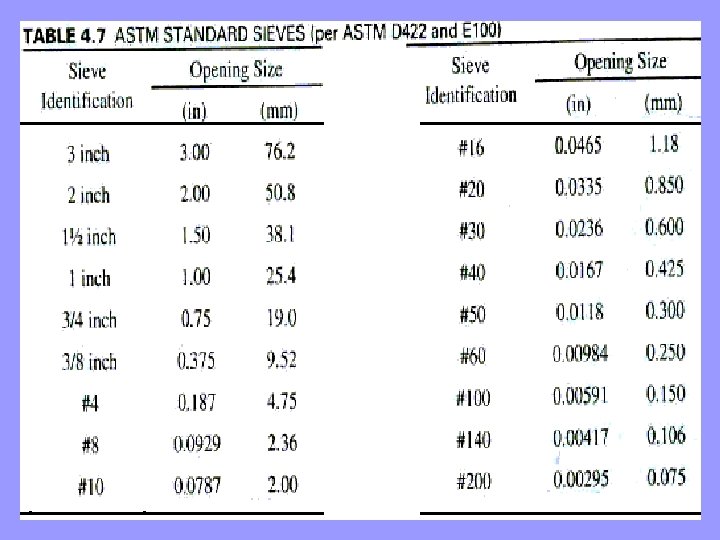
Sieve Analysis • A sieve analysis is a laboratory test that measures the grain-size distribution of a soil by passing it through a series of sieves. • The larger sieves are identified by their opening size. For example, a 3/4 -inch sieve will barely pass a 3/4 -inch diameter sphere. • Smaller sieves are numbered, with the number indicating the openings per inch. For example, a #8 sieve has 8 openings per inch or 64 per square inch. • However, the size of these openings is less than 1/8 inch because of the width of the wire. Table 4. 7 presents opening sizes for standard sieves used in North America.

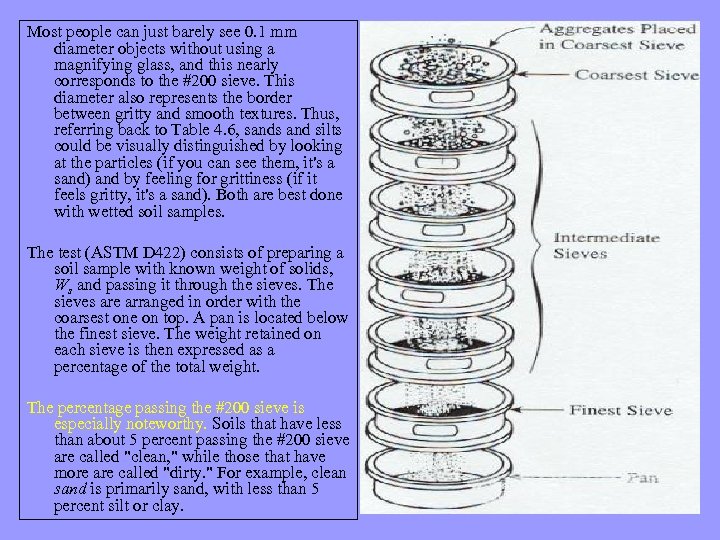Most people can just barely see 0. 1 mm diameter objects without using a magnifying glass, and this nearly corresponds to the #200 sieve. This diameter also represents the border between gritty and smooth textures. Thus, referring back to Table 4. 6, sands and silts could be visually distinguished by looking at the particles (if you can see them, it's a sand) and by feeling for grittiness (if it feels gritty, it's a sand). Both are best done with wetted soil samples. The test (ASTM D 422) consists of preparing a soil sample with known weight of solids, Ws and passing it through the sieves. The sieves are arranged in order with the coarsest one on top. A pan is located below the finest sieve. The weight retained on each sieve is then expressed as a percentage of the total weight. The percentage passing the #200 sieve is especially noteworthy. Soils that have less than about 5 percent passing the #200 sieve are called "clean, " while those that have more are called "dirty. " For example, clean sand is primarily sand, with less than 5 percent silt or clay.

Hydrometer Analysis • Although sieve analyses work very well for particles larger than the #200 sieve (sands and gravels) and they determine the total amount of fines, they do not give any insight on the distribution of finer particles (silts and clays). • The smallest clay particles are only about 1 xl 0 -4 mm in diameter, which is about the same size as a smoke particle. It is impossible to manufacture sieves this small, so we need to use another technique: The hydrometer analysis

This procedure (ASTM D 422) consists of placing a soil sample with a known Ws into a 1000 ml graduated cylinder and filling it with water. The laboratory technician vigorously shakes the cylinder to place the soil in suspension, and then places it upright on a table as shown in Figure 4. 12. Once the cylinder has been set upright, the soil particles begin to settle to the bottom.

ü The velocity is proportional to the square of the particle diameter, so large particles settle much more quickly than small ones. ü In addition, we can determine the mass of solids still in suspension by measuring the specific gravity of the soilwater mixture, which is done using the hydrometer ü Therefore, by making a series of specific gravity measurements, usually over a period of 24 hours, and employing Stoke's law, we can determine the distribution of particles sizes in the soil sample.

• The hydrometer analysis is unsuitable for particles larger than about a #100 sieve because they settle more quickly than we can measure the specific gravity. • However, by performing a sieve analysis, hydrometer analysis, or both, we can determine the distribution of particle sizes for virtually any soil.

Grain Size Distribution Curves ü Real soils rarely fall completely within only one of the categories listed in particle size classification. They almost always contain a variety of particles sizes mixed together. Therefore, we need to have an effective means of presenting the distribution of particle sizes in a soil. ü That method is the grain-size distribution curve. ü These are plots of the grain diameter (on a logarithmic scale) vs. the percentage of the solids by weight smaller than that diameter. We call the latter "percent finer" or "percent passing, " which generates mental images of that portion of the soil passing through a sieve.

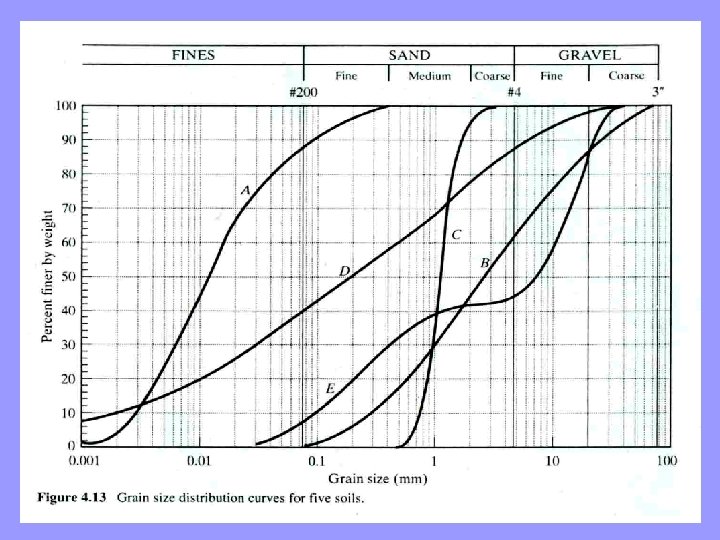
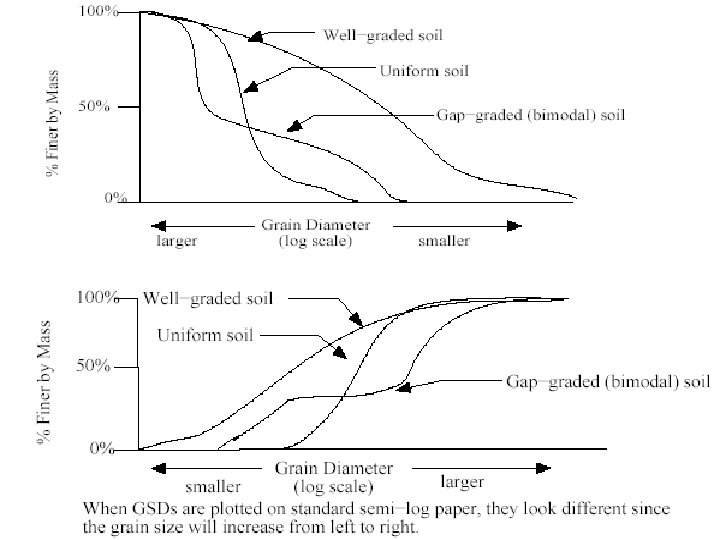
• Soil A, indicates primarily fine-grained soils (silts and clays) • Soil B, C, E indicate primarily coarse-grained soils (sands and gravels) Acording to Grain Size Disstribution Shape: • Poorly-graded soils (or uniformly-graded soils). If Steep grainsize distribution curves, such as soil C, reflect soils with a narrow range of particle sizes. • Well-graded soils. If soils with flat curves, such as soil D, containing a wide range of particle sizes • Gap-graded soils. If soils have missing particles in a certain size range in their grain-size distribution curve, such as soil E. Gapgraded soils are sometimes considered a type of poorly graded soil. Aggregates used to make concrete are typically gap graded.

We can determine the percentage of each type of soil by weight by comparing the percents passing the appropriate sieve sizes as listed in particle size classification. For example, to determine the amount of sand in a soil, subtract the percentage passing the #200 sieve from the percentage passing the #4 sieve. The particle diameters that correspond to certain percent-passing values for a given soil are known as the D-sizes. For example, D 10, is the grain size that corresponds to 10 percent passing. In other words, 10 percent of the soil is finer then D 10.

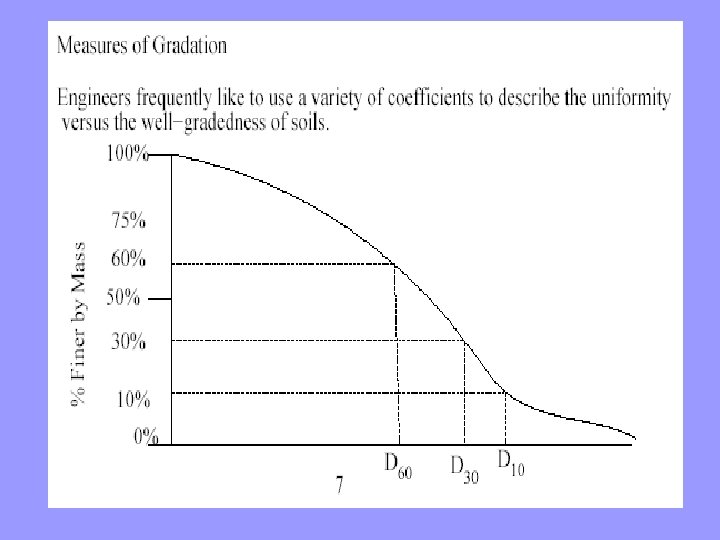
Some Engineering Parameters for Grain Size Distribution Curves • Coefficient of Uniformity • Coefficient of curvature

Ø Steep curves, which reflect poorly graded soils, have low values of Cu , while flat curves (well-graded soils) have high values. Ø Soils with smooth curves have Cc values between about 1 and 3, while irregular curves have higher or lower values. For example, most gap-graded soils have a Cc outside this range.

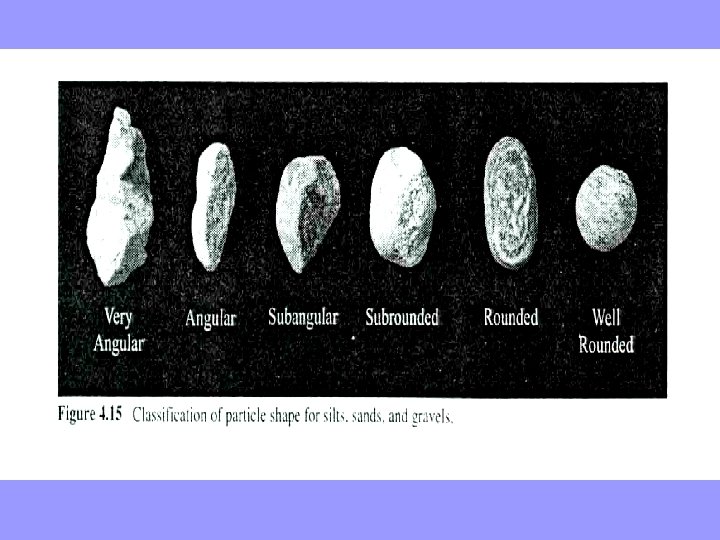
Particle Shape ü The shape of silt, sand, and gravel particles varies from very angular to well rounded. Angular particles are most often found near the rock from which they were formed, while rounded particles are most often found farther away where the soil has experienced more abrasion. ü Angular particles have a greater shear strength than smooth ones because it is more difficult to make them slide past one another. This is why aggregate base material used beneath highway pavements is often made of rocks that have been passed through a rock crusher to create very angular gravel. Clay particles have an entirely different shape, and are discussed later in the next section. ü Some non-clay particles are much flatter than any of the samples. One example is mica, which is plate-shaped. Although mica never represents a large portion of the total weight, even a small amount can affect a soil's behavior. Sands that include mica are known as micaceous sands.

Example 4 Determine the following for soil D in Figure 4. 13 given the next: • Percent gravel, sand, and fines • Cu and Cc

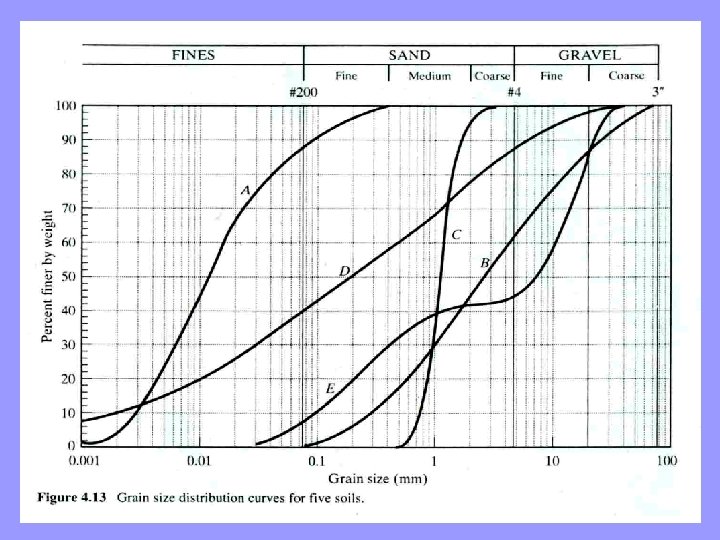
Solution Percent finer data from grain size curve: #200 — 40% #40 — 88% 3 in — 100% Percentage of each type of soil: Gravel = 3 in - #4 = 100% - 88% = 12% Sand = #4 - #200 = 88% - 40% = 48% Fines = #200 = 40% D-sizes from grain-size curve D 10 = 0. 0019 mm D 30 = 0. 030 mm D 60 = 0. 49 mm Cu and Cc : -Answer

Note: This is an exceptionally large value of Cu which reflects the very flat grain-size curve. Most Cu values are less than 20.

CLAY SOILS • Soils that consist of silt, sand, or gravel are primarily the result of physical and mild chemical weathering processes and retain much of the chemical structure of their parent rocks. • However, this is not the case with clay soils because they have experienced extensive chemical weathering and have been changed into a new material quite different from the parent rocks. • As a result, the engineering properties and behavior of clays also are quite different from other soils.

Formation and Structure of Clay Minerals Several different chemical weathering processes form clay minerals which are the materials from which clays are made. We will examine of these processes as an example. This process changes orthoclase feldspar, a mineral found in granite and many other rocks, into a clay mineral called kaolinite. The process begins when water acquires carbon dioxide as it falls through the atmosphere and seeps through soil, thus forming a weak carbonic acid (H 2 CO 3) solution. This acid reacts with orthoclase feldspar according to the following chemical formula: 4 KAl. Si 3 O 8 + 2 H 2 CO 3 + 2 H 2 O -> 2 K 2 CO 3 + Al 4(OH)8 Si 4 O 10 +8 Si. O 2 orthoclase + carbonic acid + water - potassium carbonate + kaolinite + silica Finally, the potassium carbonate and silica are carried off in solution by groundwater, ultimately to be deposited elsewhere, leaving kaolinite clay where orthoclase feldspar once existed.

v In these various chemical weathering processes, it is formed sheetlike chemical structures. v There are two types of sheets: 1) Tetrahedral or silica sheets, consist of silicon and oxygen atoms; 2) Octahedral or alumina sheets, have aluminum atoms and hydroxyls (OH). v Sometimes octahedral sheets have magnesium atoms instead of aluminum, thus forming magnesia sheets. v These sheets then combine in various ways to form dozens of different clay minerals, each with its own chemistry and structure. The three most common ones are:

• Kaolinite • Montmorillonite (also called smectite) • Illite

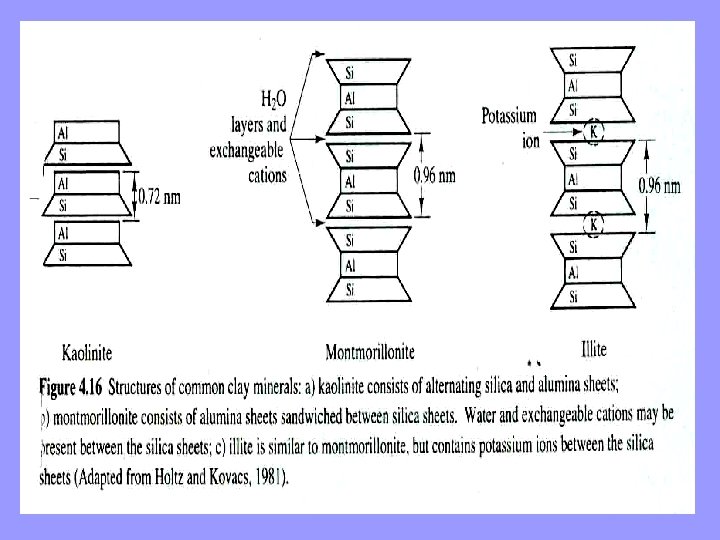
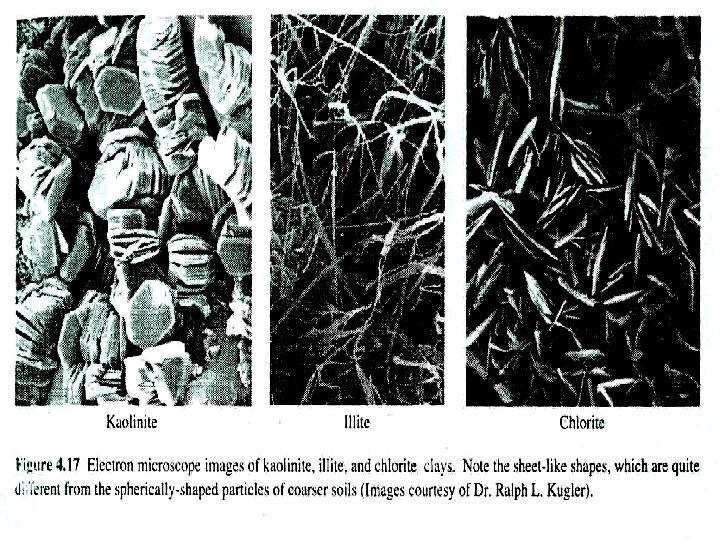
Kaolinite v Consists of alternating silica and alumina sheets. These sheets are held together with strong chemical bonds, v. So kaolinite is very stable clay. v. Unlike most other clay minerals, kaolinite does not expand appreciably when wetted. v So it is used to make pottery. v It also is an important ingredient in paper, paint, and other products, including Pharmaceuticals (i. e. , kaopectate).

Since kaolinite does not expand appreciably when wetted, It is more prefered for construction of core section with clay in embankmant dams especailly if easily obtained around

Montmorillonite v. Has layers made of two silica sheets and one alumina sheet. The bonding between these layers is very weak, so large quantities of water can easily enter and separate them, vthus causing the clay to swell. This property can be very troublesome or very useful, depending on the situation

v. Problems with soil expansion include extensive distortions in structures, highways, and other civil engineering projects. v. However, this expansive behavior and the low permeability of montmorillonite can be useful for sealing borings (especially in deep excavation by slury trench) or providing groundwater barriers. Bentonite, a type of montmorillonite, is commercially mined and sold for such purposes.

Illite v. Has layers similar to those in montmorillonite, but contains potassium ions between each layer. v. The chemical bonds in this structure are stronger than those in montmorillonite but weaker than those in kaolinite, so illite expands slightly when wetted. Glacial clays in the Great Lakes region are primarily illite. Other clay minerals include vermiculite, attapulgite, and chlorite.

Properties of Clays Because of the small particle diameter and plate-like shape of clays, the surface area to mass ratio is much greater than in other soils. This ratio is known as the specific surface. For example: Ø Montmorillonite has a specific surface of about 800 m 2/g, which means 3. 5 g of this clay has a surface area equal to that of a football field Ø Illite=> (80 -100 m 2/g) Ø Kaolinite => (10 -20) m 2/g

v. The large specific surface of clays provides more contact area between particles, and thus more opportunity for various interparticle forces to develop. v. It also provides more places for water molecules to attach, thus giving clays a much greater affinity for absorbing water. Some clay can easily absorb several times their dry weight in water. v. Montmorillonite clays have the greatest specific surface, so it is no surprise that they have the greatest affinity for water.

The interactions between this water and the clay minerals are quite complex, but the net effect is that: The engineering properties vary as the moisture content (water content) varies. For example, the shear strength of given clay at a moisture content of 50% will be less than at a moisture content of 10%.

This behavior is quite different from that in sands, because their specific surface is much smaller and the particles are more inert. Other than changes in pressure within the pore water, variations in moisture content have very little effect on the behavior of sands.

Clay Minerals compared with each other • Strength: K>I>M • Compressibilty: M>I>K • Hydraulic Conductivity: K>I>M

Formation of Clay Soils • On a slightly larger but still microscopic scale, clay minerals are assembled in various ways to form clay soils. These microscopic configurations are called the soil fabric, and depend largely on the history of formation and deposition. • For example, residual clay, which has weathered inplace and is still at its original location, will have a fabric much different from marine clay, which has been transported and deposited by sedimentation. These differences are part of the reason such soils behave differently.

• Although we sometimes encounter soil strata that consist of nearly pure clay, most clays are mixed with silts and/or sands. • Nevertheless, even a small percentage of clay significantly impacts the behavior of a soil. • When the clay content exceeds about 50 percent, the sand silt particles are essentially floating in the clay, and have very little effect on the engineering properties of the soil.

PLASTICITY AND THE ATTERBERG LIMITS • Silts and clays are two very different kinds of soils. Some classification systems draw the line between them based on particle size as determined from a hydrometer test, typically at 0. 001 to 0. 005 mm. • Although classification systems can be useful, they also can be misleading because the biggest difference between silt and clay is not their particle sizes, but their physical and chemical structures is important. • In addition, It would be impractical to use electron microscopes or other sophisticated equipment to distinguish between clays and silts on a routine works.

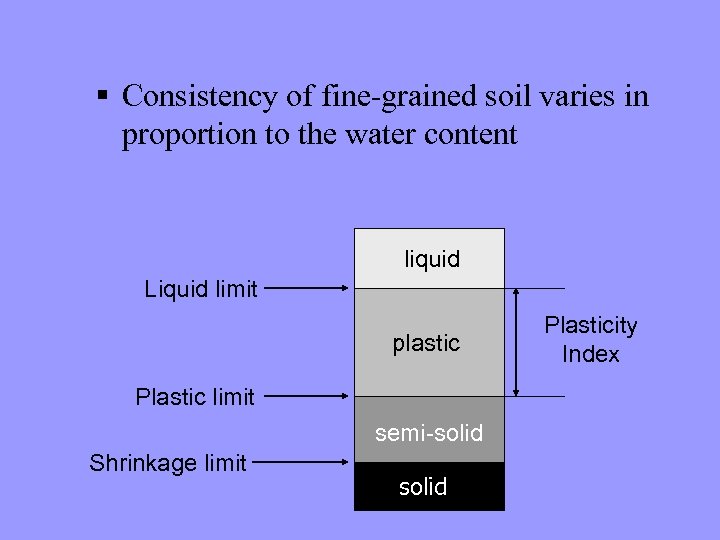
Therefore, in geotechnical engineering Plasticity is used for assesing engineering properties of clay and silt Plasticity, is described as the response of a soil to changes in moisture content.

Ø When adding water to a soil changes its consistency from hard and rigid to soft and pliable, the soil is said to be exhibiting plasticity. Ø Clays can be very plastic and silts only slightly plastic, whereas clean sands and gravels do not exhibit any plasticity at all. Ø This assessment can be made using visual-manual procedures, and with experience one can distinguish between clays and silt simply with the hands and a water bottle. ØMore formal assessments of plasticity are performed in the laboratory using the Atterberg limits tests.

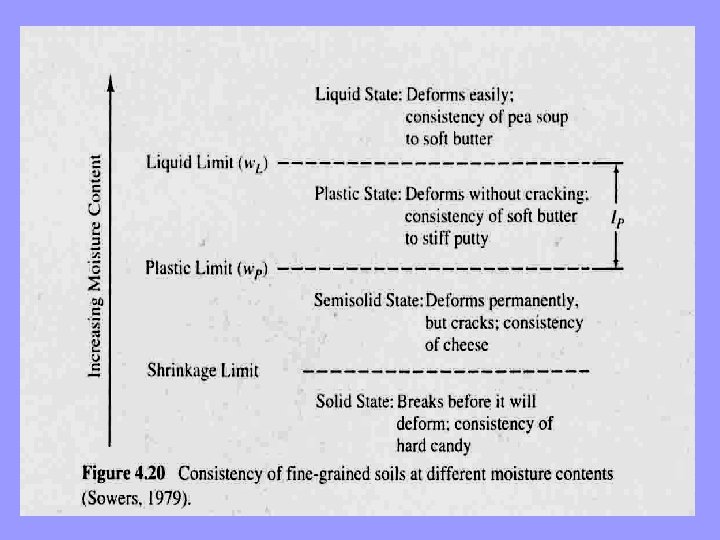
The Atterberg Limits • In 1911, the Swedish soil scientist Albert Atterberg (18461916) developed a series of tests to evaluate the relationship between moisture content and soil consistency. Then, in the 1930 s, Karl Terzaghi and Arthur Casagrande adapted these tests for civil engineering purposes, and they soon became a routine part of geotechnical engineering. • This series includes three separate tests: the liquid limit test, the plastic limit test, and the shrinkage limit test. Together they are known as the Atterberg limits tests (ASTMD 427 and. D 4318). • The liquid limit and plastic limit tests are routinely performed in many soil mechanics laboratories. However, the shrinkage limit test is less useful, and is rarely performed by civil engineers.

Liquid Limit Test: Liquid Limit • The liquid limit test uses the liquid limit device, a standard laboratory apparatus. A soil sample is placed in the device, and a groove is cut using a standard tool. The cup is then repeatedly dropped, and the number of drops required for the groove to close for a distance of onehalf inch (13 mm) is recorded. The soil is then removed and its moisture content is determined. This test is then repeated at various moisture contents, producing a plot of number of drops vs. moisture content. • By definition, the soil is said to be at its liquid limit when exactly 25 drops are required to close the groove for a distance of one-half inch (13 mm). The corresponding moisture content is determined from the test data. • The liquid limit, LL or w. L. is this moisture content expressed without a percentage sign. For example, if the moisture content is 45%, the liquid limit is 45.

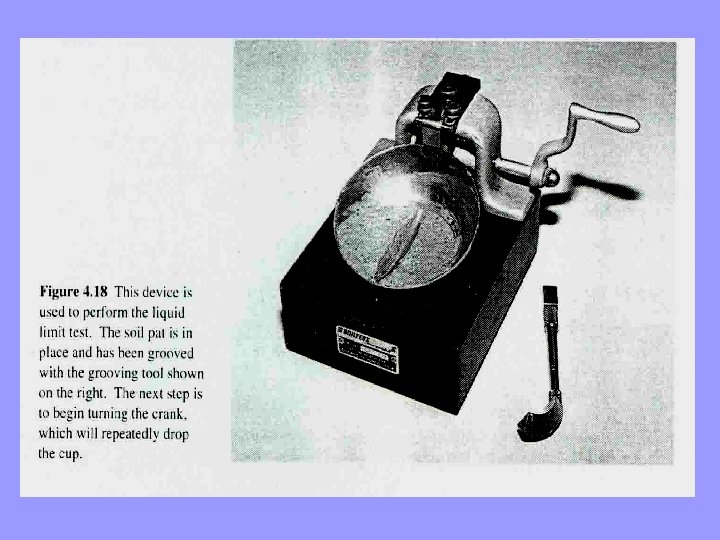
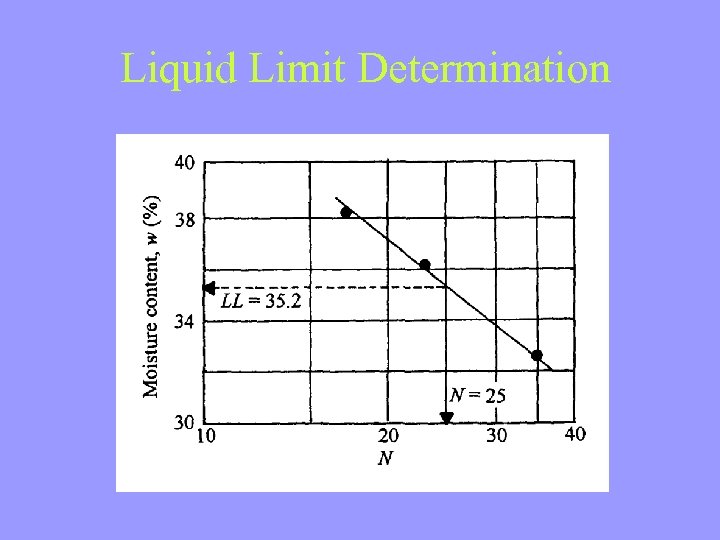Liquid Limit Determination

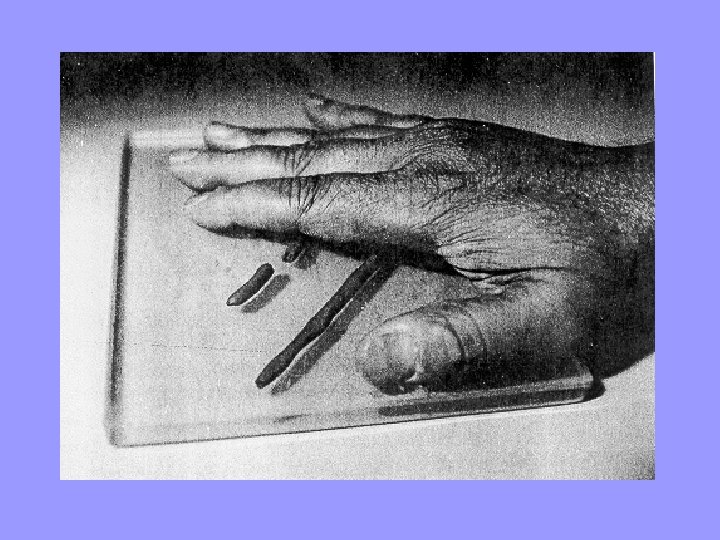
The Plastic Limit Test: Plastic Limit Ø The plastic limit test procedure involves carefully rolling the soil sample into threads. As this rolling process continues, the thread becomes thinner and eventually breaks. If the soil is dry, it breaks at a large diameter. If it is wet, it breaks at a much smaller diameter. Ø By definition, the soil is at the plastic limit when it breaks at a diameter of one-eighth of an inch (3 mm). The plastic limit, PL or wp , is this moisture content with the percent sign dropped.

Consistency and Plasticity Assessments Based on Atterberg Limits The Atterberg limits test results help engineers assess the plasticity of a soil and its consistency at various moisture contents.

§ Consistency of fine-grained soil varies in proportion to the water content liquid Liquid limit plastic Plastic limit semi-solid Shrinkage limit solid Plasticity Index

• Plasticity Index: When the soil is at a moisture content between the liquid limit and the plastic limit, it is said to be in a plastic state. It can be easily molded without cracking or breaking. The children's toy play-dough has a similar consistency. This property relates to the amount and type of clay in the soil. Ø The plasticity index, PI or IP , measure of the range of moisture contents that encompass the plastic state:

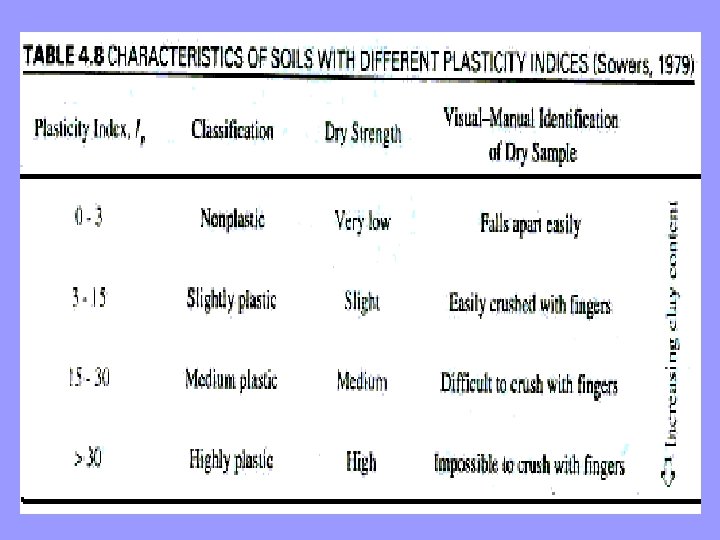
ØSoils with a large clay content retain this plastic state over a wide range of moisture contents, and thus have a large plasticity index. The opposite is true of silty soils. Table 4. 8 describes soil characteristics at various ranges of plasticity index. Clean sands and gravels are considered to be no plastic (NP).

Liquidity index: The liquidity index, IL compares the current moisture content of a soil, w, to its Atterberg limits: Thus, a liquidity index of 0 means the soil is currently at the plastic limit, and 1 means it is at the liquid limit.

STRUCTURED VS. UNSTRUCTURED SOILS Many soils contain additional physical features beyond a "simple" particulate assemblage. These are known as structured soils and include the following: Ø • Cemented soils contain cementing agents that bind the particles together. The most common cementing agents are calcium carbonate (Ca. CO 3) and iron oxides (Fe 2 O 3). Both are usually transmitted into the soil in solution within the groundwater. Ø • Fissured soils contain discontinuities similar to fissures in rock. Stiff clays are especially likely to contain fissures. Ø • Sensitive clays are those with a flocculated structure of clay particles that resemble a house of cards. These soils are very sensitive to disturbance, which destroys this delicate structure. Unstructured soils are those that do not contain such special features. Most geotechnical analyses are based on unstructured soils, and thus often need to be modified when working with structured soils.

ORGANIC SOILS Ø An organic soil is one that contains a significant amount of organic material recently derived from plants or animals. It needs to be fresh enough to still be in the process of decomposition, and thus retains a distinctive texture, color, and odor. Ø The identification of organic soils is very important, because they are much weaker and more compressible than inorganic soils, and thus do not provide suitable support for most engineering projects. If such soils are present, we usually avoid them, excavate them, or drive piles through them to reach more suitable deposits.

SUMMARY Ø 1. Soil is a particulate material, so its engineering properties depend primarily on the interaction between these particles. This is especially true of gravels, sands, and silts. Clays also are particulates, but their behavior is much more complex because of the interaction between the particles and the pore water. Ø 2. Soil can include all three phases of matter simultaneously, and their relative proportions are important. Geotechnical engineers have developed a series of weight-volume parameters to describe these proportions. Ø 3. The distribution of particle sizes in a soil also is important, and this distribution can be determined by performing a sieve analysis and/or a hydrometer analysis. The results are presented as a grain-size distribution curve. Ø 4. The solid particles also have various shapes, which impact their behavior.

Ø 5. Clays are formed by chemical weathering processes. The individual particles are much smaller than sands or silts, and their engineering behavior is much more dependent on the moisture content. Ø 6. Clays and silts are often distinguished from each other by assessing their plasticity, which reflects their affinity for water. The Atterberg limits tests, especially the plastic limit and liquid limit, help us do this. Ø 7. Structured soils are those with special features, such a cementation, fissures, or flocculated structures. They behave differently from unstructured soils, which do not contain these features. Ø 8. Organic soils are those with a significant quantity of organic matter. Their engineering properties are much worse than those of inorganic soils.

THE END