04 Системы координат пространственных данных.ppt
- Количество слайдов: 31
 4. Системы координат пространственных данных Грохольский Н. С. ГИС в геоэкологии
4. Системы координат пространственных данных Грохольский Н. С. ГИС в геоэкологии
 Геоид Физическая поверхность Земли имеет неправильную форму и потому не может быть описана замкнутыми формулами. В силу этого, для решения задач, эту поверхность заменяют математически правильной поверхностью. В самом точном приближении таковой поверхностью является поверхность геоида. Геоид – это геометрическое тело, ограниченное уровенной поверхностью морей и океанов, связанных между собой и имеющих единую водную массу. В каждой своей точке эта поверхность нормальна направлению силы тяжести.
Геоид Физическая поверхность Земли имеет неправильную форму и потому не может быть описана замкнутыми формулами. В силу этого, для решения задач, эту поверхность заменяют математически правильной поверхностью. В самом точном приближении таковой поверхностью является поверхность геоида. Геоид – это геометрическое тело, ограниченное уровенной поверхностью морей и океанов, связанных между собой и имеющих единую водную массу. В каждой своей точке эта поверхность нормальна направлению силы тяжести.
 Эллипсоид вращения Вместо геоида, в качестве поверхности используется эллипсоид вращения с малым сжатием, причем, берут его таких размеров и так ориентируют в теле Земли, чтобы он напоминал геоид. Эллипсоид вращения – это тело, образованное вращением эллипса вокруг полярной оси. Отклонения эллипсоида Красовского от геоида на территории СНГ не превышают 150 м. Название Дата Большая полуось Малая Полуось Применение Айри (Airy) 1830 6377563. 396 6356256. 91 Великобритания Бессель (Bessel) 1841 6377397. 155 6356078. 96284 Центральная Европа, Чили, Индонезия Кларк (Clarke) 1866 6378206. 4 6356583. 8 Североамериканский континент, Филиппины Хелмет (Helmet) 1907 6378200 6356818. 17 Египет Красовский 1940 6378245 6356863. 0188 СНГ, Россия, некоторые страны вост. Европы 6370997 Весь мир (мелкий масштаб) 6378137 6356752. 31 Весь Мир (GPS приемники) Сфера WGS 84 1984
Эллипсоид вращения Вместо геоида, в качестве поверхности используется эллипсоид вращения с малым сжатием, причем, берут его таких размеров и так ориентируют в теле Земли, чтобы он напоминал геоид. Эллипсоид вращения – это тело, образованное вращением эллипса вокруг полярной оси. Отклонения эллипсоида Красовского от геоида на территории СНГ не превышают 150 м. Название Дата Большая полуось Малая Полуось Применение Айри (Airy) 1830 6377563. 396 6356256. 91 Великобритания Бессель (Bessel) 1841 6377397. 155 6356078. 96284 Центральная Европа, Чили, Индонезия Кларк (Clarke) 1866 6378206. 4 6356583. 8 Североамериканский континент, Филиппины Хелмет (Helmet) 1907 6378200 6356818. 17 Египет Красовский 1940 6378245 6356863. 0188 СНГ, Россия, некоторые страны вост. Европы 6370997 Весь мир (мелкий масштаб) 6378137 6356752. 31 Весь Мир (GPS приемники) Сфера WGS 84 1984
 Системы координат: географическая Система географических (геодезических) координат Широта – угол между нормалью к поверхности эллипсоида в данной точке и плоскостью экватора Долгота – двугранный угол между меридианом данной точки и начальным меридианом (Гринвичским) Для географической системы координат в качестве нулевого меридиана принят Гринвичский меридиан, а в качестве нулевой параллели – экватор.
Системы координат: географическая Система географических (геодезических) координат Широта – угол между нормалью к поверхности эллипсоида в данной точке и плоскостью экватора Долгота – двугранный угол между меридианом данной точки и начальным меридианом (Гринвичским) Для географической системы координат в качестве нулевого меридиана принят Гринвичский меридиан, а в качестве нулевой параллели – экватор.
 Системы координат: прямоугольная Система прямоугольных координат Она основана на плоскости. Реальные географические координаты измеряются в значениях x-, y- координат от определенной начальной точки. x-, y- координаты имеют положительные величины и измеряются в метрах.
Системы координат: прямоугольная Система прямоугольных координат Она основана на плоскости. Реальные географические координаты измеряются в значениях x-, y- координат от определенной начальной точки. x-, y- координаты имеют положительные величины и измеряются в метрах.
 Системы отсчета (DATUM) Базовые геодезические параметры это набор параметров и контрольных точек, используемых для точного задания трехмерной формы Земли. В то время как сфероид аппроксимирует форму Земли, датум определяет положение сфероида по отношению к центру Земли. Являясь геоцентрическим (глобальным), то есть связанным с центром Земли, датум использует центр масс Земли в качестве начала отсчета. Наиболее широко используемым датумом является Мировая геодезическая система 1984 года (WGS 84). Она служит основой для измерения местоположений во всем мире.
Системы отсчета (DATUM) Базовые геодезические параметры это набор параметров и контрольных точек, используемых для точного задания трехмерной формы Земли. В то время как сфероид аппроксимирует форму Земли, датум определяет положение сфероида по отношению к центру Земли. Являясь геоцентрическим (глобальным), то есть связанным с центром Земли, датум использует центр масс Земли в качестве начала отсчета. Наиболее широко используемым датумом является Мировая геодезическая система 1984 года (WGS 84). Она служит основой для измерения местоположений во всем мире.
 Системы отсчета (DATUM) Молоденский разработал формулы для применения параметров сдвига к географическим координатам. здесь d. X, d. Y, d. Z - сдвиг по осям, м; a и f - большая полуось и сжатие исходного эллипсоида; da и df - разности между большой полуосью и сжатием исходного эллипсоида и целевого эллипсоида.
Системы отсчета (DATUM) Молоденский разработал формулы для применения параметров сдвига к географическим координатам. здесь d. X, d. Y, d. Z - сдвиг по осям, м; a и f - большая полуось и сжатие исходного эллипсоида; da и df - разности между большой полуосью и сжатием исходного эллипсоида и целевого эллипсоида.
 Параметры системы отсчета (Datum) Настройка навигационных систем Garmin для работы в системе координат 1942 г. Эта настройка влияет только на показания текущих координат. Garmin 12/12 XL для пересчета координат использует преобразование Молоденского. Main Menu. . . Setup Menu. . . Navigation. . . Map Datum. . . User. . . DX +28. 0 DY – 130. 0 DZ – 95. 0 DA – 108. 0 DF +0. 004808 Если вы хотите получать координаты по километровой сетке в проекции Гаусса-Крюгера: Main Menu. . . Setup Menu. . . Navigation. . . Position Frmt. . . User Grid. . . Longitude Origin Введите центральный меридиан зоны Scale 1. 000 (не 0. 9996!!!) False E 500 000 False N 0 (если карта в северном полушарии) Параметр Москва Новосибирск Владивосток DX 24 18 18 DY -130 -140 -154 DZ -86 -82 -76 DA -108 DF +0. 0048080
Параметры системы отсчета (Datum) Настройка навигационных систем Garmin для работы в системе координат 1942 г. Эта настройка влияет только на показания текущих координат. Garmin 12/12 XL для пересчета координат использует преобразование Молоденского. Main Menu. . . Setup Menu. . . Navigation. . . Map Datum. . . User. . . DX +28. 0 DY – 130. 0 DZ – 95. 0 DA – 108. 0 DF +0. 004808 Если вы хотите получать координаты по километровой сетке в проекции Гаусса-Крюгера: Main Menu. . . Setup Menu. . . Navigation. . . Position Frmt. . . User Grid. . . Longitude Origin Введите центральный меридиан зоны Scale 1. 000 (не 0. 9996!!!) False E 500 000 False N 0 (если карта в северном полушарии) Параметр Москва Новосибирск Владивосток DX 24 18 18 DY -130 -140 -154 DZ -86 -82 -76 DA -108 DF +0. 0048080
 Картографическая проекция – определенный способ отображения одной поверхности на другую, устанавливающий аналитическую зависимость между координатами точек эллипсоида (сферы) и соответствующих точек плоскости. Картографическая проекция – однозначное, дважды непрерывно дифференцируемое с определителем, отличным от нуля, соответствие между точками поверхности эллипсоида и точками плоскости.
Картографическая проекция – определенный способ отображения одной поверхности на другую, устанавливающий аналитическую зависимость между координатами точек эллипсоида (сферы) и соответствующих точек плоскости. Картографическая проекция – однозначное, дважды непрерывно дифференцируемое с определителем, отличным от нуля, соответствие между точками поверхности эллипсоида и точками плоскости.
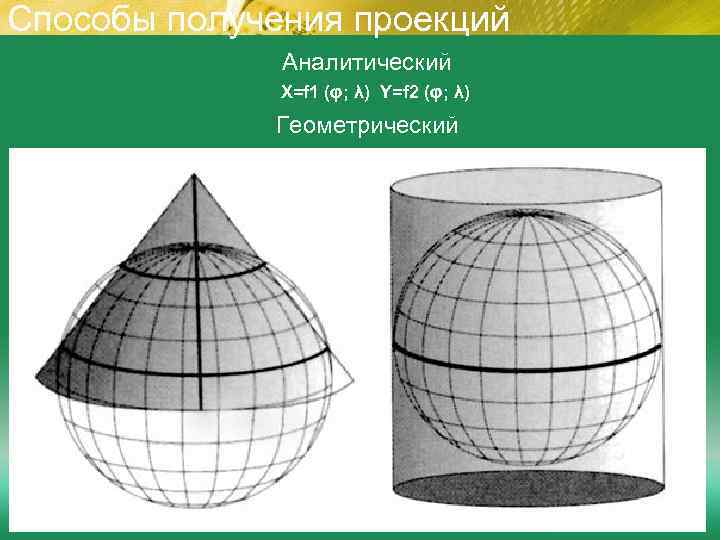 Способы получения проекций Аналитический X=f 1 (φ; λ) Y=f 2 (φ; λ) Геометрический
Способы получения проекций Аналитический X=f 1 (φ; λ) Y=f 2 (φ; λ) Геометрический
 Классификация картографических проекций 1. Характеру искажения 2. Виду меридианов и параллелей нормальной сетки 3. Положению полюса нормальной системы координат
Классификация картографических проекций 1. Характеру искажения 2. Виду меридианов и параллелей нормальной сетки 3. Положению полюса нормальной системы координат
 Классификация картографических проекций 1. Равноугольные (конформные) – углы и азимуты передаются без искажений, т. к. масштабы длин в точках не зависят от направления. Как следствие, в этих проекциях сохраняется подобие в бесконечно малых частях. Картографическая сетка в этих проекциях ортогональна. На картах в равноугольных проекциях можно измерять углы и азимуты, на них удобно производить измерение длин по всем направлениям. 2. Равновеликие (эквивалентные) – масштаб площадей остается постоянным и равным единице, а следовательно площади передаются без искажений. На картах в равновеликих проекциях можно делать сопоставление площадей. 3. Равнопромежуточные (эквидистантные) – масштаб по одному из главных направлений сохраняется и равен единице (а=1 или b=1) 4. Произвольные – присутствуют все виды искажений. По характеру искажения
Классификация картографических проекций 1. Равноугольные (конформные) – углы и азимуты передаются без искажений, т. к. масштабы длин в точках не зависят от направления. Как следствие, в этих проекциях сохраняется подобие в бесконечно малых частях. Картографическая сетка в этих проекциях ортогональна. На картах в равноугольных проекциях можно измерять углы и азимуты, на них удобно производить измерение длин по всем направлениям. 2. Равновеликие (эквивалентные) – масштаб площадей остается постоянным и равным единице, а следовательно площади передаются без искажений. На картах в равновеликих проекциях можно делать сопоставление площадей. 3. Равнопромежуточные (эквидистантные) – масштаб по одному из главных направлений сохраняется и равен единице (а=1 или b=1) 4. Произвольные – присутствуют все виды искажений. По характеру искажения
 Классификация картографических проекций Круговые – проекции, у которых меридианы и параллели изображаются окружностями. Экватор и ср. меридиан – прямые линии. Применяются для изображения всей поверхности Земли. (произвольная Гринтена, равноугольная Лагранжа). По виду меридианов и параллелей нормальной сетки
Классификация картографических проекций Круговые – проекции, у которых меридианы и параллели изображаются окружностями. Экватор и ср. меридиан – прямые линии. Применяются для изображения всей поверхности Земли. (произвольная Гринтена, равноугольная Лагранжа). По виду меридианов и параллелей нормальной сетки
 Классификация картографических проекций Азимутальные – параллели – одноцентренные окружности, меридианы – пучок прямых, расходящихся радиально из центра параллелей. Эти проекции применяются в прямом положении - для полярных территорий; в поперечном - для изображения зап. и вост. полушарий; в косом - для изображения территорий, имеющих округлую форму По виду меридианов и параллелей нормальной сетки
Классификация картографических проекций Азимутальные – параллели – одноцентренные окружности, меридианы – пучок прямых, расходящихся радиально из центра параллелей. Эти проекции применяются в прямом положении - для полярных территорий; в поперечном - для изображения зап. и вост. полушарий; в косом - для изображения территорий, имеющих округлую форму По виду меридианов и параллелей нормальной сетки
 Классификация картографических проекций Цилиндрические – параллели - параллельные прямые, перпендикулярные осевому меридиану, причем параллели всегда равноразделенные (отрезки параллелей пропорциональны разностям долгот); меридианы - Все меридианы прямые, перпендикулярные параллелям. Расстояния между меридианами пропорциональны разностям долгот. В этих проекциях можно изобразить весь земной шар. Наиболее выгодны эти проекции для изображения территорий, расположенных вблизи экваториальных широт и растянутых вдоль экватора (или вдоль некоторой стандартной параллели). По виду меридианов и параллелей нормальной сетки
Классификация картографических проекций Цилиндрические – параллели - параллельные прямые, перпендикулярные осевому меридиану, причем параллели всегда равноразделенные (отрезки параллелей пропорциональны разностям долгот); меридианы - Все меридианы прямые, перпендикулярные параллелям. Расстояния между меридианами пропорциональны разностям долгот. В этих проекциях можно изобразить весь земной шар. Наиболее выгодны эти проекции для изображения территорий, расположенных вблизи экваториальных широт и растянутых вдоль экватора (или вдоль некоторой стандартной параллели). По виду меридианов и параллелей нормальной сетки
 Классификация картографических проекций Конические – параллели - Дуги концентрических окружностей, общий центр которых лежит на осевом меридиане или его продолжении. Параллели равноразделенные, т. е. вдоль каждой параллели отрезки между меридианами одинаковые; меридианы - пучок прямых, расходящихся радиально из точки, являющейся центром параллелей. Углы между меридианами пропорциональны разностям их долгот. Эти проекции наиболее выгодны для изображения территорий, расположенных в средних широтах и растянутых вдоль параллелей. По виду меридианов и параллелей нормальной сетки
Классификация картографических проекций Конические – параллели - Дуги концентрических окружностей, общий центр которых лежит на осевом меридиане или его продолжении. Параллели равноразделенные, т. е. вдоль каждой параллели отрезки между меридианами одинаковые; меридианы - пучок прямых, расходящихся радиально из точки, являющейся центром параллелей. Углы между меридианами пропорциональны разностям их долгот. Эти проекции наиболее выгодны для изображения территорий, расположенных в средних широтах и растянутых вдоль параллелей. По виду меридианов и параллелей нормальной сетки
 Классификация картографических проекций Псевдоконические – параллели - дуги концентрических окружностей, общий центр которых лежит на осевом меридиане или его продолжении; меридианы – некоторые кривые, симметричные относительно среднего прямолинейного меридиана. Наиболее выгодны для изображения территорий, имеющих форму квадрата с вогнутыми сторонами. (проекция Бонна – применяется для карты Франции). По виду меридианов и параллелей нормальной сетки
Классификация картографических проекций Псевдоконические – параллели - дуги концентрических окружностей, общий центр которых лежит на осевом меридиане или его продолжении; меридианы – некоторые кривые, симметричные относительно среднего прямолинейного меридиана. Наиболее выгодны для изображения территорий, имеющих форму квадрата с вогнутыми сторонами. (проекция Бонна – применяется для карты Франции). По виду меридианов и параллелей нормальной сетки
 Классификация картографических проекций Псевдоцилиндрические – параллели - Параллельные прямые, перпендикулярные осевому меридиану. В большинстве случаев равноразделенные; меридианы – некоторые кривые, симметричные относительно среднего прямолинейного меридиана. Используются для изображения всей земной поверхности. Наиболее выгодны для изображения территорий растянутых вдоль среднего меридиана и экватора. (равновеликая синусоидальная проекция Сансона, равновеликая синусоидальная проекция Эккерта, равновеликая эллиптическая проекция Мольвейде). По виду меридианов и параллелей нормальной сетки
Классификация картографических проекций Псевдоцилиндрические – параллели - Параллельные прямые, перпендикулярные осевому меридиану. В большинстве случаев равноразделенные; меридианы – некоторые кривые, симметричные относительно среднего прямолинейного меридиана. Используются для изображения всей земной поверхности. Наиболее выгодны для изображения территорий растянутых вдоль среднего меридиана и экватора. (равновеликая синусоидальная проекция Сансона, равновеликая синусоидальная проекция Эккерта, равновеликая эллиптическая проекция Мольвейде). По виду меридианов и параллелей нормальной сетки
 Классификация картографических проекций Поликонические – параллели - дуги окружностей (окружности), центры которых лежат на осевом меридиане сетки или на его продолжении; меридианы – некоторые кривые, симметричные относительно среднего прямолинейного меридиана. Широко применяются для мелкомасштабных обзорных карт, выгодны для изображения территорий, растянутых вдоль среднего меридиана. (простая поликоническая проекция, видоизмененная поликоническая проекция для международной карты мира в масштабе 1: 1 000). По виду меридианов и параллелей нормальной сетки
Классификация картографических проекций Поликонические – параллели - дуги окружностей (окружности), центры которых лежат на осевом меридиане сетки или на его продолжении; меридианы – некоторые кривые, симметричные относительно среднего прямолинейного меридиана. Широко применяются для мелкомасштабных обзорных карт, выгодны для изображения территорий, растянутых вдоль среднего меридиана. (простая поликоническая проекция, видоизмененная поликоническая проекция для международной карты мира в масштабе 1: 1 000). По виду меридианов и параллелей нормальной сетки
 Классификация картографических проекций Полярная (нормальная) – полюс нормальной системы координат совпадает с географическим По положению полюса нормальной системы координат
Классификация картографических проекций Полярная (нормальная) – полюс нормальной системы координат совпадает с географическим По положению полюса нормальной системы координат
 Классификация картографических проекций Поперечная (трансверсионная) – полюс нормальной системы совпадает с экватором По положению полюса нормальной системы координат
Классификация картографических проекций Поперечная (трансверсионная) – полюс нормальной системы совпадает с экватором По положению полюса нормальной системы координат
 Классификация картографических проекций Косая (наклонная) – полюс нормальной системы координат располагается между географическим полюсом и экватором По положению полюса нормальной системы координат
Классификация картографических проекций Косая (наклонная) – полюс нормальной системы координат располагается между географическим полюсом и экватором По положению полюса нормальной системы координат
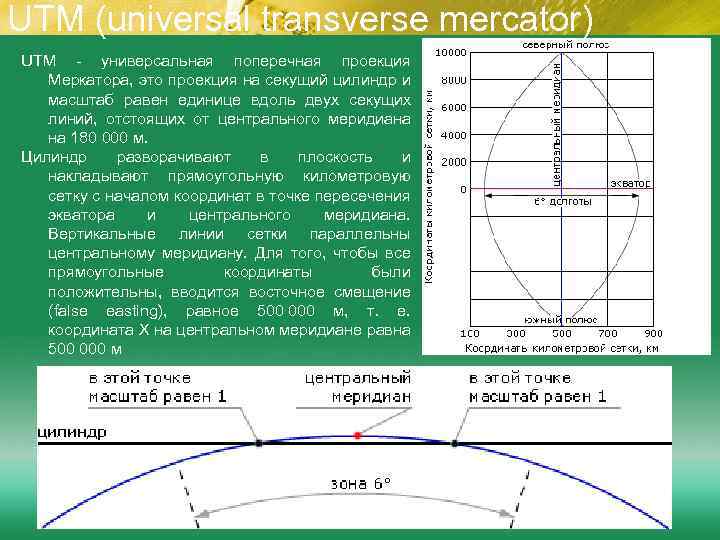 UTM (universal transverse mercator) UTM - универсальная поперечная проекция Меркатора, это проекция на секущий цилиндр и масштаб равен единице вдоль двух секущих линий, отстоящих от центрального меридиана на 180 000 м. Цилиндр разворачивают в плоскость и накладывают прямоугольную километровую сетку с началом координат в точке пересечения экватора и центрального меридиана. Вертикальные линии сетки параллельны центральному меридиану. Для того, чтобы все прямоугольные координаты были положительны, вводится восточное смещение (false easting), равное 500 000 м, т. е. координата X на центральном меридиане равна 500 000 м
UTM (universal transverse mercator) UTM - универсальная поперечная проекция Меркатора, это проекция на секущий цилиндр и масштаб равен единице вдоль двух секущих линий, отстоящих от центрального меридиана на 180 000 м. Цилиндр разворачивают в плоскость и накладывают прямоугольную километровую сетку с началом координат в точке пересечения экватора и центрального меридиана. Вертикальные линии сетки параллельны центральному меридиану. Для того, чтобы все прямоугольные координаты были положительны, вводится восточное смещение (false easting), равное 500 000 м, т. е. координата X на центральном меридиане равна 500 000 м
 Зоны UTM (universal transverse mercator)
Зоны UTM (universal transverse mercator)
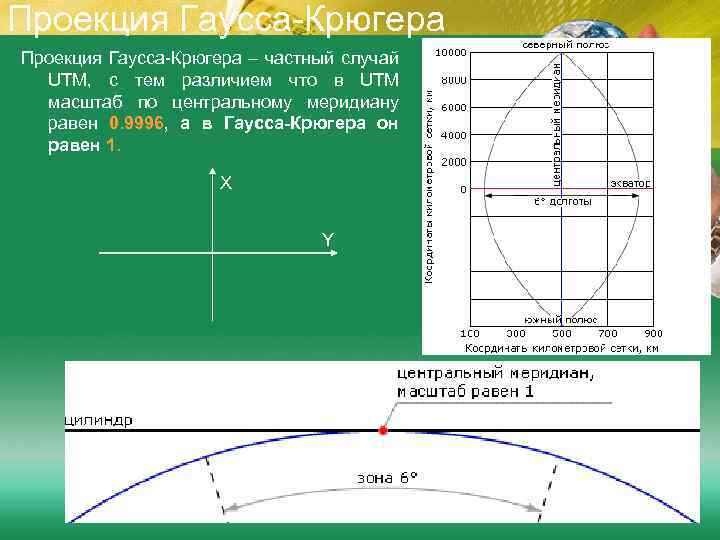 Проекция Гаусса-Крюгера – частный случай UTM, с тем различием что в UTM масштаб по центральному меридиану равен 0. 9996, а в Гаусса-Крюгера он равен 1. X Y
Проекция Гаусса-Крюгера – частный случай UTM, с тем различием что в UTM масштаб по центральному меридиану равен 0. 9996, а в Гаусса-Крюгера он равен 1. X Y
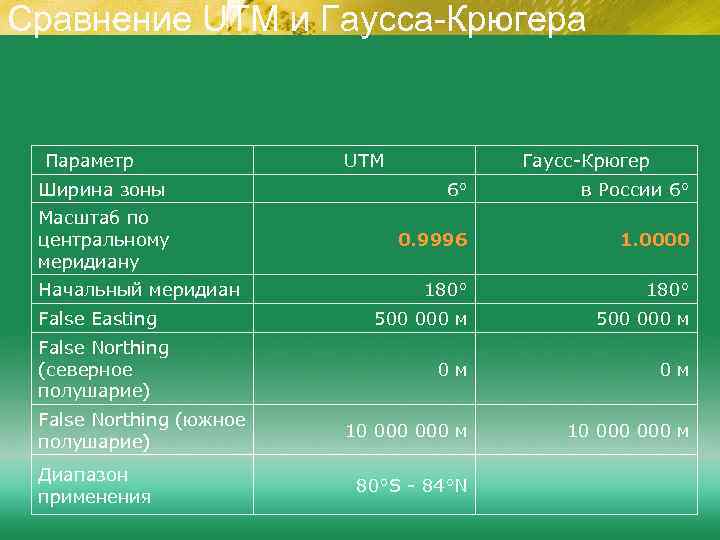 Сравнение UTM и Гаусса-Крюгера Параметр Ширина зоны Масштаб по центральному меридиану Начальный меридиан False Easting False Northing (северное полушарие) False Northing (южное полушарие) Диапазон применения UTM Гаусс-Крюгер 6° в России 6° 0. 9996 1. 0000 180° 500 000 м 0 м 10 000 000 м 80°S - 84°N
Сравнение UTM и Гаусса-Крюгера Параметр Ширина зоны Масштаб по центральному меридиану Начальный меридиан False Easting False Northing (северное полушарие) False Northing (южное полушарие) Диапазон применения UTM Гаусс-Крюгер 6° в России 6° 0. 9996 1. 0000 180° 500 000 м 0 м 10 000 000 м 80°S - 84°N
 Конические проекции EQUIDISTANT CONIC коническая равнопромежуточная LAMBERT CONFORMAL CONIC коническая равноугольная Ламберта ALBERS EQUAL-AREA CONIC коническая равновеликая Альберса
Конические проекции EQUIDISTANT CONIC коническая равнопромежуточная LAMBERT CONFORMAL CONIC коническая равноугольная Ламберта ALBERS EQUAL-AREA CONIC коническая равновеликая Альберса
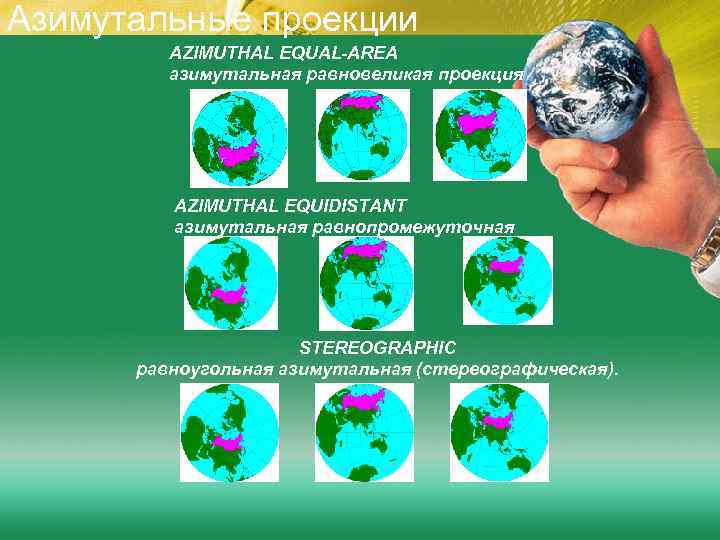 Азимутальные проекции AZIMUTHAL EQUAL-AREA азимутальная равновеликая проекция AZIMUTHAL EQUIDISTANT азимутальная равнопромежуточная STEREOGRAPHIC равноугольная азимутальная (стереографическая).
Азимутальные проекции AZIMUTHAL EQUAL-AREA азимутальная равновеликая проекция AZIMUTHAL EQUIDISTANT азимутальная равнопромежуточная STEREOGRAPHIC равноугольная азимутальная (стереографическая).
 Цилиндрические проекции CYLINDRICAL EQUAL-AREA цилиндрическая равновеликая проекция EQUIDISTANT CYLINDRICAL равнопромежуточная цилиндрическая проекция. CONFORMAL CYLINDRICAL цилиндрическая равноугольная проекция (проекция Меркатора)
Цилиндрические проекции CYLINDRICAL EQUAL-AREA цилиндрическая равновеликая проекция EQUIDISTANT CYLINDRICAL равнопромежуточная цилиндрическая проекция. CONFORMAL CYLINDRICAL цилиндрическая равноугольная проекция (проекция Меркатора)
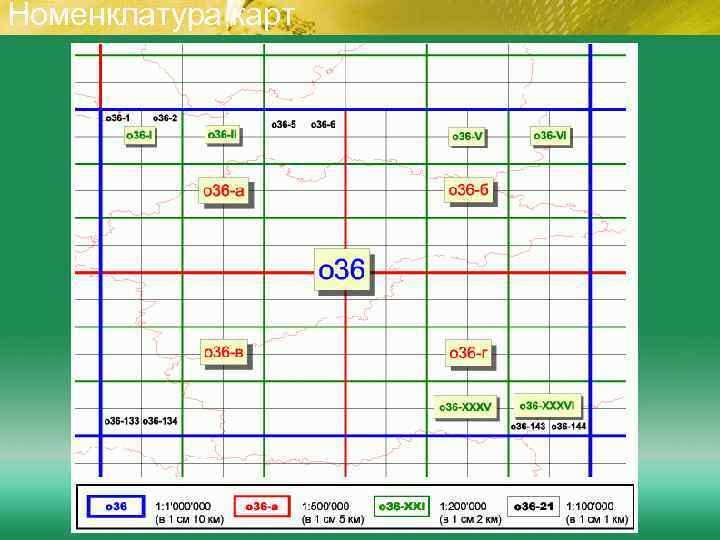 Номенклатура карт
Номенклатура карт
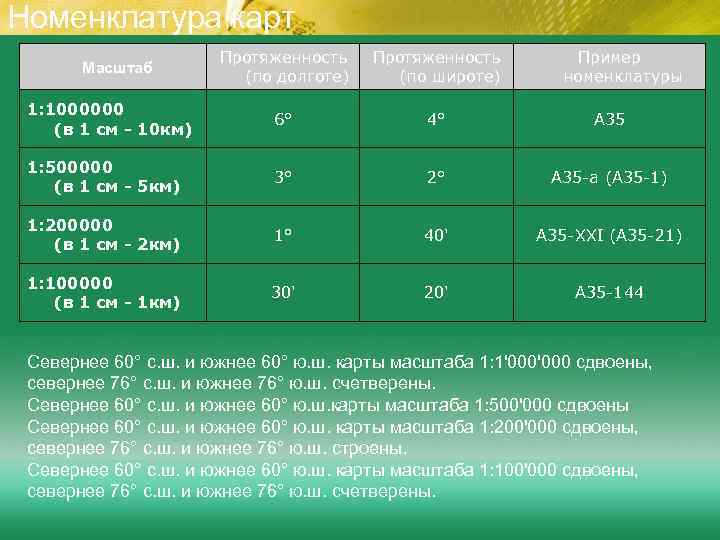 Номенклатура карт Масштаб Протяженность (по долготе) Протяженность (по широте) Пример номенклатуры 1: 1000000 (в 1 см - 10 км) 6° 4° A 35 1: 500000 (в 1 см - 5 км) 3° 2° A 35 -a (A 35 -1) 1: 200000 (в 1 см - 2 км) 1° 40' A 35 -XXI (A 35 -21) 1: 100000 (в 1 см - 1 км) 30' 20' A 35 -144 Севернее 60° с. ш. и южнее 60° ю. ш. карты масштаба 1: 1'000 сдвоены, севернее 76° с. ш. и южнее 76° ю. ш. счетверены. Севернее 60° с. ш. и южнее 60° ю. ш. карты масштаба 1: 500'000 сдвоены Севернее 60° с. ш. и южнее 60° ю. ш. карты масштаба 1: 200'000 сдвоены, севернее 76° с. ш. и южнее 76° ю. ш. строены. Севернее 60° с. ш. и южнее 60° ю. ш. карты масштаба 1: 100'000 сдвоены, севернее 76° с. ш. и южнее 76° ю. ш. счетверены.
Номенклатура карт Масштаб Протяженность (по долготе) Протяженность (по широте) Пример номенклатуры 1: 1000000 (в 1 см - 10 км) 6° 4° A 35 1: 500000 (в 1 см - 5 км) 3° 2° A 35 -a (A 35 -1) 1: 200000 (в 1 см - 2 км) 1° 40' A 35 -XXI (A 35 -21) 1: 100000 (в 1 см - 1 км) 30' 20' A 35 -144 Севернее 60° с. ш. и южнее 60° ю. ш. карты масштаба 1: 1'000 сдвоены, севернее 76° с. ш. и южнее 76° ю. ш. счетверены. Севернее 60° с. ш. и южнее 60° ю. ш. карты масштаба 1: 500'000 сдвоены Севернее 60° с. ш. и южнее 60° ю. ш. карты масштаба 1: 200'000 сдвоены, севернее 76° с. ш. и южнее 76° ю. ш. строены. Севернее 60° с. ш. и южнее 60° ю. ш. карты масштаба 1: 100'000 сдвоены, севернее 76° с. ш. и южнее 76° ю. ш. счетверены.


