4 лекция Операторный метод расчета переходных процессов ©

4 лекция Операторный метод расчета переходных процессов © 2002 Томский политехнический университет, кафедра
2 Основы операторного метода расчета переходных процессов
3 Линейные дифференциальные уравнения, характеризующие переходные процессы в линейных цепях могут быть решены при
4 Если то при
5 Имеем - прямое преобразование Лапласа
6 Где оригинал операторное изображение f(t) причем
7 Если то
8 Аналогично:
9 и т.д.
10 При имеем
11 и т.д.
12 В результате линейные дифференциальные уравнения могут быть заменены алгебраическими уравнениями
13 Например:
14 Если
15 Таким образом
16 Для определения оригинала f(t) используется обратное преобразование Лапласа
17 - обратное преобразование Лапласа
18 На основании обратного преобразования Лапласа получена теорема разложения
19 Теорема разложения
20 Если операторное изображение записано в виде
21 причем m<n корни B(p)=0 различны корни D(p)=0 и B(p)=0 различны
22 Тогда оригинал определяется так:
23 Где корни B(p)=0
24 При наличии одного корня, равного нулю:
25 Оригинал определяется так:
26 Где корни при B1(p)=0
27 Пример 1
28
29 тогда
30 Или
31 Т.е.
32 Пример 2
33 По теореме разложения:
34 Пример 3
35 По теореме разложения:
36 Пример 4
37
38 тогда
39 Или 0 0
40 0
41 Т.е.
42
43
44 Законы Ома и Кирхгофа в операторной форме
45 1. Резистивный элемент R
46 То при имеем
47 Тогда - закон Ома в операторной форме для резистивного элемента
48 Таким образом операторная схема замещения резистора:
49 2. Индуктивный элемент
50 При
51 Имеем или
52 Таким образом операторная схема замещения индуктивности:
53 при
54 3. Емкостный элемент
55 При
56 Имеем или
57 Таким образом операторная схема замещения емкости:
58 при
59 4. Пассивный двухполюсник при нулевых начальных условиях, когда
60 а в
61 При
62 - закон Ома в операторной форме при нулевых начальных условиях
63 Где Z(p) - эквивалентное операторное сопротивление двухполюсника относительно
64 Например
65
66 5. Первый закон Кирхгофа в операторной форме
67 Т.к. то
68 - первый закон Кирхгофа в операторной форме
69 Например: а
70 а
71 6. Второй закон Кирхгофа в операторной форме
72 Т.к.
73 То - второй закон Кирхгофа в операторной форме
74 Где - операторное изображение напряжения на пассивном элементе
75 Где - операторное изображение ЭДС - операторное изображение напряжения на источнике тока
76 Например:
77
78 Законы Ома и Кирхгофа в операторной форме аналогичны этим законам на постоянном токе
79 Поэтому к операторным схемам замещения применимы те же методы расчета, но в операторной
80 Метод законов Кирхгофа Метод контурных токов Метод узловых потенциалов
81 Метод наложения Метод эквивалентного генератора Метод преобразований
82 Операторная схема замещения составляется для цепи после коммутации на основании операторных схем отдельных
Скачать презентацию 4 лекция Операторный метод расчета переходных процессов © Скачать презентацию 4 лекция Операторный метод расчета переходных процессов ©

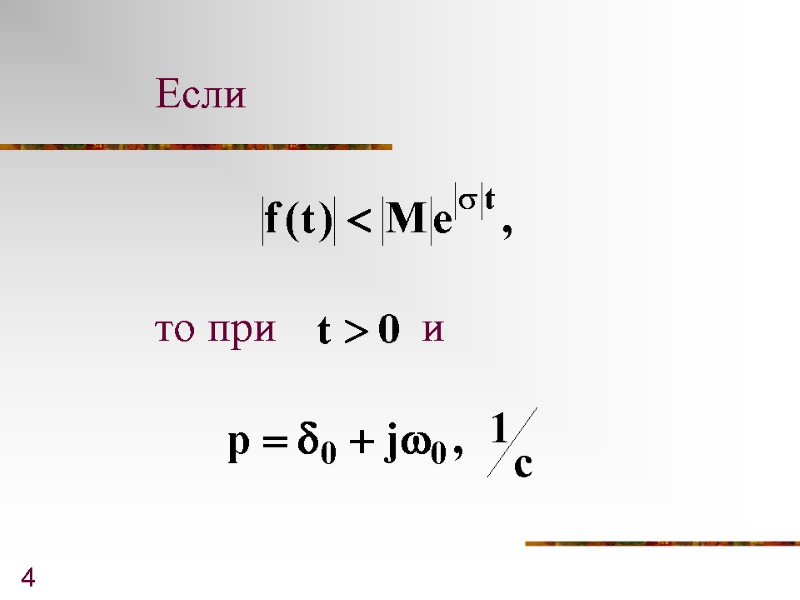
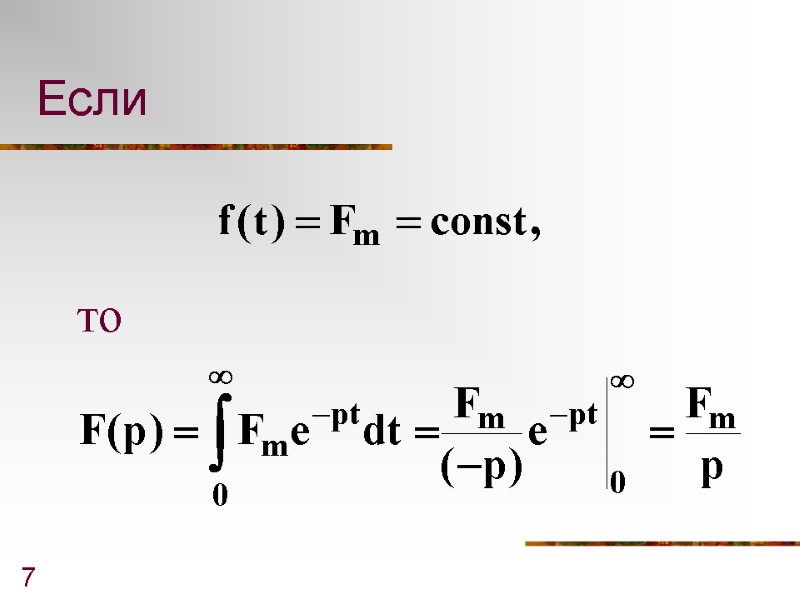
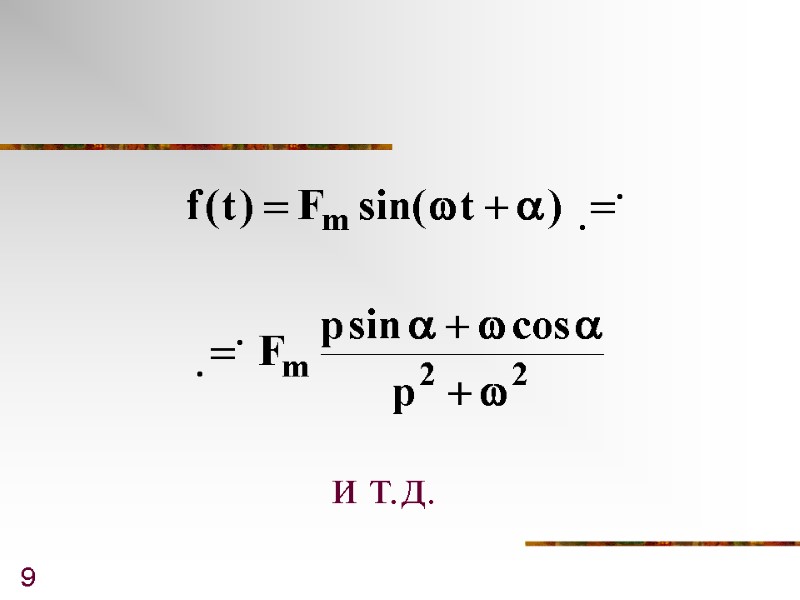
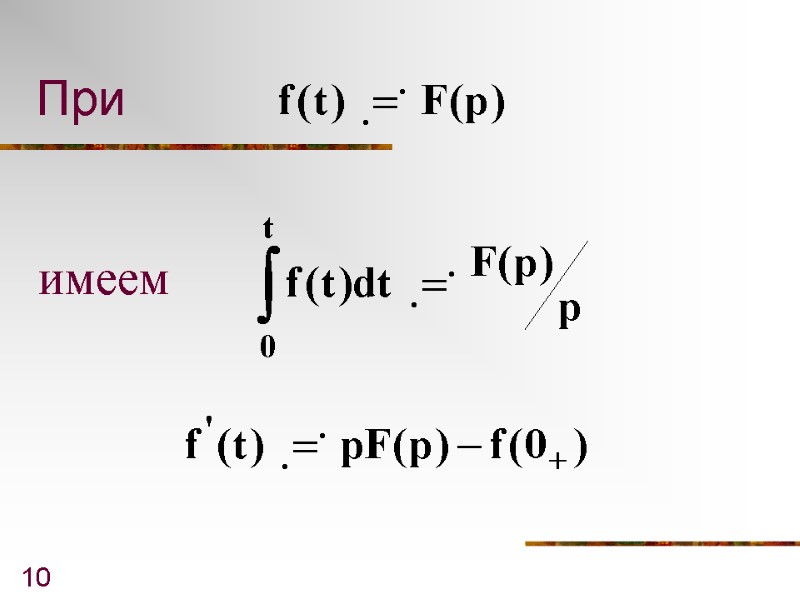
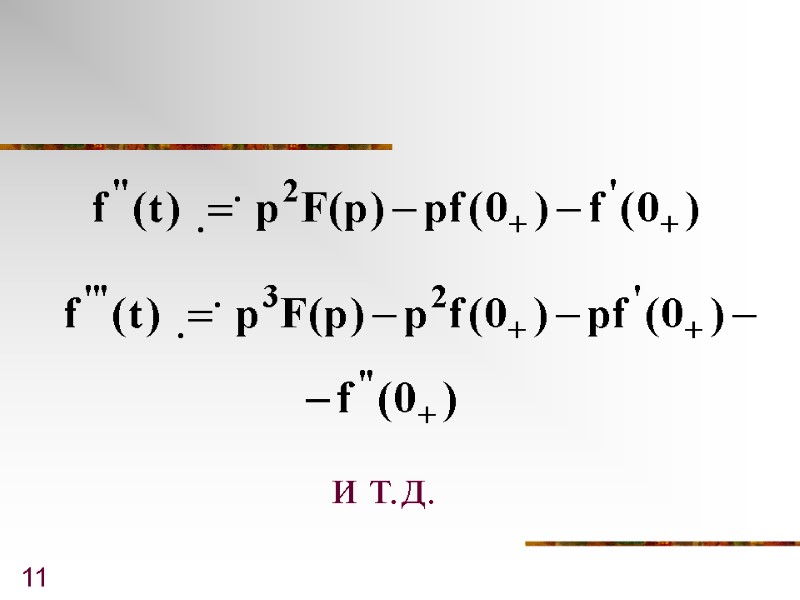
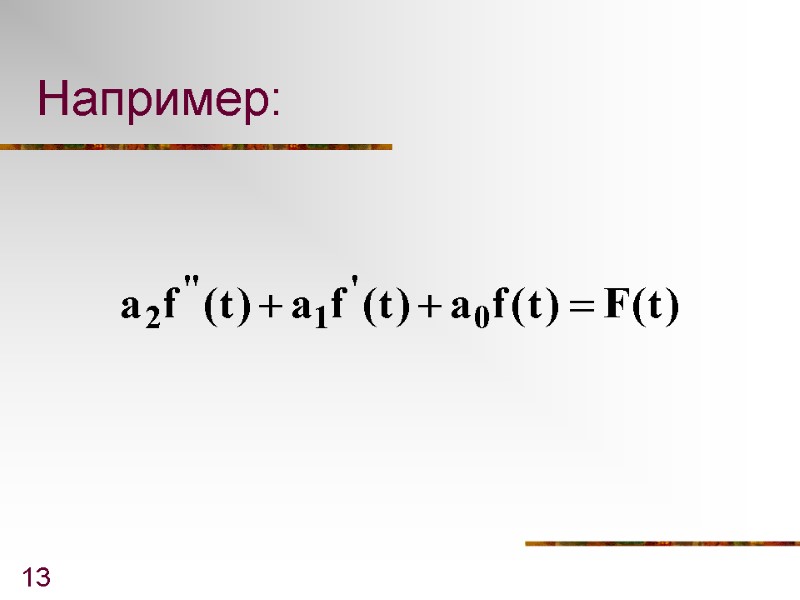
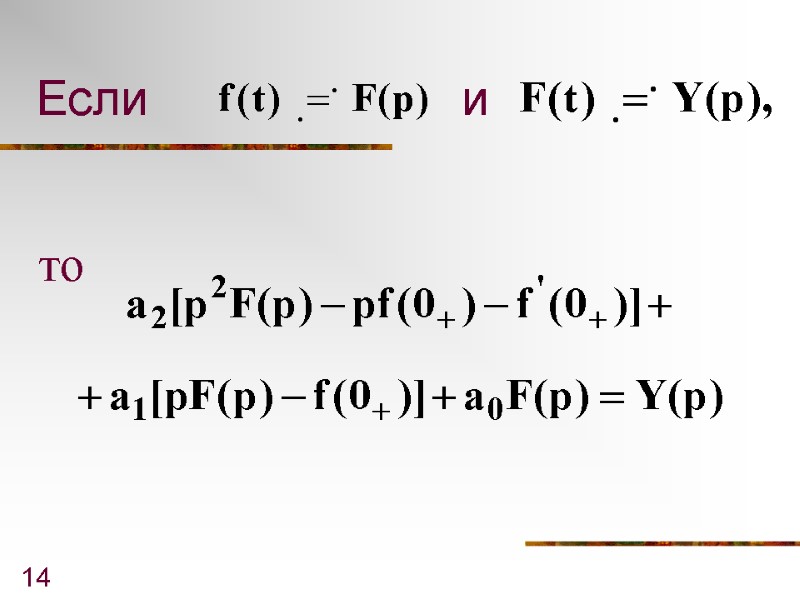
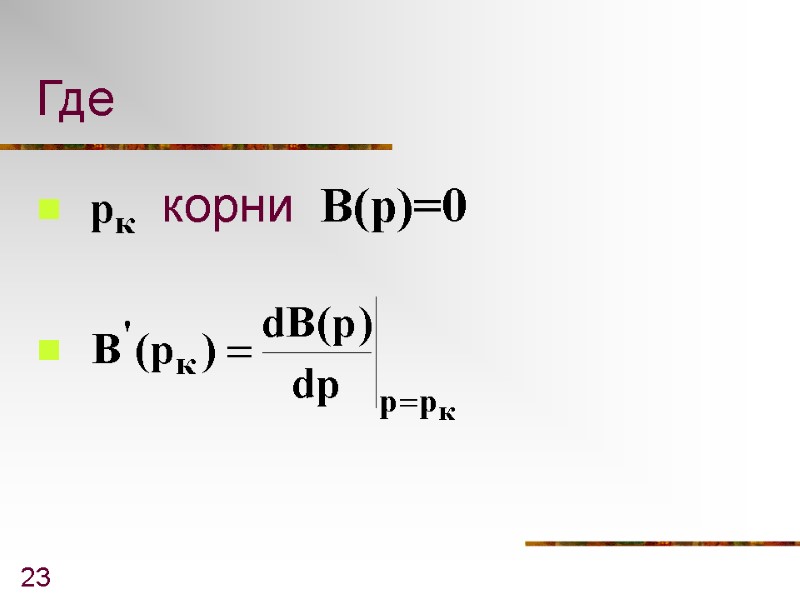
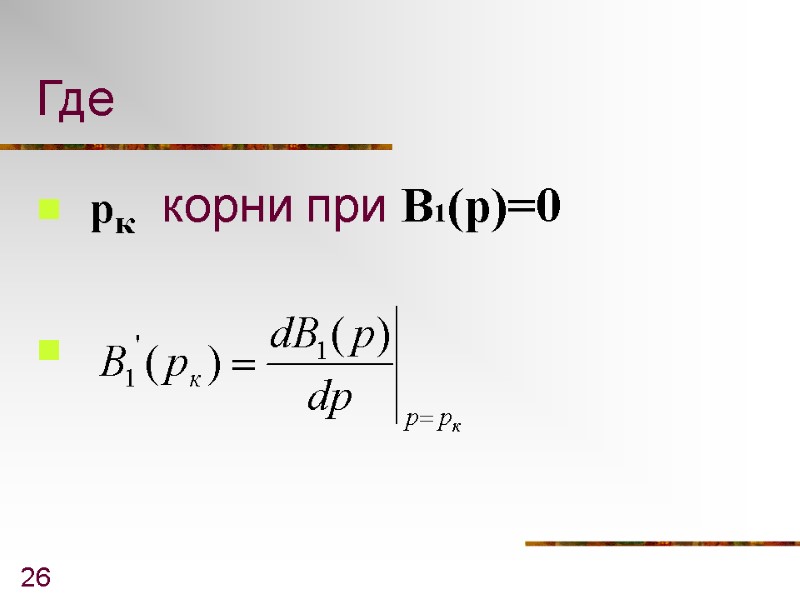
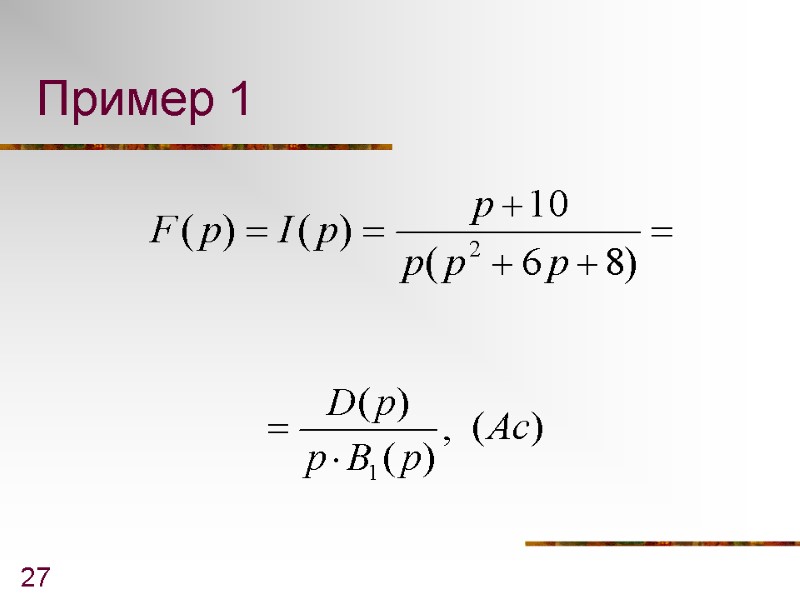
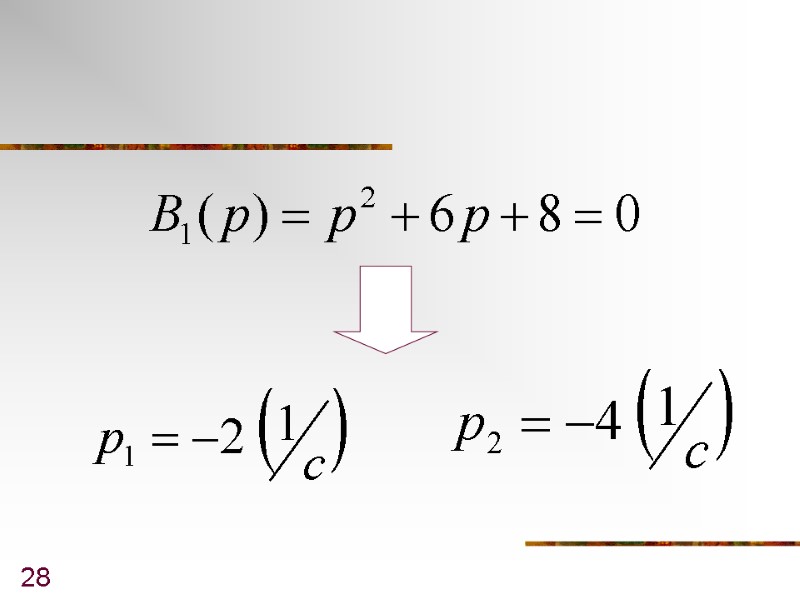
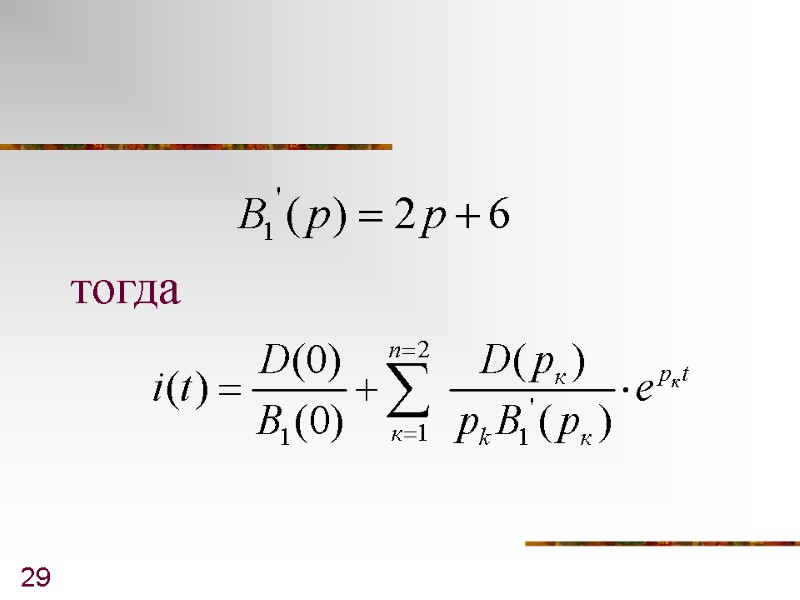
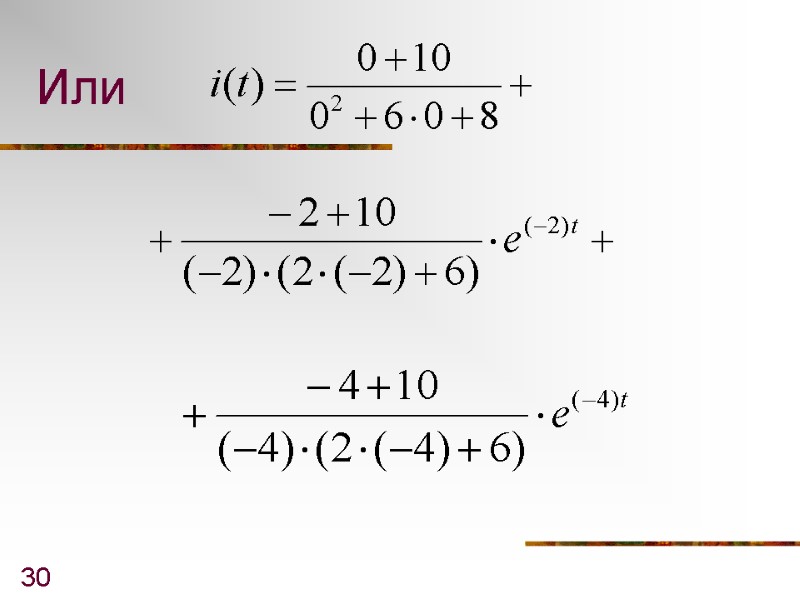
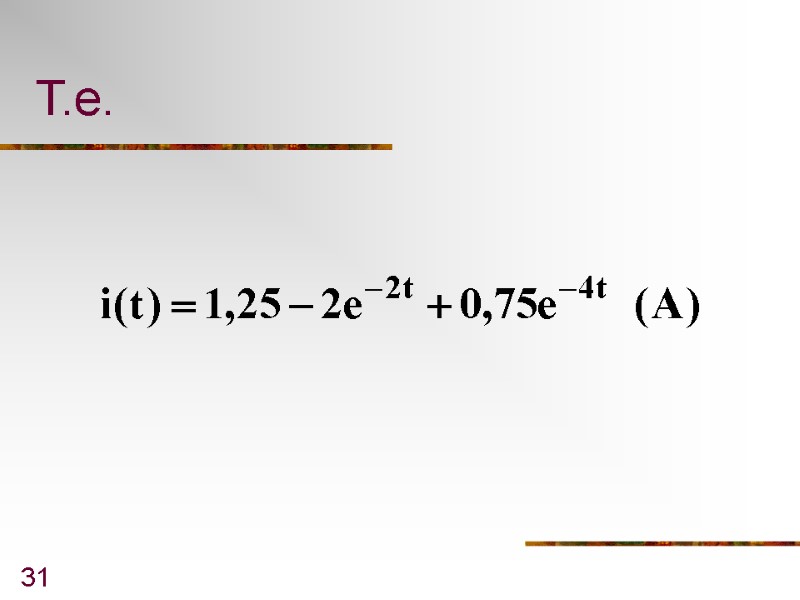
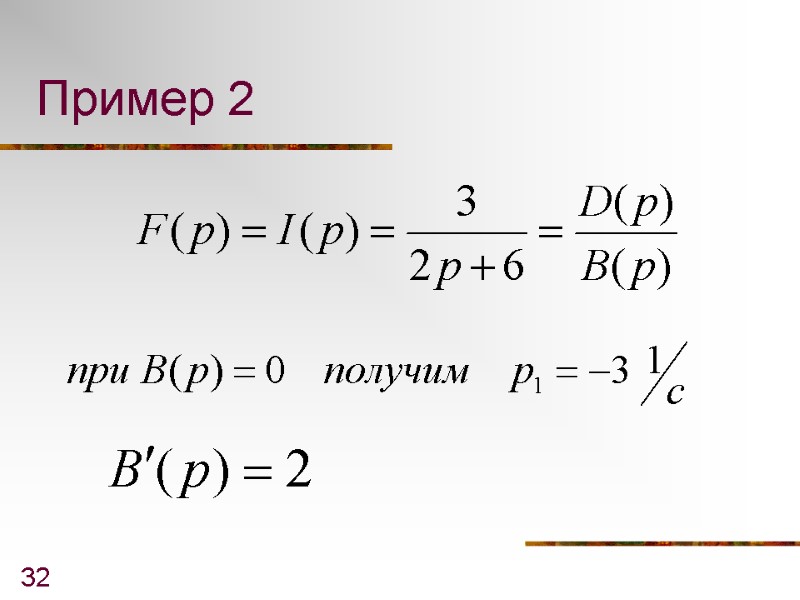
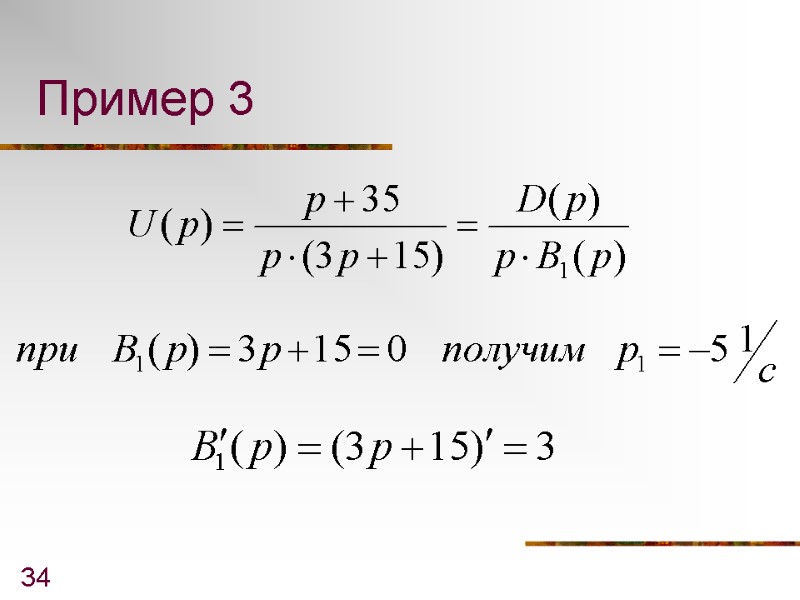
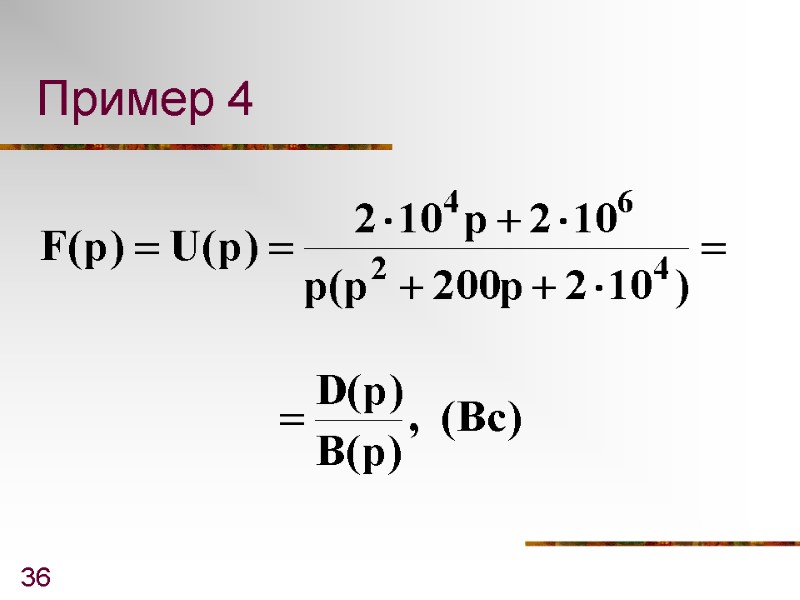
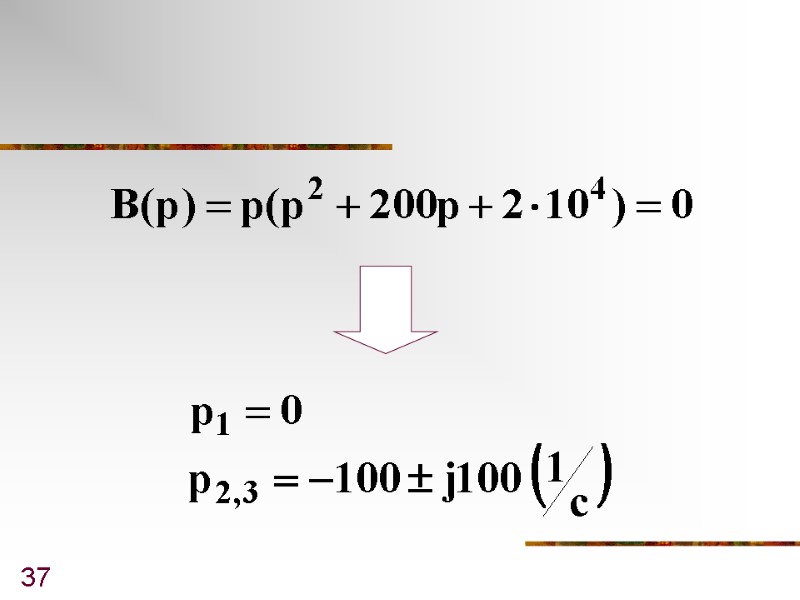
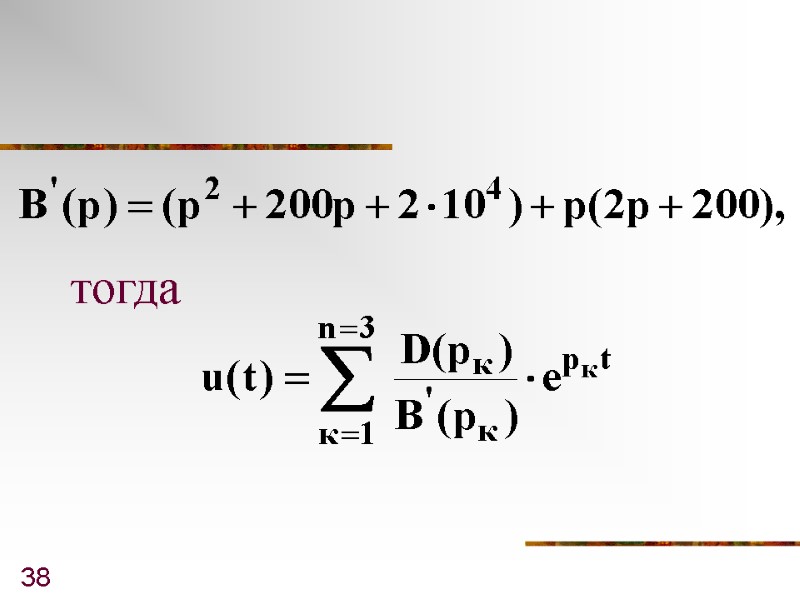
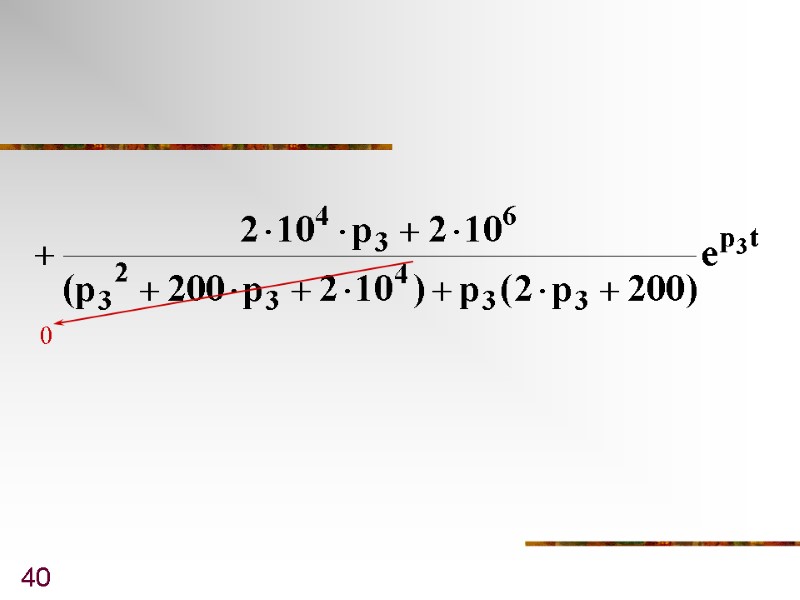
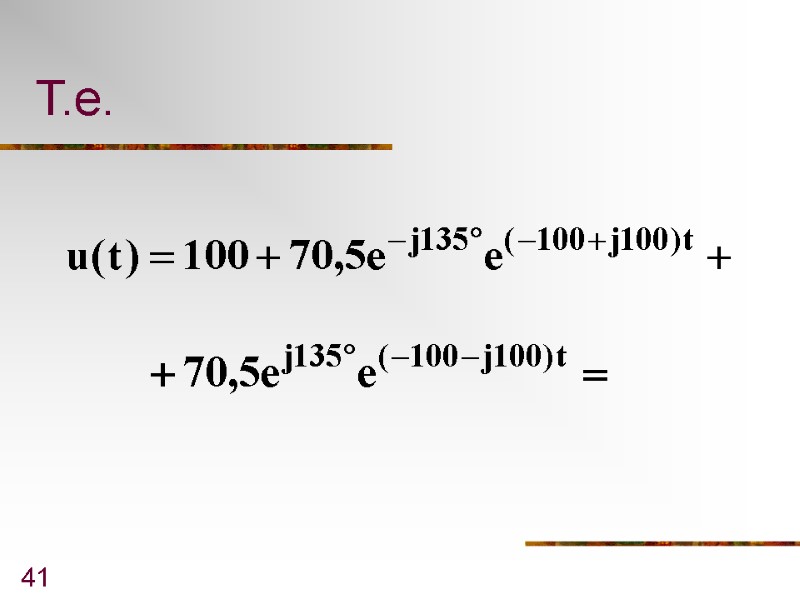
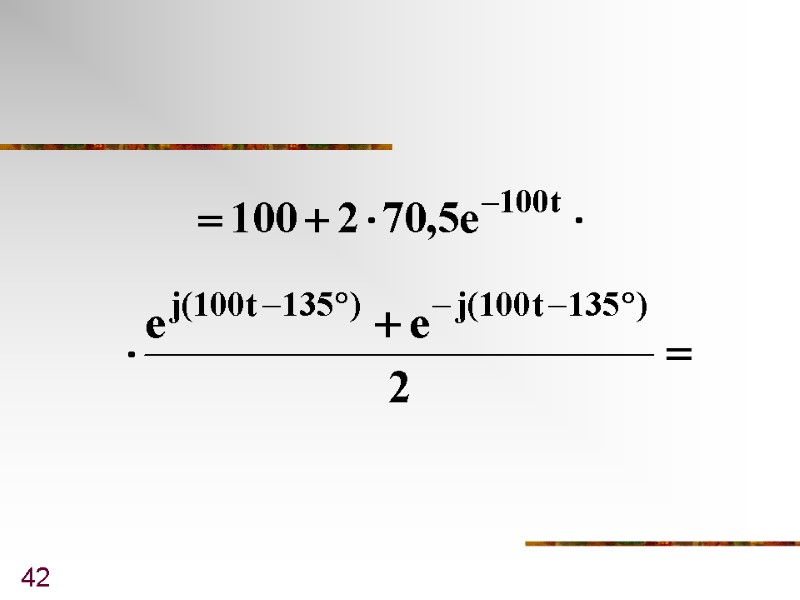
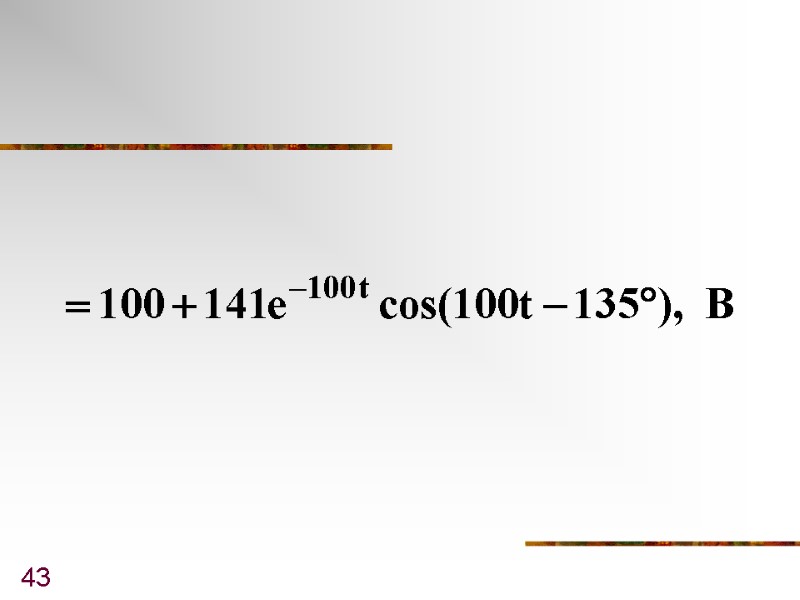
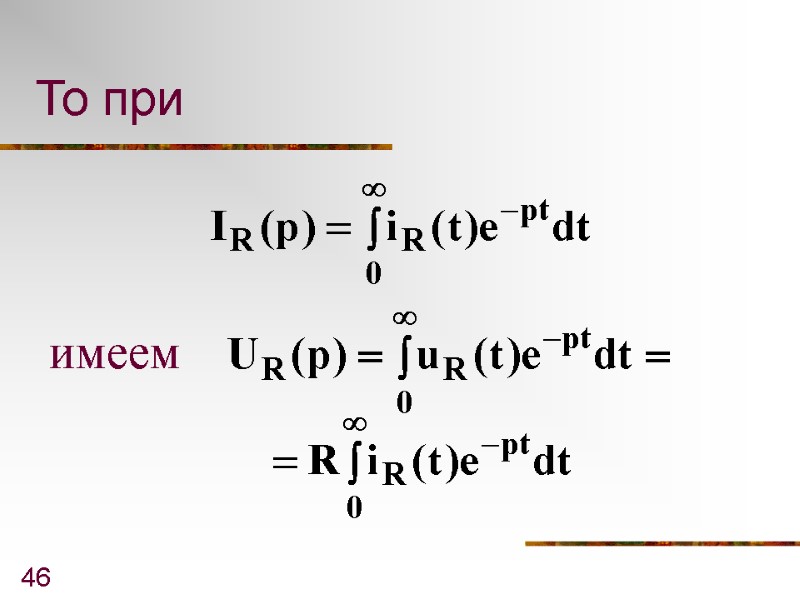
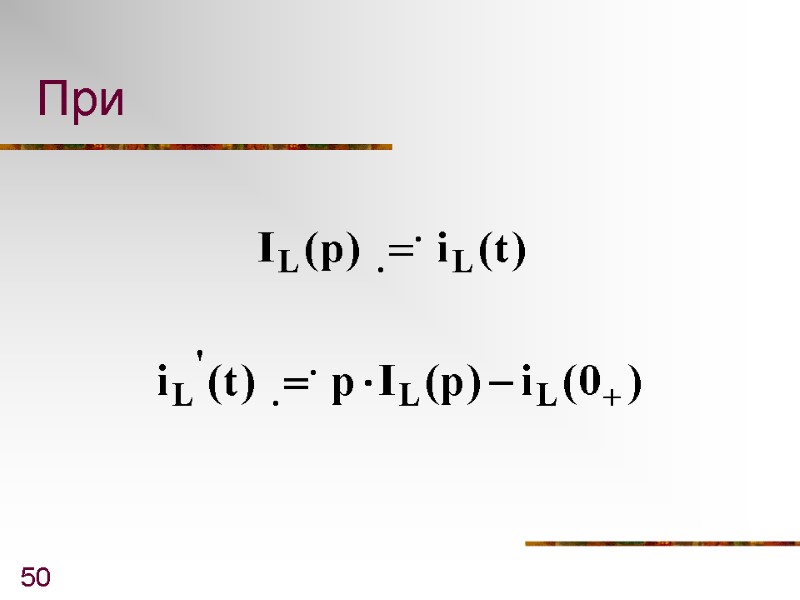
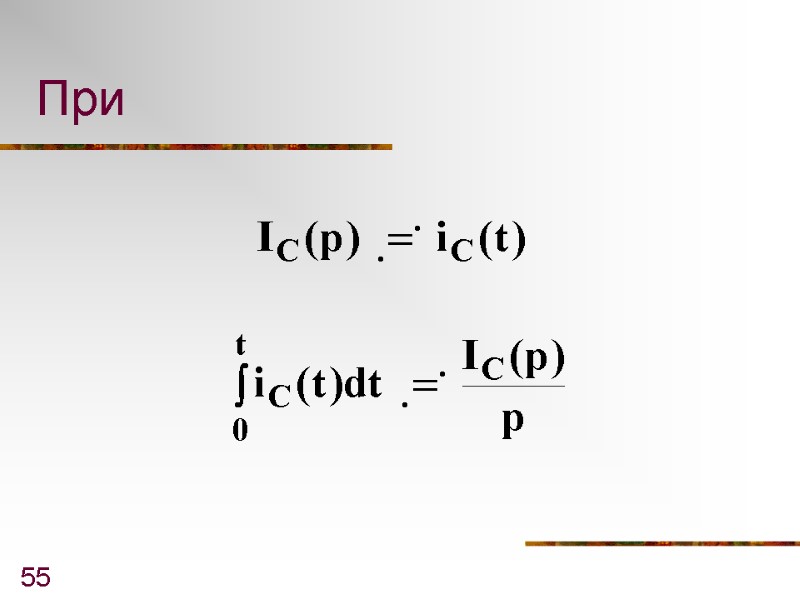
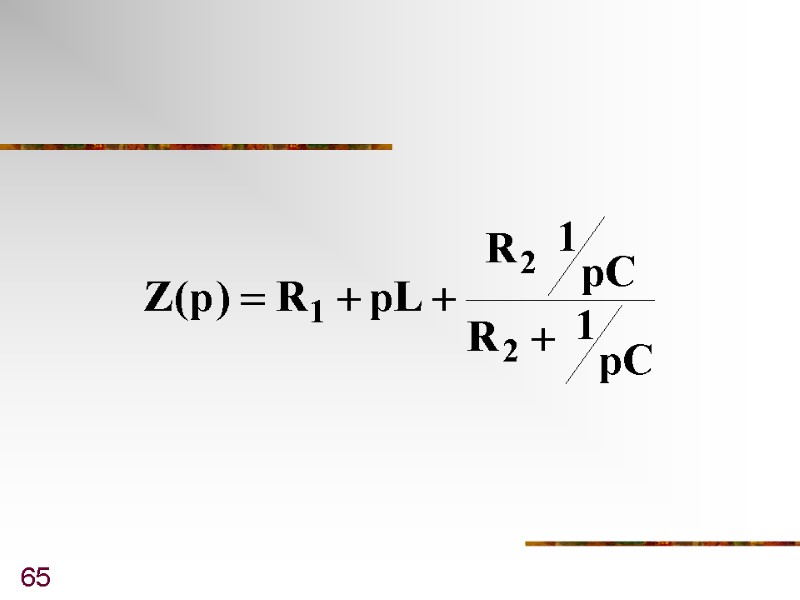
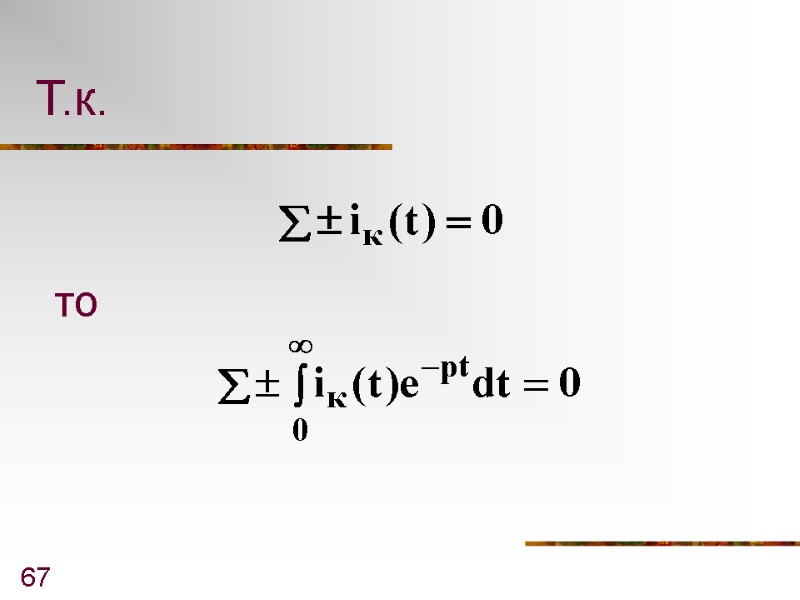
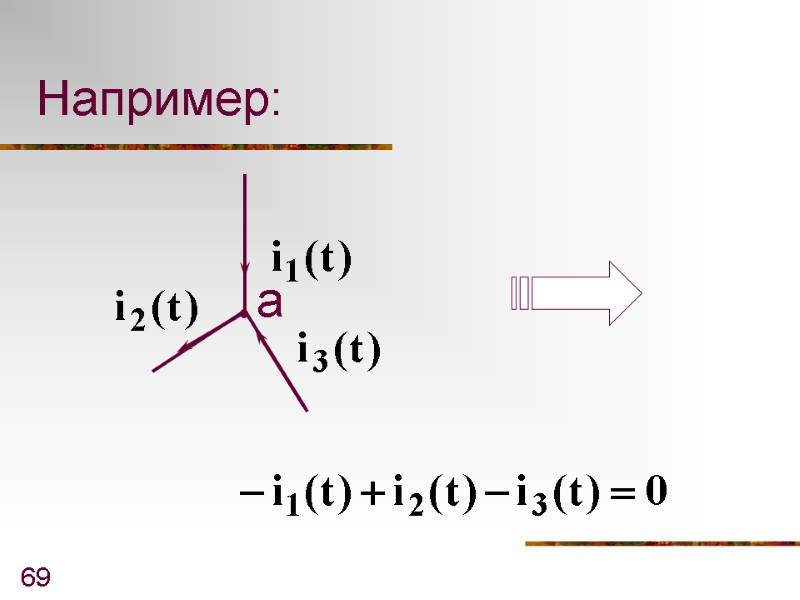
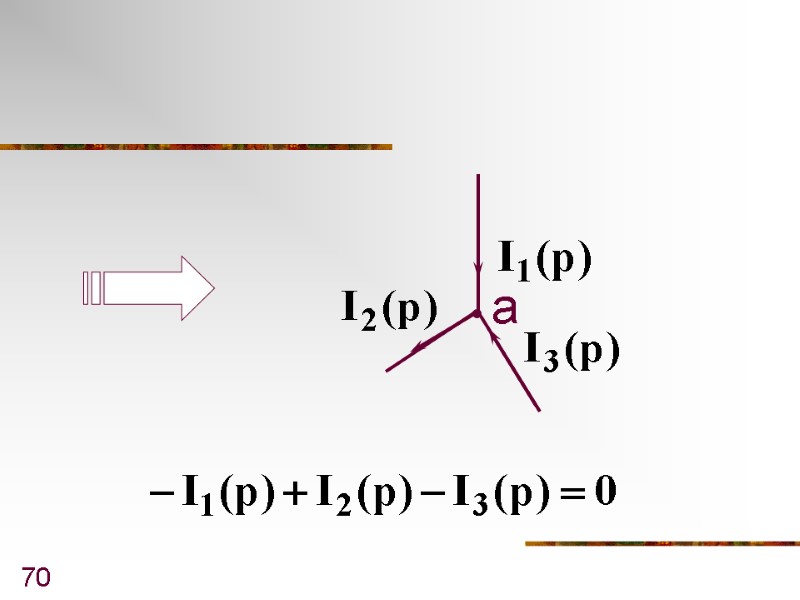
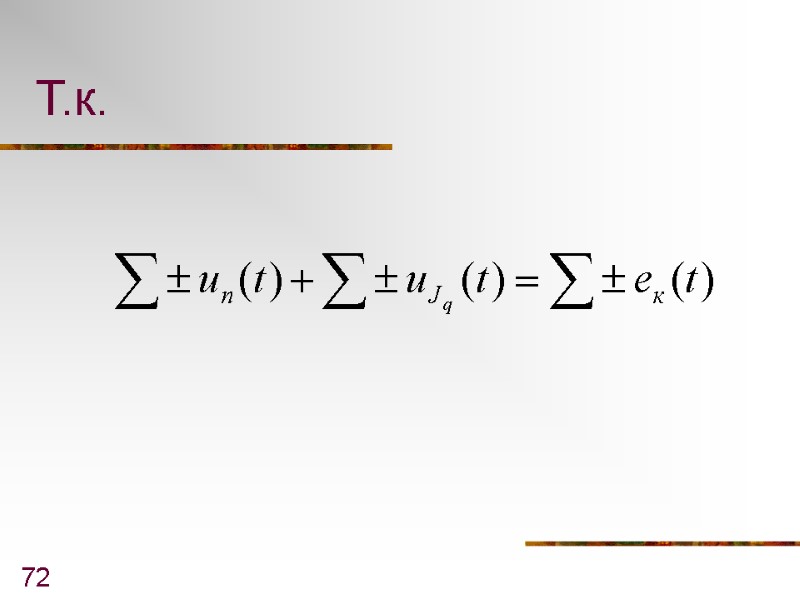
10450-el_tech_lc_14.ppt

  • Количество слайдов: 82

>4 лекция Операторный метод расчета переходных процессов © 2002 Томский политехнический университет, кафедра 4 лекция Операторный метод расчета переходных процессов © 2002 Томский политехнический университет, кафедра ТОЭ, автор Носов Геннадий Васильевич

>2 Основы операторного метода расчета переходных процессов 2 Основы операторного метода расчета переходных процессов

>3 Линейные дифференциальные уравнения, характеризующие переходные процессы в линейных цепях могут быть решены при 3 Линейные дифференциальные уравнения, характеризующие переходные процессы в линейных цепях могут быть решены при помощи интегральных преобразований Лапласа, причем из математики известно:

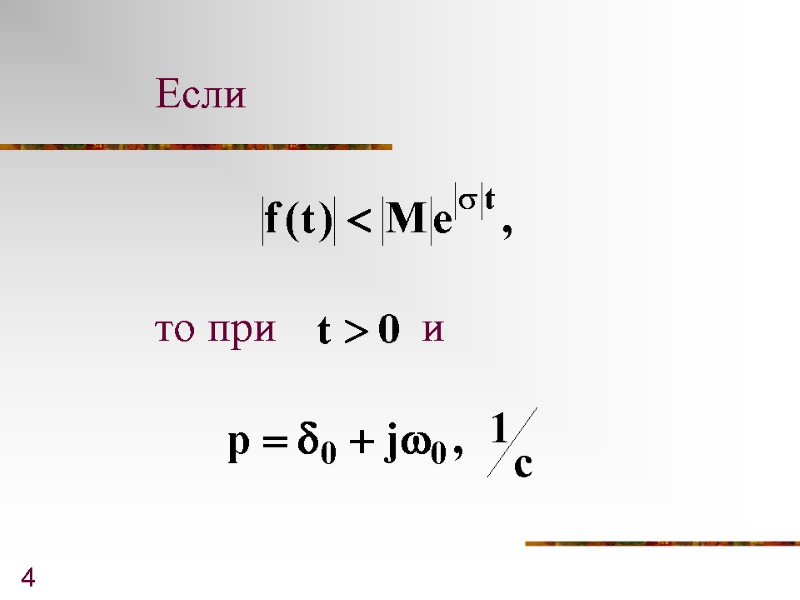>4 Если то при 4 Если то при и

>5 Имеем - прямое преобразование Лапласа 5 Имеем - прямое преобразование Лапласа

>6 Где оригинал операторное изображение f(t) причем 6 Где оригинал операторное изображение f(t) причем

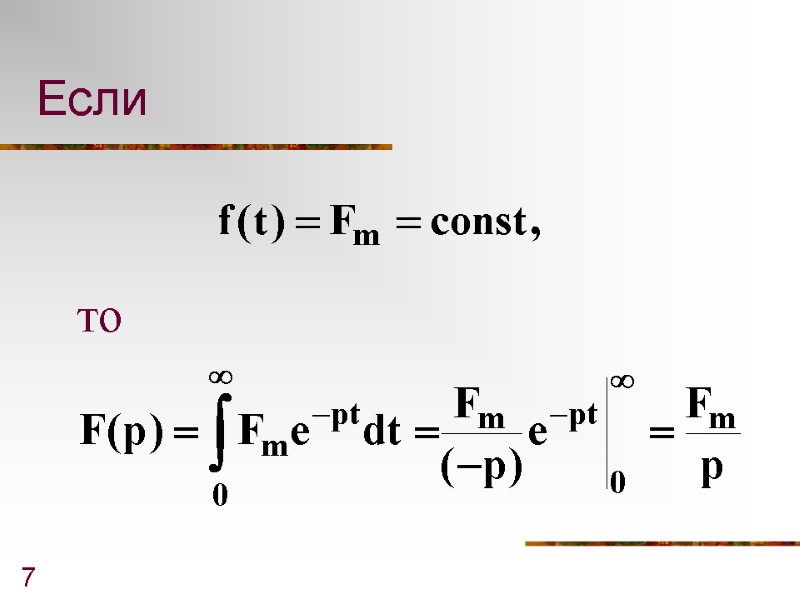>7 Если то 7 Если то

>8 Аналогично: 8 Аналогично:

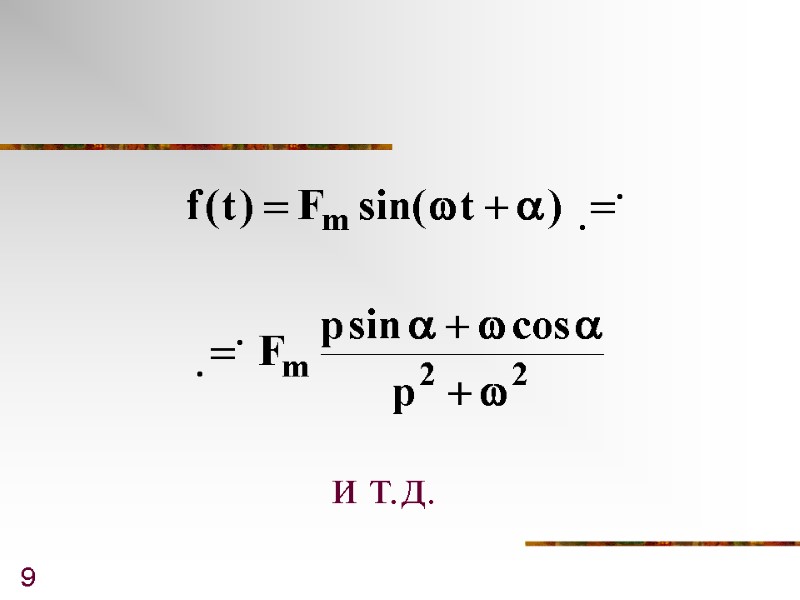>9 и т.д. 9 и т.д.

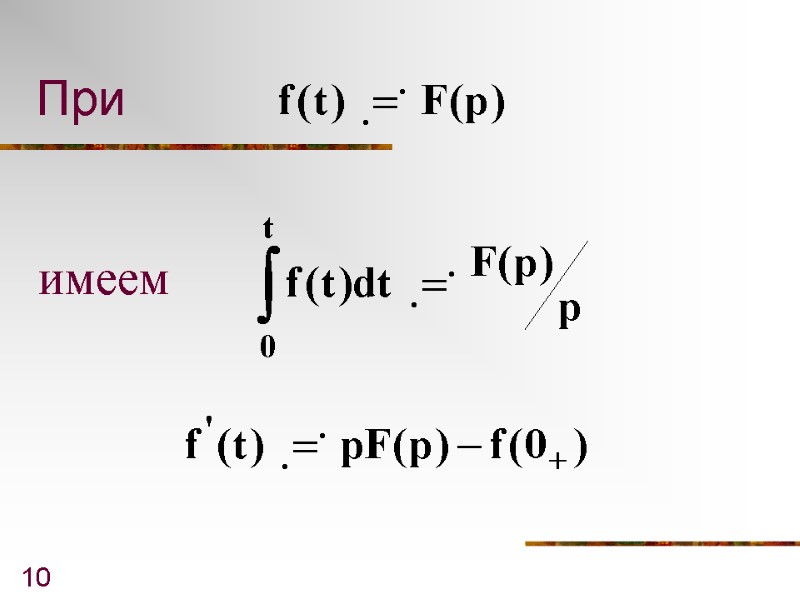>10 При имеем 10 При имеем

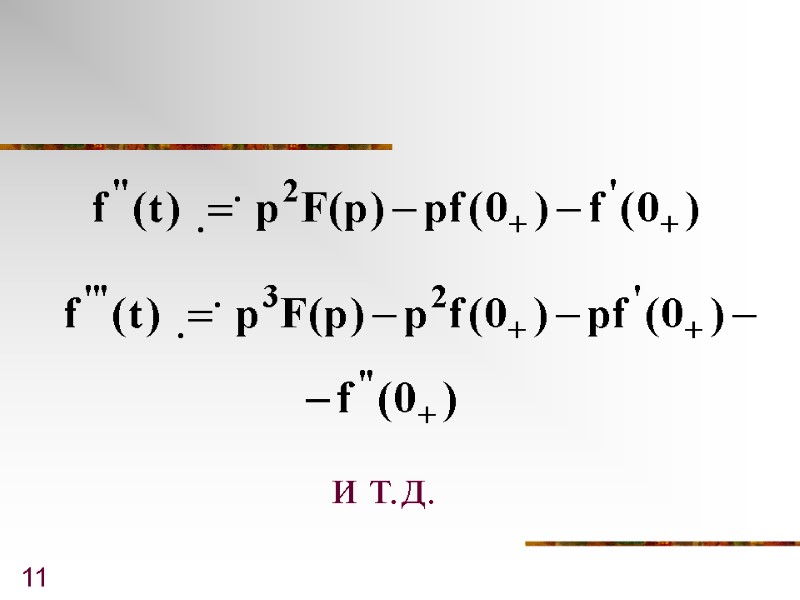>11 и т.д. 11 и т.д.

>12 В результате линейные дифференциальные уравнения могут быть заменены алгебраическими уравнениями 12 В результате линейные дифференциальные уравнения могут быть заменены алгебраическими уравнениями

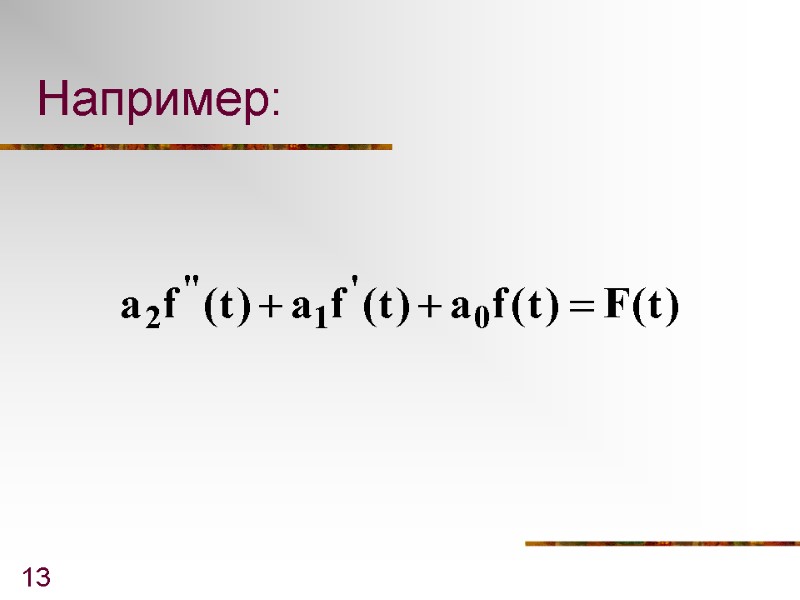>13 Например: 13 Например:

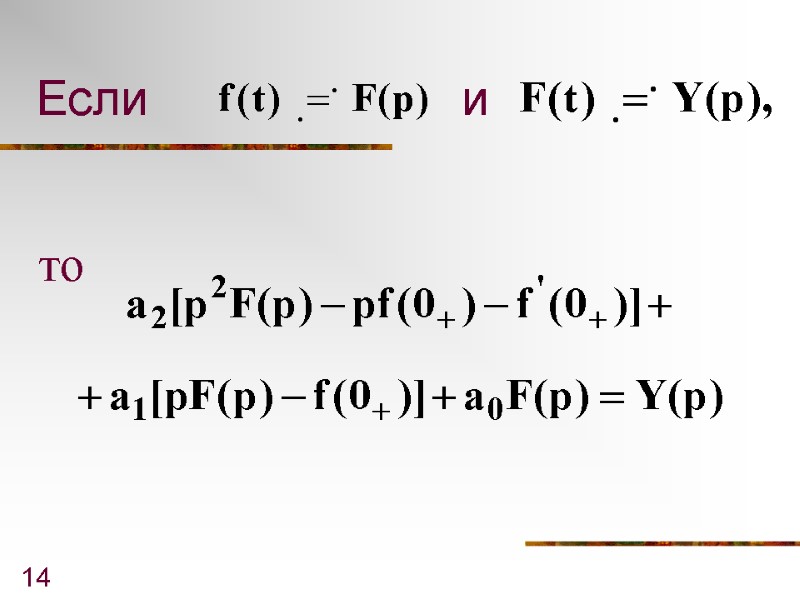>14 Если 14 Если и то

>15 Таким образом 15 Таким образом

>16 Для определения оригинала f(t) используется обратное преобразование Лапласа 16 Для определения оригинала f(t) используется обратное преобразование Лапласа

>17 - обратное преобразование Лапласа 17 - обратное преобразование Лапласа

>18 На основании обратного преобразования Лапласа получена теорема разложения 18 На основании обратного преобразования Лапласа получена теорема разложения

>19 Теорема разложения 19 Теорема разложения

>20 Если операторное изображение записано в виде 20 Если операторное изображение записано в виде

>21 причем m<n корни B(p)=0 различны корни D(p)=0 и B(p)=0 различны 21 причем m

>22 Тогда оригинал определяется так: 22 Тогда оригинал определяется так:

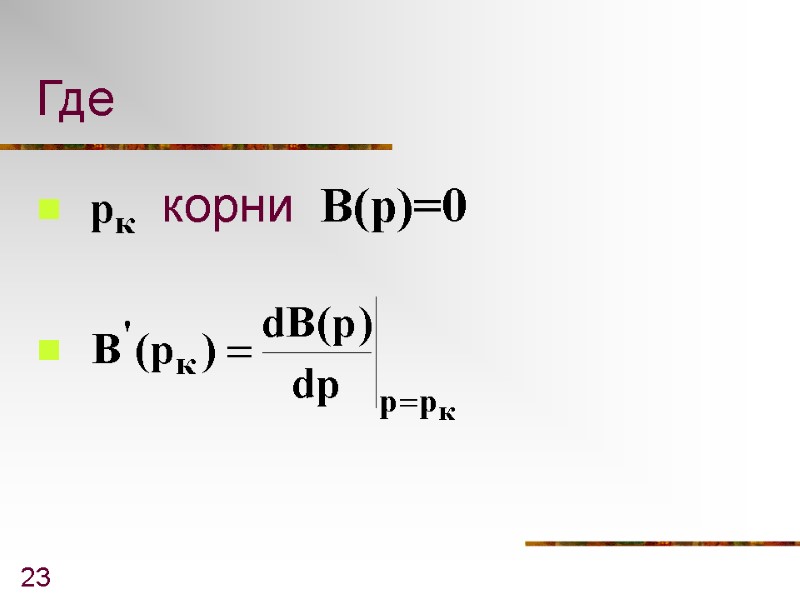>23 Где корни B(p)=0 23 Где корни B(p)=0

>24 При наличии одного корня, равного нулю: 24 При наличии одного корня, равного нулю:

>25 Оригинал определяется так: 25 Оригинал определяется так:

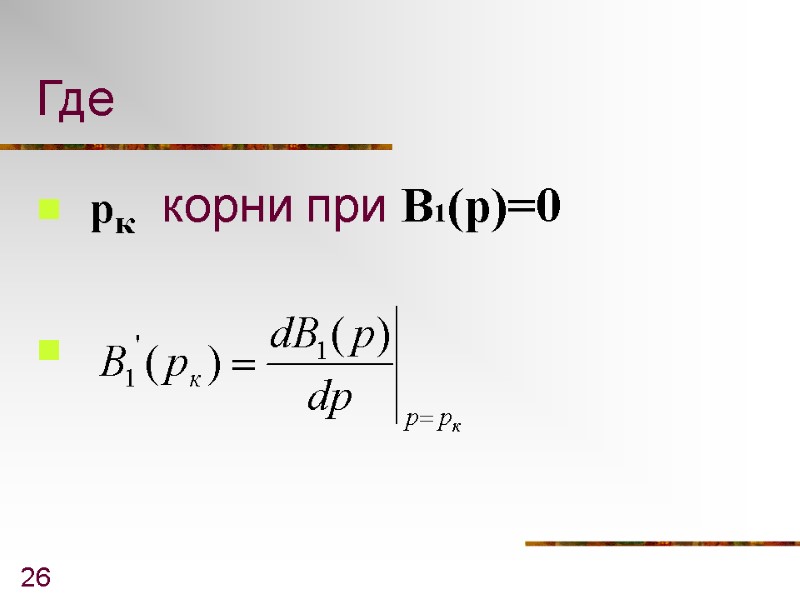>26 Где корни при B1(p)=0 26 Где корни при B1(p)=0

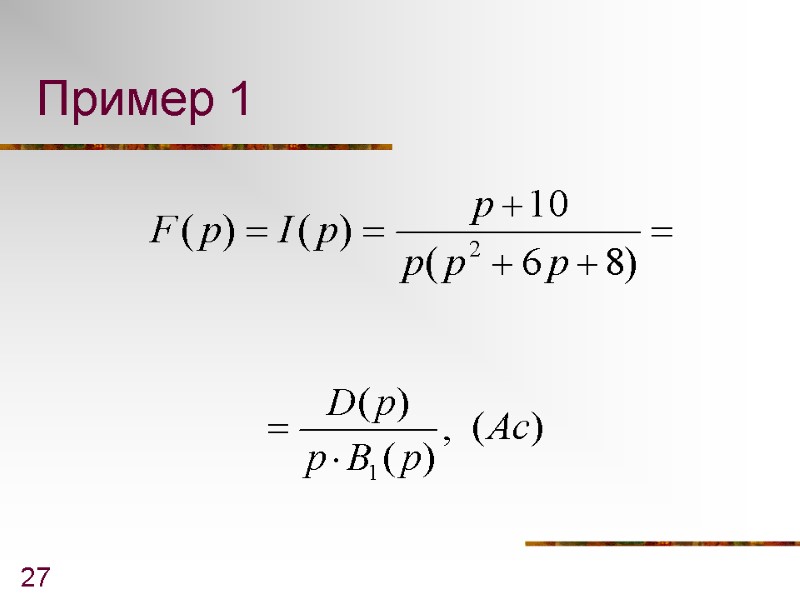>27 Пример 1 27 Пример 1

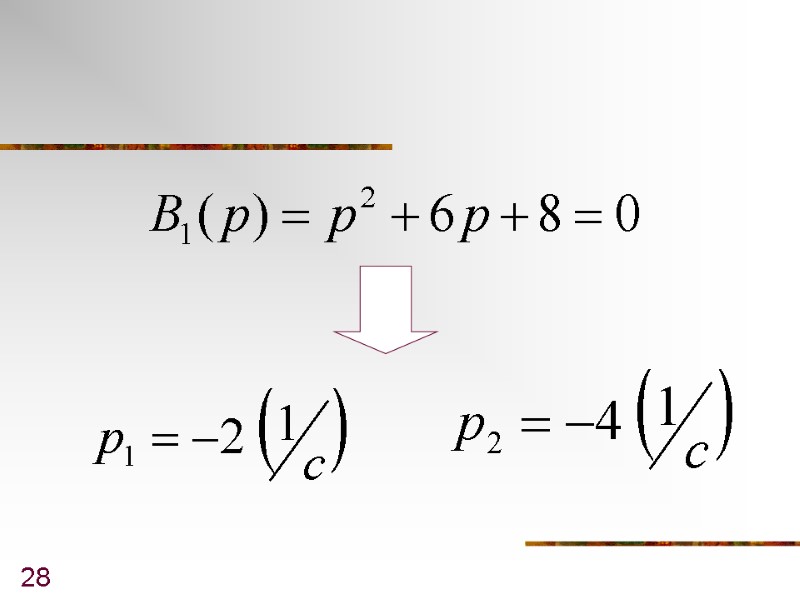>28 28

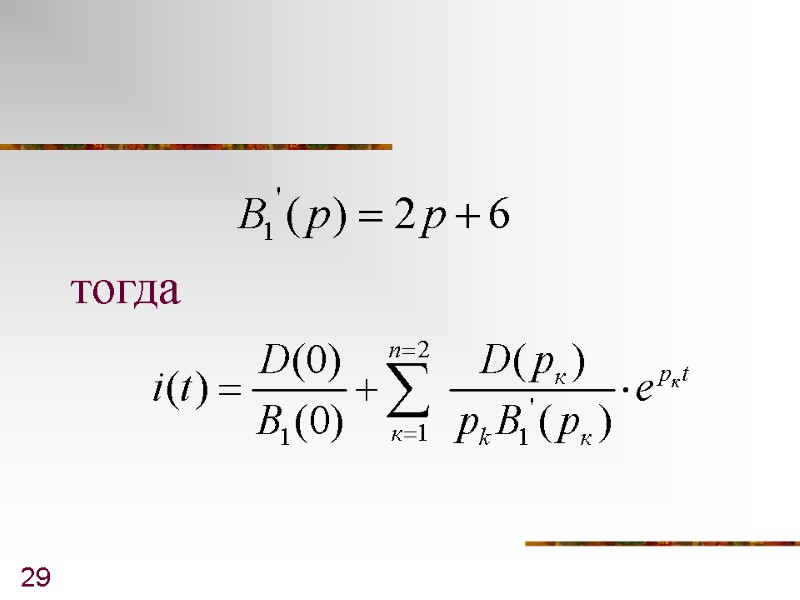>29 тогда 29 тогда

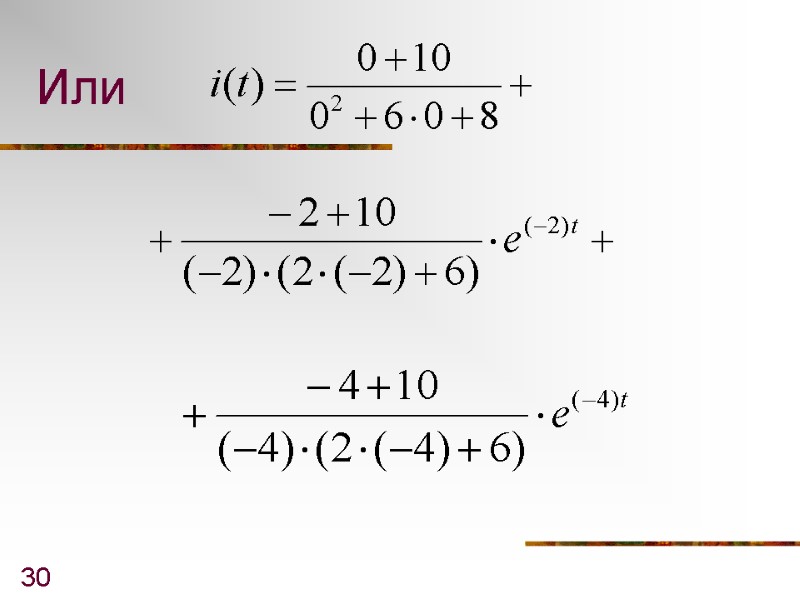>30 Или 30 Или

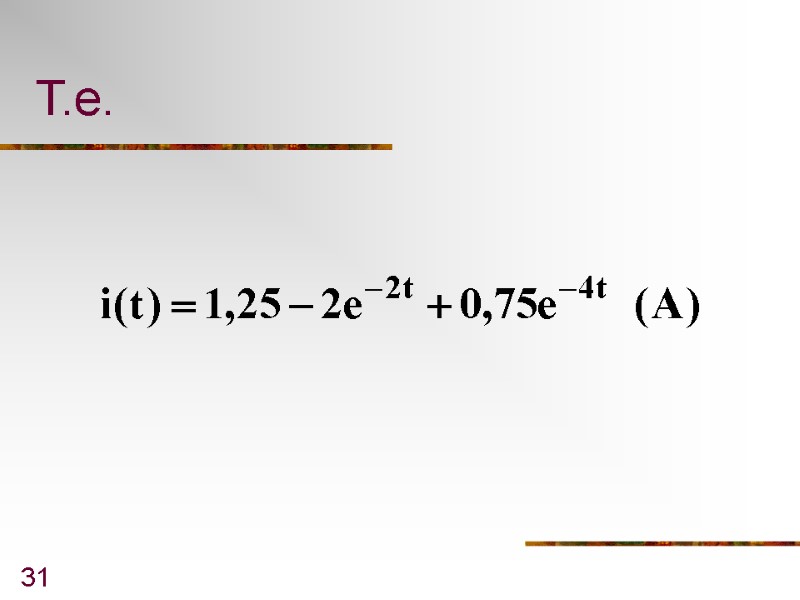>31 Т.е. 31 Т.е.

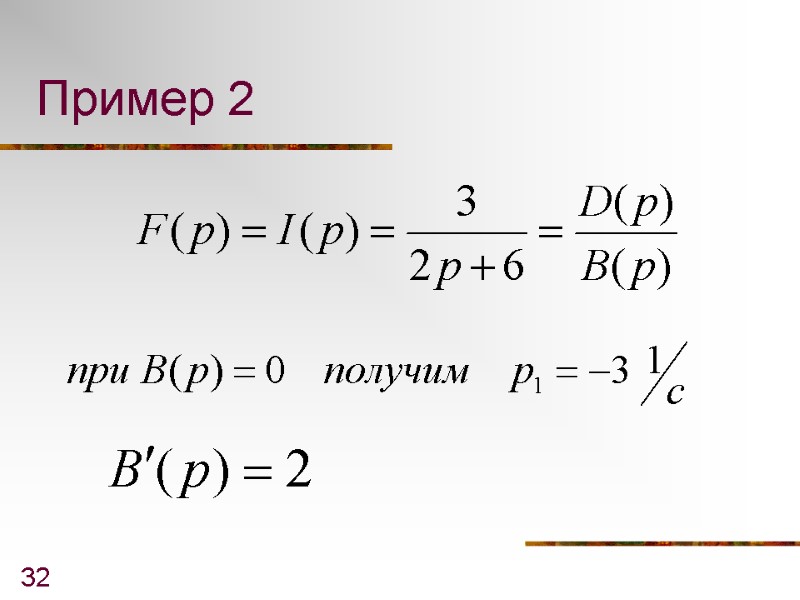>32 Пример 2 32 Пример 2

>33 По теореме разложения: 33 По теореме разложения:

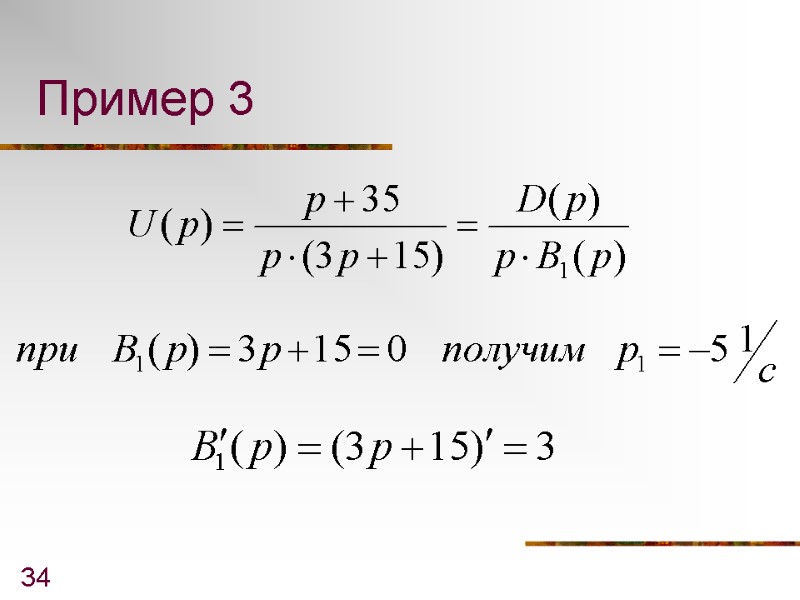>34 Пример 3 34 Пример 3

>35 По теореме разложения: 35 По теореме разложения:

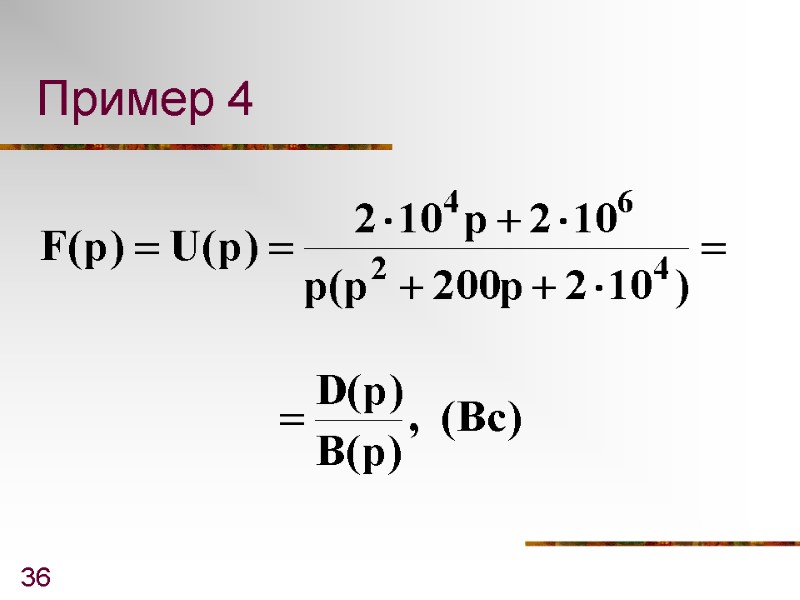>36 Пример 4 36 Пример 4

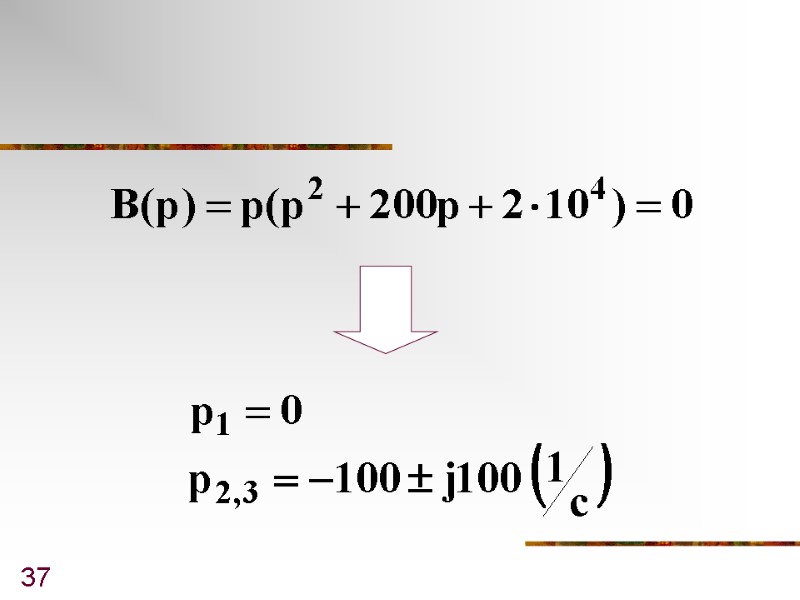>37 37

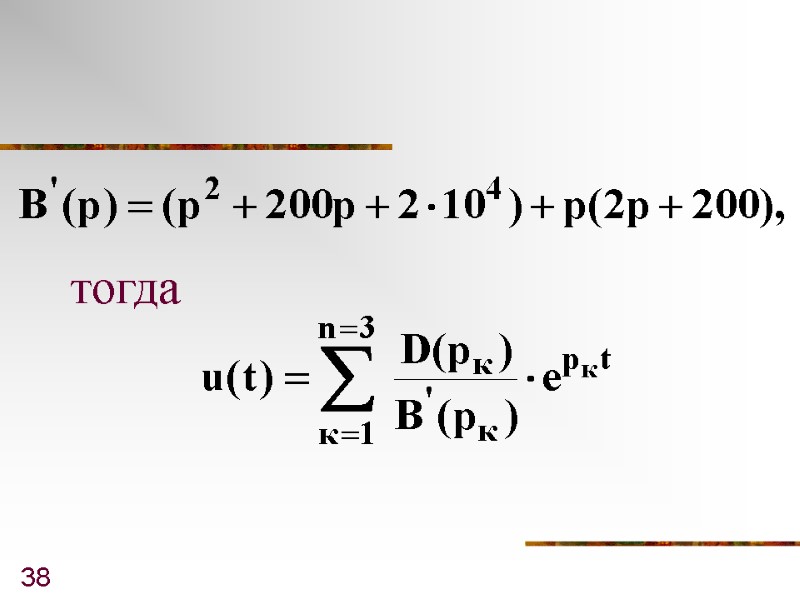>38 тогда 38 тогда

>39 Или 0 0 39 Или 0 0

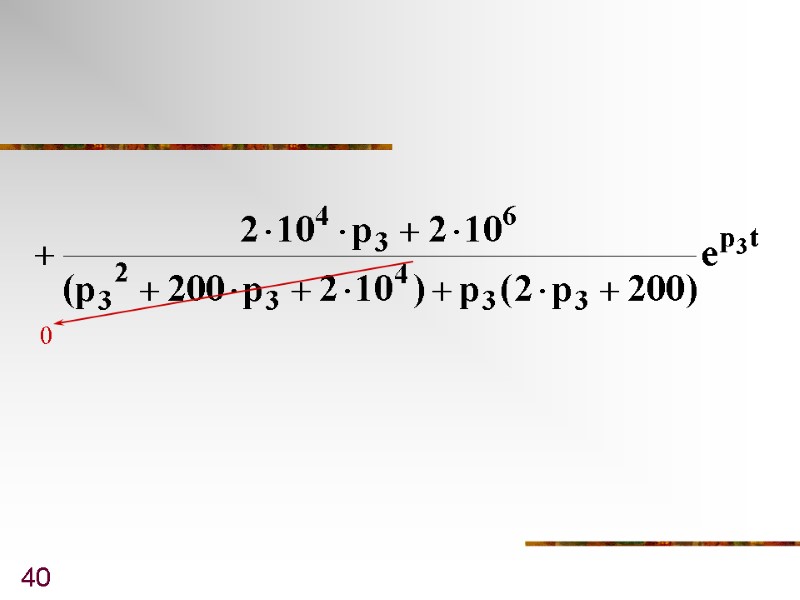>40 0 40 0

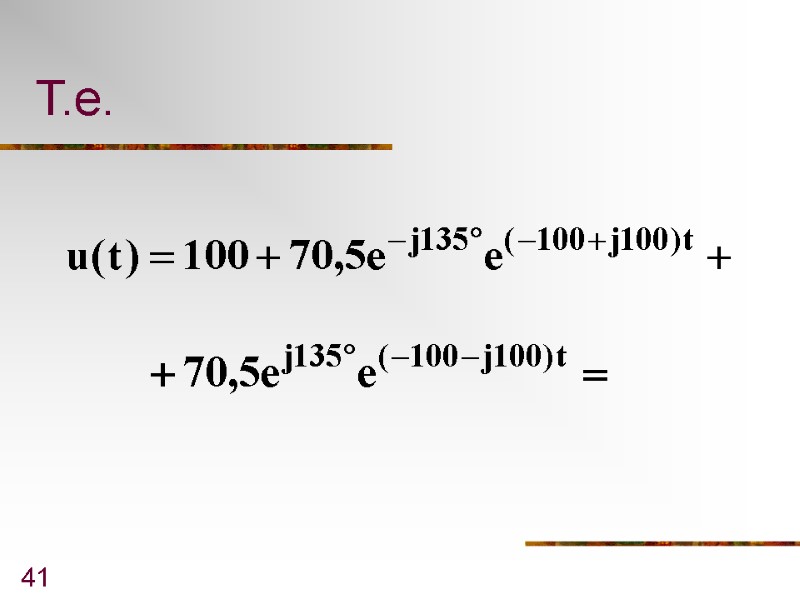>41 Т.е. 41 Т.е.

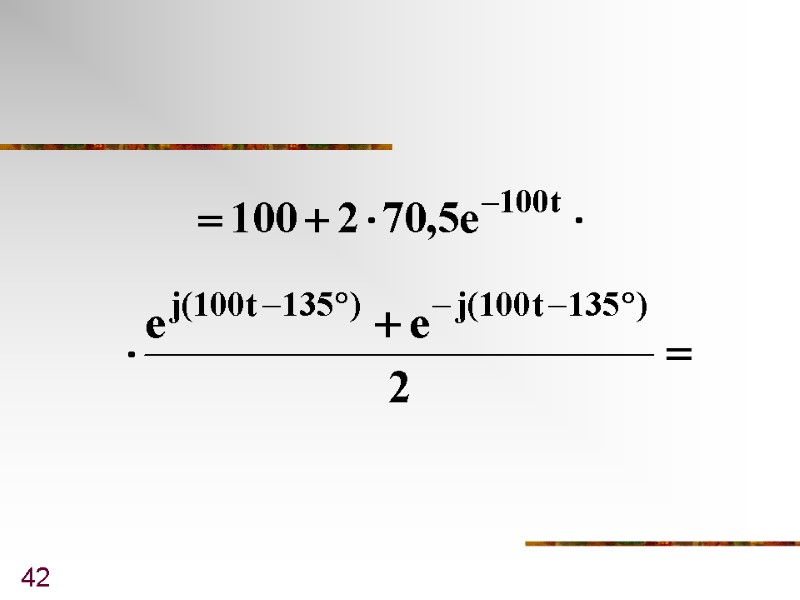>42 42

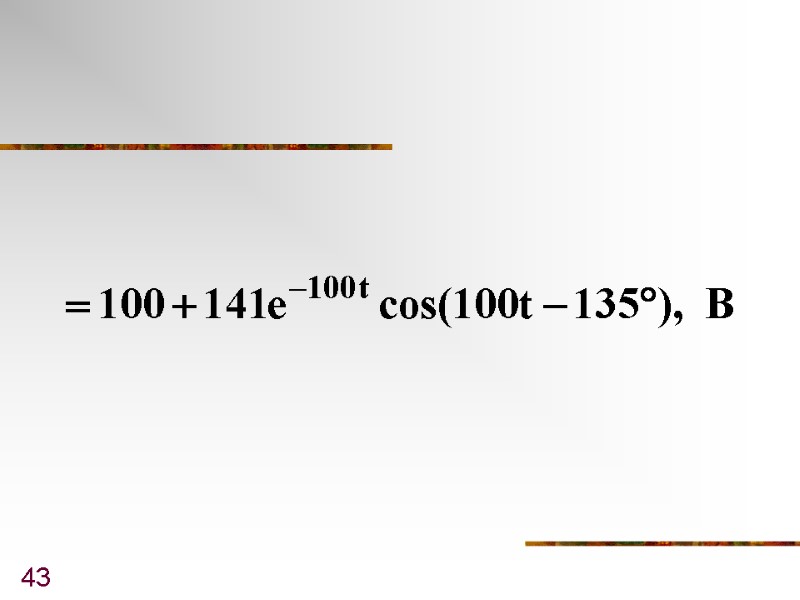>43 43

>44 Законы Ома и Кирхгофа в операторной форме 44 Законы Ома и Кирхгофа в операторной форме

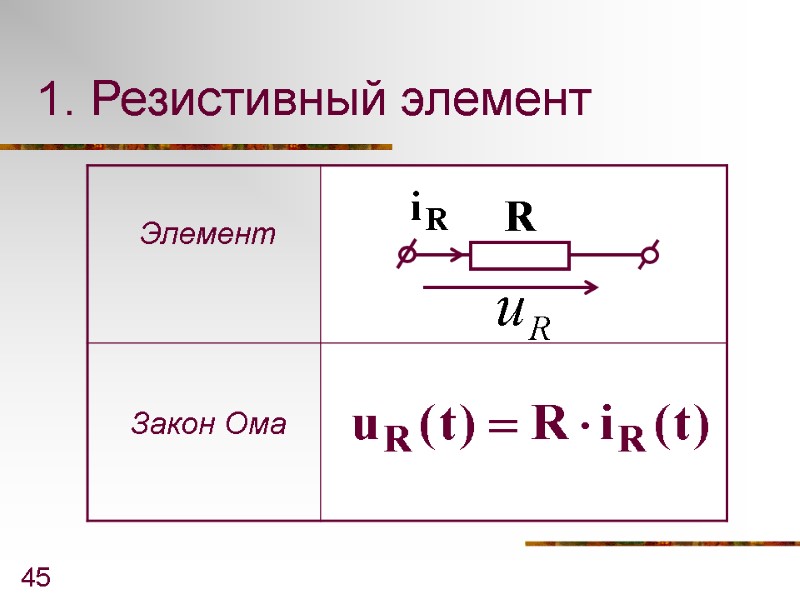
>45 1. Резистивный элемент R 45 1. Резистивный элемент R

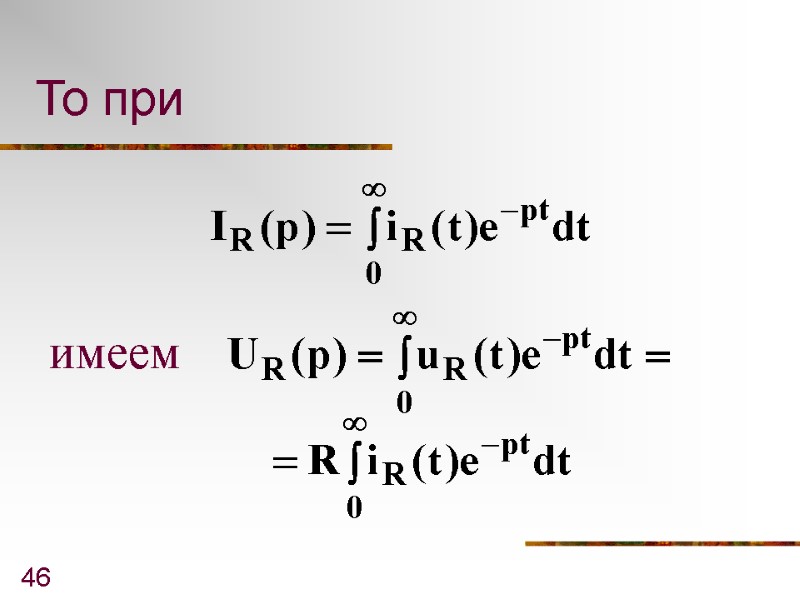>46 То при имеем 46 То при имеем

>47 Тогда - закон Ома в операторной форме для резистивного элемента 47 Тогда - закон Ома в операторной форме для резистивного элемента

>48 Таким образом операторная схема замещения резистора: 48 Таким образом операторная схема замещения резистора:

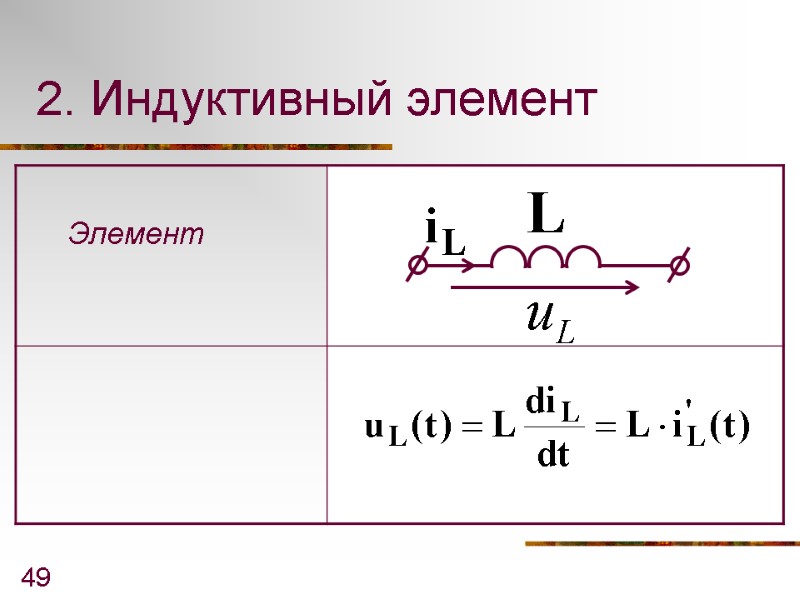
>49 2. Индуктивный элемент 49 2. Индуктивный элемент

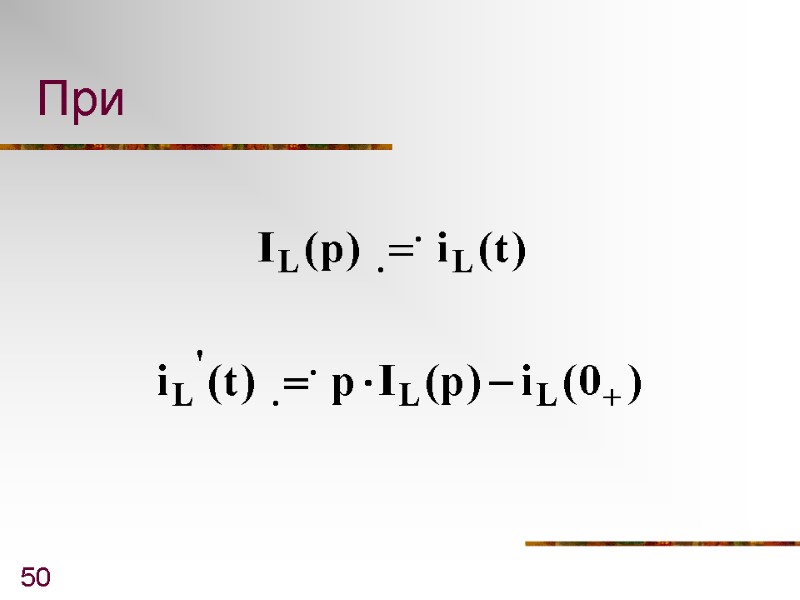>50 При 50 При

>51 Имеем или 51 Имеем или

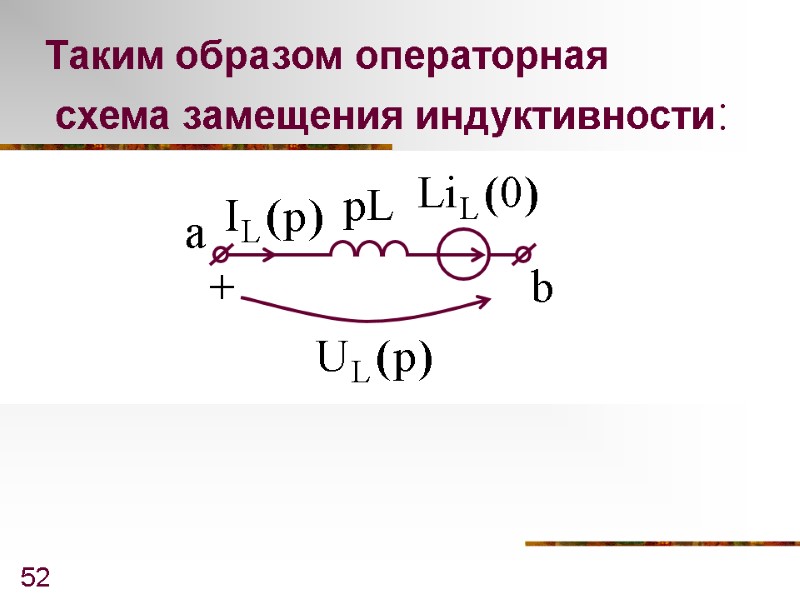
>52 Таким образом операторная схема замещения индуктивности: 52 Таким образом операторная схема замещения индуктивности:

>53 при 53 при и получаем - закон Ома в операторной форме для индуктивного элемента

>54 3. Емкостный элемент 54 3. Емкостный элемент

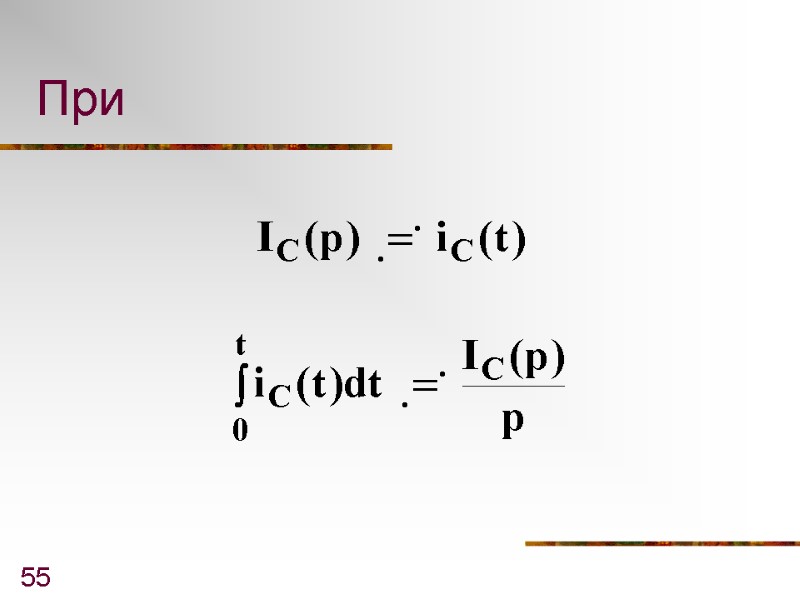>55 При 55 При

>56 Имеем или 56 Имеем или

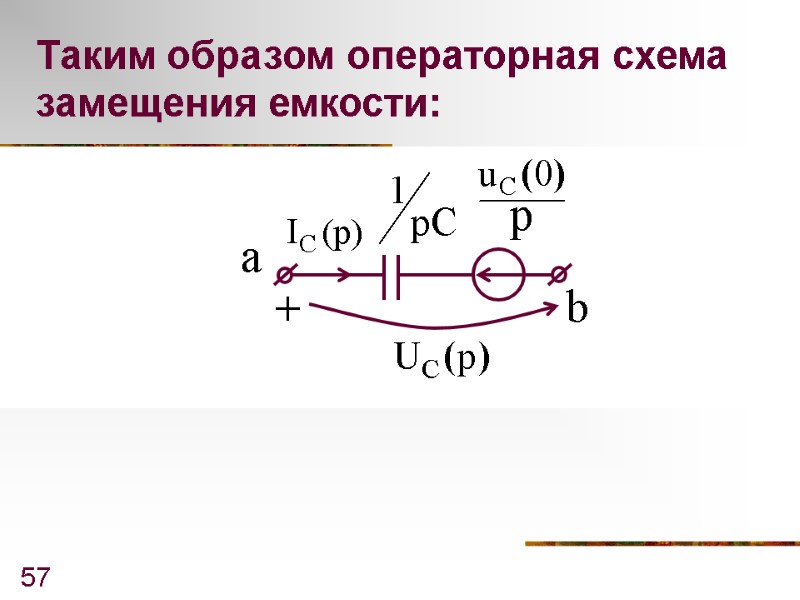
>57 Таким образом операторная схема замещения емкости: 57 Таким образом операторная схема замещения емкости:

>58 при 58 при и получаем - закон Ома в операторной форме для емкостного элемента

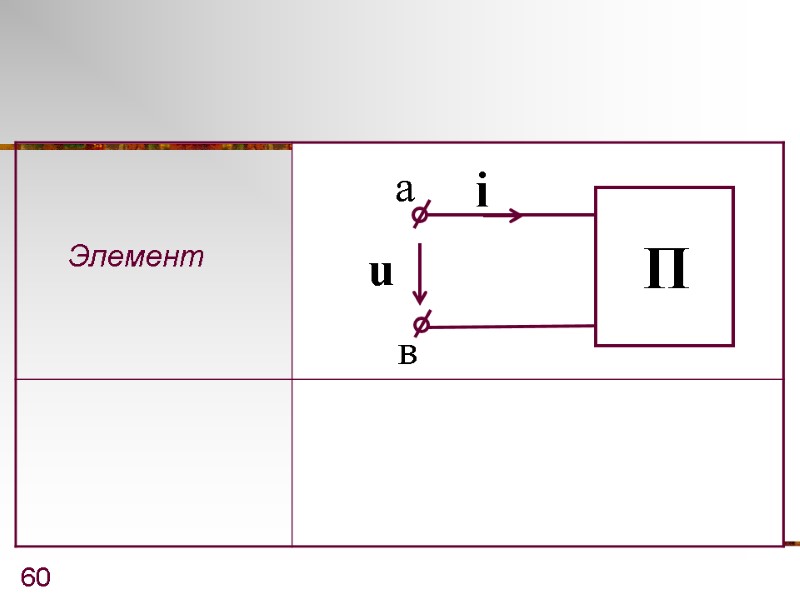
>59 4. Пассивный двухполюсник при нулевых начальных условиях, когда 59 4. Пассивный двухполюсник при нулевых начальных условиях, когда

>60 а в 60 а в

>61 При 61 При по аналогии с законом Ома для отдельных элементов можно записать операторное изображение напряжения

>62 - закон Ома в операторной форме при нулевых начальных условиях 62 - закон Ома в операторной форме при нулевых начальных условиях

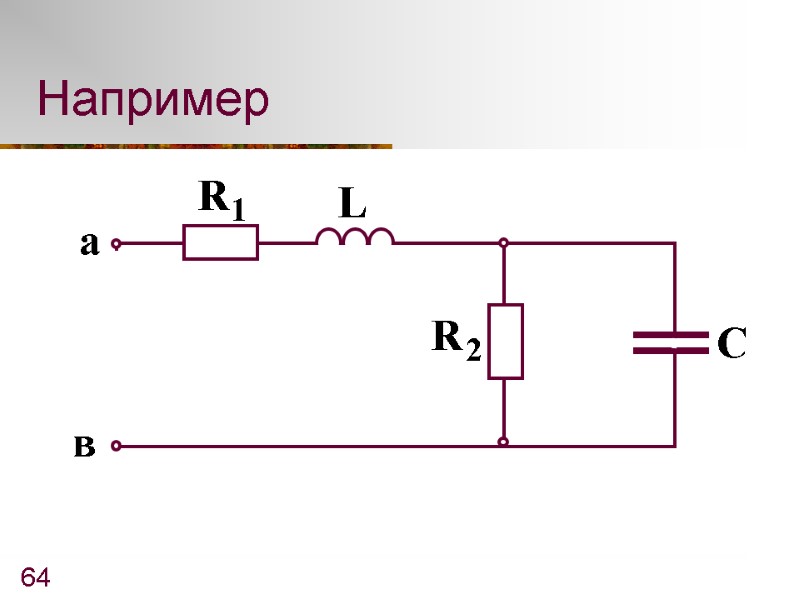
>63 Где Z(p) - эквивалентное операторное сопротивление двухполюсника относительно 63 Где Z(p) - эквивалентное операторное сопротивление двухполюсника относительно зажимов а и в

>64 Например 64 Например

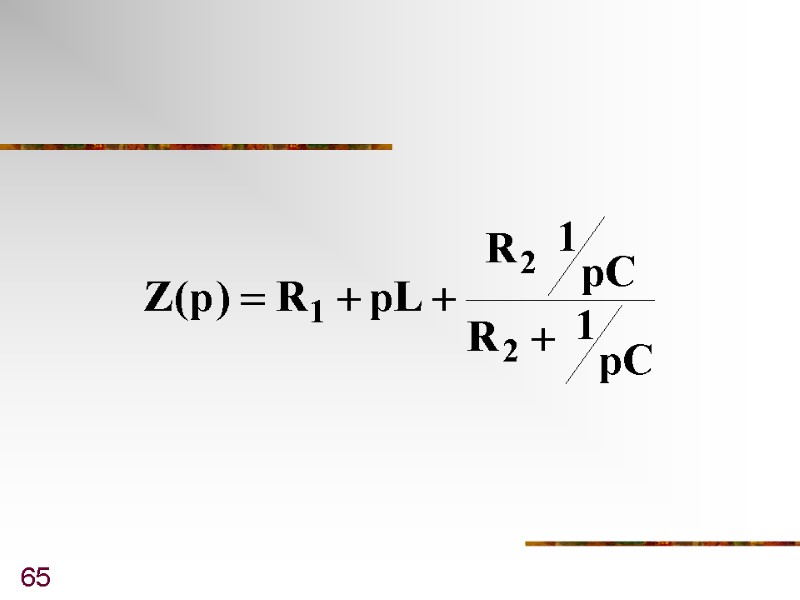>65 65

>66 5. Первый закон Кирхгофа в операторной форме 66 5. Первый закон Кирхгофа в операторной форме

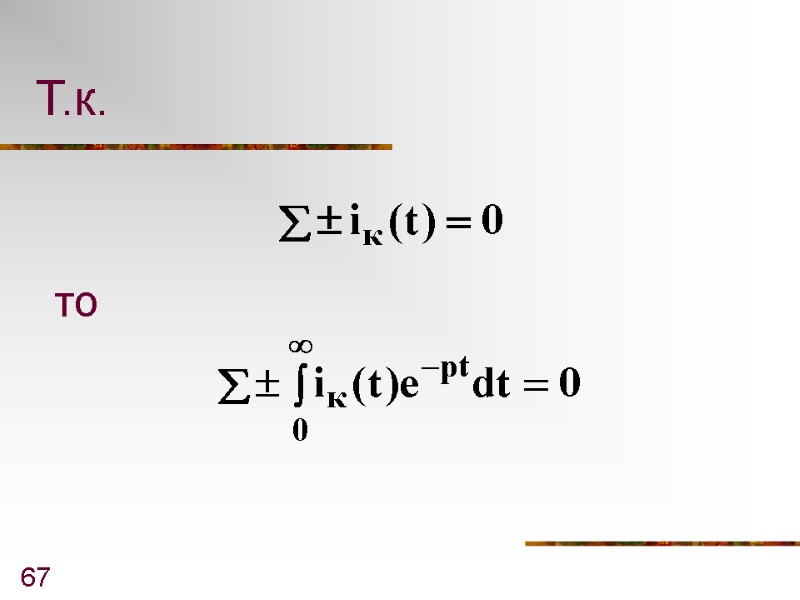>67 Т.к. то 67 Т.к. то

>68 - первый закон Кирхгофа в операторной форме 68 - первый закон Кирхгофа в операторной форме

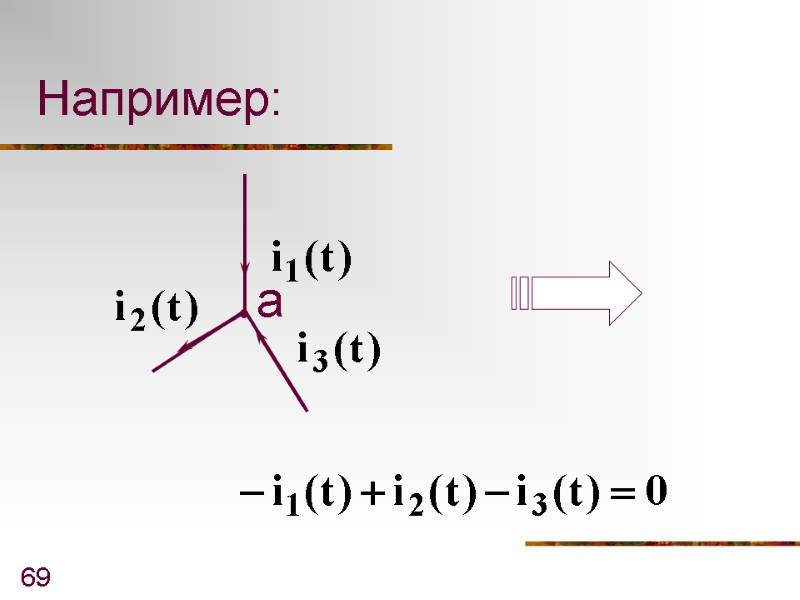>69 Например: а 69 Например: а

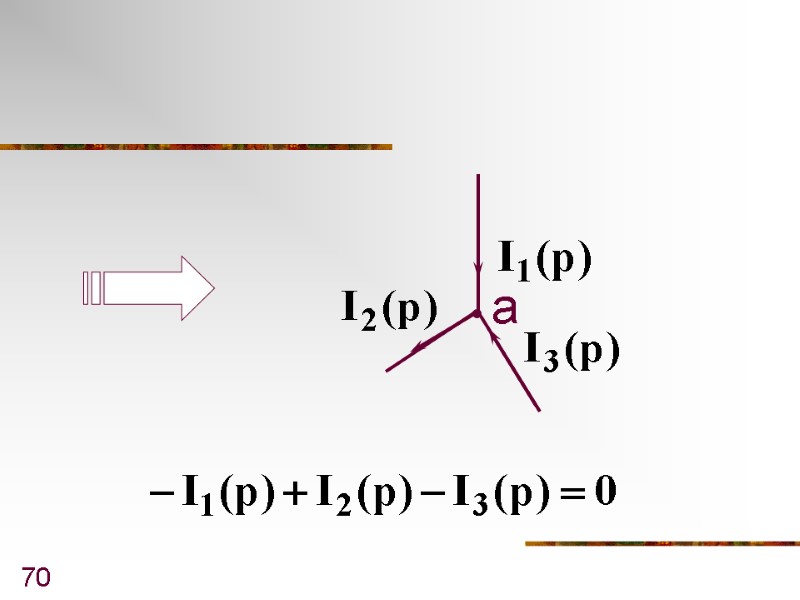>70 а 70 а

>71 6. Второй закон Кирхгофа в операторной форме 71 6. Второй закон Кирхгофа в операторной форме

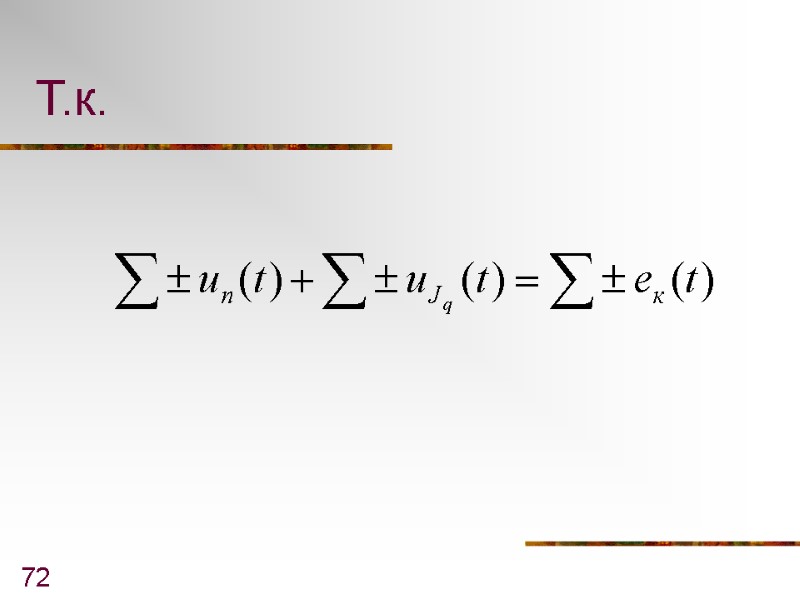>72 Т.к. 72 Т.к.

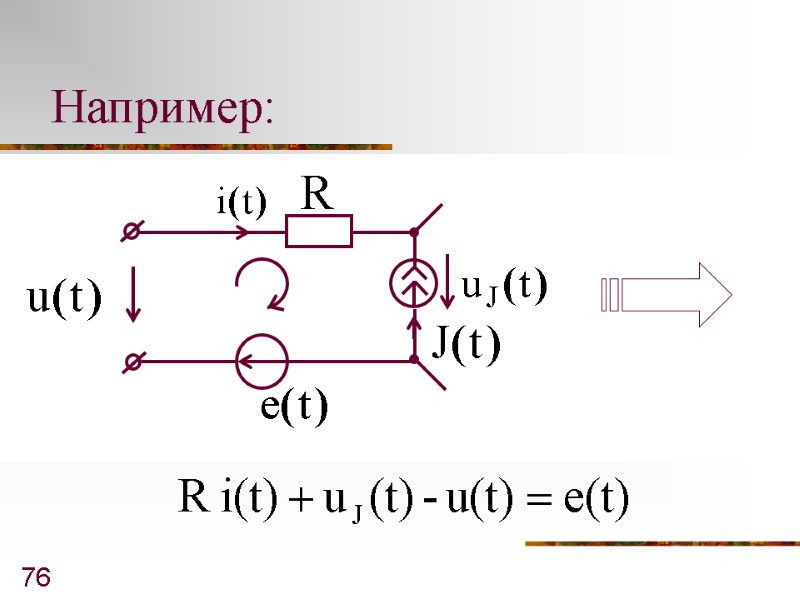
>73 То - второй закон Кирхгофа в операторной форме 73 То - второй закон Кирхгофа в операторной форме

>74 Где - операторное изображение напряжения на пассивном элементе 74 Где - операторное изображение напряжения на пассивном элементе

>75 Где - операторное изображение ЭДС - операторное изображение напряжения на источнике тока 75 Где - операторное изображение ЭДС - операторное изображение напряжения на источнике тока

>76 Например: 76 Например:

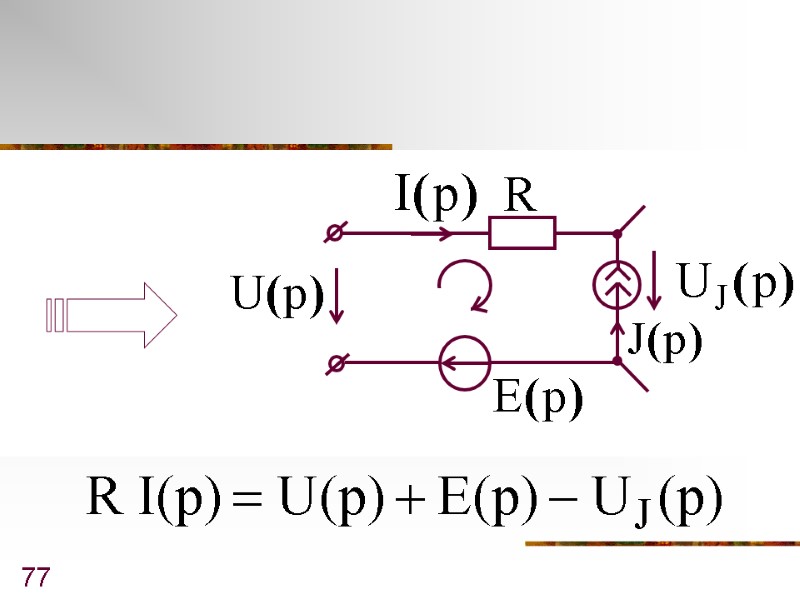
>77 77

>78 Законы Ома и Кирхгофа в операторной форме аналогичны этим законам на постоянном токе 78 Законы Ома и Кирхгофа в операторной форме аналогичны этим законам на постоянном токе

>79 Поэтому к операторным схемам замещения применимы те же методы расчета, но в операторной 79 Поэтому к операторным схемам замещения применимы те же методы расчета, но в операторной форме

>80 Метод законов Кирхгофа Метод контурных токов Метод узловых потенциалов 80 Метод законов Кирхгофа Метод контурных токов Метод узловых потенциалов

>81 Метод наложения Метод эквивалентного генератора Метод преобразований 81 Метод наложения Метод эквивалентного генератора Метод преобразований

>82 Операторная схема замещения составляется для цепи после коммутации на основании операторных схем отдельных 82 Операторная схема замещения составляется для цепи после коммутации на основании операторных схем отдельных элементов