4. Криптографическая защита информации Содержание темы: 4. 1.

4. Криптографическая защита информации Содержание темы: 4. 1. Основные определения 4. 2. Требования к современным методам шифрования 4. 3. Общая схема передачи шифрованных сообщений 4. 4. Классификация криптоалгоритмов 4. 5. Методы шифрования 4. 6. Методы кодирования 4. 7. Другие методы 4. 8. Блочные шифры 4. 9. Симметричные криптоалгоритмы 4. 10. Асимметричные криптоалгоритмы 4. 11. Электронная цифровая подпись 4. 12. Криптографические протоколы

Основные определения Шифр – совокупность обратимых преобразований множества открытых данных на множество зашифрованных данных, заданных алгоритмом криптографического преобразования. Ключ – конкретное секретное состояние некоторых параметров алгоритма криптографического преобразования данных, обеспечивающее выбор одного варианта из совокупности всевозможных для данного алгоритма. Зашифрование – процесс преобразования открытых данных в зашифрованные с помощью шифра. Расшифрование – процесс преобразования закрытых данных в открытые с помощью шифра.

Основные определения (продолжение) Дешифрование – процесс преобразования закрытых данных в открытые при неизвестном ключе и, возможно, неизвестном алгоритме. Криптостойкость – характеристика шифра, определяющая его стойкость к дешифрованию (определяется периодом времени, необходимым для дешифрования).

Требования к современным методам шифрования: 1) Стойкость шифра противостоять криптоанализу должна быть такой, чтобы вскрытие его могло быть осуществлено только путем решения задачи полного перебора ключей. 2) Криптостойкость обеспечивается не секретностью алгоритма, а секретностью ключа. 3) Шифротекст не должен существенно превосходить по объему исходную информацию. 4) Время шифрования не должно быть большим. 5) Стоимость шифрования должна быть соизмерима со стоимостью закрываемой информации.

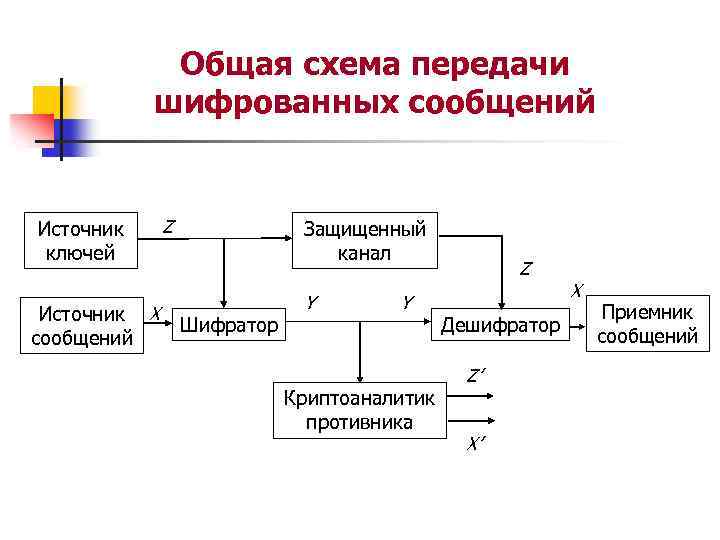Общая схема передачи шифрованных сообщений Источник ключей Источник X сообщений Z Защищенный канал Шифратор Y Y Z Дешифратор Криптоаналитик противника Z’ X’ X Приемник сообщений

Классификация криптоалгоритмов n n n По типу ключей: Симметричные – для шифрования и расшифрования требуется один и тот же ключ. Асимметричные – для шифрования требуется один ключ (открытый), а для расшифрования – другой (закрытый). По характеру воздействия на данные: Перестановочные – блоки информации (биты, байты, . . . ) не меняются сами по себе, а изменяется порядок их следования. Подстановочные – изменяются сами блоки информации. В зависимости от размера блока информации: Потоковые – шифруются побитно. Результат шифрования не зависит от зашифрованного ранее входного потока. Блочные – блок состоит из нескольких байт (обычно от 4 до 32). Результат шифрования зависит от данных всего блока.

Классификация криптоалгоритмов (продолжение) Криптоалгоритмы классифицируются также следующим образом: 1) Шифрование – преобразование элементов открытого сообщения (символов, битов, байтов, …) на основе алгоритма и ключа. 2) Кодирование – преобразование информационного (смыслового) сообщения в комбинацию символов (чисел) в соответствии с некоторой таблицей. Например: символы → числа (ASCII-код, азбука Морзе), последовательность слов → кодовое слово. 3) Другие методы.

1. Шифрование 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 1. 4. Полиграммная 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы

2. Кодирование 2. 1 Смысловое 2. 2 Символьное 2. 3 Комбинированное 3. Другие методы 3. 1 Рассечение – разнесение 3. 2 Сжатие – расширение 3. 3 Стеганография

1. 1 Шифрование заменой 1. 1. 1 Простая замена задается таблицей замен Алфавит исходного текста А ↓ Г Алфавит шифpотекста Пример. Текст: З А М Е Н А Шифр: Р Г И Ж Ф Г Е ↓ Ж З ↓ Р 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 1. 4. Полиграммная 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы М ↓ И Н. . . ↓ ↓ Ф. . .

1. 1 Шифрование заменой 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 1. 4. Полиграммная 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы 1. 1. 1 Простая замена Шифр Атбаш: алфавит шифротекста получается путем обратного порядка исходного алфавита Алфавит исходного текста А _ Алфавит шифpотекста Б В . . . Ю Я Ю. . . В Я Б _ А Шифр с кодовым словом: алфавит шифротекста начинается с символов кодового слова Алфавит исходного текста А К Алфавит шифpотекста Б В Г Д Е . . . О Д С . . . Л В

1. 1 Шифрование заменой 1. 1. 1 Простая замена 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 1. 4. Полиграммная 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы Шифр Цезаря: алфавит шифротекста получается путем сдвига исходного алфавита на 3 позиции Алфавит исходного текста А Б В Г Д . . . Ю Я Алфавит шифpотекста или шифрование: расшифрование: Ю Я _ А Б. . . Ы Ь _ Э уi = (xi + k) mod N хi = (yi + N - k) mod N где хi – номер i-го символа в алфавите исходного текста (i = 0, …, N-1) N – количество символов алфавита yi – номер i-го символа алфавита исходного текста в алфавите шифротекста k – константа (= 3) mod – остаток от деления нацело

1. 1 Шифрование заменой 1. 1. 1 Простая замена 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 1. 4. Полиграммная 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы Недостатки: 1) Сохранение статистических частот встречаемости символов в шифротексте как в открытом тексте. 2) Малое число возможных ключей шифрования. Данные методы применяются редко и только для шифрования коротких сообщений.

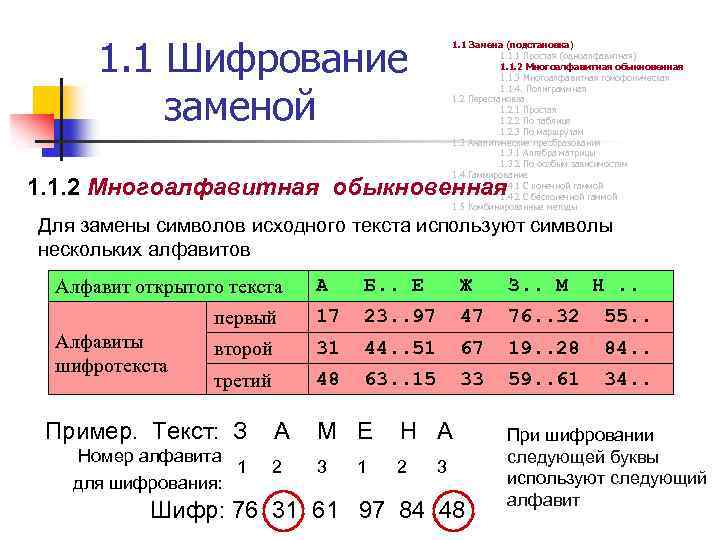1. 1 Шифрование заменой 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 1. 4. Полиграммная 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы 1. 1. 2 Многоалфавитная обыкновенная Для замены символов исходного текста используют символы нескольких алфавитов А Б. . Е Ж З. . М первый 17 23. . 97 47 76. . 32 55. . второй 31 44. . 51 67 19. . 28 84. . третий 48 63. . 15 33 59. . 61 34. . Алфавит открытого текста Алфавиты шифpотекста Пример. Текст: З Номер алфавита для шифрования: 1 А М Е Н А 2 3 2 1 3 Шифр: 76 31 61 97 84 48 Н. . При шифровании следующей буквы используют следующий алфавит

1. 1 Шифрование заменой 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы 1. 1. 2 Многоалфавитная Алфавит исходного текста обыкновенная Код А Шифр Вижинера: шифрование: уi = (xi + ki ) mod N расшифрование: хi = (yi + N – ki ) mod N Б В . . . Ю 0 1 2 . . . 30 Я _ 31 32 (у букв «Е» и «Ё» – один и тот же код) Пример шифрования где хi – код i-го символа исходного текста yi – код i-го П Я Т Н И Открытый текст символа шифротекста Ц А xi ki – код i-го символа ключа 13 8 22 0 15 31 18 Код N – количество символов алфавита К Л Ю Ч К Л Ю Ключ ki mod – остаток от деления нацело Код 10 11 30 23 10 11 30 Строка 2 + строка 4 25 42 48 36 18 33 30 Код шифра 25 9 15 3 30 Шифр Щ П Й Г 18 Т 0 А Ю xi + ki yi = (xi + ki ) mod 33

1. 1 Шифрование заменой 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы 1. 1. 2 Многоалфавитная Алфавит исходного текста обыкновенная Код Шифр Вижинера: шифрование: уi = (xi + ki ) mod N расшифрование: хi = (yi + N – ki ) mod N А Б В . . . Ю 0 1 2 . . . 30 Я _ 31 32 (у букв «Е» и «Ё» – один и тот же код) Пример расшифрования где хi – код i-го символа исходного текста y Щ шифротекста А Ю Шифр i – код i-го символа Й П Г Т ki – код i-го символа 9 15 3 18 0 30 yi 25 ключа Код шифра N – количество символов алфавита К Л Ю Ч К Л Ю Ключ ki mod – остаток от деления нацело 10 11 30 23 10 11 30 Строка 2 + 33 – строка 4 48 31 18 13 41 22 33 Код 15 31 18 13 Открытый текст П Я Т Н 8 22 И Ц 0 А yi + 33 – ki хi = (yi + 33 – ki ) mod 33

1. 1 Шифрование заменой 1. 1. 2 Многоалфавитная обыкновенная Вариации шифра Вижинера: 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы • шифр Вернама – ключ неповторяемый и неограничен по длине • шифр Бофора – шифрование: уi = (xi – ki ) mod N или уi = (ki – xi ) mod N • шифрование с автоключом – в качестве ключа используются символы открытого текста или символы шифротекста

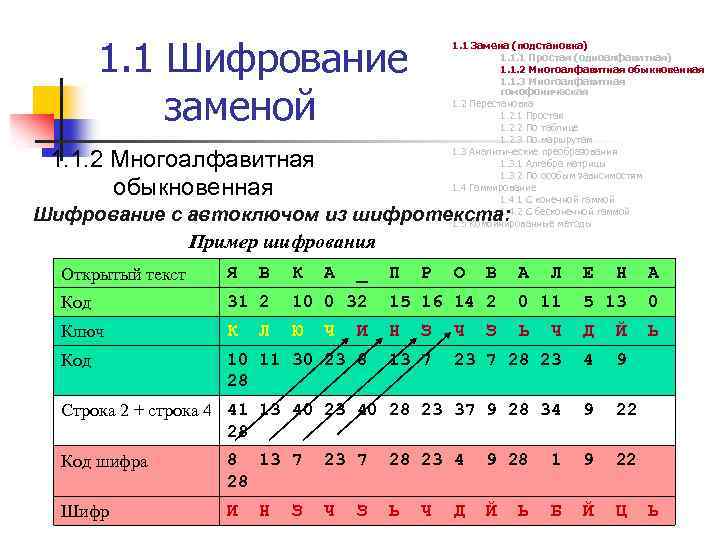1. 1 Шифрование заменой 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы 1. 1. 2 Многоалфавитная обыкновенная Шифрование с автоключом из шифротекста: Пример шифрования Открытый текст Я В Н А Код 31 2 10 0 32 15 16 14 2 0 11 5 13 0 Ключ К Ю Н Ь Ч Д Й Ь Код 10 11 30 23 8 28 23 7 28 23 4 9 Строка 2 + строка 4 41 13 40 28 23 37 9 28 34 28 9 22 Л К А Ч _ И П Р З 13 7 О Ч В З А Л Е Код шифра 8 13 7 28 23 4 9 28 1 9 22 Шифр И Ч Ь Й Б Й Ц Н З З Ч Д Ь Ь

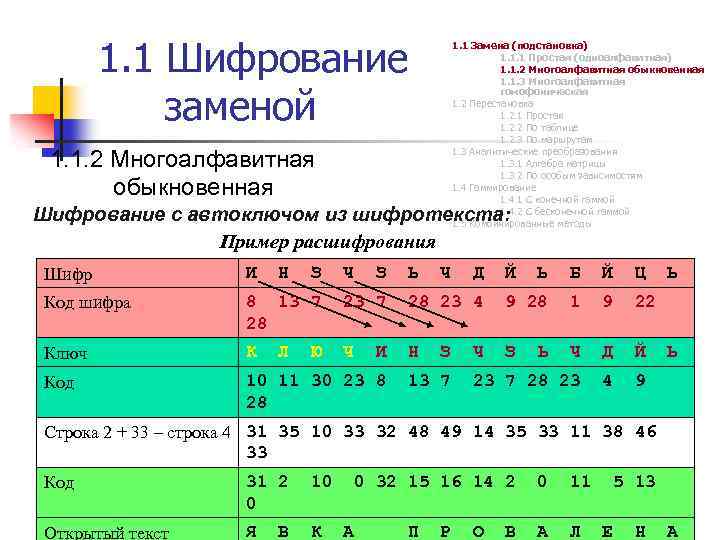1. 1 Шифрование заменой 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы 1. 1. 2 Многоалфавитная обыкновенная Шифрование с автоключом из шифротекста: Пример расшифрования Шифр И Н Код шифра 8 13 7 28 23 7 Ключ К Ч Код 10 11 30 23 8 28 Л З Ю Ч З И Ь Ч Ь Б Й Ц 28 23 4 9 28 1 9 22 Н З Ч Д Й 23 7 28 23 4 9 З 13 7 Д Ч Й Ь Ь Ь Строка 2 + 33 – строка 4 31 35 10 33 32 48 49 14 35 33 11 38 46 33 Код 31 2 0 10 Открытый текст Я К В 0 32 15 16 14 2 А _ П Р О В 0 11 А Л 5 13 Е Н А

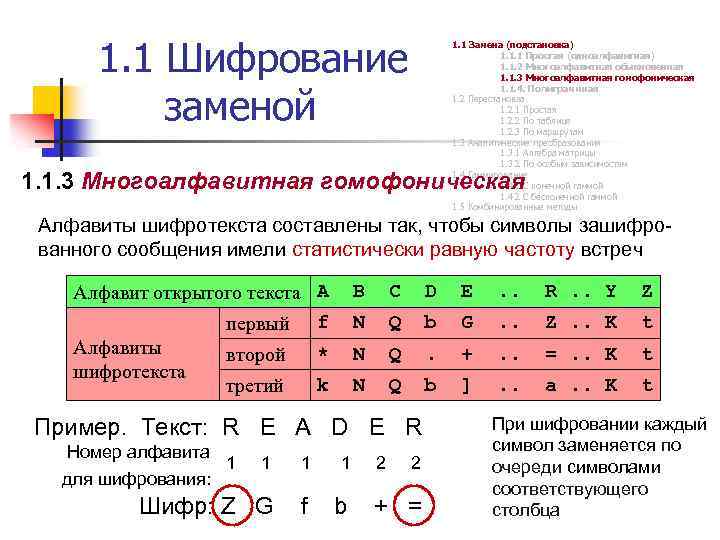1. 1 Шифрование заменой 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 1. 4. Полиграммная 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы 1. 1. 3 Многоалфавитная гомофоническая Алфавиты шифротекста составлены так, чтобы символы зашифрованного сообщения имели статистически равную частоту встреч Алфавит открытого текста A первый f Алфавиты * второй шифpотекста k третий B C D E . . R. . Y Z N Q b G . . Z. . K t N Q . + . . =. . K t N Q b ] . . a. . K t Пример. Текст: R E A D E R Номер алфавита 1 1 1 Шифр: Z G f b для шифрования: 1 2 2 + = При шифровании каждый символ заменяется по очереди символами соответствующего столбца

1. 1 Шифрование заменой 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 1. 4. Полиграммная 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы Достоинство методов многоалфавитной замены: Маскирование в шифротексте частот появления символов открытого текста.

1. 1 Шифрование заменой 1. 1. 4 Полиграммная 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 1. 4. Полиграммная 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы Шифр Плейфера Относится к шифрам полиграммной замены, когда замене подвергается не отдельный символ, а группа символов. А Ж Б М Ц Ч Г Н Ш Д Используется матрица замен (выступает в качестве ключа метода). Е Щ , Х У. З Ъ Р И С Ю В О П Й Ь К Э Т Л Я _ Ы Ф -

1. 1 Шифрование заменой Шифр Плейфера 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы Открытый текст разбивается на пары символов. Если он содержит нечетное количество символов, то перед шифрованием в конец текста добавляется специальный символ (например, тире). Каждая пара заменяется на пару символов из матрицы по следующим правилам: 1) Если символы находятся в одной строке, то каждый из символов пары заменяется на стоящий правее него (за последним символом в строке следует первый) Пример. Пара символов «ГД» заменяется на пару «НО» А Ж Ч Г Г Е Щ. З С Ю Б Н , Ъ М Ш Х Р Ц Д У И В О П Й Ь К Э Т Л Я _ Ы Ф -

1. 1 Шифрование заменой Шифр Плейфера 2) Если символы находятся в одном столбце, то каждый символ пары заменяется на символ, расположенный ниже него в столбце (за последним нижним символом следует верхний) Пример. Пара символов «СА» заменяется на пару «ЮЧ» 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы А А Ч Ч Е. Ж Г Щ З Б Н , Ъ М Ш Х Р Ц Д У И В О П Й С С Ь К Э Т Л Ю Ю Я _ Ы Ф -

1. 1 Шифрование заменой Шифр Плейфера 3) Если символы пары находятся в разных строках и столбцах, то они считаются противоположными углами прямоугольника. Символ, находящийся в левом углу, заменяется на символ, стоящий в другом левом углу; символ в правом углу заменяется на другой символ правого угла Пример. Пара символов «КО» заменяется на пару «НЛ» 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы А Ч Е. Ж Г Щ З Б Н , Ъ М Ш Х Р Ц Д У И В О П Й С Ю Ь К Э Т Л Я _ Ы Ф -

1. 1 Шифрование заменой Шифр Плейфера 4) Если в открытом тексте встречаются два одинаковых символа подряд, то перед шифрованием между ними вставляется специальный символ (например, тире) Пример. Открытый текст «РАССВЕТ» , изменяется на «РАС-СВЕТ» 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы А Ч Е. Ж Г Щ З Б Н , Ъ М Ш Х Р Ц Д У И В О П Й С Ю Ь К Э Т Л Я _ Ы Ф -

1. 2 Шифрование перестановкой 1. 2. 1 Простая перестановка 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы Символы открытого текста переставляются в соответствии с правилом, задаваемым ключом шифра. В качестве ключа перестановки можно использовать последовательность символов. Для этого: 1) отсортировать символы ключа (в алфавитном порядке) 2) каждый символ ключа заменяется на номер позиции в отсортированном ключе Пример. Ключевое слово: М И Р Отсортированный ключ: И М Р 1 2 3 Числовой ключ: 2 -1 -3 Текст: ПРО СТА Я_П ЕРЕ СТА НОВ КА Шифр: РПО ТСА _ЯП РЕЕ ТСА ОНВ АК

1. 2 Шифрование перестановкой 1. 2. 2 Перестановка по таблице 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы Символы открытого текста записываются построчно в матрицу перестановки согласно ключу1, а считываются из матрицы по столбцам согласно ключу2 Шифротекст: _ _ТЦВЙВЕИСЛН_ _ОИТТ_НППАУЯРЯЕ_З Ключ1: 5 -1 -3 -2 -4 Пример. Матрица перестановки 5 х6 Ключ1: 5 -1 -3 -2 -4, ключ2: 2 -1 -6 -5 -3 -4 Текст: СВЯЗНОЙ_ПРИЛЕТАЕТ_В_ПЯТНИЦУ Ключ2: 2 -1 -6 -5 -3 -4 1 2 3 4 5 6 1 Й _ П 2 В _ П 3 Е Т А 4 И Ц У 5 С В Я Р Я Е _ З И Т Т _ Н Л Н _ _ О

1. 2 Шифрование перестановкой 1. 2. 2 Перестановка по таблице 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы Модификации метода: § направление записи исходного текста в матрицу (построчно, по столбцам, по спирали, по диагонали); § направление чтения шифротекста из матрицы (построчно, по столбцам, по спирали, по диагонали).

1. 2 Шифрование перестановкой 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы 1. 2. 3 Перестановка по маршрутам Например, перестановка по гамильтоновым путям на графе (гамильтонов путь – замкнутый путь, проходящий через все вершины графа строго по одному разу). 1) Вершины графа нумеруют. 2) В вершины графа последовательно записывают символы открытого текста. 3) Получают шифр, путем считывания символов, согласно выбранному гамильтоновому пути.

1. 2 Шифрование перестановкой 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы Недостатки: 1) Сохранение статистических частот встречаемости символов в шифротексте как в открытом тексте. 2) Малое число возможных ключей шифрования. Достоинство: Высокая скорость шифрования.

1. 3 Аналитические преобразования 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матриц 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы Основаны на понятии односторонней функции. Функция Y = F(Х) является односторонней, если она за сравнительно небольшое число операций преобразует элемент открытого текста Х в элемент шифротекста Y, а обратная операция (вычисление X = Fобр(Y) при известном шифротексте) является вычислительно трудоемкой. В качестве односторонней функции можно использовать следующие преобразования: • умножение матриц; • решение задачи об укладке ранца; • вычисление значения полинома по модулю; • экспоненциальные преобразования и др.

1. 3 Аналитические преобразования 1. 3. 1 Метод алгебры матриц 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матриц 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы где Х – вектор элементов открытого текста, Y – вектор элементов шифротекста, А – матрица преобразования (ключ). Пример. Шифрование Расшифрование

1. 3 Аналитические преобразования 1. 3. 2 По особым зависимостям Метод укладки ранца. 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матриц 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы С = |c 1, c 2, . . . , cn| - вектор чисел, ключ Каждый символ Хi открытого текста представлен в виде n бит Хi = |x 1, x 2, . . . , xn|T, xk {0, 1}. Шифротекст получается как скалярное произведение С*Xi. Пример. Открытый текст 16 17 9 11 1 8 в двоичном виде 10000 10001 01011 00001 01000 1 3 5 7 11 Вектор С = Шифр 1 12 14 21 11 3

1. 3 Аналитические преобразования 1. 3. 2 По особым зависимостям Метод полиномов Основан на преобразовании 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матриц 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы где хi – i-й элемент открытого текста, yi – i-й элемент шифротекста, ai – целые неотрицательные числа (ключ), p – большое простое число.

1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы 1. 4 Гаммирование – процесс наложения гаммы Gi на открытые данные xi (для шифрования) или закрытые данные yi (для расшифрования). Гамма – некоторая последовательность символов (например, последовательность случайных чисел). yi = xi Gi , где – поразрядное сложение по модулю 2 (исключающее ИЛИ, XOR); вместо можно использовать и другие логические операции.

1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы 1. 4 Гаммирование – поразрядное сложение по модулю 2 (исключающее ИЛИ, XOR) Таблица истинности для операции XOR xi (вход 1) Gi (вход 2) yi (выход) 0 0 1 1 1 0 Таблица истинности содержит все возможные комбинации входных значений и соответствующие им выходные значения

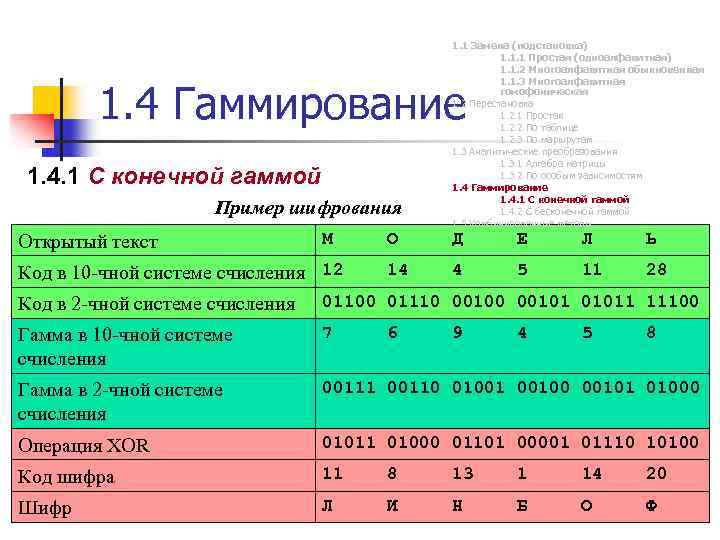1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы 1. 4 Гаммирование 1. 4. 1 С конечной гаммой Пример шифрования Открытый текст М Код в 10 -чной системе счисления 12 О Д Е Л Ь 14 4 5 11 28 Код в 2 -чной системе счисления 01100 01110 001011 11100 Гамма в 10 -чной системе счисления 7 Гамма в 2 -чной системе счисления 00111 00110 01001 00100 00101 01000 Операция XOR 01011 01000 01101 00001 01110 10100 Код шифра 11 8 13 1 14 20 Шифр Л И Н Б О Ф 6 9 4 5 8

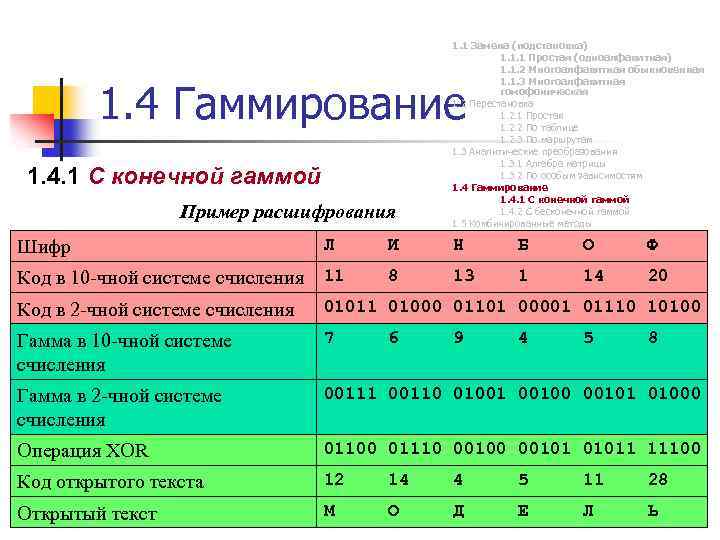1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы 1. 4 Гаммирование 1. 4. 1 С конечной гаммой Пример расшифрования Шифр Л Код в 10 -чной системе счисления 11 И Н Б О Ф 8 13 1 14 20 Код в 2 -чной системе счисления 01011 01000 01101 00001 01110 10100 Гамма в 10 -чной системе счисления 7 Гамма в 2 -чной системе счисления 00111 00110 01001 00100 00101 01000 Операция XOR 01100 01110 001011 11100 Код открытого текста 12 14 4 5 11 28 Открытый текст М О Д Е Л Ь 6 9 4 5 8

1. 5 Комбинированные методы 1. 1 Замена (подстановка) 1. 1. 1 Простая (одноалфавитная) 1. 1. 2 Многоалфавитная обыкновенная 1. 1. 3 Многоалфавитная гомофоническая 1. 2 Перестановка 1. 2. 1 Простая 1. 2. 2 По таблице 1. 2. 3 По маршрутам 1. 3 Аналитические преобразования 1. 3. 1 Алгебра матрицы 1. 3. 2 По особым зависимостям 1. 4 Гаммирование 1. 4. 1 С конечной гаммой 1. 4. 2 С бесконечной гаммой 1. 5 Комбинированные методы Последовательное использование нескольких различных методов шифрования для повышения криптостойкости. Распространенные комбинации: • подстановка + гаммирование • замена + гаммирование • гаммирование + гаммирование • замена + перестановка

2. Кодирование 2. 1 Смысловое Замена одних смысловых данных (слов, фраз) на другие. Каждому специальному сообщению – свою систему кодирования. Пример: «Имею 3 банки тушенки, привозите коробки» = «Вижу 3 танка, вызываю самолёты» 2. 2 Символьное Сопоставление символам числовых кодов (для удобства передачи, хранения, обработки). Примеры: код ASCII, азбука Морзе 2. 3 Комбинированное

3. Другие методы шифрования 3. 1 Рассечение – разнесение Сообщение разбивается на блоки, которые хранятся в разных местах. Отдельный блок не позволяет раскрыть информацию. 3. 2 Сжатие – расширение Преобразование открытых данных с целью уменьшения объема памяти для их хранения (программы-архиваторы). 3. 3 Стеганография Методы маскировки, сокрытия факта присутствия конфиденциальной информации.

3. 3 Стеганография Применительно к стеганографии различают сообщение (объект, существование и содержание которого должно быть скрыто) и контейнер (объект, в котором скрывается сообщение). При помещении сообщения в контейнер может использоваться секретный ключ, определяющий порядок помещения сообщения в контейнер. Этот же ключ должен быть задан при извлечении сообщения из контейнера. Возможно объединение методов криптографии и стеганографии, при котором сообщение предварительно зашифровывается перед помещением в контейнер.

3. 3 Стеганография Методы последнего значащего бита (Last Significant Bit, LSB) используют естественную избыточность оцифрованных графических изображений, звука и видеоинформации. Примеры: § Графические файлы в формате RGB кодируют каждую точку (пиксель) изображения тремя байтами для представления соответственно красной, зеленой и синей составляющих. Изменение каждого из трех младших битов (для хранения битов скрываемого сообщения) приведет к изменению цветовых характеристик данной точки изображения менее чем на 1%, что абсолютно незаметно для человеческого глаза. Этот метод позволяет скрыть в графическом файле размером 800 килобайт сообщение размером до 100 килобайт. § Одна секунда оцифрованного звука с частотой дискретизации 44100 Герц позволяет по методу LSB скрыть сообщение размером до 10 килобайт.

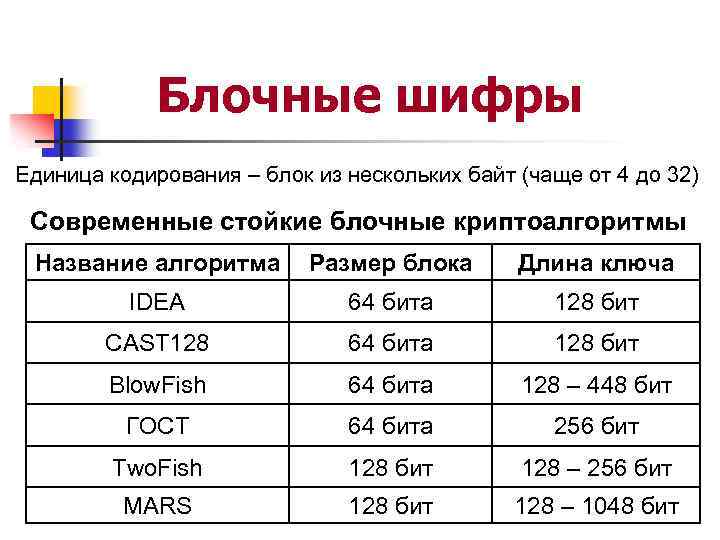Блочные шифры Единица кодирования – блок из нескольких байт (чаще от 4 до 32) Современные стойкие блочные криптоалгоритмы Название алгоритма Размер блока Длина ключа IDEA 64 бита 128 бит CAST 128 64 бита 128 бит Blow. Fish 64 бита 128 – 448 бит ГОСТ 64 бита 256 бит Two. Fish 128 бит 128 – 256 бит MARS 128 бит 128 – 1048 бит

Требования к стойкому блочному шифру: n n n Функция (алгоритм) шифрования должна быть обратимой. Не должно существовать иных методов прочтения сообщения X по известному шифру Z, кроме как полным перебором ключей Key. Не должно существовать иных методов определения, каким ключом Key было произведено преобразование известного сообщения X в шифр Z, кроме как полным перебором ключей.

Стойкость блочного криптоалгоритма Стойкость блочного шифра зависит только от длины ключа N и возрастает с ее ростом. На взлом идеально стойкого криптоалгоритма потребуется в среднем 2 N-1 проверок. Если предположить, что проверка 1 ключа происходит за 1 такт процессора, то на взлом 128 битного ключа на ЭВМ с частотой 1 ГГц потребуется: 2127 тактов = 297 с ≈ 1021 лет. На взлом 64 битного ключа: 263 тактов = 234 с ≈ 1 год.

Блок данных При блочном шифровании блок данных рассматривается как набор блоков меньшего размера, над которыми производятся различные действия 64 бита 32 бита 16 бит

Типовые действия над блоками данных Математические функции Сложение Исключающее ИЛИ X'=X+V X'=X XOR V Умножение по модулю 2 N+1 X'=(X*V) mod (2 N+1) Умножение по модулю 2 N X'=(X*V) mod (2 N) Битовые сдвиги Арифметический сдвиг влево X'=X SHL V Арифметический сдвиг вправо X'=X SHR V Циклический сдвиг влево X'=X ROL V Циклический сдвиг вправо X'=X ROR V Табличные подстановки S-box (англ. substitute) X'=Table[X, V]

Параметр V в преобразованиях данных n n n фиксированное число ( X' = X+125 ) число, получаемое из ключа ( X' = X + F(Key) ) число, получаемое из независимой части блока ( X 2' = X 2 + F(X 1) )

Сеть Фейштеля Схема шифрования, в которой шифротекст получается путем смешивания текущей части блока исходного текста с результатом некоторой функции от другой независимой части того же блока

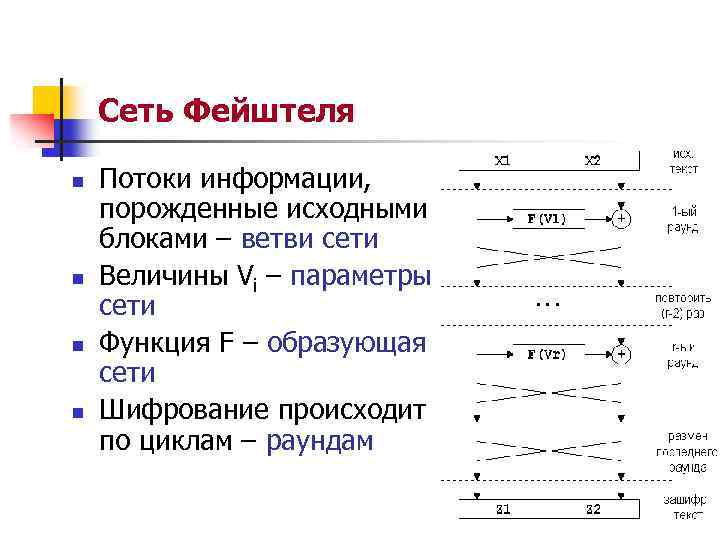Сеть Фейштеля n n Потоки информации, порожденные исходными блоками – ветви сети Величины Vi – параметры сети Функция F – образующая сети Шифрование происходит по циклам – раундам

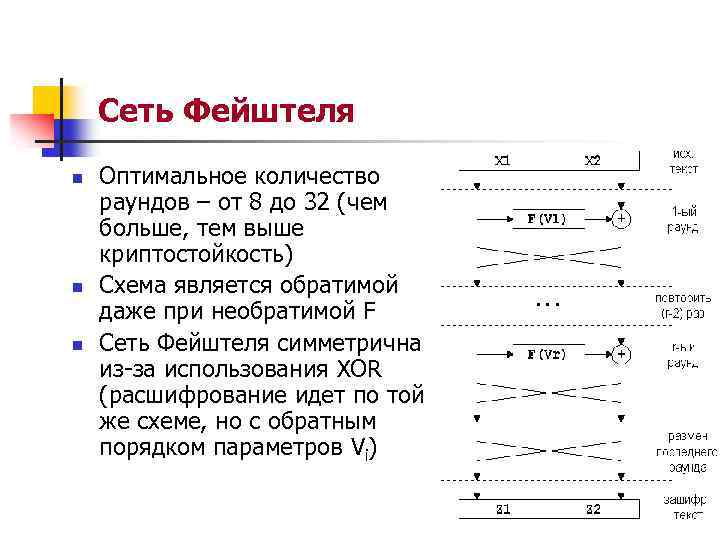Сеть Фейштеля n n n Оптимальное количество раундов – от 8 до 32 (чем больше, тем выше криптостойкость) Схема является обратимой даже при необратимой F Сеть Фейштеля симметрична из-за использования XOR (расшифрование идет по той же схеме, но с обратным порядком параметров Vi)

Модификации сети Фейштеля Абсолютно симметричная сеть Фейштеля (шифрование и расшифрование выполняется с одним и тем же набором параметров) Криптостойкость схемы недостаточно изучена, используется с большой осторожностью

Криптостойкость сети Фейштеля Криптостойкость блочного шифра, использующего сеть Фейштеля, определяется на 95% функцией F и правилом вычисления Vi из ключа. Эти функции являются объектом все новых исследований специалистов в области криптографии.

Блочный шифр TEA type TLong 2=array[0. . 1] of longint; TLong 2 x 2=array[0. . 1] of TLong 2; const Delta=$9 E 3779 B 9; var key: TLong 2 x 2; procedure En. Crypt. Routing(var data); var y, z, sum: longint; a: byte; begin y: =TLong 2(data)[0]; Размер блока – 64 бита z: =TLong 2(data)[1]; sum: =0; Длина ключа – 128 бит for a: =0 to 31 do begin Оптимизирован под 32 -х inc(sum, Delta); разрядный процессор inc(y, ((z shl 4)+key[0, 0]) xor (z+sum) xor ((z shr 5)+key[0, 1])); inc(z, ((y shl 4)+key[1, 0]) xor (y+sum) xor ((y shr 5)+key[1, 1])); Сеть шифра end; несимметрична TLong 2(data)[0]: =y; TLong 2(data)[1]: =z end; Tiny Encryption Algorithm n n

Конкурс AES (Advanced Encryption Standard) Стандартом симметричного криптоалгоритма в США в 80 -е годы был DES (Data Encryption Standard) n n Недостатки DES: длина ключа – 56 бит (мало); алгоритм был ориентирован на аппаратную реализацию, т. е. содержал операции, выполняемые на микропроцессорах за неприемлемо большое время (например, такие как перестановка бит внутри машинного слова по определенной схеме)

Конкурс AES (Advanced Encryption Standard) В 1997 году был объявлен конкурс на новый стандарт криптоалгоритма Требования: n Алгоритм должен быть симметричным n Алгоритм должен быть блочным n Длина блока – 128 бит, длина ключа – 128, 196, 256 бит Рекомендации: n Использовать операции, легко реализуемые как аппаратно, так и программно n Ориентироваться на 32 -х разрядные процессоры n Простая для исследования структура шифра

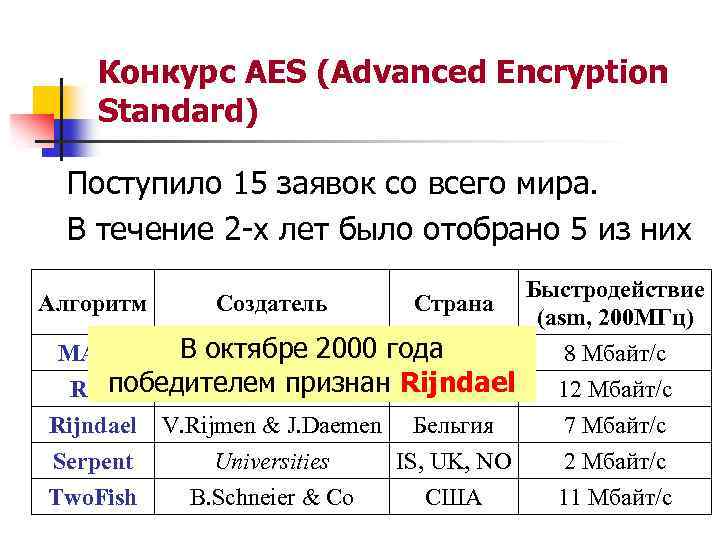Конкурс AES (Advanced Encryption Standard) Поступило 15 заявок со всего мира. В течение 2 -х лет было отобрано 5 из них Алгоритм Создатель Страна В октябре 2000 года MARS IBM США победителем признан Rijndael RC 6 R. Rivest & Co США Rijndael V. Rijmen & J. Daemen Бельгия Serpent Universities IS, UK, NO Two. Fish B. Schneier & Co США Быстродействие (asm, 200 МГц) 8 Мбайт/с 12 Мбайт/с 7 Мбайт/с 2 Мбайт/с 11 Мбайт/с

Алгоритм Rijndael n n Блочный шифр, не использующий сеть Фейштеля Каждый блок данных представляется в виде матриц 4 х4, 4 х6, 4 х8 байт Алгоритм эффективен для 32 -х разрядных процессоров Возможно параллельное выполнение преобразований (увеличение скорости в 4 раза)

Алгоритм Rijndael Алгоритм содержит 10 -14 раундов, в которых последовательно выполняются операции: 1) Byte. Sub – табличная подстановка 8 х8 бит 3) Mix. Column – математическое преобразование, 4) Add. Round. Key – добавление материала 2) Shift. Row – сдвиг строк в двумерном перемешивающее данные внутри столбца ключа операцией XOR массиве на различные смещения без сдвига циклический сдвиг на 1 циклический сдвиг на 2 циклический сдвиг на 3

Симметричные криптоалгоритмы Проблемы практического применения блочных шифров и пути их решения

Симметричные криптоалгоритмы Современные симметричные системы шифрования основаны на применении блочных криптоалгоритмов

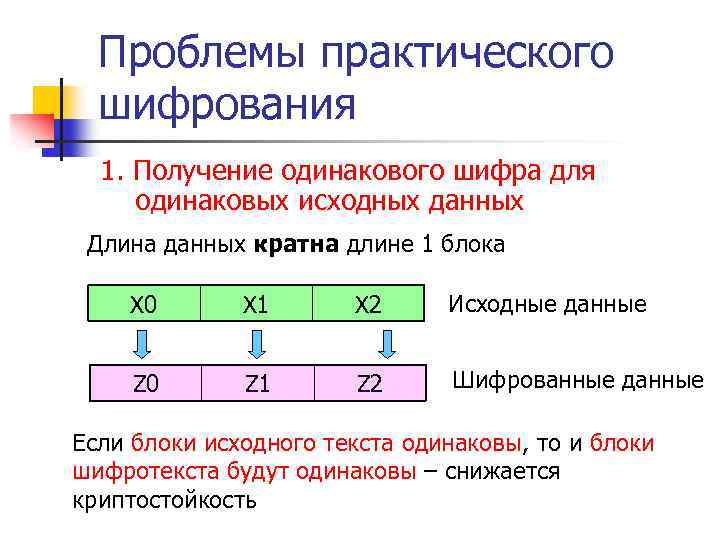Проблемы практического шифрования 1. Получение одинакового шифра для одинаковых исходных данных Длина данных кратна длине 1 блока Х 0 Х 1 Х 2 Исходные данные Z 0 Z 1 Z 2 Шифрованные данные Если блоки исходного текста одинаковы, то и блоки шифротекста будут одинаковы – снижается криптостойкость

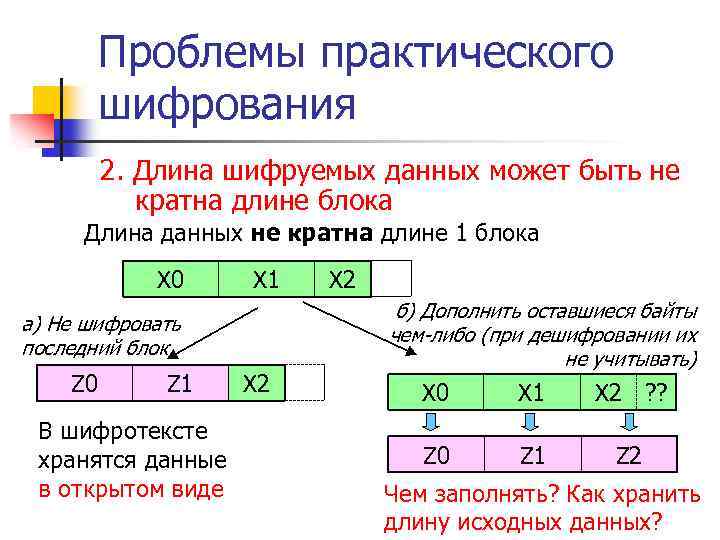Проблемы практического шифрования 2. Длина шифруемых данных может быть не кратна длине блока Длина данных не кратна длине 1 блока Х 0 Х 1 а) Не шифровать последний блок Z 0 Z 1 В шифротексте хранятся данные в открытом виде Х 2 б) Дополнить оставшиеся байты чем-либо (при дешифровании их не учитывать) Х 0 Х 1 Х 2 ? ? Z 0 Z 1 Z 2 Чем заполнять? Как хранить длину исходных данных?

Проблемы практического шифрования 3. Генерация случайной последовательности (для генерации ключей, рандомизации сообщений) Частое шифрование данных фиксированного формата одним и тем же ключом (передача информации или команд в ИС, банковские операции) приведет к мало отличающимся шифротекстам Введение случайных бит в шифруемые данные с игнорированием их на принимающей стороне Для шифрования очередных данных использовать случайный ключ (ключ сеанса) Как получать случайные (псевдослучайные) последовательности?

Проблемы практического шифрования 4. Сжатие исходных данных В криптоанализе доказано, что вероятность взлома криптосхемы при наличии корреляции (связи) между блоками исходных данных значительно выше, чем без таковой. Алгоритмы сжатия (архивации) данных устраняют избыточность данных, то есть корреляцию между исходными данными. Дополнительно уменьшается объем зашифрованных данных

Проблемы практического шифрования 5. Запоминание ключа человеком Обеспечение секретности ключа: • пользователь запоминает ключ • хранение ключа в защищенном месте Ключ 128 бит = 16 байт = 32 шестнадцатеричные цифры Предел запоминаемости человека = 8÷ 12 случайных символов Человеку проще запомнить осмысленную фразу, слово, а не последовательность цифр Использовать метод, преобразующий осмысленную строку произвольной длины (пароль) в ключ заданной длины.

Проблемы практического шифрования 6. Создание хорошего ключа шифрования • Проблема подбора пароля пользователя • Некоторые из блочных криптоалгоритмов (в частности, DES) имеют потенциально слабые ключи, используя которые получающийся шифротекст недостаточно криптостоек Решения: • Поручить генерацию ключей ЭВМ • Проверять пароли пользователя на защищенность

Проблемы практического шифрования 7. Зашифрованное сообщение может содержать непечатные символы • Часто зашифрованные должны быть переданы получателю по сети (переписка, платежи электронной коммерции, электронная почта, …) • Отдельный байт шифротекста может принимать все 256 возможных значений • Многие протоколы передачи данных корректно работают только с печатными символами (цифры, латинский алфавит, знаки препинания) Как преобразовать шифротекст в последовательность печатных символов?

Криптосистема – комплексная модель, способная шифровать и расшифровывать данные произвольного объема и подтверждать время отправки сообщения, обладающая механизмом преобразования паролей и ключей, системой транспортного кодирования (см. далее).

1. Получение одинакового шифра для одинаковых исходных данных Идея: Шифрование очередного блока сделать зависящим от соседнего блока (цепочка зависимостей) или от его позиции n n Методы создания цепочек: Электронная кодовая книга (Electronic Code Book, ECB) Сцепление блоков шифра (Cipher Block Chaining, CBC) Обратная связь по шифроблоку (Cipher Feed. Back, CFB) Обратная связь по выходу (Output Feed. Back, OFB)

Метод «Электронной кодовой книги» (ECB) Исходные данные шифруются поблочно: каждый блок – независимо от других Метод применялся в простых портативных устройствах шифрования – шифрокнижках Недостаток: для одинаковых блоков исходных данных получаются одинаковые шифроблоки Используется для коротких данных без одинаковых блоков (ключи шифрования, пароли, …)

Метод «Сцепления блоков шифра» (CBC) На очередной блок накладывается (через XOR) шифр предыдущего блока, после чего результат шифруется Для хранения шифра предыдущего блока используется блок «памяти» (Initial Value, IV) Шифрование отдельного блока зависит от всех предыдущих блоков

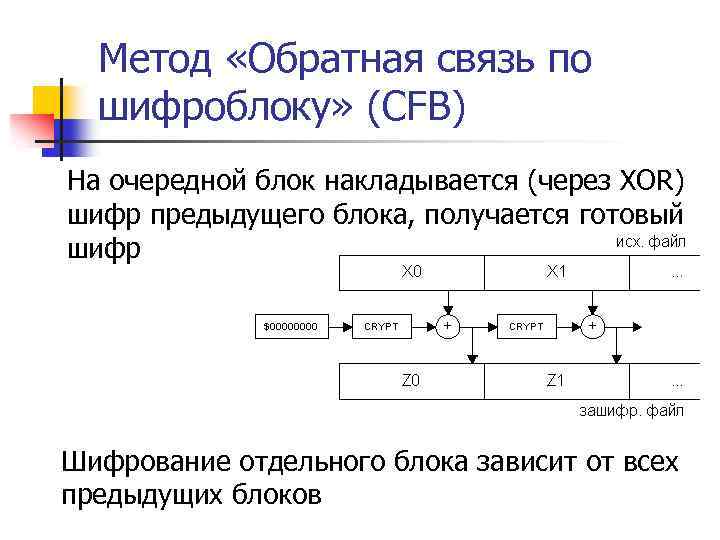Метод «Обратная связь по шифроблоку» (CFB) На очередной блок накладывается (через XOR) шифр предыдущего блока, получается готовый шифр Шифрование отдельного блока зависит от всех предыдущих блоков

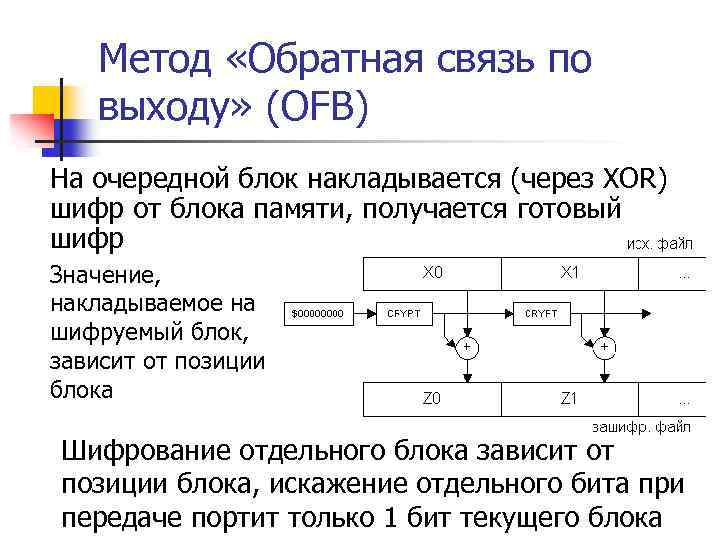Метод «Обратная связь по выходу» (ОFB) На очередной блок накладывается (через XOR) шифр от блока памяти, получается готовый шифр Значение, накладываемое на шифруемый блок, зависит от позиции блока Шифрование отдельного блока зависит от позиции блока, искажение отдельного бита при передаче портит только 1 бит текущего блока

2. Длина шифруемых данных может быть не кратной длине блока Для последнего блока следует выполнить расширение – дополнить до размера целого блока n n n Значения дополняемых байт: Значение каждого байта равно количеству дополняемых байт д д д 2 2 Значения определяются генератором псевдослучайных чисел д д д 9 44 Значение равно хеш-сумме передаваемого текста д д д х х

3. Генерация случайной последовательности n n Программные процедуры генерируют псевдослучайные величины Источники настоящих случайных величин – внешние объекты (человек, аппаратура)

Генерация с участием человека n Набор бессмысленных букв на клавиатуре человеком 1. Над приведенными символами х х х х (байтами) производят действия, повышающие случайность Результат + 2. Фиксируют интервалы времени 0 -8 бит 28 -14 бит 4 -10 бит (32 бита) между нажатиями клавиш Результат n Использование манипулятора мыши 1. Используются величины смещения указателя мыши 2. Используются псевдослучайные последовательности в момент нажатия кнопок (перемещения) мыши

Аппаратные генераторы случайных величин n n n В криптосистемах военного назначения используются генераторы чисел, основанные на физических процессах Они представляют собой платы или внешние устройства, подключаемые к ЭВМ Основные источники случайных величин – высокоточное измерение тепловых флуктуаций, запись радиоэфира на частоте, свободной от радиовещания

4. Сжатие исходных данных Современные форматы данных удобны для быстрого прочтения и работы. При этом они имеют больший объем, чем требуется для хранения данных Основные методы архивации Сжатие байт, не связанных между собой (Алгоритм Хаффмена) Сжатие последовательности байт, неоднократно встречаемых в тексте (Алгоритм Лемпела-Зива)

5. Запоминание ключа человеком Хеширование паролей – метод, преобразующий осмысленную строку произвольной длины (пароль) в ключ заданной длины Свойства хеш-функций: 1. Хеш-функция имеет бесконечную область определения (любые символы пароля); 2. Хеш-функция имеет конечную область значений (0. . 2 N -1, N – длина ключа в битах); 3. Она необратима (по выходу нельзя определить вход); 4. Изменение на входе одного бита меняет около половины всех бит выхода (результата хеш-функции).

Получение хеш-значений Требования 3 (необратимость) и 4 (сильная зависимость выхода от входа) предъявляются и к блочным криптоалгоритмам. Можно использовать блочный шифр для получения ключа, шифруя строку-пароль

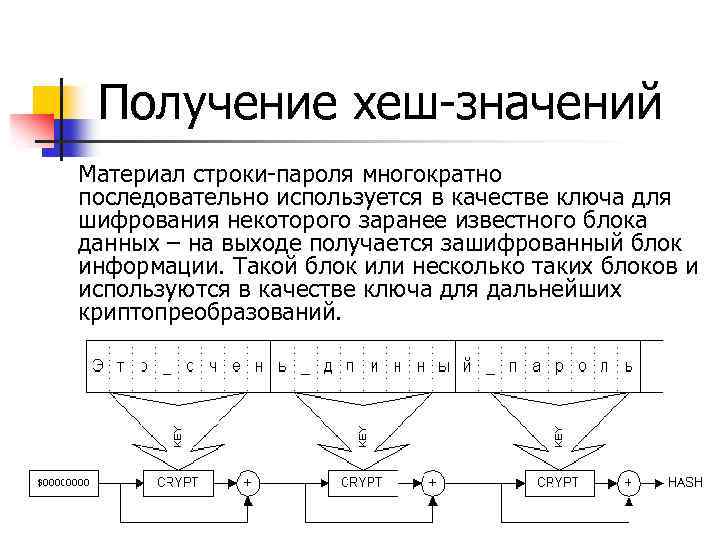Получение хеш-значений Материал строки-пароля многократно последовательно используется в качестве ключа для шифрования некоторого заранее известного блока данных – на выходе получается зашифрованный блок информации. Такой блок или несколько таких блоков и используются в качестве ключа для дальнейших криптопреобразований.

6. Создание хорошего ключа шифрования Создание ключа (пароля) пользователем n Поручить генерацию ключей ЭВМ n Проверять пароли пользователя на защищенность Наличие «слабых» ключей у криптоалгоритма n Хранить «слабые» ключи и проверять их при очередной генерации ключа

7. Зашифрованное сообщение содержит непечатные символы Отдельный байт шифротекста может принимать все 256 возможных значений, а для передачи допустимы около 68 символов 1) Запись каждого байта двумя 16 -ричными цифрами: байт со значением 252 = символы «FC» байт со значением 13 = символы « 0 D» Недостаток – слишком избыточно, в каждом байте только 4 бита информации

7. Зашифрованное сообщение содержит непечатные символы Отдельный байт шифротекста может принимать все 256 возможных значений, а для передачи допустимы около 68 символов 2) Кодировать 3 байта данных 4 -мя байтами печатных символов. Для кодирования 64 символов достаточно 6 битов. 3 байта исходных * 8 бит = 4 байта печатных * 6 бит Система Base 64 – стандарт на уровне протоколов сети Интернет

Система Base 64 Алфавит Base 64: • ПРОПИСНЫЕ «A» – «Z» (26 символов с кодами 0 – 25) • строчные «a» – «z» (26 символов с кодами 26 – 51) • цифры « 0» – « 9» (10 символов с кодами 52 – 61) • «+» , «/» (2 символа с кодами 62, 63) • «=» – символ-заполнитель Если в «хвосте» потока данных осталось менее 24 бит, то справа добавляются нулевые биты до образования целого числа 6 -битных групп. Если «хвост» входного потока имеет длину 8 или 16 бит, то в конце выходного кода добавляется два или один символ «=» соответственно.

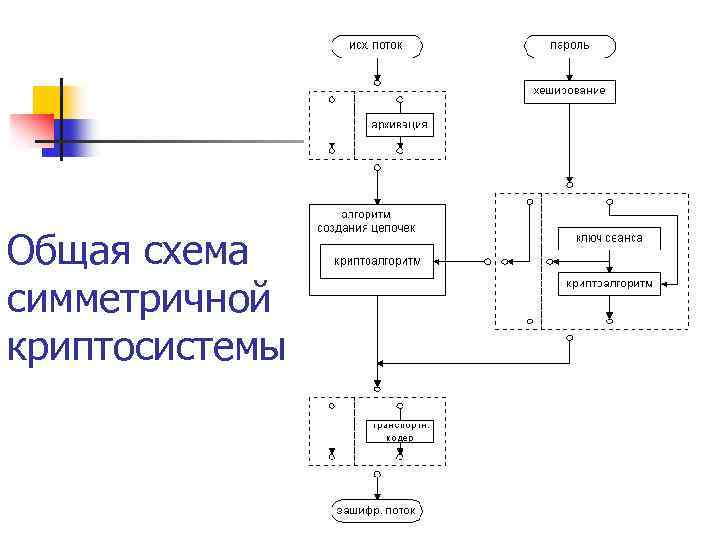Общая схема симметричной криптосистемы

Асимметричные криптоалгоритмы

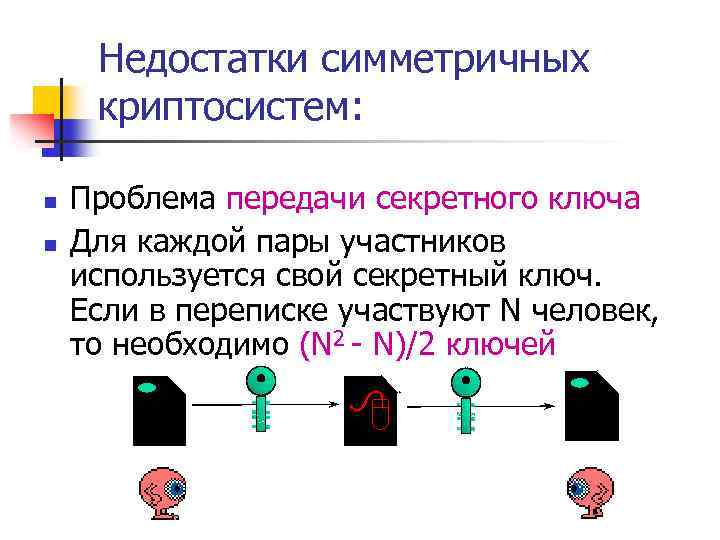Недостатки симметричных криптосистем: n n Проблема передачи секретного ключа Для каждой пары участников используется свой секретный ключ. Если в переписке участвуют N человек, то необходимо (N 2 - N)/2 ключей 8

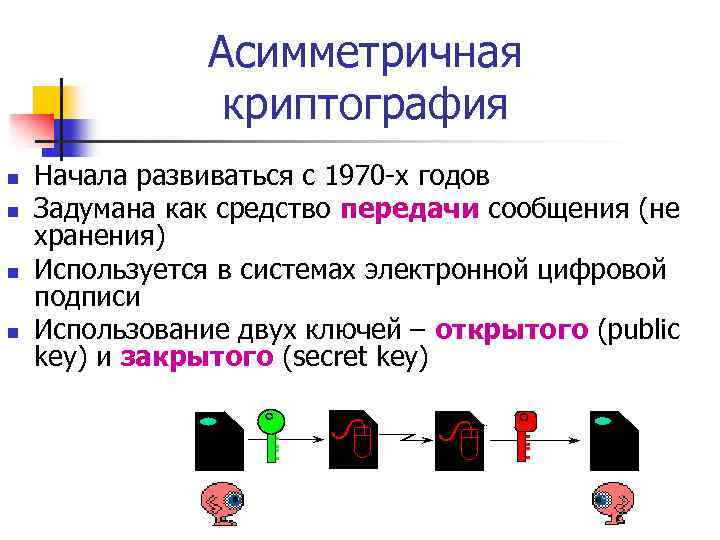Асимметричная криптография n n Начала развиваться с 1970 -х годов Задумана как средство передачи сообщения (не хранения) Используется в системах электронной цифровой подписи Использование двух ключей – открытого (public key) и закрытого (secret key) 8 8

Условия асимметричного преобразования Обозначения: n n n P – исходное сообщение Ek – процедура шифрования ключом k Dk – процедура расшифрования ключом k n n pk – открытый ключ sk – закрытый ключ Условия асимметричного преобразования: n n Dsk (Epk) = P Шифрование производится открытым ключом, расшифрование – закрытым Зная открытый ключ, нельзя определить закрытый ключ Функции D и E должны быть просты в реализации Dpk (Esk) = P Возможно использовать секретный ключ для шифрования, а открытый – для расшифрования (необязательное условие)

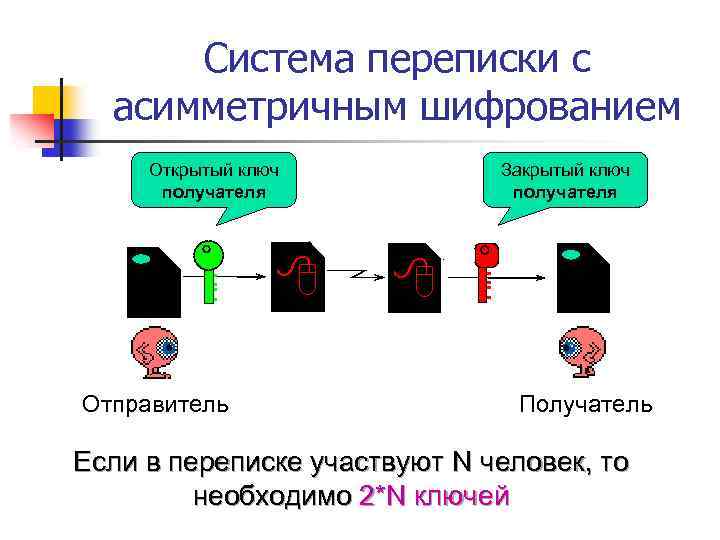Система переписки с асимметричным шифрованием Открытый ключ получателя 8 Отправитель Закрытый ключ получателя 8 Получатель Если в переписке участвуют N человек, то необходимо 2*N ключей

Современные асимметричные криптоалгоритмы: n n n n RSA Эль-Гамаля Диффи-Хеллмана Рабина Меркла-Хеллмана Месси-Омуры на основе эллиптических кривых

Алгоритм RSA стоит у истоков асимметричной криптографии. Он был предложен тремя исследователямиматематиками: Рональдом Ривестом (R. Rivest) , Ади Шамиром (A. Shamir) и Леонардом Адльманом (L. Adleman) в 1977 -78 годах.

Алгоритм RSA Создание пары ключей: 1. Выбираются два больших простых числа p и q. Простыми называются целые числа, которые делятся без остатка только на самих себя и на 1. Эти числа должны содержать больше 200 знаков. 2. Вычисляется открытая компонента ключа n: n = p · q 3. Вычисляется функция Эйлера: Функция Эйлера показывает количество целых положительных чисел от 1 до n, которые взаимно просты с n. Взаимно простыми являются такие числа, которые не имеют ни одного общего делителя, кроме 1. 4. Выбирается простое число e (e < n), которое является взаимно простым со значением f(p, q).

Алгоритм RSA Создание пары ключей (продолжение): 5. Подбирается целое число d для выполнения условия: 6. Пара чисел (e, n) принимается в качестве открытого ключа 7. Пара чисел (d, n) принимается в качестве закрытого ключа

Алгоритм RSA Процесс шифрования и расшифрования: 8. Исходная информация, независимо от ее физической природы, представляется в числовом виде. Последовательность бит разделяется на блоки длиной L бит, где L – наибольшее целое число, удовлетворяющее условию: Каждый блок рассматривается как целое положительное число X(i), принадлежащее интервалу [0, n - 1]. Таким образом, исходная информация представляется последовательностью чисел X(i), i = 1, I. Значение I определяется длиной шифруемой последовательности. 9. Зашифрованная информация получается в виде последовательности чисел Z(i), вычисляемых по формуле: 10. Для дешифрования информации используется следующая зависимость:

Алгоритм RSA Пример: Для простоты вычислений использованы минимально возможные числа 1. Выбирается p = 3 и q = 11. 2. Вычисляется n = p · q = 3 · 11 = 33. 3. Определяется функция Эйлера: f (p, q) = (p - 1) (q - 1) = (3 - 1) (11 - - 1) = 20. 4. В качестве e выберем любое число, которое является взаимно простым со значением f (p, q) = 20, например, e = 7. 5. Выбирается такое число d, которое удовлетворяло бы соотношению mod(e · d, f (p, q)) = mod(7 · d, 20) = 1. Пусть d = 3. 6. Пара чисел (e, n) принимается в качестве открытого ключа: (7, 33). 7. Пара чисел (d, n) принимается в качестве закрытого ключа: (3, 33).

Алгоритм RSA Пример (продолжение): Пусть требуется зашифровать сообщение «ГБВ» . 8. Исходное сообщение представляется как последовательность целых чисел в диапазоне 0… 32. Пусть буква «Б» соответствует числу 1, буква «В» – числу 2, а буква «Г» – числу 3. Тогда сообщение можно представить в виде последовательности чисел « 3, 1, 2» . 9. Зашифруем сообщение, используя открытый ключ (7, 33): Z(1) = mod(37, 33) = mod(2187, 33) = 9 Z(2) = mod(17, 33) = mod(1, 33) = 1 Z(3) = mod(27, 33) = mod(128, 33) = 29 В результате шифрования получаем шифротекст: « 9, 1, 29» или «ЙБЭ» .

Алгоритм RSA Пример (продолжение): Дешифруем полученный шифротекст. 10. Дешифрование сообщения Z(i) = « 9, 1, 29» , осуществляется с помощью закрытого ключа (3, 33): X(1) = mod(93, 33) = mod(729, 33) = 3 X(2) = mod(13, 33) = mod(1, 33) = 1 X(3) = mod(293, 33) = mod(24389, 33) = 2 Таким образом, в результате дешифрования последовательности Z(i) получено исходное сообщение «ГБВ» .

Алгоритм RSA Криптостойкость алгоритма RSA основывается на предположении, что исключительно трудно определить секретный ключ по известному, поскольку для этого необходимо решить задачу о существовании делителей целого числа. Данная задача не допускает в настоящее время эффективного решения. Для чисел, состоящих из 200 цифр, традиционные методы требуют выполнения огромного числа операций (около 1023).

Алгоритм Эль-Гамаля n n Разработан в 1985 г. Создание пары ключей: Выбрать большое простое число p Выбрать 2 случайных числа: g

Алгоритм Эль-Гамаля Шифрование: n n n Исходное сообщение разбить на блоки по k = [ log 2(p) ] бит Каждый блок рассматривать как число Pi Выбрать случайное число k, такое, что наибольший общий делитель (k, p-1) = 1 Вычислить шифротекст: a = mod(gk, p), Ci = mod(yk·Pi, p) Расшифрование: Вычислить Pi = mod(Ci / ax, p)

Алгоритм Диффи-Хеллмана n n Метод ключевого обмена Диффи. Хеллмана разработан в 1976 г. Предназначен для передачи секретного ключа симметричного шифрования через канал, защищенный от модификации

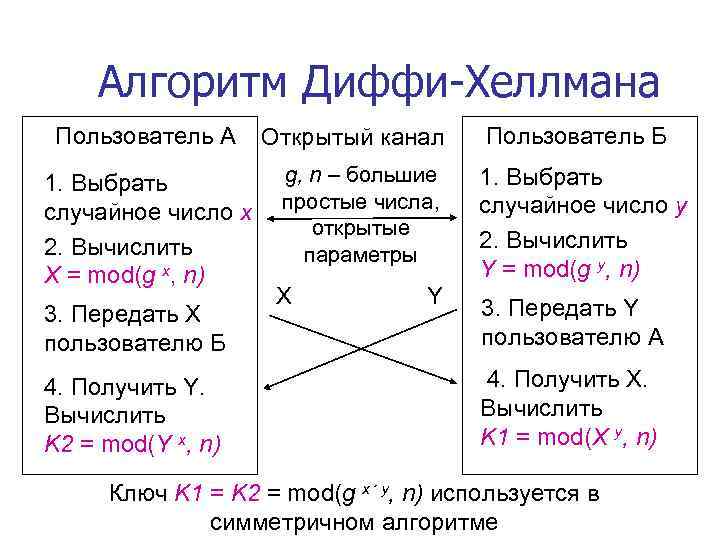Алгоритм Диффи-Хеллмана Пользователь А 1. Выбрать случайное число x 2. Вычислить Х = mod(g x, n) 3. Передать X пользователю Б 4. Получить Y. Вычислить K 2 = mod(Y x, n) Открытый канал g, n – большие простые числа, открытые параметры X Y Пользователь Б 1. Выбрать случайное число y 2. Вычислить Y = mod(g y, n) 3. Передать Y пользователю А 4. Получить X. Вычислить K 1 = mod(X y, n) Ключ K 1 = K 2 = mod(g x· y, n) используется в симметричном алгоритме

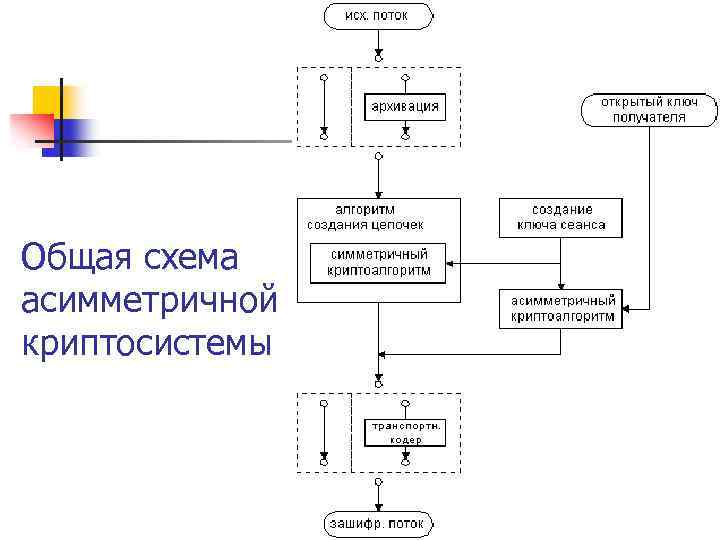Общая схема асимметричной криптосистемы

Электронная цифровая подпись (ЭЦП)

Определение ЭЦП – набор методов, которые позволяют перенести свойства рукописной подписи под документом в область электронного документооборота ЭЦП представляет собой небольшой блок данных, передаваемый вместе (реже – отдельно) с подписанным документом

Проблемы, решаемые с помощью ЭЦП: n n n Подготовка документа от имени другого пользователя ( «маскарад» ) Отказ автора документа от факта его подготовки (ренегатство) Изменение получателем документа его содержания (подмена) Изменение содержания документа третьим лицом (активный перехват) Повторная передача ранее переданного документа (повтор)

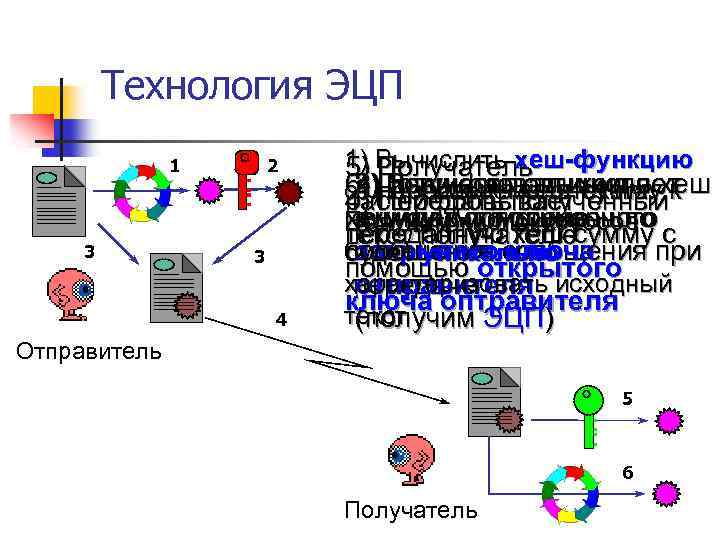Технология ЭЦП 2 1 3 3 4 1) Вычислить хеш-функцию 5) Получатель 6) передаваемого текста. хеш 7) Если есть хеш-сумму к 2) Зашифровать хеш-в 3)Передать полученный Добавить отличия от Получатель вычисляет расшифровывает 4) хеш-сумму полученного -суммахчисло, которое сумму с тотексту Получим , помощью открытому произошло с переданную хеш-сумму текст получателю сообщения при изменение ключа закрытого будет уникально помощью открытого характеризовать исходный передаче отправителя ключа оптравителя текст (получим ЭЦП) Отправитель 5 6 Получатель

Сведения, включаемые в документ при простановке ЭЦП: n n Дата и время простановки подписи Срок окончания действия секретного ключа данной подписи Реквизиты (ФИО подписывающего, должность, название организации) Идентификатор секретного ключа (для выбора соответствующего открытого ключа)

Хеширование информации От англ. hash – мелко нарезать. Хеш-функция – это односторонняя функция шифрования. Основное назначение подобных функций – получение из сообщения произвольного размера его дайджеста – значения фиксированного размера. При изменении одного бита на входе хеш-функции существенно изменяется выход.

Хеш-функция должна удовлетворять условиям: 1. Хеш-функция должна быть чувствительна к всевозможным изменениям в тексте, таким как вставки, выбросы, перестановки и т. п. 2. Хеш-функция должна обладать свойством необратимости, т. е. задача подбора документа, который обладал бы требуемым значением хеш-функции должна быть вычислительно неразрешима. 3. Вероятность того, что значения хеш-функций двух различных документов совпадут, должна быть ничтожно мала. Если хеш-функция будет удовлетворять перечисленным условиям, то формируемое ею значение будет уникально идентифицировать сообщение, и всякая попытка изменения сообщения при передаче будет обнаружена путем выполнения хеширования на принимающей стороне и сравнения с дайджестом, полученным на передающей стороне.

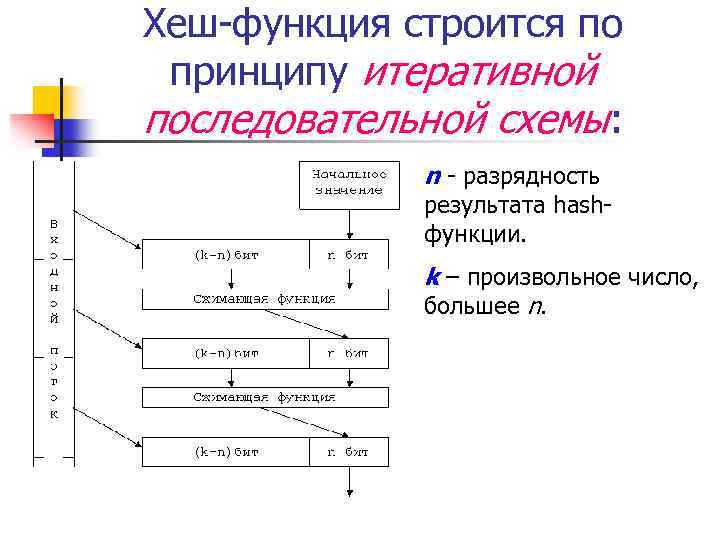Хеш-функция строится по принципу итеративной последовательной схемы: n - разрядность результата hashфункции. k – произвольное число, большее n.

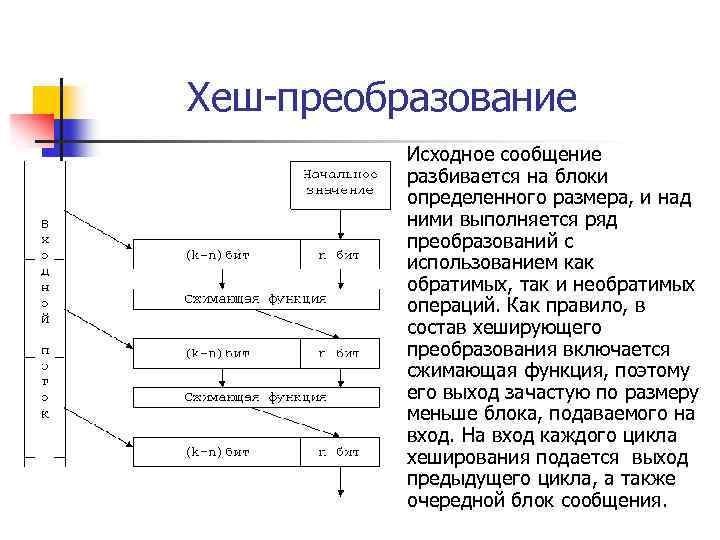Хеш-преобразование Исходное сообщение разбивается на блоки определенного размера, и над ними выполняется ряд преобразований с использованием как обратимых, так и необратимых операций. Как правило, в состав хеширующего преобразования включается сжимающая функция, поэтому его выход зачастую по размеру меньше блока, подаваемого на вход. На вход каждого цикла хеширования подается выход предыдущего цикла, а также очередной блок сообщения.

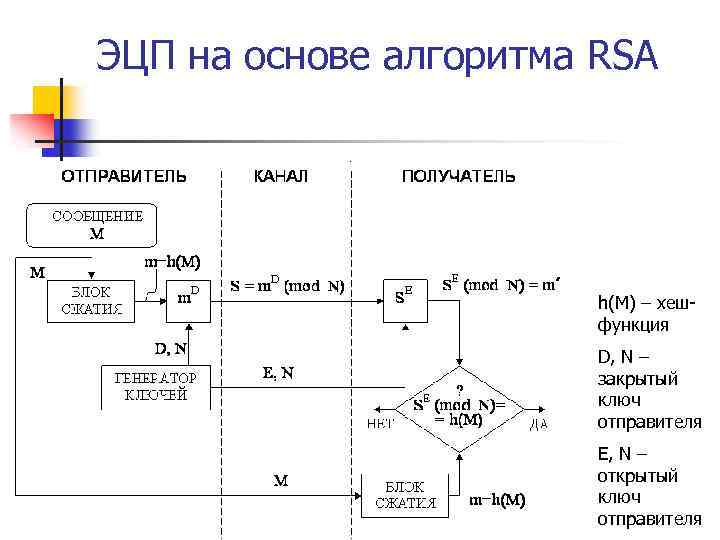ЭЦП на основе алгоритма RSA D D E h(M) – хешфункция D, N – закрытый ключ отправителя E, N – открытый ключ отправителя

Системы ЭЦП: n n RSA (на основе криптосистемы RSA) DSS (Digital Signature Standard, стандарт США на основе криптосистемы Эль-Гамаля) ГОСТ 34. 10 -94 (бывший российский стандарт ЭЦП на основе криптосистемы Эль-Гамаля ) ГОСТ 34. 10 -2001 (действующий в настоящее время российский стандарт ЭЦП, использующий криптосистему на основе эллиптических кривых)

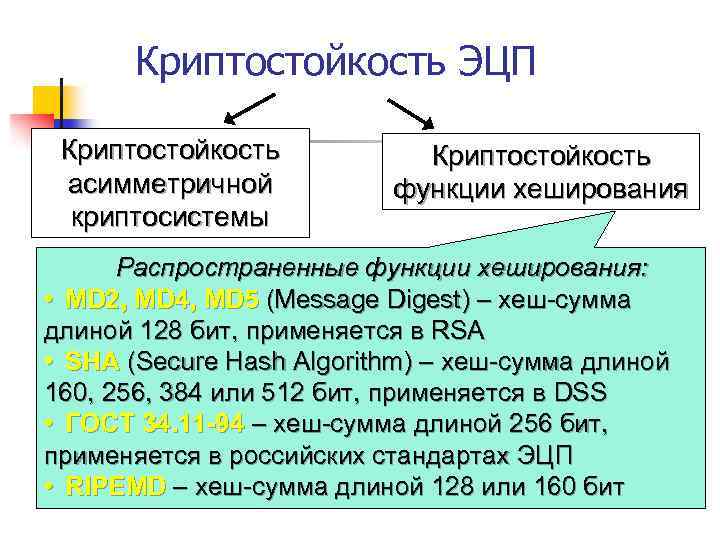Криптостойкость ЭЦП Криптостойкость асимметричной криптосистемы Криптостойкость функции хеширования Распространенные функции хеширования: • MD 2, MD 4, MD 5 (Message Digest) – хеш-сумма длиной 128 бит, применяется в RSA • SHA (Secure Hash Algorithm) – хеш-сумма длиной 160, 256, 384 или 512 бит, применяется в DSS • ГОСТ 34. 11 -94 – хеш-сумма длиной 256 бит, применяется в российских стандартах ЭЦП • RIPEMD – хеш-сумма длиной 128 или 160 бит

Алгоритм хеширования SHA (Secure Hash Algorithm) Версия SHA-1 данного алгоритма формирует 160 -битный дайджест сообщения. Хеш-функции с существенно большей длиной хеш-кода: SHA-256, SHA-384 и SHA 512 (в названиях указывается длина создаваемого этими функциями хеш-кода). Эти алгоритмы отличаются не только длиной создаваемого хеш-кода, но и длиной обрабатываемого блока, длиной слова и используемыми внутренними функциями. В данных алгоритмах размер блока сообщения равен m бит. Для SHA-256 m = 512, для SHA-384 и SHA-512 m = 1024. Каждый алгоритм оперирует с w -битными словами. Для SHA-256 w = 32, для SHA-384 и SHA-512 w = 64.

Алгоритм хеширования SHA (Secure Hash Algorithm) Алгоритмы используют следующие битовые операции: n n n n ║ – Конкатенация (Операция склеивания. Например, конкатенация слов «микро» и «мир» даст слово «микромир» ) + – Сложение and – Побитовое «И» or – Побитовое «ИЛИ» xor – Исключающее «ИЛИ» shr – Логический сдвиг вправо rotr – Циклический сдвиг вправо

Алгоритм SHA-256 Пояснения: 1) Все переменные имеют размер 32 бита и при вычислениях суммируются по модулю 232. Сложение по модулю 232 это обычное сложение с игнорированием переполнения (т. е. на результат сложения отводится 32 бита, неуместившиеся старшие биты отбрасываются). Примеры: 12 + 12 = 102 (т. е. 110 + 110 = 210). Результат сложения по модулю 21 (что то же самое – остаток от деления 102 = 210 на 21, по другому – исключающее ИЛИ, XOR): 2 mod 21 = 0. n 10102 + 1112 = 100012 (т. е. 1010 + 710 = 1710). Результат сложения по модулю 24 (что то же самое – остаток от деления 100012 = 1710 на 24): 17 mod 24 = 1. 2) message – исходное двоичное сообщение. 3) m – преобразованное сообщение. 4) «: =» – знак присваивания. n

Алгоритм SHA-256 Начальные значения переменных h 0, h 1, h 2, h 3, h 4, h 5, h 6, h 7 – первые 32 бита дробных частей квадратных корней первых восьми простых чисел. Константы k[0. . 63] – первые 32 бита дробных частей кубических корней первых 64 -х простых чисел (от 2 до 311). Предварительная обработка: m : = message ║ [единичный бит] m : = m ║ [n нулевых бит], где n – наименьшее неотрицательное число, такое, что битовая длина итогового сообщения N и число 448 сравнимы по модулю 512: mod(N - 448, 512) = 0 m : = m ║ Длина(message), где Длина(message) – длина исходного сообщения в битах в виде 64 -битного числа. Предварительная обработка необходима для того чтобы сообщение m можно было разбить на целое число блоков размером 512 бит. Например, пусть Длина(message) = 1 бит, тогда m : = message ║ [единичный бит], Длина(m) = 2 бита m : = m ║ [n нулевых бит]. Определим n. Т. к. mod(N - 448, 512) = 0, то N – 448 = 512 и N = 960, т. е. n = 958 m : = m ║ Длина(message), Длина(m) = 960 + 64 = 1024 бита, т. е. 2 блока по 512 бит.

Алгоритм SHA-256 Основная обработка: Разбить сообщение на блоки по 512 бит для каждого блока разбить блок на 16 слов длиной 32 бита: w[0. . 15]; Сгенерировать дополнительные 48 слов: для i от 16 до 63 s 0 : = (w[i-15] rotr 7) xor (w[i-15] rotr 18) xor (w[i-15] shr 3); s 1 : = (w[i-2] rotr 17) xor (w[i-2] rotr 19) xor (w[i-2] shr 10); w[i] : = w[i-16] + s 0 + w[i-7] + s 1 конец для Инициализация вспомогательных переменных: a : = h 0; b : = h 1; c : = h 2; d : = h 3; e : = h 4; f : = h 5; g : = h 6; h : = h 7

Алгоритм SHA-256 Основная обработка (продолжение): для i от 0 до 63 Σ 0 : = (a rotr 2) xor (a rotr 13) xor (a rotr 22); Ma : = (a and b) xor (a and c) xor (b and c); t 2 : = Σ 0 + Ma; Σ 1 : = (e rotr 6) xor (e rotr 11) xor (e rotr 25); Ch : = (e and f) xor ((not e) and g); t 1 : = h + Σ 1 + Ch + k[i] + w[i]; h : = g; g : = f; f : = e; e : = d + t 1; d : = c; c : = b; b : = a; a : = t 1 + t 2 конец для Добавить полученные значения к ранее вычисленному результату: h 0 : = h 0 + a; h 1 : = h 1 + b; h 2 : = h 2 + c; h 3 : = h 3 + d; h 4 : = h 4 + e; h 5 : = h 5 + f; h 6 : = h 6 + g; h 7 : = h 7 + h конец для Получить итоговое значения хеш-кода: digest = hash = h 0 ║ h 1 ║ h 2 ║ h 3 ║ h 4 ║ h 5 ║ h 6 ║ h 7

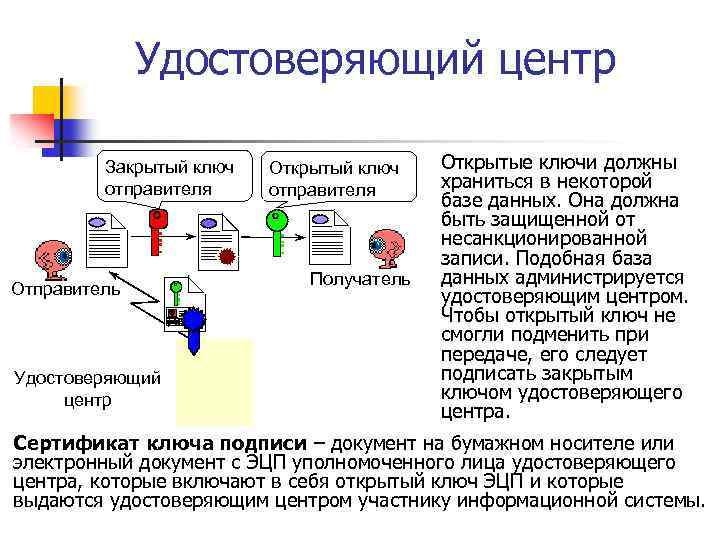Удостоверяющий центр Закрытый ключ отправителя Отправитель Удостоверяющий центр Открытый ключ отправителя Получатель Открытые ключи должны храниться в некоторой базе данных. Она должна быть защищенной от несанкционированной записи. Подобная база данных администрируется удостоверяющим центром. Чтобы открытый ключ не смогли подменить при передаче, его следует подписать закрытым ключом удостоверяющего центра. Сертификат ключа подписи – документ на бумажном носителе или электронный документ с ЭЦП уполномоченного лица удостоверяющего центра, которые включают в себя открытый ключ ЭЦП и которые выдаются удостоверяющим центром участнику информационной системы.

Сертификат ключа подписи содержит следующие сведения: § уникальный регистрационный номер, даты начала и окончания срока действия сертификата; § фамилию, имя и отчество владельца или его псевдоним (в случае использования псевдонима удостоверяющим центром вносится запись об этом в сертификат ключа подписи); § открытый ключ ЭЦП; § наименование средств ЭЦП, с которыми используется данный открытый ключ (средства ЭЦП – аппаратные и (или) программные средства, обеспечивающие реализацию хотя бы одной из следующих функций: создание ЭЦП, подтверждение подлинности ЭЦП, создание закрытых и открытых ключей ЭЦП); § наименование и место нахождения удостоверяющего центра, выдавшего сертификат.

Удостоверяющий центр выполняет следующие функции: § изготавливает и выдает сертификаты ключей подписей; § создает ключи ЭЦП по обращению участников информационной системы с гарантией сохранения в тайне закрытого ключа ЭЦП; § приостанавливает и возобновляет действие сертификатов ключей подписей, а также аннулирует их; § осуществляет по обращениям пользователей сертификатов ключей подписей подтверждение подлинности ЭЦП в электронном документе в отношении выданных им сертификатов ключей подписей. Существуют программы для создания ЭЦП и проверки подлинности файлов, например, Gnu. PT.

Криптографические протоколы Передача данных и ключей, проверка подлинности сообщения и авторства

Понятие протокола n n Протокол – это порядок действий, предпринимаемых двумя и более сторонами, предназначенный для решения определенной задачи Криптографический протокол – это протокол, использующий криптографию

Характеристики протокола n n Участники протокола должны знать протокол (последовательность и составляющие действия) Участники должны согласится следовать протоколу Протокол должен быть непротиворечивым и понятным Протокол должен быть полным (каждой возможной ситуации должно соответствовать действие)

Криптографический протокол n n Цель криптографического протокола – предотвратить или обнаружить вредительство или мошенничество Примеры: n n Обмен секретными данными Подтверждение подлинности участников Подтверждение подлинности сообщения Одновременная подпись контракта

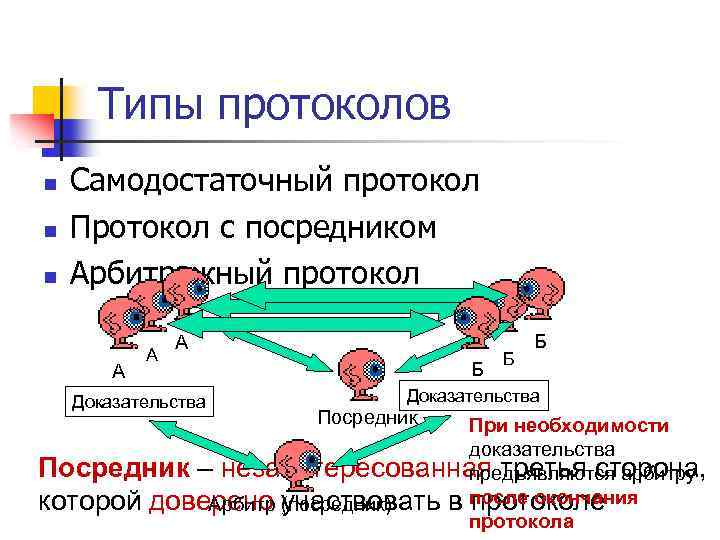Типы протоколов n n n Самодостаточный протокол Протокол с посредником Арбитражный протокол А А А Доказательства Б Б Б Доказательства Посредник При необходимости доказательства Посредник – незаинтересованная третья сторона, предъявляются арбитру которой доверено (посредник) протоколе Арбитр участвовать в после окончания протокола

Основные криптографические протоколы n n Передача данных Распределение ключей Проверка подлинности сообщения Проверка подлинности пользователя (аутентификация): см. тему № 2

Передача информации в симметричной криптографии Проблемы: 1) А и Б выбирают систему шифрования n Выбор и передача секретного 2) А и Б выбирают ключа 3) А шифрует открытый текст выбранным n При компрометации ключа алгоритмом и ключом, получая (кража, взлом) субъектом С он шифрованное сообщение может не только читать все 4) А посылает шифрованное сообщение Б шифрованные сообщения, но и 5) Б дешифрует шифротекст выбранным выдавать себя за А и Б алгоритмом и ключом, получая исходный n Большое количество ключей в текст сети из N субъектов: N (N-1)/2

Передача информации в асимметричной криптографии 1) А и Б выбирают криптосистему с открытыми ключами 2) Б посылает А свой открытый ключ Часто криптосистема согласовывается сразу для 3) А шифрует открытый текст и посылает многих пользователей, а все их его Б открытые ключи хранятся в 4) Б расшифровывает полученный общедоступной базе данных шифротекст своим закрытым ключом

Передача информации в асимметричной криптографии Проблемы: 1) А получает открытый ключ Б из базы n Достоверность открытого ключа, данных полученного из базы данных 2) А шифрует открытый текст и посылает n Медленная работа асимметричного его Б криптоалгоритма 3) Б расшифровывает полученный шифротекст своим закрытым ключом

Передача информации в смешанной криптосистеме 1) А получает открытый ключ Б из базы 2) 3) 4) 5) данных А создает случайный сеансовый ключ, Проблема: шифрует его открытым ключом Б n Достоверность открытого ключа, А посылает зашифрованный сеансовый полученного из базы данных ключ Б Б расшифровывает сеансовый ключ своим закрытым ключом А и Б шифруют свои сообщения с помощью одного сеансового ключа

Вскрытие «человек в середине» 1) А посылает запрос к базе данных для получения 2) 3) 4) 5) открытого ключа Б. М перехватывает это сообщение и посылает А свой открытый ключ А создает случайный сеансовый ключ, шифрует его Для предотвращения вскрытия открытым ключом М и посылает шифротекст Б «человек в середине» можно М перехватывает шифротекст от А, расшифровывает его, снова зашифровывает открытым ключом Б и использовать протокол посылает его Б «держась за руки» Б расшифровывает шифротекст своим закрытым ключом, получая сеансовый ключ А и Б шифруют свои сообщения с помощью одного сеансового ключа. При этом М перехватывает все шифротексты и зашифровывает их ключами А или Б

Протокол «держась за руки» 1) А получает открытый ключ Б из базы данных 2) Б получает открытый ключ А из базы данных 3) А шифрует свое сообщение открытым ключом Б. 4) 5) 6) 7) 8) Половину шифротекста отправляет Б Б шифрует свое сообщение открытым ключом А. М, перехватив половину шифротекста Половину шифротекста отправляет А на этапе 3, не сможет ее А отправляет Б вторую половину шифротекста дешифровать своим секретным Б собирает обе части шифротекста и ключом и зашифровать открытым расшифровывает их секретным ключом Б Б отправляет вторую половину своего шифротекста А собирает обе части шифротекста и расшифровывает их секретным ключом

Распределение ключей в асимметричной криптосистеме Распределение и проверку ключей в асимметричной криптосистеме можно провести с помощью: 1. Центра распределения ключей (Key Distribution Center, KDC) или Удостоверяющего центра (Certification Authority, CA) (см. выше) 2. Сетевой модели доверительных отношений

Компрометация сертификата открытого ключа n n При компрометации сертификата должна быть выполнена процедура отзыва ключа В KDC предусмотрена поддержка списка отозванных сертификатов (Certificate Revocation List, CRL)

Сетевая модель доверительных отношений n n Некоторые субъекты распределенной компьютерной системы обмениваются открытыми ключами напрямую Сертификаты открытых ключей других субъектов заверяются либо непосредственно секретным ключом известного субъекта, либо по иерархической лестнице (цепочке сертификатов) вплоть до достижения такого субъекта

Распределение ключей в симметричной криптосистеме Распределение и проверка ключей в симметричной криптосистеме осуществляется с помощью Центра распределения ключей Недостаток: Центр может читать все передаваемые сообщения

Анонимное распределение сеансовых ключей n n n skc и pkc – секретный и открытый ключи KDC ska и pka – секретный и открытый ключи А А выбирает ska и pka, сохраняя их в секрете KDC генерирует последовательность сеансовых ключей k 1, k 2, … KDC вычисляет Epkc(k 1), Epkc(k 2), …и пересылает их А А случайным образом выбирает Epkc(ki), вычисляет Epka(Epkc(ki)) и передает его в KDC вычисляет Epka(ki) = Dskc(Epka(Epkc(ki))) и пересылает его А А вычисляет ki = Dska(Epka(ki))

Проверка подлинности сообщения осуществляется посредством электронной цифровой подписи (см. выше)

Подпись документа в симметричной криптографии Т – посредник, которому все доверяют. Он выдает секретный ключ КА для А и ключ КБ для Проблемы: Б n n n А шифрует сообщение Б ключом КА и n Т участвует в каждом случае посылает его Т удостоверения подписи Т, зная ключ КА, расшифровывает n Т должен хранить удостоверенные сообщение копии в базе данных (для последующих Т добавляет к сообщению утверждение, возможных подтверждений) что это сообщение от А и шифрует новое сообщение ключом КБ n Т и его база данных должны быть Т посылает новое сообщение Б абсолютно безопасны Б расшифровывает сообщение ключом КБ

Подпись документа в асимметричной криптографии 1) А шифрует сообщение своим закрытым ключом, таким образом Проблема: подписывая его n Если документ большой, то процесс 2) А посылает подписанное сообщение Б подписания будет идти медленно 3) Б расшифровывает сообщение, Решение: используя открытый ключ А, таким n Подписывать не документ, а образом проверяя подпись значение хеш-функции этого документа

Литература 1. Информационная безопасность: учеб. пособие для студентов учреждений сред. проф. образования / В. П. Мельников, С. А. Клейменов, А. М. Петраков; под ред. С. А. Клейменова. – М. : Издательский центр «Академия» , 2010. – 336 с. (имеется в библиотеке КТИ) 2. Информационная безопасность: учеб. пособие для студентов учреждений сред. проф. образования / Т. Л. Партыка, И. И. Попов. – М. : ФОРУМ, 2008. – 432 с. (имеется в библиотеке КТИ) 3. Методы и средства защиты информации в компьютерных системах: учеб. пособие для студ. высш. учеб. заведений / П. Б. Хорев. – М. : Издательский центр «Академия» , 2008. – 256 с.