4. Красно-черные деревья 4. 1. Красно-черные деревья Бинарное

4. Красно-черные деревья

4.1. Красно-черные деревья Бинарное дерево поиска с дополнительным полем цвета в узле struct Node { int color; int key; struct Node *left, *right; struct Node *parent; }; 2

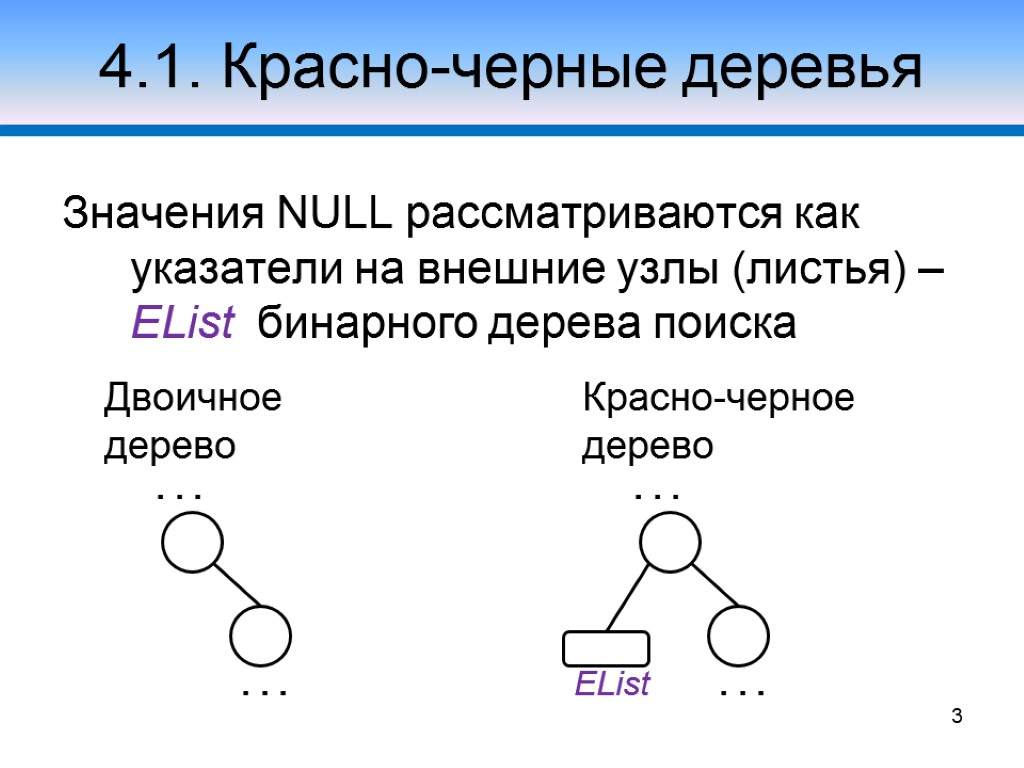
4.1. Красно-черные деревья Значения NULL рассматриваются как указатели на внешние узлы (листья) – EList бинарного дерева поиска 3 Двоичное дерево . . . . . . Красно-черное дерево . . . . . . EList

4.1. Красно-черные деревья Красно-черное бинарное дерево поиска удовлетворяет следующим свойствам: Каждый узел является красным или черным Корень дерева является черным Каждый лист дерева (EList) является черным Если узел – красный, то оба его дочерних узла – черные 4

4.1. Красно-черные деревья Для каждого узла все пути от него до листьев, являющихся потомками данного узла, содержат одно и то же количество черных узлов 5

4.1. Красно-черные деревья Количество черных узлов на пути от узла x (не считая сам узел) к листу называется черной высотой листа – bh(x) Черной высотой дерева является черная высота его корня 6

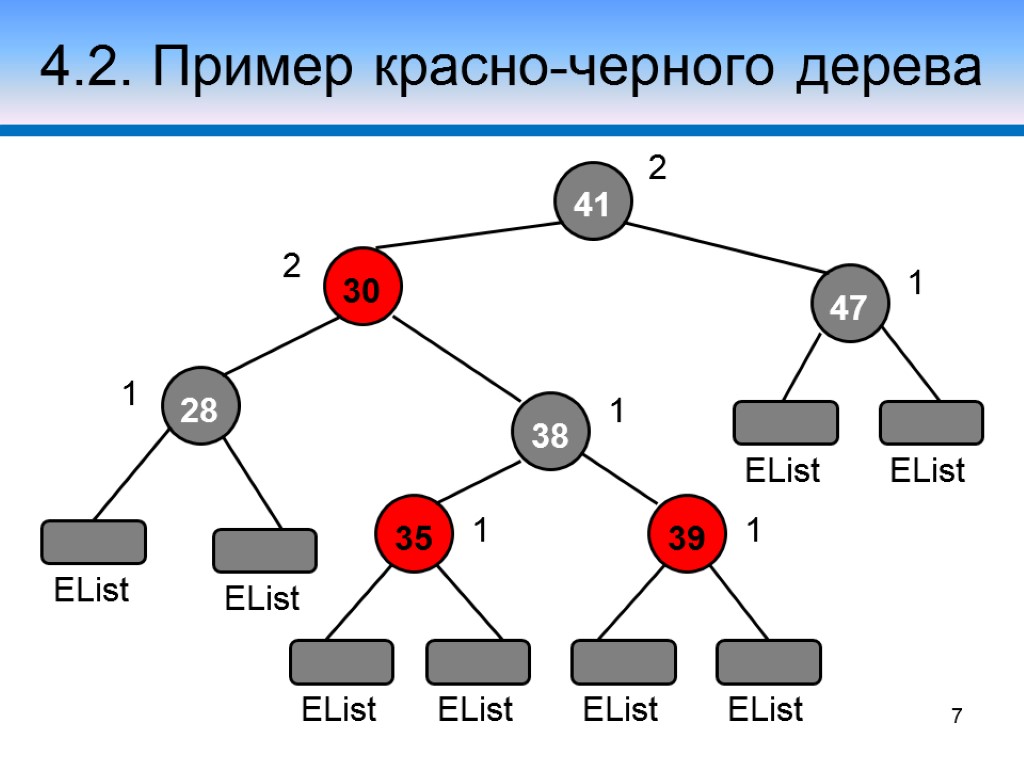
4.2. Пример красно-черного дерева 41 30 47 28 38 35 39 2 1 2 1 1 1 1 7 EList EList EList EList EList EList EList EList

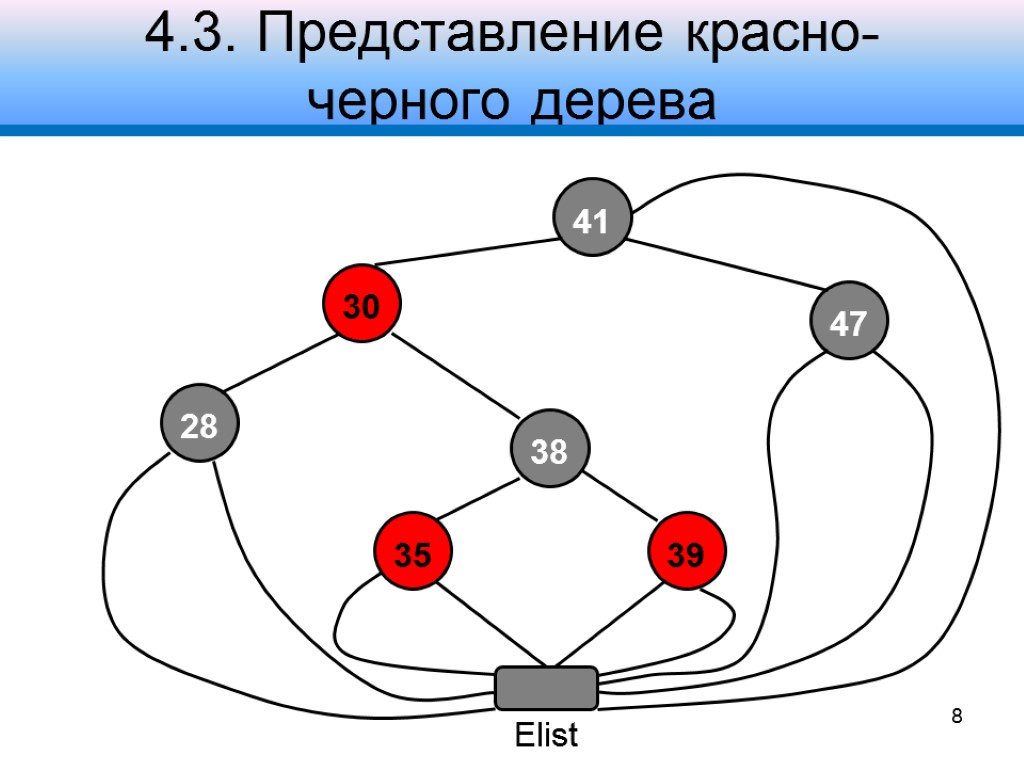
4.3. Представление красно- черного дерева 41 30 47 28 38 Elist 35 39 8

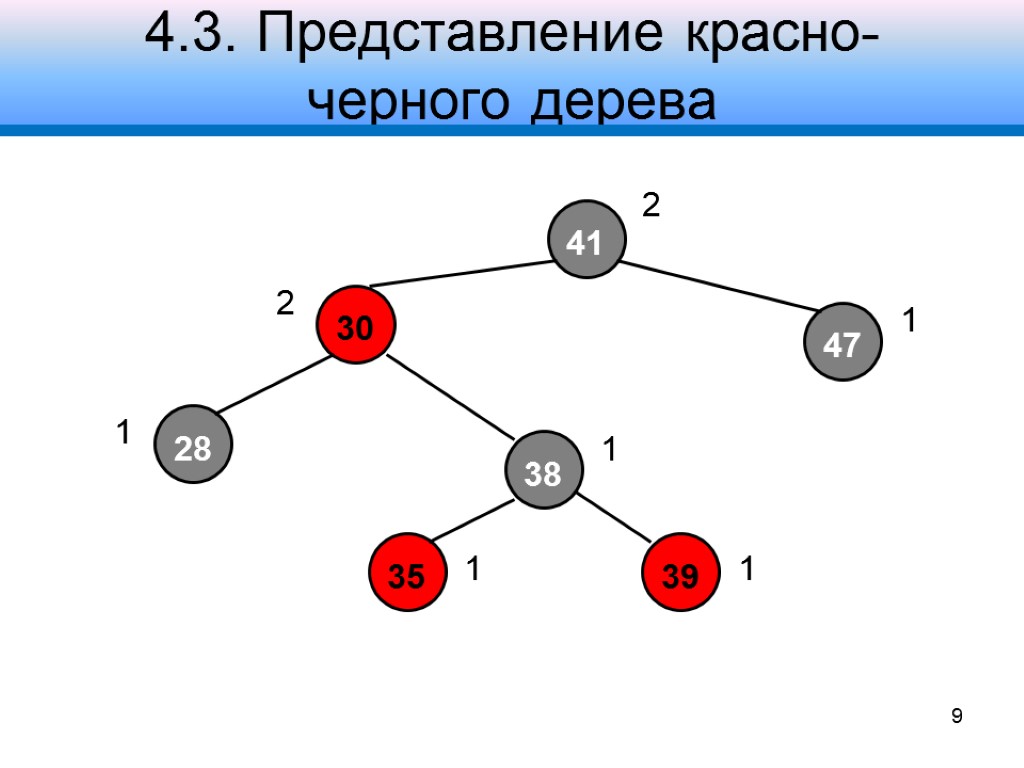
4.3. Представление красно- черного дерева 9

4.4. Характеристики красно- черного дерева Лемма Красно-черное дерево с n внутренними узлами имеет высоту h не более чем 2 lg (n + 1) Доказательство Следствие: Время поиска – O(lg(n)) 10

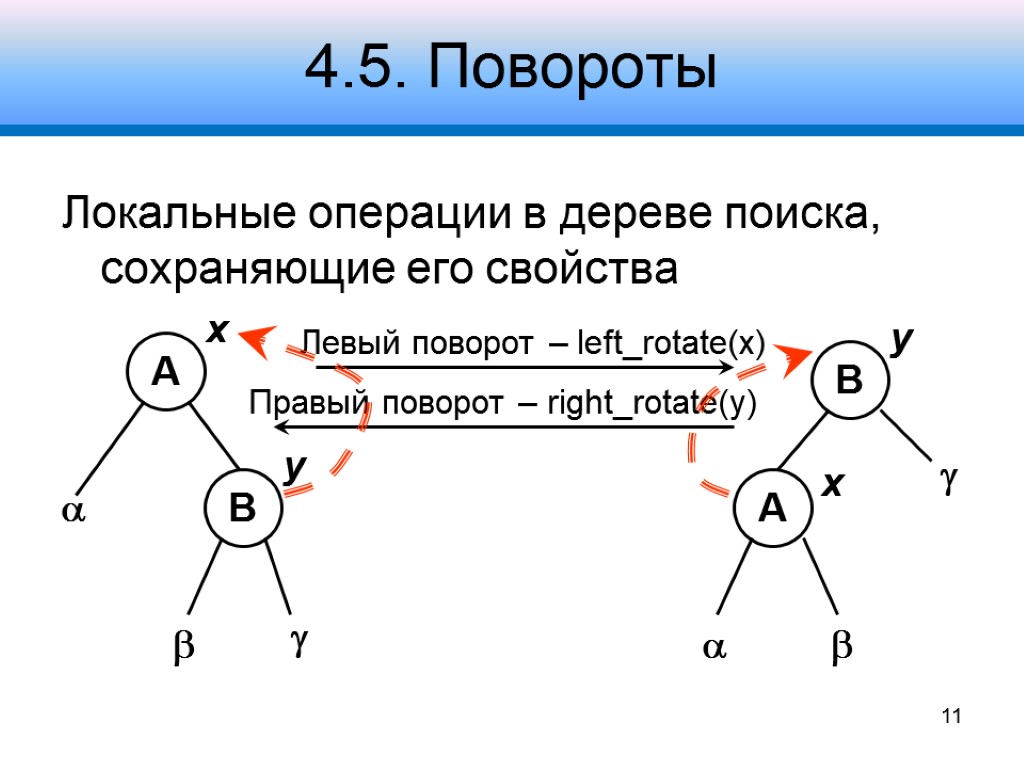
4.5. Повороты Локальные операции в дереве поиска, сохраняющие его свойства 11

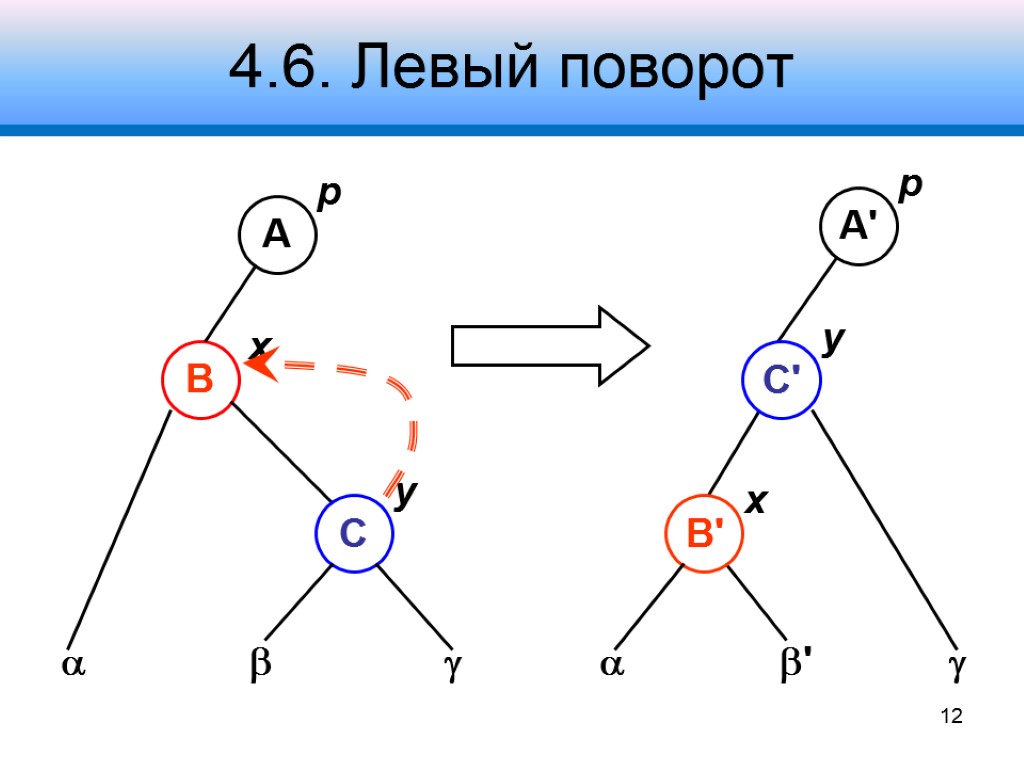
4.6. Левый поворот  ' p x   12

4.6. Левый поворот 1. Для узла x: а) переустанавливается правое поддерево б) переустанавливается родительский узел 13

4.6. Левый поворот 2. Для узла y: а) переустанавливается левое поддерево б) переустанавливается родительский узел 14

4.6. Левый поворот 3. Для узла p: переустанавливается левое (или правое) поддерево 4. Для левого поддерева узла y: переустанавливается родительский узел 15

4.7. Алгоритм Left_rotate(x) x – заданный узел y = x->right – правое поддерево узла x Переустановить правое поддерево x (1a): x->right = y->left Переустановить родительский узел левого поддерева y (если он есть) (4): if y->left ≠ EList y->left->parent = x 16

4.7. Алгоритм Left_rotate(x) Переустановить родительский узел y (2б): y->parent = x->parent Возможно, x был корнем дерева: if x->parent = EList root = y – новый корень дерева else { 17

4.7. Алгоритм Left_rotate(x) Переустановить левое или правое поддерево родительского узла x (3): if x->parent->left = x x->parent->left = y else x->parent->right = y } 18

4.7. Алгоритм Left_rotate(x) Переустановить левое поддерево y (2a): y->left = x Переустановить родительский узел для x (1б): x->parent = y Время выполнения – Ο(1) 19

4.8. Вставка в красно-черное дерево Алгоритм RB_Insert(x): Вставить узел x как в обычное бинарное дерево поиска Полям left и right нового узла присвоить значение указателя на узлы-листы Окрасить новый узел в красный цвет Перекрасить узлы и выполнить повороты 20

4.9. Алгоритм RB_Insert(x) prev = EList – родительский узел ptr = root – текущий узел while дерево не пусто: ptr ≠ EList { prev = ptr – родительский узел if x->key < ptr->key – выбор поддерева ptr = ptr->left – левое поддерево else ptr = ptr->right– правое поддерево } 21

4.9. Алгоритм RB_Insert(x) x->parent = prev – родительский узел if вставка в пустое дерево: prev = EList root = x – новый корень дерева else выбрать поддерево: if x->key < prev->key вставить в левое поддерево: prev->left = x else вставить в правое поддерево: prev->right = x 22

4.9. Алгоритм RB_Insert(x) Установить поля left и right нового узла дерева: x->left = EList x->right = EList Покрасить узел: x->color = RED Выполнить перекраску узлов и повороты дерева: RB_Insert_Fixup(x) 23

4.10. Нарушение свойств дерева при вставке 1. Каждый узел является красным или черным не нарушается 2. Корень дерева является черным может быть нарушено 3. Каждый лист дерева является черным не нарушается 24

4.10. Нарушение свойств дерева при вставке 4. Если узел – красный, то оба его дочерних узла – черные может быть нарушено 5. Для каждого узла все пути от него до листьев, являющихся потомками данного узла, содержат одно и то же количество черных узлов не нарушается 25

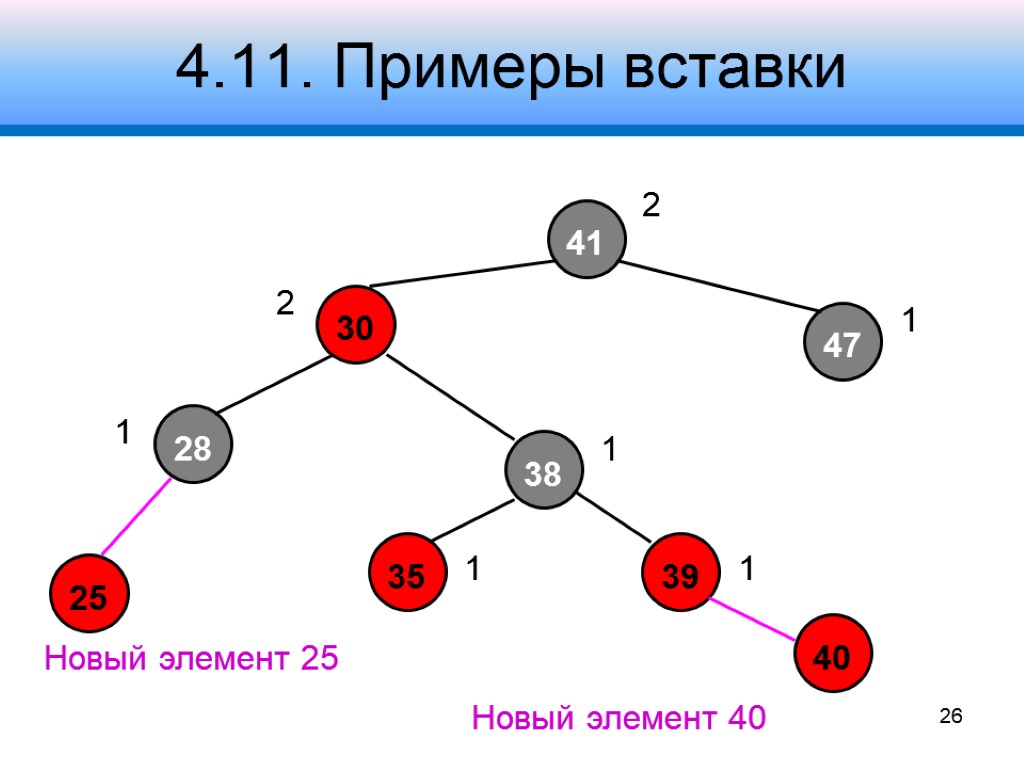
4.11. Примеры вставки 41 30 47 28 38 39 2 1 2 1 1 1 1 Новый элемент 25 Новый элемент 40 26

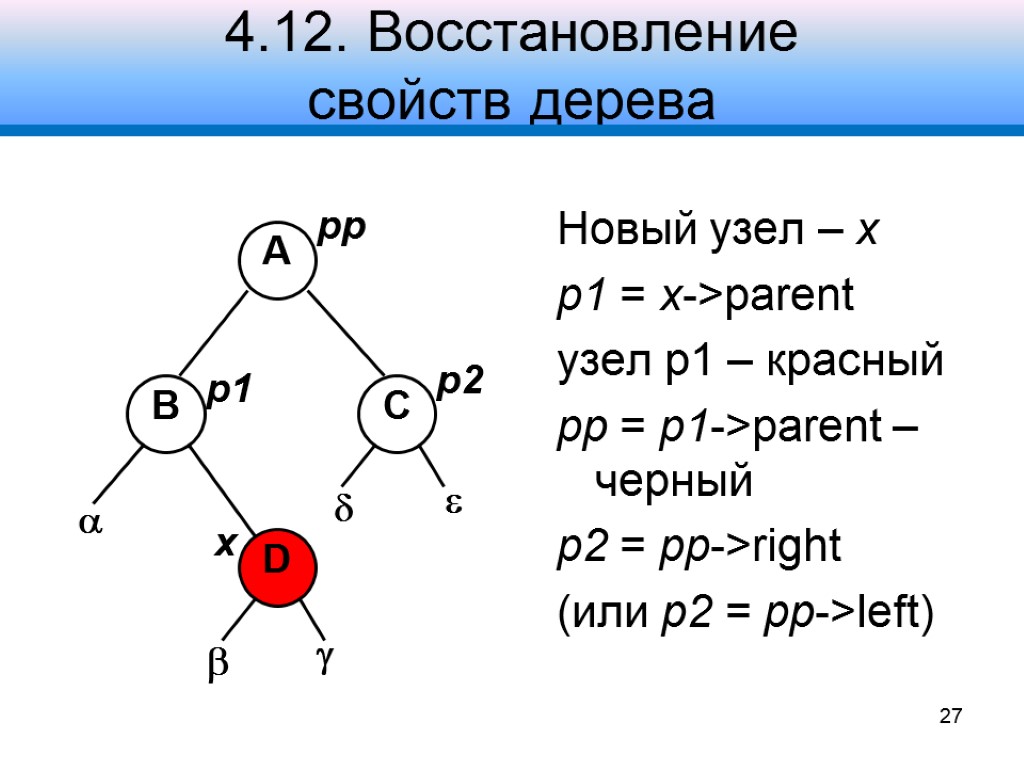
4.12. Восстановление свойств дерева Новый узел – x p1 = x->parent узел p1 – красный pp = p1->parent – черный p2 = pp->right (или p2 = pp->left) B 27

4.13. Случай 1 Узел p2 – красный Узел pp – черный Узлы , , , ,  – черные Коррекция: перекрасить узлы p1 и p2 в черный цвет, pp – в красный Переустановить узел x Продолжить коррекцию дерева 28

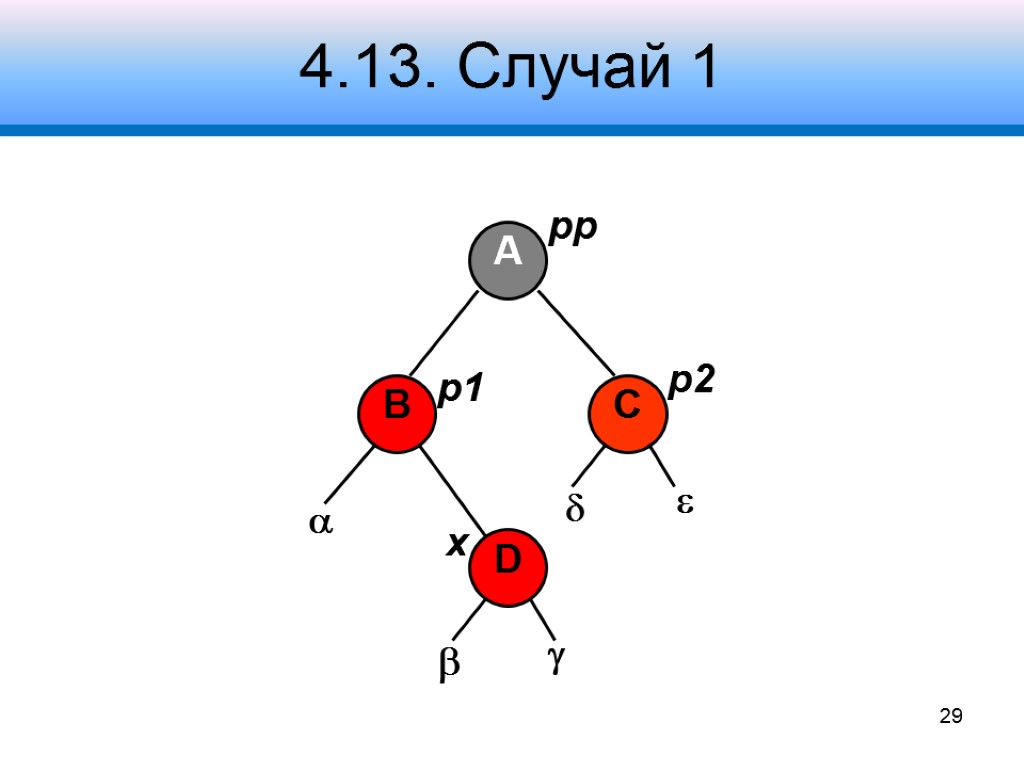
4.13. Случай 1 A B C p1 p2 pp    29

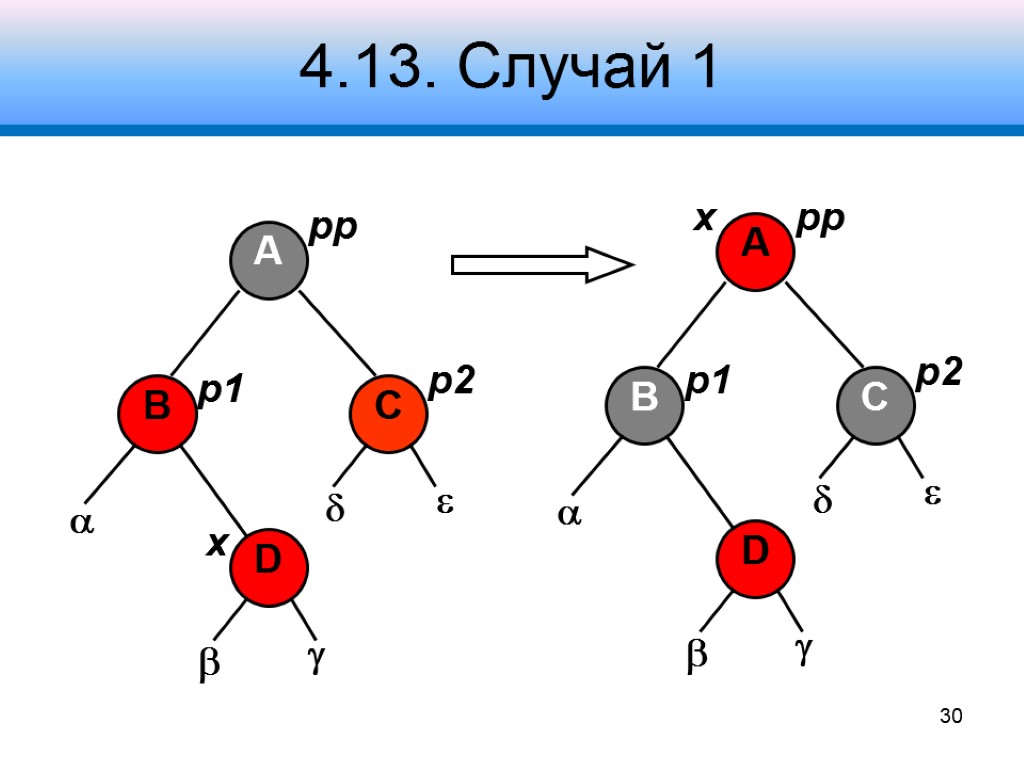
4.13. Случай 1 A B C p1 p2 pp    30

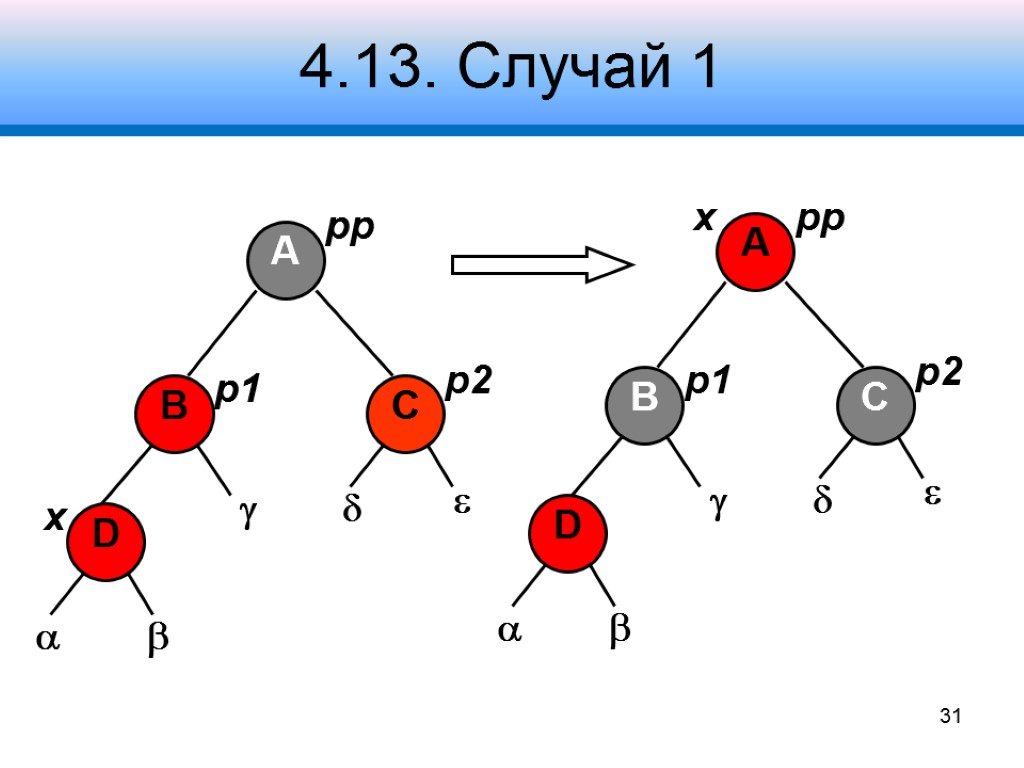
4.13. Случай 1 x p1 p2 pp      31

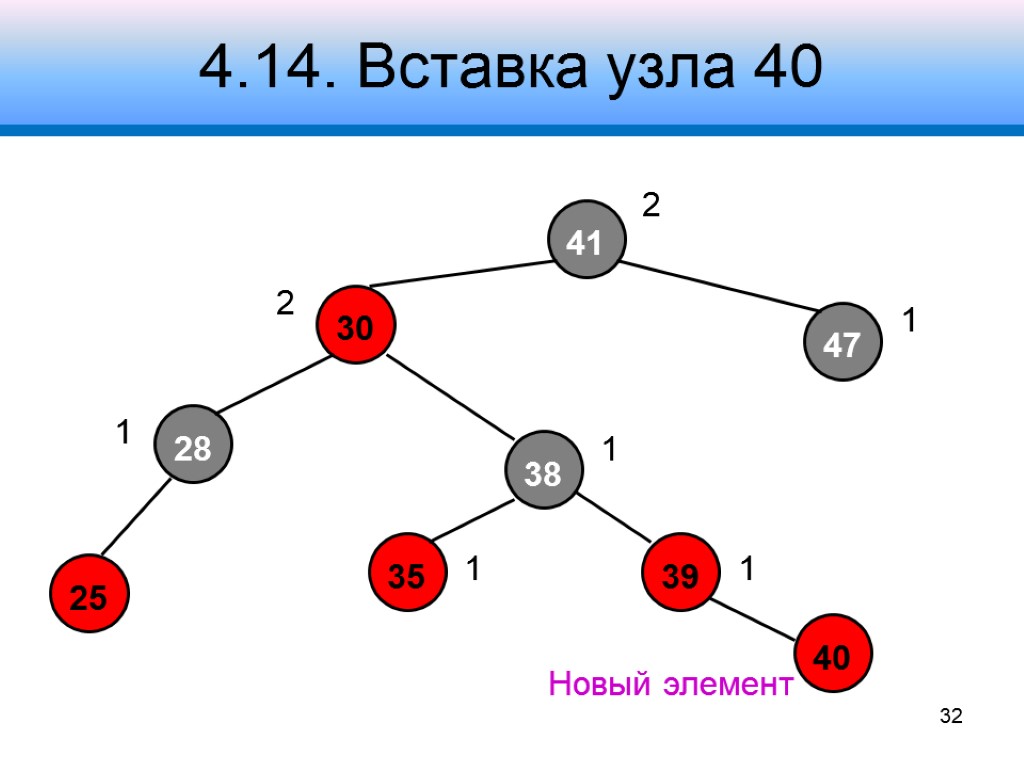
4.14. Вставка узла 40 41 30 47 28 38 39 2 1 2 1 1 1 1 Новый элемент 32

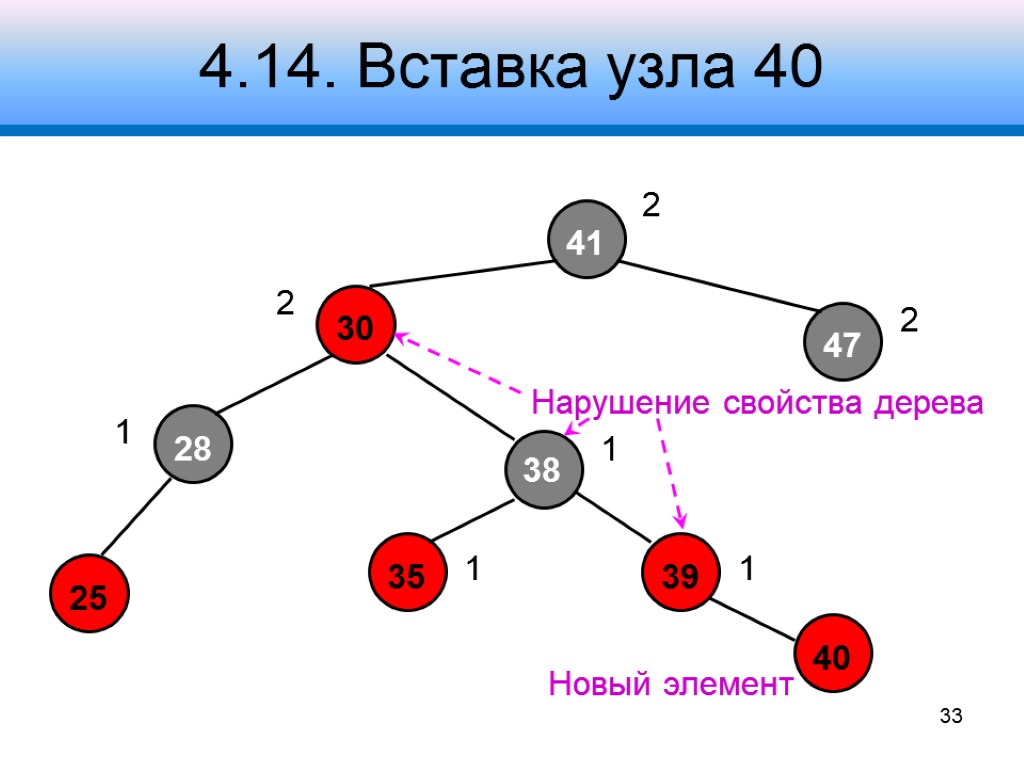
4.14. Вставка узла 40 41 30 47 28 38 35 39 2 2 2 1 1 1 1 Новый элемент Нарушение свойства дерева 33

4.15. Случай 2 Узел p2 – черный Узел x – в правом поддереве узла p1 Узел pp – черный Узлы , ,  – черные Коррекция: шаг 1 – левый поворот вокруг узла p1 Переходим к случаю 3 34

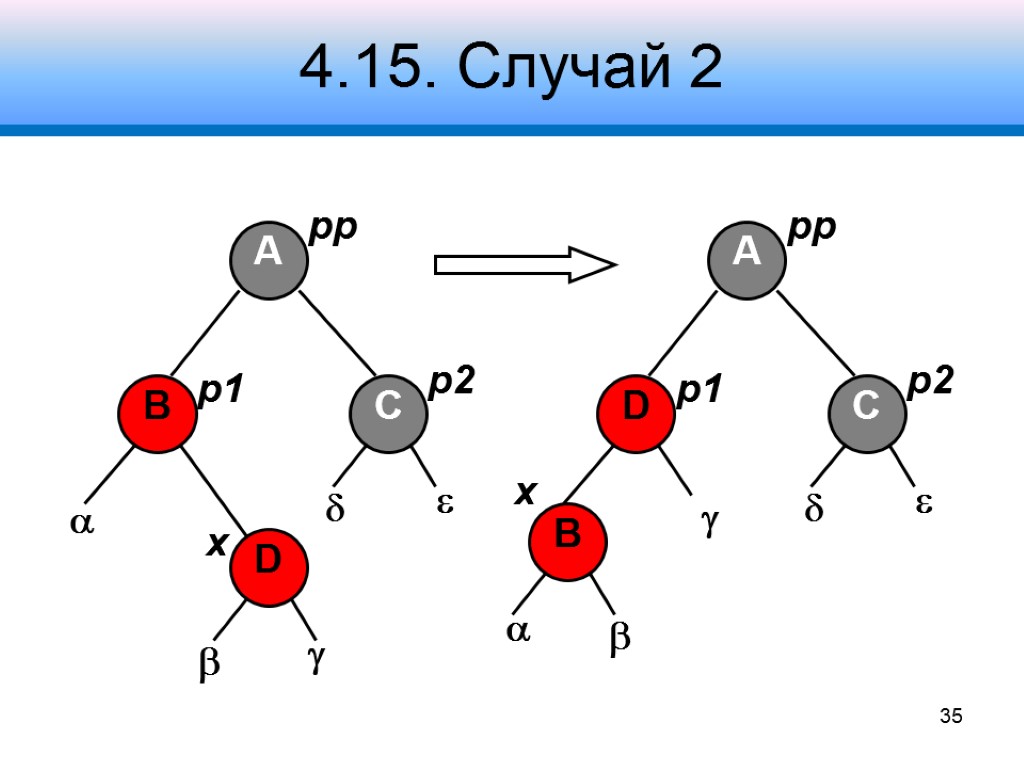
4.15. Случай 2 35

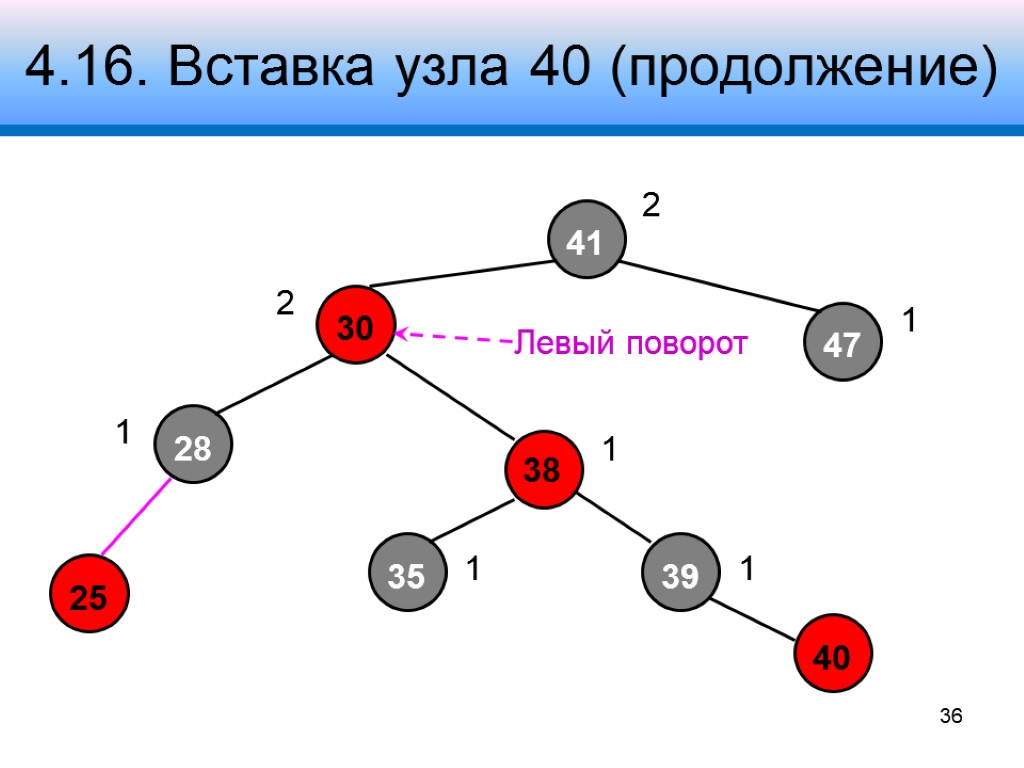
4.16. Вставка узла 40 (продолжение) 41 30 47 28 38 39 2 1 2 1 1 1 1 Левый поворот 36

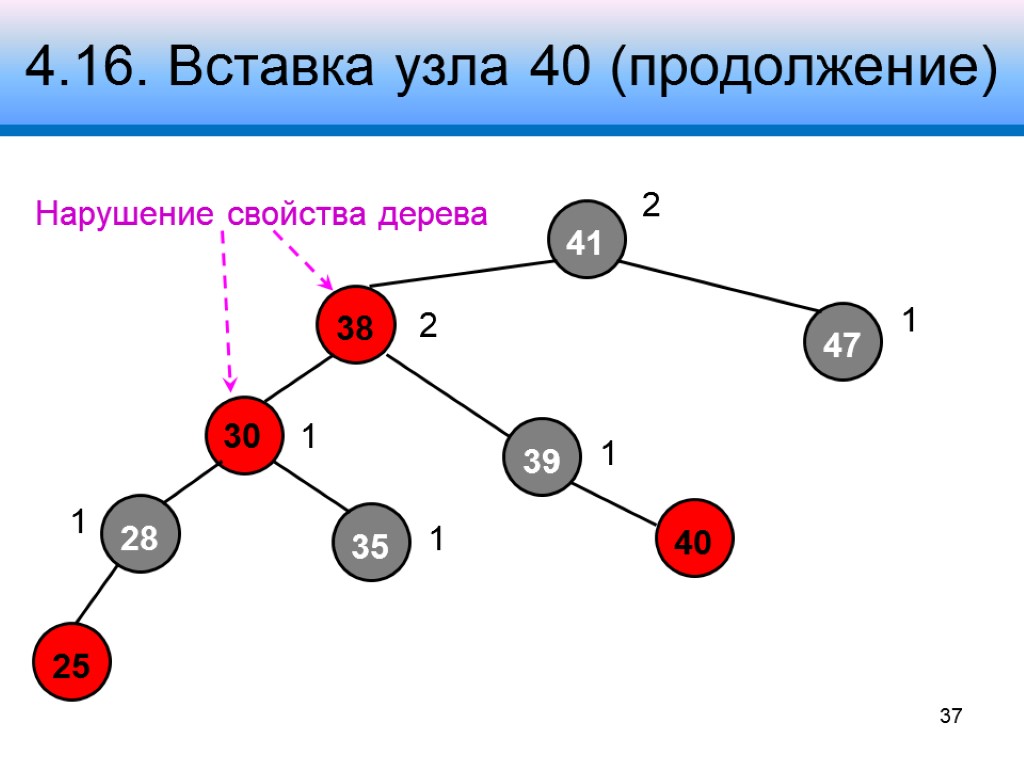
4.16. Вставка узла 40 (продолжение) 41 38 47 28 30 39 2 1 2 1 1 1 1 Нарушение свойства дерева 37

4.17. Случай 3 Узел p2 – черный Узел x – в левом поддереве узла p1 Узел pp – черный Узлы , ,  – черные Коррекция: шаг 1 – перекрасить узел p1 в черный цвет, узел pp – в красный цвет шаг 2 – правый поворот вокруг узла pp 38

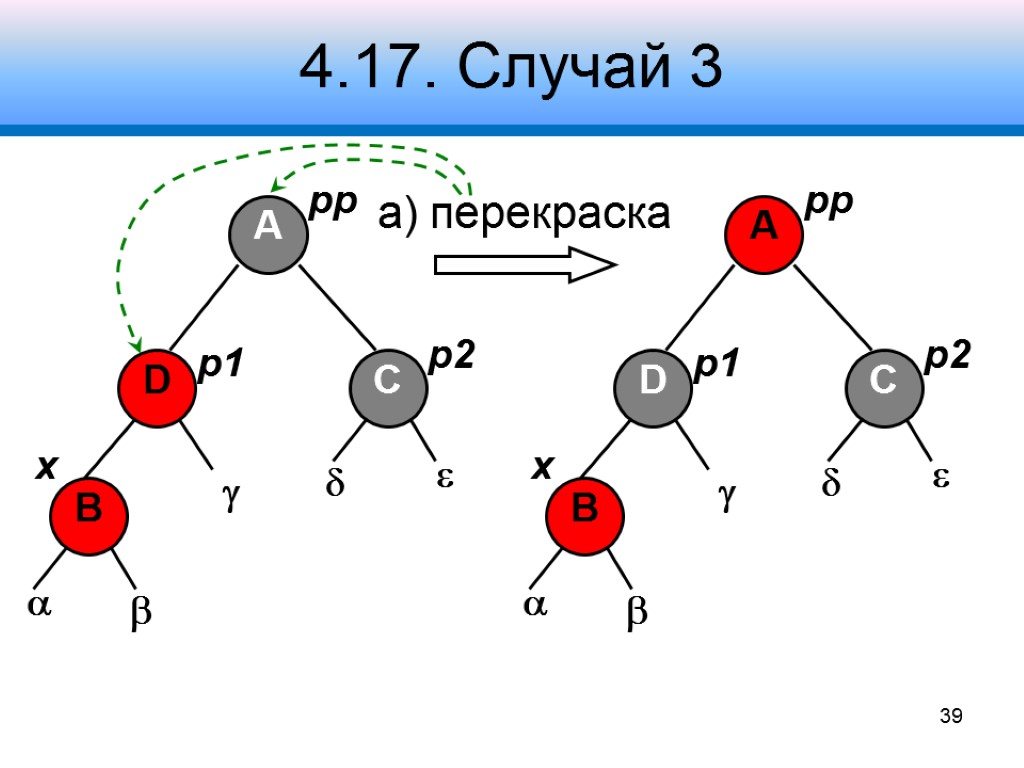
4.17. Случай 3 а) перекраска A D 39

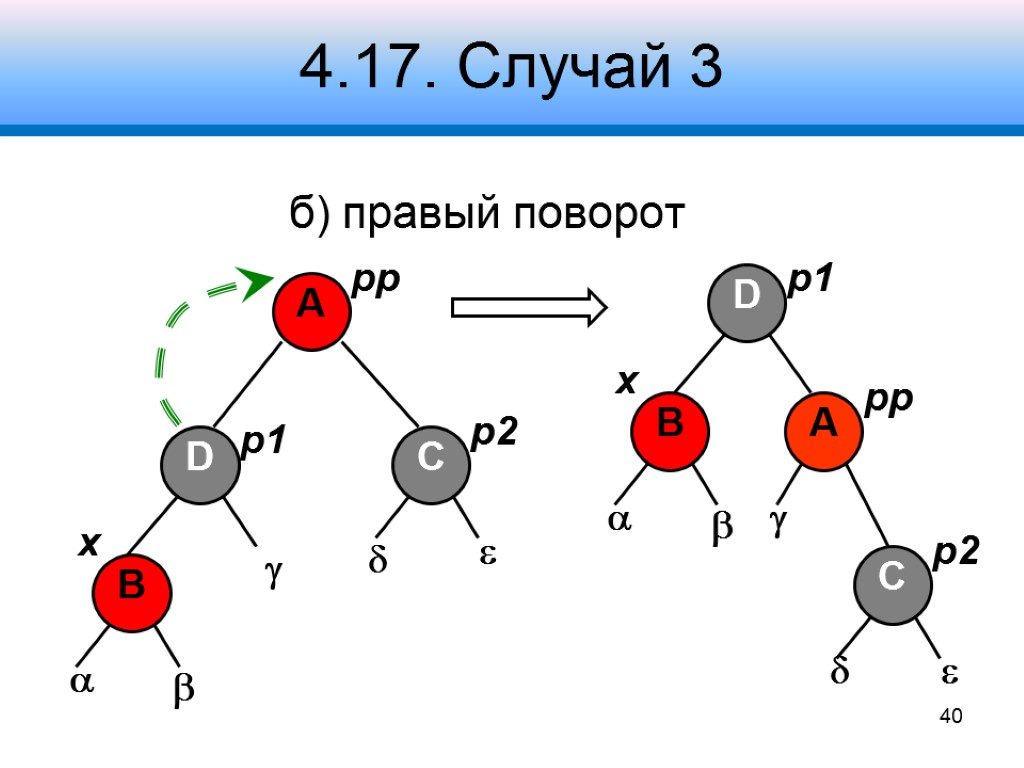
4.17. Случай 3 б) правый поворот 40

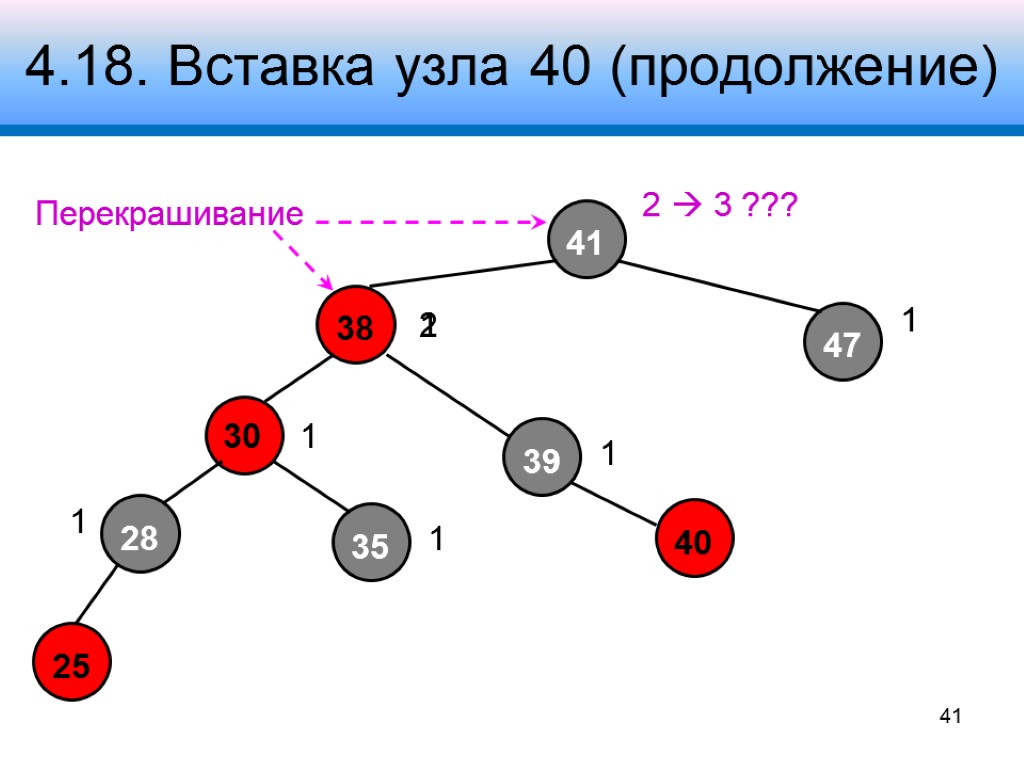
4.18. Вставка узла 40 (продолжение) 41 38 47 28 30 39 2  3 ??? 1 2 1 1 1 1 Перекрашивание 41 1

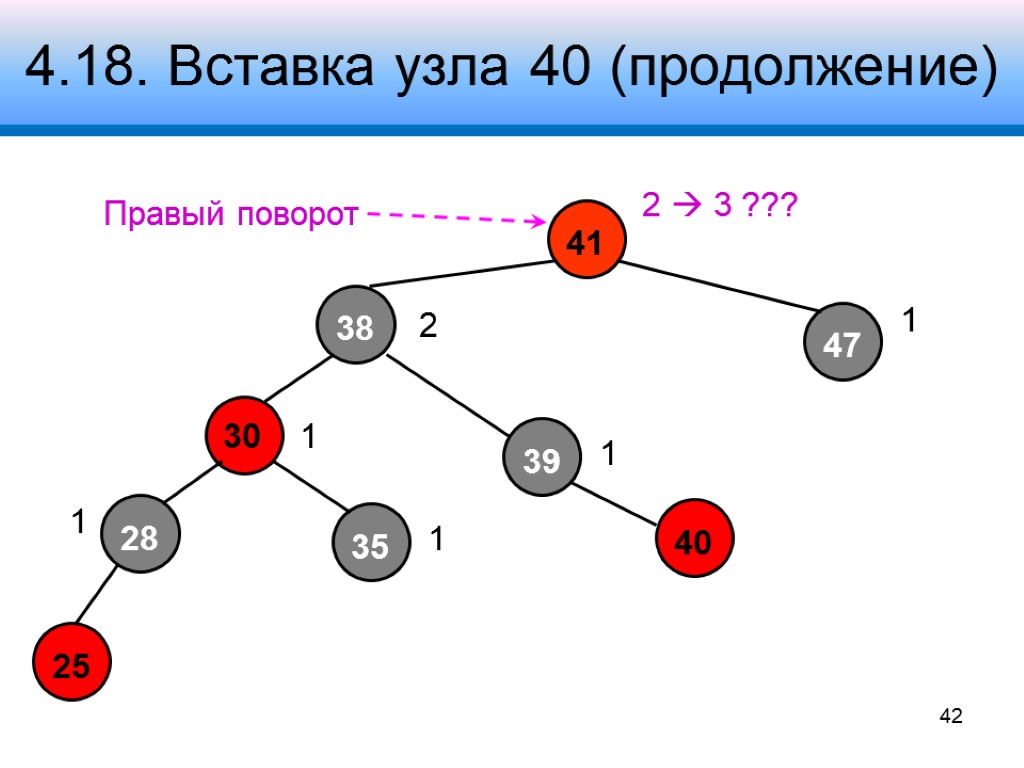
4.18. Вставка узла 40 (продолжение) 41 38 47 28 30 39 2  3 ??? 1 2 1 1 1 1 Правый поворот 42

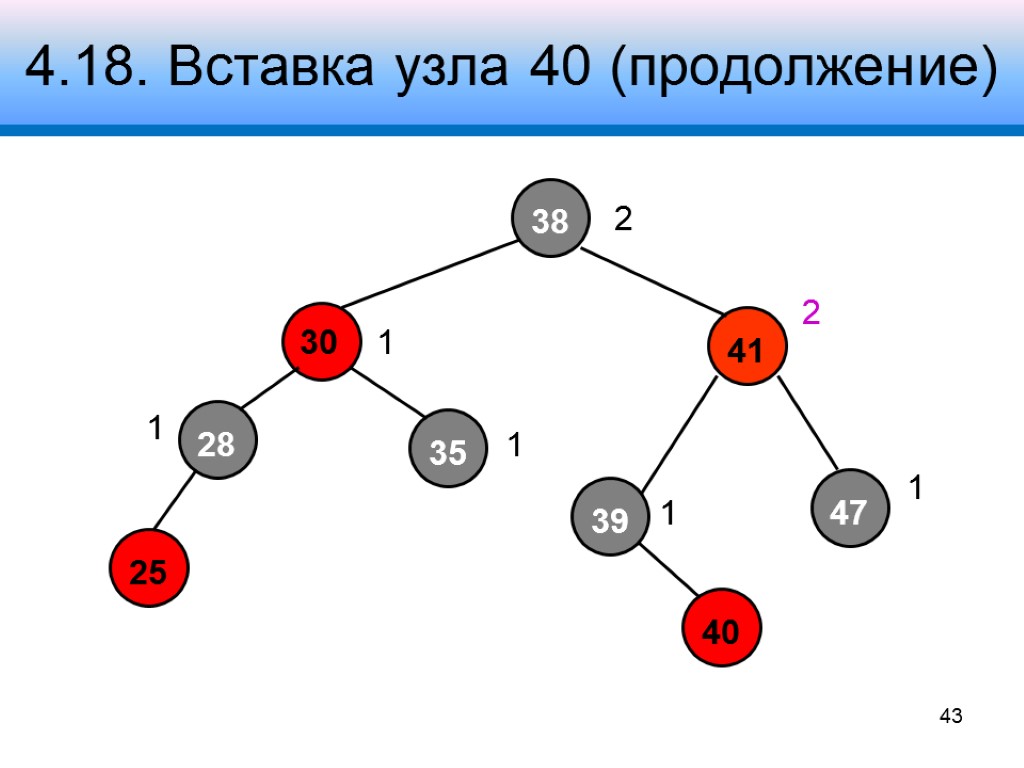
4.18. Вставка узла 40 (продолжение) 41 38 47 28 30 39 2 1 2 1 1 1 1 43

4.19. Алгоритм RB_Insert_Fixup(x) x – вставленный узел while родительский узел для x – красный (x->parent = RED) { p1 = x->parent – родительский узел x pp = p1->parent – родительский узел p1 if p1 = pp->left { #1 – начало Узел вставляется в левое поддерево p2 = pp->right 44

4.19. Алгоритм RB_Insert_Fixup(x) if p2->color = RED { случай 1: перекрасить вершины: p1->color = BLACK p2->color = BLACK pp->color = RED x = pp } 45

4.19. Алгоритм RB_Insert_Fixup(x) else { if x в правом поддереве p1 (x = p1->right) { случай 2: x = p1 левый поворот: left_rotate(x) p1 = x->parent } 46

4.19. Алгоритм RB_Insert_Fixup(x) Случай 3: перекрасить вершины: p1->color = BLACK pp->color = RED правый поворот: Right_rotate(pp) } } #1 – конец 47

4.19. Алгоритм RB_Insert_Fixup(x) else { узел вставляется в правое поддерево: повторить коды от #1 – начало до #1 – конец, заменив в них left на right, и наоборот } } – конец цикла root->color = BLACK 48

4.20. Анализ эффективности Вставка в красно-черное дерево = вставка в двоичное дерево – О(h) Коррекция красно-черного дерева Коррекция: итерации – для случая 1 – O(h) для случаев 2 и 3 – максимум два поворота h  2lg(n + 1), вставка – O(lg(n)) 49

4.21. Удаление Удалить узел как в бинарном дереве поиска; учесть представление листьев Восстановить красно-черные свойства дерева x – удаляемый узел дерева 50

4.22. Алгоритм RB_Delete(x) if x->left = Elist или x->right = Elist y = x else y = successor(x) if y->left ≠ Elist p = y->left else p = y->right 51

4.22. Алгоритм RB_Delete(x) p->parent = y->parent --- отличается! if y->parent = EList root = p else if y->parent->left = y y->parent->left = p else y->parent->right = p 52

4.22. Алгоритм RB_Delete(x) if y ≠ x { x->key = y->key копирование сопутствующих данных } if y->color = BLACK RB_Delete_Fixup(p) Успех 53

4.23. Нарушение свойств дерева при удалении Если удаляется красный узел: никакая черная высота в дереве не изменяется никакие красные узлы не становятся соседними корень остается черным 54

4.23. Нарушение свойств дерева при удалении Если удаляется черный узел: 1. Каждый узел является красным или черным не нарушается 2. Корень дерева является черным может быть нарушено 3. Каждый лист дерева является черным не нарушается 55

4.23. Нарушение свойств дерева при удалении 4. Если узел – красный, то оба его дочерних узла – черные может быть нарушено 5. Для каждого узла все пути от него до листьев, являющихся потомками данного узла, содержат одно и то же количество черных узлов нарушается!!! 56

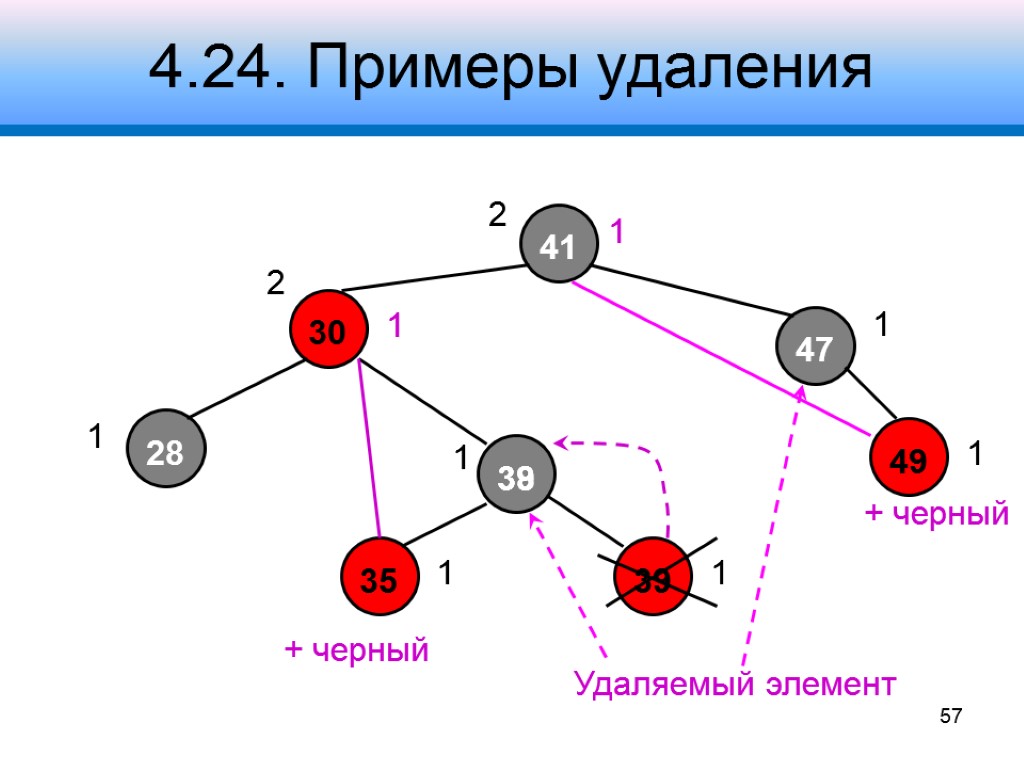
4.24. Примеры удаления 41 30 47 28 38 35 39 2 1 2 1 1 1 1 Удаляемый элемент 49 1 1 39 + черный 57 1 + черный

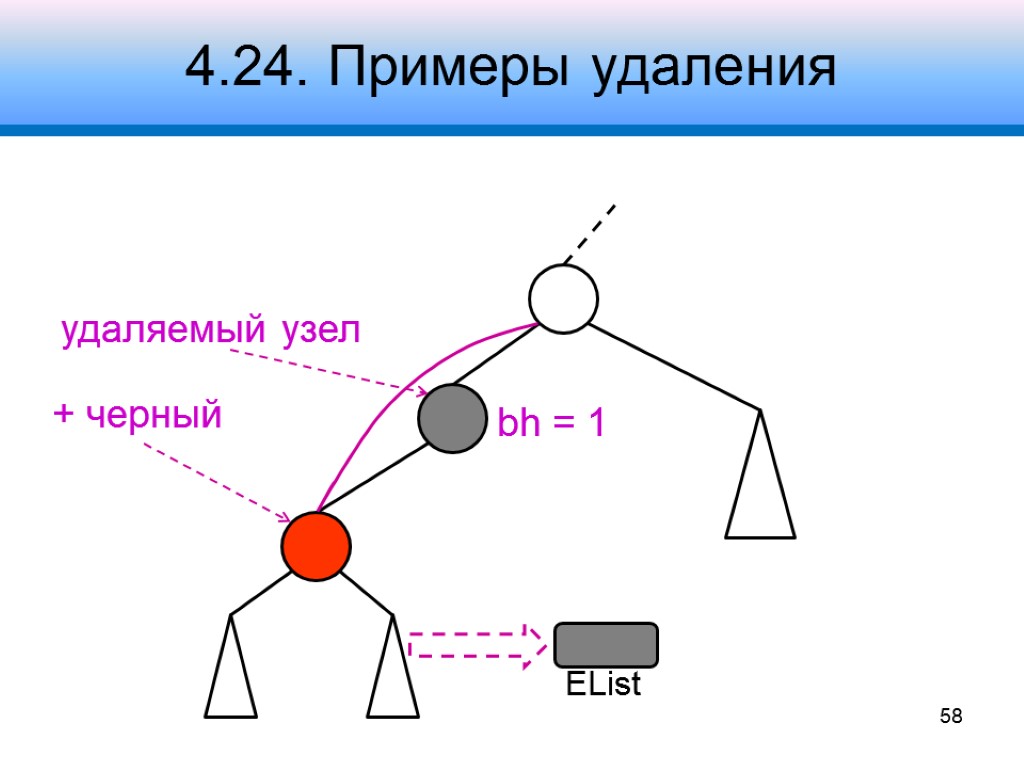
4.24. Примеры удаления 58 удаляемый узел + черный bh = 1

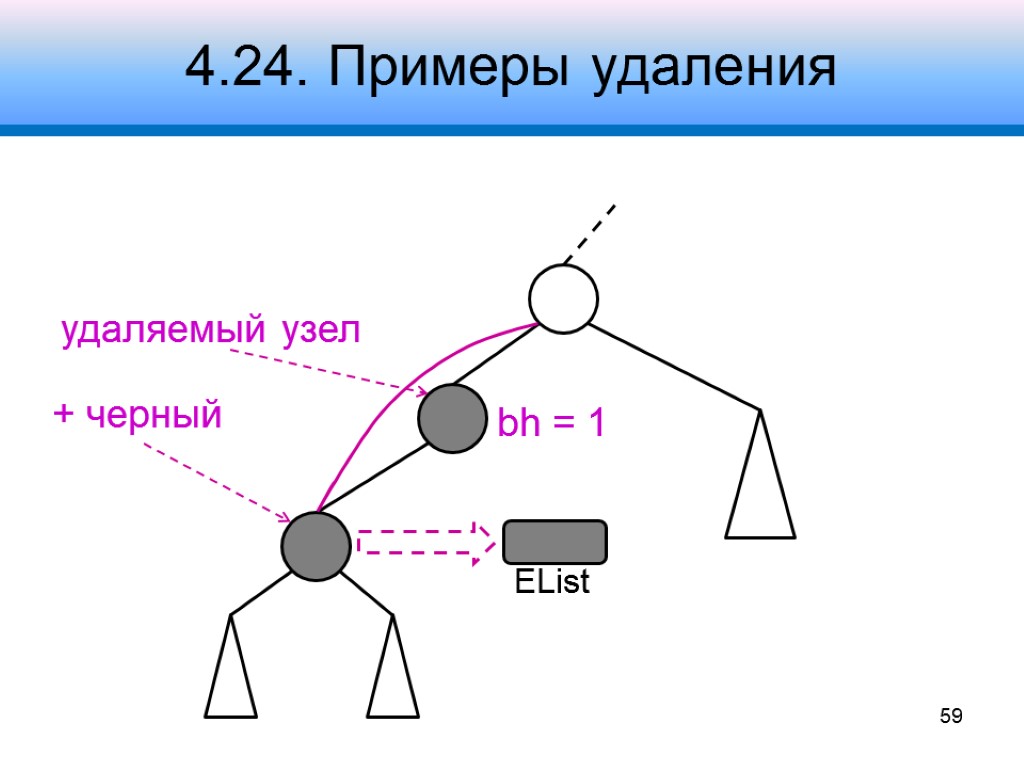
4.24. Примеры удаления 59 удаляемый узел + черный bh = 1

4.25. Восстановление черной высоты вершины У потомка – дополнительная чернота: «дважды черный» (атрибут color узла имеет значение BLACK) «красно-черный» (атрибут color узла имеет значение RED): восстанавливается свойство 5 нарушается свойство 1 – значение атрибута color узла не соответствует цвету узла 60

4.26. Восстановление цвета узла Переместить дополнительную черноту вверх по дереву: Узел является красно-черным – сделать данный узел «единожды черным» Узел является корнем дерева – убрать излишнюю черноту Выполнить повороты и перекраску, устраняющие двойную черноту 61

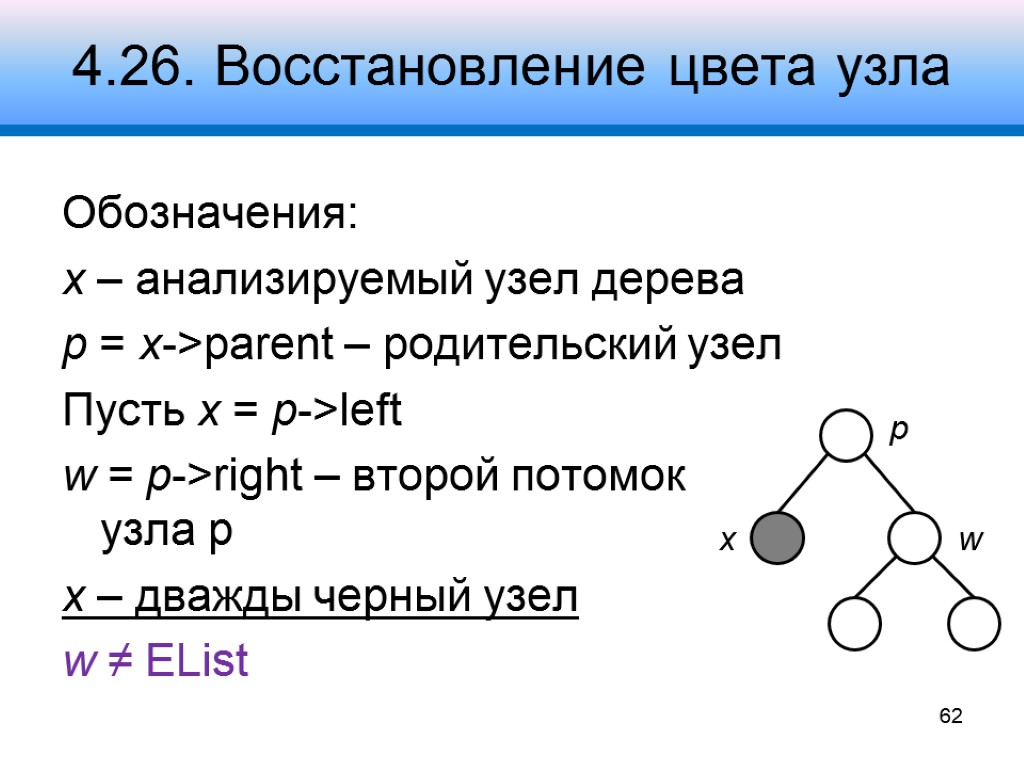
4.26. Восстановление цвета узла Обозначения: x – анализируемый узел дерева p = x->parent – родительский узел Пусть x = p->left w = p->right – второй потомок узла p x – дважды черный узел w ≠ EList 62 x p w

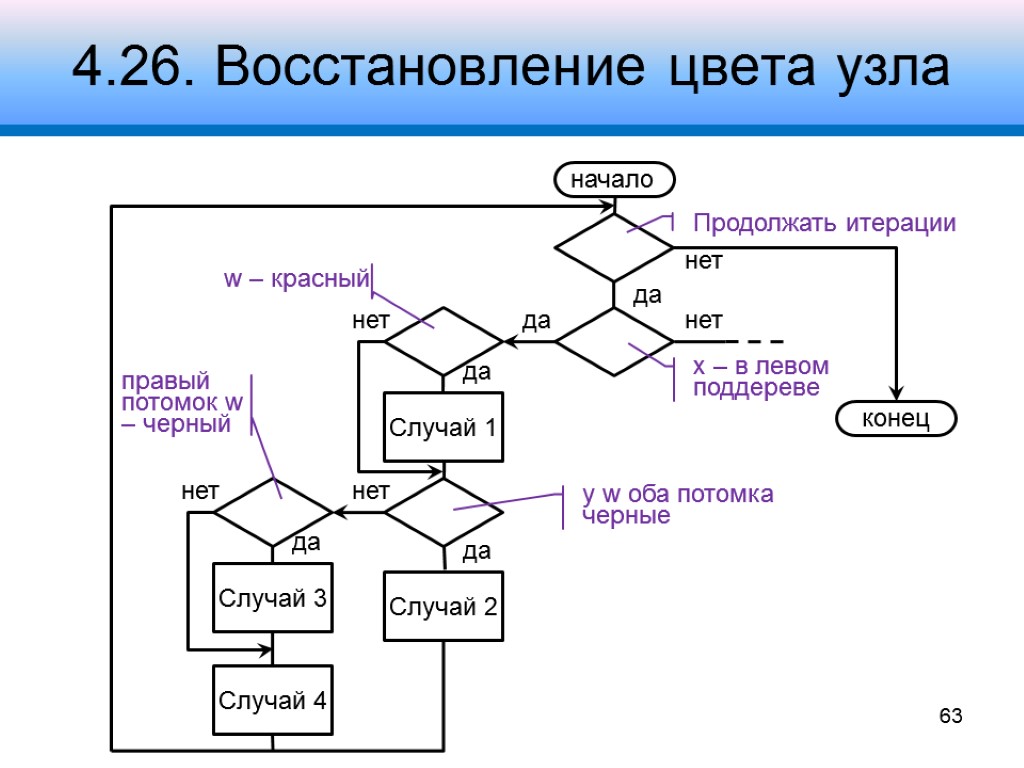
4.26. Восстановление цвета узла 63 Случай 4 нет нет нет Продолжать итерации x – в левом поддереве w – красный у w оба потомка черные правый потомок w – черный

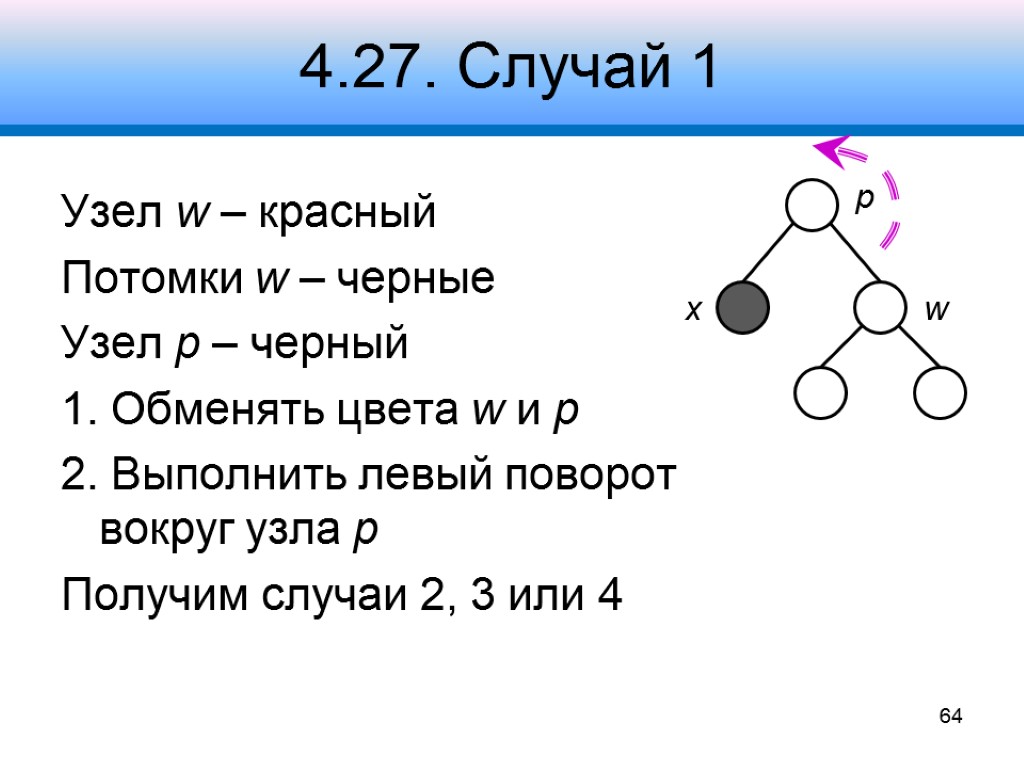
4.27. Случай 1 Узел w – красный Потомки w – черные Узел p – черный 1. Обменять цвета w и p 2. Выполнить левый поворот вокруг узла p Получим случаи 2, 3 или 4 64 x p w

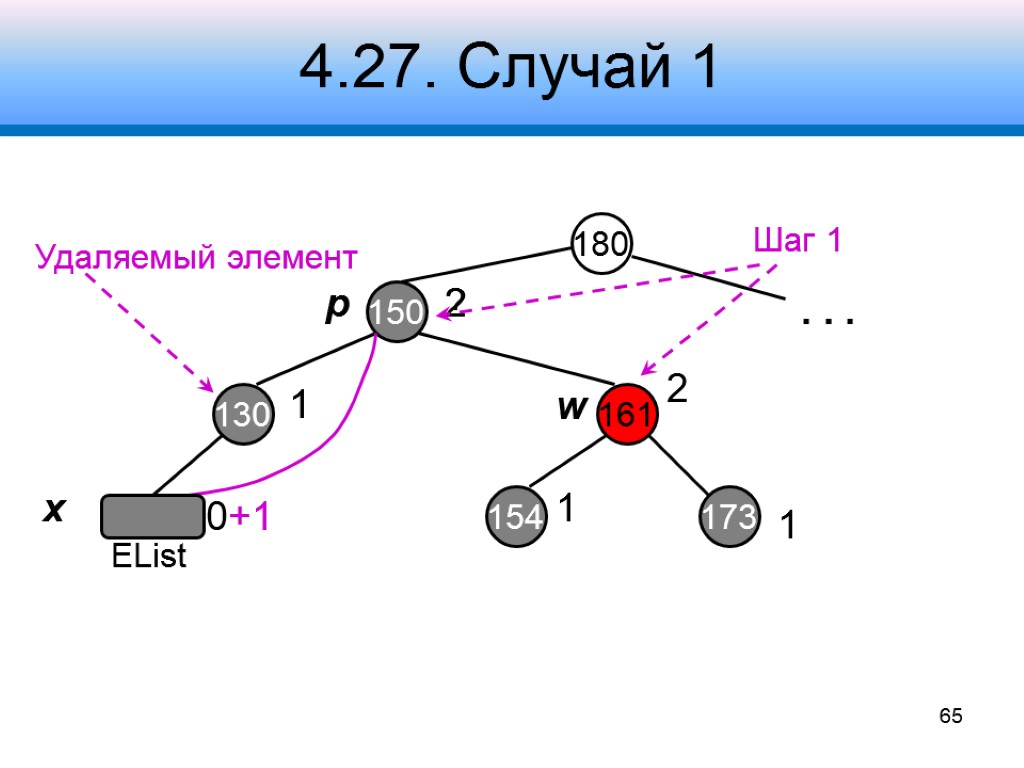
4.27. Случай 1 180 150 161 130 2 154 173 2 1 1 1 0+1 Удаляемый элемент . . . x p w 65 ? Шаг 1

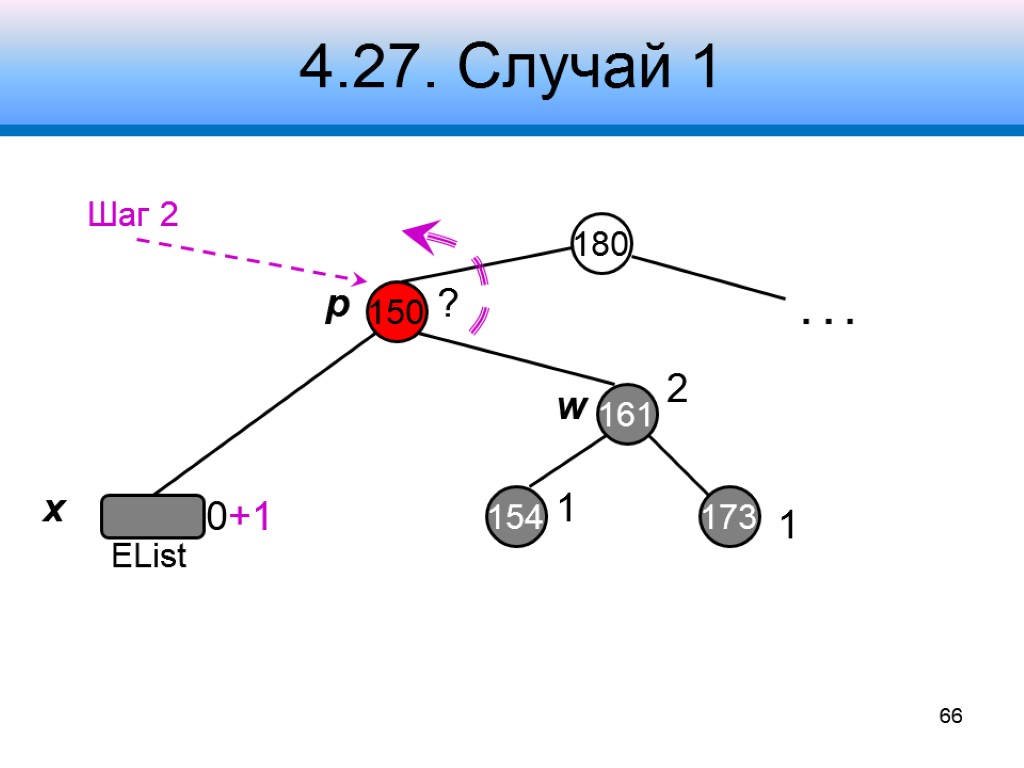
4.27. Случай 1 180 150 161 154 173 2 1 1 0+1 . . . x p w 66 ? Шаг 2

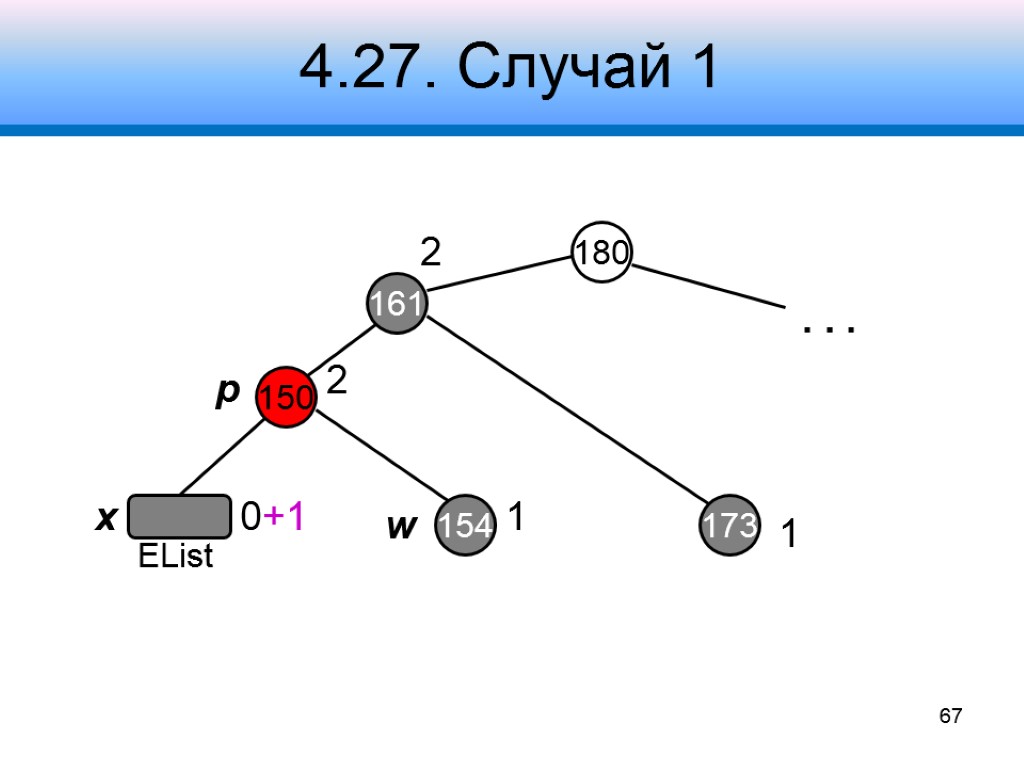
4.27. Случай 1 180 150 161 2 154 173 2 1 1 0+1 . . . x p w 67

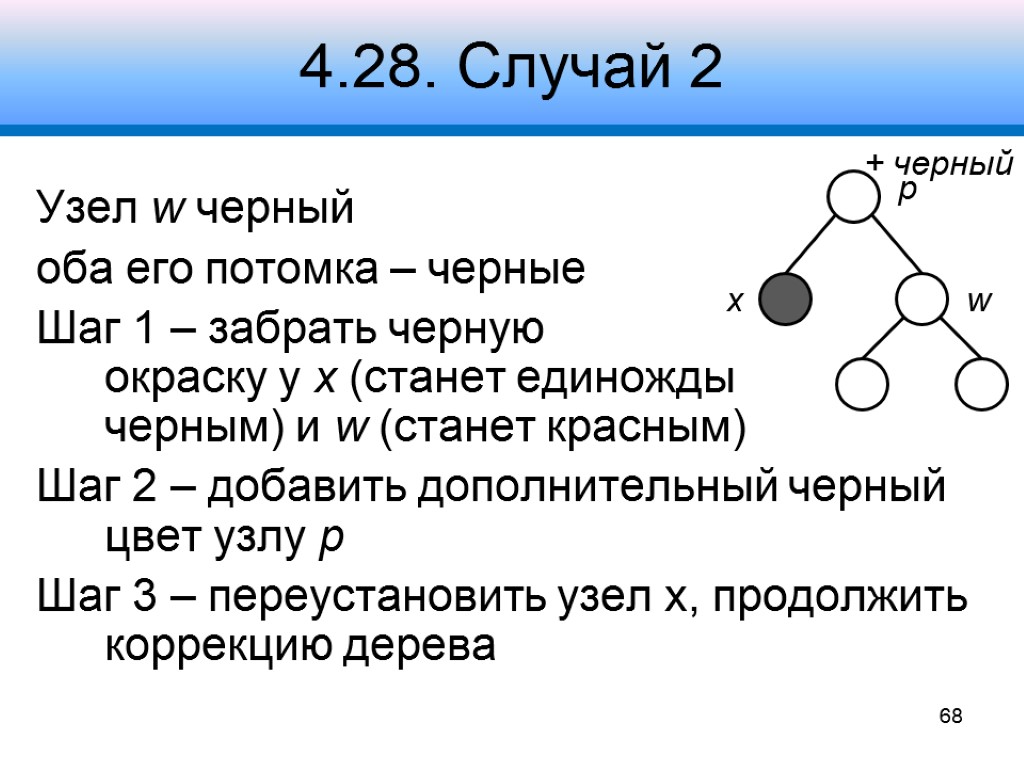
4.28. Случай 2 Узел w черный оба его потомка – черные Шаг 1 – забрать черную окраску у x (станет единожды черным) и w (станет красным) Шаг 2 – добавить дополнительный черный цвет узлу p Шаг 3 – переустановить узел x, продолжить коррекцию дерева 68 x p w + черный

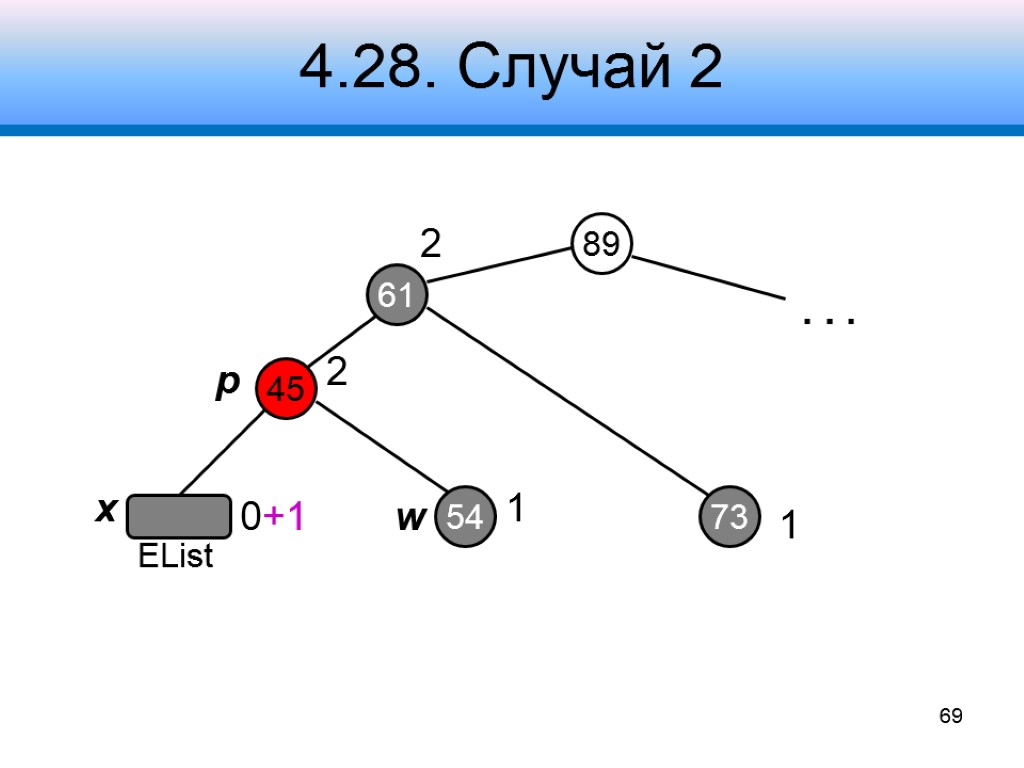
4.28. Случай 2 89 45 61 2 54 73 2 1 1 0+1 . . . x p w 69

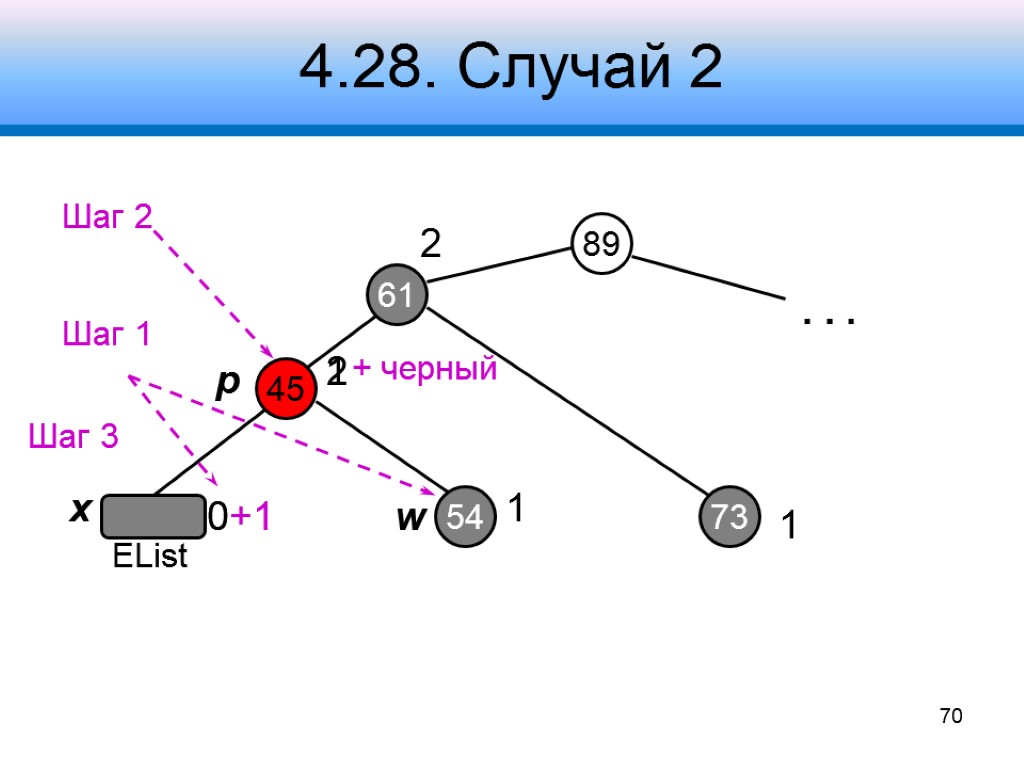
4.28. Случай 2 Шаг 2 Шаг 1 89 45 61 2 54 73 2 1 1 0+1 . . . x p w 0 1 + черный 70 Шаг 3

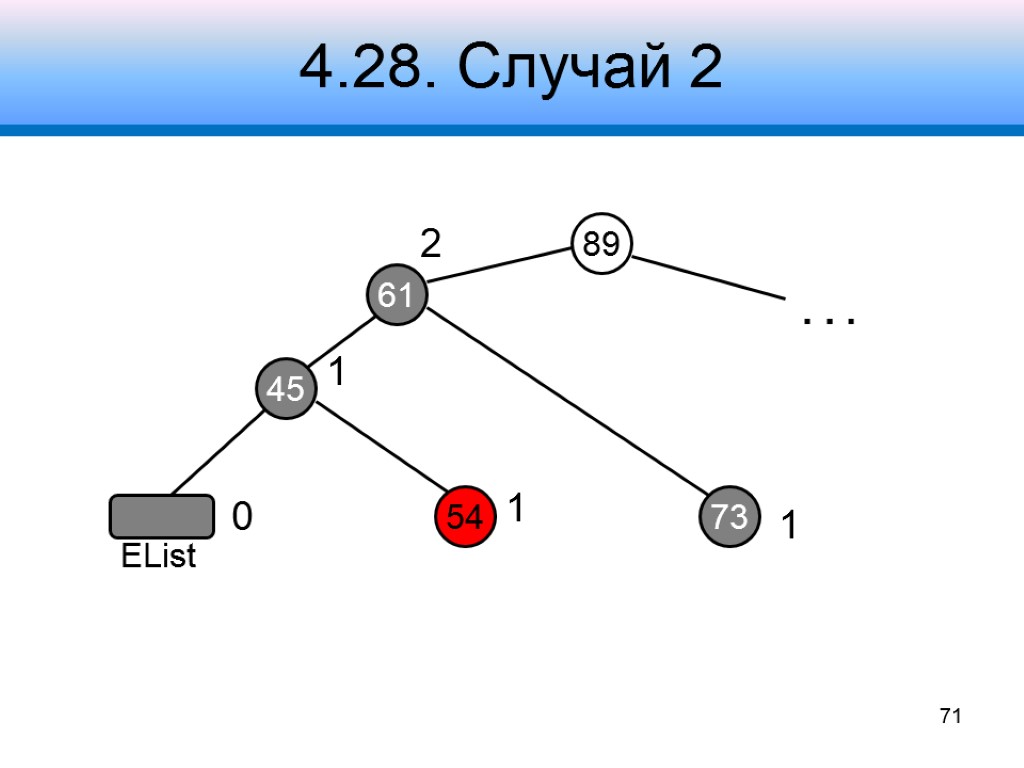
4.28. Случай 2 89 45 61 1 54 73 2 1 1 0 . . . 71

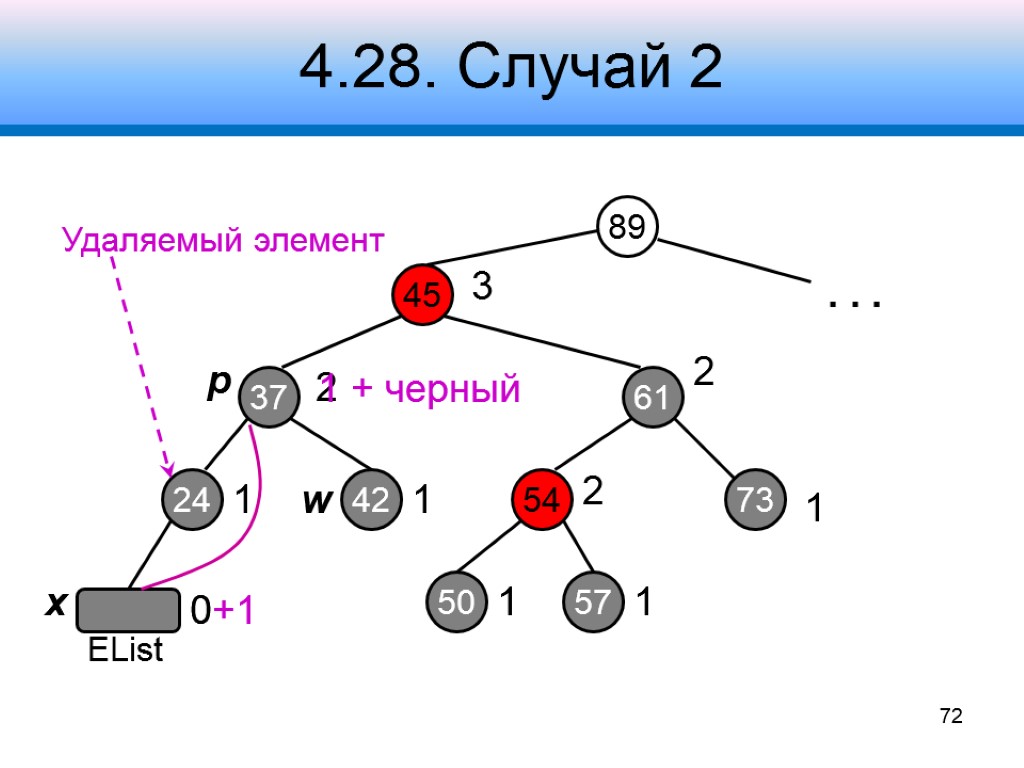
4.28. Случай 2 89 45 61 37 24 3 54 73 2 2 1 2 0+1 Удаляемый элемент . . . x p w 72 42 50 57 1 1 1 1 0 1 + черный

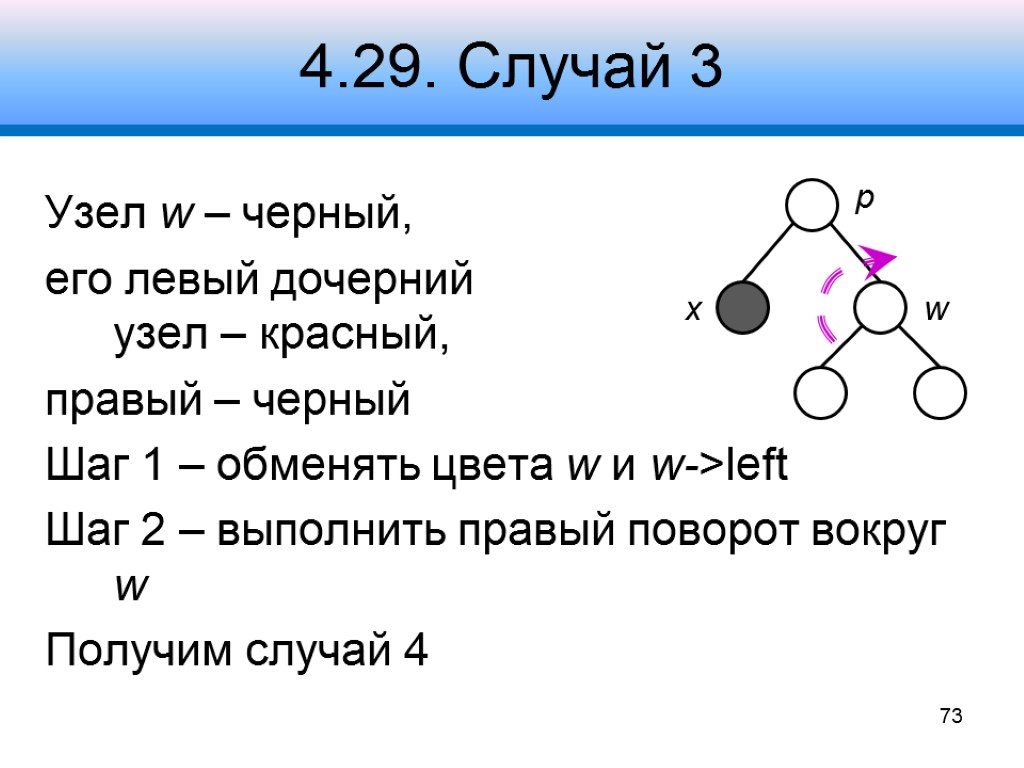
4.29. Случай 3 Узел w – черный, его левый дочерний узел – красный, правый – черный Шаг 1 – обменять цвета w и w->left Шаг 2 – выполнить правый поворот вокруг w Получим случай 4 73 x p w

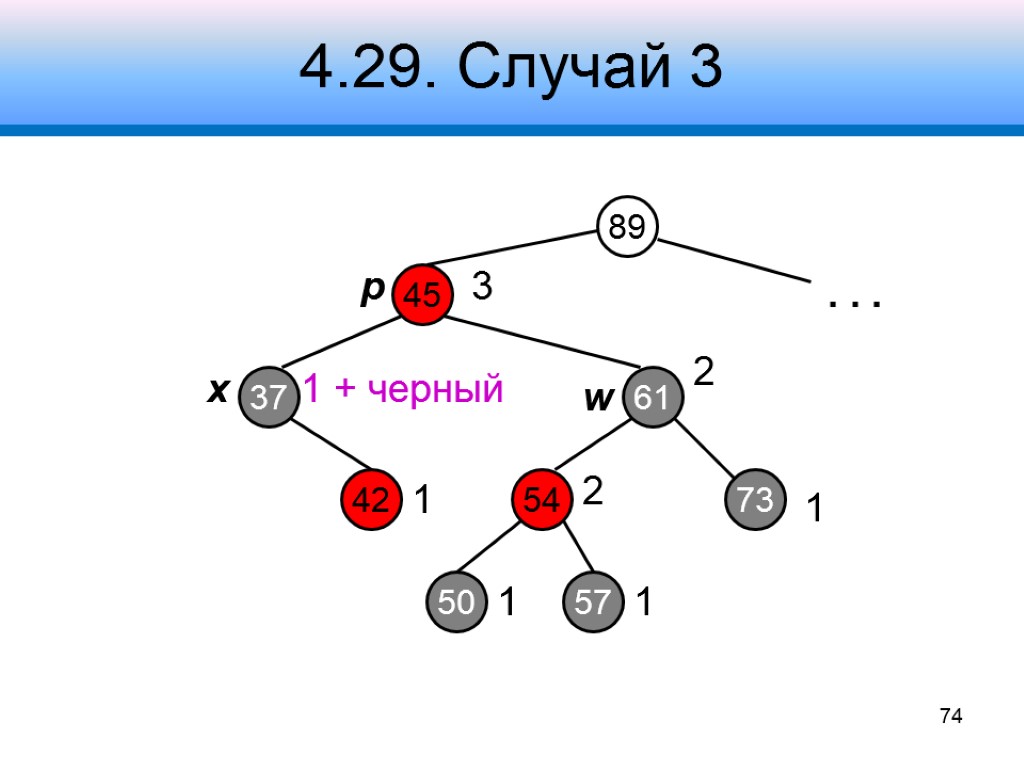
4.29. Случай 3 89 45 61 37 3 54 73 2 2 1 . . . x p w 74 42 50 57 1 1 1 + черный 1

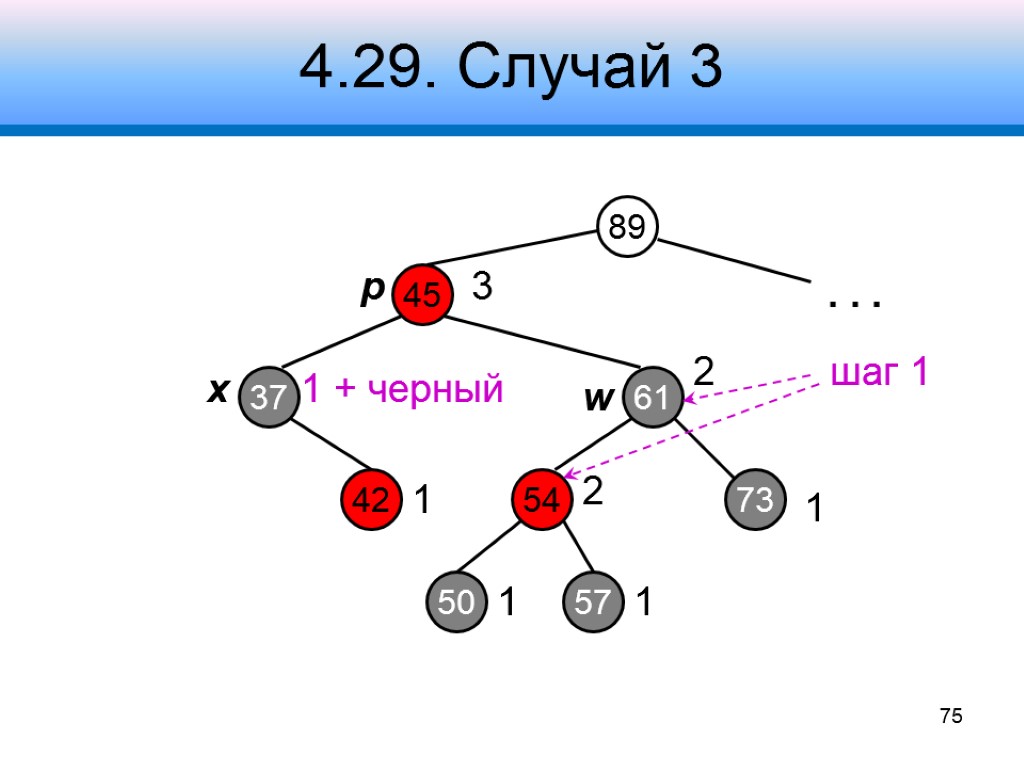
4.29. Случай 3 89 45 61 37 3 54 73 2 2 1 . . . x p w 75 42 50 57 1 1 1 + черный 1 шаг 1

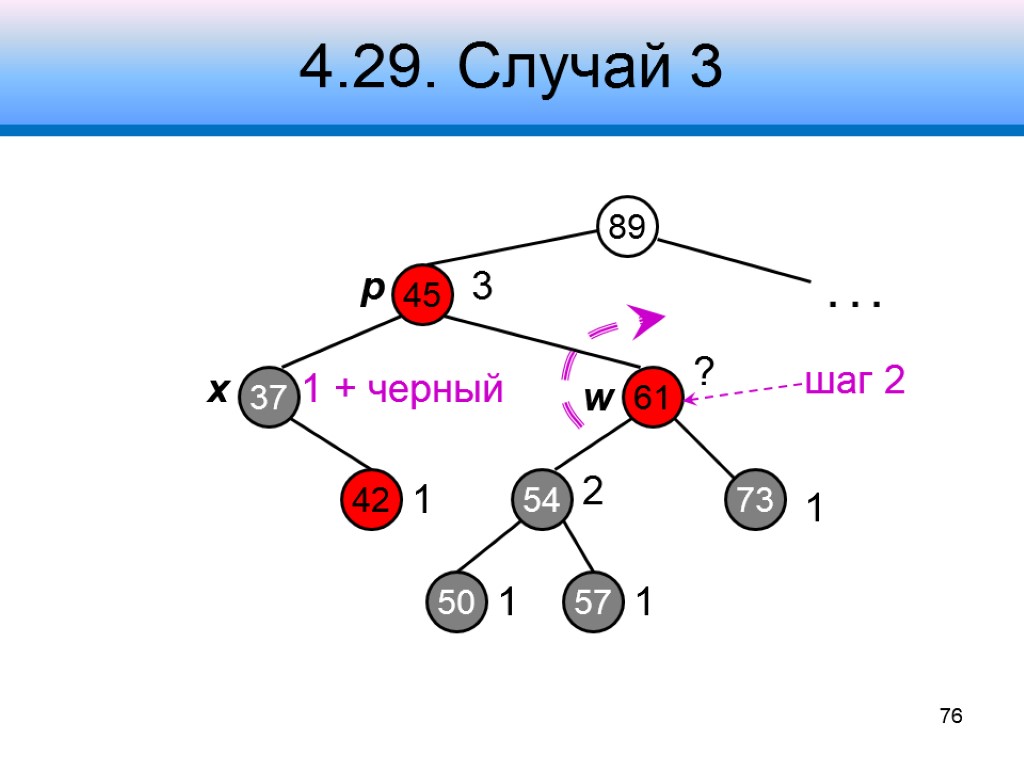
4.29. Случай 3 89 45 61 37 3 54 73 ? 2 1 . . . x p w 76 42 50 57 1 1 1 + черный 1 шаг 2

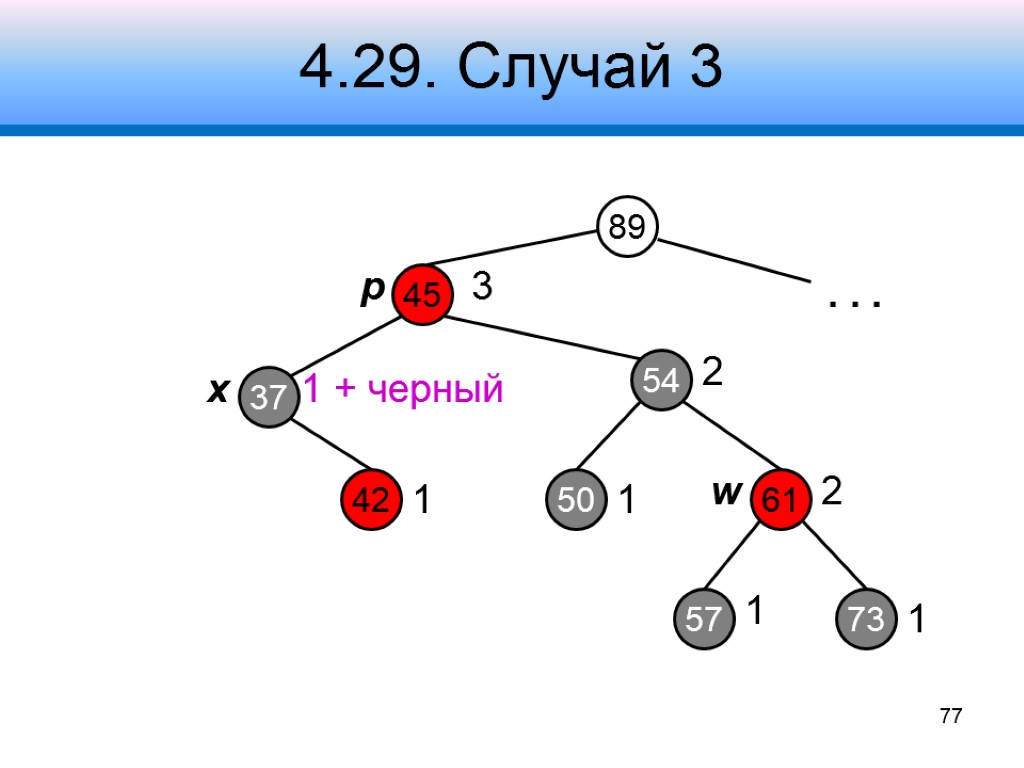
4.29. Случай 3 89 45 61 37 3 54 73 2 2 1 . . . x p w 77 42 50 57 1 1 1 + черный 1

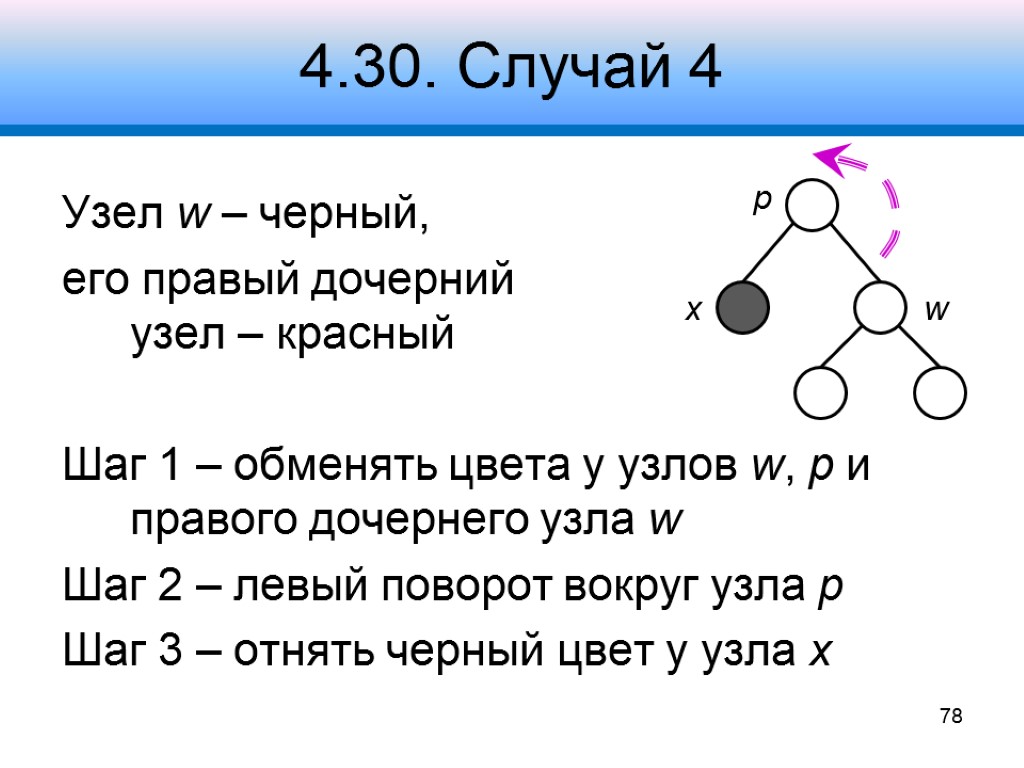
4.30. Случай 4 Узел w – черный, его правый дочерний узел – красный Шаг 1 – обменять цвета у узлов w, p и правого дочернего узла w Шаг 2 – левый поворот вокруг узла p Шаг 3 – отнять черный цвет у узла x 78 x p w

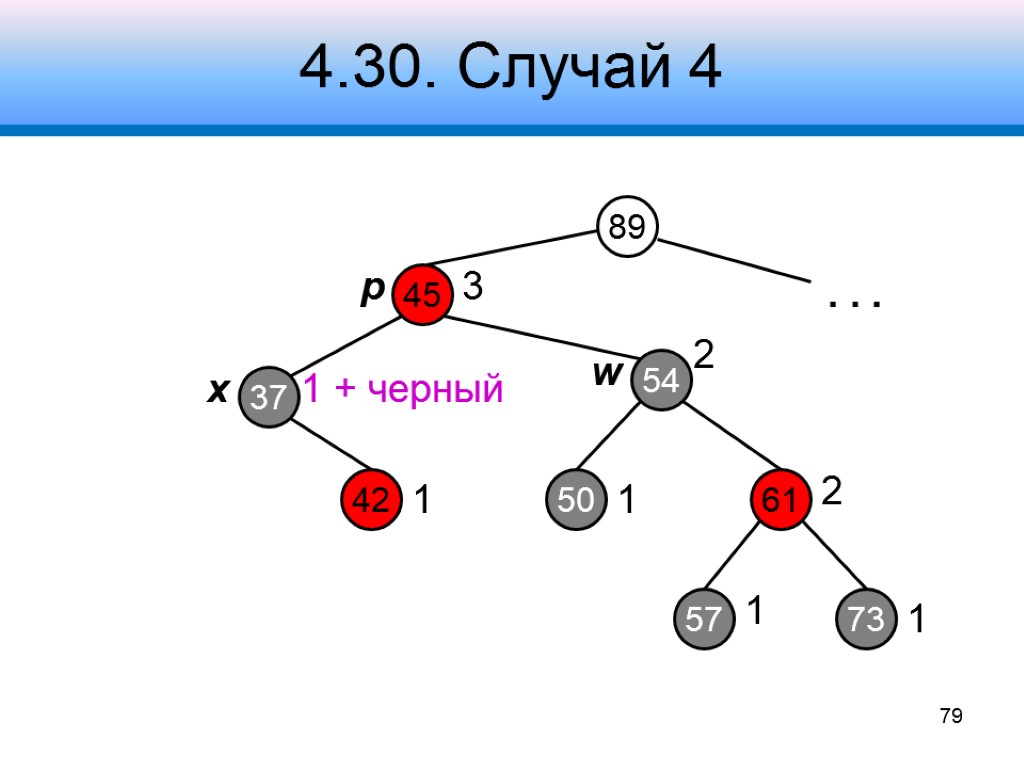
4.30. Случай 4 89 45 61 37 3 54 73 2 2 1 . . . x p w 79 42 50 57 1 1 1 + черный 1

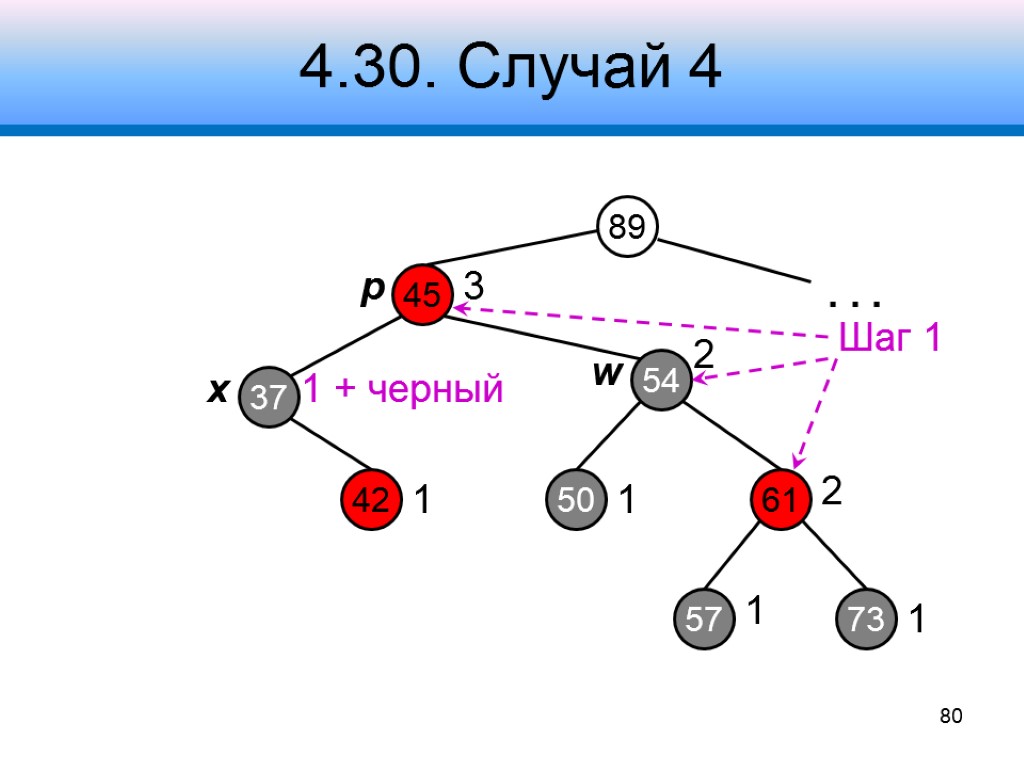
4.30. Случай 4 89 45 61 37 3 54 73 2 2 1 . . . x p w 80 42 50 57 1 1 1 + черный 1 Шаг 1

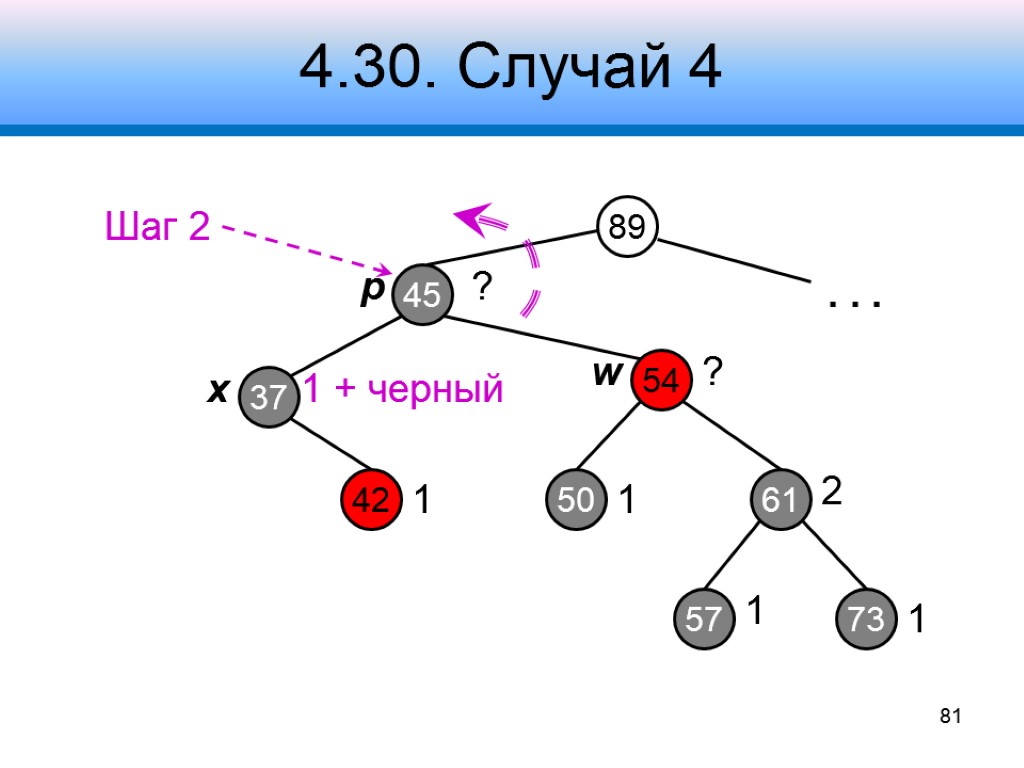
4.30. Случай 4 89 45 61 37 ? 54 73 2 ? 1 . . . x p w 81 42 50 57 1 1 1 + черный 1 Шаг 2

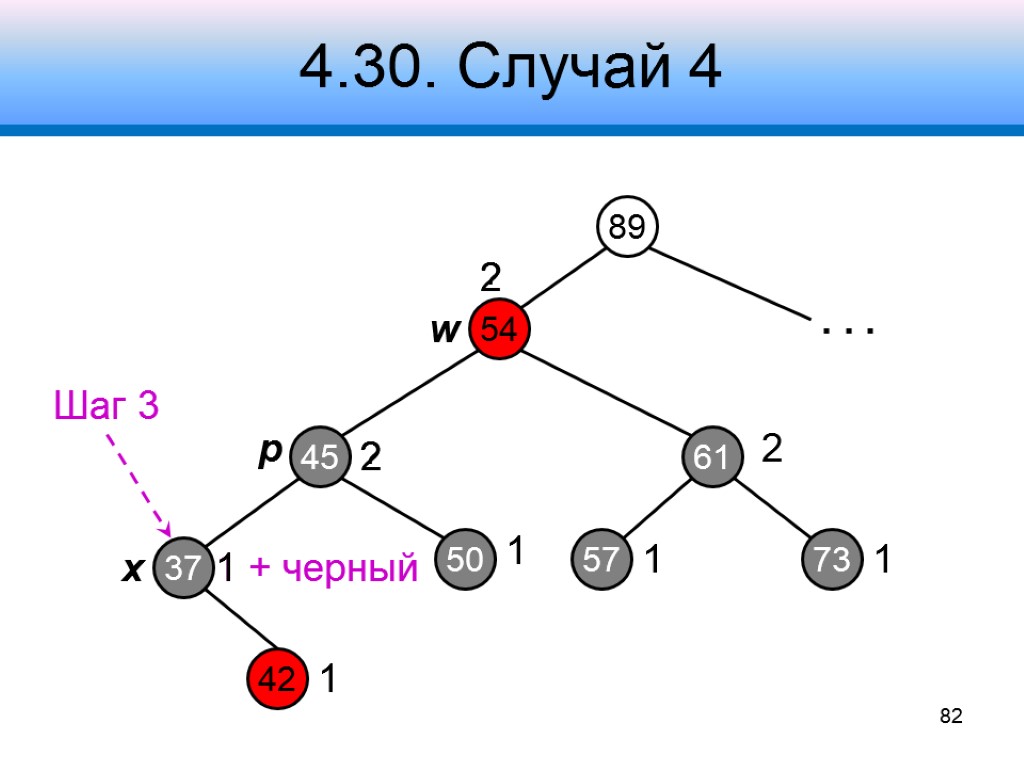
4.30. Случай 4 89 45 61 37 ? 54 73 2 2 1 . . . x p w 82 42 50 57 1 1 1 + черный 1 Шаг 3 1 2 ?

4.31. RB_Delete_Fixup(x) Обозначения: x – анализируемый узел дерева p = x->parent – родительский узел w = p->right (или p->left) – второй потомок узла p x – дважды черный узел 83

4.31. RB_Delete_Fixup(x) while продолжать итерации: x ≠ root и x->color == BLACK { проверка, в каком поддереве лежит x: p = x->parent if х – в левом поддереве: x == p->left { # 1 – начало w = p->right анализ возможных ситуаций 84

4.31. RB_Delete_Fixup(x) if w – красый: w->color == RED { – случай 1 поменять цвета у w и p: w->color = BLACK p->color = RED выполнить левый поворот вокруг p: Left_Rotate(p) w = p->right } 85

4.31. RB_Delete_Fixup(x) if у w оба потомка черные: w->left->color == BLACK и w->right->color == BLACK { – случай 2 забрать черную окраску у w: w->color = RED переместиться вверх по дереву: x = p } 86

4.31. RB_Delete_Fixup(x) else { if правый потомок w черный: w->right->color == BLACK { – случай 3 поменять цвета у w и w->left: w->color = RED w->left->color = BLACK правый поворот вокруг w: Right_Rotate(w) w = p->right } 87

4.31. RB_Delete_Fixup(x) – случай 4 поменять цвета: w->color = p->color p->color = BLACK w->right->color = BLACK левый поворот вокруг узла p Left_Rotate(p) x = root } } # 1 – конец 88

4.31. RB_Delete_Fixup(x) else { повторить коды между #1 – начало и #1 – конец, заменив left на right, и наоборот } } x->color = BLACK 89