Скачать презентацию 4 Імовірнісне моделювання 4 1 Моделювання випадкових Скачать презентацию 4 Імовірнісне моделювання 4 1 Моделювання випадкових

L4.ppt

  • Количество слайдов: 29

4. Імовірнісне моделювання 4. Імовірнісне моделювання

4. 1. Моделювання випадкових подій та дискретних величин Закон розподілу випадкових величин, якими можуть 4. 1. Моделювання випадкових подій та дискретних величин Закон розподілу випадкових величин, якими можуть бути попит, відмови устаткування, потреби, витрати та ін. – є основою імітаційного моделювання. Важливо зрозуміти цей закон. Подія (“випадкова подія”) – всякий факт, який може відбутися або не відбутися. Ймоврністю події називається чисельна міра ступеня об’єктивної можливості цієї події. (Наприклад, ймовірність події А: Р(А)=m/n, де n – загальна кількість випадків, m – кількість випадків, сприятливих події А).

Достовірною називається подія В, що в результаті досвіду неодмінно відбудеться: Р(В)=1. Неможливою називається подія Достовірною називається подія В, що в результаті досвіду неодмінно відбудеться: Р(В)=1. Неможливою називається подія С, що в результаті досвіду не може відбутися: Р(С)=0. Ймовірність будь-якої події А: 0 ≤ Р(А) ≤ 1. Випадкова величина – це величина, яка в результаті досвіду може приймати те чи інше значення, яке невідомо заздалегідь. Випадкові величини бувають дискретними або неперервними. Законом розподілу випадкової величини називається будь-яка відповідність, що встановляє зв’язок між можливими значеннями випадкової величини та відповідними ймовірностями.

МОДЕЛЮВАННЯ ВИПАДКОВИХ ПОДІЙ 4. 1. 1. Моделювання простої події • Припустимо є подія А, МОДЕЛЮВАННЯ ВИПАДКОВИХ ПОДІЙ 4. 1. 1. Моделювання простої події • Припустимо є подія А, ймовірність настання якого дорівнює РА. Потрібно виробити правило, при багатократному використанні якого частота появи події прямувала до його ймовірності. • Обираємо за допомогою датчика випадкових чисел, рівномірно розподілених у інтервалі (0, 1) деяке число z і визначимо ймовірність того, що z < P(A). Для випадкової величини z з рівномірним розподілом є справедливою залежність: • (4. 1) • Таким чином, ймовірність влучення випадкової величини у інтервал (0, РА) дорівнює величині РА. Тому, якщо при розиграшу число z потрапило у цей інтервал, то вважаємо, що подія А відбулася. Протилежна подія (не А) не відбудеться з ймовірністю (1 РА) у тому випадку, коли z PA.

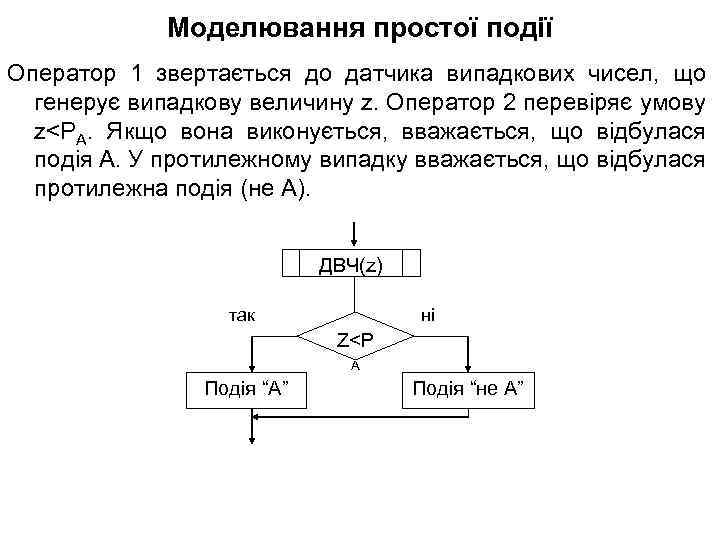Моделювання простої події Оператор 1 звертається до датчика випадкових чисел, що генерує випадкову величину Моделювання простої події Оператор 1 звертається до датчика випадкових чисел, що генерує випадкову величину z. Оператор 2 перевіряє умову z

4. 1. 2. Моделювання повної групи несумісних подій Повною групою подій називають кілька подій 4. 1. 2. Моделювання повної групи несумісних подій Повною групою подій називають кілька подій таких, що в результаті досвіду має відбутися одна з них. Кілька подій в одному досвіді називаються несумісними, якщо жодні дві з них не можуть настати разом. Нехай маємо повну групу несумісних подій (ПГНП) А 1, А 2, . . . , Аk з ймовірностями P 1, P 2, … Pk. При цьому виконується умова • Розділимо інтервал (0, 1) на k відрізків, довжини яких складають Р 1, Р 2, . . . , Рk. • Якщо випадкове число z, яке згенероване датчиком 1 випадкових чисел з рівномірним розподілом у інтервалі (0, 1), потрапило, наприклад, на відрізок Pk 1, то це означає, що відбулася подія Аk 1.

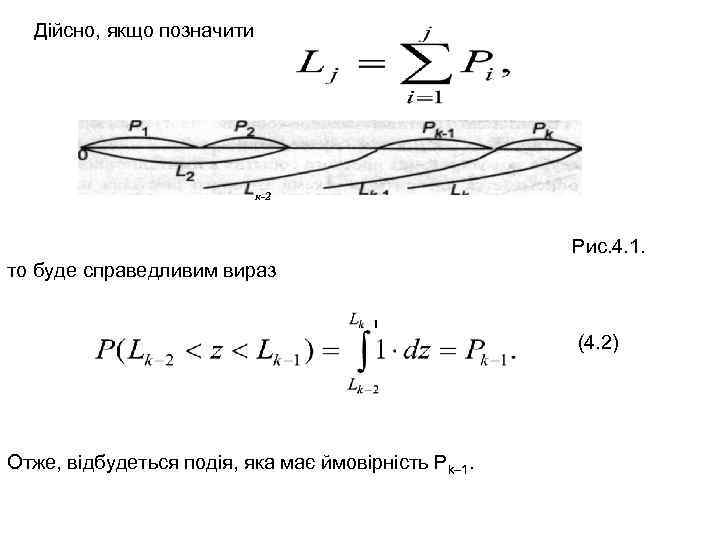Дійсно, якщо позначити к-2 Рис. 4. 1. то буде справедливим вираз (4. 2) Отже, Дійсно, якщо позначити к-2 Рис. 4. 1. то буде справедливим вираз (4. 2) Отже, відбудеться подія, яка має ймовірність Рk 1.

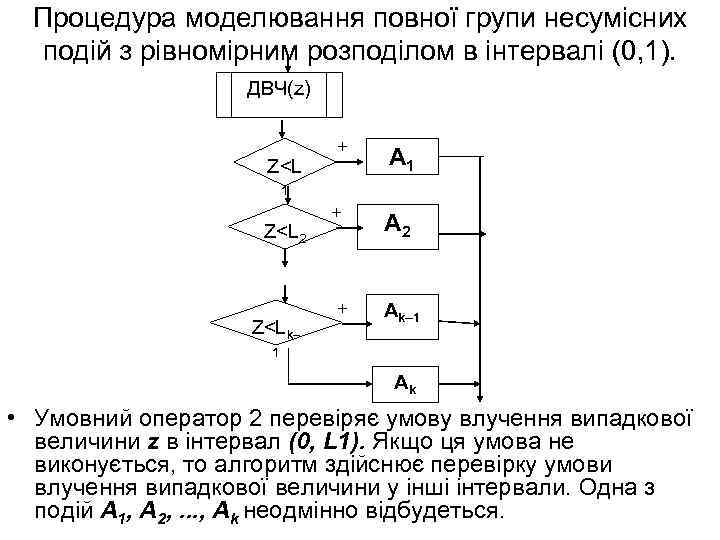Процедура моделювання повної групи несумісних подій з рівномірним розподілом в інтервалі (0, 1). ДВЧ(z) Процедура моделювання повної групи несумісних подій з рівномірним розподілом в інтервалі (0, 1). ДВЧ(z) Z

4. 1. 3. Моделювання дискретної випадкової величини Дискретна випадкова величина може бути задана табличною 4. 1. 3. Моделювання дискретної випадкової величини Дискретна випадкова величина може бути задана табличною залежністю: X x 1 x 2 … xn P p 1 p 2 … pn Тут pj ймовірність того, що дискретна випадкова величина Х прийме значення xj. При цьому p 1+p 2+…+pn=1. Розділимо інтервал (0, 1) на n відрізків, довжини яких пропорційні заданим ймовірностям.

• Якщо випадкове число z, що задається датчиком випадкових чисел, рівномірно розподілених в • Якщо випадкове число z, що задається датчиком випадкових чисел, рівномірно розподілених в інтервалі (0, 1), влучає в інтервал Рk, то випадкова величина X прийме значення xk. • Таким чином, при моделюванні дискретних випадкових величин фактично використовується та ж процедура, що й при моделюванні ПГНС.

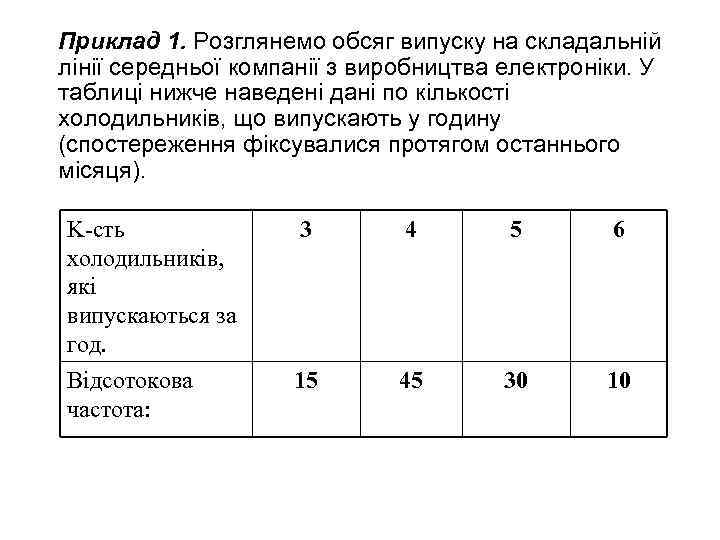Приклад 1. Розглянемо обсяг випуску на складальній лінії середньої компанії з виробництва електроніки. У Приклад 1. Розглянемо обсяг випуску на складальній лінії середньої компанії з виробництва електроніки. У таблиці нижче наведені дані по кількості холодильників, що випускають у годину (спостереження фіксувалися протягом останнього місяця). K-сть холодильників, які випускаються за год. Відсотокова частота: 3 4 5 6 15 45 30 10

Щоб змоделювати процес випуску, ми можемо довільно вибрати число, яке відповідає 100 досвідів, і Щоб змоделювати процес випуску, ми можемо довільно вибрати число, яке відповідає 100 досвідів, і використати перші 15% чисел із загальної кількості для відображення випуску 3 штук. Аналогічно, наступні 45% цих чисел будуть відображати випуск 4 штук, а випуск 5 і 6 штук представлений відповідно наступними 30 і 10%. Існує 100 двозначних випадкових чисел (00 -99). Тобто, перші 15 чисел (00 -14) можуть представляти випуск 3 штук. Наступні – 45 – випуск 4 штук і т. д. Все це можна звести в таблицю, як це показано нижче: Обсяг випуску на годину: 3 Випадкові числа: 00 -14 4 15 -59 5 60 -89 6 90 -99 Таким чином, будь-яке випадкове число від 00 до 14 покаже на випуск 3 штук, від 15 до 59 — на випуск 4 штук і т. д. Отже, якщо було згенероване випадкове число 72, то воно відповідає випуску 5 штук (тому що воно знаходиться в діапазоні від 60 до 89).

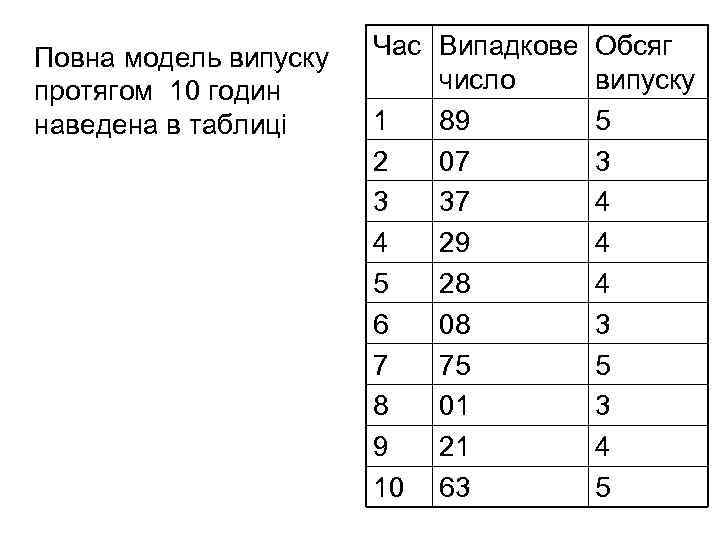Повна модель випуску протягом 10 годин наведена в таблиці Час Випадкове число 1 89 Повна модель випуску протягом 10 годин наведена в таблиці Час Випадкове число 1 89 2 07 3 37 4 29 5 28 6 08 7 75 8 01 9 21 10 63 Обсяг випуску 5 3 4 4 4 3 5 3 4 5

4. 1. 4 Рівномірний розподіл • Рівномірний розподіл ймовірностей – це такий розподіл, за 4. 1. 4 Рівномірний розподіл • Рівномірний розподіл ймовірностей – це такий розподіл, за яким всі значення у проміжку заданого діапазону можуть наступати з однаковою ймовірністю Р=1/m, де m – число можливих випадків. • Такий розподіл використовується, коли має місце випадковий альтернативний вибір: нового товару, стратегії розвитку підприємства, і заздалегідь невідомі вигоди кожного варіанту.

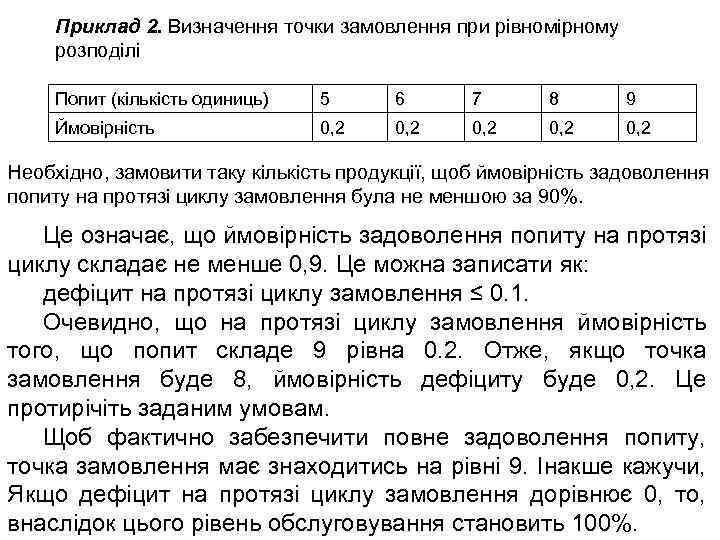Приклад 2. Визначення точки замовлення при рівномірному розподілі Попит (кількість одиниць) 5 6 7 Приклад 2. Визначення точки замовлення при рівномірному розподілі Попит (кількість одиниць) 5 6 7 8 9 Ймовірність 0, 2 0, 2 Необхідно, замовити таку кількість продукції, щоб ймовірність задоволення попиту на протязі циклу замовлення була не меншою за 90%. Це означає, що ймовірність задоволення попиту на протязі циклу складає не менше 0, 9. Це можна записати як: дефіцит на протязі циклу замовлення ≤ 0. 1. Очевидно, що на протязі циклу замовлення ймовірність того, що попит складе 9 рівна 0. 2. Отже, якщо точка замовлення буде 8, ймовірність дефіциту буде 0, 2. Це протирічіть заданим умовам. Щоб фактично забезпечити повне задоволення попиту, точка замовлення має знаходитись на рівні 9. Інакше кажучи, Якщо дефіцит на протязі циклу замовлення дорівнює 0, то, внаслідок цього рівень обслуговування становить 100%.

1. 1. 4. Біноміальний розподіл Розподіл випадкових величин, за яким може бути лише два 1. 1. 4. Біноміальний розподіл Розподіл випадкових величин, за яким може бути лише два значення: 1 – “true” та 0 – “false”. Використовується, коли оцінюється робота виконана чи ні, виріб нормальний чи бракований. Ймовірність m успішних наслідків у n незалежних випробуваннях: Функція розподілу ймовірностей має вигляд:

Залежно від n можна обрати один із двох способів моделювання. За невеликих n значення Залежно від n можна обрати один із двох способів моделювання. За невеликих n значення випадкової біноміально розподіленої величини визначається як кількість чисел у послідовності {ri} з n чисел, які не перевищують значення р. Приклад 3. Потрібно отримати випадкову величину, яка належить біноміальному розподілу з параметрами n=10, p=0, 2. Для цього спочатку генеруємо 10 випадкових значень на проміжку (0, 1): 0, 03; 0, 15; 0, 9; 0, 54; 0, 76; 0, 85; 0, 19; 0, 31; 0, 27; 0, 49. А потім рахуємо ті з них, які менше р. У даному випадку тільки три з них менші за 0, 2. Таким чином, значення випадкової величини дорівнює 3.

Для великих значень n і малих р моделювання здійснюється таким чином. Генеруються рівномірно розподілені Для великих значень n і малих р моделювання здійснюється таким чином. Генеруються рівномірно розподілені випадкові числа ri доти, доки не виконається умова: Значення випадкової величини з біноміальним розподілом дорівнює кількості випробувань n, які провели до виконання умови (4. 4).

4. 2. Моделювання неперервних випадкових величин У попередніх розділах ми познайомились з дискретним розподілом, 4. 2. Моделювання неперервних випадкових величин У попередніх розділах ми познайомились з дискретним розподілом, коли змінна, що досліджується, могла приймати лише визначені значення. У цьому розділі ми розглянемо неперервний розподіл, коли досліджувана змінна може приймати будь-яке значення у межах даного діапазону. 4. 2. 1. Метод оберненої функції Припустимо маємо деяку неперервну випадкову величину х, яка задана функцією розподілу F(x). Можна довести, що значення цієї функції рівномірно розподілені в інтервалі (0, 1). Тому між випадковою величиною z, рівномірно розподіленою у тому ж інтервалі, та функцією розподілу випадкової величини х існує взаємно однозначна відповідність, тобто z = F(x) (4. 5) Звідси x = F-1(z) (4. 6) Де – F-1 обернена функція. Отже, якщо рівняння (4. 5) має аналітичний розв’язок, то для моделювання випадкової величини х можна використати датчик випадкових чисел, що генерує величину z, а потім здійснити розрахунок за формулою (4. 6).

4. 2. 2. Моделювання випадкових величин з показниковим розподілом Якщо маємо випадкову величину х 4. 2. 2. Моделювання випадкових величин з показниковим розподілом Якщо маємо випадкову величину х з показниковим розподілом, то функція розподілу має вигляд: F(x) = 1 - e-λx, де λ – параметр розподілу. Застосуємо метод оберненої функції: z = F(x) = 1 - e-λx Звідси х = -ln(1 -z)/λ (4. 7) Оскільки випадкова величина (1 -z) має також рівномірний розподіл на інтервалі (0, 1), то (4. 7) можна замінити співвідношенням: x = -ln(z)/λ (4. 8)

4. 2. 3. Моделювання випадкових величин з нормальним розподілом Метод оберненої функції не застосовується 4. 2. 3. Моделювання випадкових величин з нормальним розподілом Метод оберненої функції не застосовується до нормального розподілу, оскільки після підстановки відповідної функції розподілу вираз (4. 5) не має аналітичного розв’язку. Нормальний розподіл є одним з найважливіших для прийняття управлінських рішень. Среднє арифметичне = m Рис. 4. 2. Нормальний розподіл

m, σ – параметри нормального розподілу: m – математичне очікування: σ – середнє квадратичне m, σ – параметри нормального розподілу: m – математичне очікування: σ – середнє квадратичне відхилення: σ2 – дисперсія. За нормальним законом зазвичай розподіляються: відсоток браку; точність виготовлення деталей; параметри технологічного процесу виготовлення; величини температури, тиску, вологості, сили струму тощо.

Нормальний закон розподілу • Випадкова величина Х має нормальний розподіл, якщо її щільність розподілу Нормальний закон розподілу • Випадкова величина Х має нормальний розподіл, якщо її щільність розподілу ймовірностей описується виразом: • Функція розподілу нормально розподіленої величини:

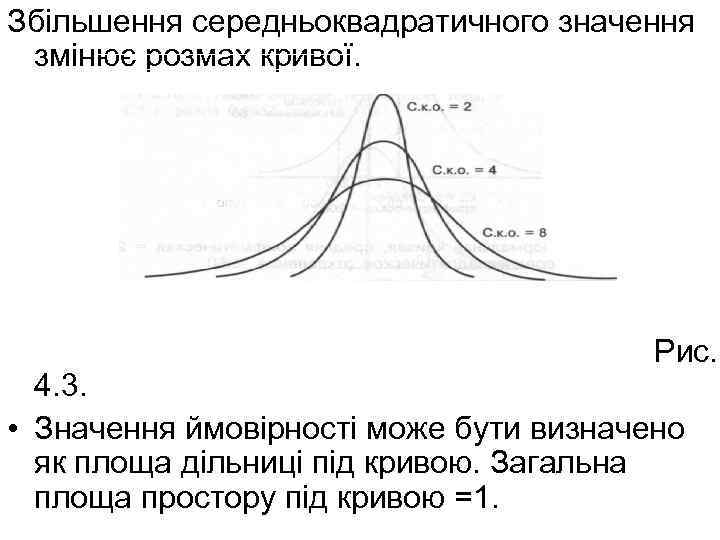Збільшення середньоквадратичного значення змінює розмах кривої. Рис. 4. 3. • Значення ймовірності може бути Збільшення середньоквадратичного значення змінює розмах кривої. Рис. 4. 3. • Значення ймовірності може бути визначено як площа дільниці під кривою. Загальна площа простору під кривою =1.

• Визначення площі під нормальною кривою потребує складної математичної формули. Тому використовують таблиці • Визначення площі під нормальною кривою потребує складної математичної формули. Тому використовують таблиці “Стандартного нормального розподілу”, де m=0, σ=1. • Будь-який нормальний розподіл із заданими m та σ можна привести до стандартного за формулою:

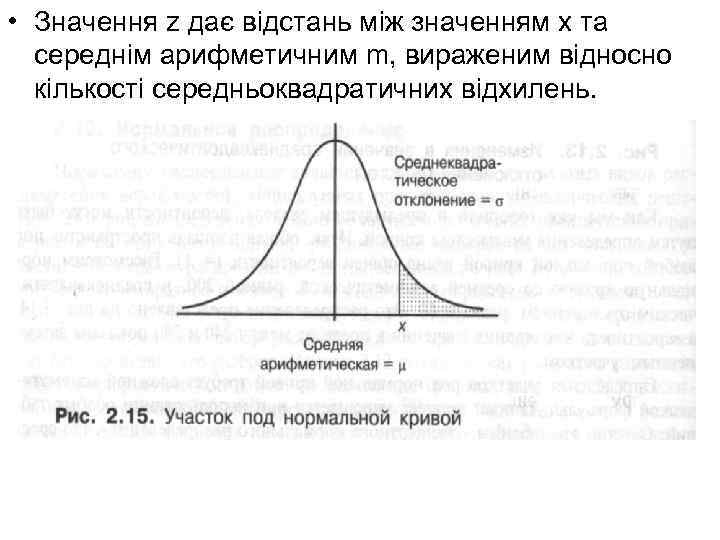• Значення z дає відстань між значенням х та середнім арифметичним m, вираженим • Значення z дає відстань між значенням х та середнім арифметичним m, вираженим відносно кількості середньоквадратичних відхилень.

Приклад. Вибіркове дослідження показало, що вага упаковки шоколаду описується нормальним розподілом із середнім значенням Приклад. Вибіркове дослідження показало, що вага упаковки шоколаду описується нормальним розподілом із середнім значенням 400 г и середньоквадратичним відхиленням в 20 г. Визначити ймовірність того, що довільна упаковка буде важити: А) більше 425 г б) до 410 г А) Знайдемо ймовірність як площу затемненої ділянки (рис. 2. 15) за х=425. Спочатку визначимо величину стандартного відхилення: Тепер за допомогою таблиці при z=1, 25 знайдемо площу затемненої дільниці, вона дорівнює 0, 1057. Отже, ймовірність того, що упаковка важить більше 425 г дорівнює 0, 1057.

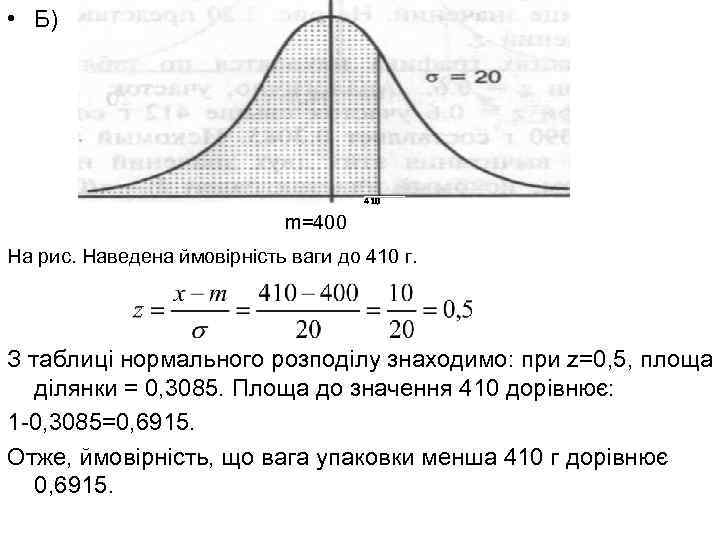• Б) 410 m=400 На рис. Наведена ймовірність ваги до 410 г. З • Б) 410 m=400 На рис. Наведена ймовірність ваги до 410 г. З таблиці нормального розподілу знаходимо: при z=0, 5, площа ділянки = 0, 3085. Площа до значення 410 дорівнює: 1 -0, 3085=0, 6915. Отже, ймовірність, що вага упаковки менша 410 г дорівнює 0, 6915.

Розглянемо нормальний розподіл з середнім m=200, середньоквадратичним відхиленням σ=50. Ймовірність знаходження значення між 240 Розглянемо нормальний розподіл з середнім m=200, середньоквадратичним відхиленням σ=50. Ймовірність знаходження значення між 240 і 280 наведено на рис. m=200 240 280 P{240 ≤ x ≤ 280} = P{240 ≤ x } - P{280 ≤ x } Обчислимо: З таблиці нормального розподілу знаходимо ймовірність для z 1 буде 0, 2119, для z 2 - 0, 0548. Отже, P{240 ≤ x ≤ 280} = 0, 2119 – 0. 0548 = 0, 1571.