4 Дифференциальные уравнения 1 -го порядка

§ 4 Дифференциальные уравнения 1 -го порядка § 4. 1 Основные понятия

Дифференциальным уравнением называется равенство, связывающее между собой независимую переменную x, функцию y(x) и ее производные. l l l Порядком ДУ называется порядок старшей производной, входящей в уравнение Решением ДУ называется такая дифференцируемая функция, определенная на некотором интервале, которая при подстановке в уравнение обращает его в тождество. Процесс нахождения всех решений ДУ называется интегрированием.

Пример. Задачей Коши или начальной задачей называют задачу нахождения решения по начальному условию: у(x 0)=y 0

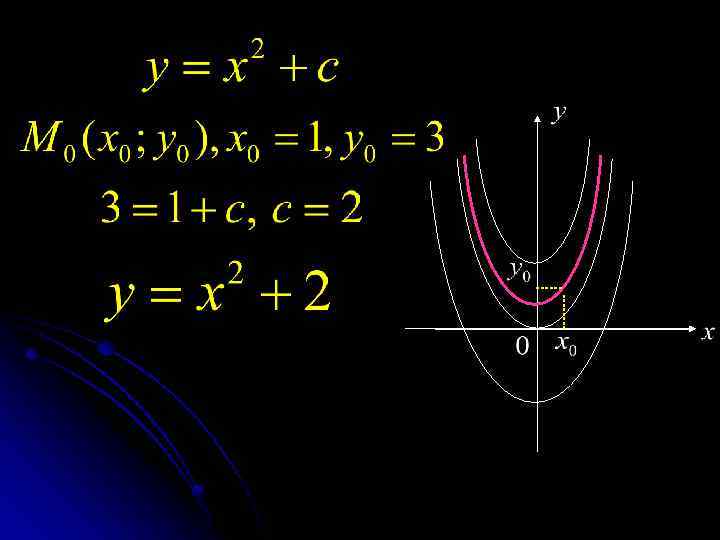
Соотношение связывающее между собой независимую переменную x, функцию y(x) и ее производную называется дифференциальным уравнением 1 -го порядка. (2) - уравнение, разрешенное относительно производной (3)- уравнение “в дифференциалах”

Переход от (2) к (3) и обратно происходит с помощью замены: При этом может измениться только область задания уравнения Решением ДУ (1) будет дифференцируемая функция определенная на некотором интервале a; b , которая при подстановке в уравнение обращает его в тождество.

Общим решением ДУ 1 -го порядка называется функция где С – произвольная константа, что: 1) функция является решением ДУ. 2) для любого допустимого начального условия найдется точка , что Частное решение – это функция получаемая из общего решения при конкретном значении произвольной постоянной. ,

С геометрической точки зрения общее решение – это множество интегральных кривых С геометрической точки зрения частное решение – это одна интегральная кривая из семейства. Задача Коши – это задача отыскания частного решения по начальному условию

Т-ма (о существовании и единственности решения задачи Коши): Пусть в ДУ функция и непрерывны в некоторой области D плоскости OXY. Тогда для любой точки существует и единственное решение этого уравнения, удовлетворяющее начальному условию

Геометрический смысл теоремы состоит в том, что через каждую точку (x 0; y 0) области D проходит одна и только одна интегральная кривая дифференциального уравнения

Решение, в каждой точке которого нарушаются условия теоремы существования и единственности решения задачи Коши называется особым. Особое решение не может быть получено из общего ни при каких числовых значениях константы С, включая

Пример. Решением является также функция y=0. Это решение нельзя получить из общего решения ни при каком числовом значении константы С.

Геометрическое толкование ДУ 1 -го порядка: уравнение устанавливает связь между координатами точки и угловым коэффициентом касательной к интегральной кривой, проходящей через эту точку.

ДУ задает поле направлений. Геометрически направление можно изобразить стрелкой, проходящей через эту точку. Решение этого дифференциального уравнения есть интегральная кривая, направление касательной к которой в каждой точке совпадает с направлением поля в этой точке.

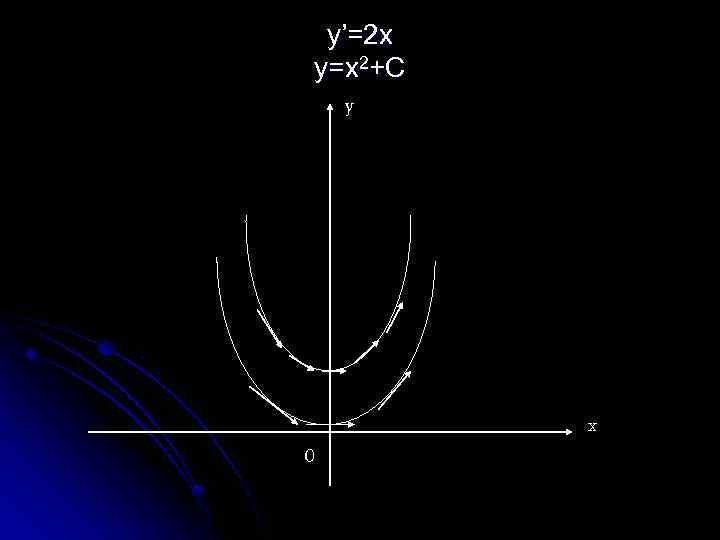y’=2 x y=x 2+C y x 0

§ 4. 2. Дифференциальные уравнения с разделяющимися переменными

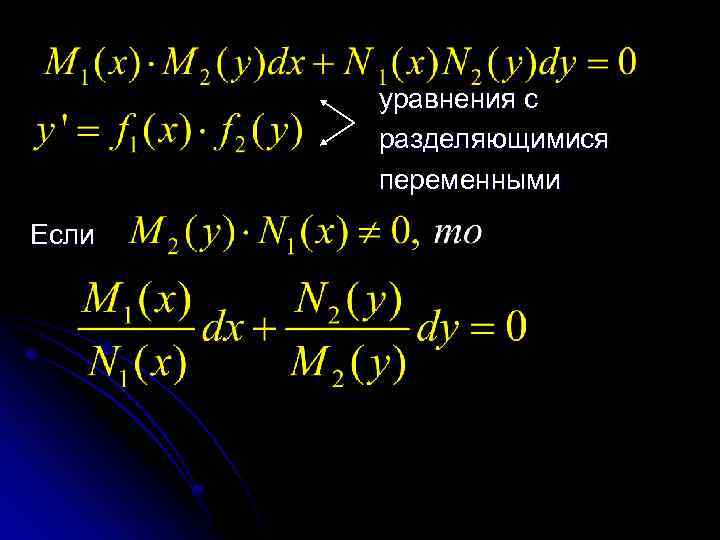уравнения с разделяющимися переменными Если

Действительные корни уравнений также являются решениями исходного уравнения. Только они могут оказаться особыми решениями

Пример. - общее решение в области

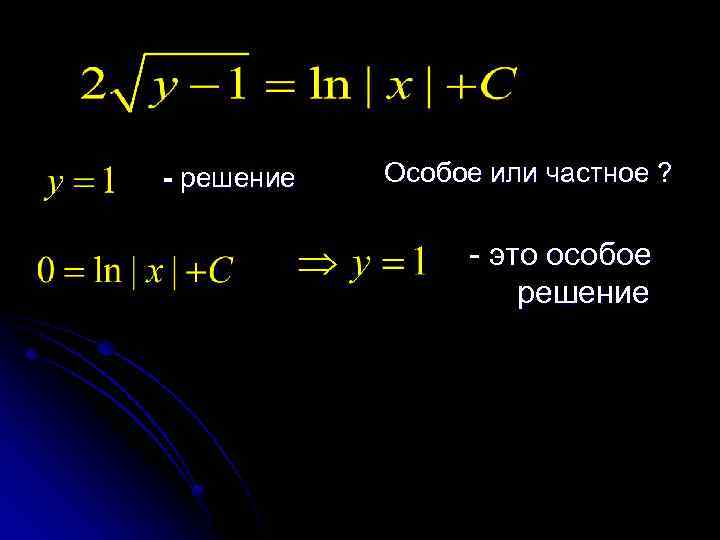- решение Особое или частное ? - это особое решение

Задача. В благоприятных для размножения условиях находится N 0 бактерий. Известно, что скорость размножения бактерий пропорциональна их количеству. Найти закон роста числа бактерий с течением времени Пусть N(t) - количество размножающихся бактерий в момент времени t: N(0)=N 0. l N’(t)=k. N(t), k>0 l

Получили уравнение с разделяющимися переменными

N(t)=Cekt - общее решение l Воспользуемся условием N(0)=N 0 , откуда N 0=C. l Окончательно получим N(t)=N 0 ekt l закон роста числа бактерий с течением времени

Математическая модель рекламы В СМИ дается реклама для ускорения реализации некоторой продукции. Найти закон распространения известий о наличии этой продукции. Решение. Пусть N – число потенциальных покупателей, то в момент времени t о наличии продукции знает y(t) покупателей.

Известно, что скорость распространения информации (скорость изменения функции y(t) ) прямо пропорциональна как числу знающих о продукции, так и числу не знающих. Получили уравнение с разделяющимися Переменными (найти решение самостоятельно)

- уравнения с разделяющимися переменными

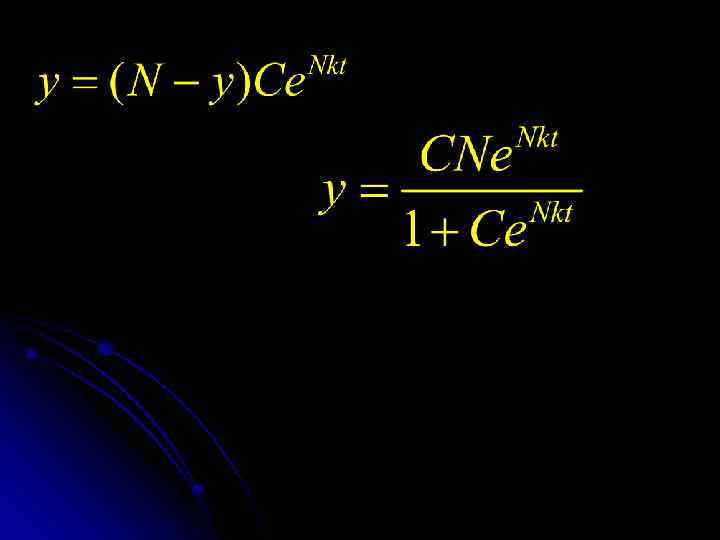
§ 4. 3 Однородные дифференциальные уравнения 1 -го порядка

- однородная функция нулевой степени - однородные функции одной степени

положив t=1/x , получим однородное ДУ сводится к уравнению с разделяющимися переменными относительно новой функции u(x) путем замены

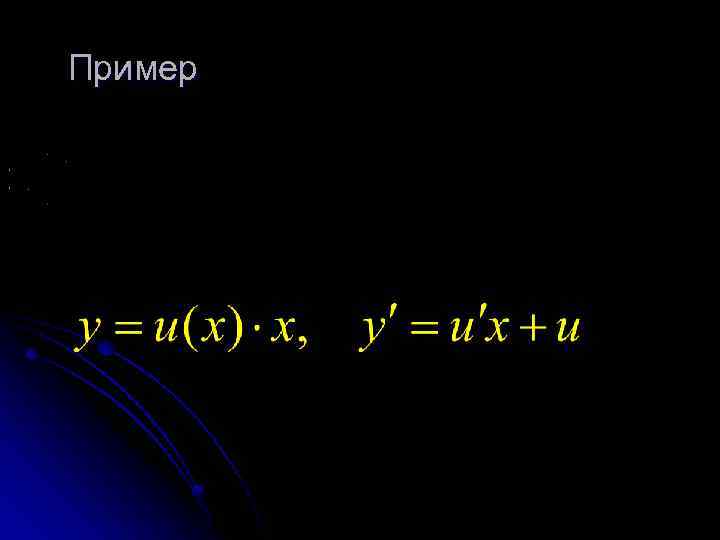Пример

§ 4. 4 Линейные уравнения 1 -го порядка. Уравнение Бернулли

- неоднородное линейное Если , то - однородное линейное уравнение I Метод Бернулли (метод подстановки) Решение уравнения ищется в виде произведения двух функций , где

Тогда Подставим все в исходное уравнение Будем подбирать функцию v(x) такой, чтобы выражение в скобках было равно нулю.

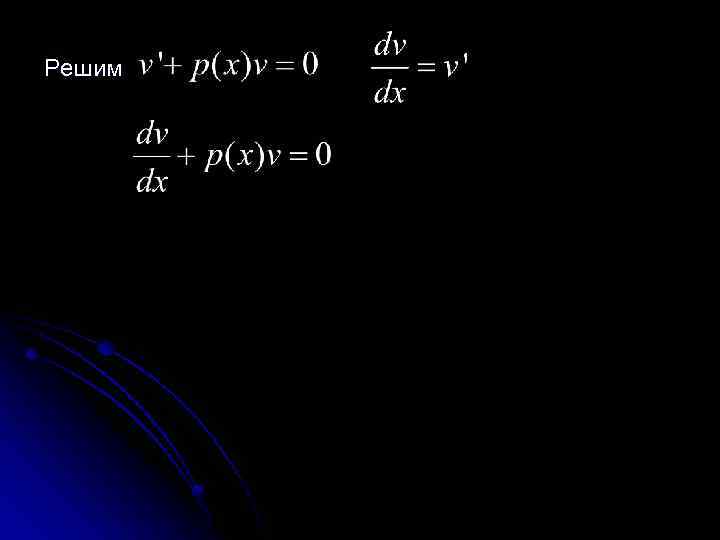Решим

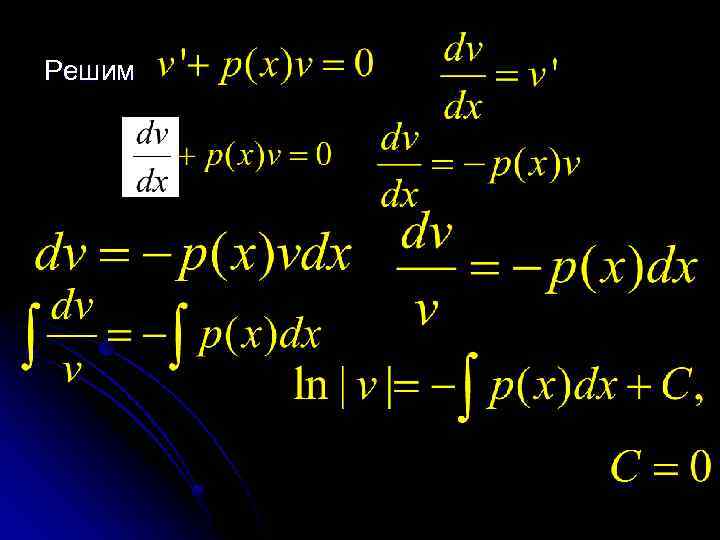Решим

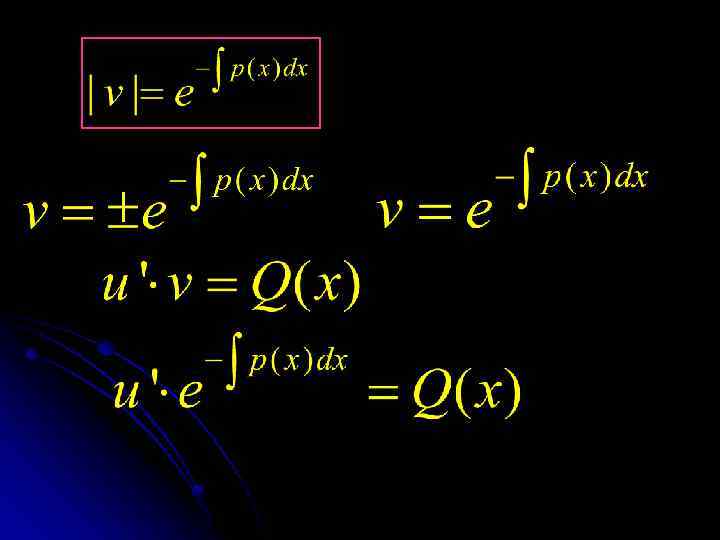
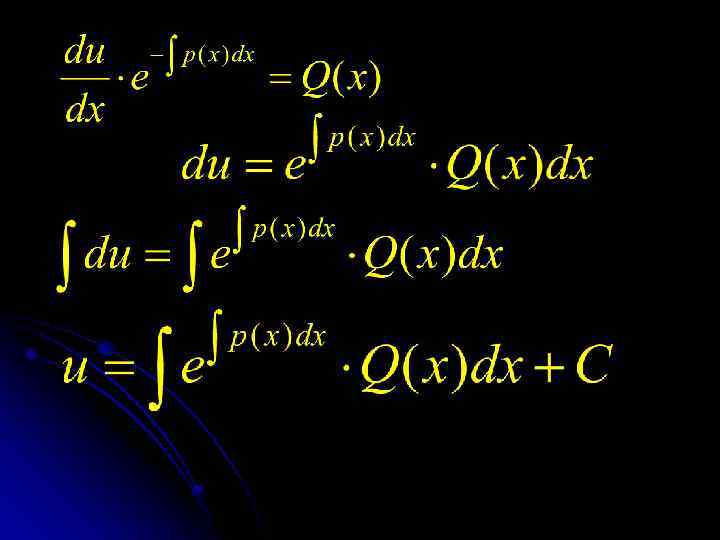
Общее решение исходного уравнения:

Пример. l Сделаем подстановку

Найдем одно частное решение первого уравнения системы l Найдем все семейство решений последнего уравнения

Решением исходного уравнения будет функция

II. Метод вариации произвольной постоянной Пример. Рассмотрим линейное однородное уравнение. Оно всегда является уравнением с разделяющимися переменными

l Будем варьировать произвольную постоянную в формуле общего решения однородного уравнения. То есть предположим, что С не константа, а некоторая неизвестная функция С=С(х). Станем искать решение неоднородного уравнения в виде

подставим все в исходное уравнение

Получим уравнение

Подставляем найденную функцию С(х) в формулу общего решения неоднородного уравнения. Получим

II Метод Лагранжа (метод вариации произвольной постоянной) Найдем решение в общем виде. Рассмотрим линейное однородное уравнение. Это уравнение с разделяющимися переменными

- общее решение однородного уравнения Варьируем произвольную постоянную, т. е. общее решение исходного неоднородного уравнения будем искать в виде - неизвестная функция

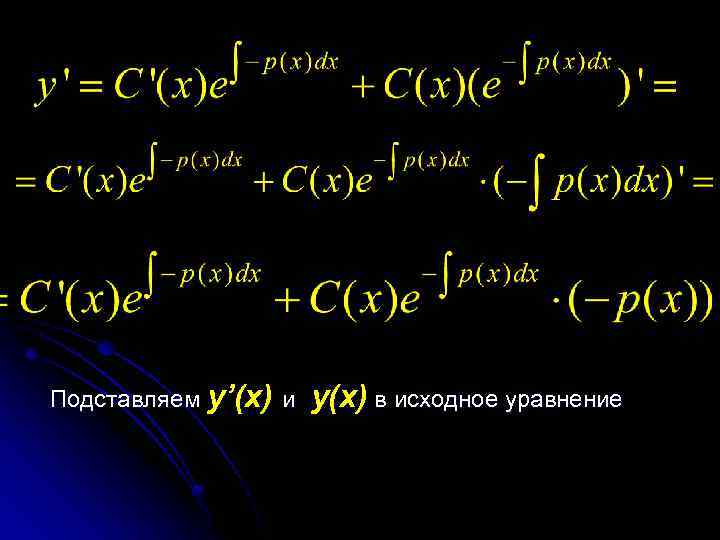Подставляем y’(x) и y(x) в исходное уравнение

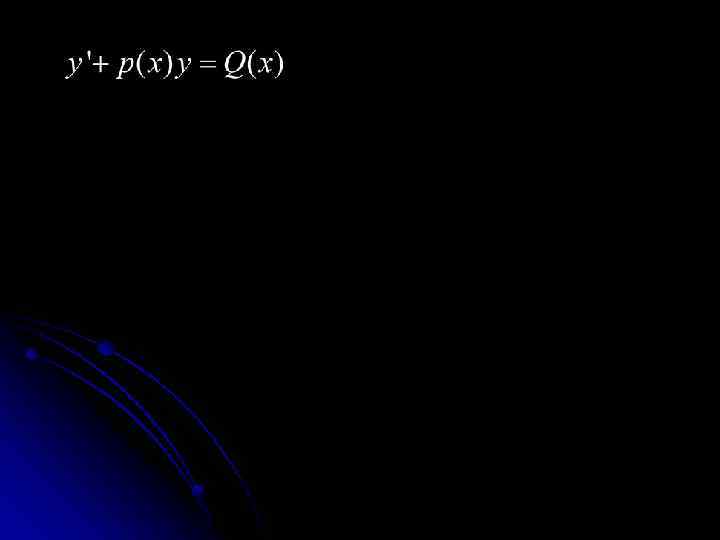
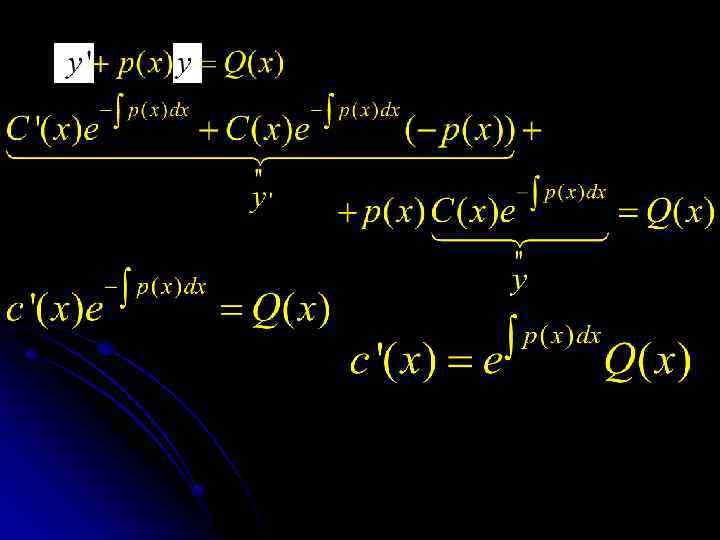
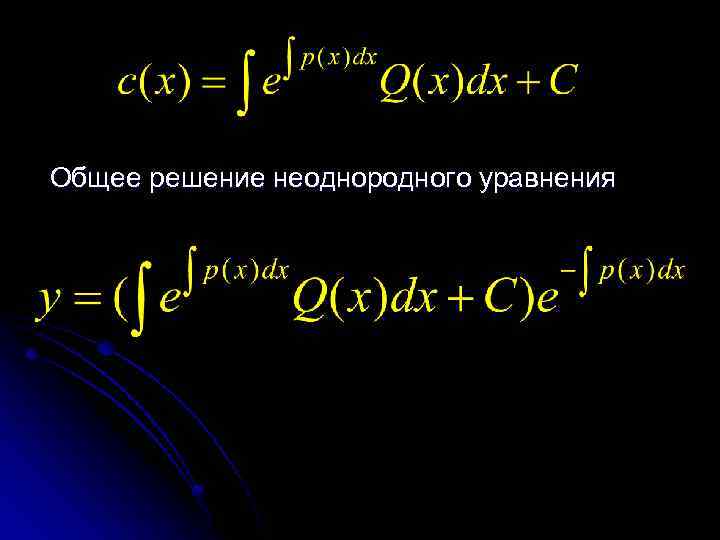Общее решение неоднородного уравнения

Уравнение Бернулли Если , то это линейное ДУ Если , то это уравнение с разделяющимися переменными Подстановка линейному. сводит уравнение к Однако, при нахождении решений уравнений Бернулли их обычно не преобразовывают в линейные, а сразу применяют подстановку y=uv или метод вариации произвольной постоянной.