Метод Хоара.ppt
- Количество слайдов: 91

4) Алгоритмы обменной сортировки 1. Прямой обмен – «пузырек» 2. Шейкер – сортировка 3. Метод Хоара-1 -2 -3 4. Поиск медианы 5. Побитовая сортировка

1. Прямой обмен – «пузырек» (bubble) Идея метода. Сравниваются пары соседних элементов и выполняется обмен при нарушении упорядоченности. Улучшение метода: «пузырек с флагом» С помощью флага фиксируется факт хотя бы одного обмена на каждом этапе сравнения. Если обмена не было – сортировка закончена.

Пример 4(1) 4(2) 3(1) 3(2) 1(1) 4(3) 4(1) 3(2) 1(1) 4(2) 4(3) 3(1) 1(1) 3(2) 4(1) 4(2) 4(3) Сортировка устойчива!!!
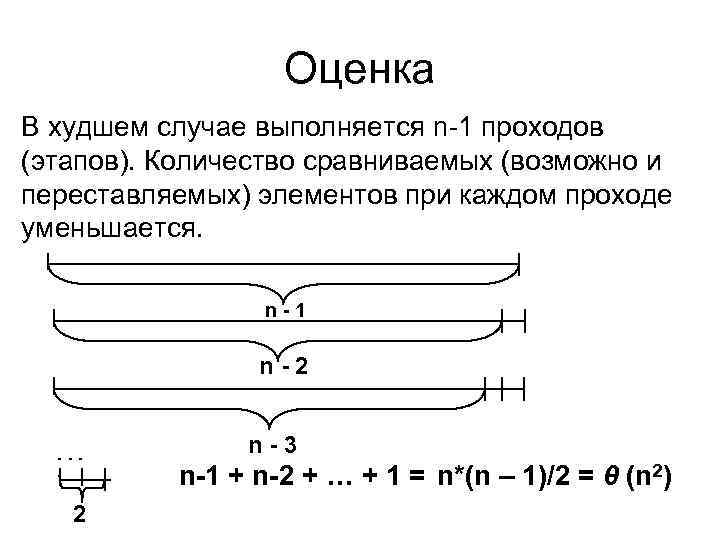
Оценка В худшем случае выполняется n-1 проходов (этапов). Количество сравниваемых (возможно и переставляемых) элементов при каждом проходе уменьшается. n-1 n-2 . . . 2 n-3 n-1 + n-2 + … + 1 = n*(n – 1)/2 = θ (n 2)

2. Шейкер-сортировка Модификация прямого обмена. Учитывает ситуации, когда в начале массива и в конце формируются упорядоченные куски. Проход по массиву выполняется с двух сторон: слева – направо и справа-налево. Фиксируется позиция последнего обмена, с которой и начинается проход в противоположном направлении.
![Прямой обмен (Shaker) [ 44 55 12 42 94 18 06 67 ] [ Прямой обмен (Shaker) [ 44 55 12 42 94 18 06 67 ] [](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-6.jpg)
Прямой обмен (Shaker) [ 44 55 12 42 94 18 06 67 ] [ 44 12 42 55 18 06 67]94 06[44 12 42 55 18 67]94 06[12 42 44 18]55 67 94 06 12 18[42 44]55 67 94 06 12 18|42 44 55 67 94 5 проходов вместо 7! Сложность сортировки θ(n 2)
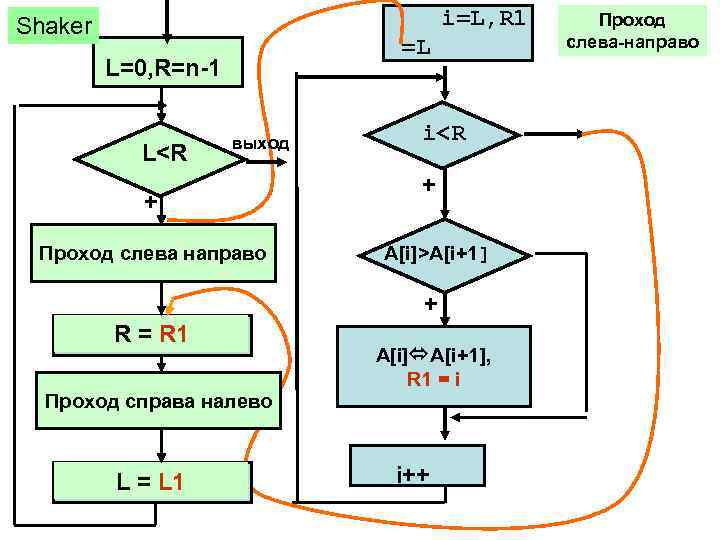
i=L, R 1 Shaker =L L=0, R=n-1 L<R выход + Проход слева направо i<R + A[i]>A[i+1] + R = R 1 Проход справа налево L = L 1 A[i] A[i+1], R 1 = i i++ Проход слева-направо

Обозначения L – номер самого левого элемента текущего прохода, R - самого правого, R 1 – номер левого элемента в последней паре обмена при проходе слева направо, L 1 – номер правого элемента в последней паре обмена при проходе справа налево. Задание. Написать проход справа налево.

Напоминаю На следующей неделе пишем самостоятельную по двум сортировкам - Шелла и пирамидальной. В работу входит • пошаговая иллюстрация работы методов; • определение одной из функций 1) вставка с фиксированным шагом (Шелл) 2) просеивание (Пирамида) • теория: определения сложности алгоритмов θ, O, Ω.

Метод Хоара - алгоритмы быстрой сортировки (Quick. Sort), - задача поиска медианы, - побитовая сортировка

3. Алгоритмы быстрой сортировки (Quick. Sort) Общая идея. На каждом этапе определяется эталонное значение. Текущий фрагмент массива делится на 2: - в одном числа <(<=) эталона; - в другом числа >=(>) эталона. Ниже рассмотрим 3 варианта сортировки Хоара.

Алгоритм Хоар_1 A = 63 42 55 12 04 32 24 05, n=8 r l Пусть дан фрагмент массива [l, r] (в примере [0, 7]), про который известно, что его значения выбирались из интервала [xl, xr] (в примере [0, 99]).

Идея алгоритма xm = (xl + xr)/2 – среднее значение для данного фрагмента ( в примере xm = 49 ). Переставим элементы фрагмента так, чтобы слева были элементы со значениями < xm, справа со значениями xm. Найдем границу между левым и правым подфрагментами. [. . . <xm. . . ][. . xm. . ] Для каждого из подфрагментов повторим описанную выше процедуру. Рекурсия!
![[ 63 42 55 12 04 32 24 05 ] [00, 99], xm [ 63 42 55 12 04 32 24 05 ] [00, 99], xm](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-14.jpg)
[ 63 42 55 12 04 32 24 05 ] [00, 99], xm = 49 [ 05 42 24 12 04 32 ] [ 55 63 ] [0, 48], xm = 24 [49, 99] [ 05 04 12 ] [ 24 42 32 ] [ 55 63 ] [0, 23], xm =11 [24, 48] [ 05 04 ] [ 12 ] [ 24 42 32] [ 55 63 ] [0, 10], xm=5 [11, 23] [ 04] [ 05 ] [ 12 ] [ 24 42 32] [ 55 63 ] [0, 4] [5, 10]
![[ 04] [ 05 ] [ 12 ] [ 24 42 32] [ [ 04] [ 05 ] [ 12 ] [ 24 42 32] [](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-15.jpg)
[ 04] [ 05 ] [ 12 ] [ 24 42 32] [ 55 63 ] [24, 48], xm = 36 [ 04] [ 05 ] [ 12 ] [ 24 32] [ 42] [ 55 63 ] [24, 35], xm=29 [36, 48] [ 04] [ 05 ] [ 12 ] [ 24] [ 32] [42] [ 55 63 ] [24, 28][29, 35] [49, 99], xm=74 [ 04] [05] [ 12 ] [ 24] [ 32] [42] [ 55 63 ][] [49, 73], xm=61 [74, 99] [ 04] [05] [ 12 ] [ 24] [ 32] [42] [ 55 ] [ 63] [] [49, 60][61, 74] [ 04 ][ 05 ][ 12 ][ 24 ][ 32 ][ 42 ] [ 55 ][ 63 ]

Обозначения: A – массив l, r – левый, правый индексы фрагмента, xl, xr – левая, правая границы значений, xm – среднее значение, (float) i – рабочий индекс, изменяется от l до j с шагом +1 j – рабочий индекс, изменяется от r до i с шагом -1

Алгоритм Хоар_1 1. Если l r или xl == xr, то выход. 2. i = l, j = r, xm = (xl+xr)/2 3. Пока i j: 3. 1. пока i j и A[i] < xm увеличиваем i на 1; 3. 2. пока j i и A[j] xm уменьшаем j на 1; 3. 3. если i < j , то A[i] ↔ A[j], увеличить i на 1, уменьшить j на 1. 4. Выполняем эту же процедуру для подмассива от l до j c интервалом значений [xl, xm-0. 5]. 5. Выполняем эту же процедуру для подмассива от i до r c интервалом [xm+0. 5, xr].

Напоминаю На следующей неделе пишем самостоятельную по двум сортировкам - Шелла и пирамидальной. В работу входит • пошаговая иллюстрация работы методов; • определение одной из функций 1) вставка с фиксированным шагом (Шелл) 2) просеивание (Пирамида) • теория: определения сложности алгоритмов θ, O, Ω.

Алгоритм Хоар_2 A = 36 42 55 12 04 32 24 05 n=8 Пусть дан фрагмент массива [l, r] (в нашем примере [0, 7]) Зададимся значением x = A[l] (в этом примере x = 36). Переставим элементы фрагмента так, чтобы: -- слева были элементы со значениями <=x, -- затем само значение x (т. е. x встало на свое место), -- справа элементы со значениями >x. Найдем границы левого и правого подфрагментов. [. . . <=x. . . ] x [. . >x. . ] Для каждого из подфрагментов повторим ( рекурсия! ) описанную выше процедуру.
![A[ l ] [ 36 42 i 55 12 04 32 24 05 ] A[ l ] [ 36 42 i 55 12 04 32 24 05 ]](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-20.jpg)
A[ l ] [ 36 42 i 55 12 04 32 24 05 ] j 36 05 24 12 04 32 j 55 i 42 j 04 ] 36 [ 55 42 ] на своем месте! [ 32 05 24 12 04 05 24 12 | 36 | 55 j i 42 04 | 05 24 12 | 36 | 55 42 04 | 05 | 12 |24 | 32 | 36 | 42 | 55

Помним!? Сегодня пишем самостоятельную по двум сортировкам - Шелла и пирамидальной. В работу входит • пошаговая иллюстрация работы методов; • определение одной из функций 1) вставка с фиксированным шагом (Шелл) 2) просеивание (Пирамида) • теория: определения сложности алгоритмов θ, O, Ω.

Алгоритм сортировки Хоар_2 1. Если l>=r , то выход. 2. Установка i = l+1, j = r, x = A[l] 3. Пока i<=j 3. 1 Пока i<=j и A[i] <=x увеличиваем i на 1. 3. 2 Пока j>=i и A[j] >x уменьшаем j на 1. 3. 3 Если i<j , то A[i] ↔ A[j] и увеличиваем i на 1, и уменьшаем j на единицу. 4. A[l] ↔ A[j], и уменьшаем j на единицу. 5. Выполняем эту же процедуру для подмассива от l до j. 6. Выполняем эту же процедуру для подмассива от i до r.

Быстрая сортировка Хоар_3 A = 36 24 55 12 04 32 24 05 n=8 Пусть дан фрагмент массива [l, r] (в нашем примере [0, 7]) Зададимся значением x, принадлежащим нашему фрагменту (в данном примере возьмем x = 24). (О том, как выбирать x – позже!) Переставим элементы фрагмента так, чтобы: -- слева были элементы со значениями <=x, -- справа элементы со значениями >=x. Найдем границы левого и правого подфрагментов. [. . . <=x. . . ] [. . >=x. . ] Для каждого из подфрагментов повторим ( рекурсия! ) описанную выше процедуру.
![x=24 [ 36 24 55 12 04 32 24 05 ] i j [ x=24 [ 36 24 55 12 04 32 24 05 ] i j [](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-24.jpg)
x=24 [ 36 24 55 12 04 32 24 05 ] i j [ 05 24 55 12 04 32 24 36 ] i j [ 05 24 04 12 55 32 24 36 ] j i [ 05 24 04 12 ][ 55 32 24 36 ] l j i r <=24 >=24 !!!

Алгоритм сортировки Хоар_3 1. Если l >= r , то выход. 2. Установка i = l, j = r, x = A[ ? ] 3. Пока i ≤ j 3. 1 Пока A[i] <x увеличиваем i на 1. 3. 2 Пока A[j] >x уменьшаем j на 1. 3. 3 Если i ≤ j , то A[i] ↔ A[j] и увеличиваем i на 1, и уменьшаем j на единицу. 4. Выполняем эту же процедуру для фрагмента от l до j. 5. Выполняем эту же процедуру для фрагмента от i до r.
![Алгоритмы сортировки методом Хоара Хоар_1: [. . . <xm. . . ][. . xm. Алгоритмы сортировки методом Хоара Хоар_1: [. . . <xm. . . ][. . xm.](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-26.jpg)
Алгоритмы сортировки методом Хоара Хоар_1: [. . . <xm. . . ][. . xm. . ], xm = (xl+xr)/2 Хоар_2: [. . . <=x. . . ] x [. . >x. . ], x = A[l] Хоар_3: [. . . <=x. . . ] [. . >=x. . ], [. . . <=x. . . ] x [. . >=x. . ], x=A[(l+r)/2]
![x=A[(l+r)/2]= A[(0+7)/2]=A[3] [ 07 08 03 07 07 09 07 01 ] i j x=A[(l+r)/2]= A[(0+7)/2]=A[3] [ 07 08 03 07 07 09 07 01 ] i j](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-27.jpg)
x=A[(l+r)/2]= A[(0+7)/2]=A[3] [ 07 08 03 07 07 09 07 01 ] i j [ 01 08 03 07 07 09 07 07 ] i j [ 01 07 03 07 07 09 08 07 ] i j [ 01 07 03 07 ][ 07 09 08 07 ] j i <=07 >=07
![[ 36 35 34 33 37 31 30 29 ] i j [ [ 36 35 34 33 37 31 30 29 ] i j [](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-28.jpg)
[ 36 35 34 33 37 31 30 29 ] i j [ 29 35 34 33 37 31 30 36 ] i j [ 29 30 34 33 37 31 35 36 ] i j [ 29 30 31 33 37 34 35 36 ] i j [ 29 30 31 ] 33 [ 37 34 35 36 ] j i <=33 >=33 3. 3 Если i ≤ j , то A[i] ↔ A[j]

Выбор эталонного значения (x): 1. Необходимо, чтобы это было значение из элементов фрагмента!! 2. Можно выбрать: -- A[l] -- A[r] --A[(l+r)/2] --A[l+random(r-l+1)] -- ….
![Выбор эталонного значения (x): 3. При выборе A[l] или A[r] при исследовании алгоритма на Выбор эталонного значения (x): 3. При выборе A[l] или A[r] при исследовании алгоритма на](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-30.jpg)
Выбор эталонного значения (x): 3. При выборе A[l] или A[r] при исследовании алгоритма на упорядоченных и антиупорядоченных массивах возможно переполнение стека рекурсии, поэтому A[(l+r)/2] или A[l+random(r-l+1)] в наших задачах предпочтительнее.
![x = A[(l+r)/2] [ 01 02 03 04 05 06 07 08 ] i x = A[(l+r)/2] [ 01 02 03 04 05 06 07 08 ] i](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-31.jpg)
x = A[(l+r)/2] [ 01 02 03 04 05 06 07 08 ] i j [ 01 02 03 04 05 06 07 08 ] ij [ 01 02 03 ] 04 [ 05 06 07 08 ] j i <=04 >=04
![x = A[l] [ 01 02 03 04 05 06 07 08 ] i x = A[l] [ 01 02 03 04 05 06 07 08 ] i](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-32.jpg)
x = A[l] [ 01 02 03 04 05 06 07 08 ] i j [01] [02 03 04 05 06 07 08 ] j i [02] [ 03 04 05 06 07 08 ] [ 03] [04 05 06 07 08 ] [04] [05 06 07 08 ] [05] [06 07 08 ] [06] [07 08 ] [07] [08 ] Глубина стека равна (n-1)

Сейчас пишем самостоятельную по двум сортировкам - Шелла и пирамидальной. В работу входит uпошаговая иллюстрация работы методов; u определение одной из функций 1) вставка с фиксированным шагом (Шелл) void ins(int* a, int h, int n){} 2) просеивание (Пирамида) void Sift 2(int *a, int n, int i){…} u теория: определения сложности алгоритмов θ, O, Ω.

Оценки ‘+’ хорошо, ‘+. ’ есть небольшое замечание, прочесть и принять во внимание ‘±’ переделать дома и сдать ‘-’ переписать в следующую пятницу соответствующий пункт с 14 -1440 Тогда же контрольную по БМ-КМП.

Объявление 9 ноября пишем контрольную работу по темам: Сортировка Хоара(2, 3) Поиск медианы Побитовая сортировка Самостоятельная должна содержать: 1. Изложение идеи метода; 2. Пошаговую иллюстрацию работы метода; 3. Определение функции; 4. Оценку метода.

Не рекурсивные алгоритмы Хоара non. Rec. H Зададим структуру, состоящую из 2 -х полей struct elem{ int L, R; }; И определим стек, как массив таких элементов elem *S = new elem[200]; При разделении на 2 фрагмента вначале в стек помещаем границы правого фрагмента, затем левого. k – вершина стека
![Алгоритм non. Rec. H 1. k = 0; S[0]. L = 0; S[0]. R Алгоритм non. Rec. H 1. k = 0; S[0]. L = 0; S[0]. R](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-37.jpg)
Алгоритм non. Rec. H 1. k = 0; S[0]. L = 0; S[0]. R = n-1 2. Пока стек не пуст (k>=0) 2. 1 l = S[k]. L; r = S[k]. R; k--; 2. 2 Если l<r , то разделить фрагменты согласно п. 2, 3 алгоритма(и п. 4 для Хоара_2) 2. 3 Кладем в стек правый фрагмент: k++; S[k]. L = i; S[k]. R = r; 2. 4 Кладем в стек левый фрагмент k++; S[k]. L = l; S[k]. R = j;

Пример (Хоар_3) l= 0 1 2 3 4 5 6 7= r 6 7 11 4 3 1 2 9 j x = A[(l+r)/2] = A[3]= 4 i 2 7 11 4 3 1 6 9 j i 2 1 11 4 3 7 6 9 j i 2 1 3 4 11 7 6 9 ij [ 2 1 3 ] 4 [11 7 6 9 j ] i S[1]: S[0]: 0 7 k L R Разделили на 2 фрагмента: сначала кладем в стек правый, затем левый 0 2 S[0]: 4 7 k L R Поэтому начинаем работать с левым: он в вершине стека S
![l= 0 2 =r 1 x = A[(l+r)/2] = A[1] = 1 2 1 l= 0 2 =r 1 x = A[(l+r)/2] = A[1] = 1 2 1](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-39.jpg)
l= 0 2 =r 1 x = A[(l+r)/2] = A[1] = 1 2 1 3 4 11 7 6 9 j i Разделили на 2 фрагмента: сначала кладем в стек правый, затем левый 1 2 3 j i 1 2 3 x=A[(l+r)/2]=A[1]=2 j i 1 2 3 Но у левого фрагмента l>r, а у правого l==r, поэтому извлекаем фрагмент [4, 7] ij 1 2 3 j i S[2]: S[1]: 0 0 S[1]: 0 2 1 2 S[0]: 4 7 k Берем левый фрагмент, но l==r, поэтому берем затем правый L R k L R 1 0 2 2 S[0]: 4 7 S[2]: S[1]: k L R

l = 4 5 6 =r 7 1 2 3 4 [11 7 6 9 ] i [6 [6 j x = A[(l+r)/2] = A[5] = 7 j ] Разделили на 2 фрагмента: 7 11 9 i сначала кладем в стек правый, затем левый j 7 11 9 ] Выбираем левый фрагмент, но l==r, правый фрагмент [6, 7] i 6 7 [ 11 9 i j j ] X = A[(l+r)/2] = A[6] = 11 i 6 7 [ 9 11 ] 1 2 3 4 6 7 9 11 6 7 [ 9 ][11 ] S[0]: 4 7 k L R S[1]: S[0]: 4 4 6 7 S[0]: 6 7 S[1]: S[0]: 6 6 7 7 Стек пуст!

4. Поиск медианы Дано: массив A размера n и целое k, 0 ≤ k < n. Найти: элемент массива x, который после сортировки массива окажется на k-м месте, т. е. x = A[k]. Если k = n/2, – это задача поиска медианы массива. Очевидный способ: отсортировать массив и вернуть A[k] (сложность О(nlogn)). Эффективный способ: используя идею метода Хоара можно сэкономить: сортировать на каждом шаге только тот фрагмент, в который попадает k. Сложность ? ? ?

Рекурсивный алгоритм поиска медианы (k-го элемента) 1. Установка i = l, j = r, x =A[ (l+r)/2]. На основе Хоара_3 2. Пока i ≤ j 2. 1 Пока A[i] <x увеличиваем i на 1. 2. 2 Пока A[j] >x уменьшаем j на 1. 2. 3 Если i ≤ j , то A[i] ↔ A[j], i ++, j --. 3. Если k в левом фрагменте (l ≤ k ≤ j), то вернуть результат рекурсии для этого фрагмента ([l, j]). Если k между фрагментами (j < k < i), то вернуть значение A[k]. Если k в правом фрагменте, то вернуть результат рекурсии для [i, r]. int Mediana. R(int *A, int l, int r, int k);

Пример поиска медианы (k-го элемента) 07 08 03 07 l = 0, r = 7; k = 6 l [ 07 08 03 07 i 07 07 [ 01 08 i 03 07 [ 01 07 03 07 i [ 01 07 03 07 01 09 07 r 01 ] j 07 09 07 j 07 ] 07 j 09 08 07 ] 07 ][ 07 j i j = 3, i = 4, k [l, j] = [0, 3] 09
![l = 4, r = 7; k = 6 k [7, 7] l=4, l = 4, r = 7; k = 6 k [7, 7] l=4,](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-44.jpg)
l = 4, r = 7; k = 6 k [7, 7] l=4, r=6; k=6, k [4, 4] l=5, r=6, k=6 [ 07 i [ 07 09 07 ] j 09 08 07 ] i j [ 07 07 08 ][ 09 ] j=6 i=7 [ 07 07 08 ] i j [ 07 ][ 07 08 ] j=4 i=5 [ 07 08 ] ij 08
![[ ] 07 [ 08 ] j=4 i=6 l=6, r=6, k=6 [ 08 ] [ ] 07 [ 08 ] j=4 i=6 l=6, r=6, k=6 [ 08 ]](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-45.jpg)
[ ] 07 [ 08 ] j=4 i=6 l=6, r=6, k=6 [ 08 ] ij [ ] 08 [ ] j=5 i=7 j=5 < k < i=7 A[6]=8

5. Побитовая сортировка Идея метода. Стратегия аналогична методу Хоара: на каждом этапе текущий фрагмент делится на 2. За критерий деления берется следующее соображение – большие числа содержат в двоичном представлении единицы в разрядах с бóльшими номерами, а меньшие – с меньшими. 25 = 11001 9 = 01001

Идея метода Алгоритм начинает анализ с самого старшего значащего разряда чисел. В левый фрагмент переносятся числа, содержащие нуль в некотором разряде, а в правый - единицы в этом же разряде. Затем алгоритм продолжает работать в этих фрагментах со следующим разрядом.
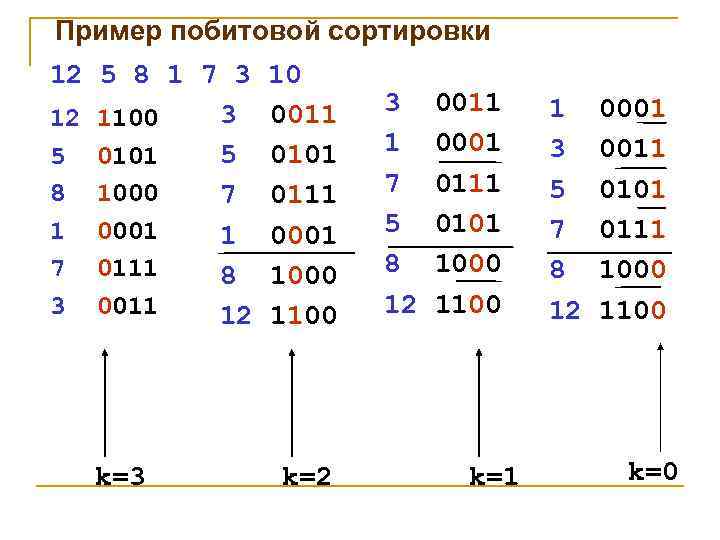
Пример побитовой сортировки 12 5 8 1 7 3 10 3 0011 12 1100 5 0101 8 1000 7 0111 1 0001 7 0111 8 1000 3 0011 12 1100 k=3 k=2 3 0011 1 0001 7 0111 5 0101 8 1000 12 1100 k=1 1 0001 3 0011 5 0101 7 0111 8 1000 12 1100 k=0

Алгоритм побитовой сортировки Вызов l = 0, r = n – 1, k = номер старшего разряда. 1. Если l ≥ r или k < 0, то выход. 2. Установка начальных значений: i = l, j = r. Используем маску! 3. Пока i ≤ j 3. 1 Пока i ≤ j и в k-ом разряде A[i] ноль, i++; 3. 2 Пока i ≤ j и в k-ом разряде A[j] единица, j--. 3. 3 Если i < j , то A[i] ↔ A[j], i ++, j --. 4. Выполняем эту же процедуру для фрагмента [l, j] по k-1 разряду. 5. Выполняем эту же процедуру для фрагмента [i, r] по k-1 разряду. Сложность: O(nlog 2 MAX)

Объявление 9 ноября пишем контрольную работу по темам: Сортировка Хоара(2, 3) Поиск медианы Побитовая сортировка Самостоятельная должна содержать: 1. Изложение идеи метода; 2. Пошаговую иллюстрацию работы метода; 3. Определение функции; 4. Оценку метода.
![Анализ сложности. Решение рекуррентных соотношений Худший случай (Хоар_2) 12345 x = A[l] [ ] Анализ сложности. Решение рекуррентных соотношений Худший случай (Хоар_2) 12345 x = A[l] [ ]](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-51.jpg)
Анализ сложности. Решение рекуррентных соотношений Худший случай (Хоар_2) 12345 x = A[l] [ ] 1 [2 3 4 5] n 2 [3 4 5] n-1 … Пусть число операций для разделения одного фрагмента из n элементов имеет оценку θ(n), включая движение и обмен. Тогда, θ (n) + θ (n-1)+. . . + θ (1) = θ (1 + 2 + 3 + …+ n) = θ (n 2)
![Лучший случай Фрагмент делится пополам. n [ n/2 [ n/4 [ ] n/2 ] Лучший случай Фрагмент делится пополам. n [ n/2 [ n/4 [ ] n/2 ]](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-52.jpg)
Лучший случай Фрагмент делится пополам. n [ n/2 [ n/4 [ ] n/2 ] [ ][ n/4 ] [ n/4 . . . [ 1 ]. . . [ 1 ] [ ] ] [ n/4 ] 1 1 ] [ log 2 n ] Пусть сложность одного этапа имеет оценку θ(n). Тогда все этапы - θ(n* log 2 n)

Рекуррентные соотношения Прежде чем перейти к оценке среднего случая, рассмотрим вопрос о решении рекуррентных соотношений. Во многих случаях сложность алгоритма подчиняется некоторому рекуррентному закону. Для построения функции сложности сначала выписывается рекуррентное соотношение, затем оно решается некоторым методом. Если не получается, то довольствуются только соотношением.

Рекуррентные соотношения «При решении многих комбинаторных задач пользуются методом сведения данной задачи к задаче, касающейся меньшего числа предметов. Метод сведения к аналогичной задаче для меньшего числа предметов называется методом рекуррентных соотношений (от латинского "recurrere" - "возвращаться"). » Н. И. Костюкова
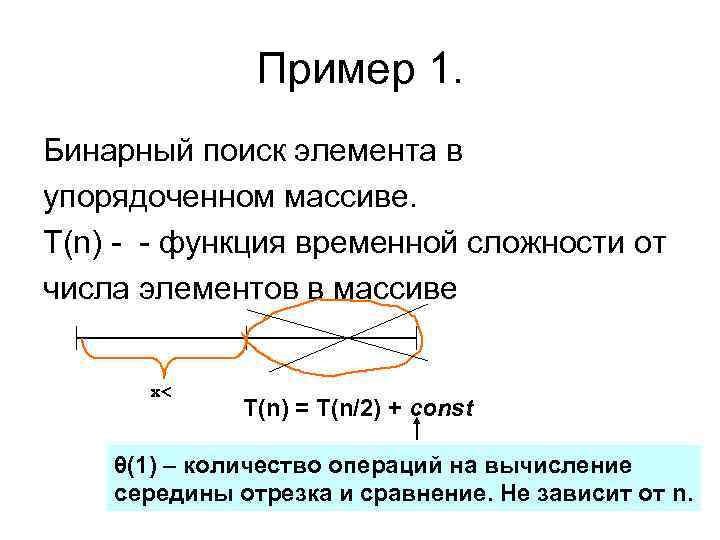
Пример 1. Бинарный поиск элемента в упорядоченном массиве. T(n) - - функция временной сложности от числа элементов в массиве x< T(n) = T(n/2) + const θ(1) – количество операций на вычисление середины отрезка и сравнение. Не зависит от n.

Пример 2 Поиск в неупорядоченном массиве. Сравнение с первым эл. n-1 T(n) = θ(1) +T(n-1)

Методы решения рекуррентных соотношений 1. Метод математической индукции. Пример 1. T(n) = 1 + T(n/2) T(1) = θ(1). Доказать: T(n) = θ(log 2 n). Док-во. По определению оценки θ требуется доказать, что c 1, c 2 и n 0 такие, что для n>n 0 c 1 log 2 n ≤ T(n) ≤c 2 log 2 n. Предположим, что оно верно для n/2 <n c 1 log 2 n/2≤T(n/2) ≤c 2 log 2 n/2 c 1 log 2 n - c 1 log 22 + 1≤T(n/2) + 1≤c 2 log 2 n- c 2 log 22 + 1 c 1 log 2 n +(1 - c 1)≤ T(n) ≤c 2 log 2 n + (1 - c 2) c 1 log 2 n ≤ T(n) ≤c 2 log 2 n для c 1 = 1/2 c 2 => T(n) = θ(log 2 n) Оценка бинарного поиска
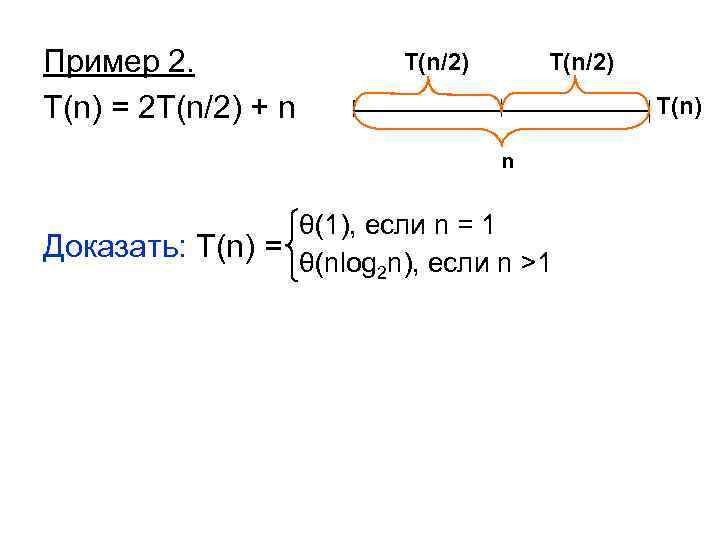
Пример 2. T(n) = 2 T(n/2) + n T(n/2) T(n) n θ(1), если n = 1 Доказать: T(n) = θ(nlog n), если n >1 2

Док-во. По определению оценки θ требуется доказать, что c 1, c 2 и n 0 такие, что для n>n 0 c 1 nlog 2 n ≤T(n)≤ c 2 nlog 2 n. Предположим, что оно верно для n/2(<n) c 1 n/2 log 2 n/2≤T(n/2) ≤c 2 n/2 log 2 n/2 *2 +n c 1 nlog 2 n/2 ≤ 2*T(n/2) ≤c 2 n log 2 n/2 c 1 nlog 2 n/2 + n ≤T(n) ≤c 2 n log 2 n/2 + n c 1 nlog 2 n - c 1 n + n ≤T(n) ≤c 2 n log 2 n - c 2 n + n c 1 nlog 2 n + n(1 - c 1) ≤T(n)≤c 2 nlog 2 n – n(c 2 -1) при c 1 = 1 и при c 2>1 c 1 nlog 2 n ≤T(n)≤ c 2 nlog 2 n => T(n) = θ(nlog 2 n) Оценка Хоара_3 в лучшем случае

2. Метод подстановки (замены переменных) Рекуррентное соотношение T(n) = 2 T(√n) + log 2 n Решение. Пусть n = 2 m => m = log 2 n T(2 m) = 2 T(2 m/2) + log 22 m (*) m Обозначим S(m) = T(2 m), из (*) следует S(m) = 2 S(m/2) + m =>S(m) = θ(mlog 2 m) => T(n) = θ(log 2 n*log 2(log 2 n)) Пример 2. из математической индукции

3. Метод итераций Рекуррентное соотношение T(n) = 2 T(n/4) + n = n + 2 T(n/4), T(1) = θ(1) Решение. T(n) = n + 2(n/4 +2 T(n/42)) = n + 2 n/4 + + 22(n/42 + 2 T(n/43)) = … = n + 2 *n/4 + n-1 +22*n/42 + 23*n/43 + …+ 2 log 4 n-1*n/4 log 4 + + 2 log 4 n*T(n/4 log 4 n) = 2 log 4 n*T(1) + n(1 + ½ + n 2 + 1/23 + …+ 1/2 log 4 n-1) ≤ θ(1)√n + n(1 + + 1/22 + …) = θ(1)√n + n*1/(1 -1/2) = = 2 n + θ(1)√n = θ(n)

Покажем, что 2 log 4 n = √n - используя формулу перехода logan = logbn*logab при a = 2 и b = 4 получим log 2 n = log 4 n*log 24 2*log 4 n = log 2 n log 4 n = ½*log 2 n 2 log 4 n = (2 log 2 n)1/2 = √n

Вернемся к оценке метода Хоара в среднем случае Вероятность того, что эталонный элемент x займет свою позицию 1/n. x q n-q Запишем рекуррентное соотношение n-1 T(n) = θ(n) + ∑ 1/n*(T(q) + T(n-q)) = q=1 n-1 = θ(n) + ∑ 2/n*T(q) q=1 (*)

Решение n-1 T(n)=θ(n) + ∑ 2/n*T(q) (*) q=1 Используя метод математической индукции покажем, что T(n) = O(n*log 2 n) Предположим, что оно справедливо q<n, т. е. T(q) = O(qlog 2 q) По определению оценки O c>0 такое, что T(q)≤ c*q*log 2 q Следовательно, вернувшись к (*), получим n-1 T(n) ≤ θ(n) + ∑ 2/n*c*q*log 2 q = q=1
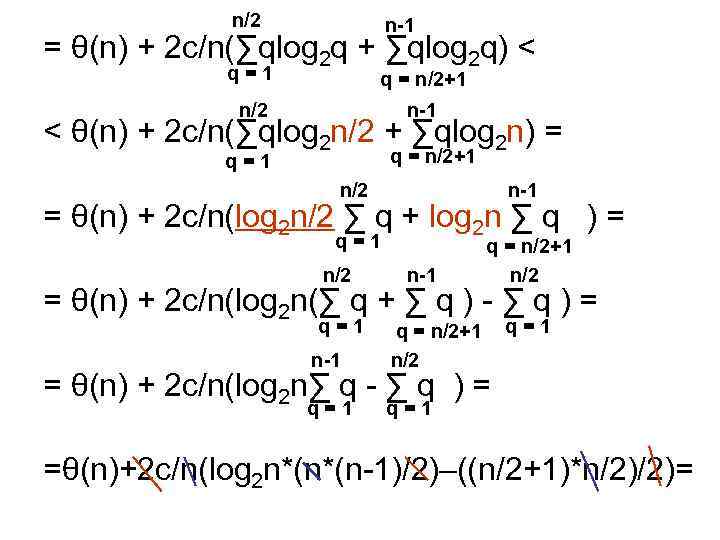
n/2 n-1 q=1 q = n/2+1 n/2 n-1 = θ(n) + 2 c/n(∑qlog 2 q + ∑qlog 2 q) < < θ(n) + 2 c/n(∑qlog 2 n/2 + ∑qlog 2 n) = q = n/2+1 q=1 n/2 n-1 = θ(n) + 2 c/n(log 2 n/2 ∑ q + log 2 n ∑ q ) = q=1 n/2 n-1 q = n/2+1 n/2 = θ(n) + 2 c/n(log 2 n(∑ q + ∑ q ) - ∑ q ) = q=1 n-1 q = n/2+1 n/2 q=1 q=1 = θ(n) + 2 c/n(log 2 n∑ q - ∑ q ) = =θ(n)+2 c/n(log 2 n*(n*(n-1)/2)–((n/2+1)*n/2)/2)=

= θ(n) + c*(n – 1)*log 2 n – c*(n/2 + 1)/2 = = c*n*log 2 n – (c*n/4 + c* log 2 n +c/2 - θ(n)) Таким образом, T(n) ≤ c*n*log 2 n, если (c*n/4 + c* log 2 n +c/2 - θ(n)) > 0, т. е. θ(n) ≤ c*n/4 + c* log 2 n +c/2. Из определения θ(n) c 2>0 такое, что f(n)=n f(n)<c 2*n ≤ c*n/4 + c* log 2 n +c/2 второе неравенство выполняется для " c>4 c 2 => T(n) ≤ c*n*log 2 n при условии c>4 c 2

Следовательно, в среднем случае оценка метода Хоара T(n) = O(n*log 2 n)

Объявление 9 ноября пишем контрольную работу по темам: Сортировка Хоара(2, 3) Поиск медианы Побитовая сортировка Самостоятельная должна содержать: 1. Изложение идеи метода; 2. Пошаговую иллюстрацию работы метода; 3. Определение функции; 4. Оценку метода.

Поиск медианы В худшем случае (k=0||k=n-1): θ(n 2). сравнений n n-1 n-2 … 1 ]x[ C=n+ n-1 + n-2 + …+ 1 = n*(n-1)/2 = θ(n 2)

В лучшем и среднем случаях: θ(n): n/2 n/4 n/8 T(n) = θ(n) + T(n/2) = θ(n)+θ(n/2)+ T(n/4) = … = = θ(n+n/2 +n/4 + n/8 +…+ 1) ≤ const *n*(1 + 1/2 + 1/4 + …) = const *2*n = θ(n) Метод итераций: T(n) = 2 T(n/4) + n => T(n) = θ(n)

Конец методам Хоара

Домашнее задание: нерекурсивный алгоритм

Нерекурсивные алгоритмы сортировки методом Хоара Утверждение 3. 2. 3. Если меньший из двух подмассивов сортируется первым, то стек никогда не содержит более записей. Доказательство. В худшем случае размер стека не должен превышать Sn, где Sn удовлетворяет рекуррентному соотношению Sn = Sn/2 + 1 при S 0 = S 1 = 0. Его решением является Sn = , что доказывает лемму.

Поиск медианы Дано: массив A размера n и целое k, 0 ≤ k < n. Найти: элемент массива x, который после сортировки массива окажется на k-м месте, т. е. x = A[k]. Если k = n/2, – это задача поиска медианы массива. Очевидный способ: отсортировать массив и вернуть A[k] (сложность О(nlogn)). Эффективный способ: используя идею метода Хоара можно сэкономить: сортировать на каждом шаге только тот фрагмент, в который попадает k. Сложность ? ? ?

Рекурсивный алгоритм поиска медианы (k-го элемента) 1. Установка i = l, j = r, x =A[ (l+r)/2]. 2. Пока i ≤ j 2. 1 Пока A[i] <x увеличиваем i на 1. 2. 2 Пока A[j] >x уменьшаем j на 1. 2. 3 Если i ≤ j , то A[i] ↔ A[j], i ++, j --. 3. Если k в левом фрагменте (l ≤ k ≤ j), то вернуть результат рекурсии для этого фрагмента ([l, j]). Если k между фрагментами (j < k < i), то вернуть значение A[k]. Если k в правом фрагменте, то вернуть результат рекурсии для [i, r]. int Mediana. R(int *A, int l, int r, int k);

Пример поиска медианы (k-го элемента) 07 08 03 07 07 09 07 01 l=0, r=7; k=6 [ 07 08 03 07 07 09 07 01 ] i j [ 01 08 03 07 07 09 07 07 ] i j [ 01 07 03 07 07 09 08 07 ] i j [ 01 07 03 07 ][ 07 09 08 07 ] j i j=3, i=4
![l=4, r=7; k=6 [ 07 09 08 07 ] i j [ 07 l=4, r=7; k=6 [ 07 09 08 07 ] i j [ 07](https://present5.com/presentation/3/30538264_152909527.pdf-img/30538264_152909527.pdf-77.jpg)
l=4, r=7; k=6 [ 07 09 08 07 ] i j [ 07 09 08 07 ] i j [ 07 07 08 ][ 09 ] j=6 i=7 l=4, r=6; k=6 [ 07 07 08 ] i j [ 07 ][ 07 08 ] j=4 i=5 l=5, r=6, k=6 [ 07 08 ] ij [] 07 [ 08 ] j=4 i=6 l=6, r=6, k=6 [ 08 ] ij [] 08 [] j=5 i=7 j=5 < k < i=7 A[6]=8

Поиск медианы Сложность ? ? ? В худшем случае: O(n 2). В лучшем и среднем случаях: O(n). Домашнее задание: нерекурсивный алгоритм.

Программа поиска медианы (k-го элемента) int Mediana. R(int *A, int l, int r, int k) { int x, i, j, tmp; i=l, j=r, x=A[ (l+r)/2]; while(i<=j){ while( A[i] <x) i++; while( A[j] >x)j--; if( i<=j) tmp=A[i], A[i++]=A[j], A[j--]=tmp; } if( l<=k&&k<=j) return Mediana. R(A, l, j, k); if( j<k&&k<i)return A[k]; return Mediana. R(A, i, r, k); }
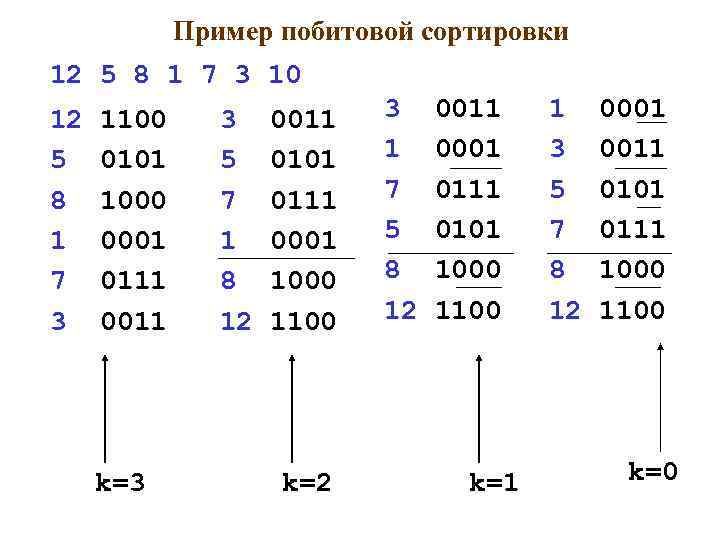
Пример побитовой сортировки 12 5 8 1 7 3 10 12 1100 5 0101 8 1000 1 0001 7 0111 3 0011 k=3 3 0011 5 0101 7 0111 1 0001 8 1000 12 1100 k=2 3 0011 1 0001 7 0111 5 0101 8 1000 12 1100 k=1 1 0001 3 0011 5 0101 7 0111 8 1000 12 1100 k=0

Алгоритм побитовой сортировки Вызов l = 0, r = n – 1, k = номер старшего разряда. 1. Если l ≥ r или k < 0, то выход. 2. Установка начальных значений: i = l, j = r. 3. Пока i ≤ j 3. 1 Пока i ≤ j и в k-ом разряде элемента A[i] ноль увеличиваем i на 1. 3. 2 Пока i ≤ j и в k-ом разряде элемента A[j] единица уменьшаем j на 1. 3. 3 Если i < j , то A[i] ↔ A[j], i ++, j --. 4. Выполняем эту же процедуру для фрагмента [l, j] по k-1 разряду. 5. Выполняем эту же процедуру для фрагмента [i, r] по k-1 разряду. Сложность: O(nlog 2 MAX)

Замечания 1. При реализации рекурсивных алгоритмов, условие прекращения рекурсии ( l < r) проверять, не в начале процедуры, а перед ее вызовом ( l < j), ( i < r). 2. Для сортировки небольших фрагментов ( ≈ 50 элементов) использовать метод вставки или выбора. 3. Не выполнять деление небольших ( ≈ 100 элементов) фрагментов. В конце применить метод вставки для всего массива (т. к. массив почти упорядочен, по аналогии с методом Шелла). 4. Метод Хоара можно применить для разделения массива на требуемое число фрагментов для их одновременной (параллельной) сортировки на многопроцессорных системах.

Методы решения рекуррентных соотношений 1. Метод математической индукции. Пример 1. T(n) = 1 + T(n/2) T(1) = θ(1). Доказать: T(n) = θ(log 2 n). Предположение: T(n/2) = θ(log 2 n/2) Док-во. По определению оценки θ: c 1, c 2 и n 0 такие, что для n>n 0 c 1 log 2 n/2≤T(n/2) ≤c 2 log 2 n/2 c 1 log 2 n - c 1 log 22 + 1≤T(n/2) + 1≤c 2 log 2 n- c 2 log 22 + 1 c 1 log 2 n +(1 - c 1)≤ T(n) ≤c 2 log 2 n + (1 - c 2) c 1 log 2 n ≤ T(n) ≤c 2 log 2 n для c 1 = 1/2 c 2 => T(n) = θ(log 2 n)

Пример 2. T(n) = 2 T(n/2) + n T(n/2) T(n) n Доказать: T(n) = θ(1), если n = 1 θ(nlog 2 n), если n >1 Предположение: Пусть оно верно для n/2 T(n/2) = θ(n/2*log 2(n/2))

Док-во. По определению оценки θ: c 1, c 2 и n 0 такие, что для n>n 0 c 1 n/2 log 2 n/2≤T(n/2) ≤c 2 n/2 log 2 n/2 *2 +n c 1 nlog 2 n/2 ≤ 2*T(n/2) ≤c 2 n log 2 n/2 c 1 nlog 2 n/2 + n ≤T(n) ≤c 2 n log 2 n/2 + n c 1 nlog 2 n - c 1 n + n ≤T(n) ≤c 2 n log 2 n - c 2 n + n c 1 nlog 2 n + n(1 - c 1) ≤T(n)≤c 2 nlog 2 n – n(c 2 -1) при c 1 = 1 и при c 2>1 c 1 nlog 2 n ≤T(n)≤ c 2 nlog 2 n => T(n) = θ(nlog 2 n)

Объявление На следующей неделе пишем самостоятельную по двум сортировкам - Шелла и пирамидальной. В работу входит § пошаговая иллюстрация работы методов; § определение одной из функций 1) вставка с фиксированным шагом (Шелл) 2) просеивание (Пирамида) 3) построение пирамиды

Объявление На следующей неделе пишем самостоятельную по двум сортировкам - Шелла и пирамидальной. В работу входит § пошаговая иллюстрация работы методов; § определение одной из функций 1) вставка с фиксированным шагом (Шелл) 2) просеивание (Пирамида) 3) построение пирамиды

Алгоритм Хоар_1 1. Если l r или xl == xr, то выход. 2. i = l, j = r, xm = (xl+xr)/2. 0 (xm тип float)!!проверить 3. Пока i j: 3. 1. пока i j и A[i] < xm увеличиваем i на 1; 3. 2. пока j i и A[j] xm уменьшаем j на 1; 3. 3. если i < j , то A[i] ↔ A[j], увеличить i на 1, уменьшить j на 1. 4. Выполняем эту же процедуру для подмассива от l до j c интервалом значений [xl, xm-0. 5]. 5. Выполняем эту же процедуру для подмассива от i до r c интервалом [xm+0. 5, xr].

Напоминаю На следующей неделе пишем самостоятельную по двум сортировкам - Шелла и пирамидальной. В работу входит • пошаговая иллюстрация работы методов; • определение одной из функций 1) вставка с фиксированным шагом (Шелл) 2) просеивание (Пирамида) • теория: определения сложности алгоритмов θ, O, Ω.

Пишем самостоятельную по двум сортировкам - Шелла и пирамидальной. В работу входит • пошаговая иллюстрация работы методов; • определение одной из функций 1) вставка с фиксированным шагом (Шелл), void insert_h(int *a, int n, int h); 2) просеивание (Пирамида) void Sift 2(int *a, int n, int i); 3) построение пирамиды void Create. Heap(int *a, int n);

Объявление Самостоятельную работу проверю к 11 ноября 2011 года.
Метод Хоара.ppt