4 2 cont Expected Value of a

4. 2 (cont. ) Expected Value of a Discrete Random Variable A measure of the “middle” of the values of a random variable

Center The mean of the probability distribution is the expected value of X, denoted E(X) is also denoted by the Greek letter µ (mu)

Mean or Expected Value Economic Scenario Profit X ($ Millions) Probability P Great x 1 10 P(X=x 1) 0. 20 Good x 2 5 P(X=x 2) 0. 40 OK x 3 1 P(X=x 3) 0. 25 Lousy x 4 -4 P(X=x 4) 0. 15 k = the number of possible values (k=4) E(x)= µ = x 1·p(x 1) + x 2·p(x 2) + x 3·p(x 3) +. . . + xk·p(xk) Weighted mean

Mean or Expected Value k = the number of outcomes (k=4) µ = x 1·p(x 1) + x 2·p(x 2) + x 3·p(x 3) +. . . + xk·p(xk) Weighted mean Each outcome is weighted by its probability

Other Weighted Means z. Stock Market: The Dow Jones Industrial Average y. The “Dow” consists of 30 companies (the 30 companies in the “Dow” change periodically) y. To compute the Dow Jones Industrial Average, a weight proportional to the company’s “size” is assigned to each company’s stock price

Other Weighted Means z GPA A=4, B=3, C=2, D=1, F=0 z Course grade: tests 40%, final exam 25%, quizzes 25%, homework 10% z "Average" ticket prices

Economic Scenario Profit X ($ Millions) Probability P x 1 10 P(X=x 1) 0. 20 Good x 2 5 P(X=x 2) 0. 40 OK x 3 1 P(X=x 3) 0. 25 Lousy Mean Great x 4 -4 P(X=x 4) 0. 15 k = the number of outcomes (k=4) µ = x 1·p(x 1) + x 2·p(x 2) + x 3·p(x 3) +. . . + xk·p(xk) EXAMPLE

Economic Scenario Profit X ($ Millions) Probability P x 1 10 P(X=x 1) 0. 20 Good x 2 5 P(X=x 2) 0. 40 OK x 3 1 P(X=x 3) 0. 25 Lousy Mean Great x 4 -4 P(X=x 4) 0. 15 k = the number of outcomes (k=4) µ = x 1·p(x 1) + x 2·p(x 2) + x 3·p(x 3) +. . . + xk·p(xk) EXAMPLE µ = 10*. 20 + 5*. 40 + 1*. 25 – 4*. 15 = 3. 65 ($ mil)

Mean µ=3. 65 k = the number of outcomes (k=4) µ = x 1·p(x 1) + x 2·p(x 2) + x 3·p(x 3) +. . . + xk·p(xk) EXAMPLE µ = 10·. 20 + 5·. 40 + 1·. 25 - 4·. 15 = 3. 65 ($ mil)

Interpretation z. E(x) is not the value of the random variable x that you “expect” to observe if you perform the experiment once

Interpretation z. E(x) is a “long run” average; if you perform the experiment many times and observe the random variable x each time, then the average x of these observed xvalues will get closer to E(x) as you observe more and more values of the random variable x.

Example: Green Mountain Lottery z. State of Vermont zchoose 3 digits from 0 through 9; repeats allowed zwin $500 x $0 $500 p(x). 999. 001 E(x)=$0(. 999) + $500(. 001) = $. 50

Example (cont. ) z. E(x)=$. 50 z. On average, each ticket wins $. 50. z. Important for Vermont to know z. E(x) is not necessarily a possible value of the random variable (values of x are $0 and $500)

Example: coin tossing z. Suppose a fair coin is tossed 3 times and we let x=the number of heads. Find m=E(x). z. First we must find the probability distribution of x.

Example (cont. ) z. Possible values of x: 0, 1, 2, 3. zp(1)? z. An outcome where x = 1: THT z. P(THT)? (½)(½)(½)=1/8 z. How many ways can we get 1 head in 3 tosses? 3 C 1=3

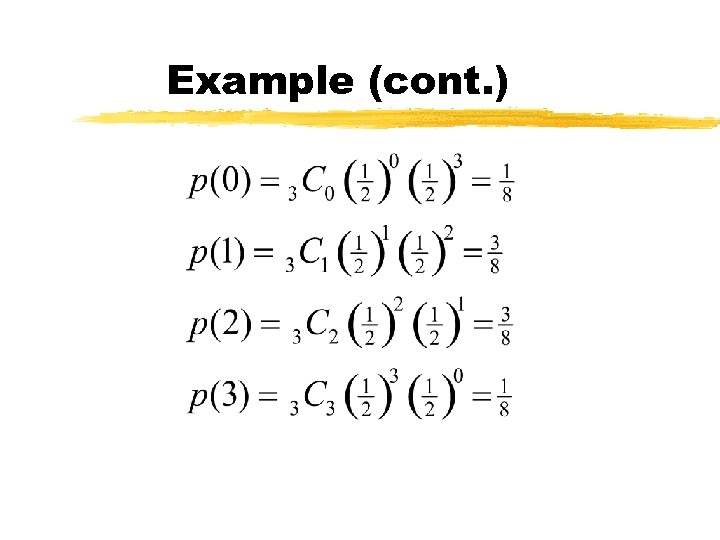Example (cont. )

Example (cont. ) z. So the probability distribution of x is: x p(x) 0 1/8 1 3/8 2 3/8 3 1/8

z So the probability distribution of x is: Example x p(x) 0 1/8 1 3/8 2 3/8 3 1/8

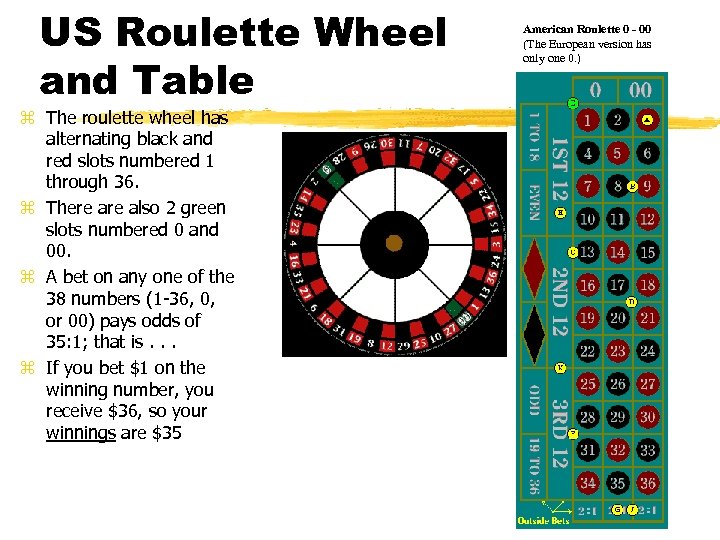US Roulette Wheel and Table z The roulette wheel has alternating black and red slots numbered 1 through 36. z There also 2 green slots numbered 0 and 00. z A bet on any one of the 38 numbers (1 -36, 0, or 00) pays odds of 35: 1; that is. . . z If you bet $1 on the winning number, you receive $36, so your winnings are $35 American Roulette 0 - 00 (The European version has only one 0. )

US Roulette Wheel: Expected Value of a $1 bet on a single number z Let x be your winnings resulting from a $1 bet on a single number; x has 2 possible values x p(x) -1 37/38 35 1/38 z E(x)= -1(37/38)+35(1/38)= -. 05 z So on average the house wins 5 cents on every such bet. A “fair” game would have E(x)=0. z The roulette wheels are spinning 24/7, winning big $$ for the house, resulting in …