4 1 Triangles The student will learn

§ 4. 1 Triangles The student will learn about: medians, altitudes, and other geometric properties of triangles. 1

§ 4. 1 Congruent Triangles We will now study some of the special segments, lines and rays associated with a triangle. 2

Median Definitions The median of a triangle is a segment whose end points are a vertex of the triangle and the midpoint of the opposite side. 3

Theorem The medians of a triangle concur. Proof: For this proof we will need parallelograms later in the course. 4

Angle Bisector Definitions A segment is an angle bisector of a triangle if it lies on the ray which bisects an angle of the triangle and its endpoints are the vertex of this angle and a point on the opposite side. 5

Theorem The angle bisectors of a triangle concur. Proof for homework. Strategy! in pairs 6

Perpendicular Bisector Definitions A line is a perpendicular bisector of a side of a triangle if it is perpendicular to that side and passes through the midpoint of that side. 7

Theorem The perpendicular bisector of a segment, is the set of all points of the plane that are equidistant from the endpoints of the segment. 8

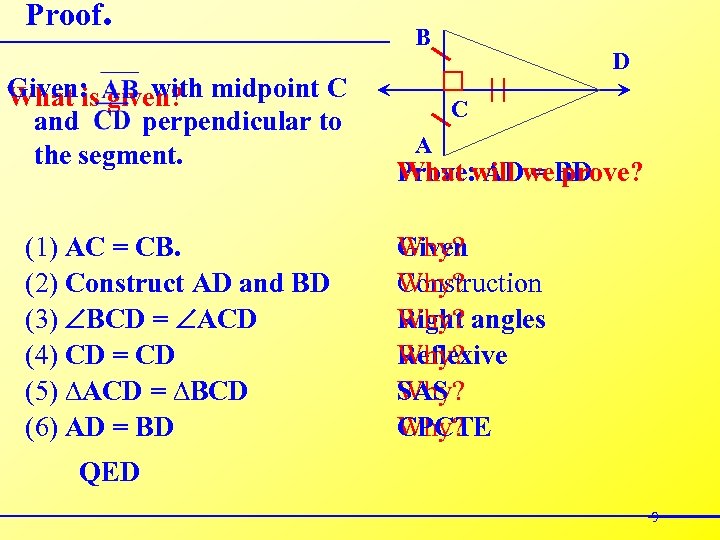Proof. Given: given? midpoint C with What is and perpendicular to the segment. (1) AC = CB. (2) Construct AD and BD (3) BCD = ACD (4) CD = CD (5) ∆ACD = ∆BCD (6) AD = BD B D C A What AD = prove? Prove: will we. BD Why? Given Why? Construction Why? Right angles Why? Reflexive SAS Why? CPCTE Why? QED 9

Theorem The perpendicular bisectors of a triangle concur. Proof left as a homework assignment. Hint: two must concur, show that the third must concur at the same point. 10

Altitude Definitions The altitude of a triangle is a perpendicular segment from a vertex of the triangle to the line containing the opposite side. 11

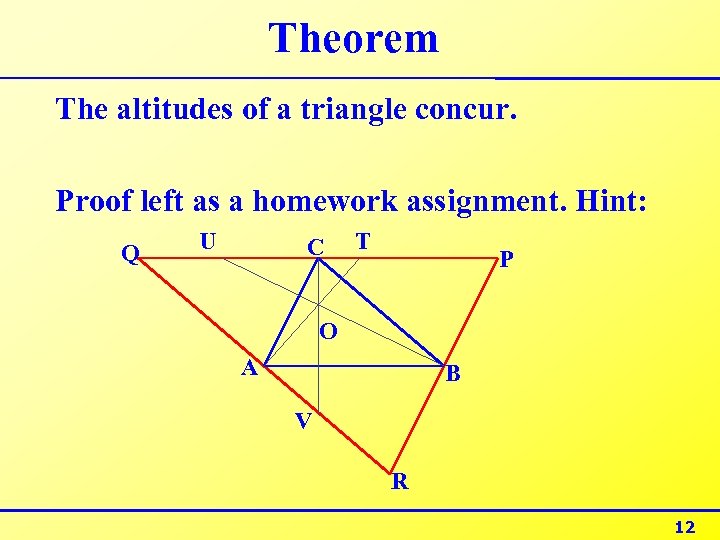Theorem The altitudes of a triangle concur. Proof left as a homework assignment. Hint: Q U C T P O A B V R 12

Exterior Angle Definitions If A – C – D, then BCD is an exterior angle of ∆ ABC. B D A C Every triangle has six exterior angles. These form three pairs of vertical angles. 13

Theorem The exterior angle of a triangle is greater than each of its remote interior angles. 14

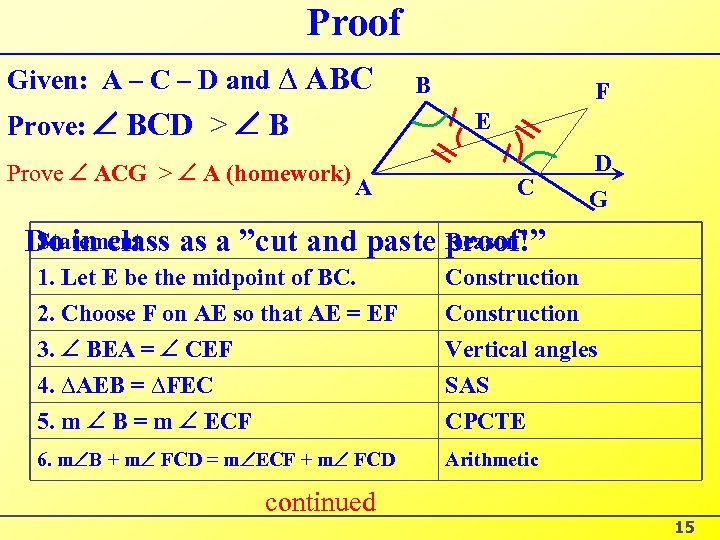Proof Given: A – C – D and ∆ ABC Prove: BCD > B Prove ACG > A (homework) B F E A C D G Statement Reason Do in class as a ”cut and paste proof!” 1. Let E be the midpoint of BC. 2. Choose F on AE so that AE = EF 3. BEA = CEF 4. ∆AEB = ∆FEC 5. m B = m ECF Construction Vertical angles SAS CPCTE 6. m B + m FCD = m ECF + m FCD Arithmetic continued 15

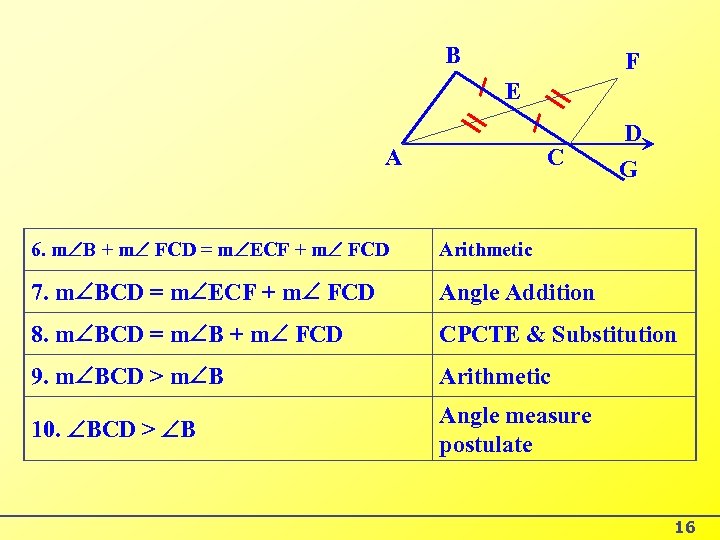B F E A C D G 6. m B + m FCD = m ECF + m FCD Arithmetic 7. m BCD = m ECF + m FCD Angle Addition 8. m BCD = m B + m FCD CPCTE & Substitution 9. m BCD > m B Arithmetic 10. BCD > B Angle measure postulate 16

Before we continue our study of quadrilaterals we will need the following information on parallelism.

Historical Background Euclid’s Fifth. If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side which are the angles less than the two right angles. n l m 1 2 A 1 + 2 < 180 then lines l and m meet on the A side of the transversal n. 18

Playfair’s Postulate Given a line l and a point P not on l, there exist one and only one line m through P parallel to l. 19

Equivalent Forms of the Fifth Area of a right triangle can be infinitely large. Angle sum of a triangle is 180. Rectangles exist. A circle can pass through three points. Parallel lines are equidistant. Given an interior point of an angle, a line can be drawn through the point intersecting both sides of the angle. 20

Euclidean Parallelism Definition. Two distinct lines l and m are said to be parallel, l || m, iff they lie in the same plane and do not meet. 21

Theorem 1: Parallelism in Absolute Geometry If two lines in the same plane are cut by a transversal so that a pair of alternate interior angles are congruent, the lines are parallel. Notice that this is a theorem and not an axiom or postulate. 22

Parallelism in Absolute Geometry Given: l, m and transversal t. and 1≅ 2 Prove: l ׀׀ m Proof by contradiction. (1) l not parallel to m, meet at R. (2) 1 is exterior angle Assumption Def (3) m 1 > m 2 Exterior angle inequality (4) → ← Given 1 ≅ 2 l t 1 m 2 B A R 23

Parallelism in Absolute Geometry Given: l, m and transversal t. and 1≅ 2 Prove: l ׀׀ m Proof by contradiction. (1) l not parallel to m, meet at R. (2) 1 is exterior angle Assumption Def (3) m 1 > m 2 Exterior angle inequality (4) → ← Given 1 ≅ 2 l t 1 m 2 B A R 24

Assignment: § 4. 1 You will need a straight edge and compass for the next two lessons. Buy them.