3 вопрос ОСНОВЫ КИНЕМАТИКИ И ДИНАМИКИ ЖИДКОСТИ И

3 вопрос ОСНОВЫ КИНЕМАТИКИ И ДИНАМИКИ ЖИДКОСТИ И ГАЗА 2012 1

3. 1. ЭЛЕМЕНТЫ КИНЕМАТИКИ И ДИНАМИКИ ЖИДКОСТЕЙ И ГАЗОВ 3. 1. 1. Определения кинематики и динамики жидкостей и газов Кинематика раздел гидромеханики, изучающий движение жидкости без учета действующих сил. Динамика жидкости раздел гидромеханики, который изучает законы движения жидкостей в зависимости от приложенных к ним сил. Причинами, вызывающими движение жидкости, являются действующие на нее силы (сила тяжести, центробежная сила, внешнее давление и т. п. ). Под действием этих сил происходит деформация жидкости, характеризующаяся изменением взаимного положения отдельных частиц жидкости. При заданных внешних силах задача динамики жидкости сводится к определению напряжений и кинематических параметров движения в каждой точке жидкости в любой момент времени, а также к определению гидродинамических сил воздействия потока на тела. 2012 2

3. 1. 2. Основные понятия о движении жидкости Движущуюся жидкость можно рассматривать как совокупное движение материальных точек. Для каждого момента времени графически можно представить положение частицы и ее скорость в виде вектора определенной длины и направление. Местная скорость жидкой частицы - скорость частицы жидкости в данной точке пространства в данный момент времени. Совокупность всех векторов скорости материальных точек представит собой поле скоростей или векторное поле (рис. 3. 1. 1). В соответствии с моментом Эйлера вектор скорости есть функция расположения данной точки и времени V=F( ŕ , t), где ŕ - радиус - вектор, ŕ =ux+uy+uz. Скорость u какой либо частицы жидкости может быть вполне определена, если станут известными проекции скорости на координатные оси ux, uy, uz. ux =f 1(x, y, z, t), uy =f 2(x, y, z, t), uz =f 3(x, y, z, t). Если основная система уравнений движения известна, то можно определить полную скорость и по направлению и по значению. Так, по правилу сложения векторов модуль скорости равен (3. 1) Полный дифференциал компонентов скорости выражается равенствами: 2012 Рис. 3. 1. 1. Составляющие скорости течения жидкости в точке 3

Геометрические характеристики движения жидкости. Траектория линия, по которой движется некоторая частица жидкости. Линия тока кривая, в каждой точке которой в данный момент времени вектор скорости жидкости касателен к кривой. Не следует смешивать понятия линии тока и траектории движущихся частиц. Касательные к траектории дают направление скорости частицы в последовательные моменты времени, между тем как касательные к линиям тока характеризуют направление скоростей разных частиц в определенный момент времени. При неустановившемся движении, когда линии тока изменяют свое положение в пространстве с течением времени, траектории и линии тока не совпадают между собой. При установившемся движении, когда линии тока не меняют своего положения в пространстве с течением времени, траектории и линии тока совпадают. Рассмотрим опорожнение сосуда с жидкостью через отверстие в его стенке (рис. 3. 1. 2). При истечении жидкости из отверстия резервуара вытекающая струя непрерывно меняет свое положение во времени. На рисунке даны три положения струи соответственно для трех моментов времени t 1, t 2, t 3, для которых условно изображены три различные линии тока (сплошные линии), кроме того, отмечены три положения частицы М для тех же моментов времени и пунктиром указана траектория этой частицы. Две различные линии тока во всех случаях не пересекаются между собой. К геометрическим характеристикам потока (траектория, линия тока) относятся и линии отмеченных точек. Линия отмеченных точек линия, на которой в данный момент времени лежат частицы жидкости, прошедшие в свое время через одну и туже начальную точку. Иллюстрацией такой линии может служить линия расположения поплавков, последовательно выпущенных из одной и той же точки. При установившемся движении все эти три линии совпадают между собой. Поверхностью тока называют поверхность, в каждой точке которой в данное мгновение вектор скорости жидкости совпадает с направлением касательной к этой поверхности, или называется поверхность, образованная линиями тока, проведенными через все точки какой нибудь заданной линии в плоскости, перпендикулярной направлению движения жидкости. Рис. 3. 1. 2 2012 4

Пульсация скорости. Осредненная и средняя скорость Скорость частиц жидкости в потоке колеблется в небольших пределах с достаточно высокой частотой относительно некоторого постоянного значения. Это явление называют пульсацией скорости. Средняя (во времени) величина скорости называется осредненной скоростью Действительная мгновенная скорость u равна сумме осредненной и пульсационной скоростей Составляющие осредненной скорости vx, vy, vz в той же точке за достаточно большой промежуток времени (t, t+T) определяются равенствами: Если осредненные скорости в каждой точке потока не зависят от времени осреднения, поток относится к установившемуся; в противном случае – к неустановившемуся. Разности между фактическими и осредненными величинами называются пульсационными скоростями и давлениями: Средняя для данного сечения скорость определяется осреднением по площади осредненных скоростей, т. е. 2012 5

3. 2. ВИДЫ ДВИЖЕНИЯ ЖИДКОСТИ 3. 2. 1. Сводная классификация видов движения жидкости Классификацию видов движения жидкости обычно проводят по следующим направлениям. В общем случае движение элементарного объема жидкости представляют как сумму трех различных движений: 1) вихревое движение (движение с вращением) движение жидкости или газа, при котором мгновенная скорость вращения элементарных объемов среды не равна нулю и всюду тождественна; 2) безвихревое движение (движение без вращения), называемое потенциальным движением движение, когда вращение элемёнтарных частиц жидкости на бесконечно малом перемещении отсутствует; 3) кроме того, рассматривают особое движение, называемое деформационным, которое обусловлено изменением формы движущихся объемов жидкости. По признаку зависимости движения жидкости от времени различают: 1) установившееся (стационарное) движение; 2) неустановившееся (нестационарное) движение, где, кроме того, рассматривают: а) медленно изменяющееся; б) быстро изменяющееся. В зависимости от геометрической формы линий тока (с учетом вопроса о деформации эпюры скоростей вдоль потока) рассматривают: 1) равномерное движение, оно же параллельноструйное (v=const, причем эпюра скоростей не деформируется вдоль потока); 2) неравномерное движение (v≠const или v=const, но эпюра скоростей деформируется вдоль потока); внутри этого вида движения также различают: а) плавно изменяющееся движение (живые сечения принимаются плоскими); б) резко изменяющееся движение (живые сечения криволинейны). В зависимости от распределения давления определяют: 1) напорное движение; 2) безнапорное движение; 3) свободные струи. В зависимости от режима движения различают: 1) ламинарный режим движения жидкости; 2) турбулентный режим движения жидкости; По характеру движения (относящемуся только к безнапорному движению): 1) спокойное движение жидкости; 2) бурное движение жидкости. В зависимости от значения компонентов скорости определяют следующий характер движения жидкости: если ux, uy, uz не равны нулю, то движение называют пространственным, если ux, или uy, или uz равны нулю, то получаем плоское движение, 2012 6 если два компонента равны нулю, то получаем одномерное движение.

3. 2. 2. Вихревое движение Определение вихревого движения. Течение жидкости, совершающей вращательное движение называют вихревым. Вихревое движение является наиболее общим видом движения. Вихревое движение жидкости или газа, при котором мгновенная скорость вращения элементарных объемов среды не равна нулю и всюду тождественна. Количественной мерой завихренности служит вектор ω=rot v, где v скорость жидкости; ω называют вектором вихря или просто завихренностью. Эквивалентной мерой завихренности, более удобной в теоретических построениях, является антисимметричная часть тензора градиента скорости ω = ½(Δv Δv. T). Движение называется безвихревым или потенциальным, если ω=0, в противном случае имеет место вихревое движение. За редким исключением, движение жидкости или газа почти всегда бывает вихревым. Так, вихревым является ламинарное течение в круглой трубе, когда скорость распределяется по параболическому закону, течение в пограничном слое при плавном обтекании тела и в следе за плохо обтекаемым телом. Вихревой характер носит любое турбулентное течение. 2012 7

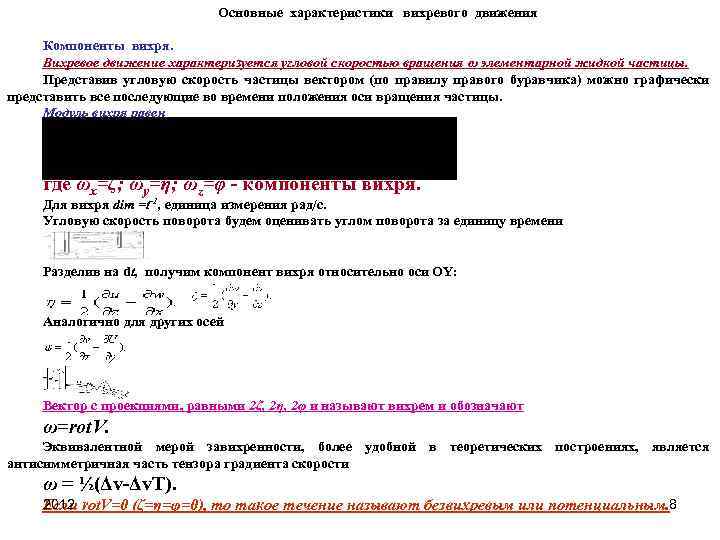Основные характеристики вихревого движения Компоненты вихря. Вихревое движение характеризуется угловой скоростью вращения ω элементарной жидкой частицы. Представив угловую скорость частицы вектором (по правилу правого буравчика) можно графически представить все последующие во времени положения оси вращения частицы. Модуль вихря равен где ωx=ζ; ωy=η; ωz=φ компоненты вихря. Для вихря dim =t-1, единица измерения рад/с. Угловую скорость поворота будем оценивать углом поворота за единицу времени Разделив на dt, получим компонент вихря относительно оси OY: Аналогично для других осей Вектор с проекциями, равными 2ζ, 2η, 2φ и называют вихрем и обозначают ω=rot. V. Эквивалентной мерой завихренности, более удобной в теоретических построениях, является антисимметричная часть тензора градиента скорости ω = ½(Δv Δv. T). 2012 Если rot. V=0 (ζ=η=φ=0), то такое течение называют безвихревым или потенциальным. 8

3. 2. 3. Потенциальное течение жидкости Определение потенциального течения Потенциальное течение - безвихревое движение жидкости, при котором каждый малый объём деформируется и перемещается поступательно, не имея вращения (вихря). Потенциальное течение может иметь место при определённых условиях только для идеальной (лишённой трения) жидкости, например, когда движение начинается из состояния покоя, когда жидкость несжимаема и в ней начинает двигаться погружённое тело или происходит удар тела о поверхность жидкости и т. п. У реальных жидкостей и газов потенциальное течение происходит в тех областях, где силы вязкости ничтожно малы по сравнению с силами давления и нет завихрений. Потенциальное течение характеризуется потенциалом скорости φ и функцией тока ψ (рис. 3. 3. 1). 2012 Рис. 3. 3. 1. Гидродинамическая сетка течения жидкости 9

Элементы потенциального течения жидкости При теоретических расчетах наиболее часто в гидрогазодинамике рассматривают струйчатое движение жидкости. При струйчатом движении жидкости различают следующие элементы: Трубка тока - называется часть движущейся жидкости, ограниченная поверхностью тока, проведенной через все точки бесконечно малого простого замкнутого контура, находящегося в области, занятой жидкостью и взятого в плоскости, перпендикулярной направлению движения жидкости. Другими словами трубка тока - множество траекторий частиц жидкости в бесконечно малом замкнутом контуре (рис. 3. 3. 2). Элементарная струйка - жидкость, протекающая внутри трубки тока, или струйка, боковая поверхность (поверхность тока) которой образована линиями тока, проходящими через точки очень малого (в пределе бесконечно малого) замкнутого контура. Другими словами элементарная струйка - масса жидкости, текущей внутри трубки тока (рис. 3. 3. 2). Рис. 3. 3. 2. Трубка тока и элементарная струйка 2012 10

3. 2. 4. Неустановившееся и установившееся движение Величины гидродинамических давлений p и скоростей u в потоке жидкости в общем случае распределены неравномерно, они меняются при переходе от одной точки потока к другой, т. е. являются функциями координат (x, y, z). Помимо этого, гидродинамические давления и скорости в одних и тех же фиксированных точках потока могут изменяться во времени как по величине, так и по направлению. Вид движения, при котором гидродинамические давления и скорости в каждой точке потока жидкости изменяются во времени по величине и направлению, называется неустановившимся движением (рис. 3. 5). Эти условия в общем виде могут быть записаны следующим образом: p = f 1(x, y, z, t); ux = f 2(x, y, z, t); uy = f 3(x, y, z, t); uz = f 4(x, y, z, t). (3. 2. 1) Примерами неустановившегося движения жидкости могут служить: движение воды в реке во время весеннего половодья или при разрушении плотины, сопровождающееся изменением во времени уровня воды, ширины потока, скорости течения и давления в каждом сечении потока. Неустановившееся движение является самым общим и самым сложным видом движения жидкости. Мы будем, в основном, рассматривать вопросы, касающиеся установившегося движения жидкости, при котором скорости и гидродинамические давления в каждой точке потока не изменяются во времени, а являются лишь функциями координат (рис. 3. 5). При установившемся движении: p = f 1(x, y, z); ux = f 2(x, y, z); uy = f 3(x, y, z); uz = f 4(x, y, z). (3. 2. 2) Примерами установившегося движения жидкости являются: движение жидкости в трубопроводе с постоянной скоростью течения; движение воды в канале постоянного сечения при постоянной глубине воды. Продольный профиль НПУ Установившееся течение h=h(x, y, z) Неустановившееся течение H=H(x, y, z, t) h 2012 Рис. 3. 5. Неустановившееся и установившееся течение H 11

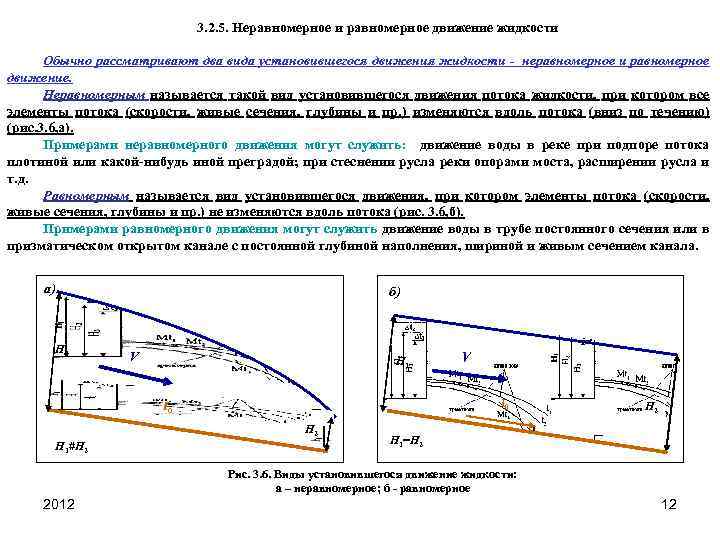3. 2. 5. Неравномерное и равномерное движение жидкости Обычно рассматривают два вида установившегося движения жидкости - неравномерное и равномерное движение. Неравномерным называется такой вид установившегося движения потока жидкости, при котором все элементы потока (скорости, живые сечения, глубины и пр. ) изменяются вдоль потока (вниз по течению) (рис. 3. 6, а). Примерами неравномерного движения могут служить: движение воды в реке при подпоре потока плотиной или какой нибудь иной преградой; при стеснении русла реки опорами моста, расширении русла и т. д. Равномерным называется вид установившегося движения, при котором элементы потока (скорости, живые сечения, глубины и пр. ) не изменяются вдоль потока (рис. 3. 6, б). Примерами равномерного движения могут служить движение воды в трубе постоянного сечения или в призматическом открытом канале с постоянной глубиной наполнения, шириной и живым сечением канала. а) H 1 б) V H 1 I 0 H 2 H 1#H 2 V H 2 H 1=H 2 Рис. 3. 6. Виды установившегося движение жидкости: а – неравномерное; б равномерное 2012 12

3. 2. 6. Напорное и безнапорное движение жидкости Как неравномерное, так и равномерное движение жидкости могут проявляться в двух формах: напорного и безнапорного движения. Напорным называется движение потока в трубе (водоводе) полным ее сечением, когда давление в жидкости больше атмосферного (Рис. 3. 7, а). Безнапорным называется движение потока со свободной поверхностью, давление над которой известно и одинаково на протяжении потока (открытые русла, каналы, канализационные трубы с частичным заполнением трубы и т. д. ) (Рис. 3. 7, б). Рис. 3. 7. Напорное и безнапорное движение жидкости а напорное движение; б, в безнапорное движение 2012 13

3. 3. ПОТОК ЖИДКОСТИ 3. 3. 1. Понятие о потоке жидкости В реальных условиях мы будет иметь дело не с отдельной элементарной струйкой, а с целым потоком жидкости (например, с потоком воды в реке, трубе, с потоком топлива в системах питания и т. п. ). Поток жидкости можно представить как совокупность элементарных струек, протекающих через площадку достаточно больших (конечных) размеров. Под живым сечением потока ω следует понимать поверхность в пределах потока, нормальную в каждой своей точке к направлению скорости u (рис. 3. 8. 1). Когда угол расхождения элементарных струек достаточно большой (рис. 3. 8. 2), а радиус их кривизны r невелик, живое сечение ω будет представлять собой выпуклую поверхность. Такой вид движения принято называть резко изменяющимся. В отдельных частных случаях движения жидкости живое сечение потока является или можно принимать плоским. Так, при параллельно струйном движении (например, в круглой цилиндрической трубе, целиком заполненной жидкостью), когда отдельные элементарные струйки строго параллельны, живые сечения потока являются плоскими. Движение, близкое к прямолинейному и параллельно струйному, при котором угол расхождения (или схождения) струек незначителен ( 0), а радиусы их кривизны большие (r ), называется плавно изменяющимся движением. При плавно изменяющемся движении живые сечения имеют небольшую кривизну, которой можно пренебречь, а живые сечения считать плоскими. 2012 Рис. 3. 8. 1. Схема потока жидкости Рис. 3. 8. 2. Схема потока жидкости 14

3. 3. 2. Гидравлические характеристики движущейся жидкости Площадь живого сечения ω. Живым сечением элементарной струйки называется поперечное сечение dω, которое нормально к направлению скорости u, и где скорости u одинаковы по всему поперечному сечению (рис. 3. 9. 1). Площадь живого сечения потока (м²) определяется как сумма элементарных живых сечений отдельных струек в потоке (рис. 3. 9) Объемный расход жидкости. Элементарным расходом d. Q называется объем жидкости d. V, проходящий через данное живое сечение dω элементарной струйки в единицу времени, называется расходом струйки или Расходом потока Q будет равен сумме расходов каждой элементарной струйки, т. е. расход потока будет составлять объем жидкости, проходящий через данное живое сечение в единицу времени. Очевидно, величину расхода потока Q можно определить путем интегрирования элементарных расходов d. Q по всему живому сечению потока (3. 3. 1) Средней скоростью потока жидкости называется отношение расхода к площади живого сечения Т. е. расход потока в данном сечении равен произведению площади живого сечения на среднюю скорость потока. (3. 3. 2) 2012 Рис. 3. 9. 1. Схема к определению площади живого сечения струйки Рис. 3. 9. 2. Схема к определению площади живого сечения потока 15

Массовый расход и массовая скорость потока жидкости (плотность массового расхода) Массовым расходом потока G будет равен сумме массовых расходов каждой элементарной струйки, т. е. (3. 4. 1) Зависимость массового G и объемного Q расхода жидкости определяется формулой (3. 4. 2) Отсюда массовая скорость потока жидкости, газа устанавливается зависимостью u=G/ω =ρv. Здесь G массовый расход вещества; Q – объемный расход; ω площадь поперечного сечения потока, v – скорость потока; u – массовая скорость; ρ плотность жидкости. 2012 16

Кроме основных элементов при расчетах движения жидкости рассматривают: Смоченный периметр , который определяется как периметр живого сечения потока или часть его, непосредственно соприкасающаяся с ограждающими стенками потока (рис. 3. 10). Гидравлический радиус - отношение площади живого сечения к смоченному периметру. Гидравлический радиус показывает, какая часть площади живого сечения приходится на единицу длины смоченного периметра. Следовательно, гидравлический радиус является обобщенной характеристикой размера и формы живого сечения данного потока. При движении жидкости в круглой трубе полным сечением Среднюю глубину потока hср, которая равна отношению площади живого сечения ω к его ширине В на уровне свободной поверхности hср=ω/B Если русло потока имеет значительную ширину при небольшой глубине, например, русло реки, то можно принять R≈χ (рис. 3. 10). Тогда на основании равенств R=χ, hср=ω/B, получим hср≈R, т. е. в этом случае гидравлический радиус можно принимать равным средней глубине потока hср. Рис. 3. 10. Гидравлические элементы потока жидкости 2012 17

3. 4. РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ 3. 4. 1. Определение режимов движения жидкости Движение жидкости, в зависимости от скорости, может проявляться в двух различных по структуре режимах - ламинарном (струйчатом) и турбулентном (беспорядочном). Для исследования режимов движения жидкости используют опытную установку, предложенной английским ученым Рейнольдсом (рис. 3. 11). В напорный бак (1) подливается вода и устанавливается постоянный напор. В бак вставляется бачок с красителем (2) с объемной массой, близкой к воде (раствор KMn). Из бака отходит труба (3) с постоянным диаметром d, скорость движения воды V по которой также регулируется краном (4). В напорный бак опускается термометр для определения температуры воды каждого опыта, по которой можно установить кинематический коэффициент вязкости. При малых скоростях движения воды раствор краски движется в виде очень тонкой струйки, параллельной образующей трубы (а). Это указывает на отсутствие обмена и перемешивания частиц жидкости. Движение струйчатое. Такой режим движения называется ламинарным. При увеличении скорости течения воды струйка краски начинает вибрировать принимает волнообразные очертания (б), а после достижения определенной – «критической» скорости струйка мгновенно смешивается с остальными частицами потока (в). Наступает беспорядочный режим движения жидкости, с сильным перемешиванием частиц, который называется турбулентным. Турбулентный режим характеризуется пульсацией скоростей и по величине и по направлению (пульсация обуславливается шероховатостью стенок и вязкостью жидкости). Ламинарный режим протекает без пульсации скоростей. Кроме турбулентного и ламинарного режимов существуют переходные режимы от ламинарного к турбулентному и от турбулентного к ламинарному (б). 2012 Рис. 3. 11. Схема установки для исследования режимов движения жидкости 18

3. 4. 2. Критерии для определения режимов движения жидкости. Смена режимов происходит вследствие изменения скорости движения жидкости в трубе. Однако существование того или иного режима обусловлено, как установил Рейнольдс, не только величиной скорости, но и плотностью жидкости , вязкостью (зависящей от температуры) и характерными размерами потока. Переход одного режима в другой происходит при определенном значении некоторого безразмерного параметра (так называемого критического числа Рейнольдса) Re (3. 5. 1) где v – скорость движения жидкости; ν=μ/ρ - кинематический коэффициент вязкости; динамический коэффициент вязкости; плотность жидкости; d диаметр трубы Число Re является безразмерным Часто в число Рейнольдса вводят гидравлический радиус, являющийся обобщенной характеристикой размера и формы живого сечения потока. Тогда оно имеет следующий вид (3. 5. 2) По опытным данным Рейнольдcа режимы движения определяются следующими значениями: ламинарный режим наблюдается, когда число Red<2300 (Re. R< 575). турбулентный режим наблюдается, когда Red>2300 (Re. R>575). Для открытых потоков Re. Rкр=300. Ламинарный режим встречается в природе в основном при движении грунтовых вод (в мелкозернистых грунтах). Турбулентный режим имеет место в трубах, каналах, реках и т. д. Поэтому в дальнейшем будем рассматривать турбулентный режим движения жидкости и его применение на практике. 2012 19

3. 4. 3. Распределение скоростей в потоке при различных режимах При ламинарном режиме, как показывают исследования, в круглой трубе наблюдается параболическое распределение скоростей, которое графически изображено на рис. 3. 12, а. У стенок трубы скорость равна нулю, т. к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. На оси трубы наблюдается максимальная скорость течения. При этом изменение скоростей от нуля до максимума идет по закону квадратичной параболы. Средняя скорость потока, определяемая по формуле vср=Q/ω, равна в этом случае половине наибольшей (максимальной) скорости в центре трубы Параболическое распределение скоростей при ламинарном режиме движения в круглой трубе наступает, в соответствии с теорией Буссинеска, подтвержденной опытом Никурадзе, на некотором расстоянии от входа в трубу. Начальный участок трубы, на котором формируется ламинарный поток, называется участком стабилизации ламинарного потока. Длина Lст определяется формулой Буссинеска где Red число Рейнольдса; d диаметр трубы (Lст 150 d при Red =2300). При ламинарном режиме наблюдается большая неравномерность распределения скоростей и т. о. большие градиенты скорости по нормали (в центре трубы ), а наибольшего значения он достигает у стенки трубы. При турбулентном режиме распределение скоростей более равномерно (рис. 3. 14, б). При этом у стенок трубы (русла) имеется вязкий подслой жидкости толщиной в, в котором сохраняется ламинарный режим (пограничный ламинарный слой), а остальное «ядро» потока движется в условиях турбулентного режима. Толщина пограничного слоя невелика десятые доли миллиметра и она уменьшается с увеличением средней скорости потока и числа Рейнольдса. Средняя скорость потока в этом случае значительно больше половины максимальной и равна vср=(0, 70… 0, 85)umax. Длина участка стабилизации турбулентного режима меньше, чем ламинарного и равна Lст≈40 d. 2012 Рис. 3. 12. Распределение скоростей в потоке: 20 а при ламинарном; б турбулентном режимах

3. 4. 4. Определение характеристик потока при ламинарном движении жидкости Определение скоростей в потоке при ламинарном режиме. Рассмотрим поток жидкости, движущийся в круглой трубе при ламинарном течении (рис. 3. 1). Приравняем силы вязкости и давления, действующие на цилиндрический объем жидкости радиуса r и длиной dx: (3. 6. 1) Отметим, что равнодействующая сил давления направлена по потоку (вдоль оси x), а сила вязкого трения, приложенная к боковой поверхности цилиндрического объема против потока, поскольку dv/dr<0. Произведя сокращение и разделив (3. 6. 1) на dx, получаем (3. 6. 2) Величина градиента давления dp/dx в (4. 14) не зависит от радиуса r, т. к. давление p=p(x) и в поперечном сечении x=const не меняется. Это позволяет проинтегрировать (3. 6. 2) по радиусу: (3. 6. 3) Уравнение (4. 15) позволяет рассчитать распределение скоростей , при условии, что у стенок трубы эта скорость равна нулю. После интегрирования (3. 6. 3) получаем (3. 6. 4) Проинтегрировав зависимость (3. 6. 4) получим уравнение, связывающее переменные υ и r (рис. 3. 13. 2), которое имеет следующий вид: (3. 7) где p 1 и p 2 давления соответственно в сечениях 1 и 2. У стенок трубы величина r = R, значит скорость υ = 0, а при r = 0 (на оси потока) скорость будет максимальной (3. 8) Следует подчеркнуть, что рассмотренные зависимости справедливы для ламинарных потоков, условие существования которых характеризуются критическим числом Рейнольдса Reкр (Re=2 Q/πRν, ν – кинематическая вязкость). При Re=Reкр ламинарное течение переходит в турбулентное. Для 2012 21 гладких круглых труб, как определено ранее Reкр =2300. Рис. 3. 1. Схема для рассмотрения ламинарного потока

Расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы (рис. 3. 13. 2), то расход жидкости численно равен объему этого параболоида. Определим этот объем. Максимальная скорость дает высоту параболоида Как известно из геометрии, объем параболоида высотой h и площадью πR 2 равен В соответствие с этим в нашем случае расход будет равен откуда (3. 9. 1) Полученная формула выражает закон Пуазейля (формула Пуазейля), в соответствие с которым определяется расход жидкости Q при истечении через трубу длиной l, диаметром R при разности давления на концах трубы Δp=p 1 -p 2. Если вместо R подставить диаметр трубы d, то последняя формула приобретет вид (3. 9. 2) Расход в трубе можно выразить через среднюю скорость: (3. 9. 3) Откуда (3. 10) 2012 22 Рис. 3. 13. 2. Схема для рассмотрения ламинарного потока

3. 4. 4. Определение характеристик потока при турбулентном течении жидкости При стационарном турбулентном течении скорость в данной точке случайным образом меняется во времени, однако среднее значение вектора скорости направлено вдоль оси трубы. Средняя скорость остается постоянной по сечению трубы, и только в очень тонком пограничном слое спадает до нуля у стенок трубы (рис. 3. 13. 3). На практике для расчета турбулентного течения жидкости по трубе используется формула, определяющая разность давлений, как функция скорости (3. 11) в которой k безразмерный гидравлический коэффициент. 2012 Рис. 3. 13. 3. Модель турбулентного режима движения 23 жидкости

4 вопрос ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ЖИДКОСТИ 2012 24

4. 1. ОСНОВНЫЕ УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ 4. 1. 1. Общее уравнение движения сплошной среды. Уравнение импульсов. Для решения многих вопросов механики жидкости возникает необходимость применения уравнения импульсов. Это уравнение позволяет находить характеристики движения на границах рассматриваемой массы жидкости в условиях, когда физические процессы, происходящие внутри этой массы, остаются неизвестными и, следовательно, не являются предметом исследования. Для материальной точки, движущейся под влиянием действующей на нее переменной силы, уравнение импульсов можно написать в следующем виде: где m масса данной материальной точки; v 2 и v 1 соответственно скорости движения этой точки в конечный и начальный моменты промежутка времени Δt = t 2 t 1, определенные в проекциях на некоторую ось; Р проекция действующей силы на ту же ось. Произведение mv называют количеством движения, а произведение Pdt импульсом силы. Общая интегральная форма уравнений количества движения и момента количества движения. Пусть проведена неподвижная замкнутая поверхность S в потоке жидкости, обтекающем неподвижное твердое тело M (рис. 4. 2). Жидкий объем, заключенный внутри S, имеет своей наружной границей поверхность S, а внутренней границей – поверхность твердого тела M. Через бесконечно малый промежуток времени dt , жидкий объем переместится в положение S', которое мы получим, отложив от каждого элемента поверхности S вектор . В случае установившегося движения уравнение сохранения количества движения τ2 где и главные векторы давлений, приложенных к S и M. Закон сохранения моментов количества движений приводит к уравнению: Q M S где и главные моменты сил гидродинамических давлений к поверхностям S и M; радиус вектор элементарной 2012 частицы dm. S' τ1 Рис. 4. 1. Схема к выводу уравнения количества движения 25

4. 1. 2. Методы исследования движения жидкости Имеются различные методы изучение движения жидкости. Наиболее разработанными методами являются метод Эйлера и Лагранжа. По методу Эйлера изучается движение жидкости в окрестности точки с координатами x, y, z. Поэтому полная скорость и давление являются функциями координат и времени: V=f 1(x, y, z, t) P=f 2(x, y, z, t) или в компонентах u=f 1(x, y, z, t) v=f 2(x, y, z, t) w=f 3(x, y, z, t) p=f 4(x, y, z, t) Переменные x, y, z, t называют переменными Эйлера. Задача сводится к решению систем дифференциальных уравнений в частных производных для каждого компонента точки жидкости. Для установившегося течения производные по времени равны нулю, поэтому V=f 1(x, y, z) P=f 2(x, y, z) По методу Лагранжа рассматривается движение жидкой частицы с первоначальными координатами a, b, c, поэтому u=f 1(a, b, c, t) v=f 2(a, b, c, t) w=f 3(a, b, c, t) p=f 4(a, b, c, t) Переменные а, b, с, и t носят название переменных Лагранжа. Задача сводится к решению систем дифференциальных уравнений в частных производных для каждой частицы жидкости. Метод Лагранжа требует более сложного математического аппарата, поэтому метод Эйлера получил большее распространение. 2012 26

4. 1. 3. Дифференциальные уравнения движения жидкости Дифференциальные уравнения Эйлера для идеальной несжимаемой жидкости. Движение идеальной (невязкой) жидкости описывается дифференциальными уравнениями Эйлера, записанными также в проекциях на оси прямоугольной декартовой системы координат, которые служат для определения vx, vy, vz, р как функций x, у, z, t: где (4. 1) Система (4. 1) описывает движение как капельной, так и газообразной жидкости. При этом считается, что течение может быть как установившемся, так и неустановившемся, потенциальным или вихревым, плотность среды может быть постоянной и зависеть от давления. В системе 3 х уравнений пять неизвестных uх, uу, uz, p и ρ, поэтому необходимо иметь еще два уравнения. Такими уравнениями являются уравнения неразрывности и характеристическое уравнение. Уравнение неразрывности или сплошности, называемое уравнением Сен Венана, является одним из уравнений гидродинамики, выражающее закон сохранения массы для любого объёма движущейся жидкости (газа). В переменных Эйлера уравнение неразрывности имеет вид где ρ плотность жидкости, v её скорость в данной точке, a vx, vy, vz проекции скорости на координатные оси. Уравнение, выражающее зависимость между плотностью и давлением, записываются в виде dp/dρ=kр/ρ. При ρ=const (для капельной жидкости) достаточно уравнения неразрывности Q=vω=const. 2012 27

Дифференциальные уравнение движения Лагранжа. Лагранж придал другую форму дифференциальным уравнениям гидродинамики. При составлении дифференциальных уравнений скорости u, v, w (а также p и ρ) рассматриваются как функции от t и от координат x, у, z точек пространства, занимаемых точками жидкости в момент t; при составлении же Лагранжевых уравнений координаты x, y, z точек жидкости в момент t рассматриваются как функции от t и от координат a, b, c той же точки в начальный момент t = 0. Уравнения Лагранжа имеют следующий вид: первое (d 2 x/dt 2)(dx/da) + (d 2 y/dt 2)(dy/da) + (d 2 z/dt 2)(dz/da) + (1/ ρ)(dp/da) = X(dx/da) + Y(dy/da) + Z(dz/da). . . (L) и два другие, отличающиеся от первого тем, что во втором входят частные производные по b, в третьем по с. Уравнение неразрывности имеет также иной вид. Впоследствии оказалось, что и эта форма дифференциальных уравнений гидродинамики также впервые указана Эйлером, хотя за нею установилось наименование Лагранжевой. 2012 28

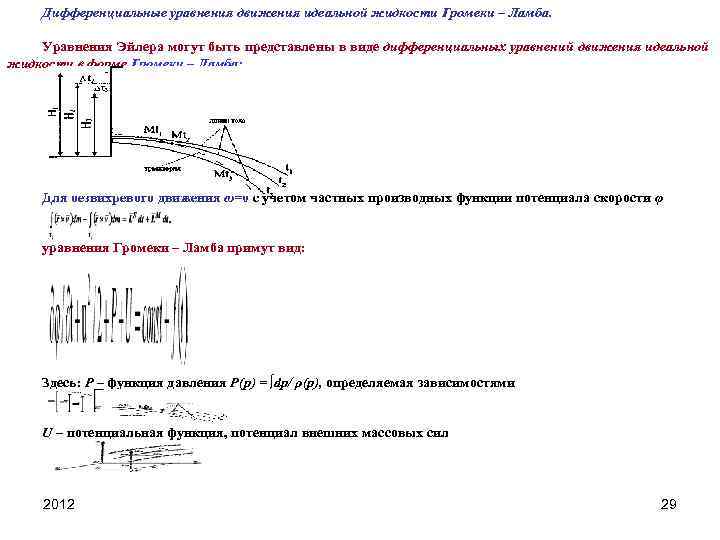Дифференциальные уравнения движения идеальной жидкости Громеки – Ламба. Уравнения Эйлера могут быть представлены в виде дифференциальных уравнений движения идеальной жидкости в форме Громеки – Ламба: Для безвихревого движения ω=0 с учетом частных производных функции потенциала скорости φ уравнения Громеки – Ламба примут вид: Здесь: Р – функция давления P(p) = ∫dp/ ρ(p), определяемая зависимостями U – потенциальная функция, потенциал внешних массовых сил 2012 29

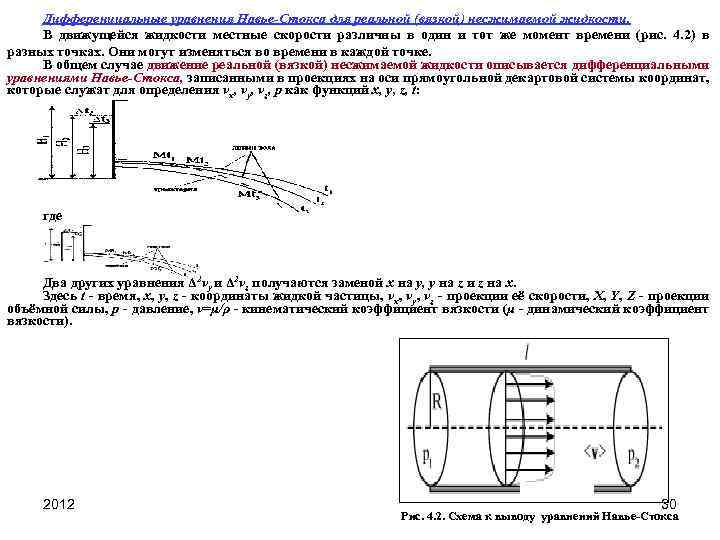Дифференциальные уравнения Навье-Стокса для реальной (вязкой) несжимаемой жидкости. В движущейся жидкости местные скорости различны в один и тот же момент времени (рис. 4. 2) в разных точках. Они могут изменяться во времени в каждой точке. В общем случае движение реальной (вязкой) несжимаемой жидкости описывается дифференциальными уравнениями Навье-Стокса, записанными в проекциях на оси прямоугольной декартовой системы координат, которые служат для определения vx, vy, vz, р как функций x, у, z, t: где Два других уравнения Δ 2 vy и Δ 2 vz получаются заменой x на у, у на z и z на x. Здесь t время, x, у, z координаты жидкой частицы, vx, vy, vz проекции её скорости, X, Y, Z проекции объёмной силы, p давление, v=μ/ρ кинематический коэффициент вязкости (μ динамический коэффициент вязкости). 2012 30 Рис. 4. 2. Схема к выводу уравнений Навье Стокса

Дифференциальными уравнениями неустановившееся движение открытого потока Сен-Венана. Математической основой любой одномерной модели неустановившегося движения и качества вод в речной сети является система уравнений Сен-Венана (уравнение неразрывности и уравнение движения), дополненная уравнением переноса, диффузии и кинетики примеси, а также моделью структуры русловой сети. Уравнение движения. ∂q/∂t+∂(vq)/∂x+gω[∂z/∂t+q|q|/K 2]=Fw+Fu (1) где ∂q/∂t – член уравнения, учитывающий изменение расхода во времени, ∂(vq)/∂x - член уравнения, учитывающий изменение скоростей по длине потока, v=q/ω средняя по сечению скорость, g ускорение силы тяжести, ∂z/∂t - дополнительный уклон, связанный с изменением глубины, z (x, t) отметка уровня воды, K=CωR 2 модуль стока, C коэффициент Шези, R=ω/χ гидравлический радиус (близкий к средней глубине h=ω/B), B ширина потока, χ(x, t) смоченный периметр, Fw, Fu дополнительные импульсы за счет соответственно скорости ветра (w) и боковой приточности (u). Уравнение неразрывности. ∂ω/∂t+∂q/∂x=u(x, t) (2) где t время, x пространственная координата, ориентированная по направлению течения, ω(x, t) площадь живого сечения водотока, q(x, t) расход воды, u(x, t) боковая приточность (склоновый сток, подземный сток и т. д. ). Уравнение продольной диффузии. ∂(ωS)/∂t+∂(q. S)/∂x=∂/∂x(Dω∂S/∂x)+ωG+u. Sl (3) где S(x, t) - концентрация вещества, d(v, R) - коэффициент продольной дисперсии, G(s, t) - кинетический член, Sl(x, t) - концентрация вещества в распределенном боковом притоке. Как показывает многолетняя практика расчетов неустановившегося движения (например, при прогнозировании паводков или обосновании эксплуатационных попусков), уравнения Сен Венана достаточно удовлетворительно отображают распространение волн перемещения, в том числе и волн попуска в реках, особенно если форма русла и поймы реки близка к призматической. Однако общее решение системы нелинейных дифференциальных уравнений гиперболического типа в частных производных, особенно с учетом реальных морфометрических характеристик рек, представляет собой большие математические трудности. Поэтому даже так называемые «строгие методы» расчета, базирующиеся на решении уравне ний ен Венана, используют, как С правило, численные методы расчета параметров волн прорыва на ЭВМ (в частности, метод характеристик, метод сеток и т. п. ). Чаще всего, в инженерной практике отказываются от непосредственного использования уравнений (1), (2), а преобразуют их или заменяют какой либо упрощенной моделью. Простота расчетов в этих моделях обычно связана с отказом от детального Рис. 4. 3. Схема неустановившегося движения открытого 2012 31 задания некоторых частей исходной информации. потока

4. 1. 4. Решения дифференциальных уравнений движения жидкости Теория интегрирования дифференциальных уравнений не дает еще средств получить решения дифференциальных уравнений ни формы Эйлера, ни формы Лагранжа в общем виде; возможно получить решения их только в некоторых простейших специальных случаях. В таких случаях по преимуществу пользуются Эйлеровой формой, когда решение требуется отыскать; но иногда обращаются и к уравнениям Лагранжа, в особенности тогда, когда представляется возможным угадать вид функций от t, а, b, с, выражающих x, y, z. Специальные категории случаев, в которых оказывается возможным решить уравнения гидродинамики, принадлежат преимущественно к тем, в которых внешние силы имеют потенциал или силовую функцию и в которых течение жидкости невихревое, то есть скорости u, v, w имеют потенциал, так что u = dφ/dx, v = dφ/dy, w = dφ/dz где φ есть функция от x, y, z, t. К числу таких вопросов относятся вопросы о течении жидкости в двух измерениях, о распространении волн, о движении твердых тел в жидкостях. Кроме этого рассмотрены некоторые вопросы о движении вихревых нитей и колец. 2012 32

Конечно разностные формы уравнений Навье Стокса. Общая схема численных методов и их реализация на ЭВМ. Разностной схемой решения краевой задачи называют совокупность разностных уравнений, заменяющих данные дифференциальные уравнения, граничные и начальные условия. Одним из способов аппроксимации дифференциальных уравнений разностными заключается в следующем. При помощи системы пересекающихся линий в рассматриваемой области вводится разностная сетка – совокупность узлов (точек пересечения линий), в которых отыскивается приближенное решение. Затем выбирается сеточная конфигурация – группа узлов, которые привлекаются для локальной аппроксимации дифференциальных уравнений. После этого каждая из производных, входящих в уравнение, заменяется отношением разности значений функции в узлах выбранной конфигурации к разности соответствующих значений аргумента. Например, рассмотрим т. н. задачу Коши для переноса Введем в плоскости (x, t) сетку из параллельных прямых и будем конструировать разностную схему при помощи трехточечной конфигурации (рис. 4. 4). Занумеруем узлы сетки парами целых чисел (k, n) и примем обозначение f(kΔx, nΔt)= . Для замены производных в узле (k, n) воспользуемся разностными отношениями Коэффициент a(x, t) , будем брать в узле (k, n). В результате замены получаем разностную схему: (k, n+1) Мы познакомились в первом приближении с порядком составления разностных схем. Существует очень много различных разностных схем для различных задач и множество способов их решения. Эти задачи решают специалисты механики (теоретики) и математики. Вы – практики должны уметь находить уже реализованные на ЭВМ нужные вам решения и применять их в своей практической деятельности. 2012 Δt (k+1, n) Δx (k, n) Рис. 4. 4 33

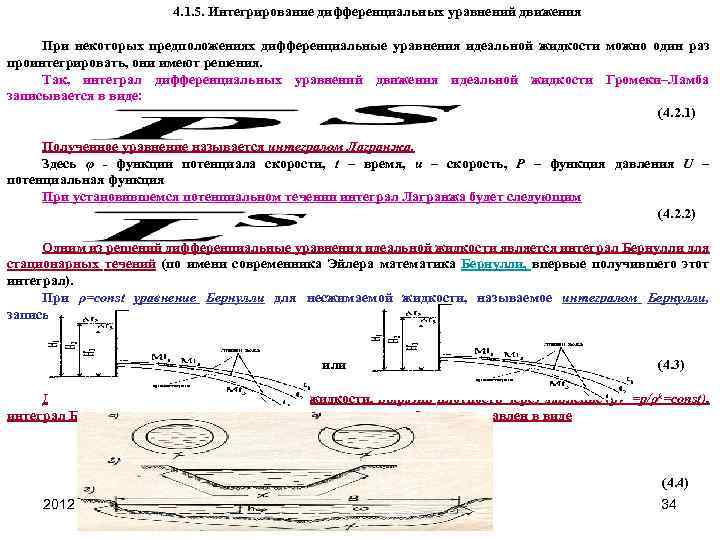4. 1. 5. Интегрирование дифференциальных уравнений движения При некоторых предположениях дифференциальные уравнения идеальной жидкости можно один раз проинтегрировать, они имеют решения. Так, интеграл дифференциальных уравнений движения идеальной жидкости Громеки–Ламба записывается в виде: (4. 2. 1) Полученное уравнение называется интегралом Лагранжа. Здесь φ - функции потенциала скорости, t – время, u – скорость, Р – функция давления U – потенциальная функция При установившемся потенциальном течении интеграл Лагранжа будет следующим (4. 2. 2) Одним из решений дифференциальные уравнения идеальной жидкости является интеграл Бернулли для стационарных течений (по имени современника Эйлера математика Бернулли, впервые получившего этот интеграл). При ρ=const уравнение Бернулли для несжимаемой жидкости, называемое интегралом Бернулли, записывается в виде: или (4. 3) Для адиабатических течений сжимаемой жидкости, выразив плотность через давление (p. Vk=р/ρk=const), интеграл Бернулли в отсутствии внешних массовых сил может быть представлен в виде (4. 4) 2012 34

4. 1. 5. Уравнения сплошности (неразрывности) течения Более подробно рассмотри уравнение сплошности (неразрывности) течения. Уравнение сплошности (неразрывности) течения для элементарной струйки. Уравнение неразрывности элементарной струйки в дифференциальной форме имеет вид Если течение установившееся, то ∂ρ/∂t=0, и условие сохранения сплошности (неразрывности) течения можно представить следующим образом: Если жидкость несжимаема (ρ=const), уравнение неразрывности принимает вид Уравнение неразрывности элементарной струйки в гидравлической форме. При установившемся движении вследствие неразрывности потока жидкости элементарный расход остается постоянным по длине элементарном струйки, т. е. d. Q=Const. Это условие для двух произвольно выбранных живых сечений струйки (например, сечений d 1 и d 2) можно записать в следующей виде (3. 2) 1 1 2 2 d. Q = u d =Const. Полученное уравнение называется гидравлическим уравнением неразрывности элементарной струйки. Из него следует, что (4. 5) т. е. скорости в различных сечениях элементарной струйки 2012 обратно пропорциональны площадям живых сечений. Рис. 3. 9. 1. Схема к выводу уравнения сплошности (неразрывности) течения 35

Гидравлическое уравнение неразрывности (или сплошности) для потока жидкости. Рассмотрим расходы жидкости в двух произвольно выбранных сечениях потока 1 1 и 2 2. Напомним, что элементарный расход какой либо струйки в этих сечениях одинаков (рис. 4. 5), т. е. d. Q=u 1 d 1=u 2 d 2=Const. Если просуммировать элементарные расходы всех струек, из которых состоит поток, в каждом из двух сечений, получим очевидные равенства: или Q 1 = Q 2. Поскольку мы выбирали произвольные живые сечения, то и для любых других сечений потока справедливо определение, что при установившемся движении жидкости расход ее в любом живом сечении потока остается постоянным Q 1 = Q 2 = Q 3 =…= Const, (4. 6. 1) Это уравнение называется гидравлическим уравнением неразрывности (или сплошности) потока жидкости, имеющим большое практическое значение. Если выразить расход потока через среднюю скорость и площадь живого сечения, то уравнение неразрывности (4. 6. 1) для двух сечений можно переписать следующим образом ω2, р2 Q 1 = Q 2 или 1 v 1 = 2 v 2, откуда (4. 6. 2) т. е. в установившемся потоке жидкости средние скорости движения обратно пропорциональны площадям живых сечений. 2012 ω1, р1 Рис. 4. 5. Схема к выводу уравнения неразрывности (или сплошности) потока жидкости 36

4. 2. УРАВНЕНИЕ Д. БЕРНУЛЛИ Уравнение Бернулли имеет большое теоретическое и практическое значение, поэтому рассмотрим его подробнее. 4. 2. 1. Уравнение Бернулли для элементарной струйки идеальной жидкости Рассмотрим элементарную струйку идеальной жидкости, где на продольном профиле выберем сечения 1 -1 и 2 -2 (рис 4. 6). В каждом сечении установим пьезометры I (один из них изображен в точке А), в которых уровень жидкости поднимается на высоту p/ρg = p/γ. Если между сечением 1 -1 и 2 -2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию, которая называется пьезометрической линией (рис. 4. 1). Кроме пьезометров в каждом сечении 1 -1 и 2 -2 установим трубки Пито II (одна из них изображена в точке А), загнутый конец которой направлен навстречу потоку жидкости. Жидкость в трубках Пито также поднимается на разную высоту, и уровень жидкости в трубке II будет выше, чем в пьезометрической трубке. Однако уровень жидкости во всех трубках Пито будет одинаков, и располагаться на равной высоте относительно произвольной горизонтальной прямой 0 -0. Уровень жидкости в трубках Пито характеризуется линией N-N, называемой напорной линией. Для двух произвольных сечений 1 -1 и 2 -2 потока идеальной жидкости уравнение Бернулли имеет следующий вид (4. 7. 1) Так как сечения 1 -1 и 2 -2 взяты произвольно, то полученное уравнение можно записать в виде (4. 7. 2) Таким образом, сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная. Уравнение Бернулли, полученное в 1738 г. , является фундаментальным уравнением гидродинамики. Уравнение Бернулли дает связь между давлением p, средней Рис. 4. 6. Схема к выводу уравнения Бернулли скоростью υ и пьезометрической высотой z в любой для элементарной струйки идеальной жидкости фиксированной точке элементарной струйки при установившемся 2012 37 движении жидкости и выражает закон сохранения энергии движущейся жидкости.

4. 2. 2. Геометрический смысл уравнения Бернулли Пользуясь методом размерностей нетрудно показать, что все члены уравнения Бернулли имеют размерность длины: z = [L[. Так где: T символ времени; L символ длины; F символ силы. Поэтому все члены уравнения Бернулли можно будет представить как высоты. Условимся, отсчет высот производить от некоторой горизонтальной плоскости координат x. Oy, которую в дальнейшем будем называть плоскостью сравнения, а след пересечения ее с плоскостью чертежа, представляющий собой горизонтальную линию, обозначим 0 -0 (рис. 4. 6). Применим метод геометрического представления к двум сечениям элементарной струйки 1 -1 и 2 -2 (рис. 4. 6). Площади живых сечений соответственно равны d 1 и d 2; скорости движения частиц в этих сечениях u 1 и u 2 в соответствии с уравнением неразрывности (3. 3) обратно пропорциональны площадям живых сечений. Выберем произвольные точки в сечениях 1 -1 и 2 -2 (в нашем случае они совпадают с центрами тяжести живых сечений d 1 и d 2). Расстояние от этих точек до плоскости сравнения 0 -0, соответственно, обозначим через z 1 и z 2. 2012 Рис. 4. 6. Схема к геометрической интерпретации членов уравнения Бернулли 38

Геометрический смысл уравнения Бернулли Первый член уравнения Бернулли - координата z измеряет высоту расположения частицы жидкости над плоскостью сравнения и называется высотой положения. Второй член называют пьезометрической высотой или высотой давления hp=р/γ, он представляет собой высоту столба жидкости, на которую может подняться уровень жидкости в открытой пьезометрической трубке I, помещенной в данную точку элементарной струйки, под действием гидродинамического давления в этой точке. Для выяснения смысла третьего члена уравнения – величины u 2/2 g рассмотрим высоту столба жидкости в трубке II (трубке Пито, называемой скоростной трубкой), помещенной в точку A элементарной струйки. Под влиянием скорости u. A уровень жидкости в трубке II поднимется выше, чем в пьезометрической трубке I на некоторую высоту h, которую мы определим из следующих соображений. Избыточная (сверх пьезометрической высоты hp=р/γ) высота h должна вызывать, согласно закону Торричелли, истечение жидкости из скоростной трубки II со скоростью С другой стороны, частицы жидкости, движущиеся в струйке, стремятся войти в отверстие скоростной трубки со скоростью u. A. Так как фактически жидкость не входит в трубку и не вытекает из нее, то откуда Следовательно, разность высот жидкости в скоростной и пьезометрической трубках и выражает собой третий член в уравнении Бернулли. Поэтому третий член в уравнении Бернулли принято называть скоростной высотой или скоростным напором Такова геометрическая интерпретация отдельных членов, входящих в уравнение Бернулли. 2012 Рис. 4. 6. Схема к геометрической интерпретации членов уравнения Бернулли 39

Геометрический смысл уравнения Бернулли Сумма высот положения и давления называется пьезометрическим напором а линия p 1 -p 2, соединяющая вершины пьезометрических напоров, называется пьезометрической линией. Сумма пьезометрического и скоростного напоров, представляющая собой сумму трех членов уравнения Бернулли, называется полным напором H (4. 7. 2) Геометрическое место вершин сумм трех высот: положения, давления и скоростной называется напорной линией N-N. Из уравнения (4. 7) видно, что для двух произвольно выбранных сечений элементарной струйки 1 -1 и 2 -2 эта сумма высот есть величина постоянная. Т. е. напорная линия N-N лежит в горизонтальной плоскости, параллельной плоскости сравнения 0 -0, на расстоянии H от нее. Отсюда геометрический смысл уравнения Бернулли (4. 7) можно сформулировать следующим образом: для элементарной струйки идеальной жидкости сумма трех высот: геометрической, пьезометрической и скоростной (т. е. полный напор) не изменяется по длине струйки. Z 2012 Рис. 4. 6. Схема к геометрической 40 интерпретации уравнения Бернулли

4. 2. 3. Энергетический смысл уравнения Бернулли Удельная энергия. Напомним, что все члены уравнения Бернулли, выраженные в единицах длины, отнесены к единице веса движущейся жидкости. Применяя метод размерностей, легко установить, что все эти члены могут быть выражены в единицах работы или энергии, отнесенных к единице веса жидкости. Энергия, отнесенная к единице веса называется удельной энергией. Таким образом, каждый из членов уравнения Бернулли представляет собой определенный вид удельной энергии движущейся жидкости. 2012 41

Энергетический смысл уравнения Бернулли. Для выявления энергетического смысла уравнения Бернулли рассмотрим вначале некоторую часть элементарной струйки массой m и объемом W, обладающей скоростью u и испытывающей гидродинамическое давление p (рис. 4. 7). Если эта масса находится на высоте z от плоскости сравнения 0 -0, то потенциальная энергия массы струйки m, зависящая от положения, будет равна ее весу, умноженному на высоту поднятия, т. е. mgz , отсюда удельная потенциальная энергия положения будет равна (4. 8. 1) Таким образом, первый член уравнения Бернулли z с энергетической точки зрения представляет собой удельную энергию положения движущейся жидкости. Так как масса струйки занимает объем W и испытывает давление p, то потенциальная энергия давления будет p. W. Поскольку вес жидкости в объеме W можно выразить, как W, то удельная потенциальная энергия давления определится соотношением (4. 8. 2) В энергетическом смысле член р/γ в уравнении Бернулли представляет собой вид удельной потенциальной энергии, обусловленной гидродинамическим давлением и называемой удельной энергией давления движущейся жидкости. Сумма удельных энергий положения и давления называется удельной потенциальной энергией движущейся жидкости eп (4. 8. 3) Третий член уравнения Бернулли u 2/2 g выражает собой величину удельной кинетической энергии eк движущейся жидкости. Действительно, кинетическая энергия, которой обладает масса m движущаяся со скоростью u будет mu 2/2. Если же эту энергию отнести к единице веса (т. е. разделить на mg), то получим (4. 8. 4) 2012 Рис. 4. 7. Схема к пояснению энергетического смысла 42 уравнения Бернулли

Энергетический смысл уравнения Бернулли. Сумма трех членов уравнения Бернулли представляет собой полную удельную энергию движущейся жидкости e, которая слагается из удельной потенциальной энергии eп (равной сумме удельной энергии положения и давления) и удельной кинетической энергии eк, т. е. (4. 9. 1) Переписав это уравнение для двух частиц (1 и 2), находящихся в одной элементарной струйке, или для двух положений одной и той же частицы движущейся жидкости, мы заметим, что (4. 9. 2) Т. е. сумма удельной потенциальной и кинетической энергии по длине элементарной струйки остается постоянной. Уравнение Бернулли в форме (4. 9. 1) или (4. 9. 2) позволят четко определить взаимосвязь между удельной потенциальной и кинетической энергией и преобразованием одного вида энергии в другой (например, части потенциальной энергии в кинетическую энергию или наоборот). Поэтому уравнение Бернулли представляет собой частное выражение общего закона сохранения энергии. Резюмируя сказанное выше, энергетический смысл уравнения Бернулли можно кратко сформулировать следующим образом: при установившемся движении идеальной жидкости удельная энергия не изменяется по длине элементарной струйки. 2012 Рис. 4. 7. Схема к пояснению энергетического смысла уравнения Бернулли 43

4. 2. 4. Уравнение Бернулли для элементарной струйки реальной жидкости При движении реальной жидкости следует учитывать ее вязкость, вследствие которой возникает сопротивление движению частиц (т. е. силы трения). На преодоление сил трения затрачивается часть энергии жидкости. Поэтому удельная энергия жидкости в сечении элементарной струйки 2 -2 (e 2 или H 2) будет меньше удельной энергии жидкости в сечении 1 -1 (e 1 или H 1) на некоторую величину h , равную (рис. 4. 8) Отсюда, с учетом выражения (1. 9), получим уравнение Бернулли для элементарной струйки реальной жидкости в следующем виде (4. 10) где h’ удельная энергия жидкости (или напор), затрачиваемая на преодоление гидравлических сопротивлений в пути между сечениями 1 -1 и 2 -2 элементарной струйки. Как и все члены уравнения, член h’ имеет размерность длины. Для струйки реальной жидкости сумма высот геометрической, пьезометрической и скоростной уже не остается постоянной, а убывает по длине струйки, что выражается отклонением напорной линии N–N’ от горизонтальной линии N-N. Величина отклонения представляет собой потерю напора или удельной энергии на соответствующем участке элементарной струйки. Линия N–N’, характеризующая величину удельной энергии жидкости в любой точке элементарной струйки, называется линией энергии. Линия p–p называется пьезометрической линией. 2012 44 Рис. 4. 8. Схема к уравнению Бернулли для элементарной струйки реальной жидкости

4. 2. 5. Уравнение Бернулли для потока реальной жидкости Для двух различных сечений потока (рис. 4. 4) при установившемся плавно изменяющемся движении уравнение Бернулли можно записать в следующем виде (4. 11) где z 1 расстояние от произвольно выбранной точки в живом сечении 1 до плоскости сравнения 0 -0; p 1 гидродинамическое давление, определенное в той же точке живого сечения потока; удельный вес жидкости; v 1 средняя скорость в живом сечении 1; g - ускорение силы тяжести; 1 коэффициент неравномерности распределения скоростей в живом сечении 1; z 2, p 2, v 2, 2 - те же величины, определенные в живом сечении ω2, hw удельная энергия (потеря напора), затраченная на преодоление гидравлических сопротивлений в пути между первым к вторым сечением. Из уравнения Бернулли для потока реальной жидкости следует, что удельная энергия уменьшается по длине потока в направлении движения, так как часть энергии затрачивается на преодоление гидравлических сопротивлений в пределах данного участка потока. 2012 Рис. 4. 4. Схема к выводу уравнения Бернулли 45 для потока реальной жидкости

4. 2. 6. Гидравлический уклон есть потеря энергии потока (напора) на единицу длины потока. Если полная потеря напора на длине L равна hw, то средняя потеря энергии (напора) средний гидравлический уклон (градиент) – равен (4. 12) 2012 46

Виды гидравлических уклонов. а) При неравномерном напорном движении, учитывая уравнение Бернулли для двух сечений потока реальной жидкости, гидравлический уклон будет равен Такой гидравлический уклон называется полным гидравлическим уклоном Id. Поскольку в нем изменяются и давление, и скорость, полный гидравлический уклон является уклоном при неравномерном напорном движении. б) При неравномерном безнапорном движении жидкости (в открытых руслах) на свободной поверхности имеет место атмосферное давление. Поэтому p 1 = p 2 = pат и выражение для гидравлического уклона получит вид в) При равномерном напорном движении жидкости (в цилиндрических трубах) v 1 = v 2, получим следующее выражение для уклона (при 1 2) Этот уклон, зависящий только от падения пьезометрического напора вдоль потока, называется пьезометрическим уклоном. Из последнего выражения видим, что для обеспечения напорного движения в цилиндрической трубе необходимо и достаточно иметь неравенство В случае напорного движения в горизонтальной трубе (z 1=z 2), пьезометрический уклон равен г) При равномерном безнапорном движении жидкости (в открытых руслах, призматический канал) v 1=v 2, p 1=p 2, тогда получим следующее выражение для уклона Т. е. гидравлический уклон, зависящий только от падения свободной поверхности потока на единицу длины, равен 2012 47 геометрическому уклону. В случае равномерного безнапорного движения уклоны свободной поверхности потока и дна русла равны и проекции их на плоскости чертежа параллельны.

4. 2. 7. Использование уравнения Бернулли для измерения характеристик потока жидкости На основе уравнения Бернулли сконструирован ряд приборов, таких, как водомер Вентури, водоструйный насос, эжектор, карбюраторы поршневых двигателей и др. С помощью уравнения Бернулли решаются многие задачи практической гидравлики. Совместное применение уравнения Бернулли к потоку конечных размеров и уравнения неразрывности позволяет решать многие инженерные задачи, связанные с движением жидкости в реках, каналах, трубах, гидравлических машинах и т. п. Например, измерение статического и скоростного давления в потоке жидкости с использованием трубок Пито (рис. 4. 11). Поместив пьезометр и трубку Пито (рис. 4. 11, а), в указанную точку, мы можем определить статический напор hs, полный напор ht и скоростной напор hv в миллиметрах ртутного (водяного) столба. Рис. 4. 11. Схемы установок пьезометров и трубок Пито для определения статический напор hs, полный напор ht и скоростной напор hv в потоке жидкости или газа: а) – установка пьезометра и трубки Пито в потоке жидкости и б) – газов; А манометр статического давления; В манометр полного давления; С дифференциальный манометр, измеряющий скоростной напор в миллиметрах ртутного (водяного) столба 2012 48

Измерение скорости потока и расхода жидкости Измерение скорости потока с использованием трубки Пито. Пусть требуется, например, измерить скорость жидкости в какой то точке потока. Поместив трубку Пито (рис. 4. 12, а), в указанную точку и составив уравнение Бернулли для сечения 1 -1 и сечения, проходящего на уровне жидкости в трубке Пито, получим или где Н столб жидкости в трубке Пито. Измерение расхода жидкости с использованием расходомера Вентури. Действие расходомера Вентури основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис. 4. 12, б). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе. Пренебрегая потерями напора и считая z 1=z 2, напишем уравнение Бернулли для сечений I-I и II-II: или Используя уравнение неразрывности Q=υ1ω1=υ2ω2 сделаем замену в полученном выражении Решая относительно Q, получим а) б) Выражение, стоящее перед √h является постоянной величиной, носящей название постоянной водомера Вентури. Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер. Рис. 4. 12. Трубка Пито и расходомер Вентури 2012 49

5 вопрос РАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ 2012 50

5. 1. ОСНОВНОЕ УРАВНЕНИЕ РАВНОМЕРНОГО ДВИЖЕНИЯ ЖИДКОСТИ 5. 1. 1. Вывод уравнения равномерного движения Рассмотрим равномерное напорное движение жидкости в цилиндрической трубе с площадью живого сечения . Сечениями 1 -1 и 2 -2 выделим участок потока длиной L и отнесем его к произвольно выбранной плоскости сравнения 0 -0. Падение пьезометрической линии P-P в пределах выделенного участка выражает собой потерю напора hf на трение по длине L (рис. 5. 1). Из определения равномерного движения следует, что ускорения и силы инерции равны нулю. Поэтому сумма проекций на любую ось всех внешних сил, приложенных к выделенному объему жидкости, должна быть равна нулю. Спроектируем эти силы на ось x-х, совпадающую с направлением движения потока жидкости. К внешним силам, действующим на выделенный объем жидкости, относятся: сила тяжести, направленная вертикально вниз, и равная весу выделенного объема жидкости G= ωL. Проекция этой силы на ось x–x Gx=Gsin ; силы P 1 и P 2, давления на торцевые сечения выделенного участка потока со стороны жидкости: P 1=p 1ω; P 2=p 2ω, где p 1 и p 2 – гидродинамические давления в центре живых сечений (в точках 1 и 2). Силы P 1 и P 2 проектируются на ось x–x без искажения, причем сила P 1 направлена в сторону движения жидкости, а сила P 2 в противоположную сторону. Равнодействующая этих сил P 1 -P 2=(p 1–p 2)ω; силы давления стенок трубы на боковую поверхность выделенного объема жидкости нормальные к этой поверхности. Проекции этих сил на направление движения равны нулю; силы сопротивления, обусловленные трением потока о стенки. Обозначив силу трения, приходящуюся на единицу поверхности соприкосновения потока со стенками, (иначе говоря, касательное напряжение «на стенке» ) через о, вычислим величину силы трения T в пределах выделенного отсека жидкости по формуле T= o L, где смоченный периметр. Составив сумму проекций всех внешних сил на направление движения, и приравняв ее к нулю, получим Gsin +P 1 -P 2–T=0. Учитывая ранее приведенные выражения для действующих сил, а также выражение sinα=(z 1 -z 2)/L (см. рис. 9. 3), уравнение равновесия рассматриваемого объема жидкости можно представить так (z 1–z 2)+ (p 1–p 2)- o L=0. (5. 1) 2012 51 Рис. 5. 1. Схема к выводу уравнения равномерного движения

Вывод уравнения равномерного движения. Рассмотрим уравнение (5. 1) (z 1 – z 2) + (p 1 – p 2) - o L = 0. Поделив все члены уравнения (5. 1) на вес жидкости L и группируя все слагаемые с одинаковыми индексами, получим (5. 2) В левой части этого равенства имеем выражение пьезометрического уклона Ip при равномерном движении. Правую часть равенства (5. 2) можно упростить, учитывая, что Тогда из равенства (5. 2) будем иметь (5. 3) 2012 52

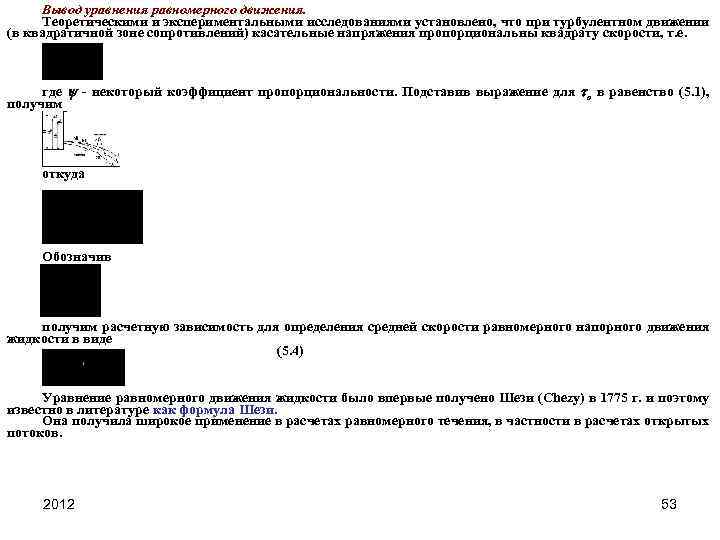Вывод уравнения равномерного движения. Теоретическими и экспериментальными исследованиями установлено, что при турбулентном движении (в квадратичной зоне сопротивлений) касательные напряжения пропорциональны квадрату скорости, т. е. где некоторый коэффициент пропорциональности. Подставив выражение для о в равенство (5. 1), получим откуда Обозначив получим расчетную зависимость для определения средней скорости равномерного напорного движения жидкости в виде (5. 4) Уравнение равномерного движения жидкости было впервые получено Шези (Chezy) в 1775 г. и поэтому известно в литературе как формула Шези. Она получила широкое применение в расчетах равномерного течения, в частности в расчетах открытых потоков. 2012 53

5. 1. 2. Расчетные формулы для скорости и расхода при равномерном движении Основная расчетная зависимость для определения средней скорости равномерного напорного движения жидкости, именуемая формулой Шези, записывается в виде (5. 4) Тогда расход жидкости определим по формуле (5. 5) Зависимости (5. 4) и (5. 5) представляют собой две формы выражения расчетного уравнения равномерного напорного движения жидкости при турбулентном режиме. Для равномерного безнапорного движения жидкости, когда гидравлический уклон равен уклону дна канала, уравнения равномерного движения примут вид (5. 6) (5. 7) В приведенных формулах: v – скорость течения, Q – расход, С – коэффициент Шези, R – гидравлический радиус, Iр – пьезометрический уклон, I 0 – уклон дна потока, ω – площадь живого сечения. 2012 54

Расчетные значения коэффициента Шези. Уравнение равномерного движения жидкости, как было отмечено ранее, было впервые получено Шези и поэтому известно в литературе как формула Шези, а коэффициент С как коэффициент Шези. В отличие от Шези, полагавшего значение коэффициента С постоянным, более поздними исследованиями было установлено, что коэффициент С изменяется в широких пределах и зависит от геометрических размеров потока (гидравлического радиуса) и шероховатости стенок труб или каналов (характеризуемой коэффициентом шероховатости n). В качестве основной зависимости для определения коэффициента С используется формула Н. Н. Павловского (5. 8) где n коэффициента шероховатости; у показатель степени, зависящий в свою очередь от гидравлического радиуса R и коэффициента шероховатости n, т. е. y=y(R, n). Значение коэффициента шероховатости n принимают в зависимости от материала труб (стальные, оцинкованные, чугунные, асбестоцементные и т. п. ), способа обработки их внутренней поверхности (без обработки, с хорошо заглаженными стыками и т. п. ) и от состояния труб (новые трубы; трубы, бывшие в эксплуатации). В некоторых гидравлических расчетах (в частности, при расчете дорожных труб) для определения коэффициента С используется формула Маннинга (5. 9) 2012 55

5. 2. ВОДОПРОВОДНАЯ ФОРМУЛА 5. 2. 1. Вывод водопроводной формулы. На участках трубопровода постоянного диаметра и расхода имеет место напорное равномерное движение жидкости, уравнение которого, как установлено, имеет вид (5. 5) Пьезометрический уклон Ip в этом уравнении представляет собой потерю напора, обусловленную трением, на единицу длины потока, т. е. Подставив последнее выражение в уравнение равномерного напорного движения и решая его относительно hf , получим (5. 10) Обозначив С 2 2 R = K 2, последнюю зависимость приведем к виду (5. 11) Это выражение называется водопроводной формулой. Здесь K 2 =С 2 2 R – модуль расхода, где С – коэффициент Шези. 2012 56

5. 2. 2. Характеристики водопроводной формулы Водопроводная формула записывается в виде (5. 12) где hf - потери напора на трение в трубе диаметром d и длиной L; Q - расход воды; K модуль расхода (или расходная характеристика), Из формулы (5. 12) видно, что потеря напора имеет размерность длины и может быть выражена в метрах столба перекачиваемой жидкости. Из уравнения (5. 5) следует, что (5. 13) откуда можно определить, что размерность модуля расхода совпадает с размерностью расхода Q. Для случая напорного равномерного движения модуль расхода является функцией диаметра трубы и ее шероховатости. При определенном постоянном значении коэффициента шероховатости (т. е. при n=const) K = f(d). Значения K для новых стальных водопроводных труб (при n=0, 012) наиболее употребительных стандартных диаметров приведены в учебниках. При расчетах водопроводных труб величину, обратную квадрату модуля расхода часто обозначают через S (5. 14) Тогда водопроводная формула (5. 12) переписывается в виде 2012 57