 № 3
№ 3
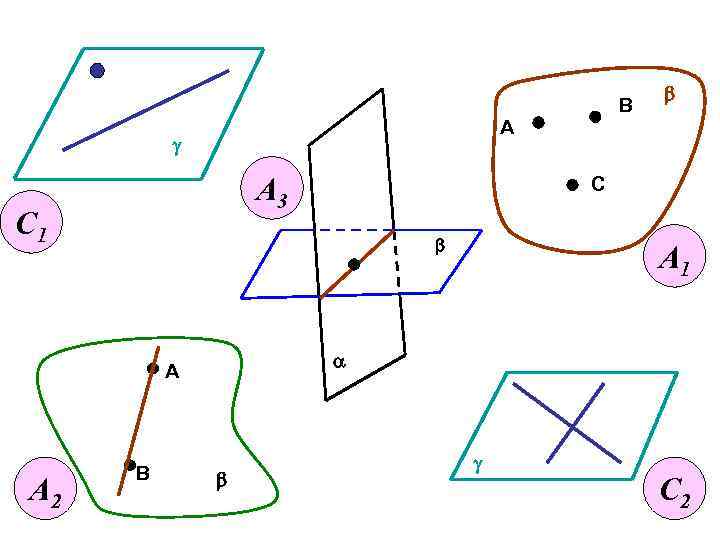 В А g А 3 2 С 1 1 А 1 3 a А А 2 4 С b В b b g С 2 5
В А g А 3 2 С 1 1 А 1 3 a А А 2 4 С b В b b g С 2 5
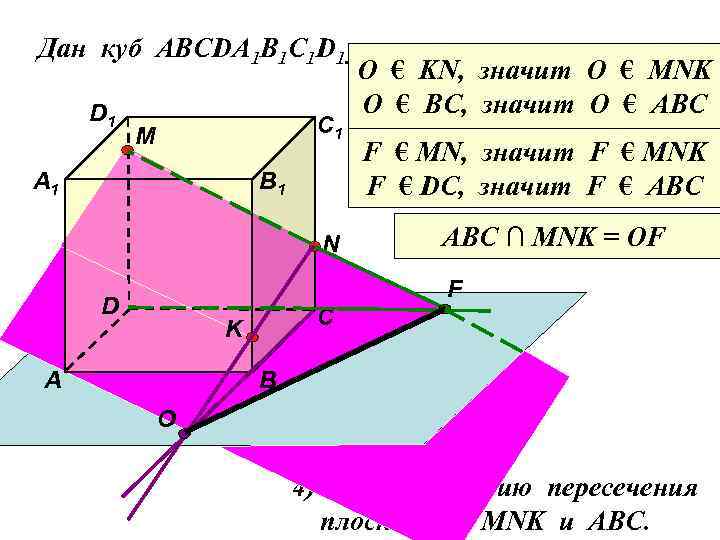 Дан куб АВСDA 1 B 1 C 1 D 1. D 1 M А 1 В 1 Точка М лежит на O € KN, значит О € МNK ребре DD 1 O € ВC, значит О € АВС С 1 Точка N лежит на F € MN, значит F € MNK ребре CC 1 F € DC, значит F € АВС Точка K лежит на ребре ∩ MNK = OF ABC BB 1 N F D С K А В O 4) Найдите линию пересечения плоскостей MNK и ABC.
Дан куб АВСDA 1 B 1 C 1 D 1. D 1 M А 1 В 1 Точка М лежит на O € KN, значит О € МNK ребре DD 1 O € ВC, значит О € АВС С 1 Точка N лежит на F € MN, значит F € MNK ребре CC 1 F € DC, значит F € АВС Точка K лежит на ребре ∩ MNK = OF ABC BB 1 N F D С K А В O 4) Найдите линию пересечения плоскостей MNK и ABC.
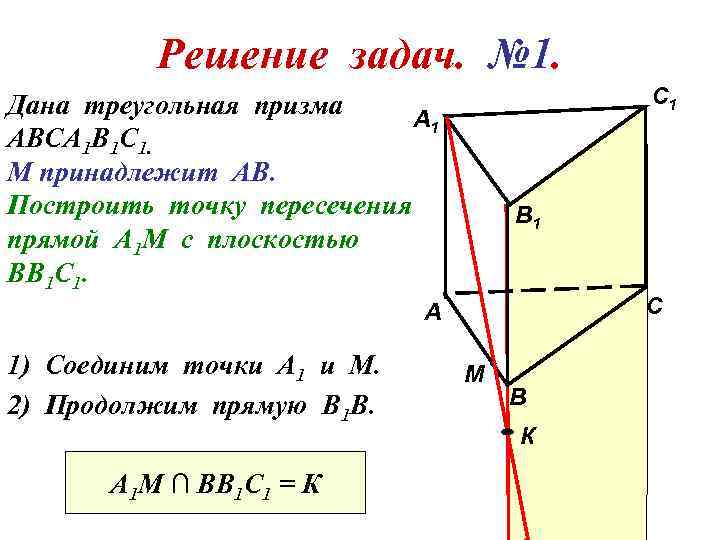 Решение задач. № 1. С 1 Дана треугольная призма А 1 АВСА 1 В 1 С 1. М принадлежит АВ. Построить точку пересечения прямой А 1 М с плоскостью ВВ 1 С 1. В 1 С А 1) Соединим точки А 1 и М. 2) Продолжим прямую В 1 В. А 1 М ∩ ВВ 1 С 1 = К М В К
Решение задач. № 1. С 1 Дана треугольная призма А 1 АВСА 1 В 1 С 1. М принадлежит АВ. Построить точку пересечения прямой А 1 М с плоскостью ВВ 1 С 1. В 1 С А 1) Соединим точки А 1 и М. 2) Продолжим прямую В 1 В. А 1 М ∩ ВВ 1 С 1 = К М В К
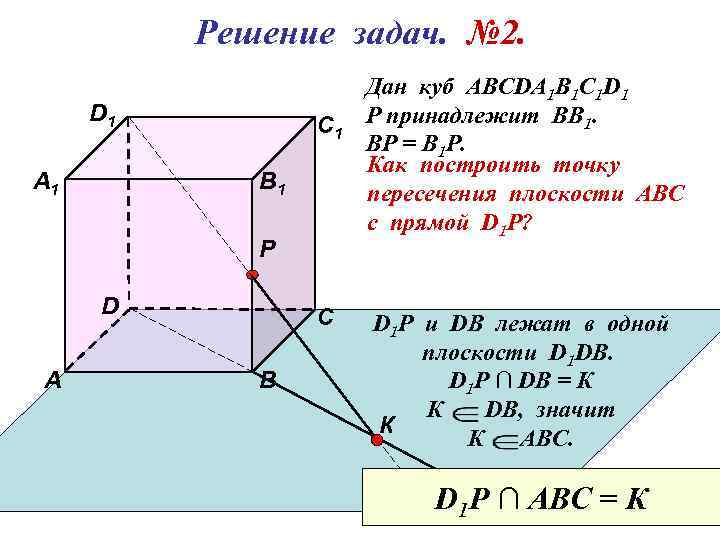 Решение задач. № 2. D 1 А 1 С 1 В 1 Р D А С В Дан куб АВСDА 1 В 1 С 1 D 1 Р принадлежит ВВ 1. ВР = В 1 Р. Как построить точку пересечения плоскости АВС с прямой D 1 P? D 1 Р u DB лежат в одной плоскости D 1 DB. D 1 P ∩ DB = К К DB, значит К К АВС. D 1 P ∩ АВС = К
Решение задач. № 2. D 1 А 1 С 1 В 1 Р D А С В Дан куб АВСDА 1 В 1 С 1 D 1 Р принадлежит ВВ 1. ВР = В 1 Р. Как построить точку пересечения плоскости АВС с прямой D 1 P? D 1 Р u DB лежат в одной плоскости D 1 DB. D 1 P ∩ DB = К К DB, значит К К АВС. D 1 P ∩ АВС = К
 Решение задач. № 3. D 1 А 1 С 1 В 1 Р D Дан куб АВСDА 1 В 1 С 1 D 1 Р принадлежит ВВ 1. ВР = В 1 Р Как построить линию пересечения плоскости АD 1 Р и АВВ 1? С Точка Р принадлежит ВВ 1, а А В значит и плоскости АВВ 1. Точка А принадлежит АВ, а значит плоскости АВВ 1 Следовательно, по аксиоме А 2, АР принадлежит АВВ 1. Аналогично АР принадлежит плоскости АD 1 P ∩ ABB 1 = AP
Решение задач. № 3. D 1 А 1 С 1 В 1 Р D Дан куб АВСDА 1 В 1 С 1 D 1 Р принадлежит ВВ 1. ВР = В 1 Р Как построить линию пересечения плоскости АD 1 Р и АВВ 1? С Точка Р принадлежит ВВ 1, а А В значит и плоскости АВВ 1. Точка А принадлежит АВ, а значит плоскости АВВ 1 Следовательно, по аксиоме А 2, АР принадлежит АВВ 1. Аналогично АР принадлежит плоскости АD 1 P ∩ ABB 1 = AP
 Диктант. № 1 Необходимо ответить на вопросы: 1 вариант. 2 вариант 1. Назовите основные фигуры на плоскости. 1. Назовите основные фигуры в пространстве. 2. Сформулируйте аксиому А 2 2. Сформулируйте аксиому А 1 3. Могут ли прямая и плоскость иметь две общие точки? 4. Сколько плоскостей можно провести через три точки? 3. Сколько плоскостей можно провести через прямую и не лежащую на ней точку? 4. Сформулируйте аксиому А 3 5. Сколько может быть общих точек у прямой и плоскости? 5. Могут ли прямая и плоскость иметь одну общую точку?
Диктант. № 1 Необходимо ответить на вопросы: 1 вариант. 2 вариант 1. Назовите основные фигуры на плоскости. 1. Назовите основные фигуры в пространстве. 2. Сформулируйте аксиому А 2 2. Сформулируйте аксиому А 1 3. Могут ли прямая и плоскость иметь две общие точки? 4. Сколько плоскостей можно провести через три точки? 3. Сколько плоскостей можно провести через прямую и не лежащую на ней точку? 4. Сформулируйте аксиому А 3 5. Сколько может быть общих точек у прямой и плоскости? 5. Могут ли прямая и плоскость иметь одну общую точку?
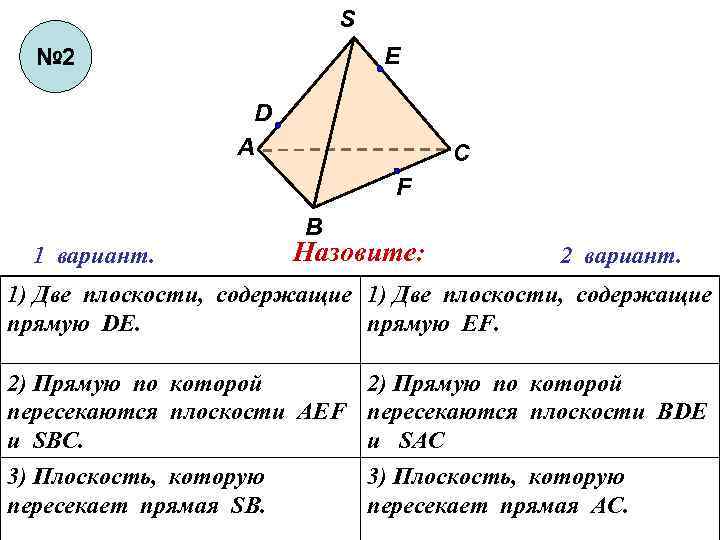 S E № 2 D А С F В 1 вариант. Назовите: 2 вариант. 1) Две плоскости, содержащие прямую DE. прямую EF. 2) Прямую по которой пересекаются плоскости АЕF пересекаются плоскости ВDE и SBC. и SAC 3) Плоскость, которую пересекает прямая SB. 3) Плоскость, которую пересекает прямая АС.
S E № 2 D А С F В 1 вариант. Назовите: 2 вариант. 1) Две плоскости, содержащие прямую DE. прямую EF. 2) Прямую по которой пересекаются плоскости АЕF пересекаются плоскости ВDE и SBC. и SAC 3) Плоскость, которую пересекает прямая SB. 3) Плоскость, которую пересекает прямая АС.