3- числовые ряды 2010.ppt
- Количество слайдов: 57
 § 3. Сходимость положительных рядов.
§ 3. Сходимость положительных рядов.
 Определение 3. 6. Числовой ряд называется знакоположительным, если все его элементы неотрицательны.
Определение 3. 6. Числовой ряд называется знакоположительным, если все его элементы неотрицательны.
 Определение 3. 6. Числовой ряд называется знакоположительным, если все его элементы неотрицательны. Следует заметить, что последовательность частичных сумм такого ряда является монотонной , точнее- неубывающей , т. е. S 1
Определение 3. 6. Числовой ряд называется знакоположительным, если все его элементы неотрицательны. Следует заметить, что последовательность частичных сумм такого ряда является монотонной , точнее- неубывающей , т. е. S 1
 Для сходимости числовой последовательности необходимо и достаточно , чтобы она была монотонной и ограниченной.
Для сходимости числовой последовательности необходимо и достаточно , чтобы она была монотонной и ограниченной.
 Теорема 3. 7 Знакоположительный ряд сходится тогда и только тогда , когда последовательность его частичных сумм ограничена.
Теорема 3. 7 Знакоположительный ряд сходится тогда и только тогда , когда последовательность его частичных сумм ограничена.
 Теорема 3. 8 : (признак сравнения) Пусть даны два положительных ряда и и для их элементов имеет место неравенство для любых , тогда :
Теорема 3. 8 : (признак сравнения) Пусть даны два положительных ряда и и для их элементов имеет место неравенство для любых , тогда :
 Теорема 3. 8 : (признак сравнения) Пусть даны два положительных ряда и и для их элементов имеет место неравенство для любых , тогда : 1) из сходимости ряда следует сходимость ряда ,
Теорема 3. 8 : (признак сравнения) Пусть даны два положительных ряда и и для их элементов имеет место неравенство для любых , тогда : 1) из сходимости ряда следует сходимость ряда ,
 Теорема 3. 8 : (признак сравнения) Пусть даны два положительных ряда и и для их элементов имеет место неравенство для любых , тогда : 1) из сходимости ряда , следует сходимость 2) из расходимости ряда следует расходимость
Теорема 3. 8 : (признак сравнения) Пусть даны два положительных ряда и и для их элементов имеет место неравенство для любых , тогда : 1) из сходимости ряда , следует сходимость 2) из расходимости ряда следует расходимость
 Доказательство 1) Пусть для любых , но так как отбрасывание конечного числа элементов ряда не влияет на сходимость , то не нарушая общности можно считать
Доказательство 1) Пусть для любых , но так как отбрасывание конечного числа элементов ряда не влияет на сходимость , то не нарушая общности можно считать
 Доказательство 1) Пусть для любых , но так как отбрасывание конечного числа элементов ряда не влияет на сходимость , то не нарушая общности можно считать 2) Если ряд сходится , то существует
Доказательство 1) Пусть для любых , но так как отбрасывание конечного числа элементов ряда не влияет на сходимость , то не нарушая общности можно считать 2) Если ряд сходится , то существует
 Доказательство 1) Пусть для любых , но так как отбрасывание конечного числа элементов ряда не влияет на сходимость , то не нарушая общности можно считать 2) Если ряд сходится , то существует 3) Тогда частичные суммы ряда значит ряд сходится. тем более ограничены и
Доказательство 1) Пусть для любых , но так как отбрасывание конечного числа элементов ряда не влияет на сходимость , то не нарушая общности можно считать 2) Если ряд сходится , то существует 3) Тогда частичные суммы ряда значит ряд сходится. тем более ограничены и
 Доказательство 1) Пусть для любых , но так как отбрасывание конечного числа элементов ряда не влияет на сходимость , то не нарушая общности можно считать 2) Если ряд сходится , то существует 3) Тогда частичные суммы ряда значит ряд сходится. тем более ограничены и 4) Если ряд расходится , то , а значит и
Доказательство 1) Пусть для любых , но так как отбрасывание конечного числа элементов ряда не влияет на сходимость , то не нарушая общности можно считать 2) Если ряд сходится , то существует 3) Тогда частичные суммы ряда значит ряд сходится. тем более ограничены и 4) Если ряд расходится , то , а значит и
 Пример 3. 7 : Исследовать на сходимость ряд
Пример 3. 7 : Исследовать на сходимость ряд
 Пример 3. 7 : Исследовать на сходимость ряд Решение: 1. Так как , а ряд пример 2. 3), то и ряд - сходится (см. - сходящийся. Примечание. Ряд в случае сходимости называют мажорантным.
Пример 3. 7 : Исследовать на сходимость ряд Решение: 1. Так как , а ряд пример 2. 3), то и ряд - сходится (см. - сходящийся. Примечание. Ряд в случае сходимости называют мажорантным.

 Доказательство 1) По определению предела следовательно
Доказательство 1) По определению предела следовательно
 Доказательство 1) По определению предела 2) следовательно
Доказательство 1) По определению предела 2) следовательно
 Доказательство 1) По определению предела 2) 3) и следовательно
Доказательство 1) По определению предела 2) 3) и следовательно
 Доказательство 1) По определению предела следовательно 2) 3) и 4) Из сходимости ряда теореме 3. 8. следует сходимость по
Доказательство 1) По определению предела следовательно 2) 3) и 4) Из сходимости ряда теореме 3. 8. следует сходимость по
 Доказательство 1) По определению предела следовательно 2) 3) и 4) Из сходимости ряда теореме 8 5) Если так как следует сходимость по – расходится , то расходится и ряд , .
Доказательство 1) По определению предела следовательно 2) 3) и 4) Из сходимости ряда теореме 8 5) Если так как следует сходимость по – расходится , то расходится и ряд , .
 Пример 3. 8. Исследовать на сходимость ряд
Пример 3. 8. Исследовать на сходимость ряд
 Пример 3. 8. Исследовать на сходимость ряд Решение: По теореме 3. 9 сходятся одновременно. , значит ряды и
Пример 3. 8. Исследовать на сходимость ряд Решение: По теореме 3. 9 сходятся одновременно. , значит ряды и
 Теорема 3. 10. (признак Д , Аламбера) Пусть для ряда существует предел Тогда если L < 1 - ряд сходится L > 1 - ряд расходится L = 1 - необходимы дополнительные исследования
Теорема 3. 10. (признак Д , Аламбера) Пусть для ряда существует предел Тогда если L < 1 - ряд сходится L > 1 - ряд расходится L = 1 - необходимы дополнительные исследования
 Доказательство: ) Пусть L <1 , тогда по определению предела при любых . 1
Доказательство: ) Пусть L <1 , тогда по определению предела при любых . 1
 Доказательство: 1) Пусть L <1 , тогда по определению предела при любых . 2) Это означает , верно неравенство
Доказательство: 1) Пусть L <1 , тогда по определению предела при любых . 2) Это означает , верно неравенство
 Доказательство: 1) Пусть L <1 , тогда по определению предела при любых 2) Это означает , верно неравенство .
Доказательство: 1) Пусть L <1 , тогда по определению предела при любых 2) Это означает , верно неравенство .
 Доказательство: 1) Пусть L <1 , тогда по определению предела при любых 2) Это означает , верно неравенство 4) следовательно .
Доказательство: 1) Пусть L <1 , тогда по определению предела при любых 2) Это означает , верно неравенство 4) следовательно .
 Доказательство: 1) Пусть L <1 , тогда по определению предела при любых 2) Это означает , верно неравенство 3) Тогда существует такое S, что L+S<1 и q=L+s. 4) следовательно 5) А также справедливы неравенства .
Доказательство: 1) Пусть L <1 , тогда по определению предела при любых 2) Это означает , верно неравенство 3) Тогда существует такое S, что L+S<1 и q=L+s. 4) следовательно 5) А также справедливы неравенства .
 Доказательство: 1) Пусть L <1 , тогда по определению предела при любых . 2) Это означает , верно неравенство 4) следовательно 5) А также справедливы неравенства 6) Просуммировав обе части данных неравенств получим . Так как ряд справа сходится как сумма бесконечно убывающей геометрической прогрессии , то и исходный ряд сходится.
Доказательство: 1) Пусть L <1 , тогда по определению предела при любых . 2) Это означает , верно неравенство 4) следовательно 5) А также справедливы неравенства 6) Просуммировав обе части данных неравенств получим . Так как ряд справа сходится как сумма бесконечно убывающей геометрической прогрессии , то и исходный ряд сходится.
 Доказательство: 7) Пусть теперь L>1, тогда И существует такое, что и
Доказательство: 7) Пусть теперь L>1, тогда И существует такое, что и
 Доказательство: 7) Пусть теперь L>1, тогда и 8)Тогда также верны неравенства и существует такое, что для , а
Доказательство: 7) Пусть теперь L>1, тогда и 8)Тогда также верны неравенства и существует такое, что для , а
 (но следовательно - расходящийся, следовательно расходится и ).
(но следовательно - расходящийся, следовательно расходится и ).
 Теорема 3. 11. (Признак Коши) Пусть для ряда верно соотношение Тогда: если L<1 - ряд сходится, если L>1 - ряд расходится, если L=1 -необходимы дополнительные исследования.
Теорема 3. 11. (Признак Коши) Пусть для ряда верно соотношение Тогда: если L<1 - ряд сходится, если L>1 - ряд расходится, если L=1 -необходимы дополнительные исследования.
 Доказательство 1)
Доказательство 1)
 Доказательство 1) 2) пусть L<1 и
Доказательство 1) 2) пусть L<1 и
 Доказательство 1) 2) пусть L<1 и 3) Просуммировав обе части неравенства получаем , так как слева – сумма бесконечно убывающей геометрической прогрессии, то она выражается конечным числом, то по признаку сравнения этот ряд сходится, следовательно исходный ряд тоже сходится.
Доказательство 1) 2) пусть L<1 и 3) Просуммировав обе части неравенства получаем , так как слева – сумма бесконечно убывающей геометрической прогрессии, то она выражается конечным числом, то по признаку сравнения этот ряд сходится, следовательно исходный ряд тоже сходится.
 Доказательство 1) 2) пусть L<1 и 3) Просуммировав обе части неравенства получаем , так как слева – сумма бесконечно убывающей геометрической прогрессии, то она выражается конечным числом, то по признаку сравнения этот ряд сходится, следовательно исходный ряд тоже сходится. 4)Пусть L>1 и ряд тоже расходится. , расходящийся следовательно исходный
Доказательство 1) 2) пусть L<1 и 3) Просуммировав обе части неравенства получаем , так как слева – сумма бесконечно убывающей геометрической прогрессии, то она выражается конечным числом, то по признаку сравнения этот ряд сходится, следовательно исходный ряд тоже сходится. 4)Пусть L>1 и ряд тоже расходится. , расходящийся следовательно исходный
 Признак Коши более сильный, чем признак Д , Аламбера, но он менее удобен.
Признак Коши более сильный, чем признак Д , Аламбера, но он менее удобен.
 Полезные формулы:
Полезные формулы:
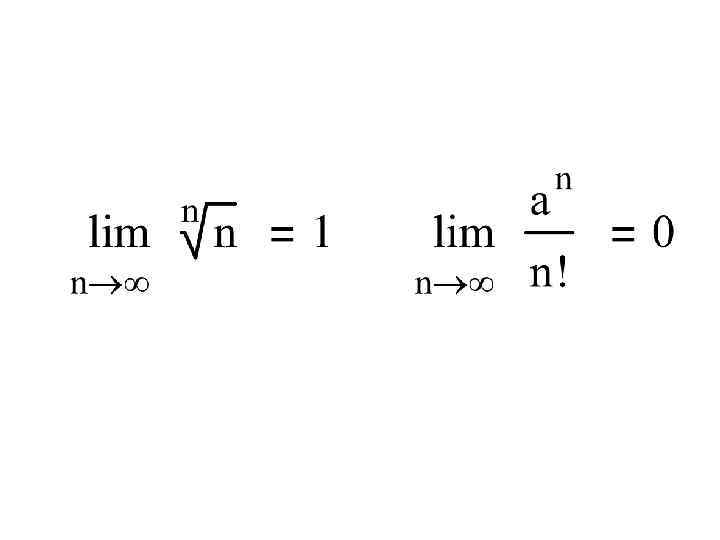
 формула Л. Стирлинга (1692 -1770 шотландский математик)
формула Л. Стирлинга (1692 -1770 шотландский математик)
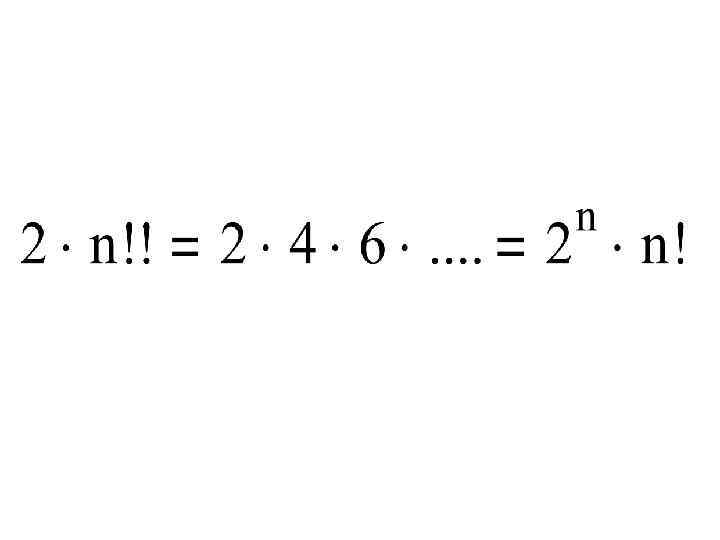
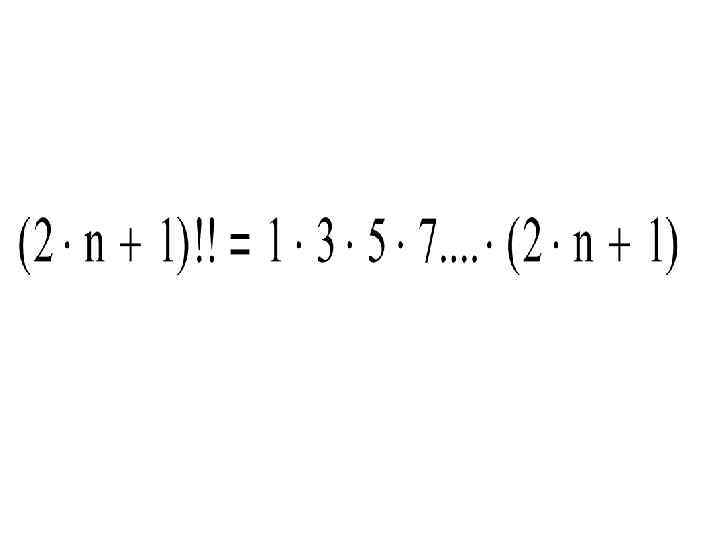
 Пример 3. 9. Исследовать на сходимость ряд .
Пример 3. 9. Исследовать на сходимость ряд .
 Теорема 3. 12. (Интегральный признак Коши) Если неотрицательная интегрируемая функция f(х) на промежутке [1, +∞] монотонно убывает и элементы ряда имеют вид: , то ряд и несобственный интеграл сходятся или расходятся одновременно Причём в случае сходимости
Теорема 3. 12. (Интегральный признак Коши) Если неотрицательная интегрируемая функция f(х) на промежутке [1, +∞] монотонно убывает и элементы ряда имеют вид: , то ряд и несобственный интеграл сходятся или расходятся одновременно Причём в случае сходимости
 Доказательство
Доказательство
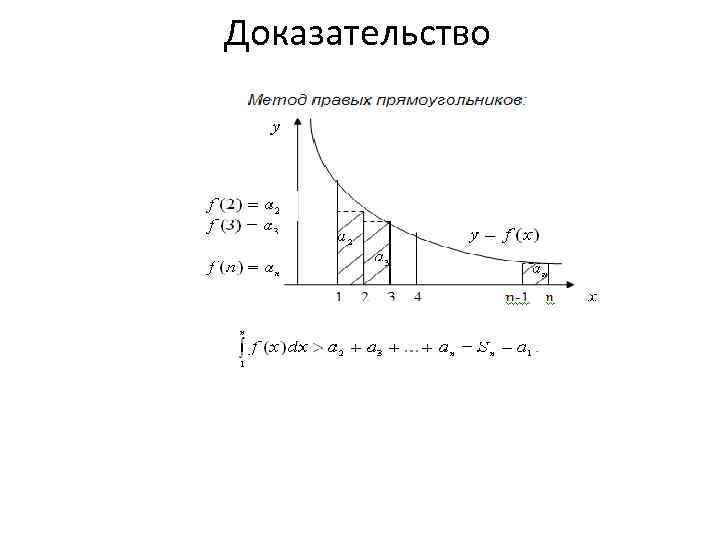 Доказательство
Доказательство
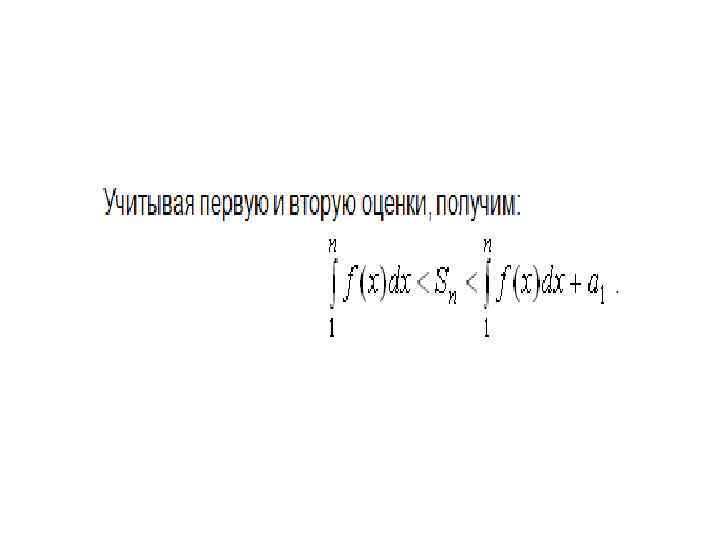
 Пример3. 10 : Исследовать на сходимость
Пример3. 10 : Исследовать на сходимость
 Пример3. 10 : Исследовать на сходимость Применим интегральный признак и рассмотрим интеграл =
Пример3. 10 : Исследовать на сходимость Применим интегральный признак и рассмотрим интеграл =
 Пример 3. 11. Исследовать на сходимость
Пример 3. 11. Исследовать на сходимость
 Пример 3. 11. Исследовать на сходимость расходится.
Пример 3. 11. Исследовать на сходимость расходится.
 Следствие (оценка остатка сходящегося ряда) 1)Из теоремы следует, что
Следствие (оценка остатка сходящегося ряда) 1)Из теоремы следует, что
 Следствие (оценка остатка сходящегося ряда) 1)Из теоремы 3. 12 следует, что 2) Заменим в нижнем пределе интегралов 1 на n+1, а т. к. S=Sn+rn, то
Следствие (оценка остатка сходящегося ряда) 1)Из теоремы 3. 12 следует, что 2) Заменим в нижнем пределе интегралов 1 на n+1, а т. к. S=Sn+rn, то
 Пример 3. 12. Найти сумму ряда с точностью до ε=0, 01. Решение Это означает, что
Пример 3. 12. Найти сумму ряда с точностью до ε=0, 01. Решение Это означает, что
 Пример 3. 12. Найти сумму ряда с …. до ε=0, 01. Решение Это означает, что Приведем к общему знаменателю
Пример 3. 12. Найти сумму ряда с …. до ε=0, 01. Решение Это означает, что Приведем к общему знаменателю
 Пример 3. 13. Найти сумму ряда с …. до ε=0, 01. Решение Это означает, что Приведем к общему знаменателю Обозначим m=n+1, тогда можно увидеть что при m≥ 8 неравенство верно, а значит n≥ 7 =>
Пример 3. 13. Найти сумму ряда с …. до ε=0, 01. Решение Это означает, что Приведем к общему знаменателю Обозначим m=n+1, тогда можно увидеть что при m≥ 8 неравенство верно, а значит n≥ 7 =>


