3 Свойства веществ в нанокристаллическом состоянии 3 1

3. Свойства веществ в нанокристаллическом состоянии. 3. 1. Оптические и электронные свойства наносистем. Оптические свойства наноцастиц металлов. Оптические свойства полупроводниковых наночастиц. Зонная структура. Зависимость зонной структуры от размера наночастиц. Дефекты на поверхности нанокристаллов. 3. 2. Фотонные кристаллы. Фотонные запрещенные зоны. Методы формирования фотонных кристаллов. Опалы как шаблон для создания трехмерных фотонных кристаллов. Материалы на основе фотонных кристаллов. Области применения. 3. 3. Магнитные свойства наносистем. Доменная структура. Суперпарамагнетизм. Энергия магнитной анизотропии. Анизотропия формы. Анизотропия механического напряжения. Обменная анизотропия. Процессы перемагничивания, вихривые поля. Магнитостатическое взаимодействие нанонитей. 3. 4. Механические свойства наносистем. Закон Холла-Петча. Структура межфазных границ. Дефекты. Влияние границ раздела. Упругие свойства. Нанокомпозиты.

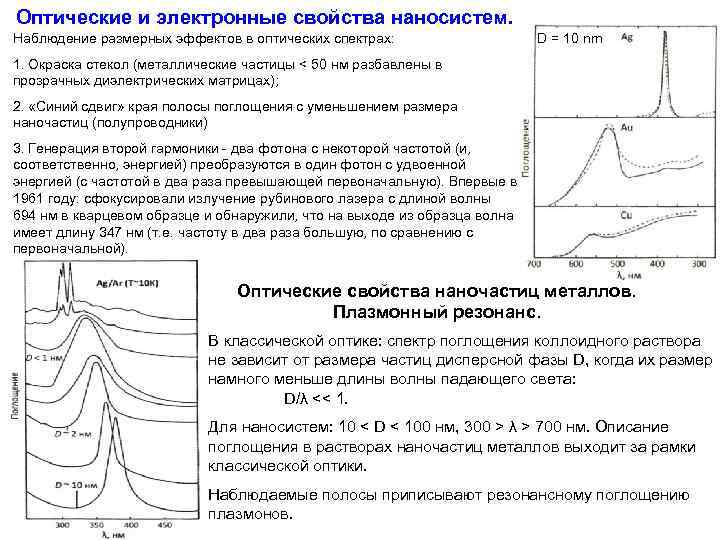Оптические и электронные свойства наносистем. Наблюдение размерных эффектов в оптических спектрах: D = 10 nm 1. Окраска стекол (металлические частицы < 50 нм разбавлены в прозрачных диэлектрических матрицах); 2. «Синий сдвиг» края полосы поглощения с уменьшением размера наночастиц (полупроводники) 3. Генерация второй гармоники - два фотона с некоторой частотой (и, соответственно, энергией) преобразуются в один фотон с удвоенной энергией (с частотой в два раза превышающей первоначальную). Впервые в 1961 году: сфокусировали излучение рубинового лазера с длиной волны 694 нм в кварцевом образце и обнаружили, что на выходе из образца волна имеет длину 347 нм (т. е. частоту в два раза большую, по сравнению с первоначальной). Оптические свойства наночастиц металлов. Плазмонный резонанс. В классической оптике: спектр поглощения коллоидного раствора не зависит от размера частиц дисперсной фазы D, когда их размер намного меньше длины волны падающего света: D/λ << 1. Для наносистем: 10 < D < 100 нм, 300 > λ > 700 нм. Описание поглощения в растворах наночастиц металлов выходит за рамки классической оптики. Наблюдаемые полосы приписывают резонансному поглощению плазмонов.

Плазмоны Плазмон – квазичастица, отвечающая коллективным колебаниям свободных электронов в металле. Плазмонный резонанс – коллективные колебания свободных электронов проводимости, которые могут сильно взаимодействовать со светом на определенных частотах. То есть совпадение частоты падающего излучения с собственной частотой плазмонов приводит к резонансному поглощению. Подвижность поверхностного плазмона определяется диэлектрическими проницаемостями металла и окружающей среды. Собственная частота колебаний электронной плотности определяет размер частиц. В приближении сплошной среды (нет электромагнитного взаимодействия между дипольными моментами кластеров) (f = Vm/Vh 10 -2 – фактор заполнения D << d Edd отсутствует) дипольный момент отдельной сферической частицы: и h диэлектрические проницаемости частицы и матрицы, Eloc – локальное поле, действующее на частицу. Соотношение Лоренца для системы со случайно распределенными диполями E 0 – внешнее поле, P – поляризация среды ~ сумме дипольных моментов частиц

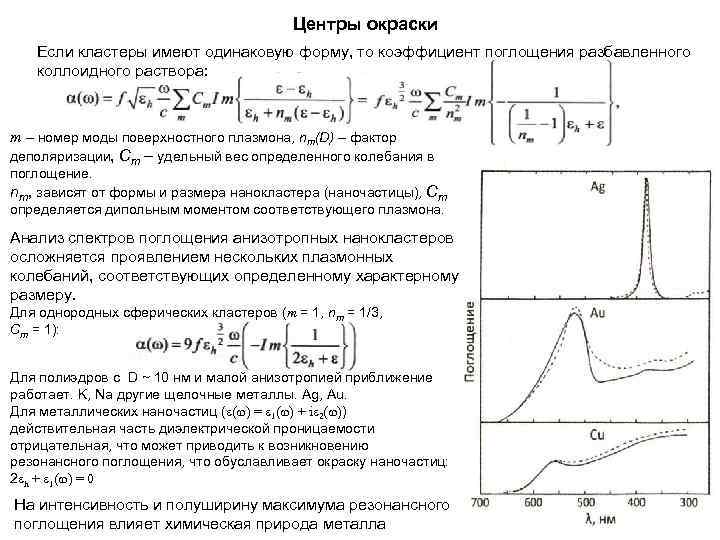Центры окраски Если кластеры имеют одинаковую форму, то коэффициент поглощения разбавленного коллоидного раствора: m – номер моды поверхностного плазмона, nm(D) – фактор деполяризации, Cm – удельный вес определенного колебания в поглощение. nm, зависят от формы и размера нанокластера (наночастицы), Cm определяется дипольным моментом соответствующего плазмона. Анализ спектров поглощения анизотропных нанокластеров осложняется проявлением нескольких плазмонных колебаний, соответствующих определенному характерному размеру. Для однородных сферических кластеров (m = 1, nm = 1/3, Cm = 1): Для полиэдров с D ~ 10 нм и малой анизотропией приближение работает. K, Na другие щелочные металлы. Ag, Au. Для металлических наночастиц (ε(ω) = ε 1(ω) + iε 2(ω)) действительная часть диэлектрической проницаемости отрицательная, что может приводить к возникновению резонансного поглощения, что обуславливает окраску наночастиц: 2εh + ε 1(ω) = 0 На интенсивность и полуширину максимума резонансного поглощения влияет химическая природа металла

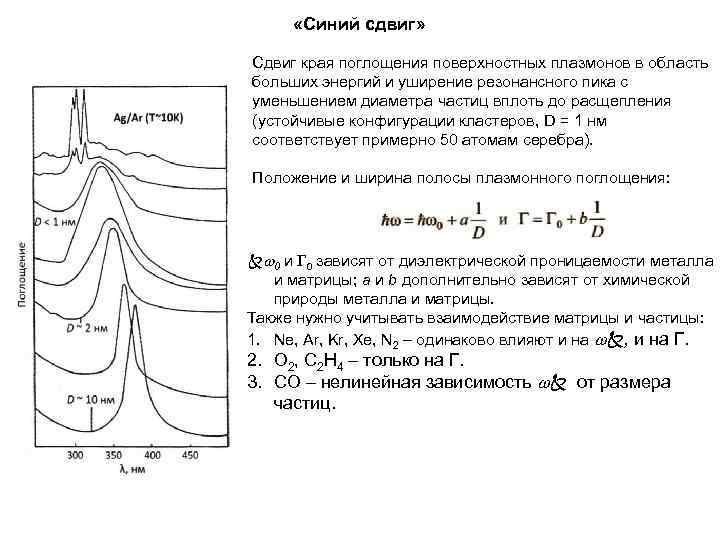«Синий сдвиг» Сдвиг края поглощения поверхностных плазмонов в область больших энергий и уширение резонансного пика с уменьшением диаметра частиц вплоть до расщепления (устойчивые конфигурации кластеров, D = 1 нм соответствует примерно 50 атомам серебра). Положение и ширина полосы плазмонного поглощения: 0 и Г 0 зависят от диэлектрической проницаемости металла и матрицы; a и b дополнительно зависят от химической природы металла и матрицы. Также нужно учитывать взаимодействие матрицы и частицы: 1. Ne, Ar, Kr, Xe, N 2 – одинаково влияют и на , и на Г. 2. O 2, C 2 H 4 – только на Г. 3. CO – нелинейная зависимость от размера частиц.

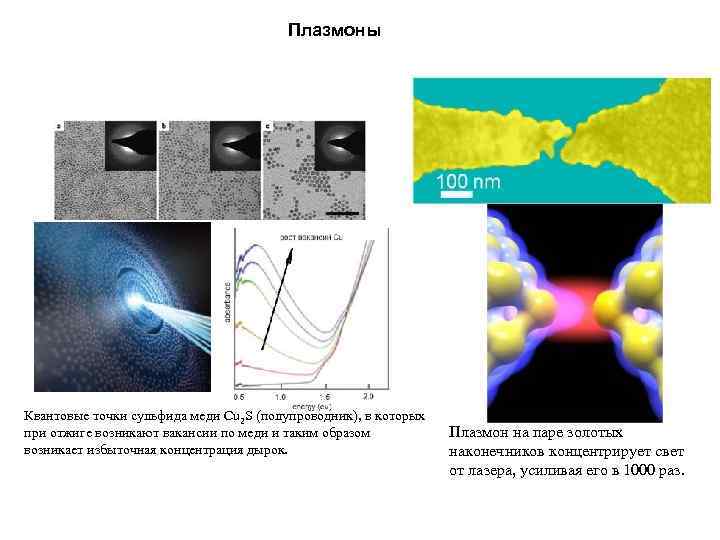Плазмоны Квантовые точки сульфида меди Cu 2 S (полупроводник), в которых при отжиге возникают вакансии по меди и таким образом возникает избыточная концентрация дырок. Плазмон на паре золотых наконечников концентрирует свет от лазера, усиливая его в 1000 раз.

Оптические свойства полупроводниковых наночастиц. Квантоворазмерный эффект. Наблюдаемые эффекты зависимости электронных свойств полупроводников от размера наночастиц: 1. Увеличение ширины запрещенной зоны с уменьшением размера частиц ( «синий сдвиг» в поглощении и фотолюминисценции полупроводников); 2. Сдвиг энергии глубинных уровней с уменьшением размера частиц; 3. Уменьшение комплексной части диэлектрической проницаемости наночастиц из-за уширения запрещенной зоны (в металлах) 4. Уменьшение комплексной ε наноразмерных полупроводников, из-за уширения запрещенной зоны (уменьшение ε может приводить к увеличению электростатических взаимодействий между электронами и дырками увеличение энергии связи экситонов. У полупроводников квантоворазмерный эффект более выражен, чем у металлов или диэлектриков. Эффект размерного квантования состоит в уменьшении одной или нескольких размерностей до величины длины волны де Бройля носителей заряда (λ = h/mv 1 нм - 100 нм) полупроводниковая частица становится резонатором спектр носителей заряда оказывается дискретным. Кроме этого для полупроводников большое значение имеет форма наночастиц.

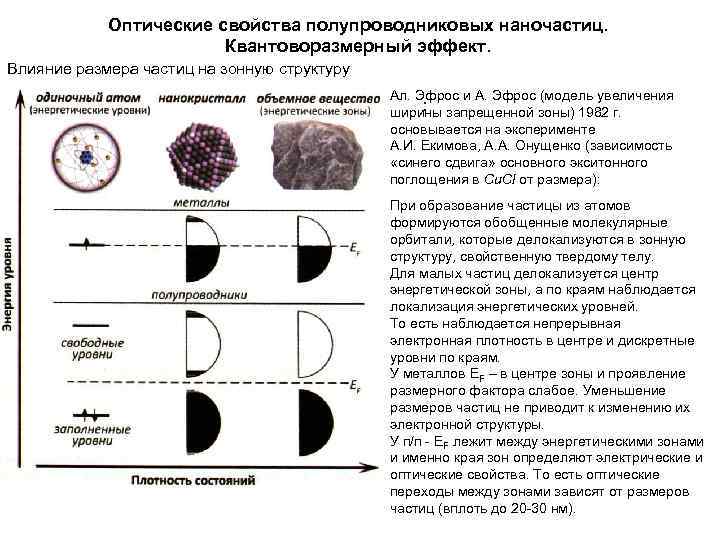Оптические свойства полупроводниковых наночастиц. Квантоворазмерный эффект. Влияние размера частиц на зонную структуру Ал. Эфрос и А. Эфрос (модель увеличения : ширины запрещенной зоны) 1982 г. основывается на эксперименте А. И. Екимова, А. А. Онущенко (зависимость «синего сдвига» основного экситонного поглощения в Cu. Cl от размера): При образование частицы из атомов формируются обобщенные молекулярные орбитали, которые делокализуются в зонную структуру, свойственную твердому телу. Для малых частиц делокализуется центр энергетической зоны, а по краям наблюдается локализация энергетических уровней. То есть наблюдается непрерывная электронная плотность в центре и дискретные уровни по краям. У металлов EF – в центре зоны и проявление размерного фактора слабое. Уменьшение размеров частиц не приводит к изменению их электронной структуры. У п/п - EF лежит между энергетическими зонами и именно края зон определяют электрические и оптические свойства. То есть оптические переходы между зонами зависят от размеров частиц (вплоть до 20 -30 нм).

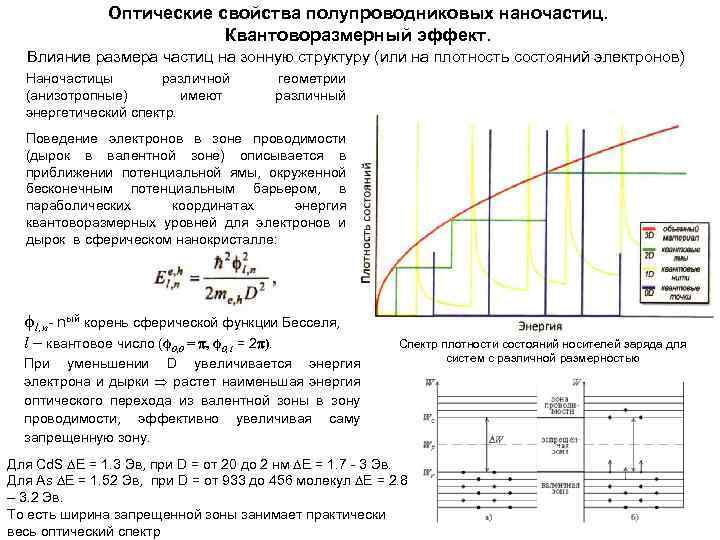Оптические свойства полупроводниковых наночастиц. Квантоворазмерный эффект. Влияние размера частиц на зонную структуру (или на плотность состояний электронов) Наночастицы различной (анизотропные) имеют энергетический спектр. геометрии различный Поведение электронов в зоне проводимости (дырок в валентной зоне) описывается в приближении потенциальной ямы, окруженной бесконечным потенциальным барьером, в параболических координатах энергия квантоворазмерных уровней для электронов и дырок в сферическом нанокристалле: ϕl, n- nый корень сферической функции Бесселя, l – квантовое число (ϕ 0, 0 = , ϕ 0, 1 = 2 ). При уменьшении D увеличивается энергия электрона и дырки растет наименьшая энергия оптического перехода из валентной зоны в зону проводимости, эффективно увеличивая саму запрещенную зону. Спектр плотности состояний носителей заряда для систем с различной размерностью Для Cd. S E = 1. 3 Эв, при D = от 20 до 2 нм E = 1. 7 - 3 Эв. Для As E = 1. 52 Эв, при D = от 933 до 456 молекул E = 2. 8 – 3. 2 Эв. То есть ширина запрещенной зоны занимает практически весь оптический спектр

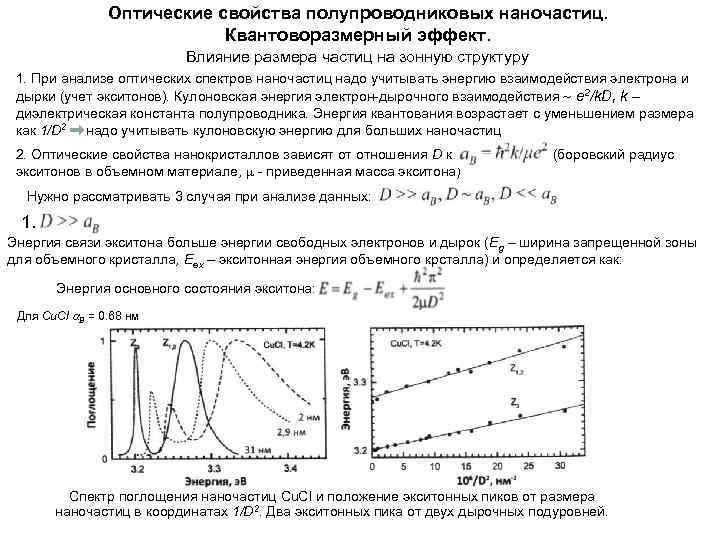Оптические свойства полупроводниковых наночастиц. Квантоворазмерный эффект. Влияние размера частиц на зонную структуру 1. При анализе оптических спектров наночастиц надо учитывать энергию взаимодействия электрона и дырки (учет экситонов). Кулоновская энергия электрон-дырочного взаимодействия e 2/k. D, k – диэлектрическая константа полупроводника. Энергия квантования возрастает с уменьшением размера как 1/D 2 надо учитывать кулоновскую энергию для больших наночастиц 2. Оптические свойства нанокристаллов зависят от отношения D к (боровский радиус экситонов в объемном материале, - приведенная масса экситона) Нужно рассматривать 3 случая при анализе данных: 1. Энергия связи экситона больше энергии свободных электронов и дырок (Eg – ширина запрещенной зоны для объемного кристалла, Eex – экситонная энергия объемного крсталла) и определяется как: Энергия основного состояния экситона: Для Cu. Cl В = 0. 68 нм Спектр поглощения наночастиц Cu. Cl и положение экситонных пиков от размера наночастиц в координатах 1/D 2. Два экситонных пика от двух дырочных подуровней.

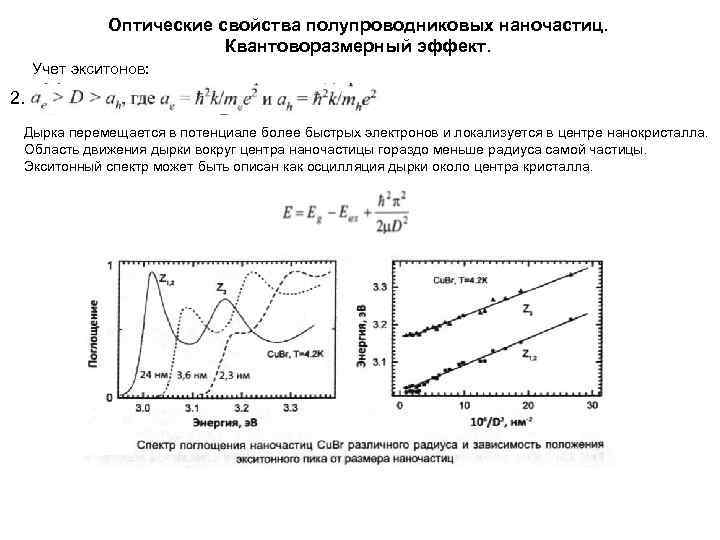Оптические свойства полупроводниковых наночастиц. Квантоворазмерный эффект. Учет экситонов: 2. Дырка перемещается в потенциале более быстрых электронов и локализуется в центре нанокристалла. Область движения дырки вокруг центра наночастицы гораздо меньше радиуса самой частицы. Экситонный спектр может быть описан как осцилляция дырки около центра кристалла.

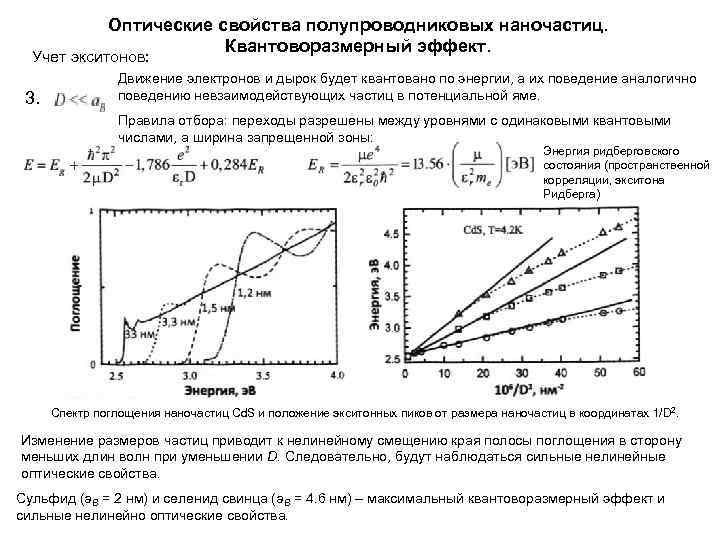Оптические свойства полупроводниковых наночастиц. Квантоворазмерный эффект. Учет экситонов: 3. Движение электронов и дырок будет квантовано по энергии, а их поведение аналогично поведению невзаимодействующих частиц в потенциальной яме. Правила отбора: переходы разрешены между уровнями с одинаковыми квантовыми числами, а ширина запрещенной зоны: Энергия ридберговского состояния (пространственной корреляции, экситона Ридберга) Спектр поглощения наночастиц Cd. S и положение экситонных пиков от размера наночастиц в координатах 1/D 2. Изменение размеров частиц приводит к нелинейному смещению края полосы поглощения в сторону меньших длин волн при уменьшении D. Следовательно, будут наблюдаться сильные нелинейные оптические свойства. Сульфид (a. B = 2 нм) и селенид свинца (a. B = 4. 6 нм) – максимальный квантоворазмерный эффект и сильные нелинейно оптические свойства.

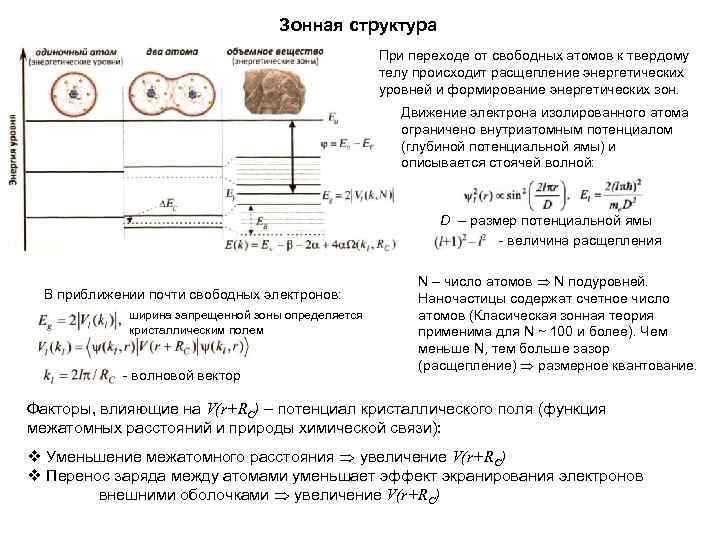Зонная структура При переходе от свободных атомов к твердому телу происходит расщепление энергетических уровней и формирование энергетических зон. Движение электрона изолированного атома ограничено внутриатомным потенциалом (глубиной потенциальной ямы) и описывается стоячей волной: D – размер потенциальной ямы - величина расщепления В приближении почти свободных электронов: ширина запрещенной зоны определяется кристаллическим полем - волновой вектор N – число атомов N подуровней. Наночастицы содержат счетное число атомов (Класическая зонная теория применима для N ~ 100 и более). Чем меньше N, тем больше зазор (расщепление) размерное квантование. Факторы, влияющие на V(r+RC) – потенциал кристаллического поля (функция межатомных расстояний и природы химической связи): v Уменьшение межатомного расстояния увеличение V(r+RC) v Перенос заряда между атомами уменьшает эффект экранирования электронов внешними оболочками увеличение V(r+RC)

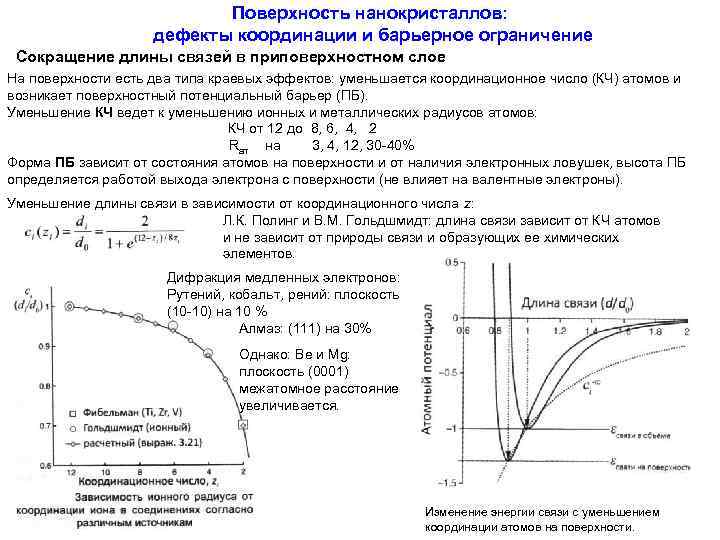Поверхность нанокристаллов: дефекты координации и барьерное ограничение Сокращение длины связей в приповерхностном слое На поверхности есть два типа краевых эффектов: уменьшается координационное число (КЧ) атомов и возникает поверхностный потенциальный барьер (ПБ). Уменьшение КЧ ведет к уменьшению ионных и металлических радиусов атомов: КЧ от 12 до 8, 6, 4, 2 Rат на 3, 4, 12, 30 -40% Форма ПБ зависит от состояния атомов на поверхности и от наличия электронных ловушек, высота ПБ определяется работой выхода электрона с поверхности (не влияет на валентные электроны). Уменьшение длины связи в зависимости от координационного числа z: Л. К. Полинг и В. М. Гольдшмидт: длина связи зависит от КЧ атомов и не зависит от природы связи и образующих ее химических элементов. Дифракция медленных электронов: Рутений, кобальт, рений: плоскость (10 -10) на 10 % Алмаз: (111) на 30% Однако: Be и Mg: плоскость (0001) межатомное расстояние увеличивается. Изменение энергии связи с уменьшением координации атомов на поверхности.

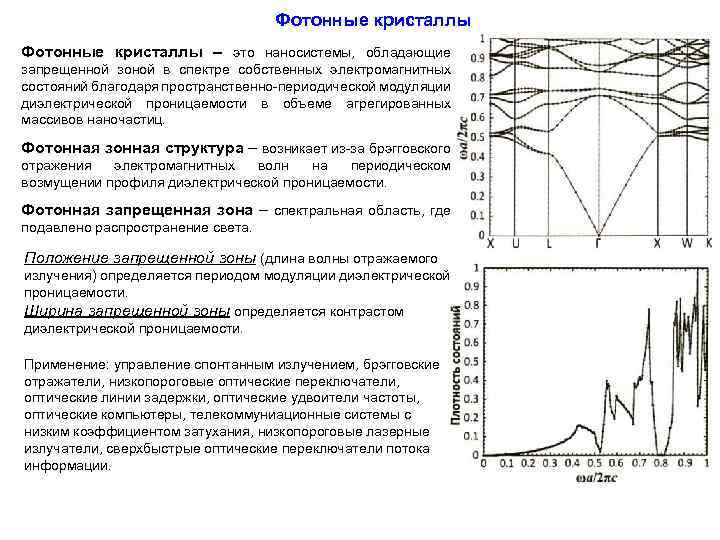Фотонные кристаллы – это наносистемы, обладающие запрещенной зоной в спектре собственных электромагнитных состояний благодаря пространственно-периодической модуляции диэлектрической проницаемости в объеме агрегированных массивов наночастиц. Фотонная зонная структура – возникает из-за брэгговского отражения электромагнитных волн на периодическом возмущении профиля диэлектрической проницаемости. Фотонная запрещенная зона – спектральная область, где подавлено распространение света. Положение запрещенной зоны (длина волны отражаемого излучения) определяется периодом модуляции диэлектрической проницаемости. Ширина запрещенной зоны определяется контрастом диэлектрической проницаемости. Применение: управление спонтанным излучением, брэгговские отражатели, низкопороговые оптические переключатели, оптические линии задержки, оптические удвоители частоты, оптические компьютеры, телекоммуниационные системы с низким коэффициентом затухания, низкопороговые лазерные излучатели, сверхбыстрые оптические переключатели потока информации.

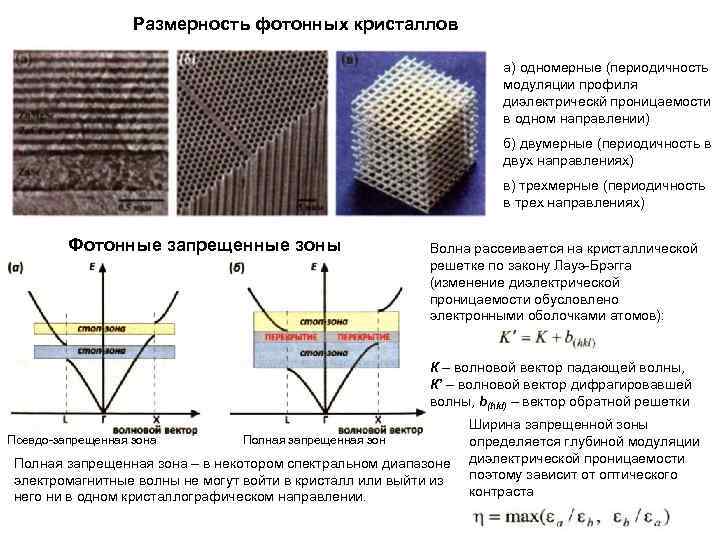Размерность фотонных кристаллов а) одномерные (периодичность модуляции профиля диэлектрическй проницаемости в одном направлении) б) двумерные (периодичность в двух направлениях) в) трехмерные (периодичность в трех направлениях) Фотонные запрещенные зоны Волна рассеивается на кристаллической решетке по закону Лауэ-Брэгга (изменение диэлектрической проницаемости обусловлено электронными оболочками атомов): К – волновой вектор падающей волны, К’ – волновой вектор дифрагировавшей волны, b(hkl) – вектор обратной решетки Псевдо-запрещенная зона Полная запрещенная зона – в некотором спектральном диапазоне электромагнитные волны не могут войти в кристалл или выйти из него ни в одном кристаллографическом направлении. Ширина запрещенной зоны определяется глубиной модуляции диэлектрической проницаемости поэтому зависит от оптического контраста

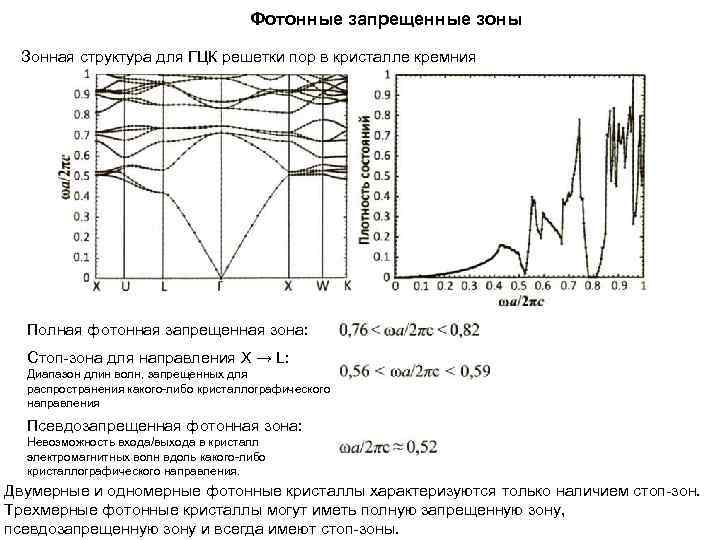Фотонные запрещенные зоны Зонная структура для ГЦК решетки пор в кристалле кремния Полная фотонная запрещенная зона: Стоп-зона для направления X → L: Диапазон длин волн, запрещенных для распространения какого-либо кристаллографического направления Псевдозапрещенная фотонная зона: Невозможность входа/выхода в кристалл электромагнитных волн вдоль какого-либо кристаллографического направления. Двумерные и одномерные фотонные кристаллы характеризуются только наличием стоп-зон. Трехмерные фотонные кристаллы могут иметь полную запрещенную зону, псевдозапрещенную зону и всегда имеют стоп-зоны.

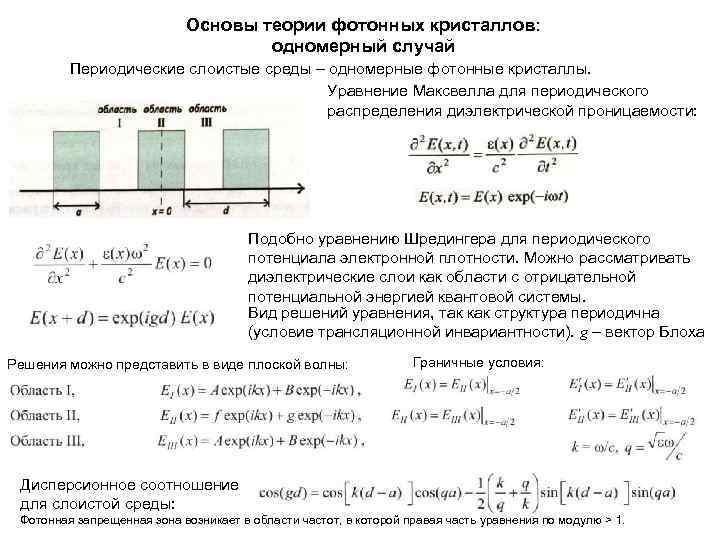Основы теории фотонных кристаллов: одномерный случай Периодические слоистые среды – одномерные фотонные кристаллы. Уравнение Максвелла для периодического распределения диэлектрической проницаемости: Подобно уравнению Шредингера для периодического потенциала электронной плотности. Можно рассматривать диэлектрические слои как области с отрицательной потенциальной энергией квантовой системы. Вид решений уравнения, так как структура периодична (условие трансляционной инвариантности). g – вектор Блоха Решения можно представить в виде плоской волны: Граничные условия: Дисперсионное соотношение для слоистой среды: Фотонная запрещенная зона возникает в области частот, в которой правая часть уравнения по модулю > 1.

Методы формирования фотонных кристаллов 1. Структура Е. Яблоновича. Период модуляции диэлектрической проницаемости 1 см. При условии совпадения масштабов модуляции диэлектрической проницаемости и длины волны зондирующего излучения спектры пропускания содержат полосы, соответствующие брэгговским отражением электромагнитных волн. 2. Самоорганизующиеся структуры (коллоидные кристаллы и опалы). 3. Создание периодической решетки в фоточувствительных материалах за счет изменения показателя преломления вещества под действием света. Дифракционная решетка, записанная в объеме халькогенидного стекла с помощью лазера. Размер 1. 5 мм x 4 мм

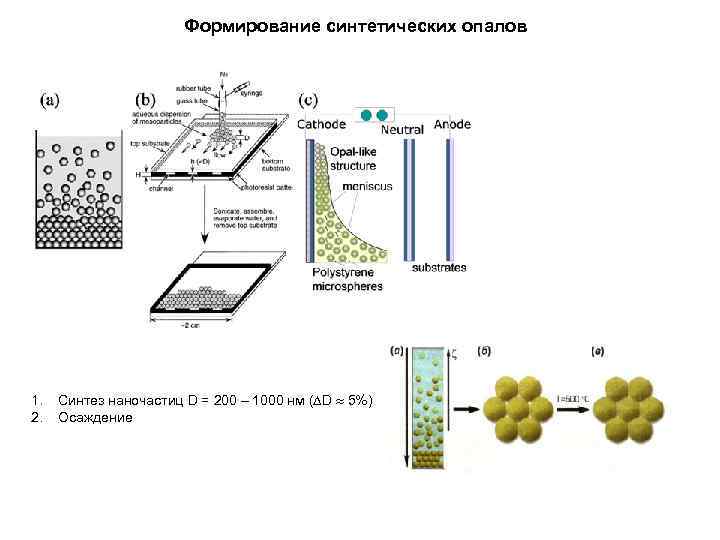Формирование синтетических опалов 1. 2. Синтез наночастиц D = 200 – 1000 нм ( D 5%) Осаждение

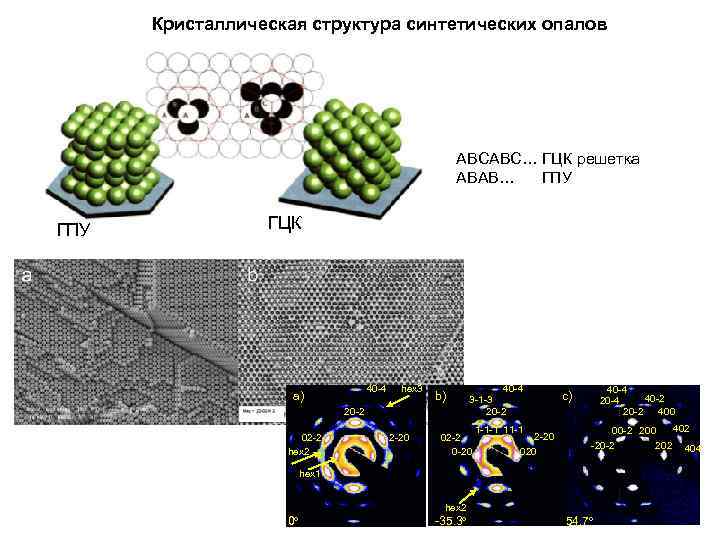Кристаллическая структура синтетических опалов АВСАВС… ГЦК решетка АВАВ… ГПУ ГЦК 40 -4 a) hex 3 b) 20 -2 02 -2 hex 2 2 -20 40 -4 3 -1 -3 20 -2 02 -2 0 -20 1 -1 -1 11 -1 2 -20 020 40 -4 40 -2 20 -4 20 -2 400 c) 402 00 -2 200 -20 -2 202 404 hex 1 hex 2 0 o -35. 3 o 54. 7 o

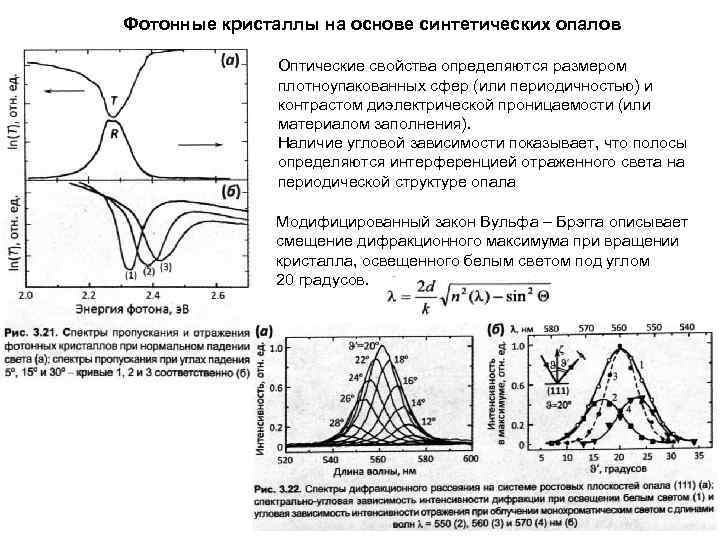Фотонные кристаллы на основе синтетических опалов Оптические свойства определяются размером плотноупакованных сфер (или периодичностью) и контрастом диэлектрической проницаемости (или материалом заполнения). Наличие угловой зависимости показывает, что полосы определяются интерференцией отраженного света на периодической структуре опала Модифицированный закон Вульфа – Брэгга описывает смещение дифракционного максимума при вращении кристалла, освещенного белым светом под углом 20 градусов.

Фотонные кристаллы на основе синтетических опалов Инвертирование позволяет «перестраивать» положение фотонной запрещенной зоны Si, Ge, Ga. P, Ga. N, Zn. O, Zr. O 2, WO 3 – высокий показатель преломления Si. O 2 WO 3 Полная запрещенная фотонная зона при nмат. /nвозд. > 2. 8 Применение: покрытия и краски на основе коллоидных микросфер, элементы светодиодов и лазеров с низкопороговой накачкой, изменение фотонных свойств под действием внешних воздействий, квантовые компьютеры и нейронные сети.

Магнитные свойства наносистем Классификация магнетиков Магнитные свойства наносистем определяются не только размерами и морфологией наночастиц, но и типом их взаимодействия между собой и с матрицей. Зависят от размерного эффекта: очень слабо зависят от размерного эффекта: Ферромагнетики, диамагнетики, Ферримагнетики, парамагнетики. Антиферромагнетики. Каждый атом – это динамическая система, состоящая из ядра и электронного облака. Магнитные свойства атома в основном определяются электронами. Электрон обладает Mсп – спиновый магнитный момент (спин) и Морб – орбитальный магнитный момент. Макроскопические характеристики твердых тел, связанные с характером взаимодействия магнитных моментов M с внешним магнитным полем Hext определяют тип магнетиков. Любое вещество во внешнем магнитном поле Hext характеризуется суммарным магнитным моментом М. [В*с*м] или [Вб*м] Намагниченность: æ для различных веществ может − магнитная постоянная, − относительная магнитная проницаемость (во сколько принимать значения как больше, так и меньше нуля: пара-, диа- и раз магнитная индукция поля в данной среде отличается от магнитной индукции в вакууме). ферромагнетики æ − магнитная восприимчивость вещества (характеризует способность вещества намагничиваться в поле напряженностью Н)

Классификация магнетиков Зависимость намагниченности от напряженности магнитного поля: 1 диамагнетик; 2 парамагнетик; Слабые поля, высокие температуры (для парамагнетиков) Сильные поля, низкие температуры (для парамагнетиков) 2 æ > 0 - парамагнетик æ < 0 - диамагнетик 3 - ферромагнетик. - Ферромагнетик (обладает спонтанной намагниченностью) 3 Магнитно-изотропные: - простое число, направление B и H совпадают. Магнитно-анизотропные: - тензорная величина, направление B и H не совпадают. Связь между магнитной проницаемостью и восприимчивостью вещества: Магнетон Бора – элементарный магнитный момент атома с одним электроном:

Классификация магнетиков Влияние магнитного поля на орбитальное движение электрона. Диамагнетизм – это способность вещества намагничиваться во внешнем магнитном поле Hext в направлении, противоположном направлению этого поля. æ < 0 Правило Ленца – всякое изменение магнитного потока, пронизывающего электрический контур, индуцирует в контуре ток такого направления, что его магнитный поток будет противодействовать указанному изменению. Магнитный момент, связанный с индуцированным током, и есть диамагнитный момент. − частота вращения электрона, T − период обращения, S - площадь круга, скорость движения электрона по орбите , круговой ток . Изменение приведет к изменению угловой скорости: При Hext= 0 на электрон действуют центробежная сила , уравновешивающая кулоновскую силу взаимодействия электрона с ядром. При Hext 0 добавляется сила Лоренца сонаправлен B, действие внешнего магнитного поля сводится к замедлению вращательного движения электрона на величину изменения угловой скорости частота Лармора

Классификация магнетиков Диамагнетизм атомных остовов Прецессия орбиты вокруг направления поля приводит к дополнительному движению электрона вокруг этого направления, накладывающемуся на его орбитальное движение. Дополнительное движение эквивалентно изменению тока: Добавочный орбитальный момент a 2 - средний квадрат расстояния от оси // В до электрона В магнитном поле каждый электрон приобретает дополнительный (индуцированный) магнитный момент. Его появление и приводит к намагничиванию, в направлении противоположном внешнему магнитному полю. Для случая z электронов: Для случая сферических орбиталей: Суммарная намагниченность Магнитная восприимчивость диамагнетика: Магнгитная восприимчивость ( ~ z) +, Cl-, полупроводниках Ge, Si, Диамагнетики: заполненные электронные оболочки – инертные газы, ионах Na Se… Анизотропия структуры и химических связей приводит к анизотропии (графен в плоскости (0001) = -6 * 10 -6, перпендикулярно плоскости (0001) = -200 * 10 -6).

Классификация магнетиков Парамагнетики Парамагнетизм − это свойство тела намагничиваться во внешнем поле H в направлении поля, т. е. парамагнитная восприимчивость − величина положительная. Благодаря межатомному взаимодействию, магнитные орбитальные моменты двух спаренных электронов взаимно погашают друга заполненные электронные оболочки имеют = 0 и не могут внести вклад в парамагнитные свойства. Поэтому парамагнетизм наблюдается у атомов с неспаренными валентными электронами. Парамагнитными свойствами обладают: атомы и молекулы, имеющие нечетное число электронов (щелочные металлы (Na, K и др. ), Al, окись азота (NO), свободные органические радикалы: трифенилметил С(С 6 Н 5)3; свободные атомы и ионы, имеющие недостроенные внутренние оболочки (элементы переходных групп, редкоземельные металлы и элементы группы актинидов); некоторые молекулы с четным числом электронов (O 2, S 2), органические бирадикалы (из-за нескомпенсированности спинов двух электронов); дефекты кристаллической решетки с нечетным числом электронов (F – центры, вакансии, бивакансии); металлы, поскольку они имеют электроны проводимости.

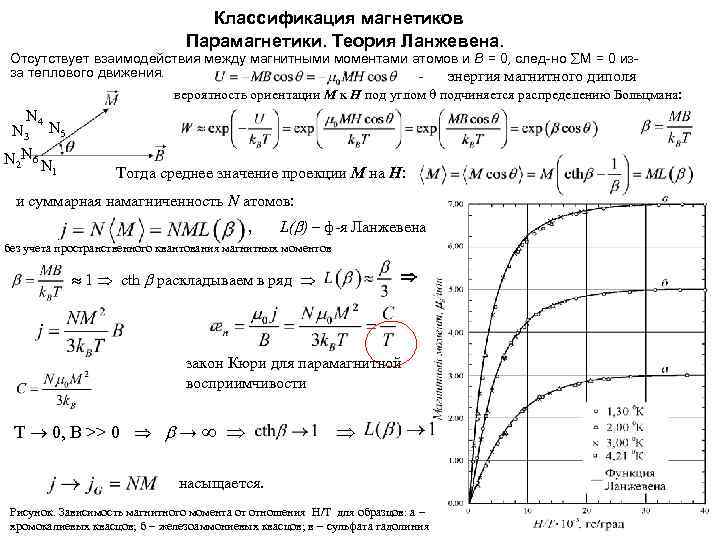Классификация магнетиков Парамагнетики. Теория Ланжевена. Отсутствует взаимодействия между магнитными моментами атомов и B = 0, след-но М = 0 изза теплового движения. - энергия магнитного диполя вероятность ориентации М к Н под углом подчиняется распределению Больцмана: N 4 N 3 N 5 N 2 N 6 N 1 Тогда среднее значение проекции М на Н: и суммарная намагниченность N атомов: , L( ) – ф-я Ланжевена без учета пространственного квантования магнитных моментов 1 cth раскладываем в ряд закон Кюри для парамагнитной восприимчивости Т 0, B >> 0 → ∞ насыщается. Рисунок. Зависимость магнитного момента от отношения Н/Т для образцов: а хромокалиевых квасцов; б железоаммониевых квасцов; в сульфата гадолиния

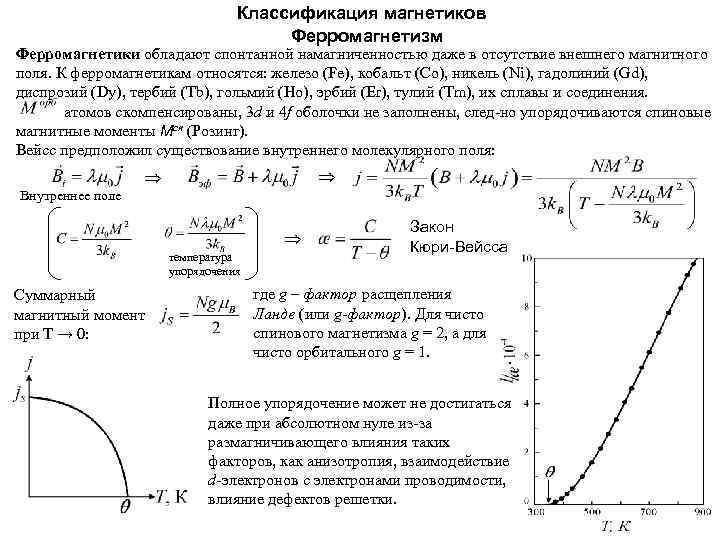Классификация магнетиков Ферромагнетизм Ферромагнетики обладают спонтанной намагниченностью даже в отсутствие внешнего магнитного поля. К ферромагнетикам относятся: железо (Fe), кобальт (Co), никель (Ni), гадолиний (Gd), диспрозий (Dy), тербий (Tb), гольмий (Ho), эрбий (Er), тулий (Tm), их сплавы и соединения. атомов скомпенсированы, 3 d и 4 f оболочки не заполнены, след-но упорядочиваются спиновые магнитные моменты Mсп (Розинг). Вейсc предположил существование внутреннего молекулярного поля: Внутреннее поле температура упорядочения Суммарный магнитный момент при Т → 0: Закон Кюри-Вейсса где g – фактор расщепления Ланде (или g-фактор). Для чисто спинового магнетизма g = 2, а для чисто орбитального g = 1. Полное упорядочение может не достигаться даже при абсолютном нуле из-за размагничивающего влияния таких факторов, как анизотропия, взаимодействие d-электронов с электронами проводимости, влияние дефектов решетки.

Классификация магнетиков Ферромагнетизм. Энергия обменного взаимодействия Какова природа внутреннего поля (Вейсса), какие силы приводят к ориентации спинов в ферромагнетике? Френкель и Гейзенберг, 1928 год: при наличии сильного электростатического взаимодействия между электронами энергетически выгодным может оказаться состояние с параллельной ориентацией спинов, т. е. намагниченное состояние. След-но, результирующая энергия взаимодействия, наряду с кулоновским членом, должна содержать член, зависящий от взаимной ориентации спинов: Энергия обменного взаимодействия - характеризует различие энергии кулоновского взаимодействия системы в случаях, когда спины параллельны и когда они антипараллельны. Для железа тепловая энергия необходимая для разрушения Не описывается 0 классическими моделями магнитного порядка при температуре Кюри: k. B 0. 1 э. В (на 1 атом) 0. 001 э. В Энергия ориентации диполя: (не квантовый механизм) Установлено, что значение обменного интеграла J зависит от отношения d/a (d – межатомное расстояние, a – диаметр недостроенной внутренней оболочки атома). Ферромагнетизм наблюдается только для элементов, у которых обменный интеграл положителен (J > 0), что выполняется для d/a > 1. 5. Из элементов группы железа ферромагнетиком является только -Fe, Co и Ni. -Fe и другие элементы этой группы ферромагнетиками не являются. Сплавы Mn-Cu-Al и соединения Mn. Sb, Mn. Bi, Cr. O 2, Mn. OFe 2 O 3 из неферромагнитных элементов - ферромагнетики. Кристаллическое строение вещества - один из факторов, определяющий ферромагнитные свойства.

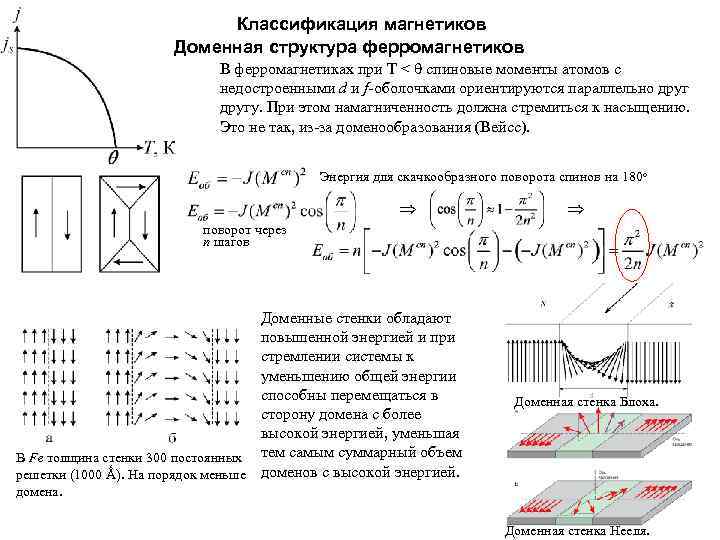Классификация магнетиков Доменная структура ферромагнетиков В ферромагнетиках при Т < спиновые моменты атомов с недостроенными d и f-оболочками ориентируются параллельно другу. При этом намагниченность должна стремиться к насыщению. Это не так, из-за доменообразования (Вейсс). Энергия для скачкообразного поворота спинов на 180 о поворот через n шагов Доменные стенки обладают повышенной энергией и при стремлении системы к уменьшению общей энергии способны перемещаться в сторону домена с более высокой энергией, уменьшая В Fe толщина стенки 300 постоянных тем самым суммарный объем решетки (1000 Ǻ). На порядок меньше доменов с высокой энергией. Доменная стенка Блоха. домена. Доменная стенка Нееля.

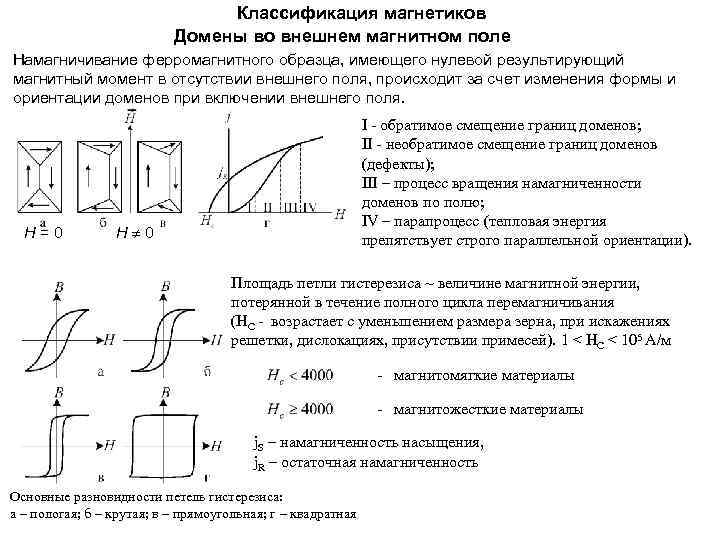Классификация магнетиков Домены во внешнем магнитном поле Намагничивание ферромагнитного образца, имеющего нулевой результирующий магнитный момент в отсутствии внешнего поля, происходит за счет изменения формы и ориентации доменов при включении внешнего поля. I - обратимое смещение границ доменов; II - необратимое смещение границ доменов (дефекты); III – процесс вращения намагниченности доменов по полю; IV – парапроцесс (тепловая энергия препятствует строго параллельной ориентации). Н = 0 Н 0 Площадь петли гистерезиса ~ величине магнитной энергии, потерянной в течение полного цикла перемагничивания (НС - возрастает с уменьшением размера зерна, при искажениях решетки, дислокациях, присутствии примесей). 1 < НС < 105 А/м - магнитомягкие материалы - магнитожесткие материалы j. S – намагниченность насыщения, j. R – остаточная намагниченность Основные разновидности петель гистерезиса: а – пологая; б – крутая; в – прямоугольная; г – квадратная

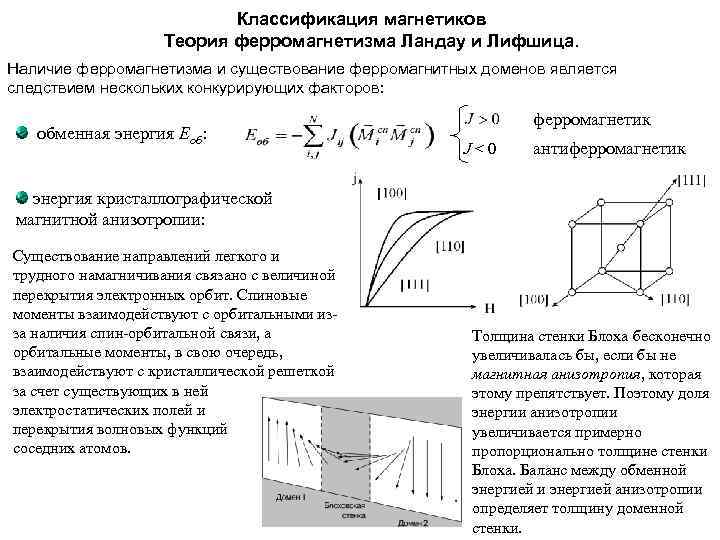Классификация магнетиков Теория ферромагнетизма Ландау и Лифшица. Наличие ферромагнетизма и существование ферромагнитных доменов является следствием нескольких конкурирующих факторов: обменная энергия Eоб: ферромагнетик J < 0 антиферромагнетик энергия кристаллографической магнитной анизотропии: Существование направлений легкого и трудного намагничивания связано с величиной перекрытия электронных орбит. Спиновые моменты взаимодействуют с орбитальными изза наличия спин-орбитальной связи, а орбитальные моменты, в свою очередь, взаимодействуют с кристаллической решеткой за счет существующих в ней электростатических полей и перекрытия волновых функций соседних атомов. Толщина стенки Блоха бесконечно увеличивалась бы, если бы не магнитная анизотропия, которая этому препятствует. Поэтому доля энергии анизотропии увеличивается примерно пропорционально толщине стенки Блоха. Баланс между обменной энергией и энергией анизотропии определяет толщину доменной стенки.

Классификация магнетиков Теория ферромагнетизма Ландау и Лифшица. Наличие ферромагнетизма и существование ферромагнитных доменов является следствием нескольких конкурирующих факторов: магнитострикционная деформация: , В − модуль объемной упругости, λS – константа магнитострикции = l / l Магнитострикция – это изменения размеров тела при его намагничивании. Например, образец из никеля при намагничивании до насыщения сжимается в направлении поля и увеличивается в поперечном направлении. Железный образец, наоборот, удлиняется в направлении поля. Анизотропная часть приводит к изменению линейной магнитострикции, что проявляется в изменении кристаллографической симметрии кристалла. Изотропный вклад приводит к изменению объемной магнитострикции и соответственно коэффициента объемного расширения. магнитостатическая энергия: NP – размагничивающий фактор, зависит от формы образца Эта энергия не связана с наличием стенок между доменами, но имеет непосредственное отношение к доменной структуре. Магнитостатическая энергия уменьшается, если образец разбивается на антипараллельные домены, и стремится к нулю, если при образовании доменов они формируются так, что магнитный поток замыкается внутри ферромагнитного вещества.

Классификация магнетиков Теория ферромагнетизма Ландау и Лифшица. Наличие ферромагнетизма и существование ферромагнитных доменов является следствием нескольких конкурирующих факторов: магнитная энергии: Это энергия ферромагнетика во внешнем магнитном поле напряженностью Н. Минимуму полной энергии соответствует не насыщенная конфигурация, а некоторая доменная структура. магнитоупругая энергия: − тензор магнитоупругого взаимодействия, − тензор упругой деформации, − направляющие косинусы вектора намагниченности Кроме магнитострикции, магнитоупругое влияние проявляется также в изменении намагниченности при деформации образца. Изменение расстояния между частицами изменяет силу магнитного взаимодействия между ними, что ведет к изменению среднего магнитного момента, температуры Кюри, . . . Различают два вклада: Полная энергия ферромагнетика определяется суммой всех конкурирующих факторов обменная энергия кристаллографической магнитной анизотропии: магнитострикционная деформация магнитостатическая энергия магнитная энергии магнитоупругая энергия:

Классификация магнетиков Антиферромагнетизм, ферримагнетизм ферромагнетик антиферромагнетик J < 0 Антиферромагнетики - это вещества, которые содержат атомы (ионы) с нескомпенсированными спинами электронов на недостроенных электронных оболочках, они также имеют доменную структуру, внутри каждого домена наблюдается строгая упорядоченная ориентация спинов. При J < 0 выгодной является антипараллельная ориентация спинов соседних узлов решетки кристалла. Антиферромагнетики: Mn. O, Mn. S, Ni. Cr, Cr 2 O 3, VO 2, Спонтанная намагниченность. Магнитная восприимчивость: N – температура Нееля Обменное взаимодействие между спинами ионов антиферромагнетика косвенно. В нем принимают участие электроны магнитно нейтральных ионов, расположенных между «магнитными ионами» . Ферриты – вещества, в которых величина магнитного момента подрешеток неодинакова, например вследствие неодинакового количества атомов в подрешетках или же их разной природы Магнетит Окись железа (Fe) + окислы лития (Li), цинка (Zn), никеля (Ni), кадмия (Cd), свинца (Pb), меди (Cu), магния (Mg), марганца (Mn) Fe. O · Fe 2 O 3 • хорошие магнетики, • HC мала, • большая величина намагниченности насыщения j. S, • высокое электрическое сопротивление.

Магнитные свойства наносистем Магнитные наноматериалы разделяются по типу организации системы и факторам , определяющим ее магнитные свойства. А – изолированные невзаимодействующие магнитные частицы. Свойства наносистемы определяются только размерным фактором. B – наночастицы «ядро в оболочке» . Свойства системы полностью определяются характером взаимодействия ядра с оболочкой. C – магнитные частицы в магнитоактивной или неактивной матрице. Свойства определяются как размерами частиц, так и характером их взаимодействия с матрицей и друг с дугом. D - наносистемы с высокой концентрацией частиц (самоорганизованные наносистемы). Свойства определяются межчастичными взаимодействиями.

Магнитные свойства наносистем Зависимость коэрцитивной силы от размера частиц Магнитные свойства многодоменных материалов во многом определяются динамикой доменных стенок. Для наночастиц энергия доменной стенки значительно превосходит энергию размагничивания и формирование доменной структуры оказывается энергетически невыгодным. м ие до ен ти ьш ос ен жн Ум дви к по ено ст Критический размер, меньше которого образование доменных стенок энергетически не выгодно. х ны ен с – const, зависит от кристаллической структуры решетки, J – обменная постоянная, a 0 – постоянная решетки, Nd = -Hd/j. R коэффициент размагничивания. Dcrit = 14 нм, 70 нм, 50 нм, 128 нм, 166 нм для Fe, Co, Ni, Fe 3 O 4, -Fe 2 O 3, соответственно. Суперпарамагнетизм - для суперпарамагнетиков после выключения полная намагниченность j релаксирует до нуля В общем случае: M = M cth MB/k. BT - k. BT/MB по экспоненциальному закону. В приближении слабого поля: M = MB/3 k. BT - характерное время релаксации - магнитокристаллическая анизтропия наночастиц определяет высоту активационного барьера E. K – коэффициент анизотропии. f 0 - частотный фактор – частота разворота магнитного момента наночастицы. Время релаксции опредедляется размером наночастиц Для f 0 109 – 1013 с-1, К = 106 эрг/см 3, Т = 300 К: R = 5. 7 нм τ = 0. 1 с R = 7. 3 нм τ = 108 с Эффективный магнитный момент будет от 100 до 1000 В по сравнению с парамагнетиками.

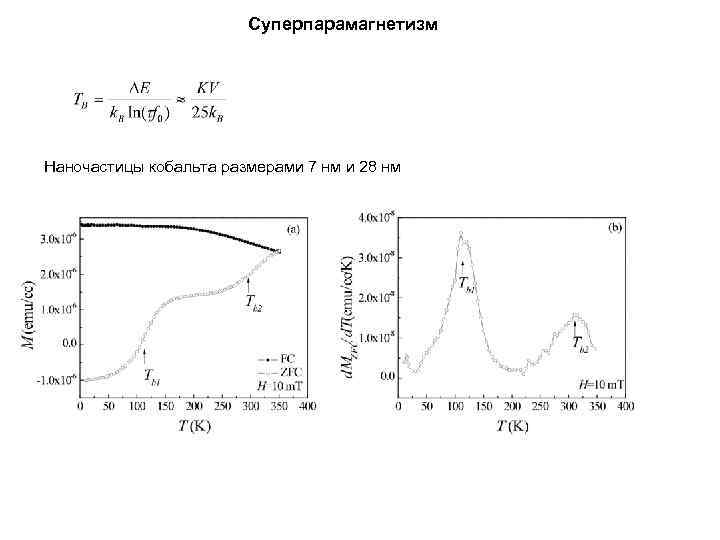Суперпарамагнетизм Наночастицы кобальта размерами 7 нм и 28 нм

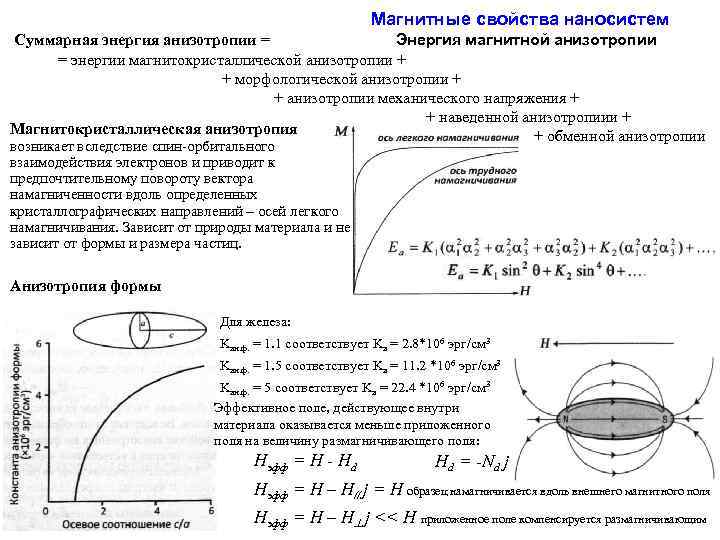Магнитные свойства наносистем Суммарная энергия анизотропии = Энергия магнитной анизотропии = энергии магнитокристаллической анизотропии + + морфологической анизотропии + + анизотропии механического напряжения + + наведенной анизотропиии + Магнитокристаллическая анизотропия + обменной анизотропии возникает вследствие спин-орбитального взаимодействия электронов и приводит к предпочтительному повороту вектора намагниченности вдоль определенных кристаллографических направлений – осей легкого намагничивания. Зависит от природы материала и не зависит от формы и размера частиц. Анизотропия формы Для железа: Kан. ф. = 1. 1 соответствует Kа = 2. 8*106 эрг/см 3 Kан. ф. = 1. 5 соответствует Kа = 11. 2 *106 эрг/см 3 Kан. ф. = 5 соответствует Kа = 22. 4 *106 эрг/см 3 Эффективное поле, действующее внутри материала оказывается меньше приложенного поля на величину размагничивающего поля: Hэфф = H - Hd Hd = -Nd j Hэфф = H – H// j = H образец намагничивается вдоль внешнего магнитного поля Hэфф = H – H j << H приложенное поле компенсируется размагничивающим

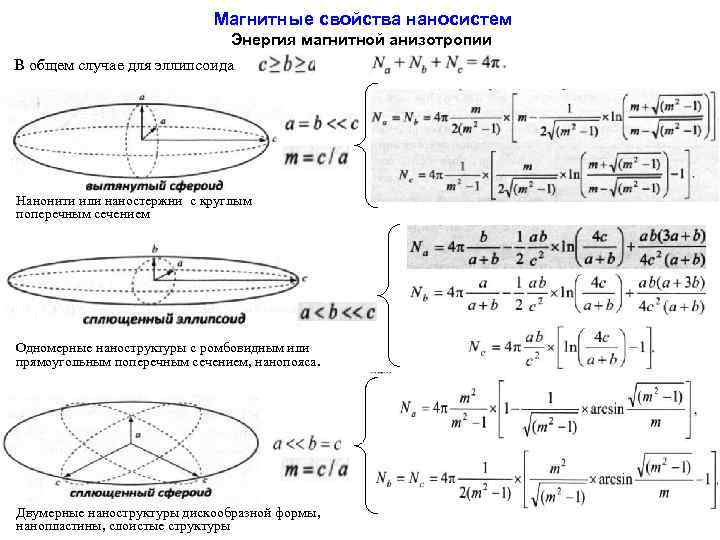Магнитные свойства наносистем Энергия магнитной анизотропии В общем случае для эллипсоида Нанонити или наностержни с круглым поперечным сечением Одномерные наноструктуры с ромбовидным или прямоугольным поперечным сечением, нанопояса. Двумерные наноструктуры дискообразной формы, нанопластины, слоистые структуры

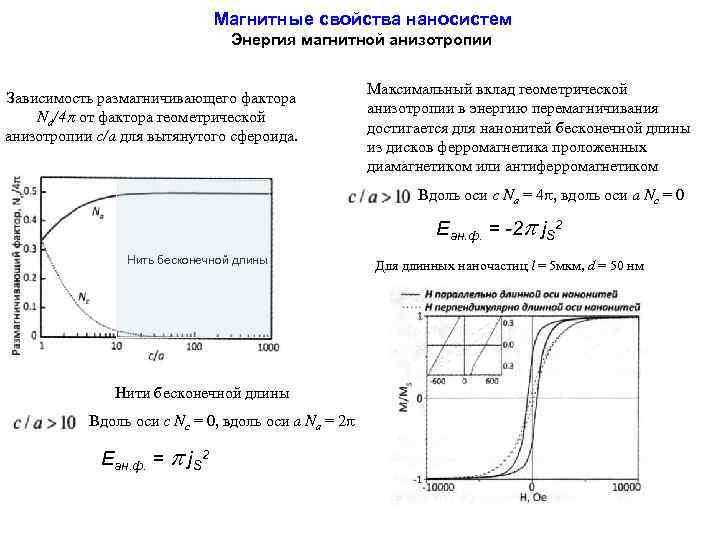Магнитные свойства наносистем Энергия магнитной анизотропии Зависимость размагничивающего фактора Nd/4 от фактора геометрической анизотропии c/a для вытянутого сфероида. Максимальный вклад геометрической анизотропии в энергию перемагничивания достигается для нанонитей бесконечной длины из дисков ферромагнетика проложенных диамагнетиком или антиферромагнетиком Вдоль оси с Na = 4 , вдоль оси a Nc = 0 Eан. ф. = -2 j. S 2 Нить бесконечной длины Нити бесконечной длины Вдоль оси с Nс = 0, вдоль оси a Nа = 2 Eан. ф. = j. S 2 Для длинных наночастиц l = 5 мкм, d = 50 нм

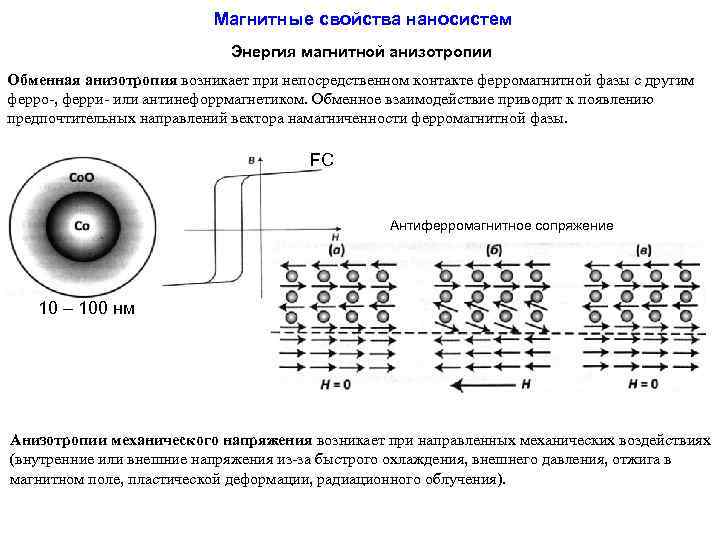Магнитные свойства наносистем Энергия магнитной анизотропии Обменная анизотропия возникает при непосредственном контакте ферромагнитной фазы с другим ферро-, ферри- или антинефоррмагнетиком. Обменное взаимодействие приводит к появлению предпочтительных направлений вектора намагниченности ферромагнитной фазы. FC Антиферромагнитное сопряжение 10 – 100 нм Анизотропии механического напряжения возникает при направленных механических воздействиях (внутренние или внешние напряжения из-за быстрого охлаждения, внешнего давления, отжига в магнитном поле, пластической деформации, радиационного облучения).

Магнитные свойства наносистем Перемагничивание однодоменных частиц Полная свободна энергия однодоменной частицы (уравнение Брауна: ) малы Еобм – обменная энергия, ЕН – Зеемановская энергия, Еа – энергия магнитокристаллической анизотропии, Еупр – энергия магнито-упругих взаимодействий, ЕD – магнитостатическая энергия Для наночастиц доменообразование невыгодно существует критический размер, соответствующий сохранению однодоменного состояния. Для вытянутого сфероида критический радиус нанонити: A – константа жесткости, Nc – размагничивающий фактор, а 0 – постоянна решетки m = c/a 1. С ростом m = c/a наблюдается значительный рост rsd 2. Изменения материала нанонити сказывается на обменных взаимодействиях в пределах одной наночастицы, что приводит к уменьшению rsd с ростом j. S Нанонить Ni с m = 10 остается однодоменной при перемагничивании вплоть до rsd 450 нм, а для Fe rsd 170 нм Co rsd 140 нм. Зависимость критического радиуса нанонитей от размагничивающего фактора

Магнитные свойства наносистем Перемагничивание однодоменных частиц Две модели: когерентное вращение магнитных моментов – Eобм → min, Nd → max, и «свертка» (curling) с образованием вихревого поля внутри частицы – Eобм → max, Nd → min. H top view H Размер частицы → min Еобм → max (из-за увеличения угла между моментами соседних атомов) более предпочтителен механизм когерентного вращения j Анизотропия частиц (m) → max Nd → max более предпочтителен curling механизм с образованием вихревого поля внутри частицы. Т. о. Механизм перемагничивания зависит от размера и форм-фактора частицы Для случая, когда поле приложено вдоль легкой оси намагничивания: Для бесконечно длинного цилиндра Na = 2 , слеовательно: q – минимальное решений ф-ции Бесселя (1. 84 для бесконечно длинного цилиндра, 2. 08 для правильного сфероида)

Магнитные свойства наносистем JS ≡ MS Перемагничивание однодоменных частиц Модели перемагничивания определяют из экспериментов по измерению угловой зависимости коэрцитивной силы. Когерентное вращение магнитных моментов Теоретический расчет по модели Стонера-Вольфорда магнитостатическая полная свободная энергия: + Зеемановская - магнитостатическая энергия, - угол между вектором намагниченности и внешним полем, 0 – угол между внешним полем и осью вытянутого сфероида. или где h = H*MS/2 Ku приведенное магнитное поле Уравнение определяет отклонение вектора намагниченности анизотропных однодоменных наночастиц от направления внешнего магнитного поля для каждого значения h. или Выделяют два участка: поле вдоль длинной оси анизотропии 0 о < θ < 30 o (h. C ~ h. S) и 30 о < θ < 90 o (h. C < h. S) Перемагничивающее поле h. S: Приведенная намагниченность: Угол перемагничивания: Уравнение позволяет рассчитать ход петли магнитного гистерезиса Коэрцитивное поле частицы (m = 0): Нет зависимости перемагничивающего поля h. S и коэрцитивного поля hc от размера частицы

Магнитные свойства наносистем Перемагничивание однодоменных частиц «Свертка» магнитных моментов с образованием вихревого поля < S < Угловая зависимость коэрцитивной силы определяется выражением: S = r/r 0 – приведенный радиус частицы (r 0 = A 1/2/MS), k = q 2 / Величина коэрцитивного поля hc зависит от размера ( частицы Так конфигурация магнитных моментов в частице стремится к минимуму свободной энергии, перемагничивание образца должно протекать по механизму, обеспечивающему минимальную коэрцитивную силу. Пороговое значений угла, при котором происходит смена механизма перемагничивания, увеличивается с увеличением диаметра нанонити и уменьшением параметра анизотропии. 1/r 2) и параметра анизотропии

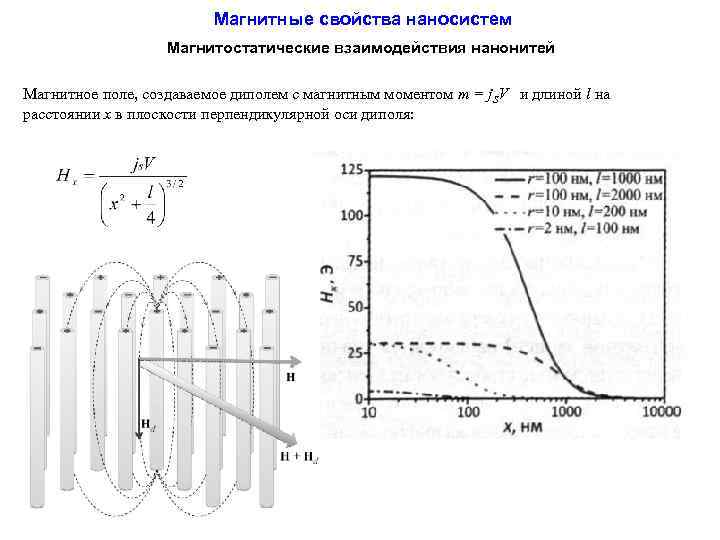Магнитные свойства наносистем Магнитостатические взаимодействия нанонитей Магнитное поле, создаваемое диполем с магнитным моментом m = j. SV и длиной l на расстоянии x в плоскости перпендикулярной оси диполя:

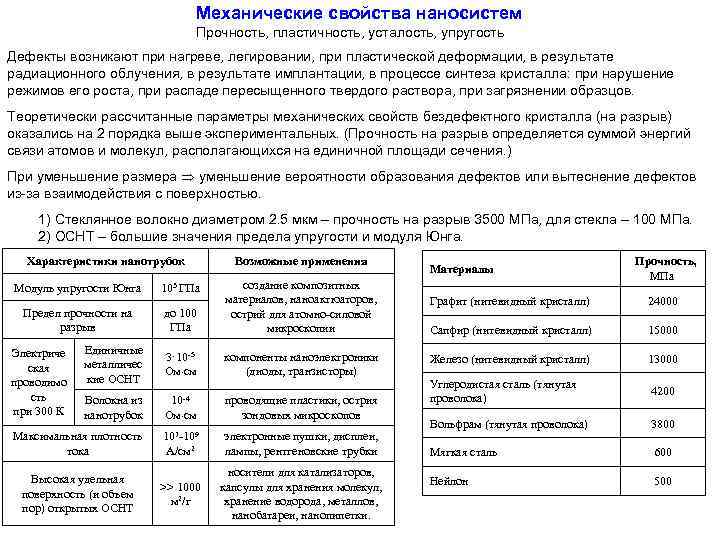Механические свойства наносистем Прочность, пластичность, усталость, упругость Дефекты возникают при нагреве, легировании, при пластической деформации, в результате радиационного облучения, в результате имплантации, в процессе синтеза кристалла: при нарушение режимов его роста, при распаде пересыщенного твердого раствора, при загрязнении образцов. Теоретически рассчитанные параметры механических свойств бездефектного кристалла (на разрыв) оказались на 2 порядка выше экспериментальных. (Прочность на разрыв определяется суммой энергий связи атомов и молекул, располагающихся на единичной площади сечения. ) При уменьшение размера уменьшение вероятности образования дефектов или вытеснение дефектов из-за взаимодействия с поверхностью. 1) Стеклянное волокно диаметром 2. 5 мкм – прочность на разрыв 3500 МПа, для стекла – 100 МПа. 2) ОСНТ – большие значения предела упругости и модуля Юнга. Характеристики нанотрубок Материалы Прочность, МПа до 100 ГПа создание композитных материалов, наноактюаторов, острий для атомно-силовой микроскопии Графит (нитевидный кристалл) 24000 Сапфир (нитевидный кристалл) 15000 Единичные металличес кие ОСНТ 3· 10 -5 Ом см компоненты наноэлектроники (диоды, транзисторы) Железо (нитевидный кристалл) 13000 Волокна из нанотрубок 10 -4 Ом см проводящие пластики, острия зондовых микроскопов Углеродистая сталь (тянутая проволока) 4200 107 -109 электронные пушки, дисплеи, лампы, рентгеновские трубки Вольфрам (тянутая проволока) 3800 Мягкая сталь 600 Нейлон 500 Модуль упругости Юнга 103 ГПа Предел прочности на разрыв Электриче ская проводимо сть при 300 К Возможные применения Максимальная плотность тока Высокая удельная поверхность (и объем пор) открытых ОСНТ A/см 2 >> 1000 м 2/г носители для катализаторов, капсулы для хранения молекул, хранение водорода, металлов, нанобатареи, нанопипетки.

Механические свойства наносистем Прочность, пластичность, усталость определяются наличием дефектов, их типом, концентрацией и распределением. Точечные дефекты: собственные - смещение или замена небольшой группы атомов, межузельный атом, вакансия; несобственные точечные дефекты – примеси внедрения, примеси замещения; комплексы, состоящие из нескольких точечных дефектов: дефект по Френкелю (вакансия + собственный междоузельный атом), бивакансия (вакансия + вакансия), А-центр (вакансия + атом кислорода в кремнии и германии). Одномерные дефекты: дефекты кристалла, размер которых по одному направлению много больше параметра решетки, а по двум другим — соизмерим с ним. К одномерным дефектам относят дислокации и дисклинации. Дислокация — граница области незавершенного сдвига в кристалле (характеризуются вектором сдвига и углом φ между ним и линией дислокации). При φ=0 дислокация называется винтовой; при φ=90° — краевой; при других углах — смешанной. Дисклинация — граница области незавершенного поворота в кристалле (характеризуется вектором поворота). Клиновая дисклинация Двумерные дефекты — поверхность кристалла, границы зёрен материала, плоскости двойникования, поверхности раздела фаз. Трехмерные дефекты - скопления вакансий, образующие поры и каналы; частицы, оседающие на различных дефектах (декорирующие), например пузырьки газов, пузырьки маточного раствора; скопления примесей в виде секторов (песочных часов) и зон роста, поры или включения примесных фаз.

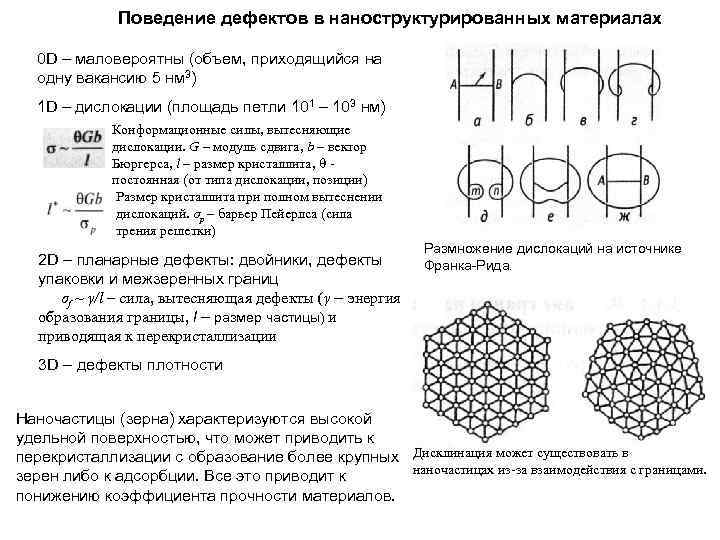Поведение дефектов в наноструктурированных материалах 0 D – маловероятны (объем, приходящийся на одну вакансию 5 нм 3) 1 D – дислокации (площадь петли 101 – 103 нм) Конформационные силы, вытесняющие дислокации. G – модуль сдвига, b – вектор Бюргерса, l – размер кристаллита, - постоянная (от типа дислокации, позиции) Размер кристаллита при полном вытеснении дислокаций. σр – барьер Пейерлса (сила трения решетки) 2 D – планарные дефекты: двойники, дефекты упаковки и межзеренных границ σf ~ γ/l – сила, вытесняющая дефекты (γ – энергия образования границы, l – размер частицы) и приводящая к перекристаллизации Размножение дислокаций на источнике Франка-Рида. 3 D – дефекты плотности Наночастицы (зерна) характеризуются высокой удельной поверхностью, что может приводить к перекристаллизации с образование более крупных Дисклинация может существовать в наночастицах из-за взаимодействия с границами. зерен либо к адсорбции. Все это приводит к понижению коэффициента прочности материалов.

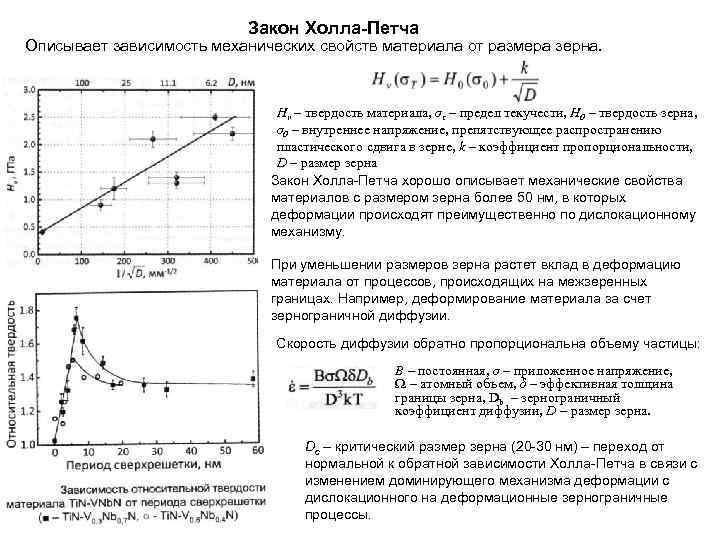Закон Холла-Петча Описывает зависимость механических свойств материала от размера зерна. Hν – твердость материала, στ – предел текучести, Н 0 – твердость зерна, σ0 – внутреннее напряжение, препятствующее распространению пластического сдвига в зерне, k – коэффициент пропорциональности, D – размер зерна Закон Холла-Петча хорошо описывает механические свойства материалов с размером зерна более 50 нм, в которых деформации происходят преимущественно по дислокационному механизму. При уменьшении размеров зерна растет вклад в деформацию материала от процессов, происходящих на межзеренных границах. Например, деформирование материала за счет зернограничной диффузии. Скорость диффузии обратно пропорциональна объему частицы: B – постоянная, σ – приложенное напряжение, – атомный объем, δ – эффективная толщина границы зерна, Db – зернограничный коэффициент диффузии, D – размер зерна. Dс – критический размер зерна (20 -30 нм) – переход от нормальной к обратной зависимости Холла-Петча в связи с изменением доминирующего механизма деформации с дислокационного на деформационные зернограничные процессы.

Механические свойства наносистем Упругие свойства. Высокотемпературная ползучесть Сверхэластические свойства – способность поликристаллических материалов испытывать значительную деформацию при растяжении без образования области шейки и разрушения (вклад диффузионной ползучести вдоль границ зерен позволяет сделать пластичными керамику и интерметаллиды). Скорость диффузии Условия для появления сверхпластичности: • малый размер зерен, играющий главную роль в зернограничной диффузии при нагружении материала; • изотропность (равноостность зерен), необходимая для проскальзывания; • высокоэнергетичные границы зерен (течение идет быстрее вдоль границ с большей энергией); • наличие второй фазы, ограничивающей рост зерен. (изменение степени деформации в единицу времени): A – постоянная, σ – приложенное напряжение, – атомный объем, δ – эффективная толщина границы зерна, Db – зернограничный коэффициент диффузии, D – размер зерна, b – вектор Бюргерса, G – модуль сдвига. для наночастиц. Модель зернограничного проскальзывания Анализ смещения показал, что деформация происходит за счет малых сдвигов атомов межзеренных границ, в которых сильно варьируются внутренние напряжения, в среднем оказывается на 10 -20 % меньше напряжений в объеме зерен. Моделирование для анализа газоподобных границ (молекулярная динамика). Белые атомы в нормальной ГЦК координации, Синие и красные – атомы с нарушением координации в первой сфере.

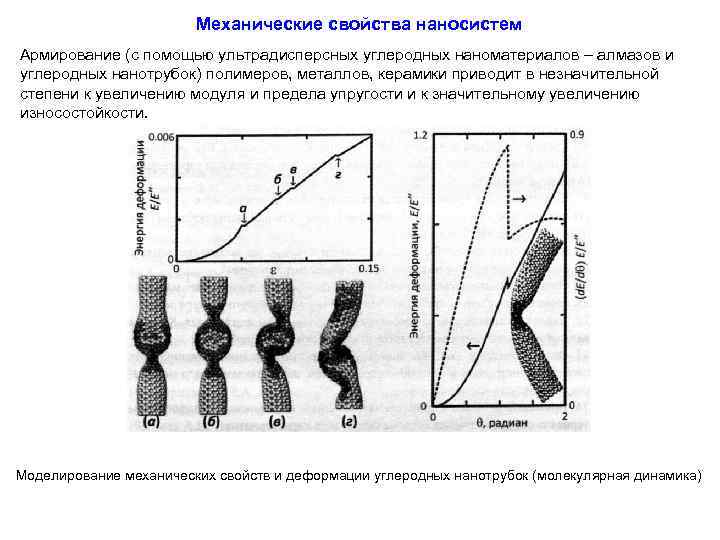Механические свойства наносистем Армирование (с помощью ультрадисперсных углеродных наноматериалов – алмазов и углеродных нанотрубок) полимеров, металлов, керамики приводит в незначительной степени к увеличению модуля и предела упругости и к значительному увеличению износостойкости. Моделирование механических свойств и деформации углеродных нанотрубок (молекулярная динамика)