математика 3 лек 3.ppt
- Количество слайдов: 39

3. Основы математической статистики Рассматриваемые вопросы: v Выборочный метод v Статистическое распределение выборки v Статистические распределения оценки параметров v Статистические оценки статистических гипотез (С) Веденяпин Е. Н. 2011 1

3. 1. Выборочный метод В отличие от теории вероятностей в математической статистике вероятностная модель определена с точностью до неизвестных параметров. Отсутствие сведений о параметрах компенсируется пробными испытаниями, на основе которых восстанавливается недостающая информация. Задачи математической статистики v разработка методов сбора и группировки статистических сведений, полученных в результате экспериментов или наблюдений; v разработка методов анализа статистических данных (оценка неизвестных вероятностей событий, а также функций распределения; оценка зависимости случайной величины от других случайных величин; проверка статистических гипотез). (С) Веденяпин Е. Н. 2011 2

Выборки Замечание: Сплошное исследование каждого объекта из совокупности на практике проводят редко. Обычно из всей совокупности отбирают ограниченное число объектов и подвергают их исследованию. Генеральная совокупность – это совокупность объектов, из которых производится выборка. Выборочная совокупность (выборка) – это совокупность случайно отобранных объектов из генеральной совокупности. Число объектов в совокупности называется объемом. Пример. Пусть из 2 000 изделий отобрано для исследования 100 изделий. Объем генеральной совокупности N=2 000, объем выборки n=100. (С) Веденяпин Е. Н. 2011 3

Способы осуществления выборки v Если после исследования объект из выборки возвращается в генеральную совокупность, то такая выборка называется повторной. v Если объект не возвращается в генеральную совокупность, то выборка называется безповторной. Репрезентативная (представительная) выборка – это выборка, по данным которой можно уверенно судить об интересующем признаке генеральной совокупности. (С) Веденяпин Е. Н. 2011 (С) Веденяпин 2011 4

Способы отбора v без расчленения генеральной совокупности на части; v с расчленением генеральной совокупности на части. Способ без расчленения на части К данному способу относятся простые случайные отборы (повторные и безповторные), когда объекты извлекаются по одному из генеральной совокупности объектов. Способ с расчленением на части v Типический отбор, при котором объекты отбираются из каждой типической части генеральной совокупности. v Механический отбор, когда генеральную совокупность делят на число групп, равное объему выборки, с последующим отбором из каждой группы по одному объекту. v Серийный отбор, при котором объекты отбираются не по одному, а сериями. (С) Веденяпин Е. Н. 2011 5

3. 2. Статистическое распределение выборки Извлечение выборки объемом N из генеральной совокупности Х x 1 x 2 x 3 x 4 … xn K k 1 k 2 k 3 k 4 … kn Варианты – это значения хi наблюдаемого признака Х. Вариационный ряд – это последовательность вариант, записанная в возрастающем порядке. Частота ki – это количество появлений хi в выборке. Относительная частота Wi (С) Веденяпин Е. Н. 2011 6

Характеристики вариационного ряда Мода М 0 – это варианта, имеющая наибольшую частоту. Медиана mе – это варианта, которая делит вариационный ряд на две части с одинаковым количеством вариант в каждой части. Замечание: Если число вариант нечетно, то есть то Если же число вариант четно, то есть то Размах варьирования – это разность между максимальной и минимальной вариантами R=x. MAX-x. MIN. (С) Веденяпин Е. Н. 2011 (С) Веденяпин 2011 7

Закон статистического распределения выборки – это перечень вариант и соответствующих им частот (относительных частот). Замечание 1: Имеется аналогия с законом распределения случайной величины: в теории вероятностей – это соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – это соответствие между наблюдаемыми величинами и их частотами (относительными частотами). Замечание 2: Сумма относительных частот равна единице (С) Веденяпин Е. Н. 2011 8

Пример нахождения основных характеристик вариационного ряда Выборка задана в виде распределения частот. Найти распределение относительных частот и основные характеристики вариационного ряда. Х 4 7 8 12 17 K 2 4 5 6 3 Объем выборки Относительные частоты (С) Веденяпин Е. Н. 2011 9

Пример нахождения основных характеристик вариационного ряда (окончание) Сумма относительных частот Закон статистического распределения Х 4 7 8 12 17 K 0. 1 0. 25 0. 3 0. 15 Мода вариационного ряда Медиана вариационного ряда (n=2· 2+1) Размах варьирования (С) Веденяпин Е. Н. 2011 10

Эмпирическая функция распределения Пусть kx – это число наблюдений, при которых наблюдалось значение признака Х, меньшее х. При объеме выборки N относительная частота события X<x равна Эмпирическая функция распределения (функция распределения выборки) – это функция, определяющая для каждого значения х относительную частоту Wx события X<x (С) Веденяпин Е. Н. 2011 11

Различие между эмпирической и теоретической функциями распределения Теоретическая функция генеральной совокупности. распределения – это функция F(х) Замечание 1: Различие между эмпирической и теоретической функциями распределения состоит в том, что теоретическая функция распределения F(х) определяет вероятность события X<x, а эмпирическая функция распределения F*(х) определяет относительную частоту этого события. Замечание 2: При больших N вероятность отличия друг от друга этих функций близка к единице (С) Веденяпин Е. Н. 2011 12

Свойства эмпирической функции распределения 1. Значения функции F*(х) принадлежат отрезку 2. Функция является неубывающей функцией. 3. Пусть xm и x. M – соответственно минимальная и максимальная варианты. Тогда и Замечание: Эмпирическая функция F*(х) служит для оценки теоретической функции F(х) генеральной совокупности. (С) Веденяпин Е. Н. 2011 13

Пример построения эмпирической функции распределения Построить эмпирическую распределению выборки. функцию распределения Х 2 4 10 15 заданному 6 K по 25 (С) Веденяпин Е. Н. 2011 14
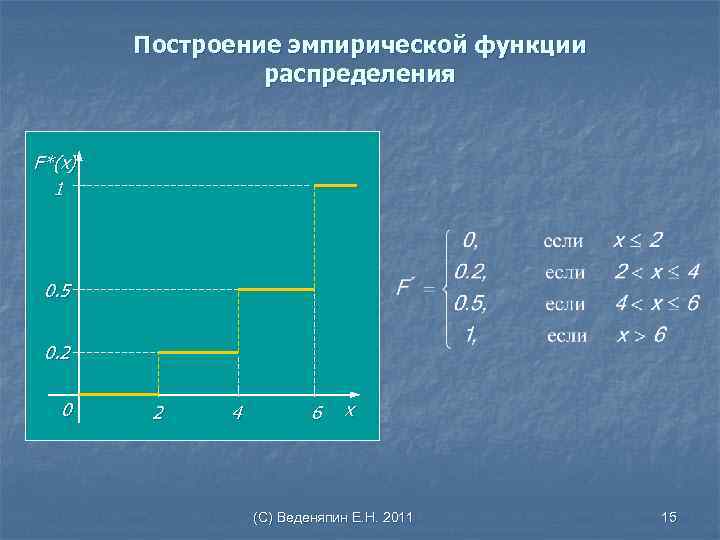
Построение эмпирической функции распределения F*(x) 1 0. 5 0. 2 0 2 4 6 x (С) Веденяпин Е. Н. 2011 15
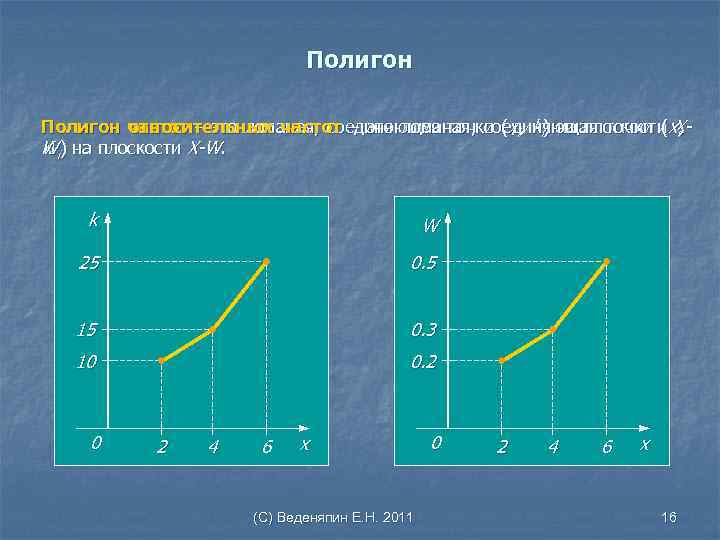
Полигон частот – это ломаная, соединяющая точки (xi, ki) на плоскости x. Xотносительных частот – это ломаная, соединяющая точки ( i, W K. i) на плоскости X-W. k W 25 0. 5 15 0. 3 10 0. 2 0 2 4 6 x (С) Веденяпин Е. Н. 2011 0 2 4 6 x 16

Гистограмма частот Ели признак Х изменяется непрерывно, то размах варьирования (x. MAX, x. MIN) разбивают несколько одинаковых частичных интервалов длиной h каждый и находят для каждого из этих интервалов сумму частот ki, попавших в него. Ступенчатая фигура, состоящая из прямоугольников с основаниями h и высотами ki/h (плотность частоты), называется гистограммой частот. Геометрический смысл гистограммы. Площадь гистограммы численно равна сумме всех частот (объему выборки). Замечание: Аналогично определяется гистограмма относительных частот. (С) Веденяпин Е. Н. 2011 17
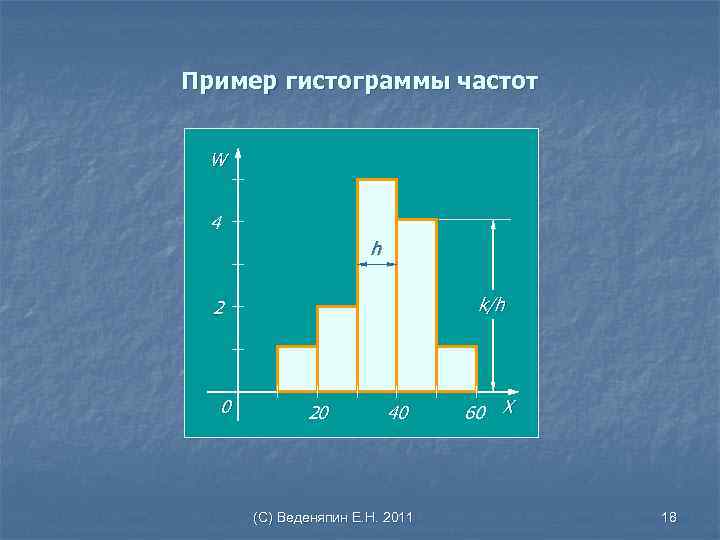
Пример гистограммы частот W 4 h k/h 2 0 20 40 (С) Веденяпин Е. Н. 2011 60 X 18

3. 3. Статистические оценки параметров распределения Рассмотрим значения некоторого признака х1, х2, х3, …, хn в выборке как независимые случайные величины Х 1, Х 2, Х 3, …, Хn. Тогда нахождение статистической оценки неизвестного параметра теоретического распределения означает отыскание функции от наблюдаемых случайных величин, которая дает приближенное значение искомого параметра. (С) Веденяпин Е. Н. 2011 19

Виды статистических оценок Несмещенная оценка статистического параметра – это статистическая оценка *, математическое ожидание которой равно оцениваемому параметру при любой выборке Смещенная оценка – это оценка, для которой Эффективная статистическая оценка – это оценка, минимальную дисперсию при заданном объеме выборки N. имеющая Состоятельная статистическая оценка – это оценка, которая при увеличении объема выборки N ∞ по вероятности стремится к оцениваемому параметру. (С) Веденяпин Е. Н. 2011 20

Средние числовые характеристики статистических оценок Генеральная средняя для изучаемого количественного признака Х по генеральной совокупности N 0 Выборочная средняя для признака Х по выборочной совокупности N Если значения признака х1, х2, х3, …, хn в выборке имеют частоты соответственно k 1, k 2, k 3, …, kn, то выборочная средняя равна Замечание: Выборочная средняя является несмещенной оценкой. (С) Веденяпин Е. Н. 2011 21

Характеристики отклонения значения признака Х от его среднего значения Генеральная дисперсия для количественного признака Х по генеральной совокупности N 0 Выборочная дисперсия для количественного признака Х по выборочной совокупности N Средние квадратические отклонения (С) Веденяпин Е. Н. 2011 22

Пример определения выборочных характеристик Выборка задана таблицей Х 1 2 3 5 K 15 20 10 5 Найти выборочные характеристики: среднюю, дисперсию и среднее квадратическое отклонение. (С) Веденяпин Е. Н. 2011 23

Эмпирические моменты Обычный эмпирический момент порядка s – это среднее значение s-ых степеней разности xi-C, где xi – наблюдаемая варианта, а С – произвольная постоянная Начальный эмпирический момент порядка s Центральный эмпирический момент порядка s (С) Веденяпин Е. Н. 2011 24

Асимметрия и эксцесс эмпирического распределения Замечание: Нормальное распределение является наиболее распространенным в применениях математической статистики. Для оценки отклонения эмпирического распределения от нормального используют следующие характеристики: v асимметрия эмпирического распределения; v эксцесс эмпирического распределения. Асимметрия эмпирического распределения Эксцесс эмпирического распределения (С) Веденяпин Е. Н. 2011 25

Применение асимметрии и эксцесса Замечание 1: Асимметрия и эксцесс служат для сравнения полигона эмпирического распределения с нормальным распределением. Замечание 2: Для нормально распределенной случайной величины асимметрия и эксцесс равны 0. Поэтому, если эти характеристики достаточно малы, можно считать, что генеральная совокупность распределена по нормальному закону. Замечание 3: Величина асимметрии характеризует «скошенность» распределения относительно симметричного нормального распределения Знак асимметрии аs указывает на расположение максимума полигона относительно математического ожидания (слева при аs>0, справа при аs<0). Замечание 4: Эксцесс характеризует «островершинность» распределения относительно нормального распределения (при ek>0 полигон более острый и высокий по сравнению с кривой нормального распределения, при ek<0 полигон более низкий и плоский). (С) Веденяпин Е. Н. 2011 26
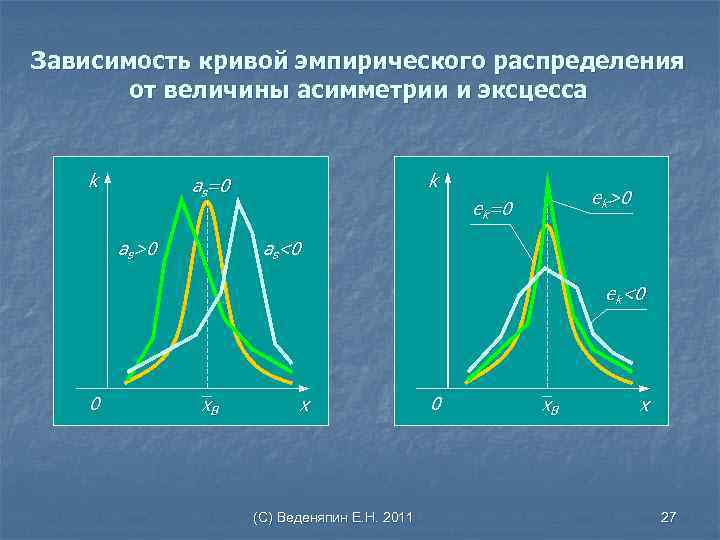
Зависимость кривой эмпирического распределения от величины асимметрии и эксцесса k k as=0 as>0 ek=0 as<0 ek<0 0 _ х. В x (С) Веденяпин Е. Н. 2011 0 _ х. В x 27

Пример определения асимметрии и эксцесса Выборка задана таблицей Х 1 2 3 4 5 6 10 K 5 10 15 35 36 15 4 Найти асимметрию и эксцесс выборочного распределения. (С) Веденяпин Е. Н. 2011 28

Пример определения асимметрии и эксцесса (окончание) (С) Веденяпин Е. Н. 2011 29

Доверительный интервал для параметра c надежностью оценки р – это числовой промежуток содержащий истинное значение данного параметра с вероятностью р где * - оценка неизвестного параметра , >0 – некоторое число. Замечание: Обычно надежность р задается числом, близким к 1. Число =1 -р называется уровнем значимости. (С) Веденяпин Е. Н. 2011 30

Схема построения доверительного интервала v Рассматриваются выборки случайных величин, с которыми связан параметр . v Подбирается случайная величина Y с известным распределением, значения которой определяются выборками и параметром : Y=Y( ). v По известному распределению Y подбираются числа Y 1 и Y 2 такие, чтобы выполнялось равенство v По значениям Y 1 и Y 2 определяется число >0 при известном *. (С) Веденяпин Е. Н. 2011 31

Пример определения доверительного интервала Найти доверительные интервалы надежности р1=0. 95 и р2=0. 99 для нормальной случайной величины Х с функцией распределения (С) Веденяпин Е. Н. 2011 32

3. 4. Статистические оценки статистических гипотез Статистическая гипотеза – это гипотеза о виде неизвестного распределения, о параметрах известных распределений, об отношениях между случайными величинами и т. д. Нулевая (основная) гипотеза – это выдвинутая гипотеза Н 0. Конкурирующая (альтернативная) гипотеза – это гипотеза Н 1, которая противоречит гипотезе Н 0. Типы гипотез v Параметрические гипотезы: при известном виде распределения предположения о неизвестных характеристиках этого распределения. v Для известной случайной величины (выборки) предположения о виде ее распределения. (С) Веденяпин Е. Н. 2011 33

Проверка статистических гипотез Статистический критерий – это случайная величина Т, которая служит для проверки статистических гипотез. Схема проверки v Для основной гипотезы Н 0 формулируется альтернативная гипотеза Н 1. v Выбирается уровень значимости (обычно 0. 01< <0. 05). v Рассматриваются теоретические выборки значений случайных величин, о которых сформулирована гипотеза Н 0 и формируется случайная величина Т. Значения и распределение Т полностью определяются по выборкам в предположении о верности гипотеза Н 0. (С) Веденяпин Е. Н. 2011 34

Схема проверки статистических гипотез (окончание) v На числовой оси задают интервал D такой, что вероятность попадания величины Т в этот интервал равна р=1 - Интервал D называется областью принятия гипотезы Н 0, а остальная область числовой оси называется критической областью. v По реализациям анализируемых теоретических выборок вычисляется наблюдаемое значение Т, равное tk и проверяется условие попадания внутрь области D принятия гипотезы Н 0. Если условие выполняется, то гипотеза Н 0 принимается в том смысле, что она не противоречит опытным данным. В противном случае гипотеза Н 0 неверна. (С) Веденяпин Е. Н. 2011 35

Ошибки проверке статистических гипотез v Ошибка первого рода. Отвергается гипотеза Н 0 при ее правильности. Вероятность такой ошибки равна . v Ошибка второго рода. Принимается гипотеза Н 0 при правильности альтернативной гипотезы Н 1. (С) Веденяпин Е. Н. 2011 36

Типы статистических критериев проверки гипотез v Критерий Пирсона; v Критерий Стьюдента; v Критерий Фишера; v Критерий Колмогорова. (С) Веденяпин Е. Н. 2011 37

Пример применения критерия Стьюдента Для независимых наблюдений х1, х2, …, xn проверить гипотезу Н 0: математическое ожидание m=m 0 при двусторонней альтернативной гипотезе m≠m 0. Уровень значимости задан. Критерий проверки Н 0 Величина Т имеет распределение Стьюдента с n-1 степенями свободы. Критическая область Гипотеза Н 0 принимается, если (С) Веденяпин Е. Н. 2011 38

(С) Веденяпин Е. Н. 2011 39
математика 3 лек 3.ppt