3. Метрика графов 3. 5. Изоморфизм Большое

3. Метрика графов 3. 5. Изоморфизм

Большое число комбинаторно-логических задач и ОЗ на графах требует установления изоморфизма или изоморфного вложения между заданными структурами. Данная проблема, является NP-полной. Поэтому разрабатываются различные эвристики для получения приемлемых практических результатов. Задача распознавания изоморфизма графов (РИГ) состоит в следующем: Для заданных графов G 1=(X 1, U 1) и G 2=(X 2, U 2) требуется определить, существует ли взаимно однозначное отображение : X 1 X 2 такое, что U=(x, y) U 1 тогда и только тогда, когда ( (x), (y)) U 2. 2

В настоящее время известны полиномиальные алгоритмы для следующих классов графов: графы ограниченной степени; графы с ограниченной кратностью собственных значений; к - разделимые графы; k - стягиваемые графы и т. д. Особое внимание заслуживают сильнорегулярные графы (СГ). Граф G=(X, , n 111, n 011), |x|=n называется n– вершинным регулярным графом степени , если в нем любая пара смежных вершин имеет n 111 общих соседей, а любая пара несмежных вершин - n 011. Известно, что СГ образуют класс наиболее трудных задач для РИГ. Для СГ известен алгоритм с ВСА 0(exp 2 n log 2 n) 3

Известно, что задача изоморфного вложения графа является NP- полной задачей [198]. Она имеет много сходства и в то же время существенно (по сложности) отличается от РИГ. Например, для решения задачи изоморфизма подграфа G 1 с использованием известных алгоритмов РИГ необходимо разработать процедуру выделения в графе G подмножества X 1 X равномощного с множеством вершин X 2 графа G 2. 4

Данная процедура включает k 1 действий, где , n=|X|, n 2=|X 2|. Следовательно k 2 раз надо применять и алгоритм РИГ. Поэтому при выделении каждого подграфа G 1 в графе G необходимо выполнять k 2 действий, где (m 1 количество ребер в подграфе G 1, m 2 - в графе G 2, m 1>m 2). 5

Следовательно, даже если есть полиномиальный алгоритм РИГ, с его помощью невозможно решить задачу изоморфного вложения за полиномиальное время. Она может быть решена за полиномиальное время, если G 1– лес, а G 2 – дерево. 6

Наибольшую трудоемкость представляет установление изоморфизма однородных графов, имеющих автоморфные подграфы. Для решения таких задач используются методы разбиения исследуемых графов на различные уровни. При этом ВСА алгоритма снижается с О(n!) до О(k!), где n - число элементов в графе, а k - число элементов в наибольшем автоморфном подграфе, т. е. в таком подграфе, где не имеет значения выбор вершин для установления соответствия. 7

Основная идея таких алгоритмов заключается в следующем. В графах, исследуемых на изоморфизм, выбираются две предполагаемо изоморфные вершины. Относительно них производится разбиение всех оставшихся вершин на два класса. В первый класс включаются вершины, смежные предполагаемо изоморфным, а во второй нет. Например, на рис. 3. 27, а, б показаны два графа G и G’. G = (Х, U), G’ = (Х’, U’), |Х| = |Х’| = 6, |U| = |U'| = 9, локальные степени всех вершин графа равны трем. 8

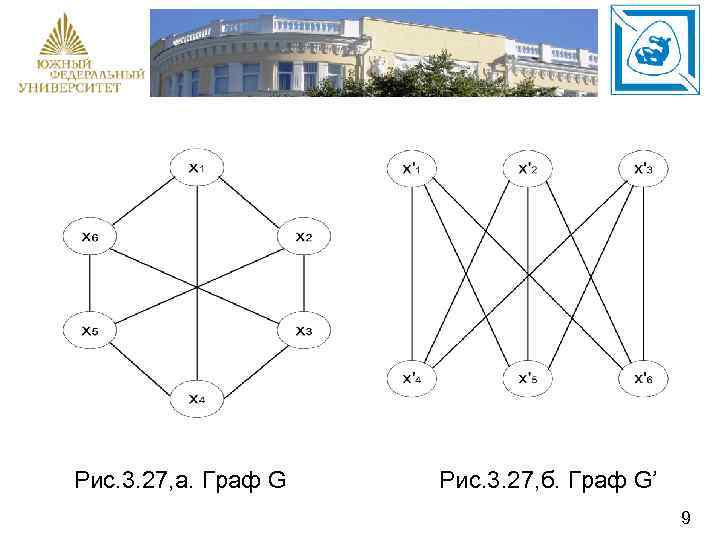
Рис. 3. 27, а. Граф G Рис. 3. 27, б. Граф G’ 9

Необходимо установить изоморфизм графов G и G’. Другими словами, необходимо определить, существует ли отношение эквивалентности: Х Х’, U U’ такое, что, если ребро (xi, xj) ребру (x’i, x’j), (3. 31) тогда xi x’i, xj x’j, xi, xj, X, x’i, x’j, X’. Покажем на примере реализацию эвристики разбиения для установления изоморфизма однородных графов. Выберем одну вершину в графе G и одну в графе G’. И относительно них выполним указанное выше разбиение: {1} {2}, 4, 6}1+ {3, 5}1 - (G), {1’} {4’, 5’, 6’}1’+ {2’, 3’}1’- (G’). 10

В данном разбиении вершины х2, х4, х6 смежны вершине х1, а вершины, х3, х5 не смежны вершине х1 графа G. Аналогичное разбиение выполнено для графа G'. Здесь считается, что вершины х1 и х’ 1 предполагаемо изоморфны (П - изоморфны). Далее, выбираются подмножества меньшей мощности и внутри них проверяется смежность вершин. В нашем примере вершины х3, х5 и х’ 2, х’ 3 не смежны. Поэтому процесс разбиения продолжается. {1} {1’} {3}1 - {{2, 4, 6}3+}1+ {{5}3 -}1 -, {2’}1’- {{4’, 5’, 6’}2’+}1’+ {{3’}2’-}1’-. 11

Продолжая процесс аналогично, получим, что граф G изоморфен графу G'. Подстановка вершин запишется В рассматриваемом примере подмножества вершин {х2, х4, х6} и {х’ 4, х’ 5, х’ 6} являются автморфными, т. е. каждая вершина в одном подграфе может быть изоморфна любой вершине второго подграфа. 12

13

G` преобразовали в G на основе подстановки Следовательно G изоморфен G` 14

В примере (рис. 3. 27) ВСА РИГ О(6!) была сведена к ВСА РИГ О(3!). В алгоритмах такого типа необходим перебор между элементами автоморфных подграфов. Причем, как следует из рассмотрения примера, такой перебор здесь выполняется последовательно для всех вершин, кроме последней в подграфе. В этой связи применение новых архитектур локальный поиск позволяет повысить скорость установления изоморфизма графов. 15

Например, на рис. 3. 28, а, б показаны нетривиальные, неоднородные (трудные) графы G и G’. В этих графах |Х| = |Х’| = 7, |U| = |U'| = 8, 1=1, 2=3, 3=3, 4=3, 5=3, 6=2, 7=1; a=1, b=3, c=3, d=3, e=3, f=2, g=1. Вершина 1 может быть П–изоморфна вершине a или g. В первом случае нас ждет тупик, а во втором успех. Мы предположили, что вершина 1 П–изоморфна вершине g. Тогда на основе связности графа и эвристики разбиения следует, что вершина 7 П–изоморфна вершине a. После этого вытекает, что вершина 6 П– изоморфна вершине f. 16

Далее необходимо установить существует ли соответствие между подмножествами автоморфных вершин {2, 3, 4, 5} и {b, c, d, e}. В этом случае, как отмечалось выше, в общем, необходимо выполнить полный перебор между этими подмножествами вершин. Для этих подмножеств это - 4!. Выполняя такие преобразования, получим, что вершина 2 П–изоморфна вершине b, вершина 3 П–изоморфна вершине d, 4 – c и 5 – e. Отсюда следует, что графы G и G' (рис. 3. 28, а, б) изоморфны, а подстановка изоморфизма, переводящая один граф в другой, запишется 17

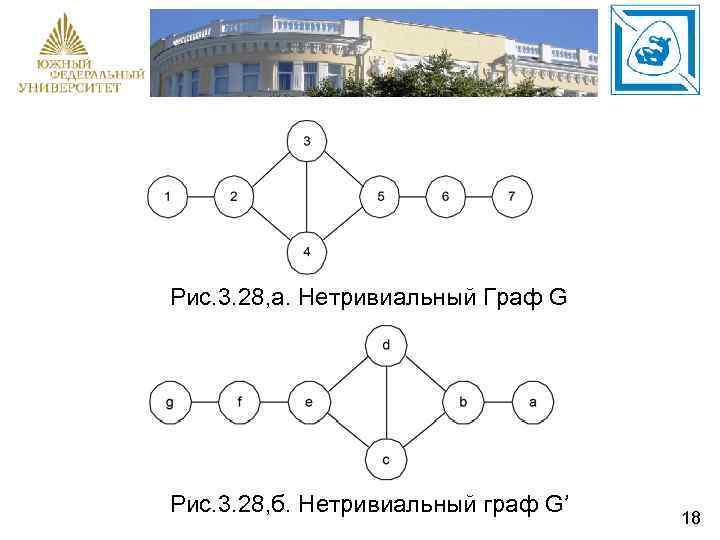
Рис. 3. 28, а. Нетривиальный Граф G Рис. 3. 28, б. Нетривиальный граф G’ 18

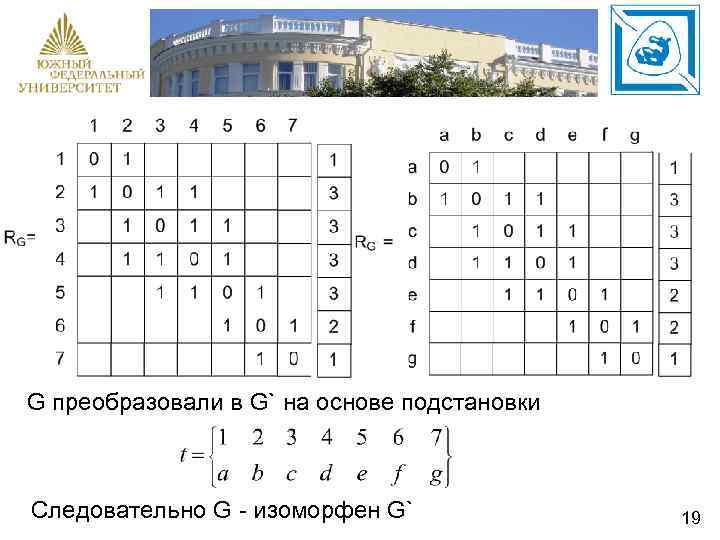
G преобразовали в G` на основе подстановки Следовательно G - изоморфен G` 19

Как видно, наличие вершин с различными локальными степенями упрощает процесс РИГ. Это позволяет выбирать начальные условия для эвристики разбиения. В примере (рис3. 28, а, б) всего два способа для выбора разбиения, в то время, как в графах (рис3. 27, а, б) шесть возможных способов разбиения. В однородных графах все степени вершин одинаковы, поэтому начальные условия выбираются произвольно случайным образом. 20

В этой связи при установлении изоморфизма в однородных графах ВСА в самом лучшем случае О( n), в самом худшем случае О( n!). Если графы неизоморфны, то за одну итерацию установить результат невозможно. Необходимо провести сравнение на изоморфизм одной случайно выбранной вершины из одного графа со всеми остальными вершинами другого графа. 21

Например, пусть заданы два графа (рис. 3. 29, а, б) G и G’. При этом G = (Х, U), G’ = (Х’, U’), |Х| = |Х’| = 6, |U| = |U'| = 9, локальные степени всех вершин графа равны трем. Для РИГ применим эвристику разбиения. Предположим, что вершина 1 графа G П – изоморфна вершине a графа G’. Тогда получим: {1} {a} {2, 4, 6}1+ {b, d, f}1’+ {3, 5}1 -(G), {e, c}1’ (G’). 22

Для дальнейшего анализа выбираем соответствующие подмножества наименьшей мощности {3, 5} и {e, c}. Вершины (3, 5) в графе G (рис. 3. 29, а) смежны, а вершины (c, e) в графе G’ – нет. Следовательно, вершина 1 не может быть изоморфна вершине a. В этой связи необходимо провести аналогичные операции для проверки изоморфизма вершины 1 с остальными вершинами графа G’. Далее получим: {1} {b} {2, 4, 6}1+ {3, 5}1 - (G), {a, c, e}1’+ {d, f}1’(G’). 23

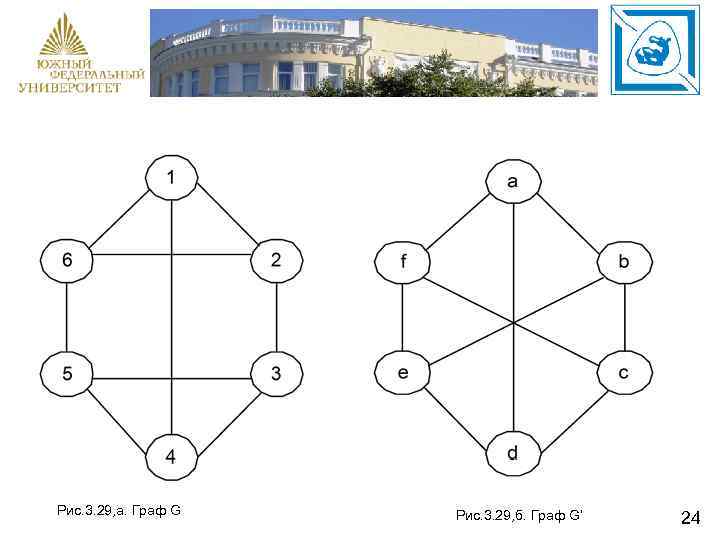
Рис. 3. 29, а. Граф G Рис. 3. 29, б. Граф G’ 24

Вершины (3, 5) в графе G (рис. 3. 29, а) смежны, а вершины (d, f) в графе G’ – нет. Следовательно, вершина 1 не может быть изоморфна вершине b. Продолжая аналогичные построения, имеем, что вершина 1 не может быть изоморфна вершинам c, d, e. Наконец, предположим, что вершина 1 графа G П– изоморфна вершине f графа G’. Тогда получим: {1} {2, 4, 6}1+ {3, 5}1(G), {f} {a, c, e}1’+ {b, d}1’(G’). 25

Вершины (3, 5) в графе G (рис. 3. 29, а) смежны, а вершины (b, d) в графе G’ – нет. Следовательно, вершина 1 не может быть изоморфна вершине b. Проанализированы все вершины графа G’ на предмет изоморфизма с вершиной 1 графа G. Во всех случаях ответ отрицательный. Поэтому граф G неизоморфен графу G’. 26

Рассмотрим пример РИГ (рис. 3. 30, а, б) G и G’. При этом G = (Х, U), G’ = (Х’, U’), |Х| = |Х’| = 10, |U| = |U'| = 15, локальные степени всех вершин графа равны трем. Предположим, что вершина 1 графа G П – изоморфна вершине a графа G’. Тогда получим: {1} {a} {2, 5, 6}1+ {3, 4, 7, 8, 910}1 - (G), {b, e, f}1’+ {c, d, h, g, k, i}1’- (G’). 27

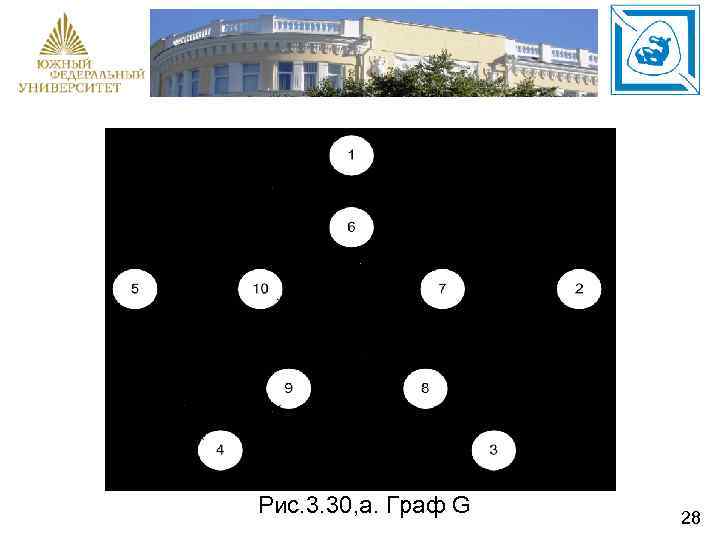
Рис. 3. 30, а. Граф G 28

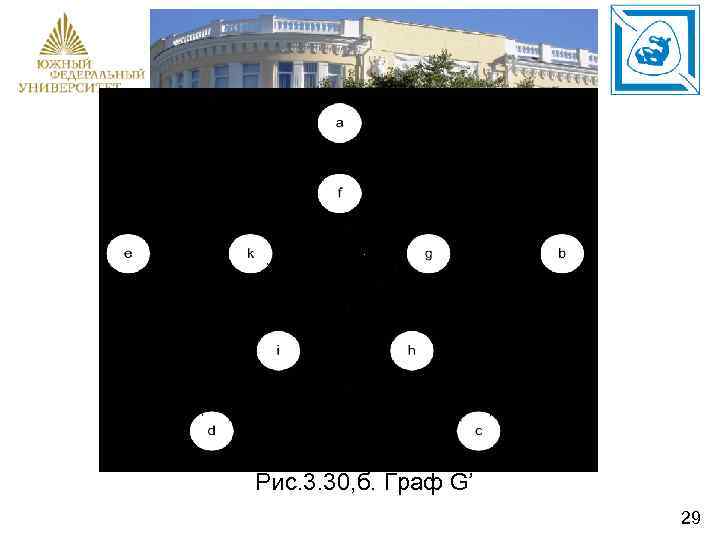
Рис. 3. 30, б. Граф G’ 29

Для дальнейшего анализа выбираем соответствующие подмножества наименьшей мощности {2, 5, 6} и {b, e, f}. Предположим, что вершина 2 Пизоморфна вершине b. В этом случае получим: {1} {2, }1+ [{5, 6}1+]1 - [{7, 3}1+, {, 4, 8, 910}1 -]1{a} {b, }1’+ [{e, f}1’+]1’- [{g, c}1’+, {d, h, k, i}1’-]1’- (G), (G’). Как видно П- изоморфизм сохраняется. Продолжая далее, запишем {1} {2, }1+ [{5, 6}1+]1 - [[{7}1+, {3}1+]1+, [{9, 10}1 -, {4, 8}1 -]1 -]1 - (G), {a} {b, }1’+ [{e, f}1’+]1’- [[{g}1’+, {c}1’+]1’+, [{i, k}1’-, {h, d, }1’-]1’- (G’). 30

Так как вершины (h, d) в графе G’ (рис. 3. 30, б) смежны, а вершины (4, 8) в графе G (рис. 3. 30, а) – нет. Следовательно, вершина 1 не может быть изоморфна вершине а, вершина 2 -b, вершина 7 -g и вершина 3 -c. Продолжая аналогично, получим, что граф G не изоморфен графу G’. 31

Определение изоморфизма графов позволяет определять одинаковые графы, которые расположены на плоскости по разному. 32