3 Group Technology Cellular Manufacturing Inselfertigung c

3 Group Technology / Cellular Manufacturing (Inselfertigung) (c) Prof. Richard F. Hartl Layout & Design

Group Technology (GT) n n Observation already in 1920 ies: product-oriented departments to manufacture standardized products in machine companies lead to reduced transportation Can be considered the start of Group Technology (GT): Parts with similar features are manufactured together with standardized processes small "focused factories" are created as independent operating units within large facilities. More generally, GT can be considered a “theory of management” based on the principle "similar things should be done similarly“ "things". . product design, process planning, fabrication, assembly, and production control (here); but also other activities, including administrative functions. (c) Prof. Richard F. Hartl Layout & Design 2

When to use GT? n n See also Chapter 1 (Figure 1. 5) Pure item flow lines are possible, if volumes are very large. If volumes are very small, and parts are very different, a functional layout (job shop) is usually appropriate In the intermediate case of medium-variety, mediumvolume environments, group configuration is most appropriate (c) Prof. Richard F. Hartl Layout & Design 3

Cellular Manufacturing n n Principle of GT: divide the manufacturing facility into small groups or cells of machines cellular manufacturing Each cell is dedicated to a specified family of part types (or few “similar” families). ¨ Preferably, all parts are completed within one cell ¨ n Typically, it consists of ¨ a small group of machines, tools, and handling equipment (c) Prof. Richard F. Hartl Layout & Design 4

Different Versions of GT n The idea of GT can also be used to build larger groups, such as for instance, a department, possibly composed of several automated cells or several manned machines of various types. n GT flow line classical GT cell GT center n n (c) Prof. Richard F. Hartl Layout & Design 5

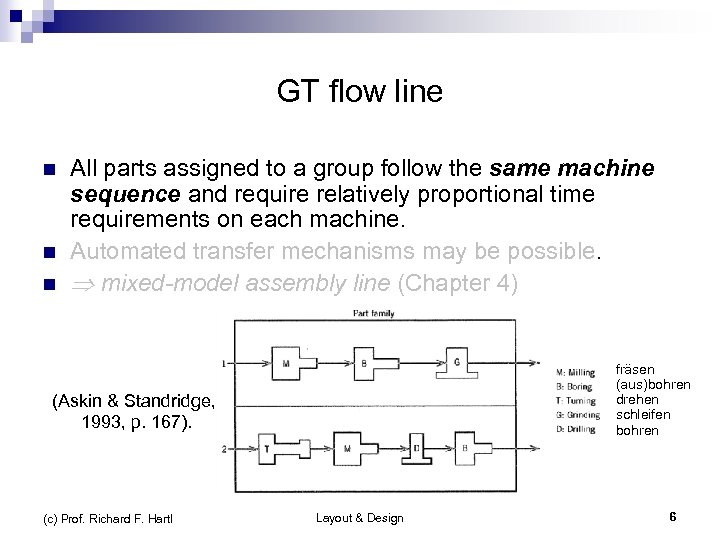GT flow line n n n All parts assigned to a group follow the same machine sequence and require relatively proportional time requirements on each machine. Automated transfer mechanisms may be possible. mixed-model assembly line (Chapter 4) fräsen (aus)bohren drehen schleifen bohren (Askin & Standridge, 1993, p. 167). (c) Prof. Richard F. Hartl Layout & Design 6

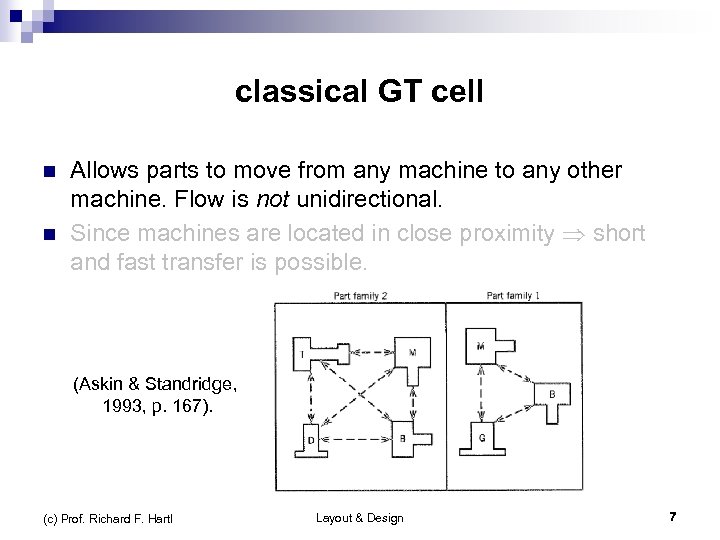classical GT cell n n Allows parts to move from any machine to any other machine. Flow is not unidirectional. Since machines are located in close proximity short and fast transfer is possible. (Askin & Standridge, 1993, p. 167). (c) Prof. Richard F. Hartl Layout & Design 7

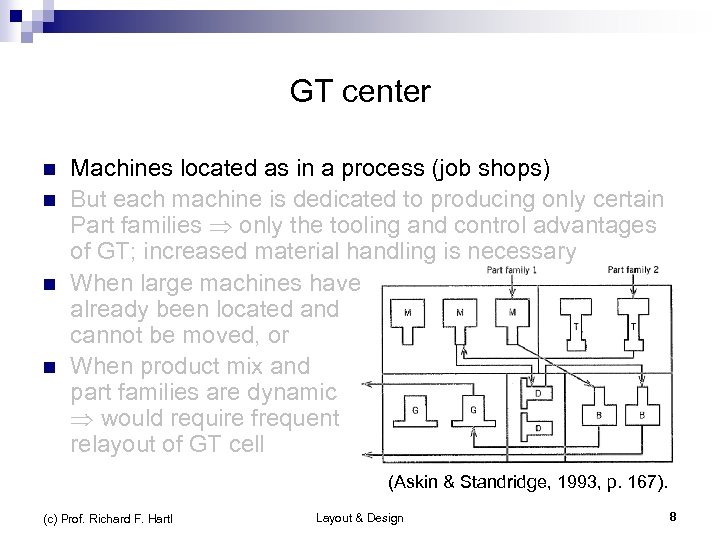GT center n n Machines located as in a process (job shops) But each machine is dedicated to producing only certain Part families only the tooling and control advantages of GT; increased material handling is necessary When large machines have already been located and cannot be moved, or When product mix and part families are dynamic would require frequent relayout of GT cell (Askin & Standridge, 1993, p. 167). (c) Prof. Richard F. Hartl Layout & Design 8

Typical Manufacturing Cell (1) n n n Often u-shaped for short transport Even if process layout not possible Often typical material flow (c) Prof. Richard F. Hartl Layout & Design 9

Typical Manufacturing Cell (2) n n Example with 3 workers Also u-shaped (c) Prof. Richard F. Hartl Layout & Design 10

Advantages of GT Cell n Short transportation and handling (usually within cell) n Short setup times because often same tools and fixtures can be used (products are similar) n High flexibility (quick reaction on changes) n Investment cost low (no advanced technology necessary) n Clear arrangement, few tools/machines easy to control n High motivation and satisfaction of workers (identification with “their" products) n Small lot sizes possible n short flow times (c) Prof. Richard F. Hartl Layout & Design 11

How to Build Groups/Cells n n Basic Idea: Typical Part Families Items that look alike ¨ Items that are made with the same equipment ¨ (c) Prof. Richard F. Hartl Layout & Design 12

Items That Look Alike n n n Most products that look similar are manufactured using similar production techniques (if similar material) Parts are grouped because they have similar geometry (about the same size and shape) they should represent a part family, e. g. cog wheels (gear wheels) of similar size and material (c) Prof. Richard F. Hartl Layout & Design 13

Items That Are Made with Same Equipment (c) Prof. Richard F. Hartl Layout & Design 14

How to Build Groups/Cells n Visual inspection “Items that look alike” may use photos or part prints ¨ utilizes subjective judgment (experience) ¨ n Classification & coding by examination of design & production data (same equipment) most common in industry ¨ time consuming & complicated ¨ (c) Prof. Richard F. Hartl Layout & Design 15

Codes n n n The code should be sufficiently flexible to handle future as well as current parts The scope of part types must be known (e. g. parts rotational, prismatic, sheet metal, etc. ? ) The code must discriminate between parts with different values for key attributes (material, tolerances, required machines, etc. ) (c) Prof. Richard F. Hartl Layout & Design 16

Codes n Many coding systems have been developed None is universally applicable ¨ Most implementations require some customization ¨ n Functional classification coding based on part design attributes ¨ coding based on part manufacturing attributes ¨ coding based on combination of design & manuf. attributes ¨ n Structural classification Hierarchical Structure ¨ Chain Type Structure ¨ Hybrid structure (combination) ¨ (c) Prof. Richard F. Hartl Layout & Design 17

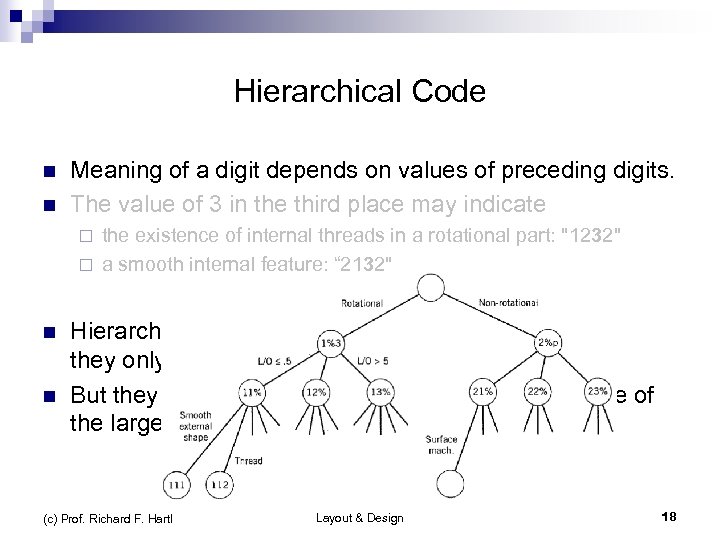Hierarchical Code n n Meaning of a digit depends on values of preceding digits. The value of 3 in the third place may indicate the existence of internal threads in a rotational part: "1232" ¨ a smooth internal feature: “ 2132" ¨ n n Hierarchical codes are efficient: they only consider relevant information at each digit But they are difficult to learn and remember because of the large number of conditional inferences. (c) Prof. Richard F. Hartl Layout & Design 18

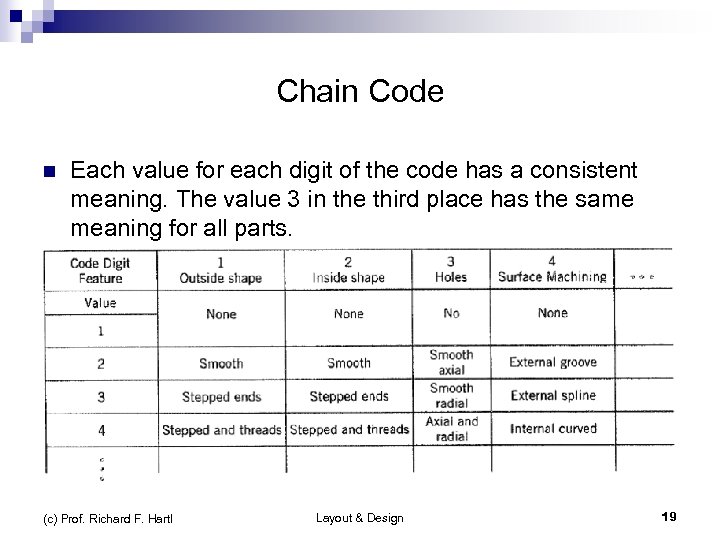Chain Code n Each value for each digit of the code has a consistent meaning. The value 3 in the third place has the same meaning for all parts. n Easier to learn but less efficient (longer for same info) Certain digits may be meaningless for some/many parts. n (c) Prof. Richard F. Hartl Layout & Design 19

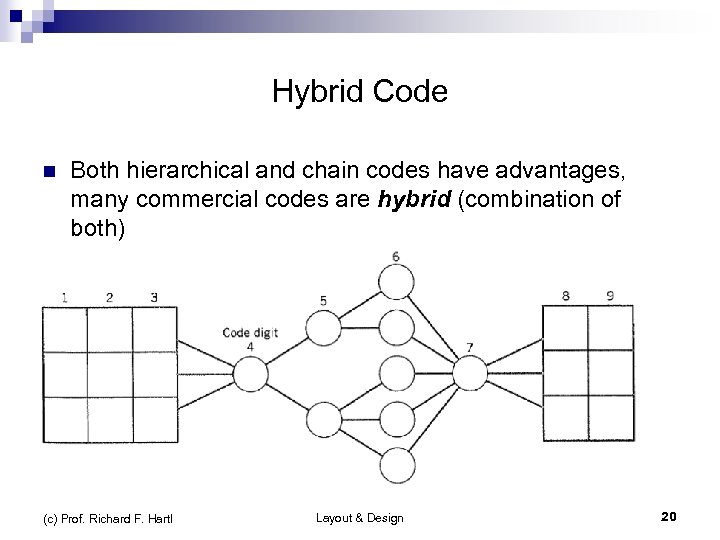Hybrid Code n n Both hierarchical and chain codes have advantages, many commercial codes are hybrid (combination of both) Some section of the code is a chain code and then several hierarchical digits further detail the specified characteristics. Several such sections may exist. One example of a hybrid code is Opitz (c) Prof. Richard F. Hartl Layout & Design 20

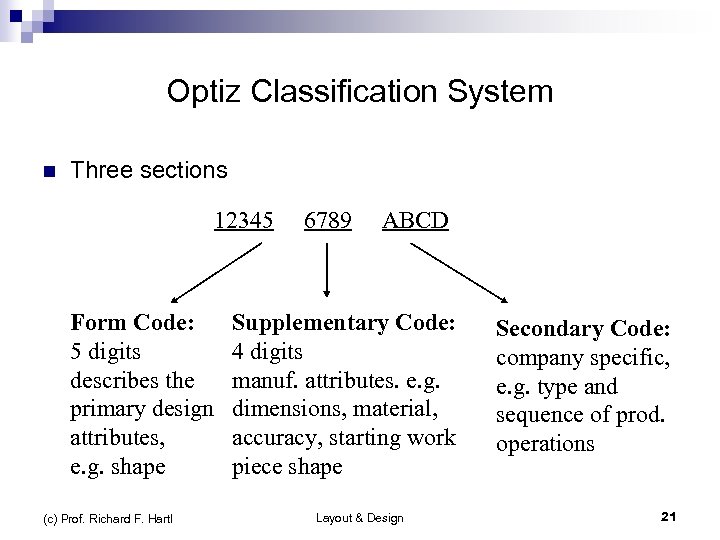Optiz Classification System n Three sections 12345 Form Code: 5 digits describes the primary design attributes, e. g. shape (c) Prof. Richard F. Hartl 6789 ABCD Supplementary Code: 4 digits manuf. attributes. e. g. dimensions, material, accuracy, starting work piece shape Layout & Design Secondary Code: company specific, e. g. type and sequence of prod. operations 21

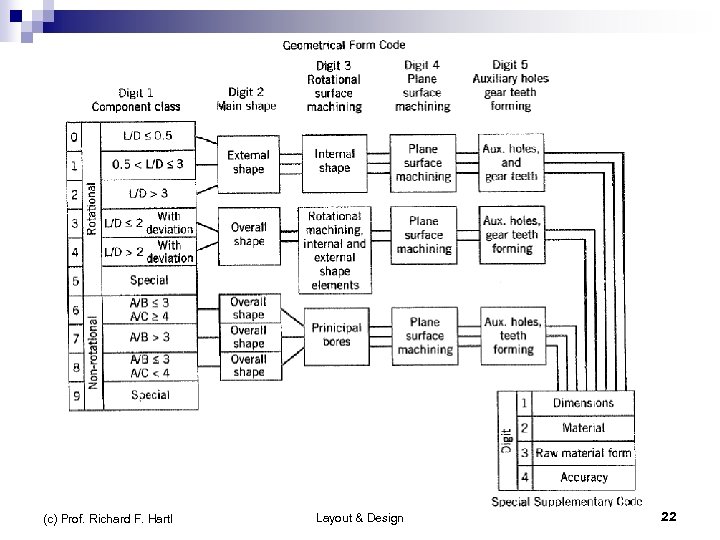Optiz Classification System (c) Prof. Richard F. Hartl Layout & Design 22

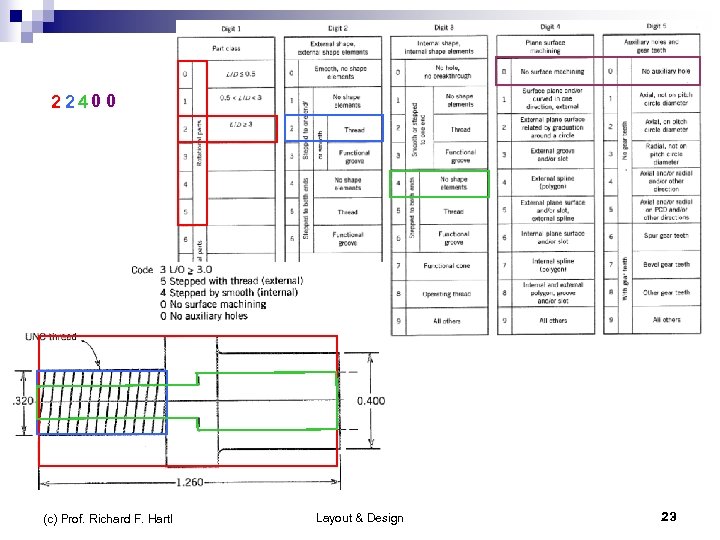2240 0 (c) Prof. Richard F. Hartl Optiz in More Detail Layout & Design 23

Production Flow Analysis (PFA) n n Basic idea: Items that are made with the same processes / the same equipment These parts are assembled into a part family Can be grouped into a cell to minimize material handling requirements. (c) Prof. Richard F. Hartl Layout & Design 25

How to Build Groups/Cells using PFA n n Many clustering methods have been developed Can be classified into: Part family grouping: Form part families and then group machines into cells ¨ Machine grouping: Form machine cells based upon similarities in part routing and then allocate parts to cells ¨ Machine-part grouping: Form part families and machine cells simultaneously. ¨ (c) Prof. Richard F. Hartl Layout & Design 26

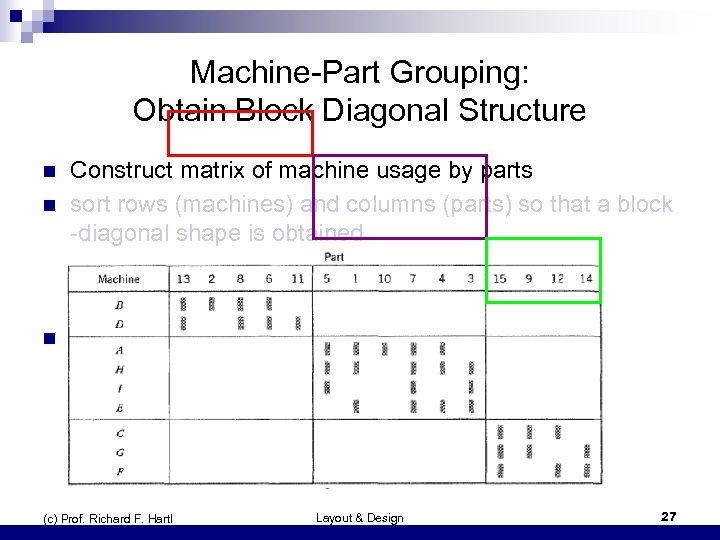Machine-Part Grouping: Obtain Block Diagonal Structure n Construct matrix of machine usage by parts sort rows (machines) and columns (parts) so that a block -diagonal shape is obtained n Then it is easy to build groups: n Group 1: parts {13, 2, 8, 6, 11 }, machines {B, D} ¨ Group 2: parts { 5, 1, 10, 7, 4, 3}, machines {A, H, I, E} ¨ Group 3: parts { 15, 9, 12, 14}, machines {C, G, F} ¨ (c) Prof. Richard F. Hartl Layout & Design 27

King’s Algorithm (Rank Order Clustering) Binary Ordering n n n How to obtain block-diagonal shape? Example: 5 machines; 6 parts: Interpret rows and columns as binary numbers Sort rows w. r. t. decreasing binary numbers Sort columns w. r. t. decreasing binary numbers (c) Prof. Richard F. Hartl part machine 1 2 3 4 5 6 A - 1 - - B 1 - 1 1 C - 1 1 1 - 1 D 1 - - - 1 1 E - - - 1 1 - Layout & Design 28

Binary Ordering § Sort rows w. r. t. decreasing binary numbers part value machine 1 2 3 4 5 6 A - 1 - - B 1 - 1 1 0101002 = 22 + 24 = 20 20 + 21 + 2 3 + 25 = 43 C - 1 1 1 - 1 20 + 22 + 2 3 + 24 = 29 D 1 - - - 1 1 20 + 21 + 2 5 = 35 E - - - 1 1 - 21 + 22 = 6 25 24 23 22 21 32 16 8 4 2 20 1 § New ordering of machines: B – D – C – A - E (c) Prof. Richard F. Hartl Layout & Design 29

Binary Ordering n Sort columns w. r. t. decreasing binary numbers part 6 value 24 = 16 B 1 - 1 1 43 23 = 8 D 1 - - - 1 1 35 22 =4 C - 1 1 1 - 1 29 21 = 2 A - 1 - - 20 20 = 1 E - - - 1 1 - 6 value (c) Prof. Richard F. Hartl Layout & Design 22+23+24=28 5 20+23+24=25 4 20+21+22=7 3 22 + 24 = 20 2 21 + 22 = 6 1 23 + 24 = 24 machine n n New ordering of parts: 6 -5 -1 -3 -4 -2 30

Result of Binary Ordering n No complete block-diagonal structure part machine 5 1 3 4 2 B 1 1 - 1 1 1 - - - C 1 - - 1 1 1 A - - 1 1 E - 1 - 7 6 value n n n - D 6 28 25 24 20 2 groups: Group 1: parts {6, 5, 1 }, machines {B, D} ¨ Group 2: parts { 3, 4, 2}, machines {C, A, E} ¨ n Parts 1, 4, and 2 can be produced in one cell Remaining items: 6, 5, and 3 produced in both cells Or machines B, C, and E have to be duplicated (c) Prof. Richard F. Hartl Layout & Design 31

Repeated Binary Ordering n n Binary Ordering is a simple heuristic no guarantee that „optimal“ ordering is obtained Sometimes a better block-diagonal structure is obtained by repeatingthe Binary Ordering until there is no change anymore (c) Prof. Richard F. Hartl Layout & Design 32

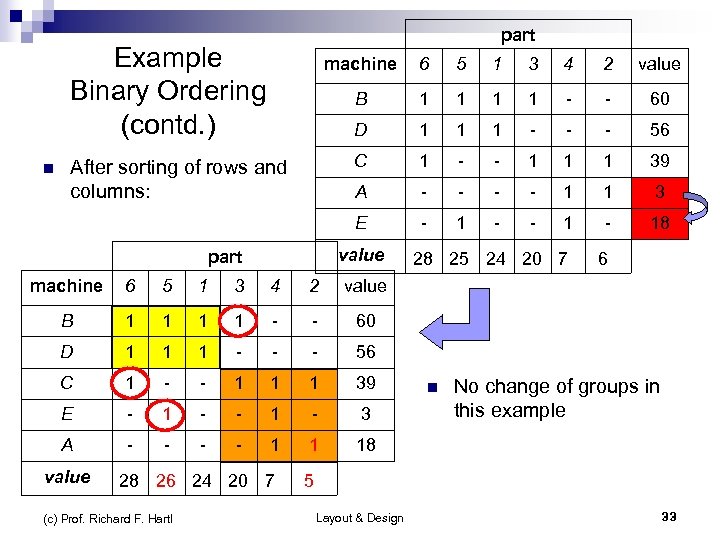part Example Binary Ordering (contd. ) 5 1 3 4 2 value B 1 1 - - 60 D 1 1 1 - - - 56 C 1 - - 1 1 1 39 A After sorting of rows and columns: 6 - - 1 1 3 E n machine - 1 - 18 28 25 24 20 7 6 value part machine 6 5 1 3 4 2 value B 1 1 - - 60 D 1 1 1 - - - 56 C 1 - - 1 1 1 39 E - 1 - 3 A - - 1 1 18 value 28 26 24 20 7 (c) Prof. Richard F. Hartl n No change of groups in this example 5 Layout & Design 33

Single-Pass Heuristic Considering Capacities (Askin and Standridge) extension of simple rule with binary sorting: n All parts must be processed in one cell (machines must be duplicated, if off-diagonal elements in matrix) n All machines have capacities (normalized to be 1) n Constraints on number of identical machines in a group n Constraints on total number of machines in a group (c) Prof. Richard F. Hartl Layout & Design 34

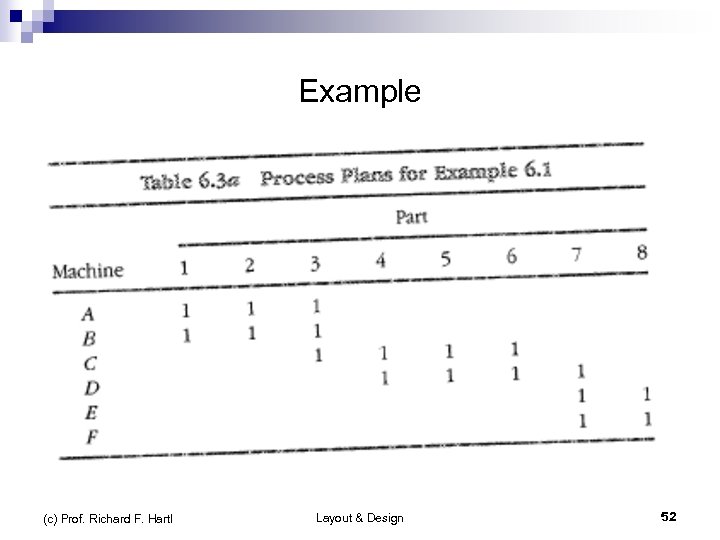
Example Single-Pass Heuristic (Askin and Standridge) n 7 parts, 6 machines Given matrix of processing times (incl. set up times) for typical lot size of parts on machines Entries in matrix not just 0/1 for used/not used) All times as percentage of total machine capacity n At most 4 machines in a group n Not mot than one copy of each machine in each group n n n (c) Prof. Richard F. Hartl Layout & Design 35

Example Single-Pass Heuristic (contd. ) part machine 1 2 3 4 5 6 7 sum min. # machines A 0. 3 - - - 0. 6 - - 0. 9 1 B - 0. 3 - - 0. 1 0. 7 1 C 0. 4 - - 0. 5 - 0. 3 - 1. 2 2 D 0. 2 - 0. 4 - 0. 3 - 0. 5 1. 4 2 E - 0. 4 - - - 0. 5 - 0. 9 1 F - 0. 2 0. 3 0. 4 - - 0. 2 1. 1 2 = 9 machines (c) Prof. Richard F. Hartl Layout & Design 36

Example Single-Pass Heuristic (contd. ) n n n At least 9 machines are needed Not more than 4 machines in a group at least 9/4 = 2, 25 groups, i. e. at least 3 groups Step 1: acquire block diagonal structure e. g. using binary sorting Step 2: build groups (c) Prof. Richard F. Hartl Layout & Design 37

Example - Step 1: Binary Sorting n n For binary sorting treat all entries as 1 s. Result is part machine 1 5 7 3 D 0. 2 0. 3 0. 5 0. 4 C 0. 4 A 0. 3 0. 6 - - - 4 6 2 - - - 0. 5 0. 3 - - F - 0. 2 0. 3 0. 4 - 0. 2 B - - 0. 1 - 0. 3 E (c) Prof. Richard F. Hartl - - - Layout & Design 0. 5 0. 4 solution 38

Step 2: Build Groups n Assign parts to groups (in sorting order) n Necessary machines are also included in group n Add parts to group until either the capacity of some machine would be exceeded, or ¨ the maximum number of machines would be exceeded ¨ (c) Prof. Richard F. Hartl Layout & Design 39

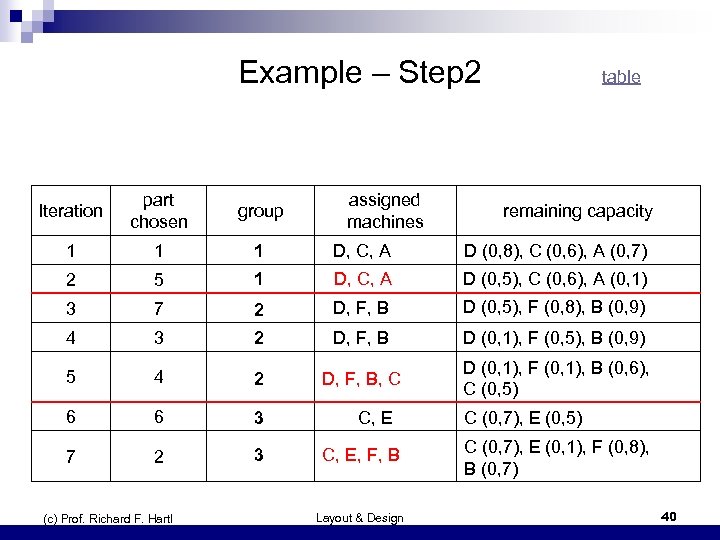Example – Step 2 Iteration part chosen group 1 1 1 D, C, A D (0, 8), C (0, 6), A (0, 7) 2 5 1 D, C, A D (0, 5), C (0, 6), A (0, 1) 3 7 2 D, F, B D (0, 5), F (0, 8), B (0, 9) 4 3 2 D, F, B D (0, 1), F (0, 5), B (0, 9) 5 4 2 D, F, B, C D (0, 1), F (0, 1), B (0, 6), C (0, 5) 6 6 3 7 2 3 (c) Prof. Richard F. Hartl assigned machines table C, E, F, B Layout & Design remaining capacity C (0, 7), E (0, 5) C (0, 7), E (0, 1), F (0, 8), B (0, 7) 40

Results of Example n Machines used: One machine each of types: A, E ¨ Two machines of types: B, D, F ¨ Three machines of type: C ¨ n n Single-pass heuristic of Askin und Standridge is a simple heuristic not necessarily optimal solution (min possible number of machines) Compare result with theoretical min number of machines (c) Prof. Richard F. Hartl Layout & Design 41

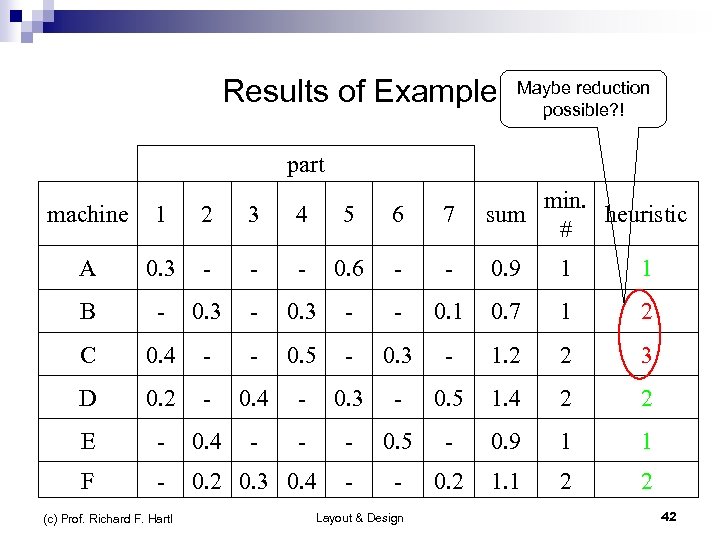Results of Example part Maybe reduction possible? ! machine 1 2 3 4 5 6 7 min. sum heuristic # A 0. 3 - - - 0. 6 - - 0. 9 1 1 B - 0. 3 - - 0. 1 0. 7 1 2 C 0. 4 - - 0. 5 - 0. 3 - 1. 2 2 3 D 0. 2 - 0. 4 - 0. 3 - 0. 5 1. 4 2 2 E - 0. 4 - - - 0. 5 - 0. 9 1 1 F - 0. 2 0. 3 0. 4 - - 0. 2 1. 1 2 2 (c) Prof. Richard F. Hartl Layout & Design 42

LP for min Number of Machines n Minimize total (or weighted) number of machines used when the number of groups is given n Previous example: At least 9 machines necessary ¨ Every group has at most M = 4 machines ¨ at least 3 groups (try 3) ¨ (c) Prof. Richard F. Hartl Layout & Design 43

Given Data ajk . . . capacity of machine k needed for part j i I . . . groups (cells) j J . . . parts k K. . . machines M. . . maximum number of machines per group (c) Prof. Richard F. Hartl Layout & Design 44

Decision Variables = 1, if part j is assigned to group i 0, otherwise 1, if machine of type k is assigned to group i = 0, otherwise (c) Prof. Richard F. Hartl Layout & Design 45

LP objective: constraints: each part must be assigned to one group respect capacity of machine k in group i not more than M machines in group i binary variables (c) Prof. Richard F. Hartl Layout & Design 46

Solution of LP group 1 n n machines B, C, E, F remaining capacity B (0. 4), C (0. 2), E (0. 1), F (0. 4) 2 3 n parts 2, 4, 6 1, 5 3, 7 A, C, D B, D, F A (0. 1), C (0. 6), D (0. 5) B (0. 9), D (0. 1), F (0. 5) Optimal solution with 10 machines Theoretical minimum number was 9 machines (not reached because of constraints) Single pass heuristic used 11 machines (c) Prof. Richard F. Hartl Layout & Design 47

Other Approaches for Clustering n Constructive algorithms for sorting: ¨ n Use similarity coefficients for clustering ¨ n E. g. „direct clustering“ instead of binary sorting Askin Standridge § 6. 4. 4 Group analysis after binary ordering ¨ Askin Standridge § 6. 4. 1 (c) Prof. Richard F. Hartl Layout & Design 48

Clustering using Similarity Coefficients n Define ni . . . Number of parts visiting machine i nij . . . Number of parts visiting machines i and j n Similarity coefficient between machines i and j Proportion of parts visting machine i that also visit machine j (c) Prof. Richard F. Hartl Layout & Design 49

Example for Similarity Coefficients n Machine-part matrix (c) Prof. Richard F. Hartl Layout & Design 50

Group analysis after binary ordering (c) Prof. Richard F. Hartl Layout & Design 51

Example (c) Prof. Richard F. Hartl Layout & Design 52