3 Двоичная восьмеричная шестнадцатеричная системы счисления 1 Системы

3. Двоичная, восьмеричная, шестнадцатеричная системы счисления. 1 Системы счисления Непозиционные Системы счисления, в которых каждой цифре соответствует величина, не зависящая от её места в записи числа Древнегреческая, кириллическая, римская Позиционные Системы счисления, в которых вклад каждой цифры в величину числа зависит от её положения (позиции) в последовательности цифр, изображающей число Десятичная, двоичная и т. д.

Римская нумерация 2 Пример 1. IV – римская 4, но I имеет значение 1, а V – значение 5, VI – римская 6, но I – всё равно 1, а V – всё равно 5 Пример 2. девяносто шесть—XCVI (сто минус десять плюс пять и плюс еще один) и т. д.

Основные понятия позиционных систем 3 Система счисления — совокупность приемов наименования и обозначения чисел с помощью набора символов, называемых цифрами. Количество цифр (знаков), используемых для представления чисел называют основанием системы счисления.

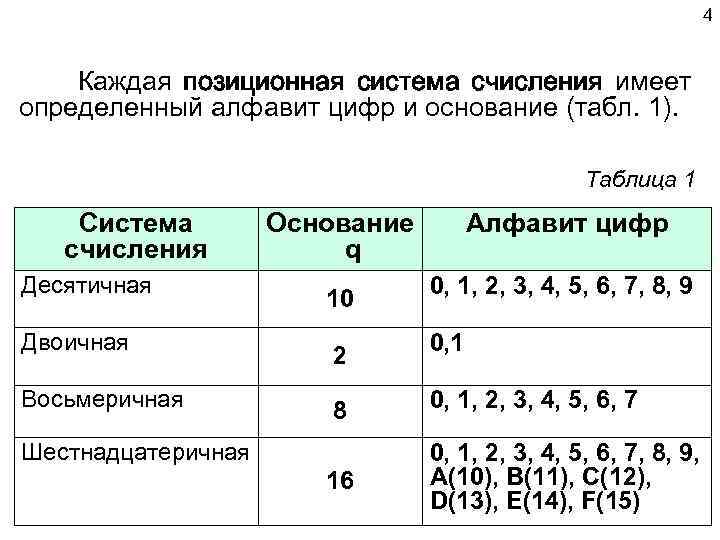4 Каждая позиционная система счисления имеет определенный алфавит цифр и основание (табл. 1). Таблица 1 Система счисления Десятичная Двоичная Восьмеричная Основание q 10 2 Алфавит цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1 8 0, 1, 2, 3, 4, 5, 6, 7 16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A(10), B(11), C(12), D(13), E(14), F(15) Шестнадцатеричная

22 Способы перевода чисел из одной системы счисления в другую

Развернутая форма числа в десятичной системе ai — цифры системы счисления q — основание системы счисления n — число целых разрядов m — число дробных разрядов

Перевод целых чисел из десятичной системы счисления в q-ичную 1) разделить целое число на основание новой системы счисления q, записать частное от деления и остаток; 2) затем полученное частное снова разделить на q и записать частное и остаток; и так делить до тех пор, пока в частном не получится ноль; 3) составить число в новой системе счисления, записав полученные остатки в обратном порядке.

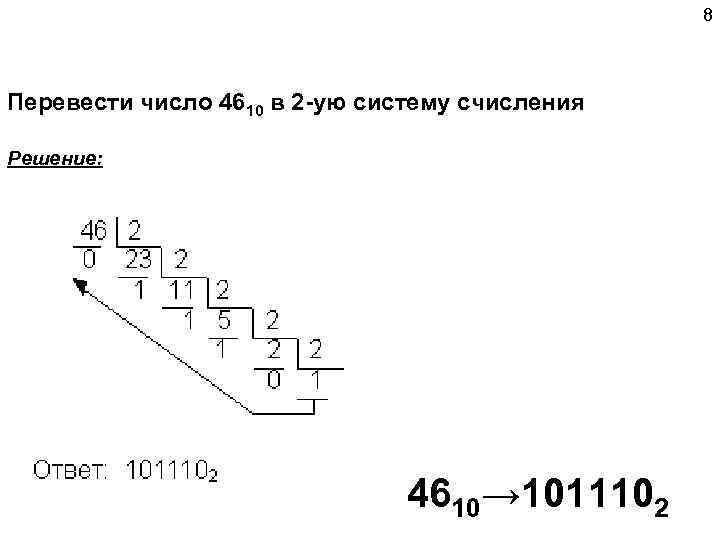8 Перевести число 4610 в 2 -ую систему счисления Решение: 4610→ 1011102

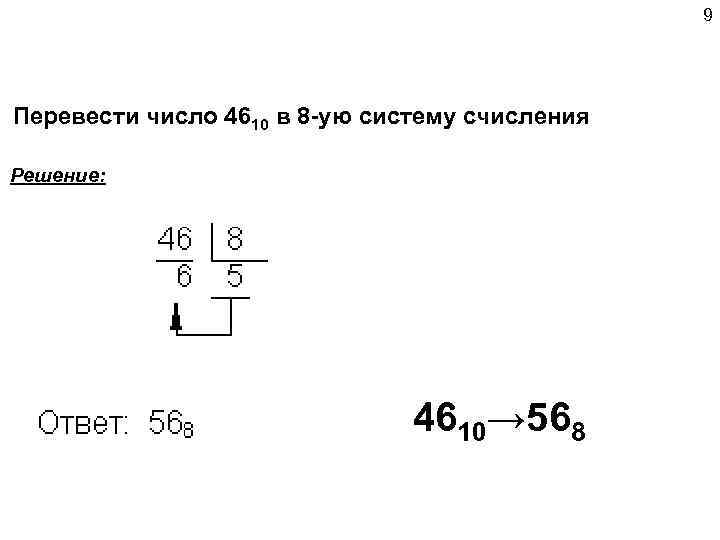9 Перевести число 4610 в 8 -ую систему счисления Решение: 4610→ 568

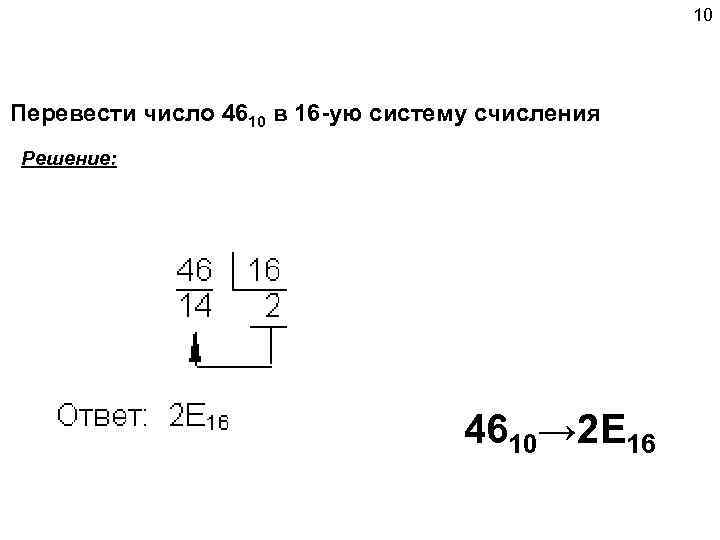10 Перевести число 4610 в 16 -ую систему счисления Решение: 4610→ 2 E 16

Округление В процессе перевода следует вычислять на одну цифру больше, а затем, применяя правила округления, сокращать эту цифру. Выполняя округление, нужно соблюдать следующее правило: если первая отбрасываемая цифра больше или равна n/2 (n — основание системы), то к сохраняемому младшему разряду числа прибавляется единица. Например, округление восьмеричного числа 32, 324718 до одного знака после запятой даст в результате 32, 3; округление до двух знаков после запятой — 32, 33.

Перевод чисел из q-ичной системы счисления в десятичную 12 1) пронумеровать каждую цифру q-ичного числа следующим образом: целую часть нумеруем, начиная с 0, справа налево в сторону увеличения, а дробную часть, начиная с – 1, слева направо в сторону уменьшения; 2) каждую цифру q-ичного числа умножить на основание системы счисления q в соответствующей степени; 3) выполнить арифметические действия.

13 Перевести число 1011102 в 10 -ю систему счисления Решение: 1011102→ 4610

14 Перевести число 568 в 10 -ю систему счисления Решение: 568→ 4610

15 Перевести число 2 E 16 в 10 -ю систему счисления Решение: 2 E 16→ 4610

Перевод чисел из 2 -ичной системы счисления в 2 n-ичную Таблица 2 Двоично-восьмеричная таблица 16

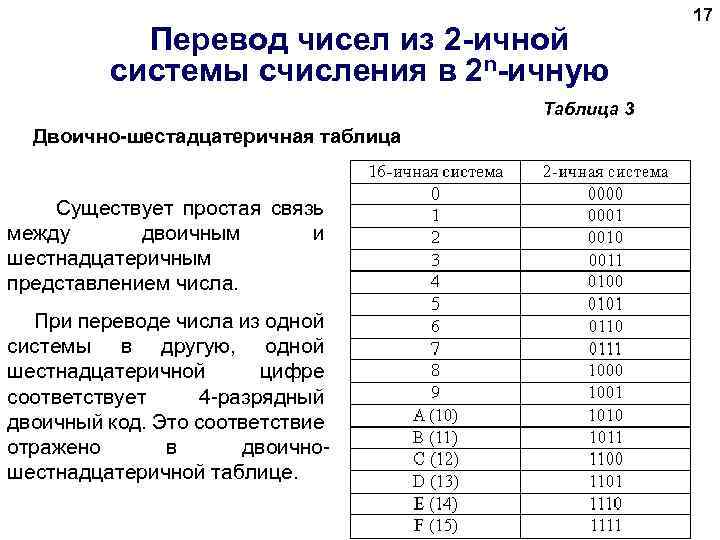Перевод чисел из 2 -ичной системы счисления в 2 n-ичную Таблица 3 Двоично-шестадцатеричная таблица Существует простая связь между двоичным и шестнадцатеричным представлением числа. При переводе числа из одной системы в другую, одной шестнадцатеричной цифре соответствует 4 -разрядный двоичный код. Это соответствие отражено в двоичношестнадцатеричной таблице. 17

Перевод чисел из 2 -ичной системы счисления в 2 n-ичную 18 1) разбить исходное число на группы по n цифр в каждой (целая часть – налево, дробная часть - направо), дописав слева и справа нужное количество нулей; 2) перевести каждую группу в систему счисления с основанием 2 n (см. табл. 2 и 3).

19 Перевести число 1011102 в 8 -ую систему счисления 8=23 выделить триаду в записи двоичного числа Решение: заменить каждую группу соответствующим восьмеричным числом 1011102→ 568

20 Перевести число 1011102 в 16 -ую систему счисления 16=24 выделить тетраду в записи двоичного числа Решение: заменить каждую группу соответствующим шестнадцатеричным числом 1011102→ 2 E 16

Перевод чисел из 2 n-ичной системы счисления в двоичную Обратный переход из системы счисления с основанием 2 n осуществляется заменой каждой цифры исходного числа соответствующим nразрядным двоичным числом. Для перевода в 8 -ичную и 16 -ичную систему счисления используйте таблицу, рассмотренную ранее (см. табл. 3). 21

22 Перевести число 568 в 2 -ую систему счисления Решение: 568→ 1011102

23 Перевести число 2 E 16 в 2 -ую систему счисления Решение: 2 E 16→ 101110 2

24 Перевод чисел из 8 -й системы счисления в 16 -ую Перевести число 568 в 16 -ую систему счисления Решение: N 8= триада в записи 2 -го числа тетрада в записи 2 -го числа 568→ 2 E 16