3 D reconstruction Class 16 3 D

3 D reconstruction Class 16

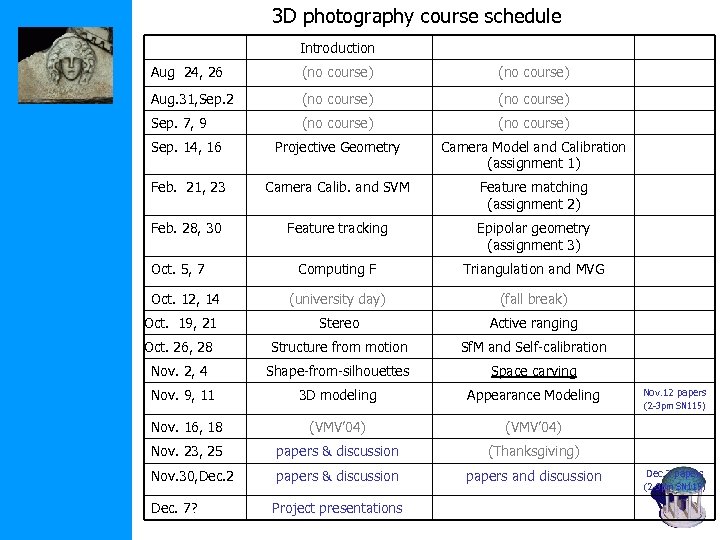3 D photography course schedule Introduction Aug 24, 26 (no course) Aug. 31, Sep. 2 (no course) Sep. 7, 9 (no course) Sep. 14, 16 Projective Geometry Camera Model and Calibration (assignment 1) Feb. 21, 23 Camera Calib. and SVM Feature matching (assignment 2) Feb. 28, 30 Feature tracking Epipolar geometry (assignment 3) Computing F Triangulation and MVG (university day) (fall break) Oct. 19, 21 Stereo Active ranging Oct. 26, 28 Structure from motion Sf. M and Self-calibration Nov. 2, 4 Shape-from-silhouettes Space carving Nov. 9, 11 3 D modeling Appearance Modeling Nov. 16, 18 (VMV’ 04) Nov. 23, 25 papers & discussion (Thanksgiving) Nov. 30, Dec. 2 papers & discussion papers and discussion Dec. 7? Project presentations Oct. 5, 7 Oct. 12, 14 Nov. 12 papers (2 -3 pm SN 115) Dec. 3 papers (2 -3 pm SN 115)

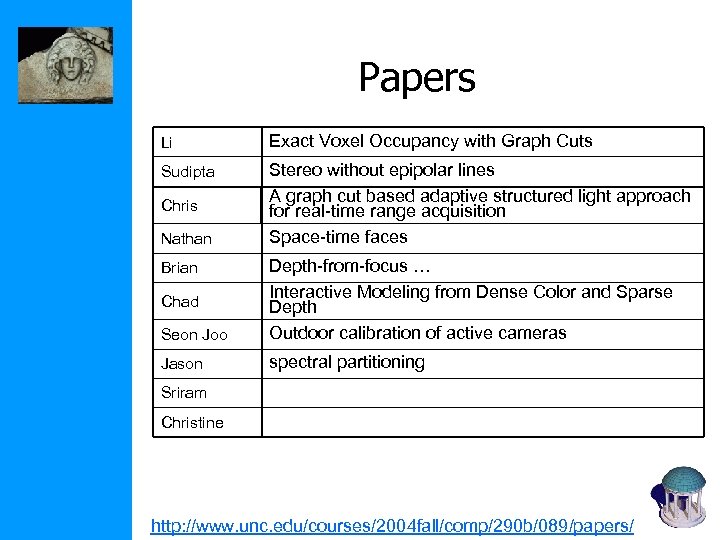Papers Li Exact Voxel Occupancy with Graph Cuts Sudipta Stereo without epipolar lines A graph cut based adaptive structured light approach for real-time range acquisition Space-time faces Chris Nathan Seon Joo Depth-from-focus … Interactive Modeling from Dense Color and Sparse Depth Outdoor calibration of active cameras Jason spectral partitioning Brian Chad Sriram Christine http: //www. unc. edu/courses/2004 fall/comp/290 b/089/papers/

Ideas for a project? Chris Wide-area display reconstruction Nathan ? Brian Depth-from-focus/defocus Li Visual-hulls with occlusions Chad Laser scanner for 3 D environments Seon Joo Collaborative 3 D tracking Jason Sf. M for long sequences Sudipta Combining exact silhouettes and photoconsistency Sriram Panoramic cameras self-calibration Christine desktop lamp scanner

3 D modeling • Aligning range images • Pairwise • Globally • Surface reconstruction • Single range image • Merged (some slides from S. Rusinkiewicz, J. Ponce, …)

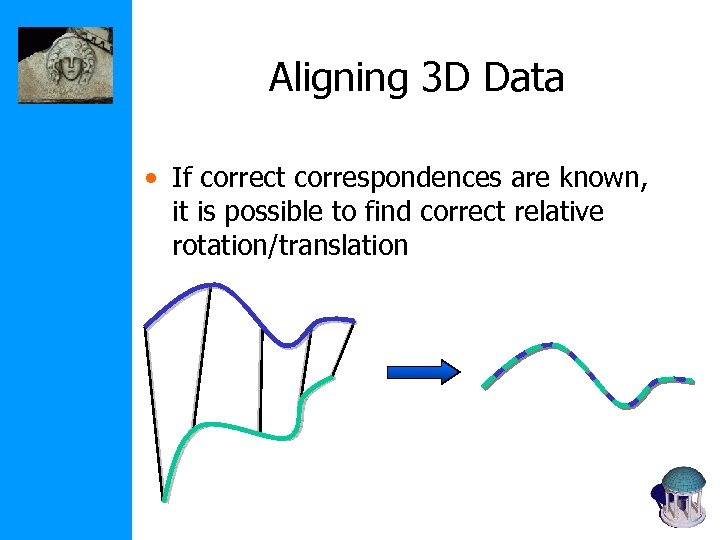Aligning 3 D Data • If correct correspondences are known, it is possible to find correct relative rotation/translation

Intermezzo: quaternions q = a+ q is a quaternion, a 2 R is its real part, and 2 R 3 is its imaginary part. Operations on quaternions: • Sum of quaternions: • Multiplication by a scalar: • Quaternion product: • Conjugate: ) • Norm: Note:

Intermezzo: quaternions and rotations Let R denote the rotation of angle about the unit vector u. Define Then for any vector , Reciprocally, if q = a + ( b, c, d )T is a unit quaternion, the corresponding rotation matrix is:

Estimate rigid transformation Problem: Find the rotation matrix R and the vector t that minimize n E = | xi’ – R xi – t |2. i=1 n At a minimum: 0 = E/ t = – 2 ( xi’ – R xi – t ). Or. . t = x’ – R x. i=1 If yi = xi –x and yi’ = xi’ –x’, the error is (at a minimum): n E = | y i’ – R y i i=1 |2 n = | y i’ – q y i i=1 Or E = Linear least squares !! q|2|q|2 n = | y i ’ q – q y i |2 i=1

Aligning 3 D Data • How to find corresponding points? • Previous systems based on user input, feature matching, surface signatures, etc.

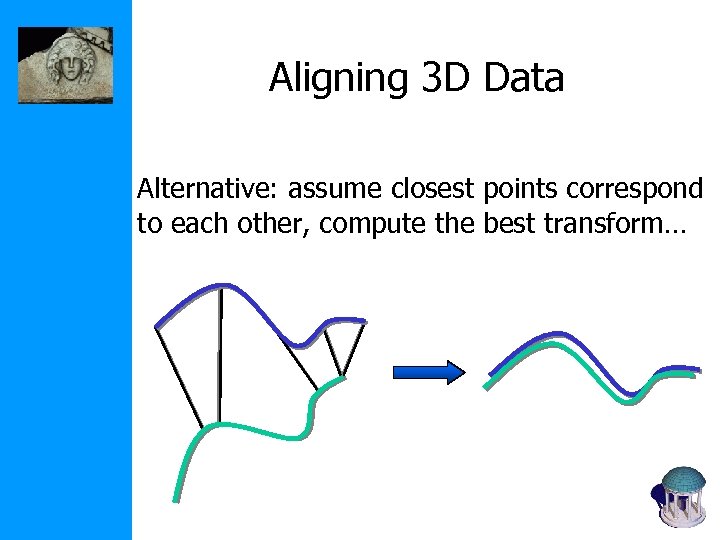Aligning 3 D Data Alternative: assume closest points correspond to each other, compute the best transform…

Aligning 3 D Data … and iterate to find alignment Iterated Closest Points (ICP) [Besl & Mc. Kay 92] Converges if starting position “close enough“

ICP Variants • Classic ICP algorithm not real-time • To improve speed: examine stages of ICP and evaluate proposed variants 1. 2. 3. 4. 5. 6. Selecting source points (from one or both meshes) Matching to points in the other mesh Weighting the correspondences Rejecting certain (outlier) point pairs Assigning an error metric to the current transform Minimizing the error metric [Rusinkiewicz & Levoy, 3 DIM 2001]

ICP Variant – Point-to-Plane Error Metric • Using point-to-plane distance instead of point-topoint lets flat regions slide along each other more easily [Chen & Medioni 91]

Finding Corresponding Points • Finding closest point is most expensive stage of ICP • Brute force search – O(n) • Spatial data structure (e. g. , k-d tree) – O(log n) • Voxel grid – O(1), but large constant, slow preprocessing

Finding Corresponding Points • For range images, simply project point [Blais 95] • Constant-time, fast • Does not require precomputing a spatial data structure

High-Speed ICP Algorithm • ICP algorithm with projection-based correspondences, point-to-plane matching can align meshes in a few tens of ms. (cf. over 1 sec. with closest-point) [Rusinkiewicz & Levoy, 3 DIM 2001]

3 D Global Registration

3 D Global registration The problem: • Given: n scans around an object • Goal: align them all • First attempt: ICP each scan to one other

3 D Global registration • Want method for distributing accumulated error among all scans

Approach #1: Avoid the Problem • In some cases have 1 scan that covers large part of surface (e. g. , cylindrical scan) • Align all other scans to this “anchor” • Disadvantage: not always practical to obtain anchor scan

Approach #2: The Greedy Solution • Align each new scan to all previous scans • Disadvantages: • Order dependent • Doesn’t spread out error

Approach #3: Brute-Force Solution • While not converged: • For each scan: • For each point: – For every other scan » Find closest point • Minimize error w. r. t. transforms of all scans • Disadvantage: • Solve (np) matrix equation, where n is number of scans and p is number of points per scan

Approach #3 a: Slightly Less Brute. Force • While not converged: • For each scan: • For each point: – For every other scan » Find closest point • Minimize error w. r. t. transform of this scan • Faster than previous method (matrices are p p)

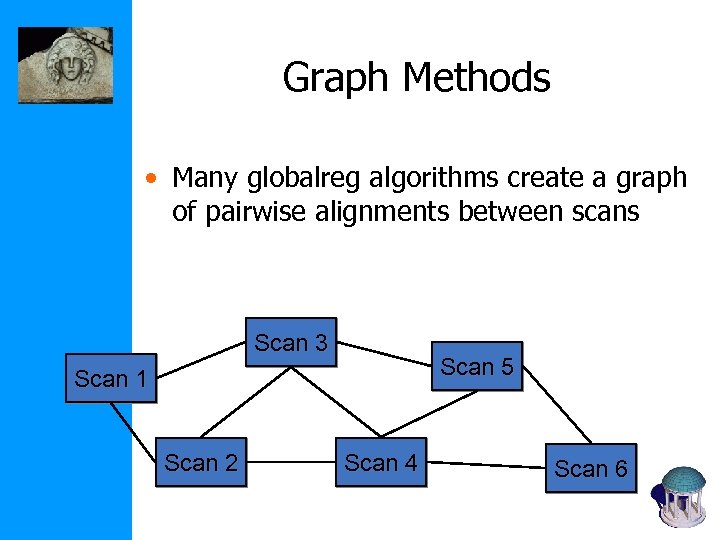Graph Methods • Many globalreg algorithms create a graph of pairwise alignments between scans Scan 3 Scan 5 Scan 1 Scan 2 Scan 4 Scan 6

Pulli’s Algorithm • Perform pairwise ICPs, record sample (e. g. 200) of corresponding points • For each scan, starting w. most connected • Align scan to existing set • While (change in error) > threshold • Align each scan to others • All alignments during globalreg phase use precomputed corresponding points

Sharp et al. Algorithm • Perform pairwise ICPs, record only optimal rotation/translation for each • Decompose alignment graph into cycles • While (change in error) > tolerance • For each cycle: • Spread out error equally among all scans in the cycle • For each scan belonging to more than 1 cycle: • Assign average transform to scan

Lu and Milios Algorithm • Perform pairwise ICPs, record optimal rotation/translation and covariance for each • Least squares simultaneous minimization of all errors (covariance-weighted) • Requires linearization of rotations • Worse than the ICP case, since don’t converge to (incremental rotation) = 0

Open Questions in Global Registration • Best way to do correctly-weighted globalreg without linearizing rotations? • How to prevent bias (if many scans in one area, few scans in another)? • Robust outlier detection • For graph methods, pairwise ICP often automated • One bad ICP can throw off the entire model

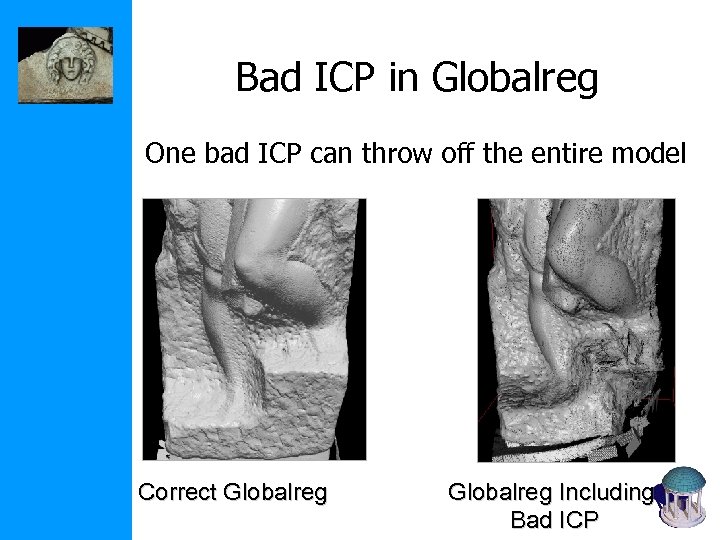Bad ICP in Globalreg One bad ICP can throw off the entire model Correct Globalreg Including Bad ICP

Huber’s Automatic Modeling System • Start with unaligned cans • Generate candidate pairwise alignments using spin images • Incrementally add scans, checking consistency • ICP error in overlapping regions • Free space consistency • Occupied space consistency

Spin Images • Johnson and Hebert • “Signature” that captures local shape • Similar shapes similar spin images

Computing Spin Images • Start with a point on a 3 D model • Find (averaged) surface normal at that point • Define coordinate system centered at this point, oriented according to surface normal and two (arbitrary) tangents • Express other points (within some distance) in terms of the new coordinates

Computing Spin Images • Compute histogram of locations of other points, in new coordinate system, ignoring rotation around normal:

Computing Spin Images

Spin Image Parameters • Size of neighborhood • Determines whether local or global shape is captured • Big neighborhood: more discriminatory power • Small neighborhood: resistance to clutter • Size of bins in histogram: • Big bins: less sensitive to noise • Small bins: captures more detail, less storage

Using Spin Images for Alignment Not robust

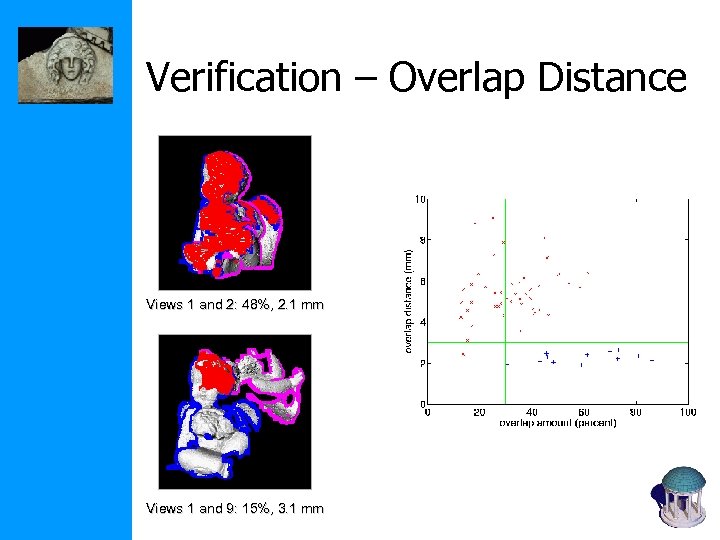Verification – Overlap Distance Views 1 and 2: 48%, 2. 1 mm Views 1 and 9: 15%, 3. 1 mm

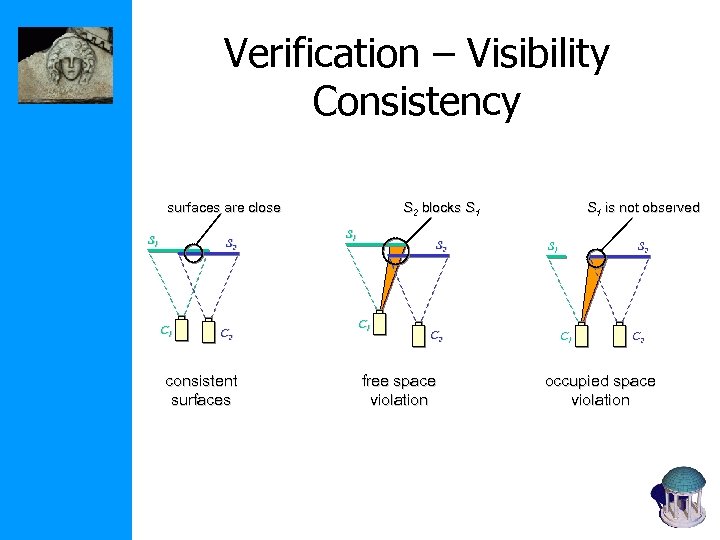Verification – Visibility Consistency surfaces are close S 1 S 2 C 1 C 2 consistent surfaces S 2 blocks S 1 S 2 C 1 C 2 free space violation S 1 is not observed S 1 S 2 C 1 C 2 occupied space violation

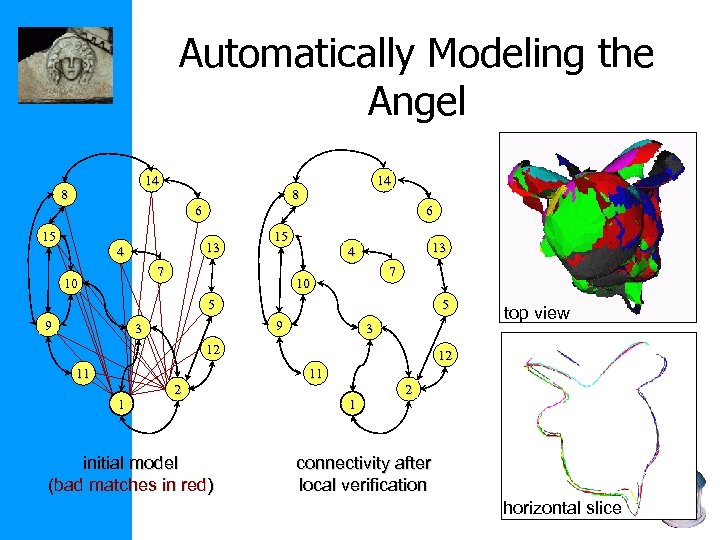Automatically Modeling the Angel 14 8 6 15 13 4 6 15 7 10 14 8 13 4 7 10 5 9 3 3 12 11 1 2 initial model (bad matches in red) top view 12 11 1 2 connectivity after local verification horizontal slice

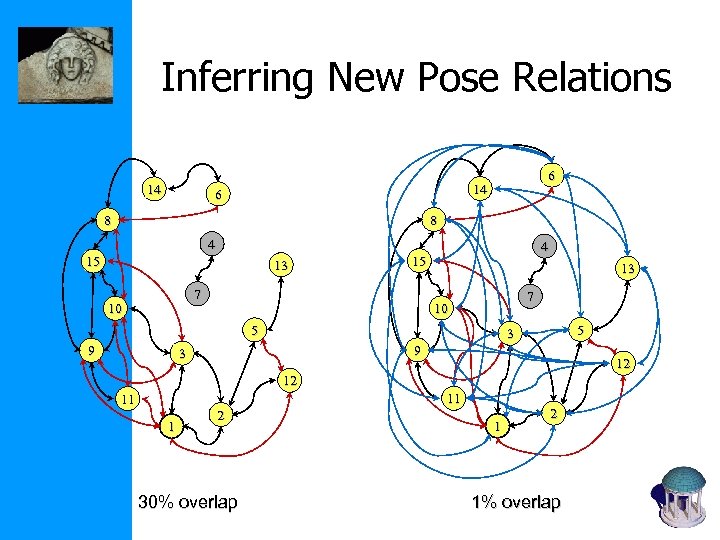Inferring New Pose Relations 14 6 8 8 4 15 13 15 7 10 4 13 7 10 5 9 5 3 9 3 12 12 11 11 1 2 30% overlap 1 2 1% overlap

The Final Angel Model top view horizontal slice

Problems With Reconstruction from Point Clouds

Surface Reconstruction from Range Images • Often an easier problem than reconstruction from arbitrary point clouds • Implicit information about adjacency, connectivity • Roughly uniform spacing

Surface Reconstruction From Range Images • First, construct surface from each range image • Then, merge resulting surfaces • Obtain average surface in overlapping regions • Control point density

Range Image Tesselation • Given a range image, connect up the neighbors

3 D surface model Depth image Triangle mesh Texture image Textured 3 D Wireframe model

Range Image Tesselation • Caveat #1: can’t be too aggressive • Introduce distance threshold for tesselation

Range Image Tesselation • Caveat #2: Which way to triangulate? • Possible heuristics: • • Shorter diagonal Dihedral angle closer to 180 Maximize smallest angle in both triangles Always the same way (best triangle strips)

Scan Merging Using Zippering • • Turk & Levoy, 1994 Erode geometry in overlapping areas Stitch scans together along seam Re-introduce all data • Weighted average

Zippering

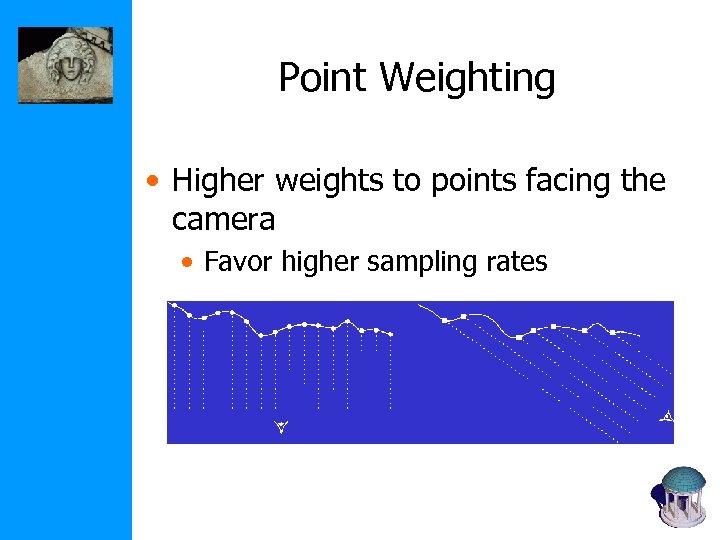Point Weighting • Higher weights to points facing the camera • Favor higher sampling rates

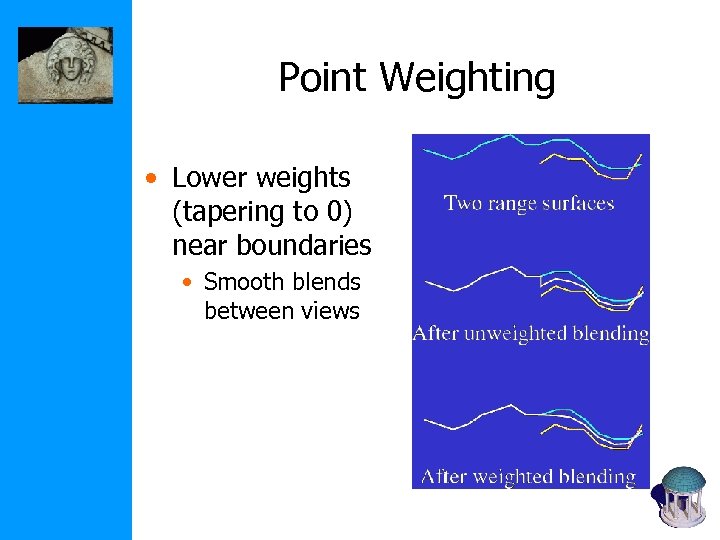Point Weighting • Lower weights (tapering to 0) near boundaries • Smooth blends between views

Volumetric Reconstruction • Implicit function defined volumetrically • Usually stored sampled on a 3 D grid • Can be compressed (e. g. , using RLE) • Another possibility: hierarchical data structures • Can extract isosurface (i. e. , subset of space where implicit function = some constant)

Volumetric Reconstruction Overview • Generate signed distance function (or something close to it) for each scan • Compute average (possibly weighted) • Extract isosurface

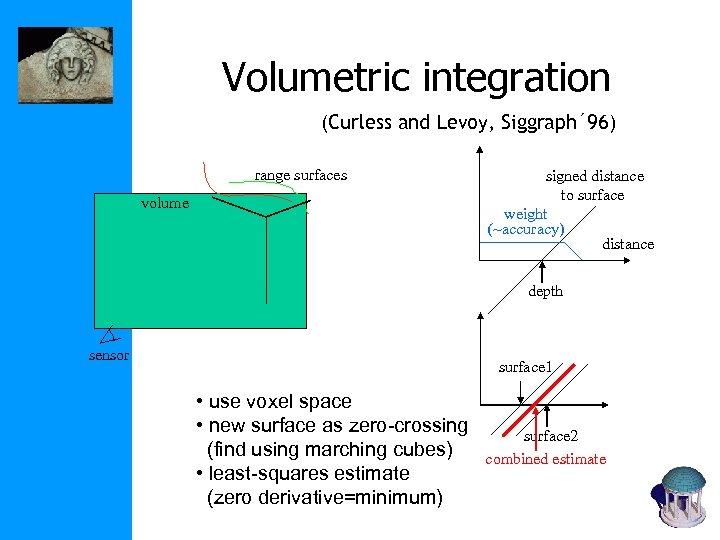Volumetric integration (Curless and Levoy, Siggraph´ 96) range surfaces volume signed distance to surface weight (~accuracy) distance depth sensor surface 1 • use voxel space • new surface as zero-crossing (find using marching cubes) • least-squares estimate (zero derivative=minimum) surface 2 combined estimate

Volumetric Reconstruction Benefits • Always generates a manifold surface • Can control sampling density • Averaging of signed distance functions corresponds to averaging the surfaces

Volumetric Reconstruction Drawbacks • Represent a 3 D entity rather than 2 D • Running time • Storage • Resampling step – bandlimits the function • Generates consistent topology, but not always the topology you wanted • Problems with very thin surfaces

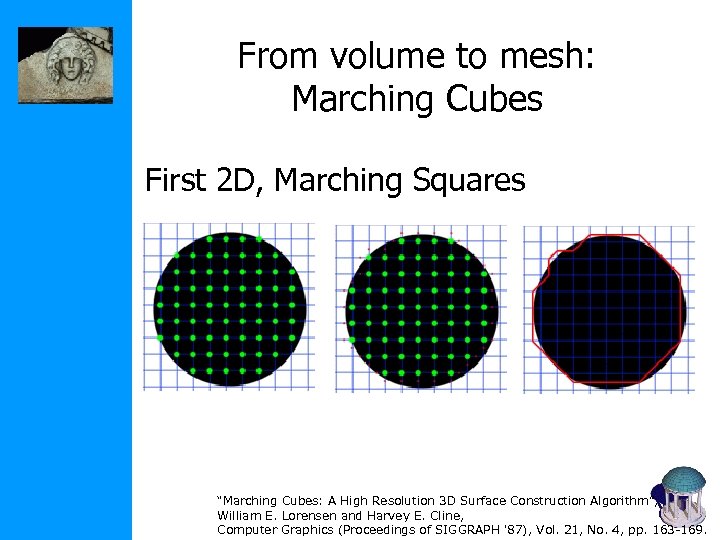From volume to mesh: Marching Cubes First 2 D, Marching Squares “Marching Cubes: A High Resolution 3 D Surface Construction Algorithm”, William E. Lorensen and Harvey E. Cline, Computer Graphics (Proceedings of SIGGRAPH '87), Vol. 21, No. 4, pp. 163 -169.

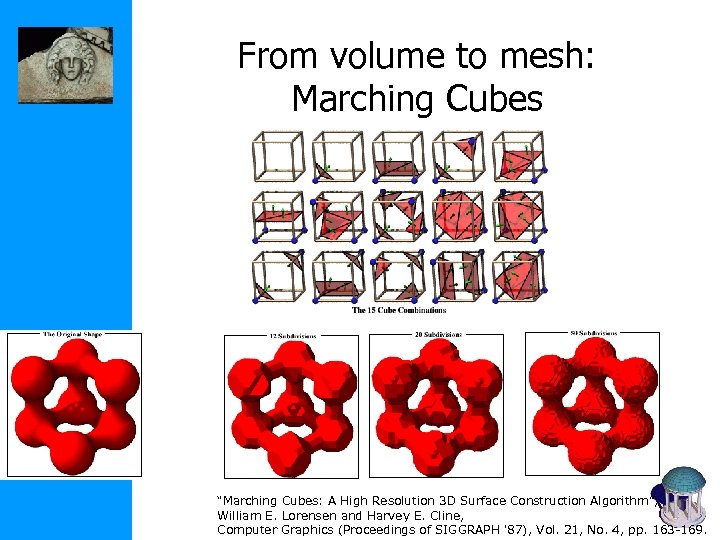From volume to mesh: Marching Cubes “Marching Cubes: A High Resolution 3 D Surface Construction Algorithm”, William E. Lorensen and Harvey E. Cline, Computer Graphics (Proceedings of SIGGRAPH '87), Vol. 21, No. 4, pp. 163 -169.

From volume to mesh: Marching Cubes Improvement “Marching Cubes: A High Resolution 3 D Surface Construction Algorithm”, William E. Lorensen and Harvey E. Cline, Computer Graphics (Proceedings of SIGGRAPH '87), Vol. 21, No. 4, pp. 163 -169.

Volumetric 3 D integration Multiple depth images Volumetric integration

Next class: appearance modeling