3 D Long-Wave Oscillatory Patterns in Thermocapillary Convection

3 D Long-Wave Oscillatory Patterns in Thermocapillary Convection with Soret Effect A. Nepomnyashchy, A. Oron Technion, Haifa, Israel, and S. Shklyaev, Technion, Haifa, Israel, Perm State University, Russia

This work is supported by the Israel Science Foundation I am grateful to Isaac Newton Institute for the invitation and for the financial support 2

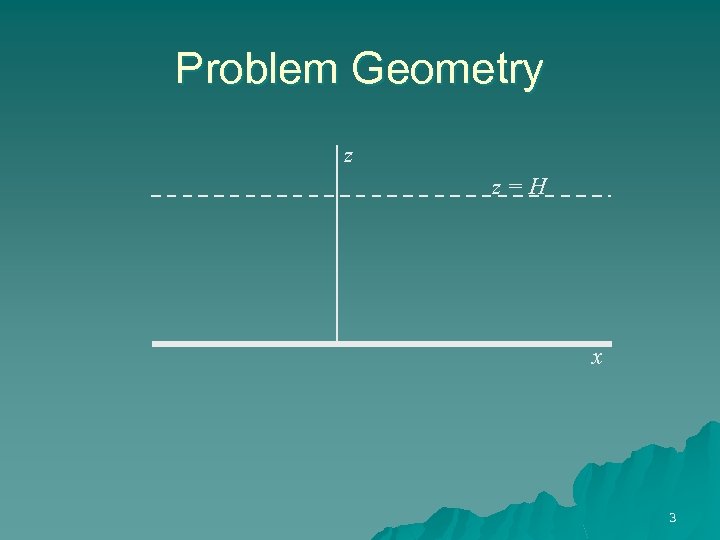Problem Geometry z z=H x 3

Previous results Linear stability analysis Pure liquid: • J. R. A. Pearson, JFM (1958); • S. H. Davis, Annu. Rev. Fluid Mech. (1987). Double-diffusive Marangoni convection: • J. L. Castillo and M. G. Velarde, JFM (1982); • C. L. Mc. Taggart, JFM (1983). Linear stability problem with Soret effect: • C. F. Chen, C. C. Chen, Phys. Fluids (1994); • J. R. L. Skarda, D. Jackmin, and F. E. Mc. Caughan, JFM (1998). 4

Nonlinear analysis of long-wave perturbations Marangoni convection in pure liquids: • E. Knobloch, Physica D (1990); • A. A. Golovin, A. A. Nepomnyashchy, nd L. M. Pismen, Physica D (1995); Marangoni convection in solutions: • L. Braverman, A. Oron, J. Eng. Math. (1997); • A. Oron and A. A. Nepomnyashchy, Phys. Rev. E (2004). Oscillatory mode in Rayleigh-Benard convection • L. M. Pismen, Phys. Rev. A (1988). 5

Basic assumptions Gravity is negligible; u Free surface is nondeformable; u Surface tension linearly depends on both the temperature and the concentration: u u Soret effect plays an important role: The heat flux is fixed at the rigid plate; u The Newton law of cooling governs the heat transfer at the free surface: u 6

Governing equations 7

Boundary conditions At the rigid wall: At the interface: Here is the differential operator in plane x-y 8

Dimensionless parameters u The Prandtl number u The Schmidt number u The Soret number u The Marangoni number u The Biot number u The Lewis number 9

Basic state There exist the equilibrium state corresponding to the linear temperature and concentration distribution: 10

Equation for perturbations P, Q, S are the perturbations of the pressure, the temperature and the concentration, respectively; here and below 11

Previous results Linear and nonlinear stability analysis of above conductive state with respect to long-wave perturbations was carried out by A. Oron and A. Nepomnyashchy (PRE, 2004): Linear stability problem was studied; u Monotonous mode was found and weakly nonlinear analysis was performed; u Oscillatory mode was revealed; u The set of amplitude equations to study 2 D oscillatory convective motion was obtained. u 12

Multi-scale expansion for the analysis of long wave perturbations Rescaled coordinates: Rescaled components of the velocity: “Slow” times : 13

Multi-scale expansion for the analysis of long wave perturbations Small Biot number: Expansion with respect to e: 14

The zeroth order solution Z X 15

The second order The solvability conditions: The plane wave solution: 16

The second order Critical Marangoni number: The dispersion relation: The solution of the second order: 17

The fourth order The solvability conditions: 18

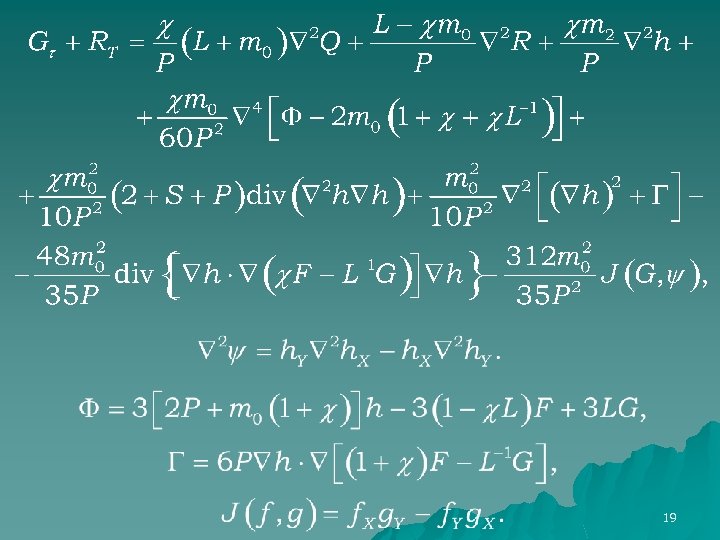19

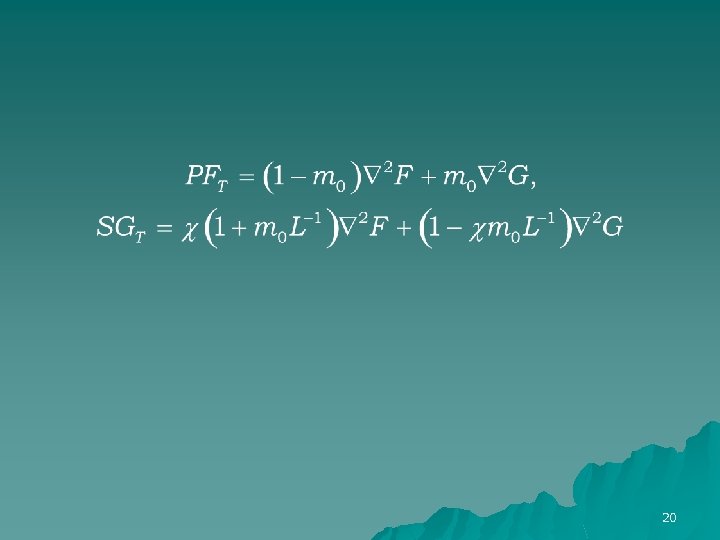20

Linear stability analysis Oron, Nepomnyashchy, PRE, 2004 Neutral curve for 21

2 D regimes. Bifurcation analysis Oron, Nepomnyashchy, PRE, 2004 Interaction of two plane waves Solvability conditions: Here i. e. in 2 D case traveling waves are selected, standing waves are unstable 22

2 D regimes. Numerical results Solvability condition leads to the dynamic system for only if the resonant conditions are held: 23

Numerical simulations show, that system evolve to traveling wave index l depends on the initial conditions Stability region for simple traveling wave Plane wave with fixed k exists above white line and it is stable with respect to 2 D perturbations above green line 24

3 D-patterns. Bifurcation analysis Interaction of two plane waves Y X For the simplicity we set 25

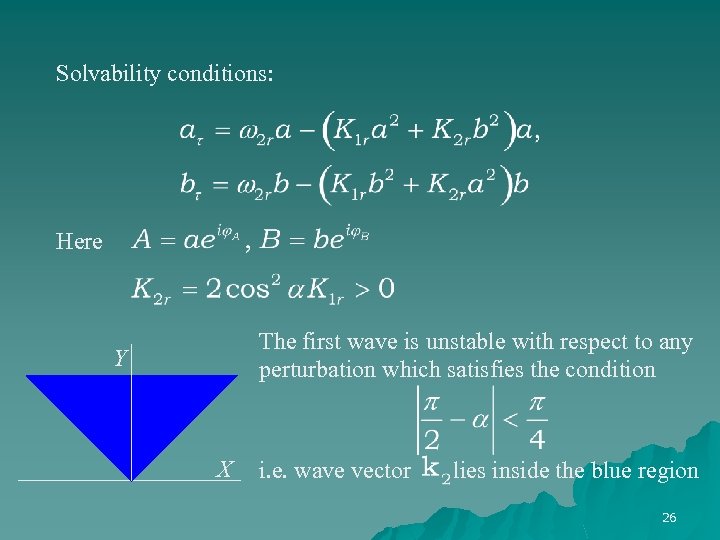Solvability conditions: Here The first wave is unstable with respect to any perturbation which satisfies the condition Y X i. e. wave vector lies inside the blue region 26

“Three-mode” solution Y X The solvability conditions gives the set of 4 ODEs for 27

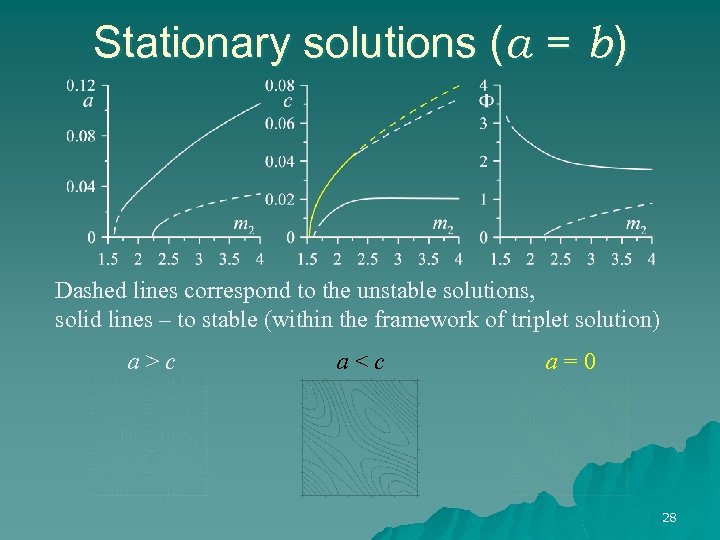Stationary solutions (a = b) Dashed lines correspond to the unstable solutions, solid lines – to stable (within the framework of triplet solution) a>c a

Numerical results The solvability condition gives the dynamic system for only if the resonant conditions are held: 29

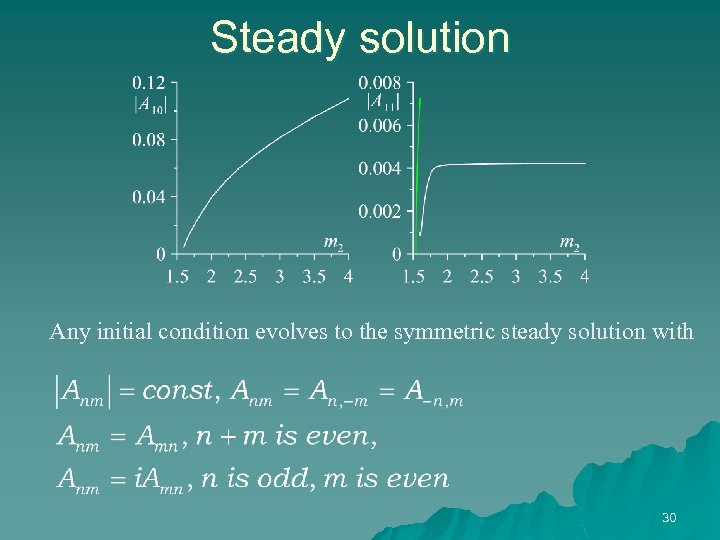Steady solution Any initial condition evolves to the symmetric steady solution with 30

Evolution of h in T 31

Conclusions u 2 D oscillatory long-wave convection is studied numerically. It is shown, that plane wave is realized after some evolution; u The set of equations describing the 3 D long-wave oscillatory convection is obtained; u The instability of a plane wave solution with respect to 3 D perturbations is demonstrated; u The simplest 3 D structure (triplet) is studied; u The numerical solution of the problem shows that 3 D standing wave is realized; u The harmonics with critical wave number are the dominant ones. 32

Thank you for the attention!