Отдел_Корней_Алгебр_Трансц_Уравн.ppt
- Количество слайдов: 27

3. Численные методы 3. 1. Решение алгебраических и трансцендентных уравнений 3. 1. 1. Отделение корней уравнений

3. 1. 1. 1 Отделение корней алгебраических уравнений В общем виде алгебраическое уравнение с одним неизвестным имеет вид: ( 3. 1 ) o Отделение корней – определение числового интервала, содержащего только один корень уравнения (3. 1). o Уточнение значения корня – процедура сужения границ найденного интервала с целью определения значения корня уравнения (3. 1) с любой наперед заданной точностью e.

3. 1. 1. 1 Отделение корней алгебраических уравнений Для алгебраического уравнения (3. 1) с действительными коэффициентами верхняя граница положительных корней определяется по формуле Лагранжа где k≥ 1 – номер (индекс) первого из отрицательных коэффициентов уравнения (3. 1); В = |-аi|max – наибольшее из абсолютных значений отрицательных коэффициентов уравнения (3. 1). Нижнюю границу положительных действительных корней определяют из вспомогательного уравнения: ( 3. 2 )

3. 1. 1. 1 Отделение корней алгебраических уравнений o Итак, положительные корни х+ уравнения (3. 1), если они существуют, удовлетворяют неравенству Для отыскания границ отрицательных корней следует в уравнении (3. 1) заменить х на –х и определить нижнюю границу по Формуле Лагранжа для вспомогательного уравнения: ( 3. 3 ) Верхняя граница отрицательных корней определяется также из вспомогательного уравнения ( 3. 4 )

3. 1. 1. 1 Отделение корней алгебраических уравнений Итак, отрицательные корни х ‾ уравнения (3. 1), если они существуют, удовлетворяют неравенству Таким образом, все корни алгебраического уравнения (3. 1) находятся на отрезке т. е. от нижней границы отрицательных корней до верхней границы положительных корней

3. 1. 1. 1 Отделение корней алгебраических уравнений o Пример. Определить границы действительных корней алгебраического уравнения: Для правильного определения индексов коэффициентов исходного уравнения запишем его в общем виде: где

3. 1. 1. 1 Отделение корней алгебраических уравнений По формуле Лагранжа находим верхнюю границу положительных корней заданного уравнения. Здесь k=1; B=9; a 0=3; Для определения нижней границы положительных корней разрабатываем вспомогательное уравнение вида (3. 2): или ( 3. 2. 1 )

3. 1. 1. 1 Отделение корней алгебраических уравнений В уравнении (3. 2. 1): k=8; B=3; a 0=3. Тогда Для нахождения границ отрицательных корней, составляем вспомогательные уравнения вида (3. 3) и (3. 4). Нижняя граница действительных отрицательных корней: Здесь k=8; B=9; a 0=3.

3. 1. 1. 1 Отделение корней алгебраических уравнений Верхняя граница отрицательных корней: Здесь k=1; B=6; a 0=9. Итак, действительные корни заданного уравнения, если они существуют, находятся на отрезках: положительные 0, 53 ≤ x+ ≤ 4; отрицательные -2, 15 ≤ x- ≤ -0, 6. Все корни находятся на отрезке: -2, 15 ≤ x ≤ 4.

3. 1. 1. 1 Отделение корней алгебраических уравнений Правило знаков Декарта 1. Число положительных корней алгебраического уравнения либо равно числу N перемен знака в последовательности коэффициентов аi, причем учитываются коэффициенты, равные нулю, либо меньше числа N на четное число. 2. Если перемен знаков нет, то алгебраическое уравнение положительных корней не имеет. 3. Если есть одна смена знака, то уравнение имеет только один положительный корень. 4. Применяя это правило к уравнению f(-x), получаем аналогичное правило для отрицательных корней.

3. 1. 1. 1 Отделение корней алгебраических уравнений Схема Горнера для отделения корней алгебраических уравнений Значение многочлена (3, 1) легко вычислить, используя схему Горнера. Так, разделив уравнение (3. 1) на двучлен (х-с), получаем: f(x)=(x-c) (x)+r, где (x)-частное (многочлен на порядок ниже f(x)); r-остаток. Коэффициенты bi уравнения (x) рассчитываются по формулам: b 0=a 0; b 1= b 0 c+a 1; b 2=b 1 c+a 2; . . bn=r=bn-1 c+an. r = bn. где bn числено равен значению многочлена при подстановке в него вместо Х значение С.
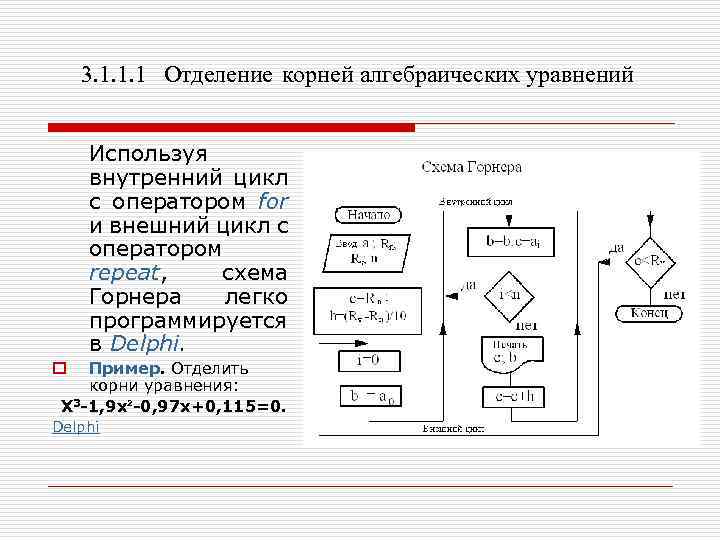
3. 1. 1. 1 Отделение корней алгебраических уравнений Используя внутренний цикл с оператором for и внешний цикл с оператором repeat, схема Горнера легко программируется в Delphi. Пример. Отделить корни уравнения: X 3 -1, 9 x²-0, 97 x+0, 115=0. o Delphi

3. 1. 1. 1 Отделение корней алгебраических уравнений Рассмотрим содержание подпрограммы Gorner. Procedure Gorner(c: real; A: Mas; Var b: real); Var i : integer; begin for i: =1 to n do b: =b*c+A[i]; end; где «с» изменяется во внешнем цикле от нижней границы отрицательных корней до верхней границы положительных корней с некоторым шагом h; b – численное значение многочлена при подстановке в него вместо «х» значение «с» . Обращение к подпрограмме Gorner в вызывающей программе: Gorner(c, A, b);

3. 1. 1. 1 Отделение корней алгебраических уравнений Подпрограммы головного модуля Unit 1. 1. Вызов калькулятора. procedure TForm 1. Bit. Btn 2 Click(Sender: TObject); begin Win. Exec('Calc', sw_Restore); end; 2. Удаление файлов при щелчке по кнопке «Выход» procedure TForm 1. Bit. Btn 5 Click(Sender: TObject); begin Delete. File('A. Rez'); Delete. File('Gr. Dat'); Close; end;

3. 1. 1. 1 Отделение корней алгебраических уравнений 3. Подпрограмма «Создание главной формы» . procedure TForm 1. Form. Create(Sender: TObject); Var i : integer; begin Decimal. Separator: ='. '; Assign. File(Fr, 'A. Dat'); Reset(Fr); readln(Fr, FIO); //Чтение данных из файла «А. Dat» readln(Fr, n. Gr); readln(Fr, n); for i: =0 to n do read(Fr, A[i]); readln(Fr, Rn, Rv); Close. File(Fr);

3. 1. 1. 1 Отделение корней алгебраических уравнений Edit 1. Text: =FIO; //Размещение данных по окнам Edit 2. Text: =n. Gr; Edit 3. Text: =Int. To. Str(n); Edit 4. Text: =Float. To. Str(Rn); Edit 5. Text: =Float. To. Str(Rv); with String. Grid 1 do //Оформление компоненты String. Grid 1 begin Col. Count: =n+2; //Число столбцов Row. Count: =2; //Число строк for i: =0 to 11 do Cells[i+1, 0]: ='a'+Int. To. Str(i); for i: =1 to 10 do Cells[0, i]: =Int. To. Str(i); for i: =1 to n+1 do Cells[i, 1]: =Float. To. Str(A[i-1]); end; //Конец подпрограммы TForm 1. Form. Create
3. 1. 1. 1 Отделение корней алгебраических уравнений 4. Головная программа procedure TForm 1. Bit. Btn 4 Click(Sender: TObject); Var h, b: real; i : integer; begin FIO: =Edit 1. Text; n. Gr: =Edit 2. Text; n: =Str. To. Int(Edit 3. Text); Rn: =Str. To. Float(Edit 4. Text); Rv: =Str. To. Float(Edit 5. Text); with String. Grid 1 do //Заполнение данными ячеек //String. Grid 1 for i: =1 to n+1 do A[i-1]: =Str. To. Float(Cells[i, 1]);

3. 1. 1. 1 Отделение корней алгебраических уравнений Assign. File(Fw, 'A. Dat'); //Обновление файла «A. Dat); » Rewrite(Fw); writeln(Fw, FIO); writeln(Fw, n. Gr); writeln(Fw, n); for i: =1 to n+1 do write(Fw, A[i-1]: 8: 3); writeln(Fw, Rn: 10: 3, Rv: 10: 3); Close. File(Fw); h: =(Rv-Rn)/20; //Вычисление шага изменения «с» c: =Rn; //Присвоение «с» 1 -го значения - Rn

3. 1. 1. 1 Отделение корней алгебраических уравнений Assign. File(Fw, 'A. Rez'); //Открытие файла для записи Rewrite(Fw); Assign. File(Fww, 'Gr. Dat'); Rewrite(Fww); Tabl; //Оформление «шапки» таблицы результатов repeat //Внешний цикл по «с» b: =A[0]; Gorner(c, A, b); writeln(Fw, '': 13, c: 10: 3, b: 23: 3); writeln(Fww, '': 2, c: 10: 3, b: 10: 3); c: =c+h; until (c>Rv);

3. 1. 1. 1 Отделение корней алгебраических уравнений Lin(5, 15, 0, 1, '-'); write(Fw, ' *** Конец расчета *** '); 3. 1. 1. 1 Lin(0, 15, 0, 1, '-'); Close. File(Fww); Form 1. Visible: =False; //Показать результаты расчета with TForm 2. Create(Application) do try Show. Modal; finally free; end; Form 1. Visible: =True; end; //Конец головной программы

3. 1. 1. 1 Отделение корней алгебраических уравнений 5. Показать блок-схему вычисления значения многочлена по схеме Горнера procedure TForm 1. Bit. Btn 3 Click(Sender: TObject); begin Form 4. Show. Modal; end; 6. Показать содержание информации «О программе» procedure TForm 1. Bit. Btn 1 Click(Sender: TObject); begin Form 5. Show. Modal; end. //Конец модуля Unit 1

3. 1. 1. 2. Отделение корней трансцендентных уравнений o В общем виде трансцендентное уравнение с одним неизвестных записывается так : f(x) = 0, ( 3. 5 ) где f(x) – некоторая функция от «х» . Для отделения корней трансцендентных уравнений обычно применяют графический метод, который заключается в том, что непосредственно строят график функции f(x), либо исходную функцию представляют в виде суммы нескольких более простых функций, т. е. f(x) = f 1(x) + f 2(x).

3. 1. 1. 2. Отделение корней трансцендентных уравнений В первом случае находят пересечение графика функции f(x) с осью абсцисс, во втором – точки пересечения функций f 1(x) и f 2(x). Таким образом, чтобы отделить все действительные корни уравнения (5), требуется найти интервалы, на которых функция монотонна, и определить знаки функции на концах каждого интервала. Если знаки различны, то исследуемый интервал содержит один корень. Признаком монотонности функции f(x) на некотором интервале является неизменность знака производной функции. Следовательно, для поиска интервалов, содержащих корни уравнения (5), необходимо найти такие значения «х» , для которых производная не меняет знак. Поэтому задача отделения корней сводится к задаче отыскания точек, в которых производная равна нулю или имеет разрыв, и определению знака функции f(x) в найденных точках.

3. 1. 1. 2. Отделение корней трансцендентных уравнений o Пример. Отделить корни уравнения x 2 – sinx = 0. Функция f(x)=x 2 -sinx и ее производная f’(x)=2 x-cosx непрерывны на всей числовой оси. При х=0 имеем f(0)=0, т. е. это один из корней заданного уравнения. Определим интервалы монотонности функции f(x), т. е. решим уравнение f’(x)=2 x-cosx =0. Имеем : при х1=p/4, f’(x 1)=p/2, а при х 2=p/2, Таким образом, найден следующий отрезок монотонности функции f(x): Так как при х= p/4 f(x)= , а при х=p/2 , то на концах найденного отрезка функция f(x) меняет знак, т. е. найденный интервал содержит один корень. Delphi

3. 1. 1. 2. Отделение корней трансцендентных уравнений Покажем особенности нахождения значения трансцендентного уравнения. procedure TForm 1. Bit. Btn 1 Click(Sender: TObject); Var Rn, Rv, h, fx, x : real; begin Decimal. Separator: ='. '; Rn: =Str. To. Float(Edit 1. Text); Rv: =Str. To. Float(Edit 2. Text); h: =(Rv-Rn)/10; x: =Rn; repeat fx: =x*x-sin(x); //Исследуемая функция Series 1. Add. XY(x, fx, '', cl. Tee. Color); x: =x+h; until(x>Rv); end; //Конец головной программы

3. 1. 1. Отделение корней уравнений Построить графики и тем самым отделить корни заданного уравнения можно с помощью пакетов Math. CAD и Excel. Построим графики, рассмотренных уравнений с помощью этих пакетов. Math. CAD: Excel. Таким образом, основным методом отделения корней алгебраических и трансцендентных уравнений является графический метод. Однако для отделения корней алгебраических уравнений наиболее удобна схема Горнера. Графики заданного уравнения можно строить по готовой программе, написанной в Delphi или использовать пакеты Math. CAD или Excel.

3. 1. 1. Отделение корней уравнений
Отдел_Корней_Алгебр_Трансц_Уравн.ppt