3 Алгебра логики как раздел математической логики изучает

3. Алгебра логики как раздел математической логики изучает строение логических формул и способы установления их истинности с помощью алгебраических методов. Основные объекты алгебры логики – формулы алгебры логики, состоящие из букв, знаков, логических операций и скобок. Каждая формула задаёт логическую функцию – функцию от логических переменных, которая может принимать только два логических значения.

Пусть B={0, 1} – бинарное множество, элементами которого являются формальные символы 1 и 0 – { «да» , «нет» } , { «истина» , «ложь» } и т. д. Алгебра логики – алгебра, образованная множеством B={0, 1} вместе со всеми возможными операциями на нем.

Функцией алгебры логики (логической функцией) f от n переменных f(x 1, x 2, …, xn) называется n-арная логическая операция на B, т. е. f: Bn → B. Множество всех логических функций обозначается P 2. Множество всех логических операций n переменных – P 2(n).

Любую логическую функцию f(x 1, x 2, …, xn) можно задать таблицей истинности. Число всех возможных различающихся наборов значений n переменных функции f(x 1, x 2, …, xn) равно 2 n. Число всех различных функций n переменных равно 22ⁿ, т. е. |P 2(n)|=22ⁿ.

Особую роль в алгебре логики играют логические функции одной и двух переменных – унарные и бинарные логические операции, поскольку очевидным образом интерпретируются естественными логическими связками «не» , «или» и т. д.

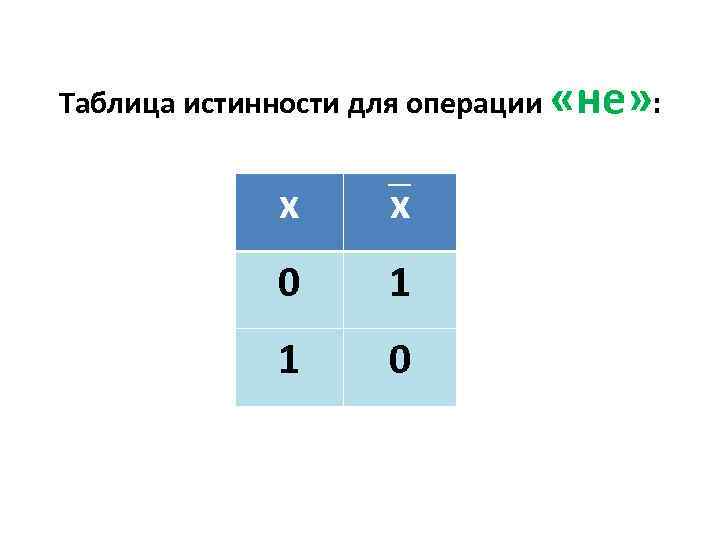
Таблица истинности для операции «не» : x x 0 1 1 0

Таблица истинности логических функций одной переменной: |P 2(1)|=4 • 3 – значения не зависят от х; 0 и х – несущественная (фиктивная) для этих функций; • – повторение переменной; 1(x)=x • – отрицание переменной 2(x)=x х 0 1 0 1 x 2 1 0 x 3 1 1 x

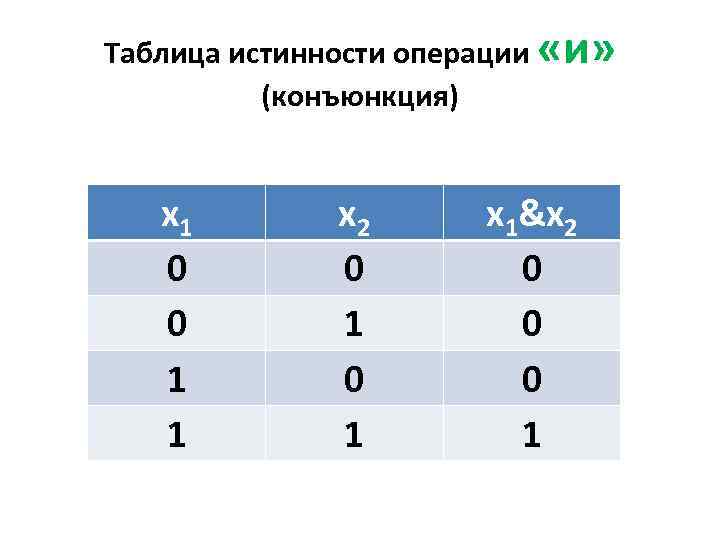
Таблица истинности операции «и» (конъюнкция) x 1 0 0 1 1 x 2 0 1 x 1&x 2 0 0 0 1

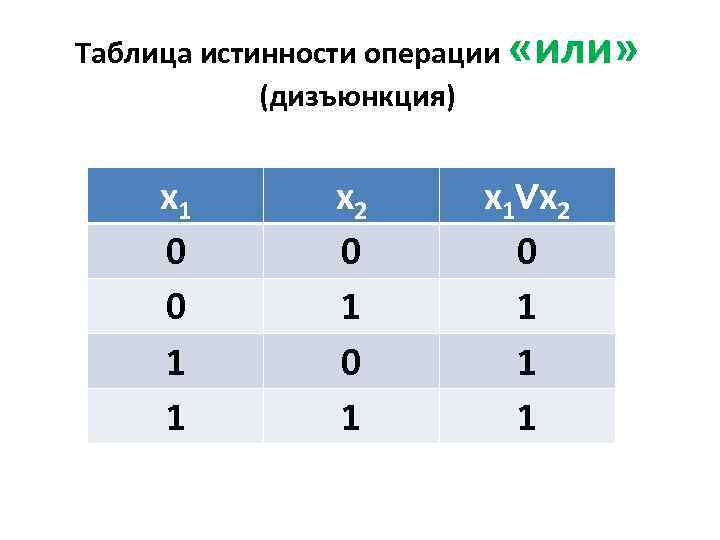
Таблица истинности операции «или» (дизъюнкция) x 1 0 0 1 1 x 2 0 1 x 1∨x 2 0 1 1 1

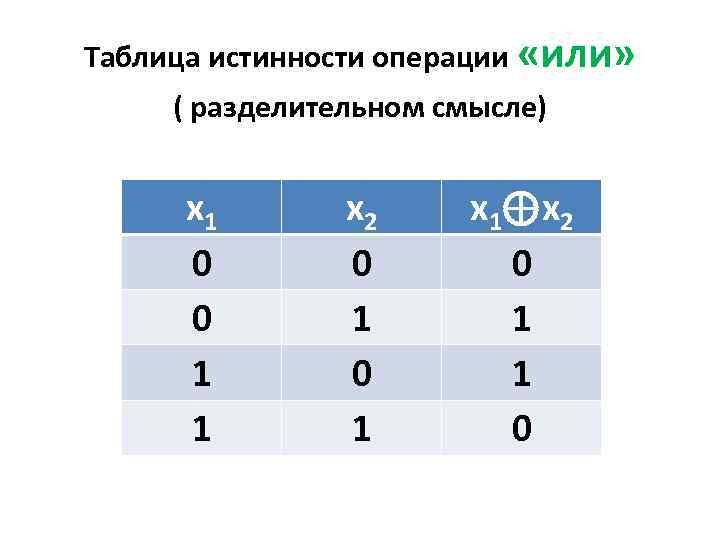
Таблица истинности операции «или» ( разделительном смысле) x 1 0 0 1 1 x 2 0 1 x 1⊕x 2 0 1 1 0

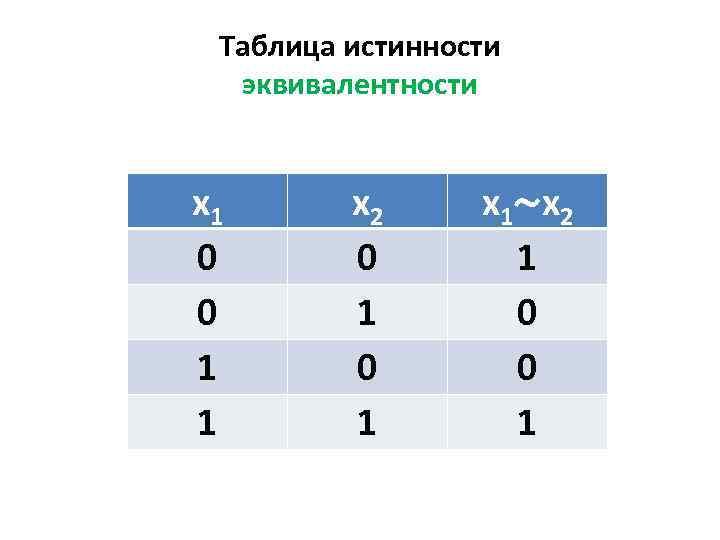
Таблица истинности эквивалентности x 1 0 0 1 1 x 2 0 1 x 1∼x 2 1 0 0 1

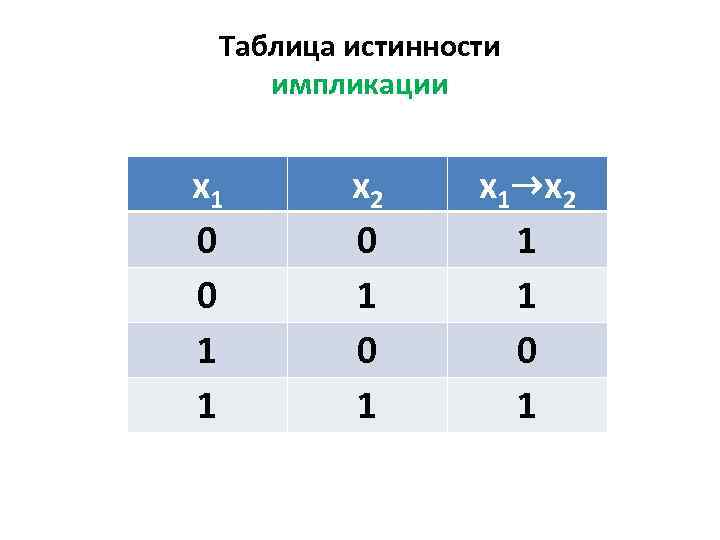
Таблица истинности импликации x 1 0 0 1 1 x 2 0 1 x 1→x 2 1 1 0 1

Множество всех логических функций двух переменных P 2(n) – бинарных логических операций – так же можно свести в общую таблицу истинности. !!! Помним, что |P (n)|=16 функций. 2

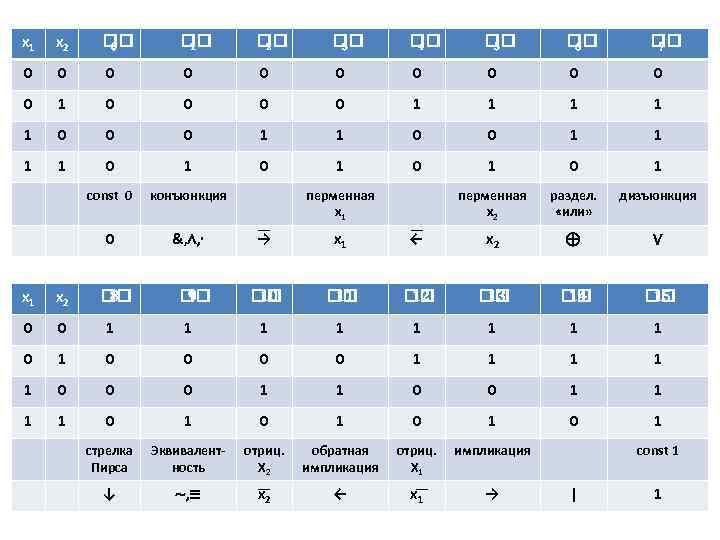
x 1 x 2 0 1 2 3 4 5 6 7 0 0 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 1 0 1 const 0 конъюнкция перменная x 2 раздел. «или» дизъюнкция 0 &, ∧, ∙ перменная x 1 → x 1 ← x 2 ⊕ ∨ 10 11 12 13 14 15 x 1 x 2 0 0 1 1 1 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 1 0 1 стрелка Пирса Эквивалентность отриц. X 2 обратная импликация отриц. X 1 импликация ↓ ∼, ≡ x 2 ← x 1 → 8 9 const 1 | 1

Из этих 16 -ти функций 6 имеют фиктивные переменные. Значение любой логической функции 3 -х и более переменных можно вычислить используя эту таблицу. Формула наряду с таблицей служит способом задания и вычисления функции. В общем случае формула описывает логическую функцию как суперпозицию других более простых функций. Эквивалентными (равносильными) называются формулы, представляющие одну и ту же функцию.

Как установить равносильность двух формул? 1. По каждой формуле восстановить таблицу истинности. 2. Полученные таблицы сравнить по каждому набору значений переменных.

Пример 1 Логическая функция трех переменных задана формулой в префиксной форме: f(x 1, x 2, x 3)=f 3(f 1(x 3, x 1), f 2(x 1, f 3(x 1, x 2))). Представить f в инфиксной форме, если f 1 – &; f 2 – ⊕; f 3 – ∨. Вычислить f на наборе (0; 1; 1), т. е. х1=0; x 2=1; x 3=1.

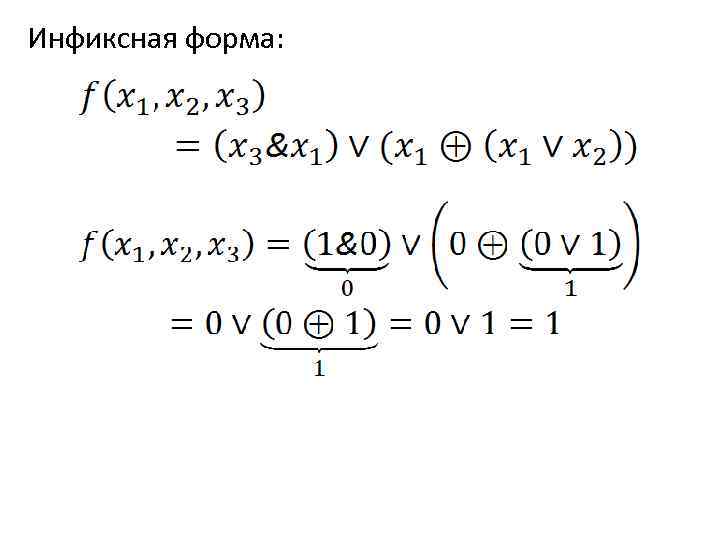
Инфиксная форма:

Пример 2 Составить таблицу истинности функции трёх переменных:

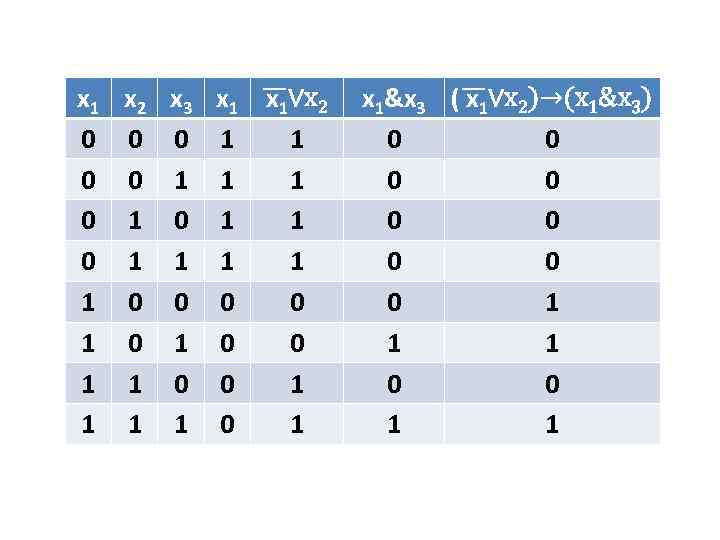
x 1 x 2 x 3 x 1∨x 2 0 0 0 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 1 x 1&x 3 ( x 1∨x 2)→(x 1&x 3) 0 0 0 0 0 1 1 1 0 0 1 1

Пример 3 (самостоятельно) Доказать эквивалентность формул: а) б)