3 15 2018 Waves Waves revision Watch a Mexican

3/15/2018 Waves

Waves revision Watch a “Mexican Wave” 3/15/2018

Some definitions… 1) Amplitude – this is “how high” the wave is: 2) Wavelength ( ) – this is the distance between two corresponding points on the wave and is measured in metres: 3) Frequency – this is how many waves pass by every second and is measured in Hertz (Hz) 3/15/2018

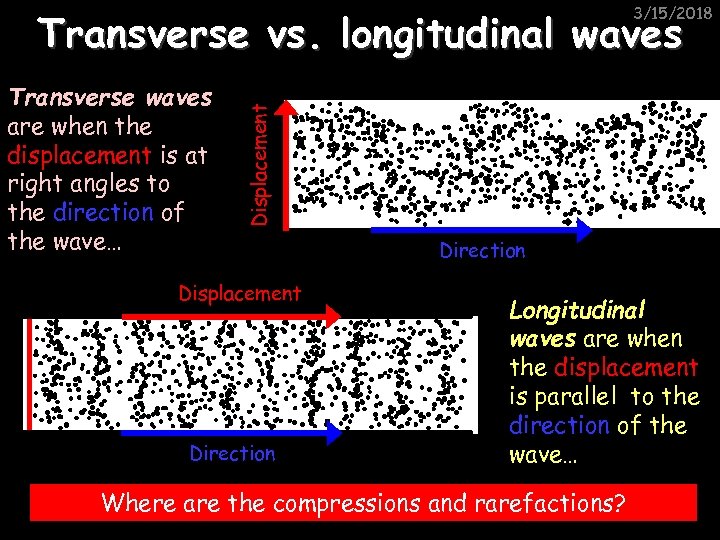3/15/2018 Transverse waves are when the displacement is at right angles to the direction of the wave… Displacement Transverse vs. longitudinal waves Displacement Direction Longitudinal waves are when the displacement is parallel to the direction of the wave… Where are the compressions and rarefactions?

Oscillating Systems 3/15/2018 Design an experiment that determines what the period of oscillation depends on for these two oscillating systems: T = 2π l g T = 2π m k

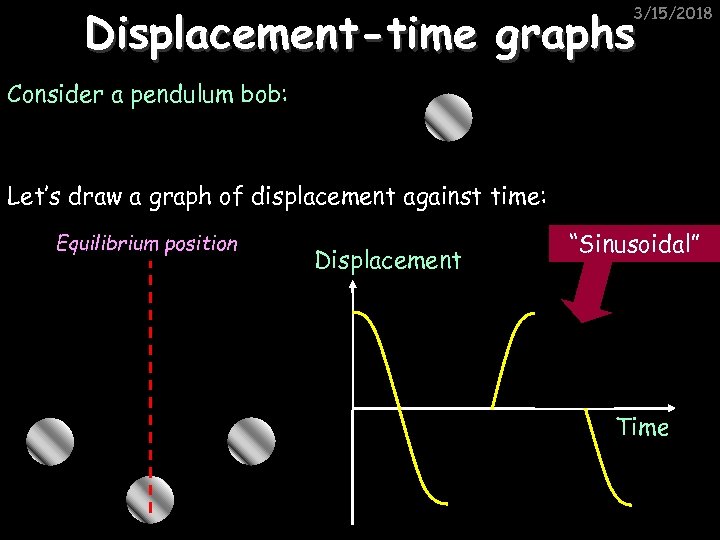Displacement-time graphs 3/15/2018 Consider a pendulum bob: Let’s draw a graph of displacement against time: Equilibrium position Displacement “Sinusoidal” Time

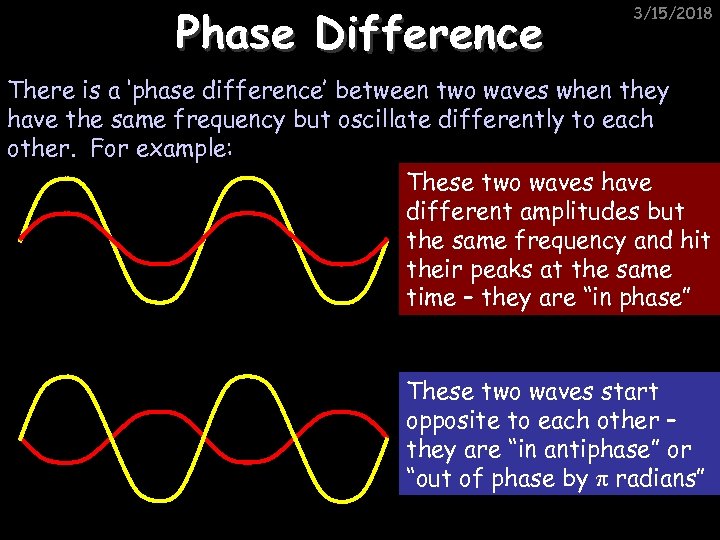Phase Difference 3/15/2018 There is a ‘phase difference’ between two waves when they have the same frequency but oscillate differently to each other. For example: These two waves have different amplitudes but the same frequency and hit their peaks at the same time – they are “in phase” These two waves start opposite to each other – they are “in antiphase” or “out of phase by π radians”

Phase Difference What is the phase difference between each of these waves? 3/15/2018

The Wave Equation 3/15/2018 The wave equation relates the speed of the wave to its frequency and wavelength: Wave speed (v) = frequency (f) x wavelength ( ) in ms-1 in Hz in m V f

Some example wave equation questions 3/15/2018 1) A water wave has a frequency of 2 Hz and a wavelength of 0. 3 m. How fast is it moving? 0. 6 ms-1 2) A water wave travels through a pond with a speed of 1 ms-1 and a frequency of 5 Hz. What is the wavelength of the waves? 0. 2 m 3) The speed of sound is 330 ms-1 (in air). When Dave hears this sound his ear vibrates 660 times a second. What was the wavelength of the sound? 0. 5 m 4) Purple light has a wavelength of around 6 x 10 -7 m and a frequency of 5 x 1014 Hz. What is the speed of purple light? 3 x 108 ms-1

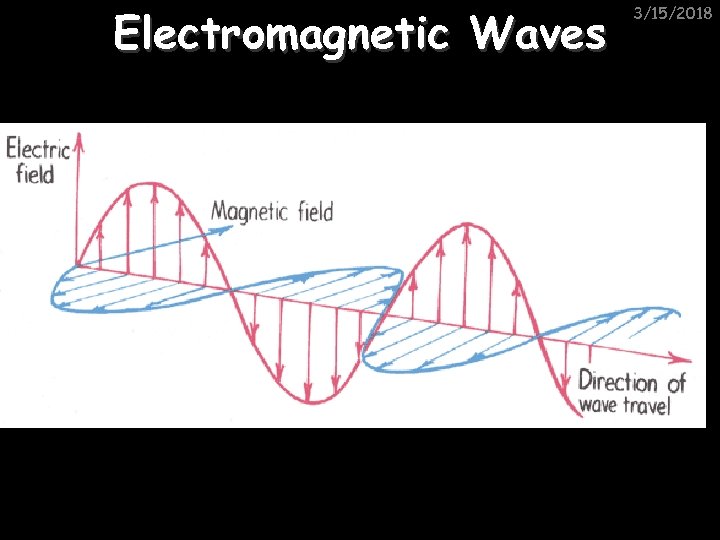Electromagnetic Waves 3/15/2018

Electromagnetic Radiation 3/15/2018 E-M radiation is basically a movement of energy in the form of a wave. Some examples:

The Electromagnetic Spectrum 3/15/2018 Each type of radiation shown in the electromagnetic spectrum has a different wavelength and a different frequency: High frequency, _____ wavelength Gamma rays X-rays Low frequency, _____ (high) wavelength Ultra violet Visible light Infra red Microwaves Radio/TV γ Each of these types travels at the same speed through a _______ (300, 000 ms-1), and different wavelengths are absorbed by different surfaces (e. g. infra red is absorbed very well by ______ surfaces). This absorption may heat the material up (like infra red and _______) or cause an alternating current (like in a __ _______). Words – black, microwaves, long, short, TV aerial, vacuum

The Electromagnetic Spectrum 3/15/2018 Type of radiation Uses Dangers Gamma rays Treating cancer, sterilisation Cell mutation X rays Medical Cell mutation Ultra violet Sun beds Skin cancer Visible light Seeing things None (unless you look at the sun) Infra red Remote controls, heat transfer Sunburn Microwaves Satellites, phones Very few TV/radio Communications Very few

Water Waves 3/15/2018 Q. Design an experiment that explores the relationship between the depth of water and the speed of a wave in that water.

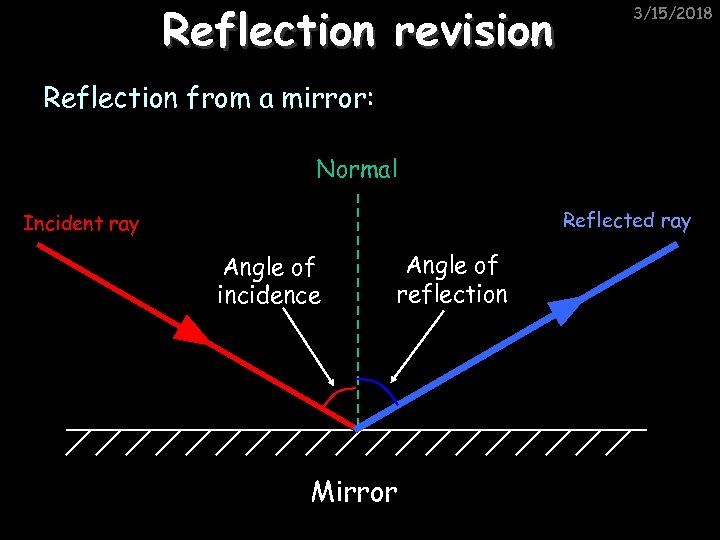Reflection revision 3/15/2018 Reflection from a mirror: Normal Reflected ray Incident ray Angle of incidence Angle of reflection Mirror

Refraction Revision 3/15/2018

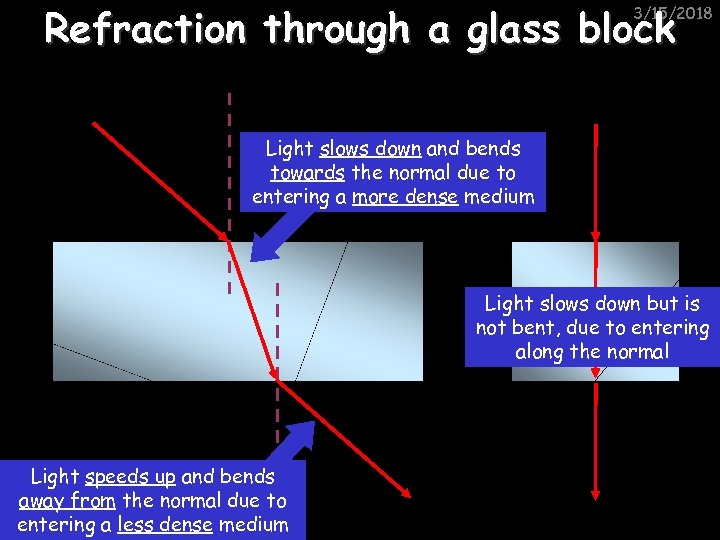Refraction through a glass block 3/15/2018 Light slows down and bends towards the normal due to entering a more dense medium Light slows down but is not bent, due to entering along the normal Light speeds up and bends away from the normal due to entering a less dense medium

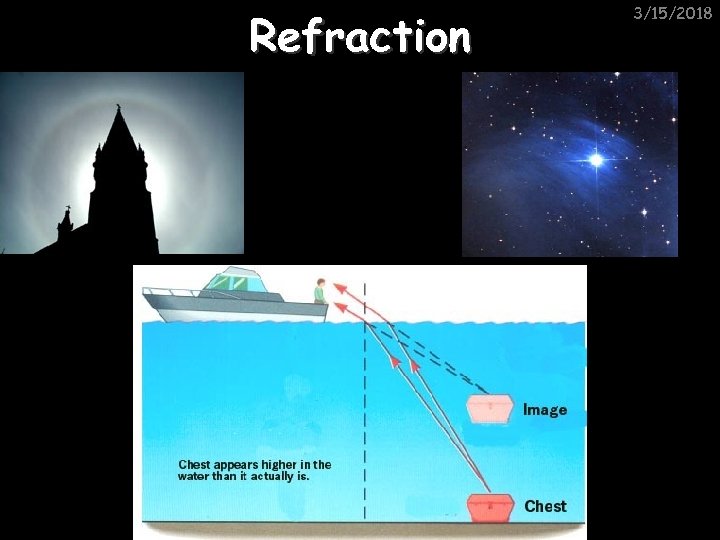Refraction 3/15/2018

Refractive Index 3/15/2018 The Refractive Index of a material is a measure of the factor by which the material will slow down light: Speed in medium 1 Refractive index = Speed in medium 2 Using some interesting maths I turned this relationship into Snell’s Law: 1μ 2 = sinθ 1 sinθ 2 = sin i sin r Willebrord Snellius, 1580 -1626 1μ 2 = v 1 v 2

3/15/2018 Questions on the Refractive Index The speed of light is 3 x 108 ms-1 in air, 2. 3 x 108 ms-1 in water and 2 x 108 ms-1 in glass. 1) Calculate the refractive index for light passing from air into water, from air into glass and from water into glass. Air 2) Calculate the angles θW and θG for light incident at 40 O to the air-water boundary: Water Glass

More Questions… 3/15/2018 My law can often be stated as this: μ 1 sin θ 1 = μ 2 sin θ 2 1) Light passes from water (refractive index of 1. 3) into crystal with a refractive index of 1. 5. Calculate the angles of refraction for light incident at 20 O, 30 O, 40 O and 50 O. 2) A ray of light travels through a vacuum and is incident upon a glass block (of refractive index 1. 5) at an angle of 30 O. The ray then passes into water. Draw an accurate diagram to show the path of this light as it travels from the vacuum through the glass and into the water.

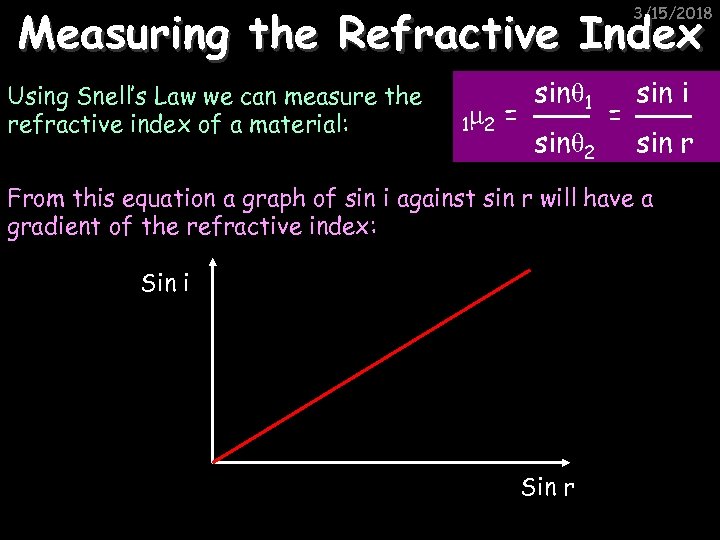Measuring the Refractive Index 3/15/2018 Using Snell’s Law we can measure the refractive index of a material: 1μ 2 = sinθ 1 sinθ 2 = sin i sin r From this equation a graph of sin i against sin r will have a gradient of the refractive index: Sin i Sin r

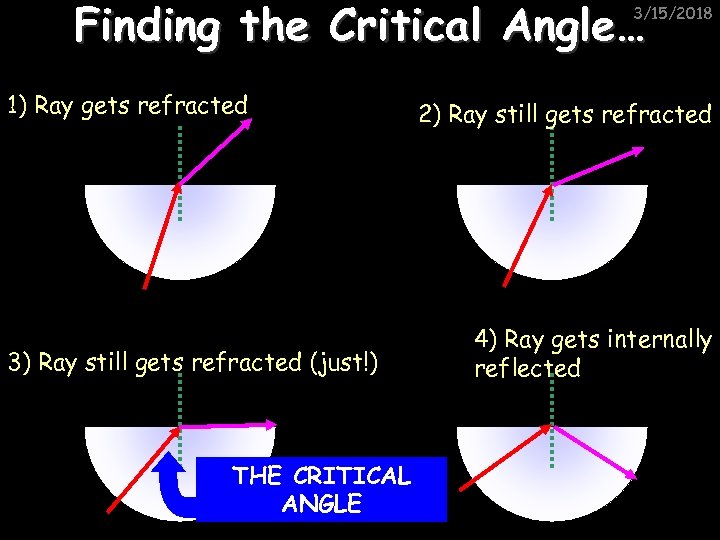Finding the Critical Angle… 3/15/2018 1) Ray gets refracted 3) Ray still gets refracted (just!) THE CRITICAL ANGLE 2) Ray still gets refracted 4) Ray gets internally reflected

3/15/2018 Uses of Total Internal Reflection Optical fibres: An optical fibre is a long, thin, _______ rod made of glass or plastic. Light is _______ reflected from one end to the other, making it possible to send ____ chunks of information Optical fibres can be used for _____ by sending electrical signals through the cable. The main advantage of this is a reduced ______ loss. Words – communications, internally, large, transparent, signal

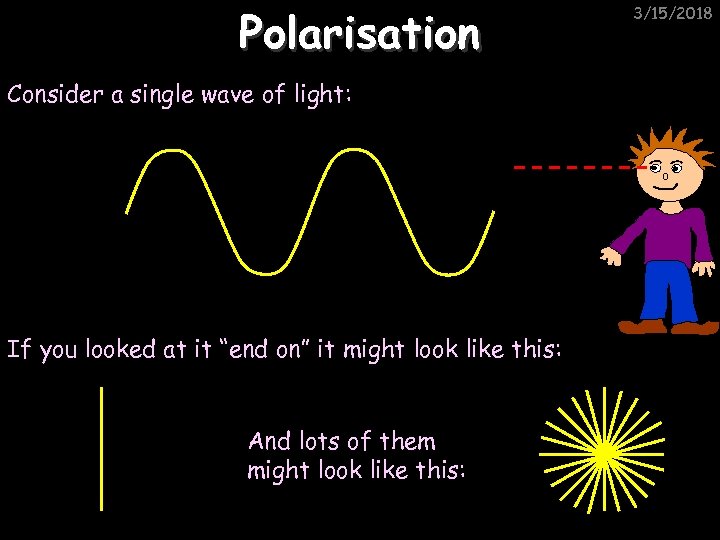Polarisation Consider a single wave of light: If you looked at it “end on” it might look like this: And lots of them might look like this: 3/15/2018

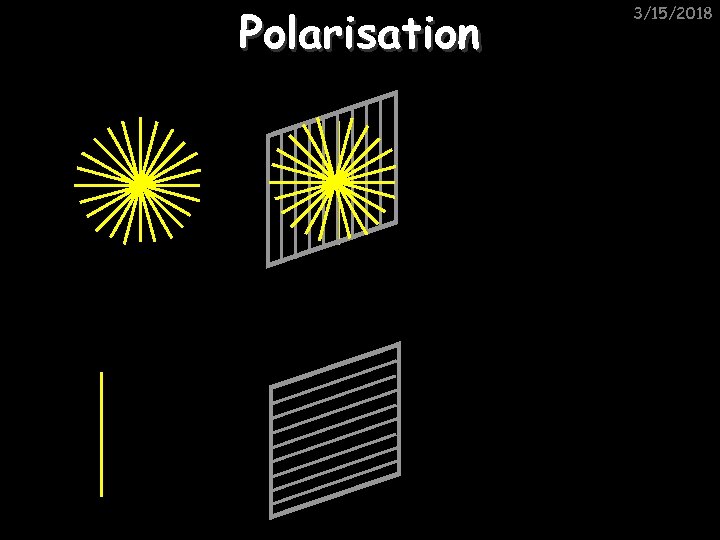Polarisation 3/15/2018

Polarisation and Microwaves 3/15/2018 Describe an experiment that demonstrates that microwaves are polarised.

3/15/2018 Sugar Solution and Polarised Light Task: To investigate the amount of sugar dissolved in a solution using polarised light. Method: 1) Measure and dissolve 10 g, 20 g, 30 g, 40 g and 50 g of sugar into 100 ml of water 2) Investigate the angle of rotation needed to block out a light source using the solution and two polaroid filters 3) Draw a graph of angle against concentration 4) Use this graph to determine the amount of sugar in unknown solution x.

3/15/2018 Using polarized light to see stress

Pulse-Echo techniques 3/15/2018 In pulse-echo techniques sound is reflected from an object to measure the distance to that object:

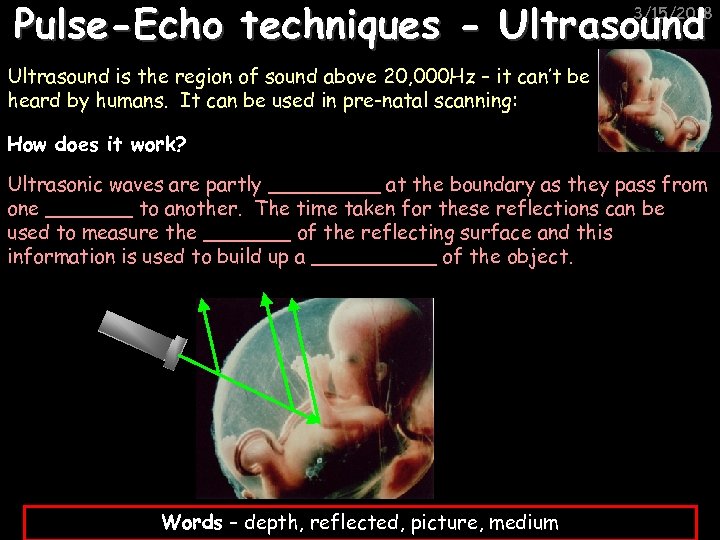Pulse-Echo techniques - Ultrasound 3/15/2018 Ultrasound is the region of sound above 20, 000 Hz – it can’t be heard by humans. It can be used in pre-natal scanning: How does it work? Ultrasonic waves are partly _____ at the boundary as they pass from one _______ to another. The time taken for these reflections can be used to measure the _______ of the reflecting surface and this information is used to build up a _____ of the object. Words – depth, reflected, picture, medium

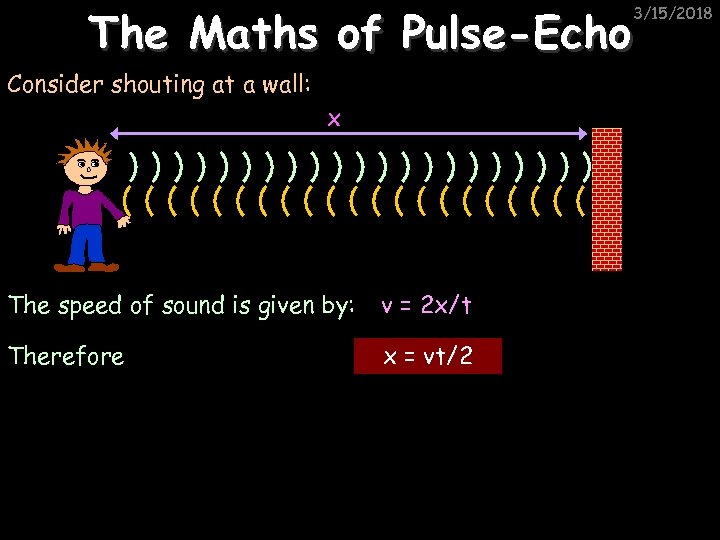The Maths of Pulse-Echo 3/15/2018 Consider shouting at a wall: x The speed of sound is given by: v = 2 x/t Therefore x = vt/2

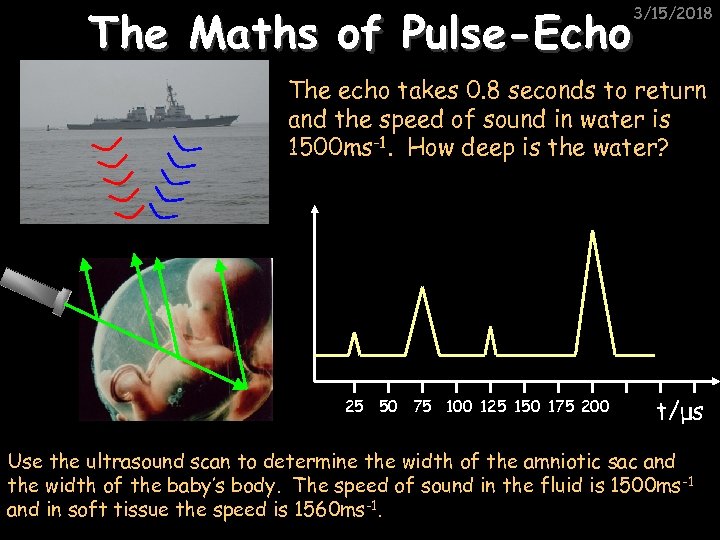The Maths of Pulse-Echo 3/15/2018 The echo takes 0. 8 seconds to return and the speed of sound in water is 1500 ms-1. How deep is the water? 25 50 75 100 125 150 175 200 t/μs Use the ultrasound scan to determine the width of the amniotic sac and the width of the baby’s body. The speed of sound in the fluid is 1500 ms -1 and in soft tissue the speed is 1560 ms-1.

Ultrasound vs X Rays 1) Why are X Rays better than ultrasound? 2) Why is ultrasound better than X Rays? 3/15/2018

The Doppler Effect 3/15/2018

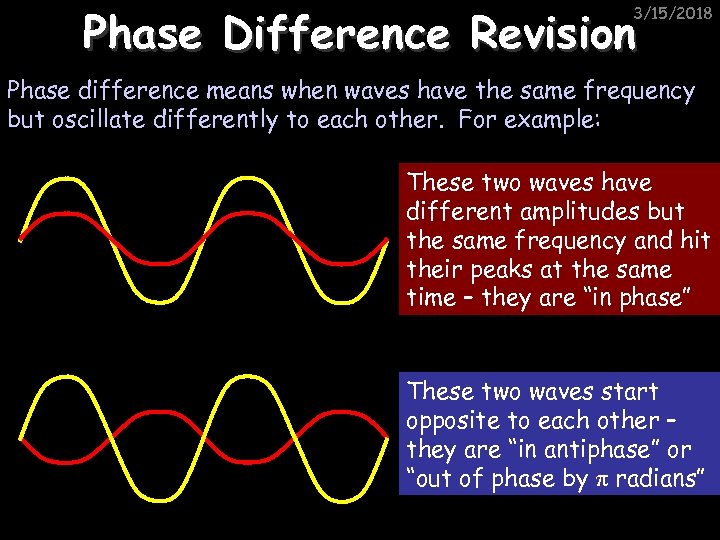Phase Difference Revision 3/15/2018 Phase difference means when waves have the same frequency but oscillate differently to each other. For example: These two waves have different amplitudes but the same frequency and hit their peaks at the same time – they are “in phase” These two waves start opposite to each other – they are “in antiphase” or “out of phase by π radians”

Coherence 3/15/2018 Two waves are said to be “coherent” if they have the same frequency and the same constant phase difference. For example: These waves have a different frequency, so phase is irrelevant.

Coherence 3/15/2018 These waves have the same frequency and the same constant phase difference, so they are “coherent”

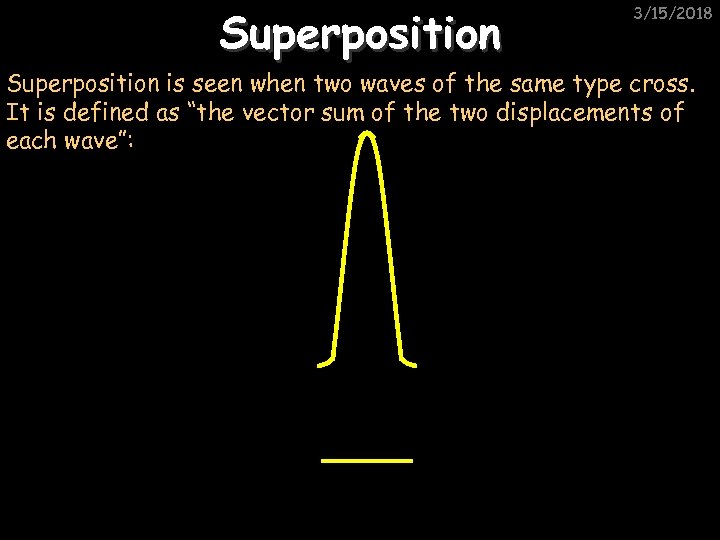Superposition 3/15/2018 Superposition is seen when two waves of the same type cross. It is defined as “the vector sum of the two displacements of each wave”:

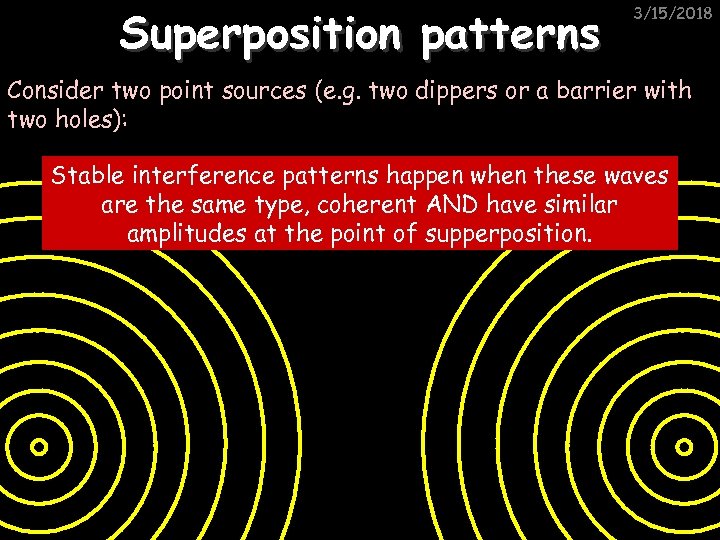Superposition patterns 3/15/2018 Consider two point sources (e. g. two dippers or a barrier with two holes): Stable interference patterns happen when these waves are the same type, coherent AND have similar amplitudes at the point of supperposition.

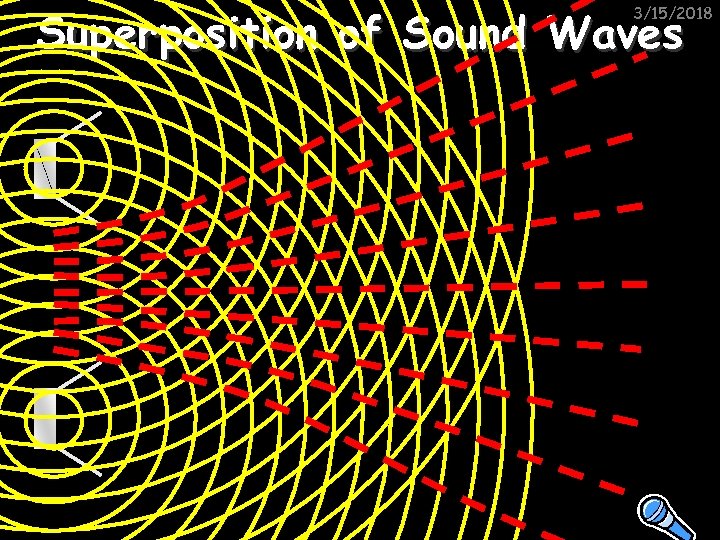Superposition of Sound Waves 3/15/2018

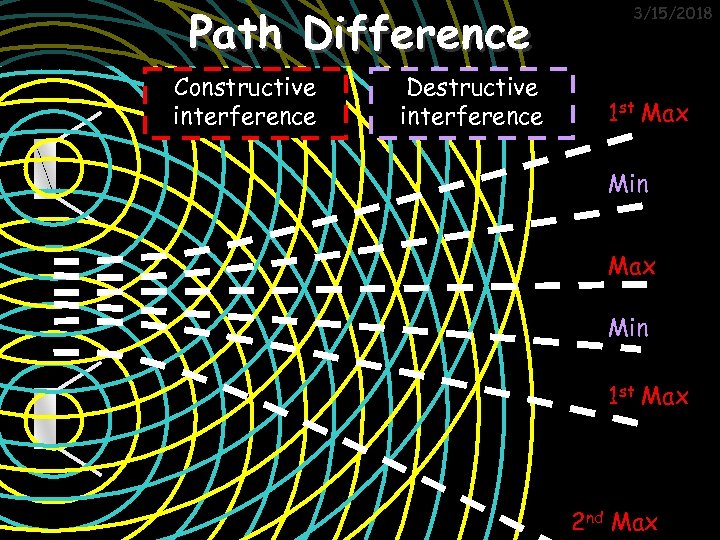Path Difference Constructive interference Destructive interference 3/15/2018 1 st Max Min 1 st Max 2 nd Max

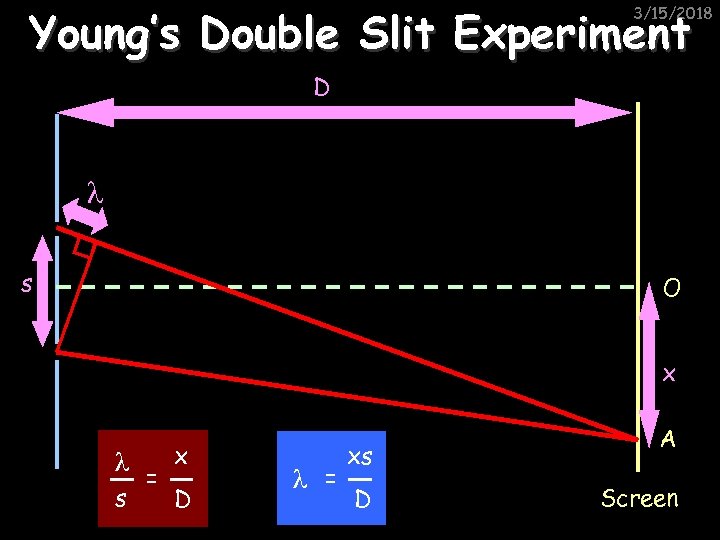Young’s Double Slit Experiment 3/15/2018 D λ s O x λ s = x D λ = xs D A Screen

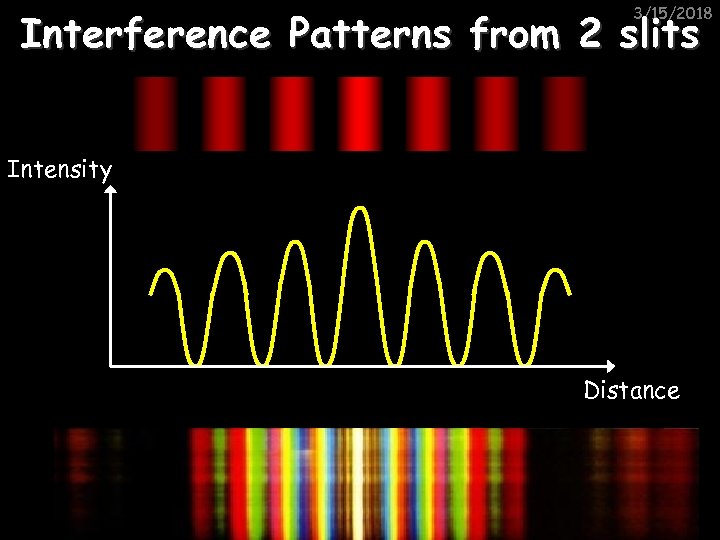3/15/2018 Interference Patterns from 2 slits Intensity Distance

Interferometers 3/15/2018 Task: Find out what an interferometer is. Include the following: 1) Where they are used 2) A diagram of how they are used 3) Some pictures 4) The physics principle behind how they work (i. e. the use of a path difference)

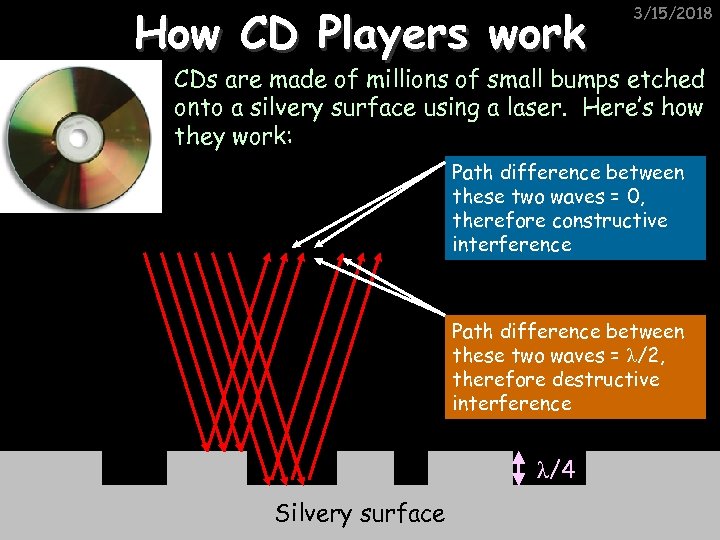How CD Players work 3/15/2018 CDs are made of millions of small bumps etched onto a silvery surface using a laser. Here’s how they work: Path difference between these two waves = 0, therefore constructive interference Path difference between these two waves = λ/2, therefore destructive interference λ/4 Silvery surface

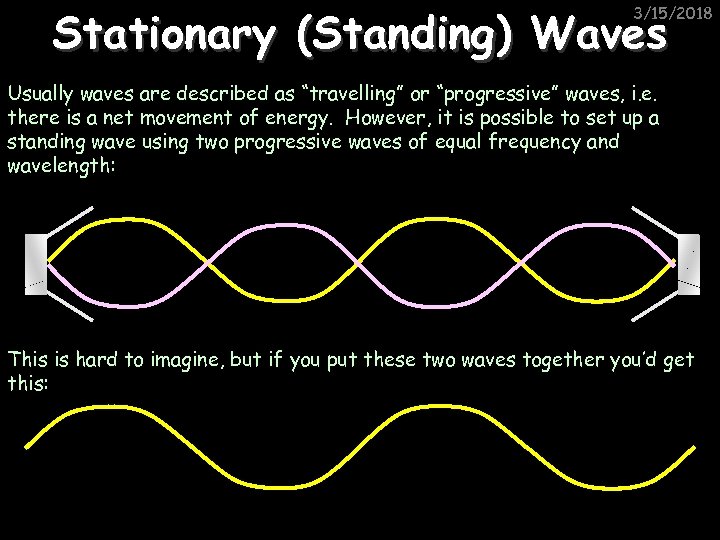Stationary (Standing) Waves 3/15/2018 Usually waves are described as “travelling” or “progressive” waves, i. e. there is a net movement of energy. However, it is possible to set up a standing wave using two progressive waves of equal frequency and wavelength: This is hard to imagine, but if you put these two waves together you’d get this:

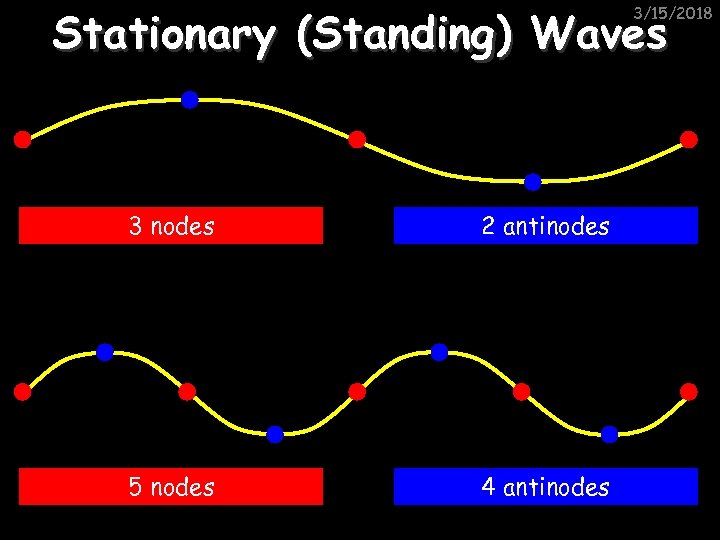Stationary (Standing) Waves 3/15/2018 3 nodes 2 antinodes 5 nodes 4 antinodes

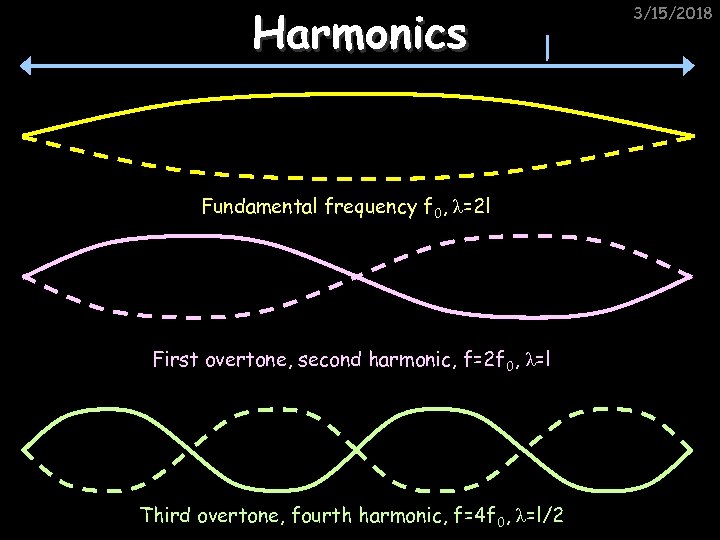Harmonics 3/15/2018 l Fundamental frequency f 0, λ=2 l First overtone, second harmonic, f=2 f 0, λ=l Third overtone, fourth harmonic, f=4 f 0, λ=l/2

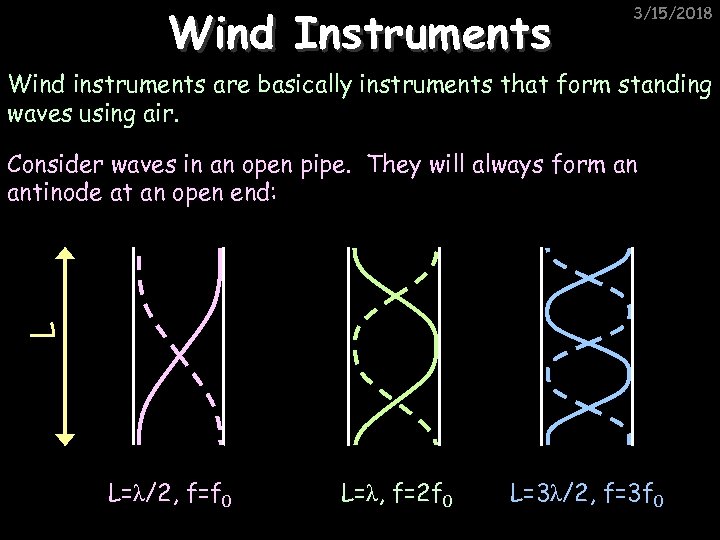Wind Instruments 3/15/2018 Wind instruments are basically instruments that form standing waves using air. L Consider waves in an open pipe. They will always form an antinode at an open end: L=λ/2, f=f 0 L=λ, f=2 f 0 L=3λ/2, f=3 f 0

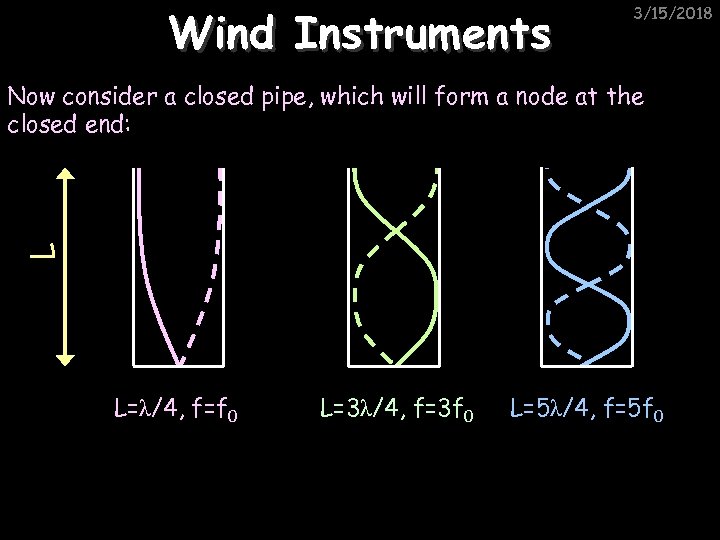Wind Instruments 3/15/2018 L Now consider a closed pipe, which will form a node at the closed end: L=λ/4, f=f 0 L=3λ/4, f=3 f 0 L=5λ/4, f=5 f 0

Example Questions 3/15/2018 A tuning fork emits a frequency of 512 Hz. It is held above a glass tube filled to the top with water. The water is allowed to drain out of the tube. When 17 cm of water has drained out a standing wave is formed and resonance occurs. Calculate: 1) The wavelength of the sound From the previous slide 17 cm=λ/4, therefore λ=68 cm 2) The speed of sound in air v=fλ, therefore v=512 x 0. 68 = 348 ms-1 3) How far the water must run to form the next resonance Next standing wave and resonance occurs at 3λ/4 = 51 cm

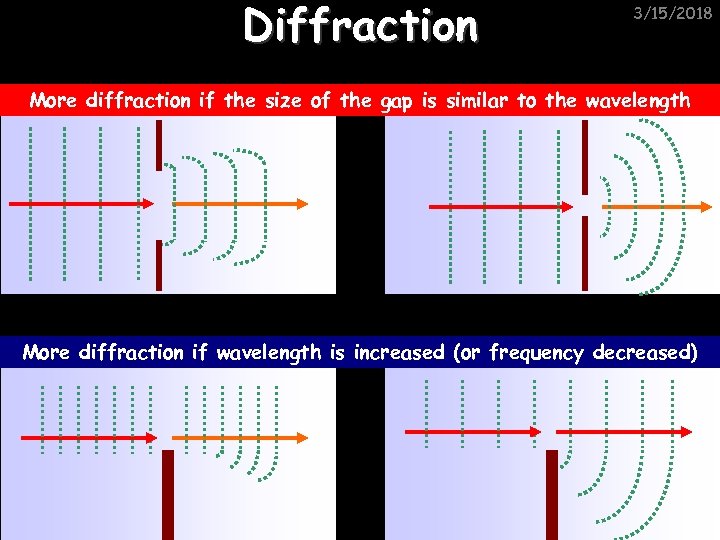Diffraction 3/15/2018 More diffraction if the size of the gap is similar to the wavelength More diffraction if wavelength is increased (or frequency decreased)

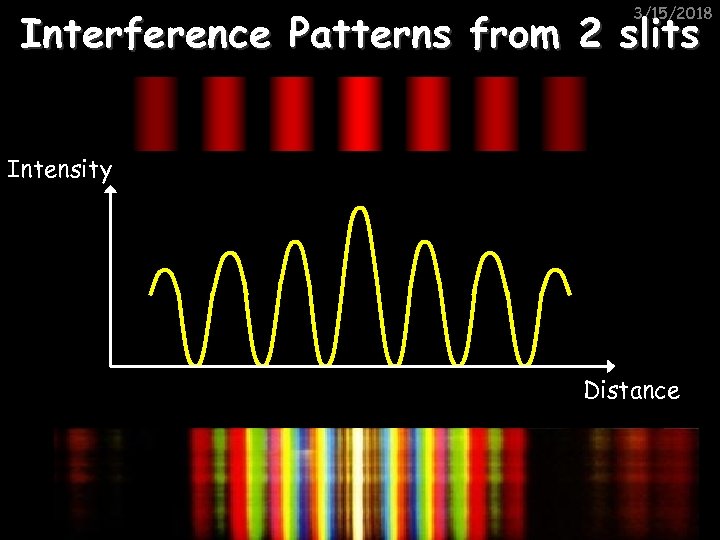3/15/2018 Interference Patterns from 2 slits Intensity Distance

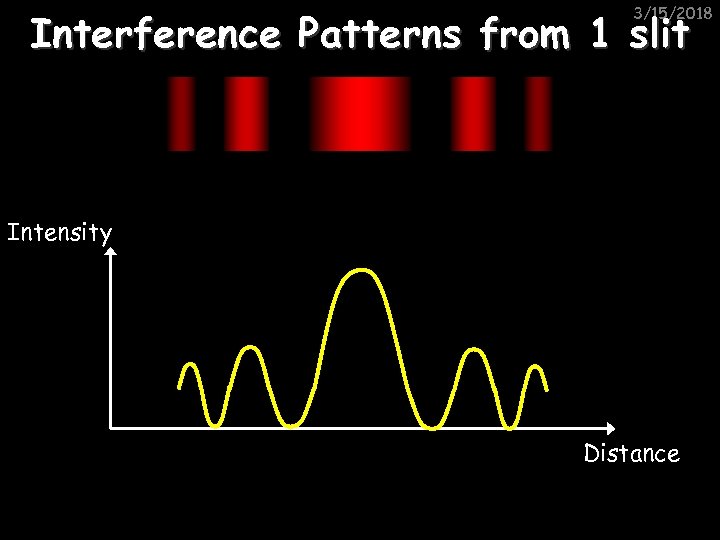3/15/2018 Interference Patterns from 1 slit Intensity Distance

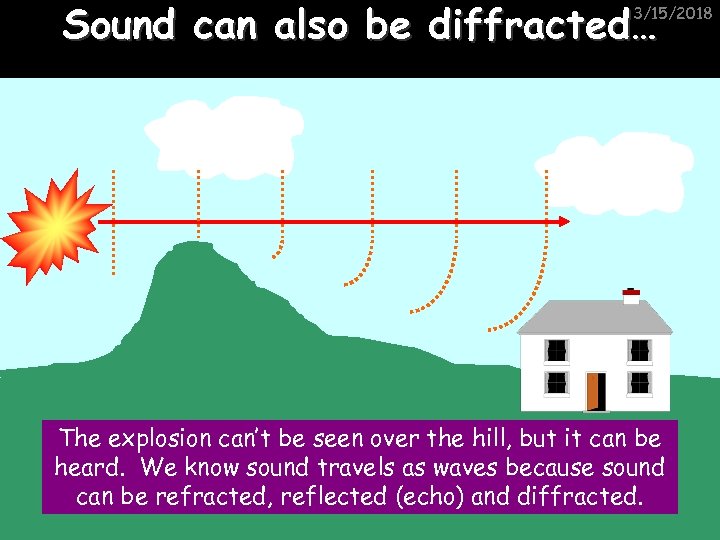Sound can also be diffracted… 3/15/2018 The explosion can’t be seen over the hill, but it can be heard. We know sound travels as waves because sound can be refracted, reflected (echo) and diffracted.

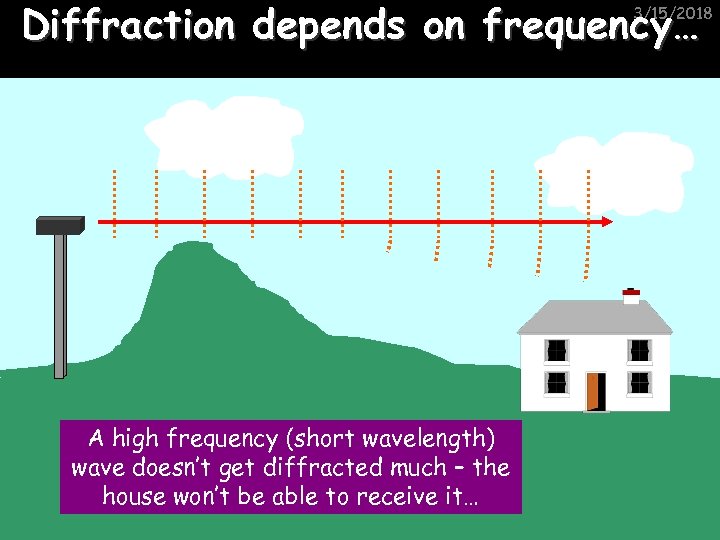Diffraction depends on frequency… 3/15/2018 A high frequency (short wavelength) wave doesn’t get diffracted much – the house won’t be able to receive it…

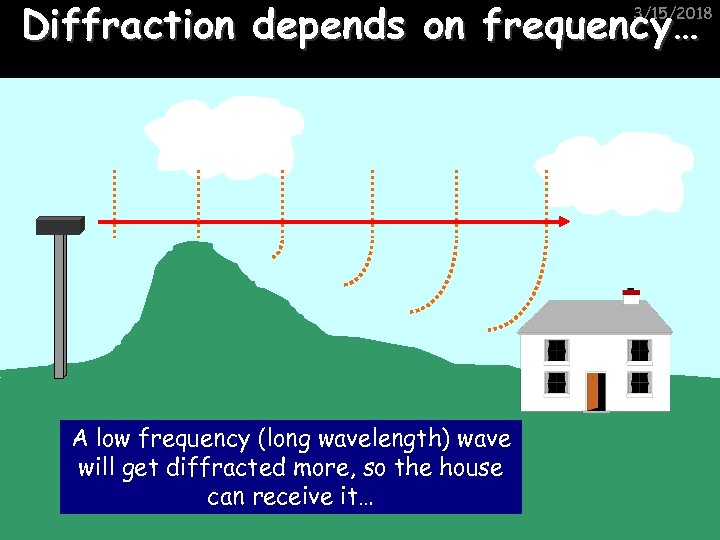Diffraction depends on frequency… 3/15/2018 A low frequency (long wavelength) wave will get diffracted more, so the house can receive it…

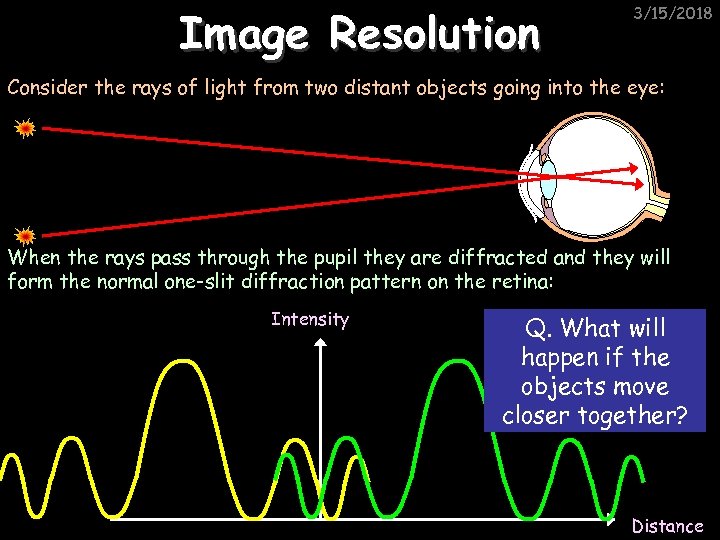Image Resolution 3/15/2018 Consider the rays of light from two distant objects going into the eye: When the rays pass through the pupil they are diffracted and they will form the normal one-slit diffraction pattern on the retina: Intensity Q. What will happen if the objects move closer together? Distance

Electron Diffraction 3/15/2018 Electron diffraction patterns are seen when electrons are passed through graphite crystal. Diffraction is seen because the distance between the atoms is of the same order as the de Broglie wavelength of the electrons. de Broglie wavelength λ = h mv 1) What is the de Broglie wavelength of electrons travelling at around 2 x 107 ms-1 (electron mass = 9. 1 x 10 -31 kg)? 2) What would happen to the diffraction pattern if the voltage to the electrons (and therefore their speed) was increased?

3/15/2018 Electricity

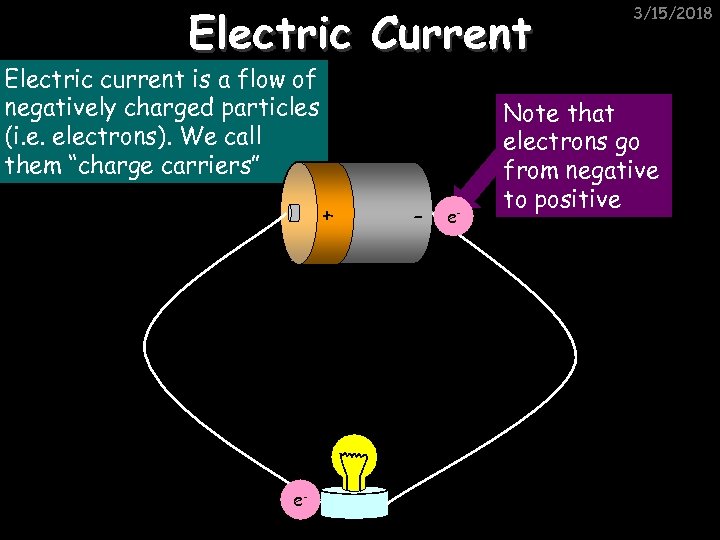Electric Current Electric current is a flow of negatively charged particles (i. e. electrons). We call them “charge carriers” + e- - e- 3/15/2018 Note that electrons go from negative to positive

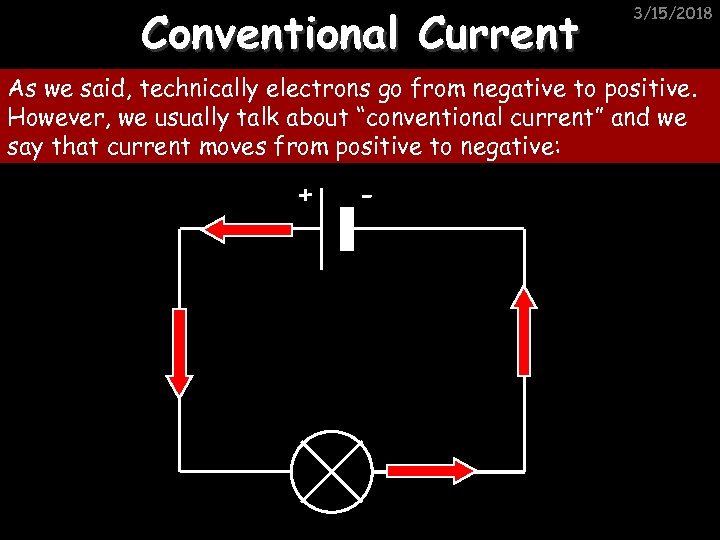Conventional Current 3/15/2018 As we said, technically electrons go from negative to positive. However, we usually talk about “conventional current” and we say that current moves from positive to negative: + -

Basic ideas… 3/15/2018 Electric current is when electrons start to flow around a circuit. We use an _____ to measure it and it is measured in ____. Potential difference (also called _______) is how big the push on the electrons is. We use a ____ to measure it and it is measured in ______, a unit named after Volta. Resistance is anything that resists an electric current. It is measured in _____. Words: volts, amps, ohms, voltage, ammeter, voltmeter

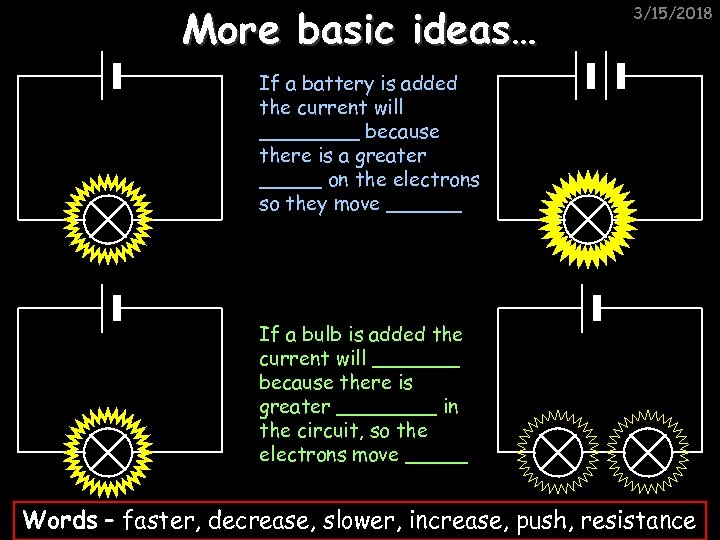More basic ideas… 3/15/2018 If a battery is added the current will ____ because there is a greater _____ on the electrons so they move ______ If a bulb is added the current will _______ because there is greater ____ in the circuit, so the electrons move _____ Words – faster, decrease, slower, increase, push, resistance

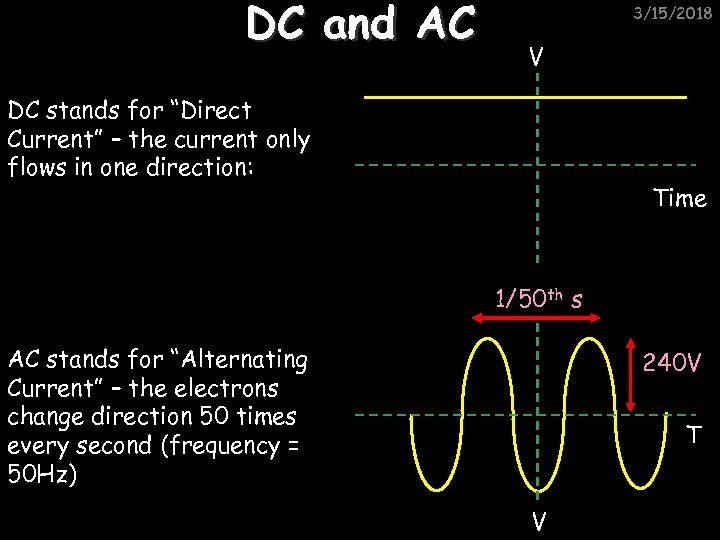DC and AC 3/15/2018 V DC stands for “Direct Current” – the current only flows in one direction: Time 1/50 th s AC stands for “Alternating Current” – the electrons change direction 50 times every second (frequency = 50 Hz) 240 V T V

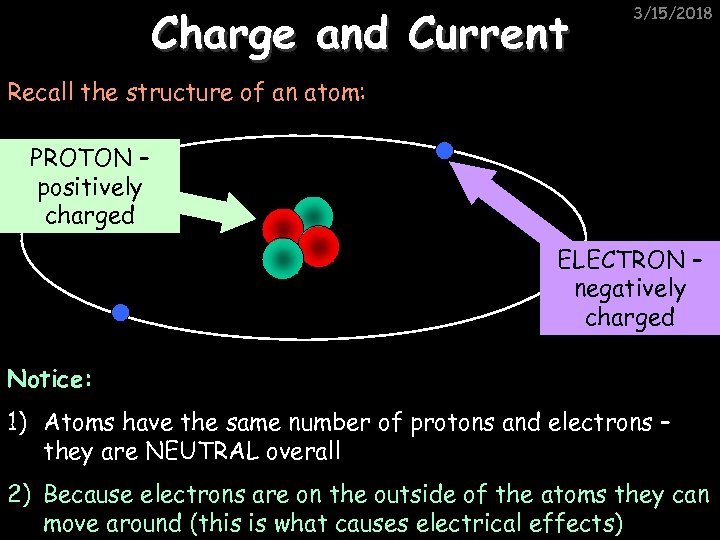Charge and Current 3/15/2018 Recall the structure of an atom: PROTON – positively charged ELECTRON – negatively charged Notice: 1) Atoms have the same number of protons and electrons – they are NEUTRAL overall 2) Because electrons are on the outside of the atoms they can move around (this is what causes electrical effects)

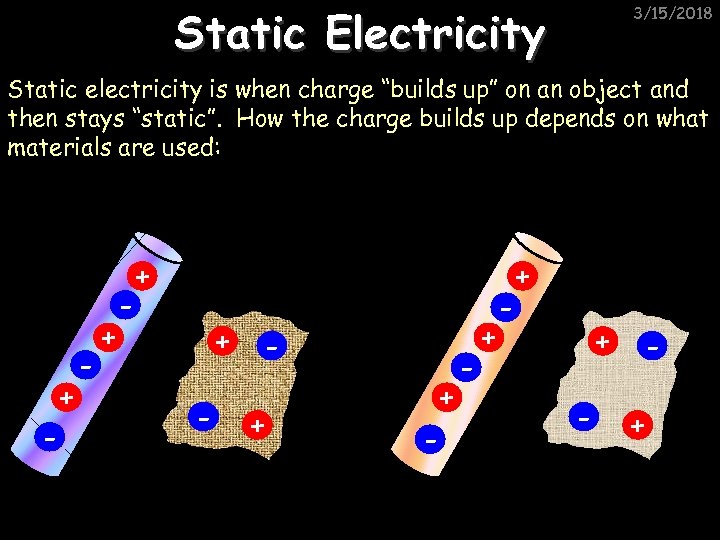Static Electricity 3/15/2018 Static electricity is when charge “builds up” on an object and then stays “static”. How the charge builds up depends on what materials are used: - + - + - +

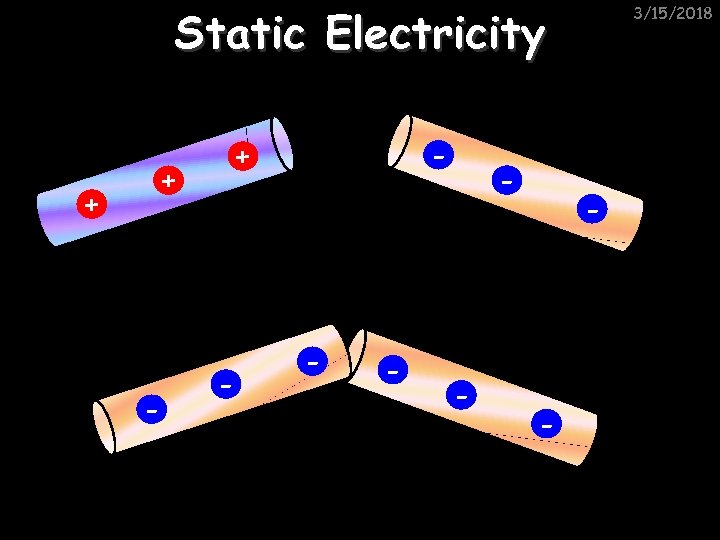Static Electricity + + - - - - - 3/15/2018 - -

Measuring Charge 3/15/2018 The charge on an electron is very small, so we measure charge using units called “coulombs” (C). One electron has a charge of 1. 6 x 10 -19 C. Charge can be measured using a coulombmeter, and they usually measure in nanocoloumbs (1 n. C = 10 -9 C). For example, a charged polythene rod may carry a charge of a few hundred nanocoulombs

Calculating Charge (Q) 3/15/2018 By definition, current is the rate of flow of charge. In other words, its how much charge flows per second. One amp (1 A) is equal to one coulomb per second (1 Cs-1). Charge and current are related by the equation: Current = rate of flow of charge I = ΔQ ΔT 1. A battery supplies 10 C over a period of 50 seconds. What is the current? 2. Another battery is connected for 2 minutes and provided a current of 0. 4 A. How much charge flowed? 3. A car battery has a capacity of 24 Ah (amp hours). If it provides a current of 48 A how long can it be used for? How much charge (in coulombs) does it contain?

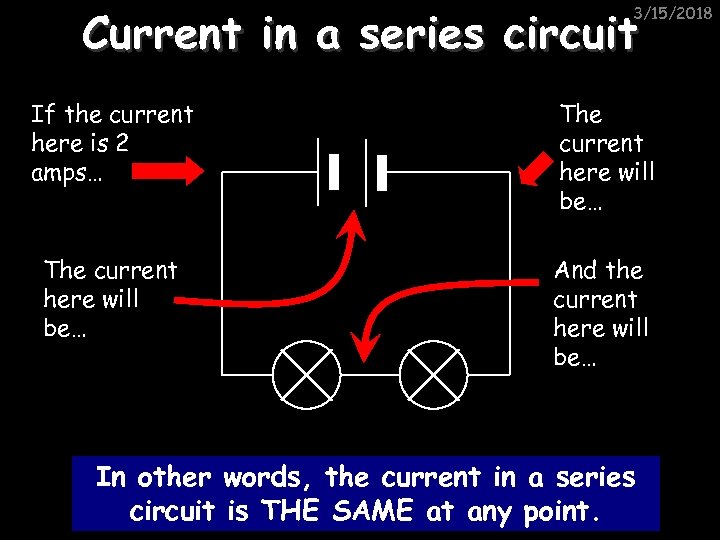Current in a series circuit 3/15/2018 If the current here is 2 amps… The current here will be… And the current here will be… In other words, the current in a series circuit is THE SAME at any point.

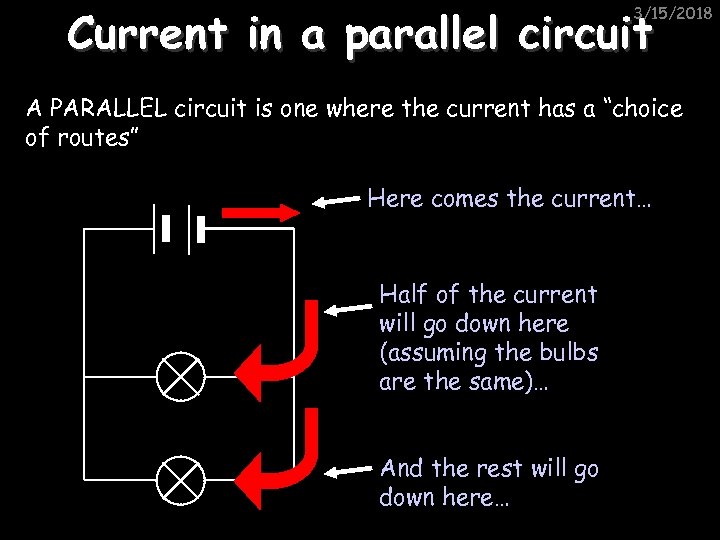Current in a parallel circuit 3/15/2018 A PARALLEL circuit is one where the current has a “choice of routes” Here comes the current… Half of the current will go down here (assuming the bulbs are the same)… And the rest will go down here…

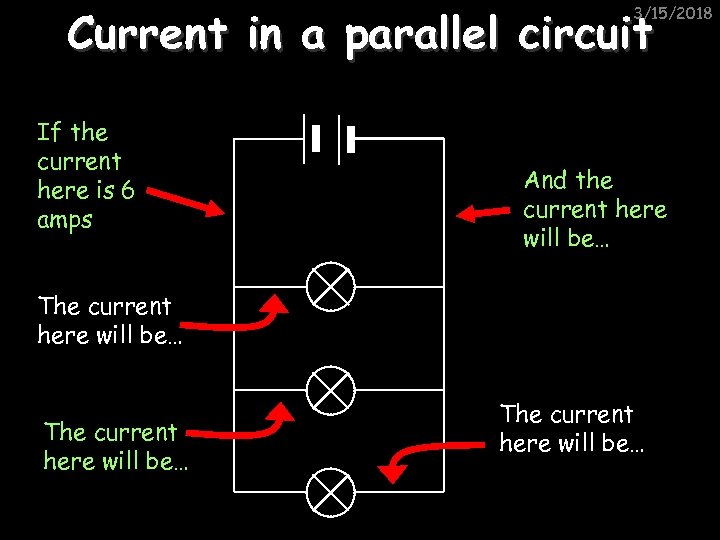Current in a parallel circuit 3/15/2018 If the current here is 6 amps And the current here will be… The current here will be…

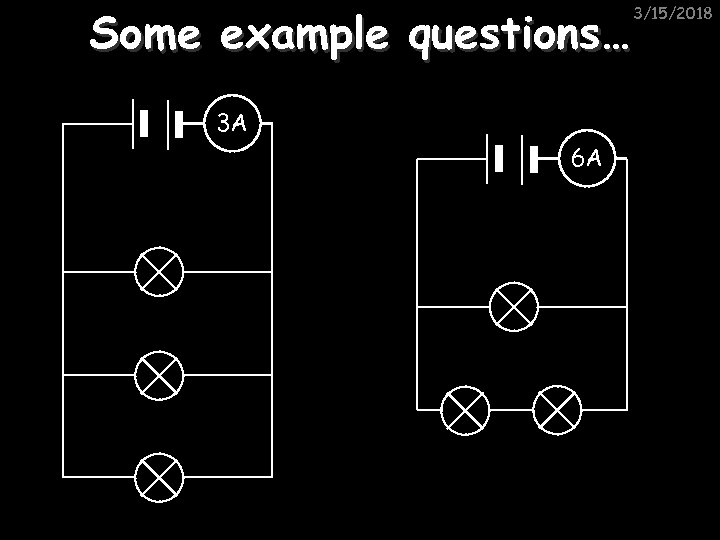Some example questions… 3 A 6 A 3/15/2018

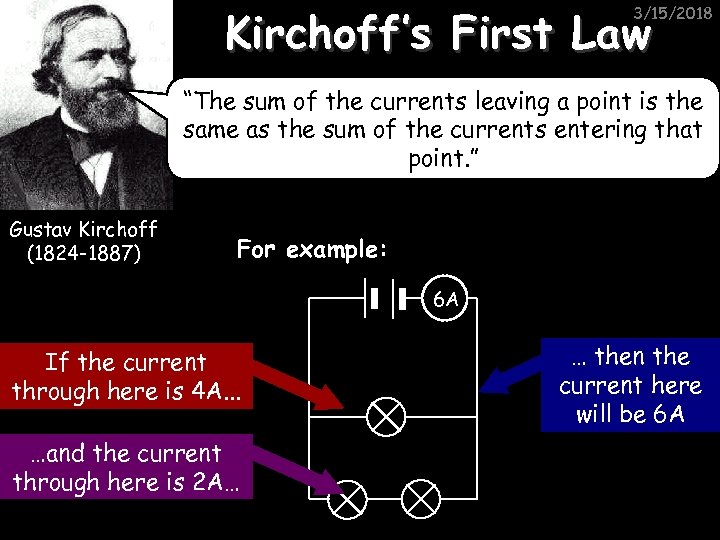Kirchoff’s First Law 3/15/2018 “The sum of the currents leaving a point is the same as the sum of the currents entering that point. ” Gustav Kirchoff (1824 -1887) For example: 6 A If the current through here is 4 A. . . …and the current through here is 2 A… … then the current here will be 6 A

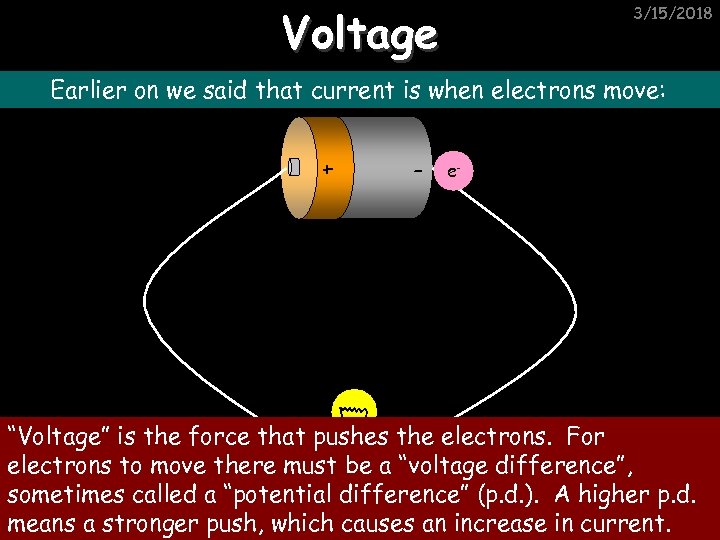Voltage 3/15/2018 Earlier on we said that current is when electrons move: + - e- “Voltage” is the force that- pushes the electrons. For e electrons to move there must be a “voltage difference”, sometimes called a “potential difference” (p. d. ). A higher p. d. means a stronger push, which causes an increase in current.

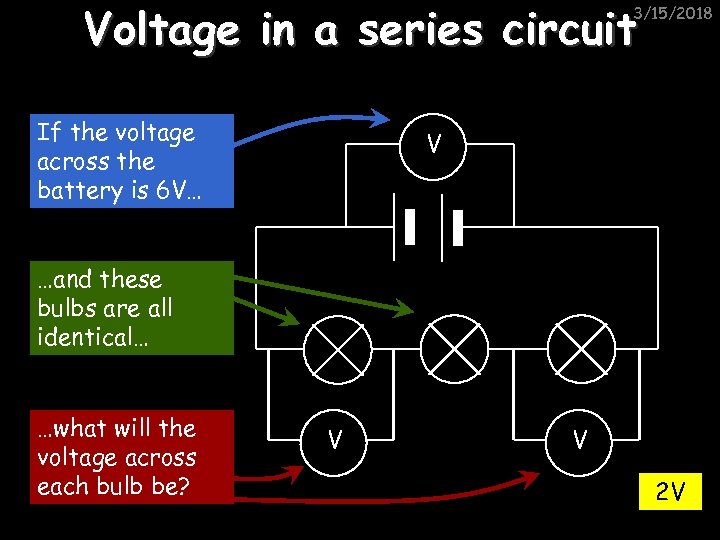Voltage in a series circuit 3/15/2018 If the voltage across the battery is 6 V… V …and these bulbs are all identical… …what will the voltage across each bulb be? V V 2 V

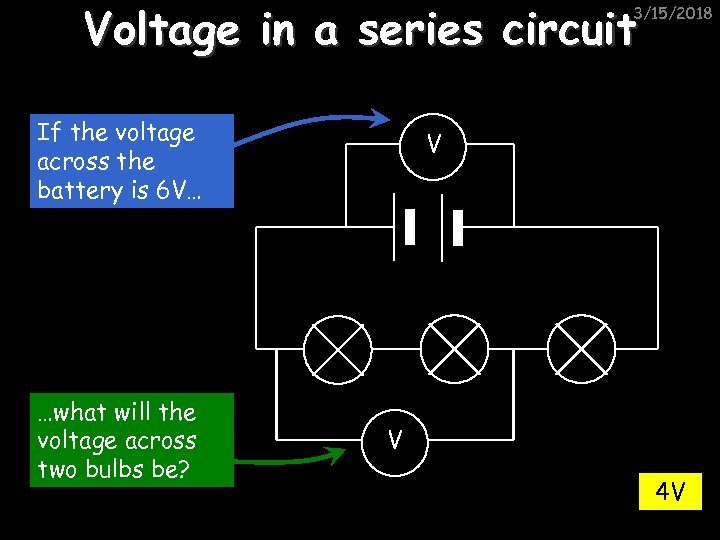Voltage in a series circuit 3/15/2018 If the voltage across the battery is 6 V… …what will the voltage across two bulbs be? V V 4 V

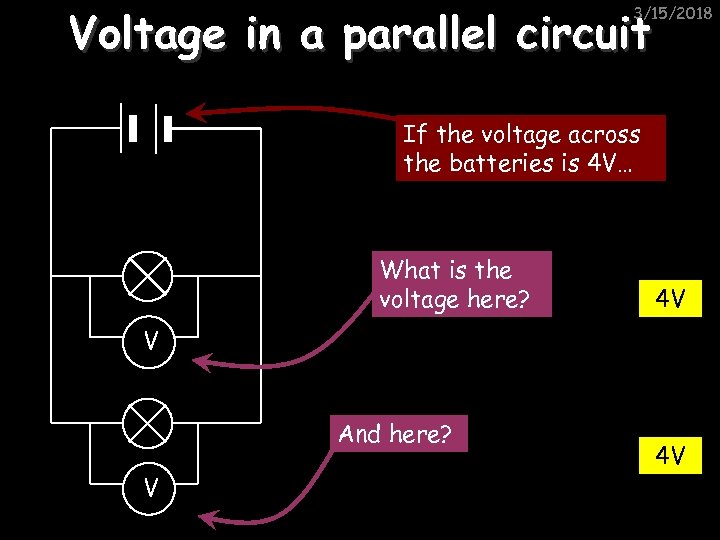Voltage in a parallel circuit 3/15/2018 If the voltage across the batteries is 4 V… What is the voltage here? 4 V V And here? V 4 V

Summary 3/15/2018 In a SERIES circuit: Current is THE SAME at any point Voltage SPLITS UP over each component In a PARALLEL circuit: Current SPLITS UP down each “strand” Voltage is THE SAME across each”strand”

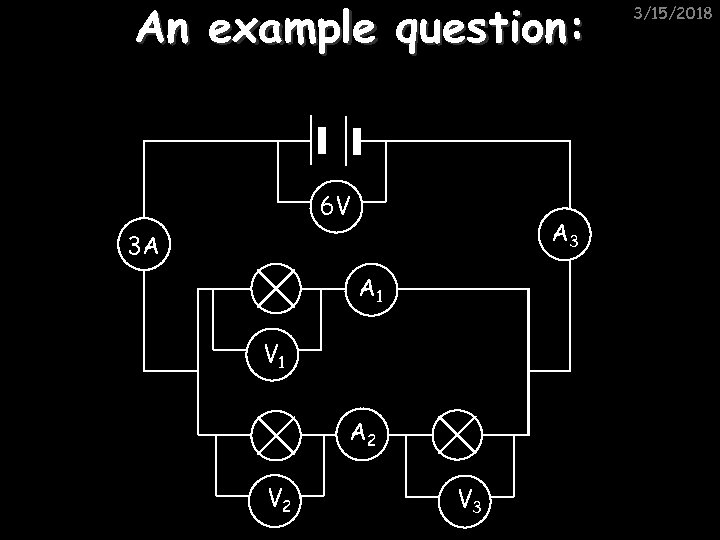An example question: 6 V A 3 3 A A 1 V 1 A 2 V 3 3/15/2018

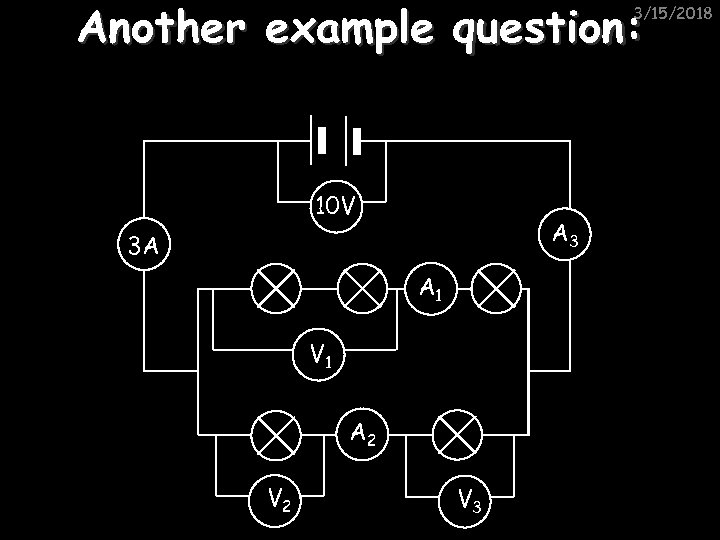Another example question: 3/15/2018 10 V A 3 3 A A 1 V 1 A 2 V 3

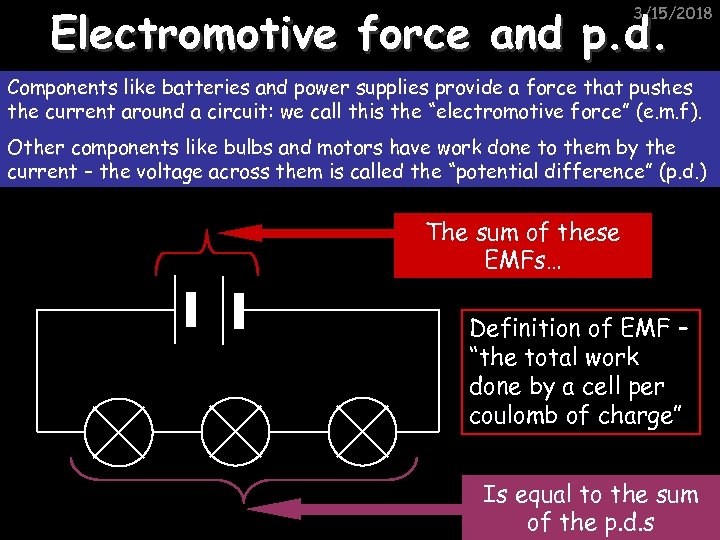Electromotive force and p. d. 3/15/2018 Components like batteries and power supplies provide a force that pushes the current around a circuit: we call this the “electromotive force” (e. m. f). Other components like bulbs and motors have work done to them by the current – the voltage across them is called the “potential difference” (p. d. ) The sum of these EMFs… Definition of EMF – “the total work done by a cell per coulomb of charge” Is equal to the sum of the p. d. s

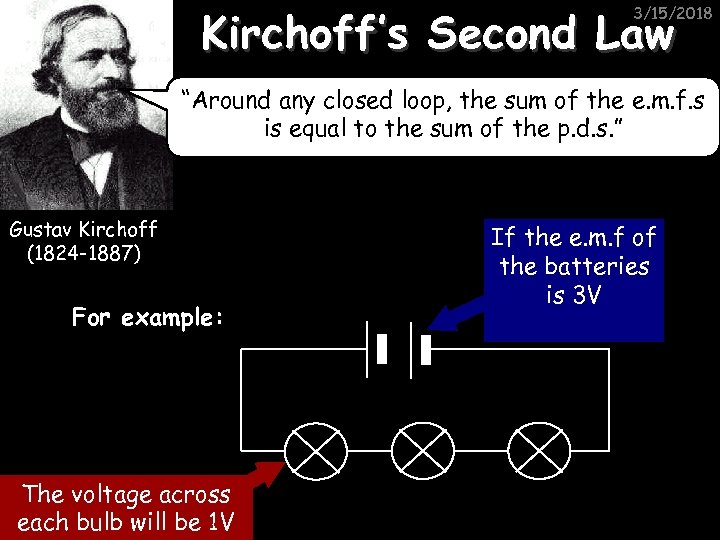Kirchoff’s Second Law 3/15/2018 “Around any closed loop, the sum of the e. m. f. s is equal to the sum of the p. d. s. ” Gustav Kirchoff (1824 -1887) For example: The voltage across each bulb will be 1 V If the e. m. f of the batteries is 3 V

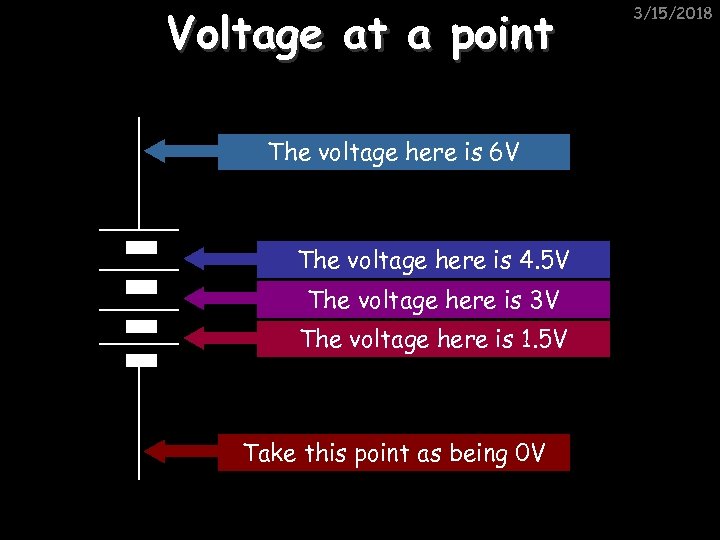Voltage at a point The voltage here is 6 V The voltage here is 4. 5 V The voltage here is 3 V The voltage here is 1. 5 V Take this point as being 0 V 3/15/2018

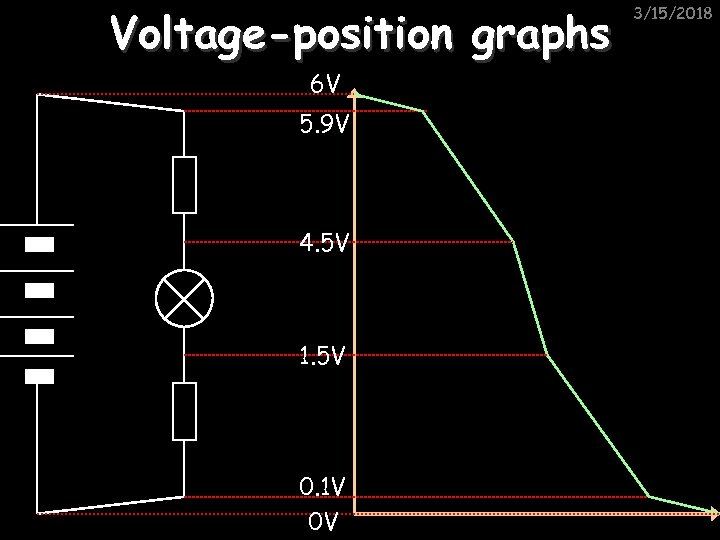Voltage-position graphs 6 V 5. 9 V 4. 5 V 1. 5 V 0. 1 V 0 V 3/15/2018

Work done 3/15/2018 Definition of a volt: The voltage between two points is the work done per coulomb travelling between the two points Voltage = work done charge We can see that 1 V = 1 JC-1 V=W Q

Example Questions 3/15/2018 1) A battery does 9 J of work. If it transfers 6 C of charge what is the battery’s voltage? 2) A powerpack does 100 J of work in transferring 20 C of charge. What is the voltage? 3) A 9 V battery transfers 20 C of charge. How much work did it do? 4) If the current of the battery is 0. 2 A how long was it used for? 5) 240 J of work is done to a 12 V motor. How much charge flowed through it? 6) If this motor was used for 40 seconds how much current did it draw?

Electrical Power Voltage = work done 1) Recall: charge 2) Also, recall that power = rate of doing work 3) Therefore 4) But I = Q so T 3/15/2018 W = QV Power = work done P=W time T Power = charge x voltage P = Q x V time Power = current x voltage P = IV or V 2/R or I 2 R T

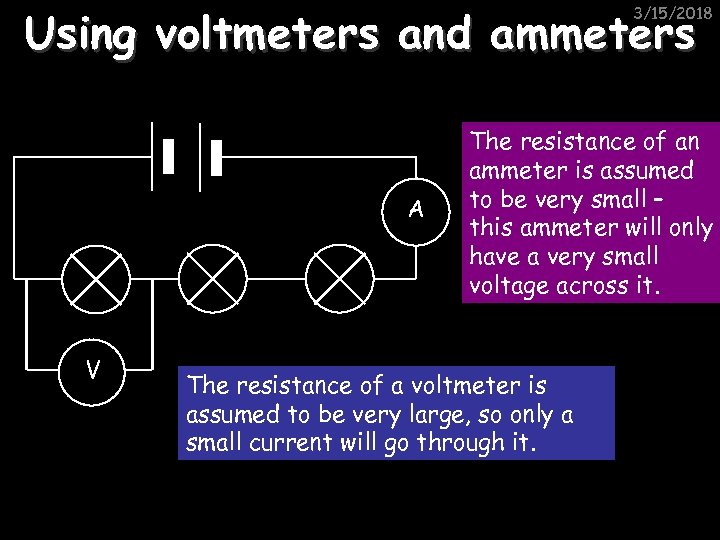Using voltmeters and ammeters 3/15/2018 A V The resistance of an ammeter is assumed to be very small – this ammeter will only have a very small voltage across it. The resistance of a voltmeter is assumed to be very large, so only a small current will go through it.

Resistance 3/15/2018 Resistance is anything that will RESIST a current. It is measured in Ohms, a unit named after me. Georg Simon Ohm 1789 -1854 The resistance of a component can be calculated using Ohm’s Law: Resistance (in ) = V Voltage (in V) Current (in A) I R

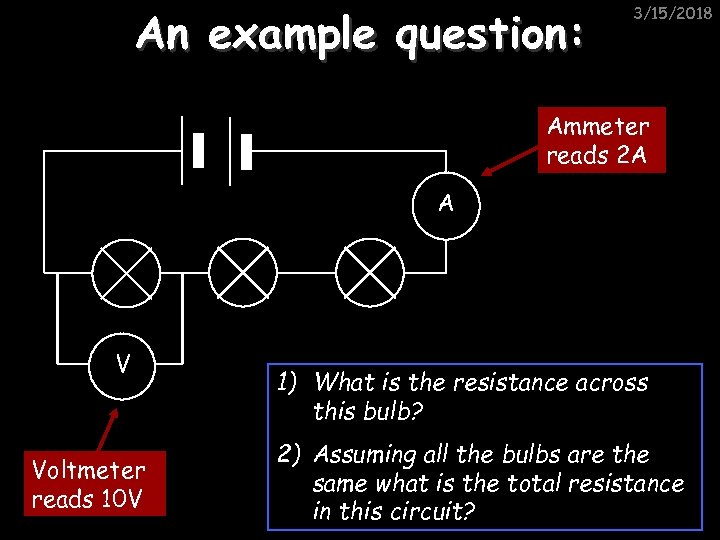An example question: 3/15/2018 Ammeter reads 2 A A V Voltmeter reads 10 V 1) What is the resistance across this bulb? 2) Assuming all the bulbs are the same what is the total resistance in this circuit?

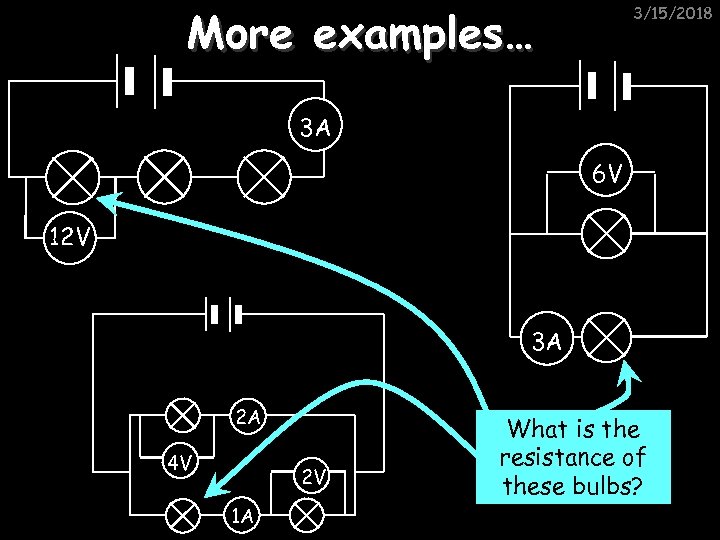More examples… 3/15/2018 3 A 6 V 12 V 3 A 2 A 4 V 2 V 1 A What is the resistance of these bulbs?

Resistance 3/15/2018 Resistance is anything that opposes an electric current. Resistance (Ohms, ) = Potential Difference (volts, V) Current (amps, A) What is the resistance of the following: 1) A bulb with a voltage of 3 V and a current of 1 A. 2) A resistor with a voltage of 12 V and a current of 3 A 3) A diode with a voltage of 240 V and a current of 40 A 4) A thermistor with a current of 0. 5 A and a voltage of 10 V

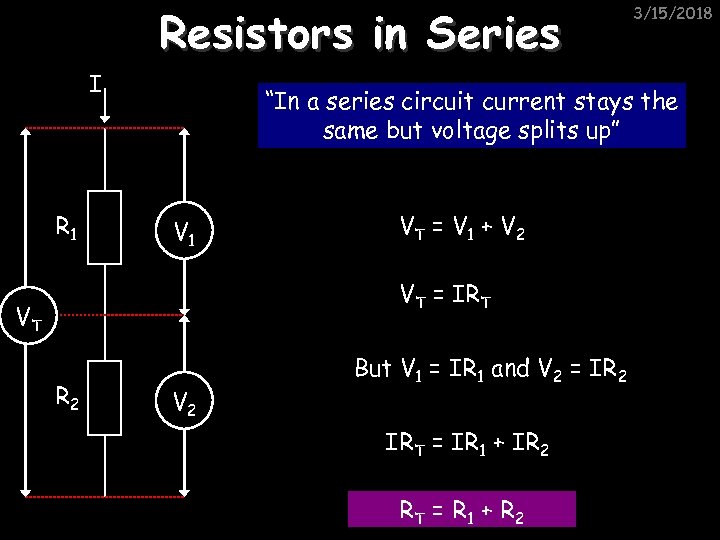Resistors in Series I R 1 “In a series circuit current stays the same but voltage splits up” V 1 VT = V 1 + V 2 VT = IRT VT R 2 3/15/2018 V 2 But V 1 = IR 1 and V 2 = IR 2 IRT = IR 1 + IR 2 RT = R 1 + R 2

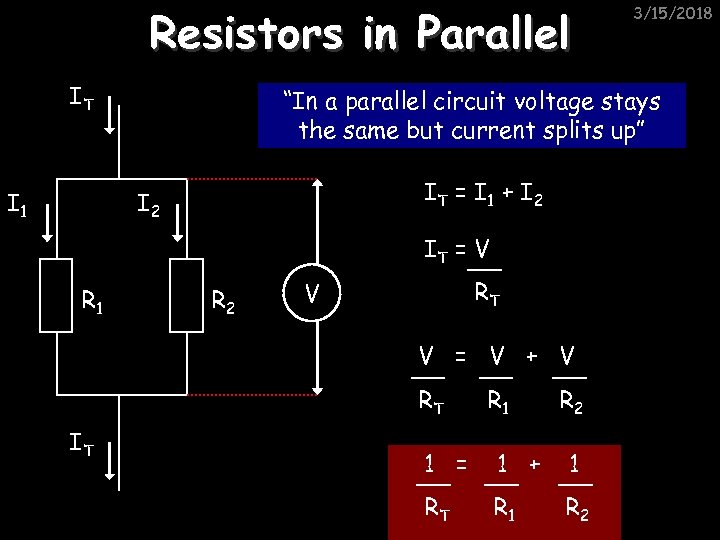Resistors in Parallel IT I 1 “In a parallel circuit voltage stays the same but current splits up” IT = I 1 + I 2 IT = V R 1 R 2 RT V V = V + V RT IT 3/15/2018 R 1 R 2 1 = 1 + 1 RT R 1 R 2

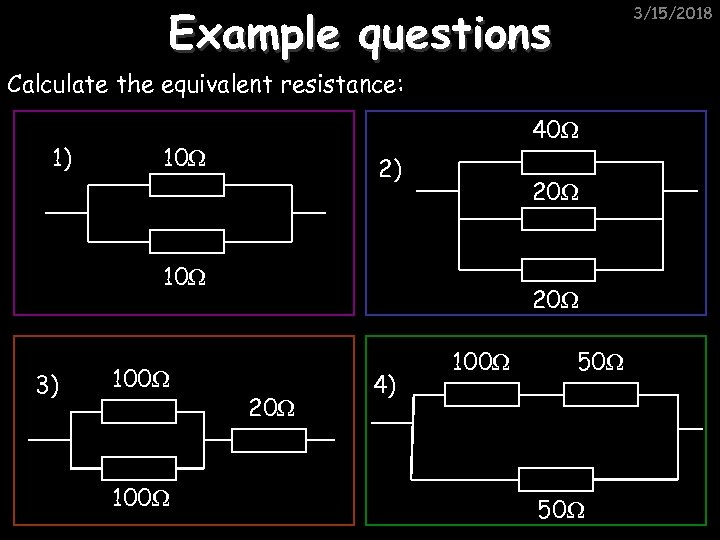Example questions 3/15/2018 Calculate the equivalent resistance: 1) 40Ω 10Ω 2) 20Ω 10Ω 3) 100Ω 20Ω 4) 100Ω 50Ω

Power through a resistor Recall: 1) P = IV Putting these two equations together gives us: 3/15/2018 2) V = IR Power = I x IR = I 2 R or V 2/R 1) A 10Ω resistor has 2 A flowing through it. Calculate the power dissipated by the resistor. 2) A motor takes a current of 10 A. If its resistance is 2. 2 MΩ calculate the power dissipated by the motor. 3) A 2 KW heater has a resistance of 20 Ω. Calculate the current through it.

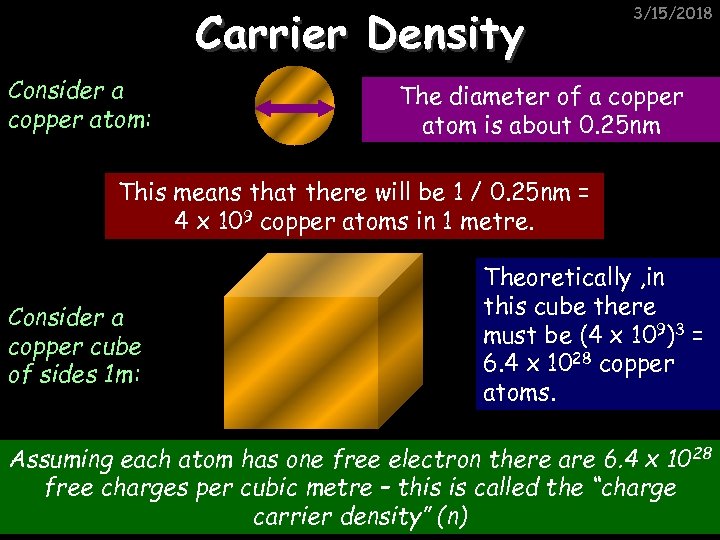Carrier Density Consider a copper atom: 3/15/2018 The diameter of a copper atom is about 0. 25 nm This means that there will be 1 / 0. 25 nm = 4 x 109 copper atoms in 1 metre. Consider a copper cube of sides 1 m: Theoretically , in this cube there must be (4 x 109)3 = 6. 4 x 1028 copper atoms. Assuming each atom has one free electron there are 6. 4 x 10 28 free charges per cubic metre – this is called the “charge carrier density” (n)

Some questions… 3/15/2018 1) If, for copper, n = 6. 4 x 1028 and each electron has a charge of 1. 6 x 10 -19 C how much free charge was in the cubic metre? 2) How much free charge would be in 1 mm 3 instead? 3) Calculate the carrier density for a cubic metre of another atom with diameter 0. 3 nm. Assume each atom has one free electron again.

Drift Speed 3/15/2018 Definition: Drift speed is the speed with which electrons will move down a wire. How do we work it out? Consider a wire of cross sectional area A and charge carrier density n, where each carrier has the charge q and they are moving with a drift speed of v. 1) Every second the volume of charge carriers that pass a point will be Av 2) Therefore the number of charge carriers that pass by every second is given by n. Av 3) Therefore the charge that passes by every second will be n. Avq 4) But charge per second IS current, so… I = n. Aqv

Example questions 3/15/2018 1) Calculate the current down a 1 mm 2 wire where the drift speed is 1 mms-1 and the carrier density is 6. 4 x 1028 m-3 (remember that the charge on an electron is 1. 6 x 10 -19 C) 2) Calculate the drift speed down a 2 mm 2 wire which has a current of 0. 5 A passing through it and a carrier density of 6. 4 x 1028 m-3.

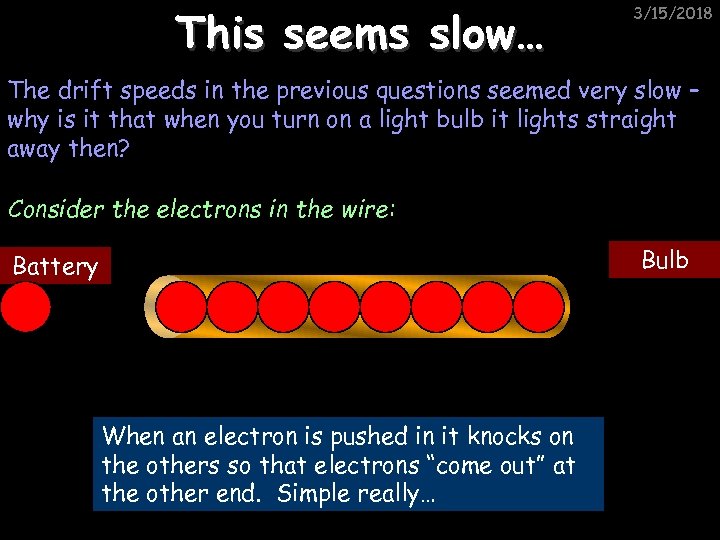This seems slow… 3/15/2018 The drift speeds in the previous questions seemed very slow – why is it that when you turn on a light bulb it lights straight away then? Consider the electrons in the wire: Bulb Battery When an electron is pushed in it knocks on the others so that electrons “come out” at the other end. Simple really…

Comparing Drift Speeds 3/15/2018 Consider two wires connected in series: 1 2 Q. The area of wire 2 is twice that of wire 1. Which wire do electrons travel fastest in? In wire 1 I 1 = n 1 A 1 q 1 v 1 In wire 2 I 2 = n 2 A 2 q 2 v 2 However, in series I 1=I 2 therefore n 1 A 1 q 1 v 1 = n 2 A 2 q 2 v 2 Also, q 1 = q 2 and n 1 = n 2… Therefore A 1 v 1 = A 2 v 2

Resistivity 3/15/2018 The resistance of a wire depends on 3 things: the length of the wire, the width of the wire and what the wire is made of: Resistance = resistivity x length area R = ρL A Calculate the following: 1) The resistance of a copper wire of length 2 m, area 2 mm 2 and resistivity 1. 7 x 10 -8 Ωm 2) The resistance of an iron wire of length 100 m, area 5 mm 2 and resistivity 1 x 10 -7 Ωm 3) A copper wire has a resistance of 5Ω. If the wire is 20 m long and the wire is cylindrical what is the radius of the wire?

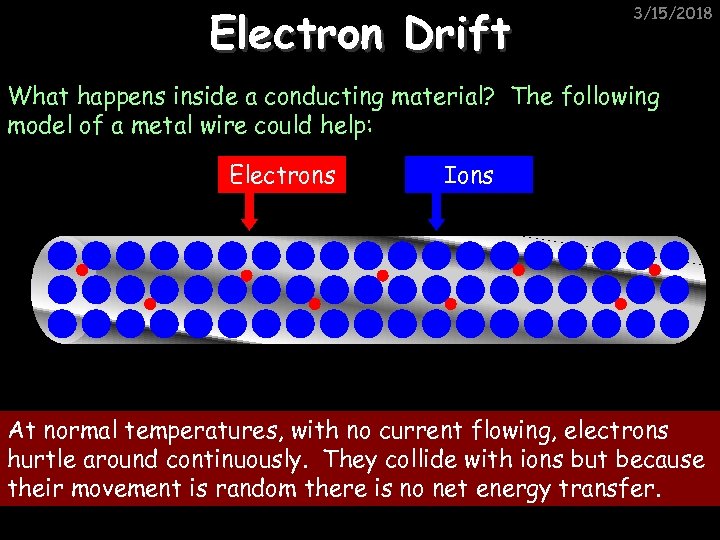Electron Drift 3/15/2018 What happens inside a conducting material? The following model of a metal wire could help: Electrons Ions At normal temperatures, with no current flowing, electrons hurtle around continuously. They collide with ions but because their movement is random there is no net energy transfer.

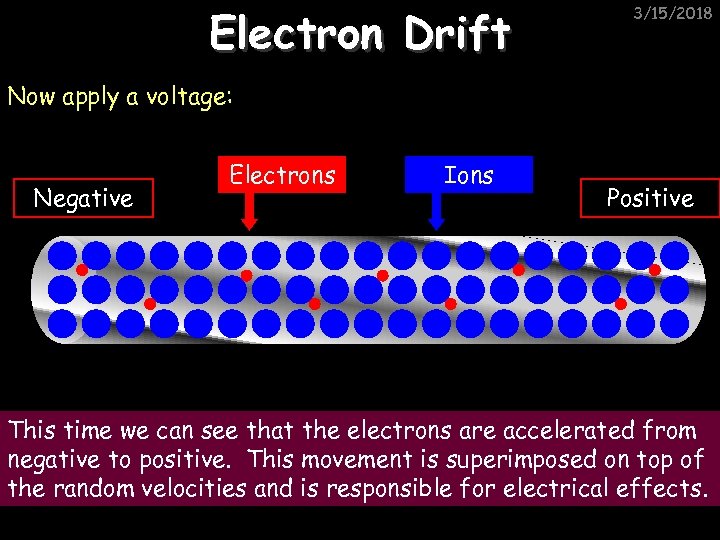Electron Drift 3/15/2018 Now apply a voltage: Negative Electrons Ions Positive This time we can see that the electrons are accelerated from negative to positive. This movement is superimposed on top of the random velocities and is responsible for electrical effects.

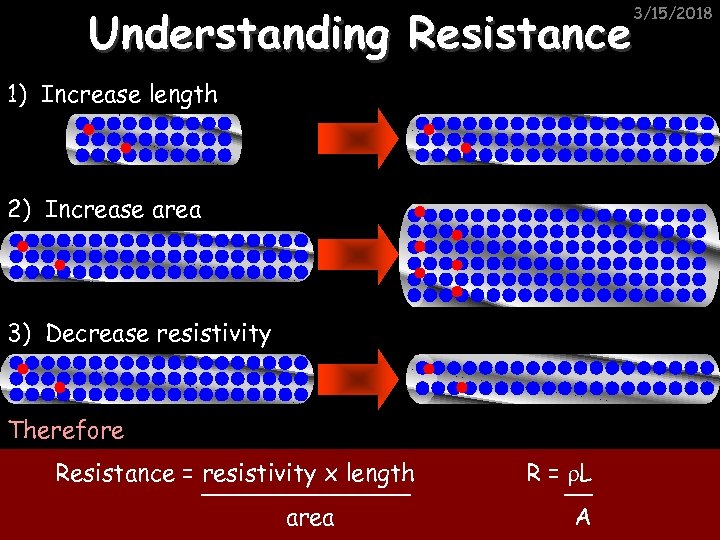Understanding Resistance 3/15/2018 1) Increase length 2) Increase area 3) Decrease resistivity Therefore Resistance = resistivity x length area R = ρL A

Understanding Current Recall the equation: 3/15/2018 Increasing the temperature of a metal will increase the ______ of the ions. This will increase the ____ of the metal and decrease the current because it lowers the _____. I = n. Aqv In semiconductors the carrier density is small but _____ with temperature, so the resistivity of a semiconductor decreases with temperature (e. g. a ____). These devices have a “negative temperature coefficient”. In insulators n is very low. Words – thermistor, resistivity, vibrations, drift speed, increases

Potential Dividers 3/15/2018 VIN R 1 VOUT R 2 0 V 0 V The Potential Divider equation: VOUT VIN (R 2) x (R 1 + R 2)

Some example questions 12 V 50 V 100 0 V 10 VOUT 0 V 3 V 75 0 V VOUT 0 V 1. 5 V 75 25 0 V 3/15/2018 50 VOUT 0 V 45 0 V VOUT 0 V

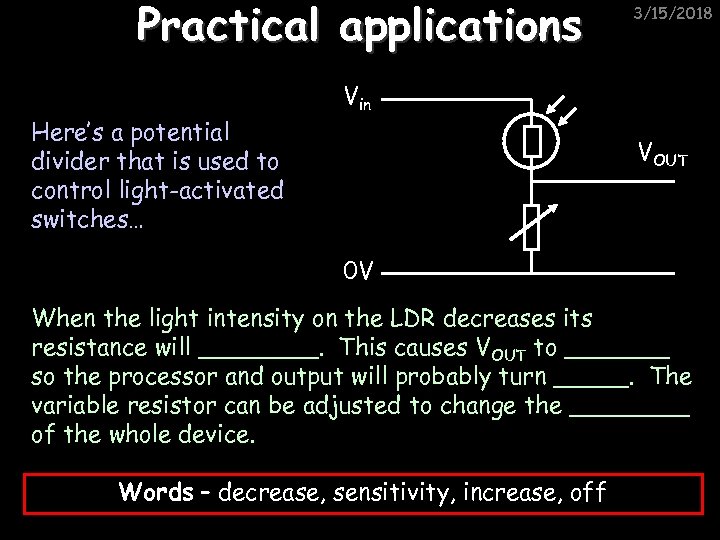Practical applications Here’s a potential divider that is used to control light-activated switches… 3/15/2018 Vin VOUT 0 V When the light intensity on the LDR decreases its resistance will ____. This causes VOUT to _______ so the processor and output will probably turn _____. The variable resistor can be adjusted to change the ____ of the whole device. Words – decrease, sensitivity, increase, off

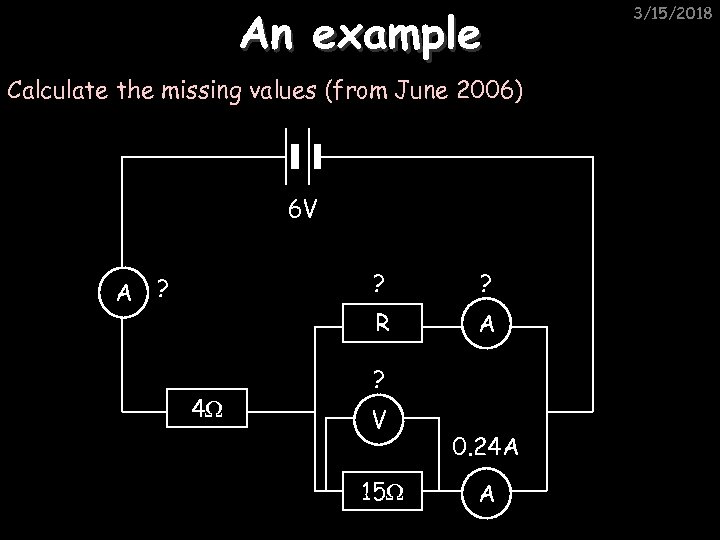An example Calculate the missing values (from June 2006) 6 V A ? 4Ω ? R ? A ? V 15Ω 0. 24 A A 3/15/2018

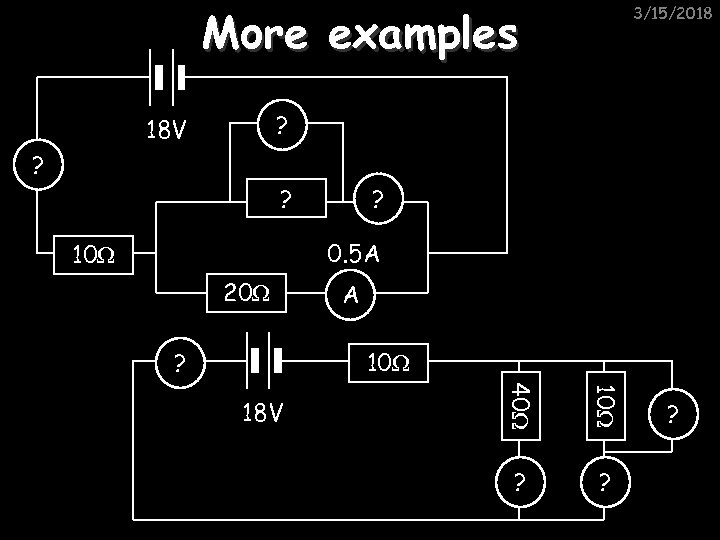More examples 3/15/2018 ? 18 V ? ? ? 0. 5 A 10Ω 20Ω A 10Ω ? 40Ω 18 V ? ? ?

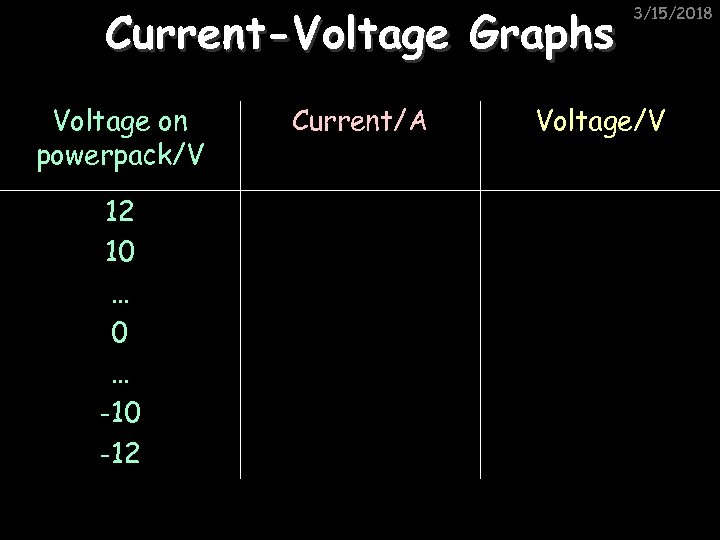Current-Voltage Graphs Voltage on powerpack/V 12 10 … -10 -12 Current/A 3/15/2018 Voltage/V

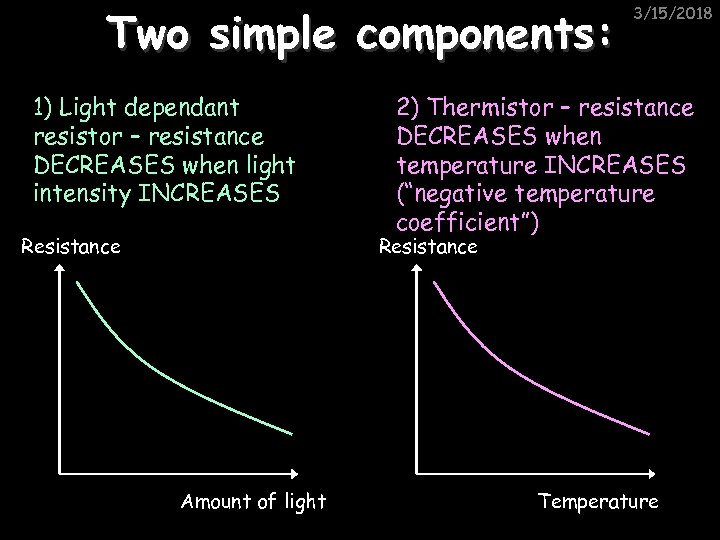Two simple components: 1) Light dependant resistor – resistance DECREASES when light intensity INCREASES Resistance 3/15/2018 2) Thermistor – resistance DECREASES when temperature INCREASES (“negative temperature coefficient”) Resistance Amount of light Temperature

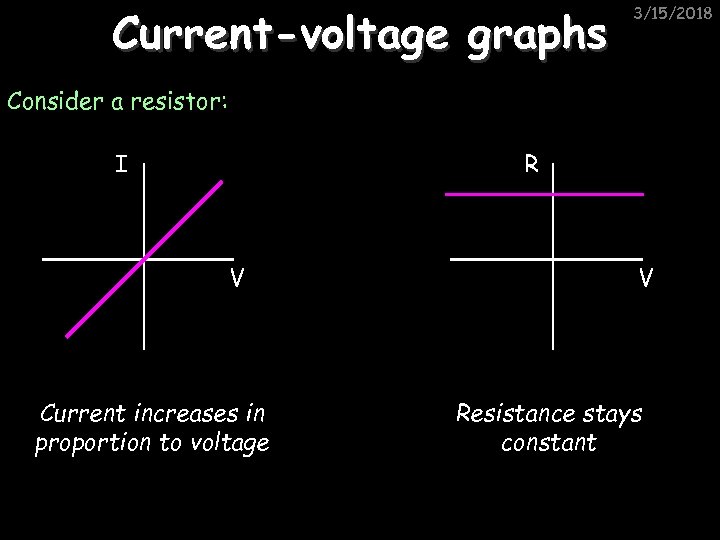Current-voltage graphs 3/15/2018 Consider a resistor: I R V Current increases in proportion to voltage V Resistance stays constant

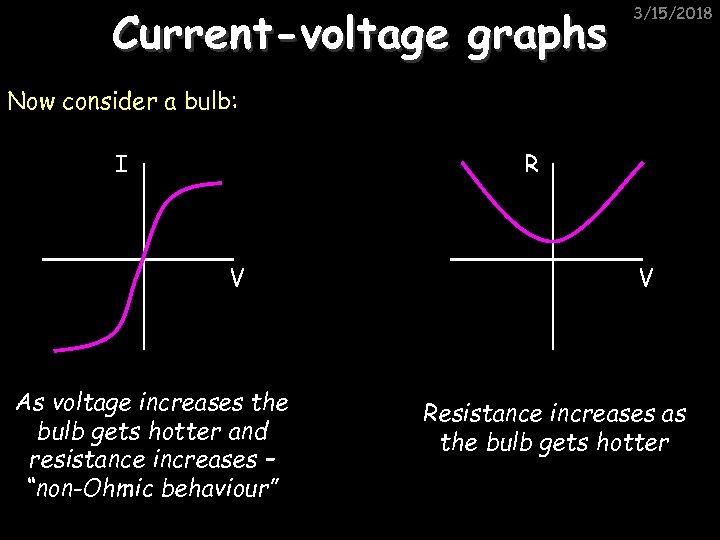Current-voltage graphs 3/15/2018 Now consider a bulb: I R V As voltage increases the bulb gets hotter and resistance increases – “non-Ohmic behaviour” V Resistance increases as the bulb gets hotter

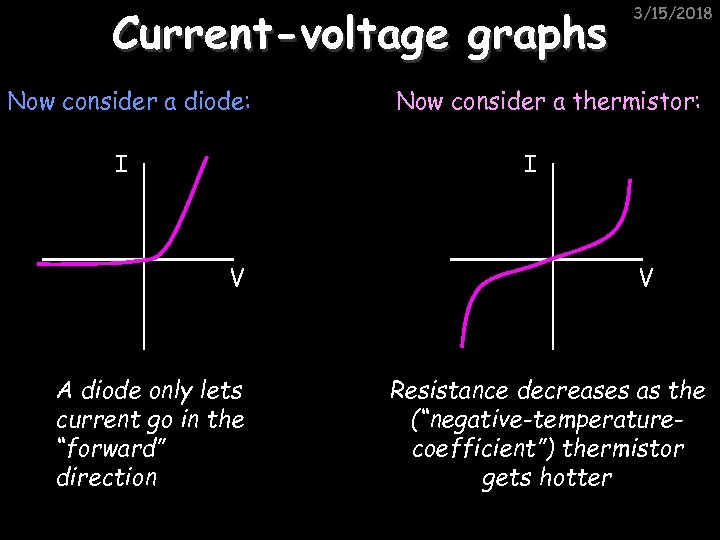Current-voltage graphs Now consider a diode: I 3/15/2018 Now consider a thermistor: I V A diode only lets current go in the “forward” direction V Resistance decreases as the (“negative-temperaturecoefficient”) thermistor gets hotter

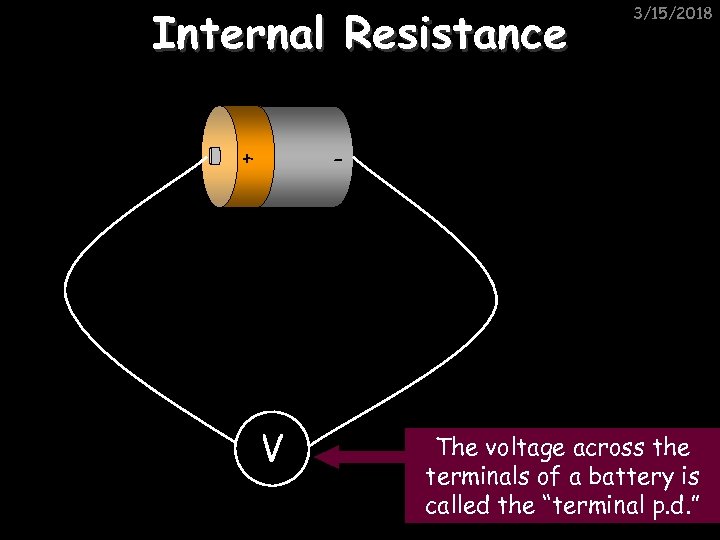Internal Resistance + 3/15/2018 - V The voltage across the terminals of a battery is called the “terminal p. d. ”

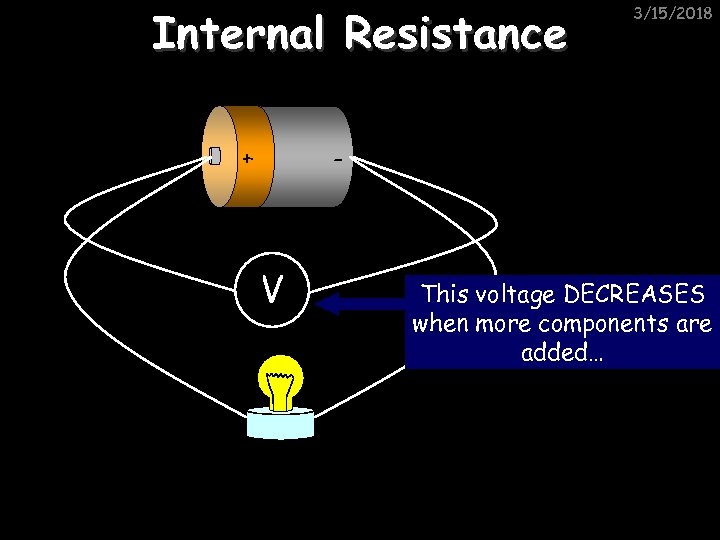Internal Resistance + 3/15/2018 - V This voltage DECREASES when more components are added…

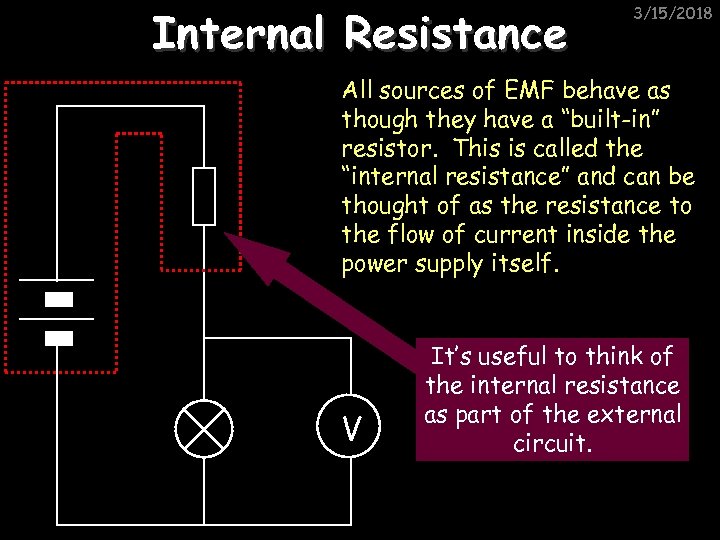Internal Resistance 3/15/2018 All sources of EMF behave as though they have a “built-in” resistor. This is called the “internal resistance” and can be thought of as the resistance to the flow of current inside the power supply itself. V It’s useful to think of the internal resistance as part of the external circuit.

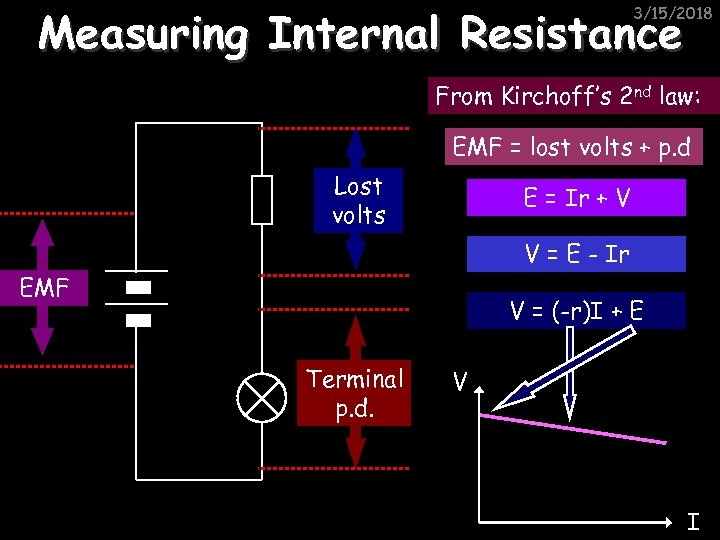Measuring Internal Resistance 3/15/2018 From Kirchoff’s 2 nd law: EMF = lost volts + p. d Lost volts E = Ir + V V = E - Ir EMF V = (-r)I + E Terminal p. d. V I

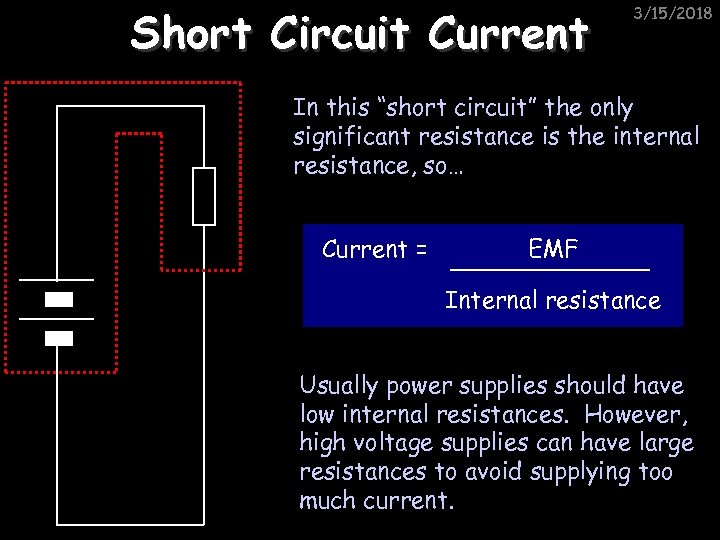Short Circuit Current 3/15/2018 In this “short circuit” the only significant resistance is the internal resistance, so… Current = EMF Internal resistance Usually power supplies should have low internal resistances. However, high voltage supplies can have large resistances to avoid supplying too much current.

Numerical quiz 3/15/2018 1) What is the resistance of a bulb with a voltage of 12 V and a current of 2 A through it? 2) This bulb transfers 100 C of electrical energy. How long was it used for? 3) A power supply does 4, 800 J of work. If it transfers 20 C of charge what is the EMF of the supply? 4) What is the resistance of a thermistor when the p. d. across it is 20 V and the current through it is 2 A? 5) Work out the total resistance of the following: 10Ω each 20Ω each

Numerical quiz 3/15/2018 6) A thermistor has a resistance of 200 when 20 V is applied across it. What is the current through thermistor? 7) The same thermistor is put in a warm water bath. The resistance drops to 120. What is the current through it now? 8) A resistor takes a current of 2 A. If the resistor has a resistance of 10Ω calculate the power dissipated in the resistor. 9) A piece of copper wire has a length of 2 m, an area of 1 mm 2 and a resistivity of 1. 7 x 10 -8Ωm. Calculate the resistance. 10) Calculate the charge carrier density in this wire if the drift speed is 1 mms-1 and the current through it is 2 A.

Numerical quiz 3/15/2018 11) How many electrons does it take to have a charge of 20 C? 12) A bulb dissipates 800 W of power. If its resistance is 200Ω calculate the current through it. 13) What is the voltage across this bulb? 14) An electric fire uses 1200 C of charge over 2 minutes. What current did it draw? 15) Calculate the following output voltages: 12 V 20 V 50 150 0 V 4 VOUT 0 V 6 0 V VOUT 0 V

3/15/2018 The Nature of Light W Richards The Weald School

Intensity 3/15/2018 Definition: “Intensity” means the strength of light arriving at a certain point, and can also be called “Radiation flux density” Energy dissipation Clearly, a wave will get weaker the further it travels. Assuming the wave comes from a point source and travels out equally in all directions we can say: Energy flux = Power (in W) (in Wm-2) Area (in m 2) φ= P 4πr 2 An “inverse square law”

Introduction 3/15/2018 Some basic principles: 1) The wavelength of blue light is around 400 nm (4 x 10 -7 m) 2) The wavelength of red light is around 650 nm (6. 5 x 10 -7 m) 3) Therefore blue light is higher frequency than red light 4) Light is treated as being a wave. Therefore the amount of energy a light wave contains should depend on its intensity or brightness.

Photoelectric Emission 3/15/2018 Consider a gold-leaf electroscope… Now charge the top: -- - --5000 V +

Photoelectric Emission 3/15/2018 Let’s put a piece of zinc on top: Now shine some UV light onto it: lt U et ol vi ra - - - Ultra-violet light is causing the zinc to emit electrons – this is “Photoelectric Emission”.

Some definitions… 3/15/2018 For zinc, this effect is only seen when UV light is used, i. e. when the light has a frequency of 1 x 1015 Hz or higher. This is called the “Threshold Frequency” and is generally lower for more reactive metals. Max Planck (1858 -1947) proposed that electromagnetic radiation, like light, comes in small packets. The general name for these packets is “quanta”. In the specific case of electromagnetic radiation, a quanta is called a “photon” and its energy depends on its frequency, not how bright it is. The amount of energy needed to release an electron from a metal is called the “work function” and is given the symbol φ. Generally, work functions are lower for more reactive metals.

Photoelectron Energy 3/15/2018 …and some energy is given to the electron as kinetic energy. - Some energy is needed to release the electron (the work function φ)… Photon Energy = work function + kinetic energy of electron

Calculating Photon Energy 3/15/2018 I think that the energy of a photon is proportional to its frequency, so E=hf, where h = Planck’s Constant = 6. 63 x 10 -34 Js. On the previous slide we said that… Photon energy = work function + kinetic energy of electron hf = φ + 1/2 mv 2

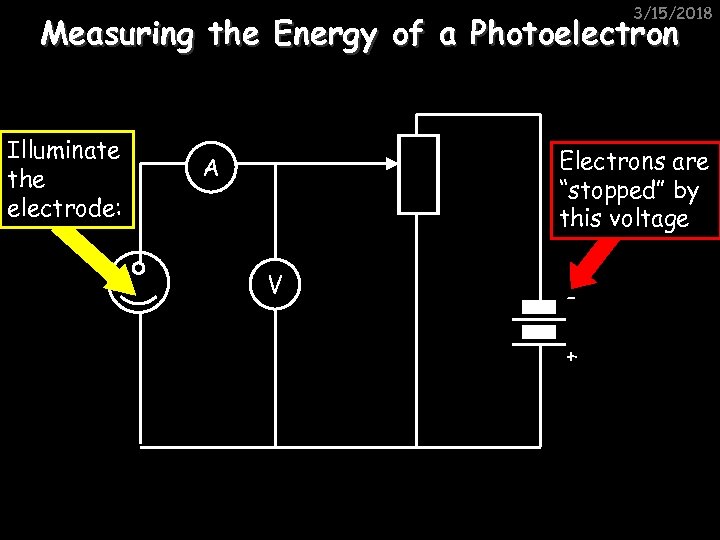3/15/2018 Measuring the Energy of a Photoelectron Illuminate the electrode: Electrons are “stopped” by this voltage A V +

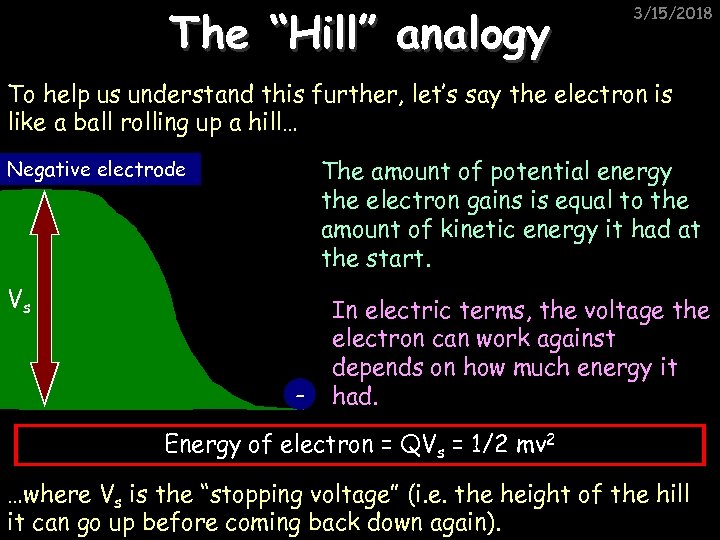The “Hill” analogy 3/15/2018 To help us understand this further, let’s say the electron is like a ball rolling up a hill… The amount of potential energy the electron gains is equal to the amount of kinetic energy it had at the start. Negative electrode Vs - In electric terms, the voltage the electron can work against depends on how much energy it had. Energy of electron = QVs = 1/2 mv 2 …where Vs is the “stopping voltage” (i. e. the height of the hill it can go up before coming back down again).

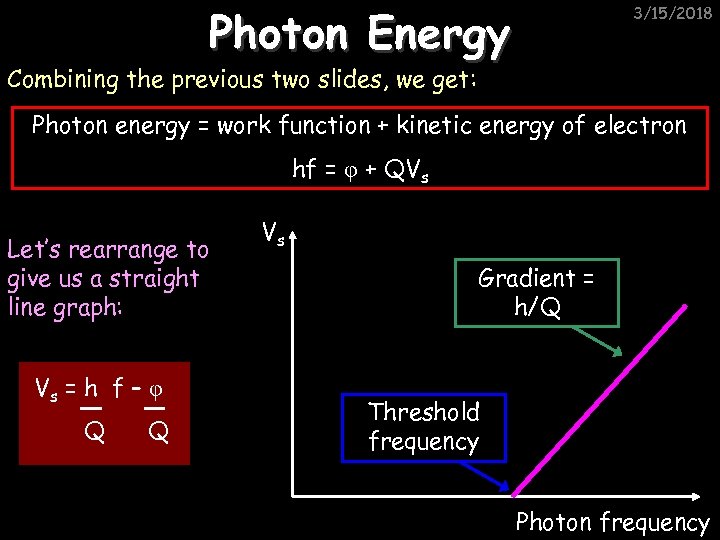Photon Energy 3/15/2018 Combining the previous two slides, we get: Photon energy = work function + kinetic energy of electron hf = φ + QVs Let’s rearrange to give us a straight line graph: Vs = h f – φ Q Q Vs Gradient = h/Q Threshold frequency Photon frequency

Spectra – introduction 3/15/2018

Spectra Source of light 3/15/2018 “Spectra”

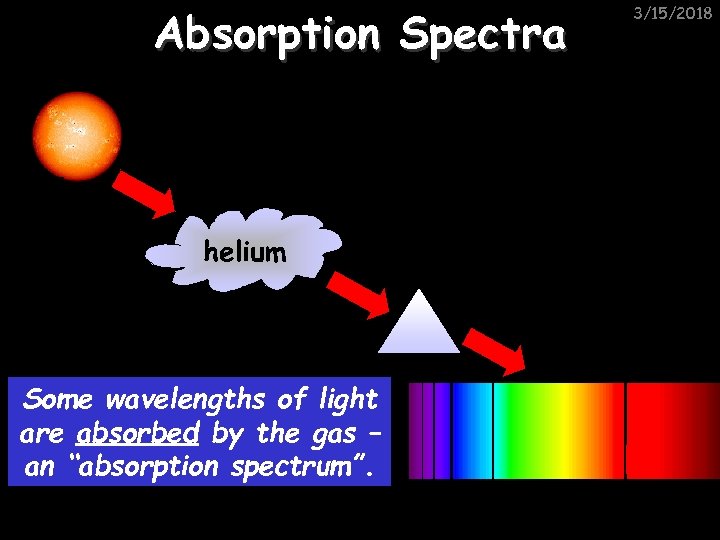Absorption Spectra helium Some wavelengths of light are absorbed by the gas – an “absorption spectrum”. 3/15/2018

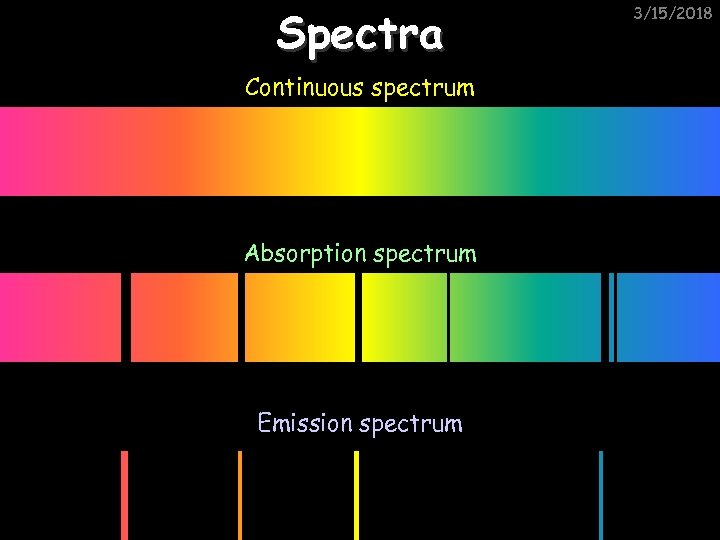Spectra Continuous spectrum Absorption spectrum Emission spectrum 3/15/2018

Emission Spectra Hydrogen Helium Sodium 3/15/2018

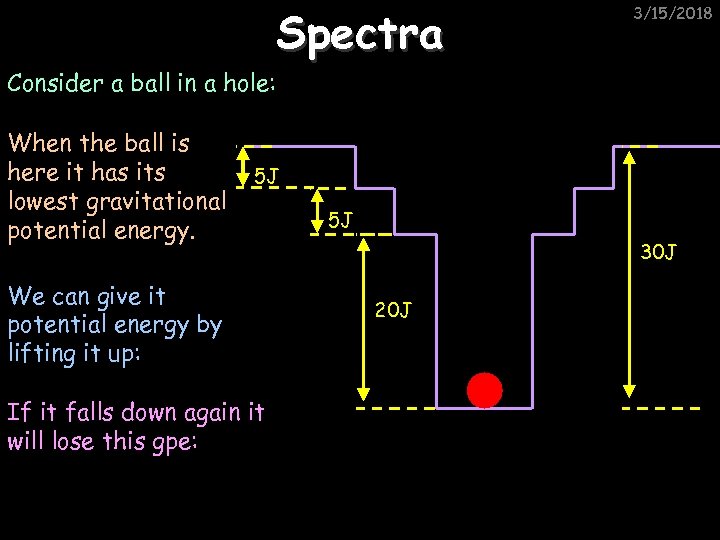Spectra 3/15/2018 Consider a ball in a hole: When the ball is here it has its lowest gravitational potential energy. 5 J We can give it potential energy by lifting it up: If it falls down again it will lose this gpe: 5 J 30 J 20 J

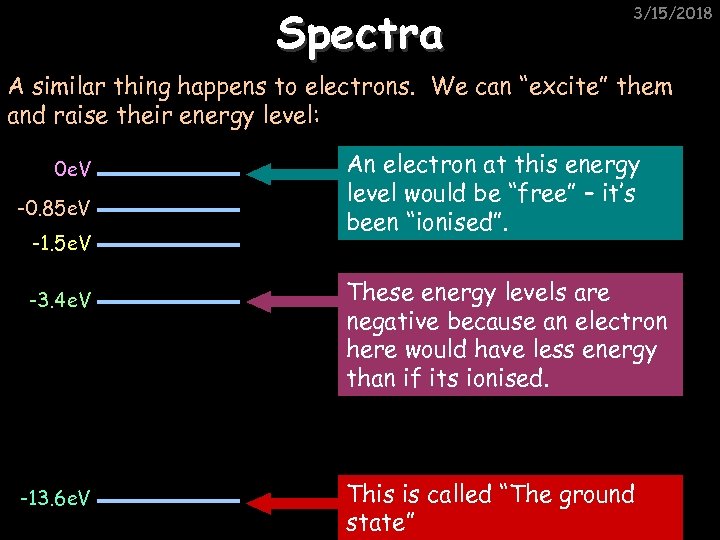Spectra 3/15/2018 A similar thing happens to electrons. We can “excite” them and raise their energy level: 0 e. V -0. 85 e. V -1. 5 e. V -3. 4 e. V -13. 6 e. V An electron at this energy level would be “free” – it’s been “ionised”. These energy levels are negative because an electron here would have less energy than if its ionised. This is called “The ground state”

Spectra 3/15/2018 If we illuminate the atom we can excite the electron: Q. What wavelength of light would be needed to excite this electron to ionise it? 0 e. V -0. 85 e. V -1. 5 e. V -3. 4 e. V Light Energy change = 3. 4 e. V = 5. 44 x 10 -19 J. Using E=hc/λ wavelength = 3. 66 x 10 -7 m -13. 6 e. V (In other words, ultra violet light)

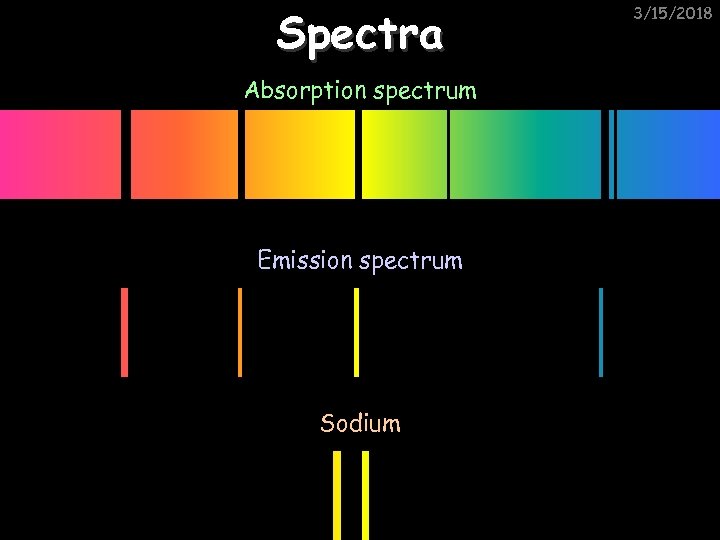Spectra Absorption spectrum Emission spectrum Sodium 3/15/2018

Example questions 1) State the ionisation energy of this atom in e. V. 2) Calculate this ionisation energy in joules. 3) Calculate the wavelength of light needed to ionise the atom. 0 e. V -0. 85 e. V -1. 5 e. V -3. 4 e. V 4) An electron falls from the -1. 5 e. V to the -3. 4 e. V level. What wavelength of light does it emit and what is the colour? 5) Light of frequency 1 x 1014 Hz is incident upon the atom. Will it be able to ionise the atom? -13. 6 e. V 3/15/2018

Electron Diffraction 3/15/2018 Electron diffraction patterns are seen when electrons are passed through graphite crystal. Diffraction is seen because the distance between the atoms is of the same order as the de Broglie wavelength of the electrons. de Broglie wavelength λ = h mv 1) What is the de Broglie wavelength of electrons travelling at around 2 x 107 ms-1 (electron mass = 9. 1 x 10 -31 kg)? 2) What would happen to the diffraction pattern if the voltage to the electrons (and therefore their speed) was increased?