f4072fa15baadb9a8832efda8ceed4c5.ppt
- Количество слайдов: 30

272: Software Engineering Fall 2012 Instructor: Tevfik Bultan Lecture 1: Software Verification with Spin and Bandera

State of the art in verification: Model Checking • What is model checking? – Automated verification technique – Focuses on bug finding rather than proving correctness – The basic idea is to exhaustively search for bugs in software – Has many flavors • Explicit-state model checking • Symbolic model checking • Bounded model checking • …

Model Checking and Temporal Logics • Model checking tools assume that the properties that one wants to check about a system are expressed using temporal logics • Temporal logics are a type of modal logics – Modal logics were developed to express modalities such as “necessity” or “possibility” – Temporal logics focus on the modality of temporal progression • Temporal logics can be used to express, for example, that: – an assertion is an invariant (i. e. , it is true all the time) – an assertion eventually becomes true (i. e. , it will become true sometime in the future)

Temporal Logics • We will assume that there is a set of basic atomic properties called – These are used to write the basic (non-temporal) assertions about the program – Examples: a=true, pc 0=c, x=y+1 • We will use the usual boolean connectives: , , • We will also use four temporal operators: Invariant p : Gp (aka p or [] p) Eventually p : Fp (aka p or <> p) Next p : Xp (aka p) p Until q : p. Uq (Globally) (Future) (ne. Xt) (Until)
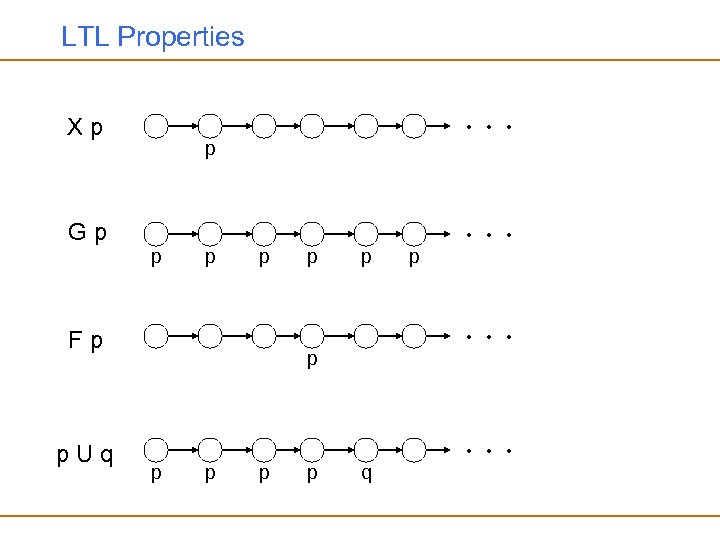
LTL Properties . . . Xp p . . . Gp p p . . . Fp p. Uq p p . . . p p q

Example Properties Examples: mutual exclusion: Two processes are not in the critical section (cs) at the same time: G ( (pc 1=cs pc 2=cs)) starvation freedom: If a process starts waiting (wait) it will eventually get in the critical section: G(pc 1=wait F(pc 1=cs)) G(pc 2=wait F(pc 2=cs))
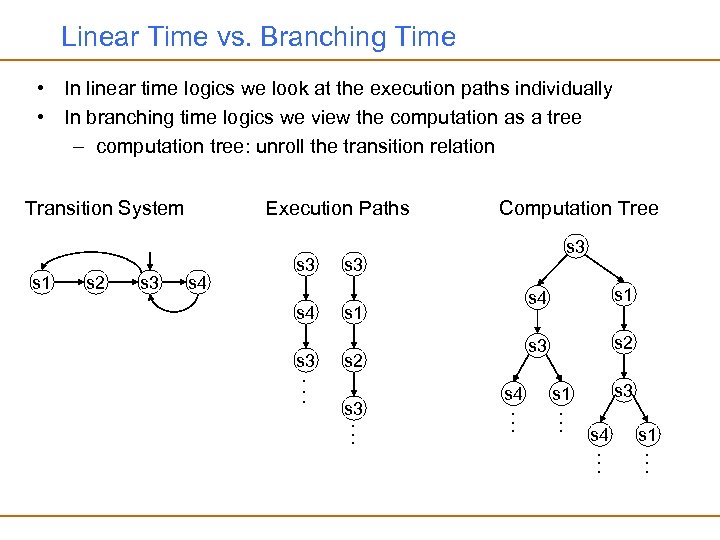
Linear Time vs. Branching Time • In linear time logics we look at the execution paths individually • In branching time logics we view the computation as a tree – computation tree: unroll the transition relation Transition System s 1 s 2 s 3 Execution Paths s 4 s 3. . . Computation Tree s 3 s 4 s 3 s 1 s 2 s 3. . . s 4. . . s 1 s 2 s 3 s 1. . . s 4. . . s 1. . .

Computation Tree Logic (CTL) • In CTL we quantify over the paths in the computation tree • We use the same four temporal operators: X, G, F, U • However we attach path quantifiers to these temporal operators: – A : for all paths – E : there exists a path • We end up with eight temporal operators: – AX, EX, AG, EG, AF, EF, AU, EU • Expressive power of CTL and LTL are not comparable – There are properties that can be expressed in LTL but cannot be expressed in CTL, and visa versa – There are temporal logics which are more powerful than both CTL and LTL (CTL*, mu-calculus)

Model Checking Model checking problem: Given a transition system (a sate machine) and a temporal logic property, determine if all the paths (or all the computation trees) starting from the initial states satisfy the property. • A model checker is a tool that can automatically answer this question • If the property fails, then the model checker generates a counterexample behavior: An execution path that demonstrates the violation of the property If the input system has a finite number of states then model checking can be done fully automatically – Its complexity is linear in the size of the input transition system but could be exponential in the size of the formula

Model Checking Tools • Two model checking tools that had significant impact – Spin model checker: An explicit state model checker that focuses on verification of concurrent protocols – SMV model checker: A BDD-based symbolic model checker that focuses on hardware specifications • Spin and SMV have their own input specification languages – To check a specification using them, you need to write your system in their input specification language • This requires translation of the system to be verified to the input language of the model checker – Most of the time these translations are not automated and use adhoc simplifications and abstractions

Automata-based LTL Model Checking • Büchi automata: Finite state automata that accept infinite strings – The better known variant of finite state automata accept finite strings (used in lexical analysis for example) • A Büchi automaton accepts a string when the corresponding run visits an accepting state infinitely often – Note that an infinite run never ends, so we cannot say that an accepting run ends at an accepting state • LTL properties can be translated to Büchi automata – The automaton accepts a path if and only if the path satisfies the corresponding LTL property
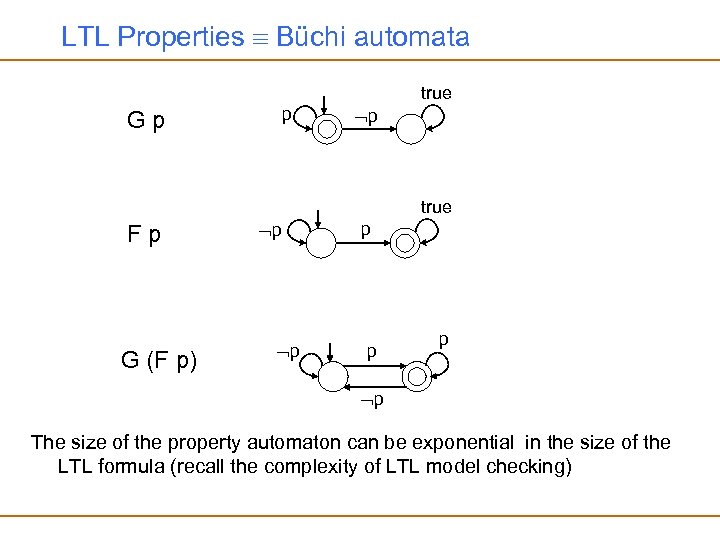
LTL Properties Büchi automata true Gp p p true Fp G (F p) p p The size of the property automaton can be exponential in the size of the LTL formula (recall the complexity of LTL model checking)

Büchi Automata: Language Emptiness Check • Given a Buchi automaton, one interesting question is: – Is the language accepted by the automaton empty? • i. e. , does it accept any string? • A Büchi automaton accepts a string when the corresponding run visits an accepting state infinitely often • To check emptiness: – Look for a cycle which contains an accepting state and is reachable from the initial state • Find a strongly connected component that contains an accepting state, and is reachable from the initial state – If no such cycle can be found the language accepted by the automaton is empty

LTL Model Checking • Generate the property automaton from the negated LTL property • Generate the product of the property automaton and the transition system • Show that there is no accepting cycle in the product automaton (check language emptiness) – i. e. , show that the intersection of the paths generated by the transition system and the paths accepted by the (negated) property automaton is empty • If there is a cycle, it corresponds to a counterexample behavior that demonstrates the bug
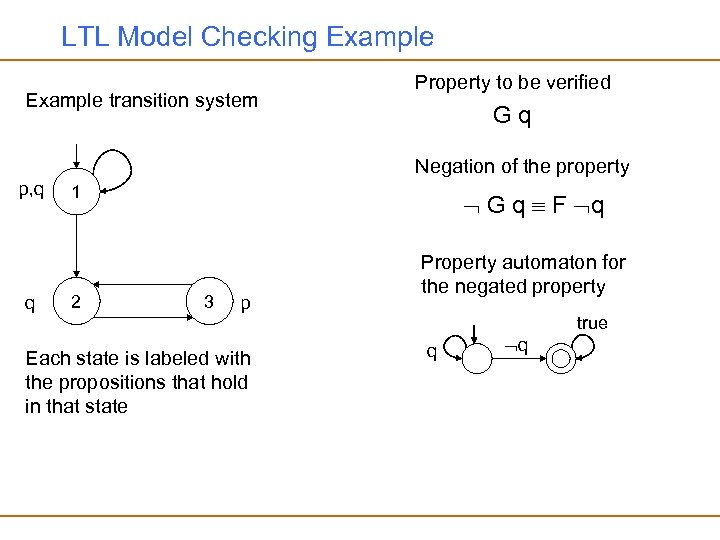
LTL Model Checking Example transition system Property to be verified Gq Negation of the property p, q q 1 2 G q F q 3 p Each state is labeled with the propositions that hold in that state Property automaton for the negated property true q q
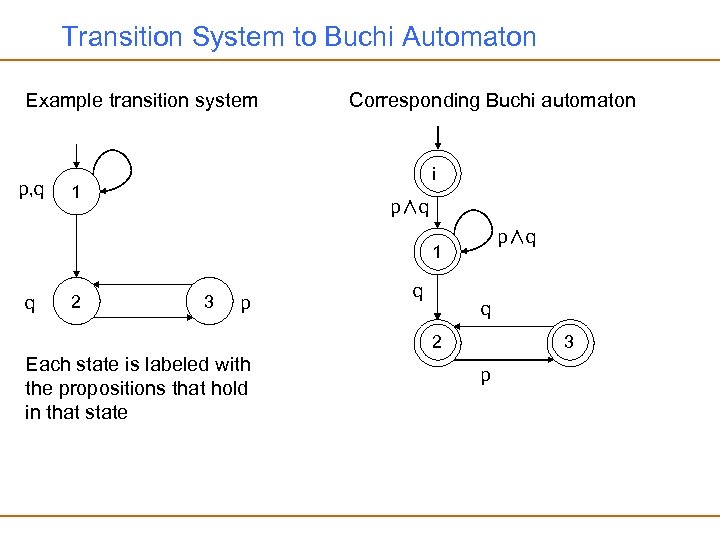
Transition System to Buchi Automaton Example transition system p, q Corresponding Buchi automaton i 1 p∧q 1 q 2 3 p q q 2 Each state is labeled with the propositions that hold in that state 3 p
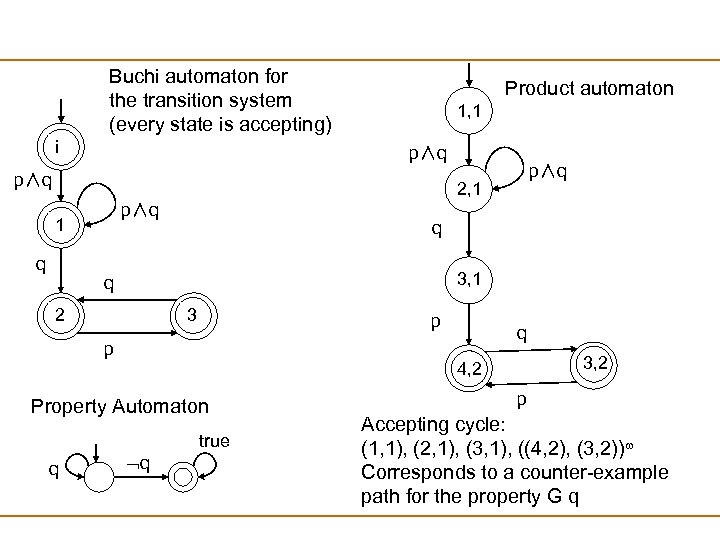
Buchi automaton for the transition system (every state is accepting) i Product automaton 1, 1 p∧q p∧q 2, 1 p∧q 1 q q 3, 1 q 2 3 p q p 3, 2 4, 2 Property Automaton true q q p Accepting cycle: (1, 1), (2, 1), (3, 1), ((4, 2), (3, 2)) Corresponds to a counter-example path for the property G q

Automata Theoretic LTL Model Checking Input: A transition system T and an LTL property f • Translate the transition system T to a Buchi automaton AT • Negate the LTL property and translate the negated property f to a Buchi automaton A f • Check if the intersection of the languages accepted by AT and A f is empty – Is L(AT) L(A f) = ? – If L(AT) L(A f) , then the transition system T violates the property f

Automata Theoretic LTL Model Checking • Note that – L(AT) L(A f) = if and only if L(AT) L(Af) • By negating the property f we are converting language subsumption check to language intersection followed by language emptiness check • Given the Buchi automata AT and A f we will construct a product automaton AT A f such that – L(AT A f) = L(AT) L(A f) • So all we have to do is to check if the language accepted by the Buchi automaton AT A f is empty

SPIN • • A model checking tool Checks finite state systems Properties are specified using temporal logic LTL Input language: PROMELA – Asynchronous processes – Shared variables – Message passing through (bounded) communication channels – Variables: boolean, char, integer (bounded), arrays (fixed size) – Structured data types

SPIN Verification in SPIN • Uses automata-theoretic LTL model checking approach • Constructs the product automaton on-the-fly – It is possible to find an accepting cycle (i. e. a counter-example) without constructing the whole state space • Uses a nested depth-first search algorithm to look for an accepting cycle • Uses various heuristics to improve the efficiency of the nested depth first search: – partial order reduction – state compression

Example Mutual Exclusion Protocol in Promela #define cs 1 process 1@cs Two concurrently executing processes #define cs 2 process 2@cs trying to enter a critical section without #define wait 1 process 1@wait violating mutual exclusion #define wait 2 process 2@wait #define true 1 #define false 0 bool a; bool b; bool turn; proctype process 1() { out: a = true; turn = true; wait: (b == false || turn == false); cs: a = false; goto out; } proctype process 2() { out: b = true; turn = false; wait: (a == false || turn == true); cs: b = false; goto out; } init { run process 1(); run process 2() } are
![Property automaton generation % spin -f "! [] (! (cs 1 && cs 2))“ Property automaton generation % spin -f "! [] (! (cs 1 && cs 2))“](https://present5.com/presentation/f4072fa15baadb9a8832efda8ceed4c5/image-23.jpg)
Property automaton generation % spin -f "! [] (! (cs 1 && cs 2))“ never { T 0_init: /* ! [] (! (cs 1 && cs 2)) */ if : : ((cs 1) && (cs 2)) -> goto accept_all : : (1) -> goto T 0_init fi; accept_all: skip } % spin -f "!([](wait 1 -> <>(cs 1)))“ never { T 0_init: /* !([](wait 1 -> <>(cs 1))) */ if : : ( !((cs 1)) && (wait 1) ) -> goto accept_S 4 : : (1) -> goto T 0_init fi; accept_S 4: if : : (! ((cs 1))) -> goto accept_S 4 fi; } • Input formula “[]” means G “<>” means F • “spin –f” option generates a Buchi automaton for the input LTL formula Concatanate the generated never claims to the end of the specification file

SPIN • “spin –a mutex. spin” generates a C program “pan. c” from the specification file – This C program implements the on-the-fly nested-depth first search algorithm – You compile “pan. c” and run it to the model checking • Spin generates a counter-example trace if it finds out that a property is violated

%mutex -a warning: for p. o. reduction to be valid the never claim must be stutter-invariant (never claims generated from LTL formulae are stutter-invariant) (Spin Version 4. 2. 6 -- 27 October 2005) + Partial Order Reduction Full statespace search for: never claim assertion violations acceptance cycles invalid end states + + (if within scope of claim) + (fairness disabled) - (disabled by never claim) State-vector 28 byte, depth reached 33, errors: 0 22 states, stored 15 states, matched 37 transitions (= stored+matched) 0 atomic steps hash conflicts: 0 (resolved) 2. 622 memory usage (Mbyte) unreached in proctype process 1 line 18, state 6, "-end-" (1 of 6 states) unreached in proctype process 2 line 27, state 6, "-end-" (1 of 6 states) unreached in proctype : init: (0 of 3 states)

Bandera • A tool set for model checking Java source code • Automated compact finite state model extraction from Java source code • Uses existing model checkers, translates into an existing model checker's input language – Promela (input language of the Spin model checker), SMV, etc. • The properties to be verified are specified in Bandera Specification Language (BSL) – Supports both pre and post conditions and also temporal properties

Design criteria for Bandera • Reuse of existing verification technologies • Automated support for abstractions used by experienced model developers • Specialized models for specific properties • An open design for extensibility • Synergistic integration with existing testing and debugging techniques

Strategy for model checking software • Irrelevant component elimination: Many parts of the code can be irrelevant for the property that we want to check • Data abstraction: State space of the program can be reduced using data abstraction • Component restriction: Using a bounded search that searches only a part of the full state space can still reveal bugs since many bugs reveal themselves even in small versions of a system

Bandera • It uses various techniques to reduce the size of the state space of the program – Slicing to automatically eliminate irrelevant components – Abstraction engine for reduction of the domains of the variables • Uses an intermediate language: Bandera Intermediate Language (BIR) • Maps the error trace generated by the model checkers to the source code • Abstraction library – Users can define their own abstractions for data domains or use one of the existing abstractions from the abstraction library – Users can write abstraction in Bandera Abstraction Specification Language (BASL)

Component based tool architecture • Slicer: Slicing component compresses paths in the program by removing control points variables and data structures that are irrelevant for checking a given property • Abstraction Engine: Allows user to reduce the cardinality of data sets associated with data variables. Includes a language for specifying abstractions which can be collected in an abstraction library for reuse. • Back End: Generates BIR: a low-level intermediate language based on guarded commands that abstracts common model checker input languages. The back end also contains a translator each model checker supported. • User Interface: An advanced graphical user interface that facilitates interaction with various components and displays counter-examples to the user like on the source code like a debugger.
f4072fa15baadb9a8832efda8ceed4c5.ppt