25. 11. 2015
Устно:
Устно:
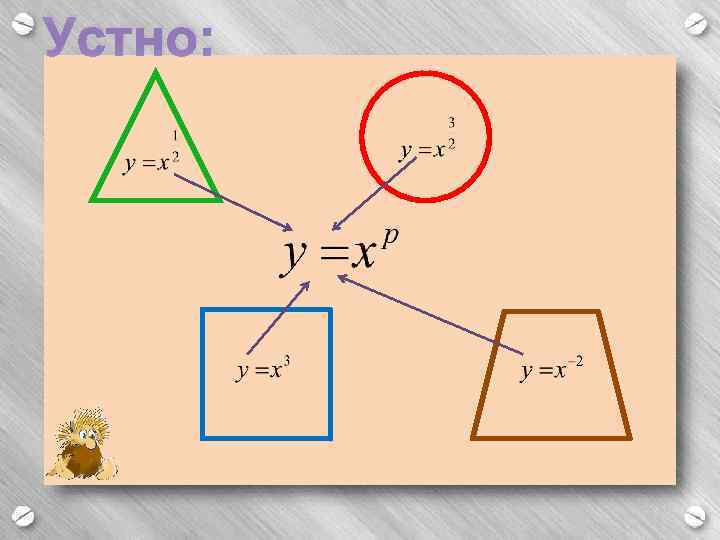Устно:
10. 2007
У=х 2 Функция у -5 - 4 - 3 8 7 6 5 4 3 2 1 -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 0 х 1 2 3 4 5 6 1) D (у) = R; 2) E (у) = [0; + ); 3) Чётная, т. к. (-х)2= х2; 4) Функция возрастает при х [0; + ), функция убывает при х (– ; 0].
Функция , 2 n где показатель р=2 n – чётное натуральное число -5 - 4 - 3 8 7 6 5 4 3 2 1 -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 У=х у 0 х 1 2 3 4 5 6 1) D (у) = R; 2) E (у) = [0; + ); 3) Чётная, т. к. (-х)2 n= х2 n; 4) Функция возрастает при х [0; + ), функция убывает при х (– ; 0].
3 Функция -5 - 4 - 3 8 7 6 5 4 3 2 1 -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 У=х у 0 х 1 2 3 4 5 6 1) D (у) = R; 2) E (у) = R; 3) Нечётная, т. к. (-х)3= -х3; 4) Функция возрастает при х (- ; + ).
Функция 2 n- 1 где показатель р=2 n-1 – нечётное натуральное число -5 - 4 - 3 8 7 6 5 4 3 2 1 -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 У=х у 0 х 1 2 3 4 5 6 1) D (у) = R; 2) E (у) = R; 3) Нечётная, т. к. (-х)2 n-1= -х2 n-1; 4) Функция возрастает при х (- ; + ).
Функция у -5 - 4 - 3 8 7 6 5 4 3 2 1 -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 0 У= х 1 2 3 4 5 6 1) D (у) = R, кроме х=0; 2) E (у) = (0; + ); 3) Чётная, т. к. = ; 4) Функция возрастает при х (– ; 0), функция убывает при х (0; + ).
Функция где показатель р= -2 n и n - натуральное число, т. е. р – чётное отрицательное число у -5 - 4 - 3 8 7 6 5 4 3 2 1 -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 0 У= х 1 2 3 4 5 6 1) D (у) = R, кроме х=0; 2) E (у) = (0; + ); 3) Чётная, т. к. = ; 4) Функция возрастает при х (– ; 0), функция убывает при х (0; + )
Функция -5 - 4 - 3 8 7 6 5 4 3 2 1 -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 0 х 1 2 3 4 5 6 1) D (у) = R, кроме х = 0; 2) E (у) = R, кроме у = 0; 3) Нечётная, т. к. =4) Функция убывает при х (– ; 0) (0; + ). ∩ у ;
Функция где показатель р= -(2 n-1) и n - натуральное число, т. е. р – нечётное отрицательное число у -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 0 1) D (у) = R, кроме х = 0; 2) E (у) = R, кроме у = 0; 3) Нечётная, т. к. =х 1 2 3 4 5 6 4) Функция убывает при х (– ; 0) (0; + ). ∩ -5 - 4 - 3 8 7 6 5 4 3 2 1 ;
Функция у -5 - 4 - 3 8 7 6 5 4 3 2 1 -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 0 х 1 2 3 4 5 1) D (у) = [0; + ); 2) E (у) = [0; + ); 3)Функция возрастает при х [0; + ). 6 Функция 1) D (у) = [0; + ); 2) E (у) = [0; + ); 3) Функция возрастает при х [0; + ).
Функция где р – положительное нецелое число , где 0< p <1 у -5 - 4 - 3 8 7 6 5 4 3 2 1 -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 0 p >1 0< p <1 х 1 2 3 4 5 1) D (у) = [0; + ); 2) E (у) = [0; + ); 3)Функция возрастает при х [0; + ). 6 , где p >1 1) D (у) = [0; + ); 2) E (у) = [0; + ); 3) Функция возрастает при х [0; + ).
Функция у -5 - 4 -3 -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 1) D (у) = (0; + ); 2) E (у) = (0; + ); 3)Функция убывает при х (0; + ), 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 х
Функция где р – отрицательное действительное нецелое число у -5 - 4 -3 -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 1) D (у) = (0; + ); 2) E (у) = (0; + ); 3)Функция убывает при х (0; + ) 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 х
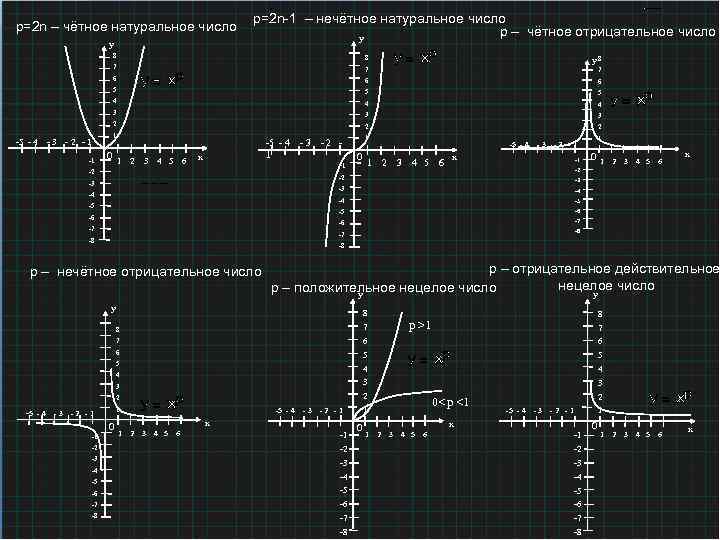р=2 n – чётное натуральное число у р=2 n-1 – нечётное натуральное число р – чётное отрицательное число у 8 5 4 4 3 3 3 2 2 2 1 -1 6 5 4 -2 -1 7 6 5 -3 у8 7 6 -5 - 4 8 7 1 0 1 2 3 4 5 6 -5 - 4 - 3 1 х -2 -2 -1 0 -5 - 4 1 2 3 4 5 6 -3 х -1 -8 р – отрицательное действительное нецелое число р – положительное нецелое число у у у 8 8 p >1 8 7 7 6 6 6 5 5 4 4 3 3 3 2 2 5 4 -4 -3 1 -2 -1 0 -1 1 -5 - 4 2 3 4 5 6 -3 -1 0< p <1 1 -2 -1 х 0 7 2 -5 - 4 -3 1 -2 -1 х 1 2 3 4 5 6 -1 -2 -2 -2 -3 -3 -3 -4 -4 -6 -5 -5 -7 -6 -6 -8 -7 -7 -8 -8 -4 -5 х -8 р – нечётное отрицательное число -5 6 -7 -7 -8 4 5 -6 -6 -7 3 -5 -5 -6 2 -4 -4 -5 1 -3 -3 -4 0 -2 -2 -3 1 -2 -1 0 1 2 3 4 5 6 х
Самостоятельно: 1 вариант. Решив графически уравнение и выбрав правильный вариант ответа, мы узнаем имя математика, который впервые ввёл в 1694 году термин «функция» . -2; -1; 0 0 2 вариант. Решив неравенство и выбрав правильный вариант ответа, мы узнаем годы его жизни. (0; 1) X>1 [0; 1]
Самостоятельно: 1 вариант. Решив графически уравнение и выбрав правильный вариант ответа, мы узнаем имя математика, который впервые ввёл в 1694 году термин «функция» . Г. В. Лейбниц 2 вариант. Решив неравенство и выбрав правильный вариант ответа, мы узнаем годы его жизни. (0; 1) X>1 [0; 1]
Самостоятельно: 1 вариант. Решив графически уравнение и выбрав правильный вариант ответа, мы узнаем имя математика, который впервые ввёл в 1694 году термин «функция» . Г. В. Лейбниц 2 вариант. Решив неравенство и выбрав правильный вариант ответа, мы узнаем годы его жизни. 1646 -1716
Дома: § 6, № 126(2, 4), 130*(2)