25 09 13 Лекция 2 Предикатное программирование

25. 09. 13 Лекция 2 Предикатное программирование Логика программы 2. Задачи дедуктивной верификации Программа в виде тройки Хоара, однозначность программы, тотальность и однозначность спецификации Тотальная корректность программы Теорема тождества спецификации и программы 3. Язык исчисления вычислимых предикатов Структура программы на языке CCP Система типов данных

Основные свойства программы: • автоматическая вычислимость • наличие спецификации программы • логика программы Свойство 2. Программа должна соответствовать спецификации.

Классификация программ 1. Программы-функции (преобразователи) 2. Программы-процессы ………. Языковые процессоры Операционные системы Объектно-ориентированное расширение классов Базис классификации: • внешняя форма (интерфейс с окружением) • минимальное ядро языка программирования; • формы определения спецификации программы; • виды условий корректности программы vs спецификации. Разные классы требуют разных методов и технологий

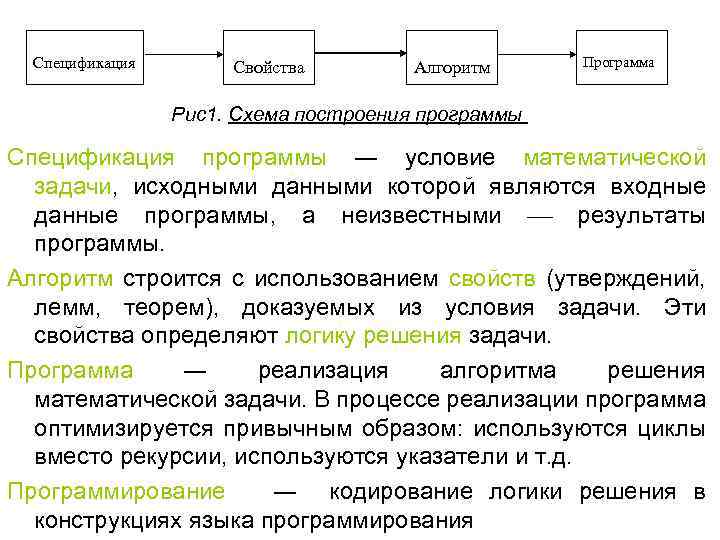Спецификация Свойства Алгоритм Программа Рис1. Схема построения программы Спецификация программы ― условие математической задачи, исходными данными которой являются входные данные программы, а неизвестными результаты программы. Алгоритм строится с использованием свойств (утверждений, лемм, теорем), доказуемых из условия задачи. Эти свойства определяют логику решения задачи. Программа ― реализация алгоритма решения математической задачи. В процессе реализации программа оптимизируется привычным образом: используются циклы вместо рекурсии, используются указатели и т. д. Программирование ― кодирование логики решения в конструкциях языка программирования

Логика программы Предикат A сильнее B A B L(S) – логика программы-функции S: сильнейший предикат, истинный при завершении исполнения S. sp(P, S) – сильнейшее постусловие программы S при истинности предусловия P L(S) = sp(true, S) Ограничение: программа не взаимодействует с окружением Класс программ-функций (невзаимодействующих программ)

Логика базисных операторов L(B; C) ? Необходима специализация S(x: y) оператор S(x, y) с аргументами x и результатами y. Оператор суперпозиции B(x: z); C(z: y), параллельный оператор B(x: y) || C(x: z) x, y и z – разные наборы переменных L(B(x: z); C(z: y)) z. L(B(x: z)) & L(C(z: y)) L(B(x: y) || C(x: z)) L(B(x: y)) & L(C(x: z)) L(if (E) B(x: y) else C(x: y)) E & L(B(x: y)) E & L(C(x: y)) if (E) L(B(x: y)) else L(C(x: y))

Логика оператора цикла W(u, x) – while E do B(u, x) end proc W(u, x) { if (E) { B(u, x); W(u, x)}} L(W(u, x: x’)) = if (E) z. L(B(u, x: z) & L(W(u, z: x’)) else x’ = x наименьшая неподвижная точка Логика бесконечного цикла не существует ( = false)

Корректность логики программы определяется как согласованность логики с операционной семантикой языка программирования для любых выражений и операторов. Программа – оператор S(x, y) x и y наборы переменных, аргументы и результаты. RUN(S, x, y) любое исполнение оператора S для аргументов со значениями x завершается и значения результатов есть y. x, y. L(S(x, y)) RUN(S, x, y)

2. Задача дедуктивной верификации для класса невзаимодействующих программ

Программа – оператор S(x, y) x аргументы набор входных данных, y результаты набор выходных данных. Предикатная спецификация программы формула P(x) & Q(x, y) P(x) предусловие, истинное перед исполнением программы, Q(x, y) постусловие, истинное после исполнения программы. Спецификация изображается в виде: [ P (x), Q(x, y) ] Программа со спецификацией представляется тройкой Хоара {P(x)} S(x, y) {Q(x, y)}.

P(x) { S (x, y) } Q(x, y) L(S(x, y)) – логика программы (2. 1) Однозначность программы S(x, y) : P(x) & L(S(x, y 1)) & L(S(x, y 2)) y 1 = y 2 Однозначность спецификации [P(x), Q(x, y)] : P(x) & Q(x, y 1) & Q(x, y 2) y 1 = y 2 Тотальность спецификации [P(x), Q(x, y)] : P(x) y. Q(x, y) Свойство 2. Программа должна соответствовать спецификации. Конкретизация закона соответствия программы и спецификации: - аргументы x должны соответствовать предусловию P(x) перед исполнением программы; - аргументы x и результаты y должны удовлетворять постусловию Q(x, y) после завершения исполнения программы.

P(x) { S (x, y) } Q(x, y) (2. 1) Предусловие P(x) не следует из L(S(x, y)). Оно должно быть доказано ранее – перед вызовом S(x, y). Здесь же оно должно быть истинно априори, и поэтому должно быть посылкой, т. е. : P(x) & L(S(x, y)) Q(x, y) (2. 3) Данное условие определяет частичную корректность программы S (x, y). Условие завершения программы: P(x) y. L(S(x, y)) (2. 4) Тотальная корректность программы S(x, y) относительно спецификации [P(x), Q(x, y)] складывается из частичной корректности и условия завершения программы: P(x) [L(S(x, y)) Q(x, y)] & y. L(S(x, y)) (2. 5) Частичная корректность Условие завершения программы

P(x) & L(S(x, y)) Q(x, y) (2. 3) P(x) y. L(S(x, y)) (2. 4) Термин «корректность» далее используется в смысле тотальной корректности. Лемма 2. 1. Если программа корректна относительно спецификации, то спецификация тотальна. Доказательство. Пусть истинно P(x). Необходимо доказать истинность y. Q(x, y). Из условия (2. 4) следует истинность y. L(S(x, y)). Допустим, истинность этой формулы реализуется для некоторого y 0. Из условия (2. 3) получаем истинность Q(x, y 0), а значит и y. Q(x, y). □

Предикат A(x, y) является однозначным в области X, если: x X. A(x, y 1) & A(x, y 2) y 1 = y 2 Лемма 2. 2. Допустим, предикат D(x, y) является однозначным в области X, а предикат Z(x, y) тотальный в области X. Пусть истинна формула x X. Z(x, y) D(x, y). Тогда истинна следующая формула: x X. D(x, y) Z(x, y). Как следствие, предикаты D и Z оказываются тождественными в области X. Доказательство. Пусть истинно D(x, y) для некоторого x X. Докажем истинность Z(x, y). Поскольку предикат Z тотальный, то существует некоторый y’, для которого истинно Z(x, y’). Из Z(x, y) D(x, y) получаем истинность D(x, y’). Поскольку истинны D(x, y) и D(x, y’), то из однозначности D следует y = y’. Тогда истинно Z(x, y). □

Теорема 2. 1 тождества спецификации и программы P(x) { S (x, y) } Q(x, y) (2. 1) Оператор S(x, y) является однозначным, а спецификация [P(x), Q(x, y)] тотальной. Пусть истина формула: P(x) & Q(x, y) L(x, y) (2. 6) Тогда программа (2. 1) является корректной. Доказательство. Достаточно доказать (2. 5), т. е. : P(x) [L(S(x, y)) Q(x, y)] & y. L(S(x, y)) (2. 5) Пусть предусловие P(x) истинно. Докажем истинность y. L(S(x, y)). Из тотальности спецификации следует y. Q(x, y). Пусть эта формула истинна для некоторого y’. Тогда из (2. 6) истинна L(S(x, y’)) и, следовательно, y. L(S(x, y)).

Докажем истинность формулы L(S(x, y)) Q(x, y). Поскольку истинны P(x) и формула (2. 6), то истинна формула Q(x, y) L(S(x, y)). В соответствии с леммой 2. 2 истинна формула L(S(x, y)) Q(x, y), поскольку постусловие Q(x, y) тотально, а L(S(x, y)) однозначно. □ Лемма 2. 8. В условиях теоремы 2. 1 истинна ф-ла: P(x) (L(S(x, y)) Q(x, y)) Доказательство. Допустим, предусловие P(x) истинно. Истинность формулы L(S(x, y)) Q(x, y) установлена при доказательстве теоремы 2. 1. Обратная импликация следует из (2. 16). □ Следствие леммы 2. 8: спецификация [P(x), Q(x, y)] является однозначной.

Лемма 2. 9. Допустим, программа (2. 1) является корректной, а ее спецификация однозначной. Тогда истинна формула (2. 6), т. е. L(S(x, y)) выводима из спецификации. Доказательство. Допустим, истинны P(x) и Q(x, y). Докажем истинность L(S(x, y)). Из корректности программы (2. 1) по формуле (2. 5) следует истинность формулы L(S(x, y)) Q(x, y), а также тотальность L(S(x, y)). Пусть для некоторого y’ истинно L(S(x, y’)). Тогда истинно Q(x, y’), а из однозначности Q следует y = y’. Следовательно, истинно L(S(x, y)). □

3. Язык исчисления вычислимых предикатов

Исчисление вычислимых предикатов ― множество вычислимых формул языка исчисления предикатов ― язык CCP (Calculus of Computable Predicates) ― ядро класса программ-функций, используемое для построения языка предикатного программирования

Структура программы на языке CCP Программа ─ набор определений предикатов Определение A K предикат A , оператор K параллельный оператор, оператор суперпозиции, условный оператор Вызов предиката (d 1, d 2, …, dn : e 1, e 2, …, em) (3. 1) φ ─ имя предиката или переменной предикатного типа, n 0, m > 0, d 1, d 2, …, dn ─ имена переменных ─ аргументы вызова, e 1, e 2, …, em ─ результаты вызова Вычисление предиката Вызов φ(d: e), где d = d 1, d 2, …, dn, e = e 1, e 2, …, em – наборы переменных n = 0 – вызов предикта соответствует константе Значение φ(d) φ(d: b) , где b ─ переменная логического типа Определение предиката A(x: y) K(x: y) (3. 2) A имя предиката; набор x аргументы предиката, набор y результаты предиката, K(x: y) – оператор. Предикат – определяемый, базисный, значение переменной. Тип данных определяет набор базисных предикатов со значениями типа Система типов определяет совокупность всех базисных предикатов

Система типов данных Тип ― множество значений, имя типа Система типов: примитивные типы, подмножество типа и структурные типы Примитивные типы: логический BOOL, целый INT, вещественный REAL и литерный CHAR. Базисные предикаты: +(x, y: z) z = x + y, -(x, y: z) z = x - y, -(x: y) y = -x, <(x, y: b) b = x < y и др. Предикаты равенства =(x: y) y = x и =(x, y: b) b = (x = y) для всех примитивных типов

Предикаты Cons. Int. Zero( : x) x = 0 Cons. Int. One( : x) x = 1 x переменная типа T, d возможно пустой набор переменных – параметров типа Подмножество типа T на базе предиката P(x, d) S = Subset(T, x, P, d) = {x T | P(x, d)} (3. 3) Subset стандартное имя, P вычислимый, d параметры типа NAT = Subset(INT, x, GE 0) = {x INT | x 0}. DIAP(n) = Subset(INT, x, IN 1_n, n) = {x INT | x 1 x n}

Структурный тип ― композиция компонентных типов Структурные типы: произведение типов (кортеж), объединение типов, множество подмножеств типа, предикатный тип (в т. ч. массив). Базисные предикаты конструкторы, деструкторы и другие операции Конструктор по значениям компонентных типов строит значение структурного типа. Деструктор для значения структурного типа определяет соответствующие значения компонент. Нет типов указателей !

Произведение типов Z = X Y = {(x, y) | x X, y Y} (3. 4) x X, y Y, z Z Конструктор Cons. Struct(x, y: z) z = (x, y) Деструктор Comp. Struct(z: x, y) z = (x, y) Объединение типов Z = X + Y = {(1, x) | x X} {(2, y) | y Y} (3. 5) Первая компонента (1 или 2) ― тег значения Конструктор Cons. Union 1(x: z) z = (1, x). Конструктор Cons. Union 2(y: z) z = (2, y) Деструктор Comp. Union(z: i, x, y) либо z = (1, x) и i = 1, либо z = (2, y) и i = 2. Если i = 1, то y не определено. Если i = 2, то x не определено

Множество подмножеств конечного типа X: Z = Set(X) = {z | z X} (3. 6) Конструктор Cons. Set. Empty( : z) z = Конструктор Cons. Set. Elem(x : z) z = {x} Предикат Comp. Set(z, x: b) b = x z Предикатный тип Z = Pred(D: E) = { (d: e) | d D, e E, - вычислимый} (3. 7) ― множество вычислимых предикатов вида (d: e) для непересекающихся списков переменных d и e Z = { (d: e) | d D, e E, CCP} Конструктор предиката Cons. Pred будет определен позже Z ― тип массива D не пуст & типы D конечны & Z d D e (d: e) ― массив с индексом d и элементом массива e Конструктор предиката Cons. Array будет определен позже Деструктор Comp. Array(a, i: x) x = a(i) a(i: x)

Произвольный тип либо примитивный, либо вводится следующим определением: <имя типа> = <типовый терм> Z = Subset(T, x, P, d) (3. 3) Z = X Y (3. 4) Z = X + Y (3. 5) Z = Set(X) (3. 6) Z = Pred(D: E) (3. 7) Z, T, X, Y, D, E ― имена типов, примитивных или определяемых.

Тип “подмножество типа” может быть параметризован набором переменных d Структурный тип параметризован, если параметризован один из его компонентных типов. В качестве параметра может выступать также имя типа. Если <имя типа>, встречающееся в правой части определения типа, не есть имя примитивного типа и этот тип не объявлен как параметр, то должно существовать определение для этого типа Замкнутая совокупность определений типов ― любой встречающийся тип либо является примитивным, либо имеет определение, либо считается параметром для некоторых типов из совокупности определений Рекурсивный тип ― определение типа прямо или косвенно, через совокупность определений, использует этот тип

Примеры рекурсивных типов Специальный тип NIL = { nil }; nil обозначает пустую последовательность Тип последовательности, составленной из элементов типа T: Seq(T) = NIL + (T Seq) Тип списка LIST для языка Лисп: LIST = Seq(ATOM) ATOM = NIL + NUM + SYMBOL + LIST NUM = INT + REAL SYMBOL = STRING = Seq(CHAR)

4. Математические основы 4. 1. Отношения порядка 4. 2. Наименьшая неподвижная точка

Отношения порядка (D, R) ― отношение порядка R D D; a R b (a, b) R a D. a R a ― рефлексивность a D. a R a ― иррефлексивность a, b D. a R b b R a ― симметричность a, b D. a R b & b R a a = b ― антисимметричность a, b, c D. a R b & b R c a R c ― транзитивность (D, ⊑) ― частично упорядоченное множество (чум) ⊑ - рефлексивно, антисимметрично, транзитивно; ⊑ - частичный порядок Частичный порядок ⊑ линейный (или тотальный) a, b D. (a ⊑ b b ⊑ a). ⊏ - строгий частичный порядок ⊏ - иррефлексивно, антисимметрично, транзитивно. (D, ⊑) ― предпорядок ⊑ - рефлексивно и транзитивно (D, R) ― отношение эквивалентности R рефлексивно, симметрично и транзитивно

a S ― наименьший (наибольший) элемент S D s S. a⊑s ( s S. s⊑a ) ⊥ (bottom) и ⊤ (top) a D ― верхняя грань S D s S. s⊑a a D ― наименьшая верхняя грань S D b D. (b ― верхняя грань a⊑b) a = lub(S) least upper bound a S ― минимальный элемент S D b S. (b⊑a b=a) нижняя грань, наибольшая нижняя грань, максимальный элемент нижняя полурешетка ч у м с нижней гранью полная решетка ч у м с нижней и верхней гранью Лемма 4. 1. Нижняя (верхняя) полурешетка является полной решеткой. вполне упорядоченное множество ― всякое подмножество имеет нижнюю грань ч у м со свойством обрыва бесконечно убывающих цепей (well-founded partial order) ― всякое подмножество имеет минимальный элемент

Наименьшая неподвижная точка (D, ⊑, ⊥) ― частично упорядоченное множество с нижней гранью: a D. ⊥⊑a - нижняя полурешетка Последовательность {am}m 0 является возрастающей цепью, если a 0 ⊑ a 1 ⊑ … ⊑ am ⊑ …. F: D→D ― монотонная функция a, b D. a⊑b F(a)⊑F(b) Лемма 4. 2. {Fn(⊥)}n≥ 0 ― для монотонной функции F определяют возрастающую цепь: ⊥⊑F(⊥)⊑F 2(⊥)⊑…⊑Fn(⊥)⊑… Лемма 4. 3. Если F ― монотонна и a 0⊑a 1⊑a 2⊑… ― возрастающая цепь, то F(a 0)⊑F(a 1)⊑F(a 2)⊑… ― также возрастающая цепь

m 0 am lub {am}m 0 ― наименьшая верхняя грань цепи F: D→D ― непрерывная функция возрастающей цепи {am}m 0. F( m 0 am) = m 0 F( am) Лемма 4. 4. Непрерывная функция является монотонной. x = F(x) ― решением этого уравнения является неподвижная точка функции F Теорема 4. 1 Клини. F ― непрерывна. Тогда n 0{Fn(⊥)} ― наименьшая неподвижная точка F

Рекурсивные типы данных Z = Subset(T, x, P, d) (1) Z = X Y (2) Z = X + Y (3) Z = Set(X) (4) Z = Pred(D: E) (5) типовый терм φ(X, Y) Xk = φk(X 1, X 2, …, Xn, T 1, T 2, …, Ts ); k = 1, …, n; n > 0, s≥ 0 (3. 8) ― система типовых уравнений X = (X 1, X 2, …, Xn), φ = (φ1, φ2, …, φn) X = φ(X) ― векторная форма (3. 9) (Γ, , ) ― множество типов; Z Γ. Z ― нижняя грань Вектора типов X ⊑ Y k=1. . n (Xk Yk) = ( , , …, ) ― нижняя грань (Φ, ⊑, ) ― множество векторов типов Лемма. (Φ, ⊑, ) является нижней полурешеткой

X 0 = , Xm+1 = φ(Xm), m 0. (3. 10) Лемма. {Ym}m 0 возрастающая цепь типов. a m 0 Ym ( k. n>k. a Yn) Лемма. Произведение Y Z и объединение Y + Z непрерывны относительно вхождений компонентных типов Y и Z. {Ym}m 0 и {Zm}m 0 возрастающие цепи типов. m 0(Ym Zm) = ( m 0 Ym) ( m 0 Zm). Лемма 3. 1. Функция φ системы (3. 9) определений рекурсивных типов X = φ(X) является непрерывной относительно произведения и объединения. По теореме Клини решением системы X = φ(X) является наименьшая неподвижная точка, определяемая как m 0 Xm, при условии, что рекурсия реализуется через произведение и объединение

Запрещается рекурсия Y = Q(Subset(H(Y))) Z = Q(Set(H(Z))) A = Q(PRED(H(A), …: …) B = Q(PRED(…: H(B), …), где Q и H ― некоторые функционалы, представленные типовыми термами

Q

Логика по всей программе z – набор переменных p – произвольная точка в программе S(z) Логика Lp(S(z)) истинна исполнение программы, достигающее точку p с теми же значениями z Lp(S(z)) – сильнейший предикат, истинный в точке p. Для доказательства истинности свойства X в точке p достаточно доказать истинность формулы Lp(S(z)) X

Аппроксимация логики программы Предикат R называется аппроксимацией логики Lp(S(z)) , если Lp(S(z)) R Если R X, то свойство X доказуемо из логики: Lp(S(z)) X Логика программы – сильнейшая из аппроксимаций Тождественно истинный предикат true – надежная, но бесполезная аппроксимация логики Lp(S(z)) Инвариант цикла – достаточно сильная аппроксимация логики в начале цикла Другие примеры: результаты статического анализа, бизнес-логика – в реинжиниринге, абстрактные предикаты в статическом анализаторе достижимости места ошибки

x, y ― наборы переменных Оператор S(x: y) Предикаты P(x), Q(x, y) Тройка Хоара {P(x)} S(x: y) {Q(x, y)} истинна P(x) истинно перед исполнением S Q(x, y) истинно после исполнения S Q = sp(S, P) ― сильнейшее постусловие относительно P {P} S {Q} & ({P} S {Q’} (Q Q’)) Важнейший факт: L(S(x: y)) sp(S, true).