23 10 13 Лекция 6 Предикатное программирование 5

23. 10. 13 Лекция 6 Предикатное программирование 5. Построение языка предикатного программирования. Методы доказательства корректности предикатных программ (прод) Методы доказательства корректности рекурсивных программ Примеры 6. Язык предикатного программирования Лексемы, предикаты, операторы, выражения, типы, массивы, формулы, императивное расширение. Примеры

Метод индукции, использующий меру t X. [ ( y X. m(y) < m(t) W(y) ) W(t) ] u X. W(u) (3. 5) Функция m: X nat называется мерой Вместо типа nat может использоваться ЧУМ со свойством обрыва бесконечно убывающих цепей (well-founded partial order) Induct(t, W) y. m(y) < m(t) W(y)) t X. [ Induct(t, W) W(t) ] u X. W(u) (3. 5) RR: Induct(t, W) W(t) W(x) RR 1: Induct(t, W)) W(t) Induct(t, W) ├ W(t)

5. Построение языка предикатного программирования. Методы доказательства корректности предикатных программ (продолжение )

Методы доказательства корректности рекурсивных программ Определения предикатов рекурсивного кольца A 1, A 2, …, An: Aj(xj: yj) Pj(xj) {Kj(xj: yj)} Qj(xj, yj); j=1…n; n > 0 (3. 36’) Здесь Pj и Qj ― предусловие и постусловие предиката Aj; xj, yj ― различающиеся наборы переменных. Рекурсивное кольцо из единственного определения предиката: A(x: y) pre P(x) { K(x: y) } post Q(x, y) measure m(x); T 0: y. P(x) & L(S(x: y)) Q(x, y); P(x) y. L(S(x: y)) Corr(S, P, Q)(x) Induct(t, W) y. m(y) < m(t) W(y)) Induct(t, W) ├ W(t) W(x) = Corr(S, P, Q)(x) Induct(A, P, Q)(t) ≌ ∀u (m(u) < m(t) ⇒ Corr(A, P, Q)(u))

Обобщение на случай рекурсии Corr*(B, PB, QB)(x); Corr*(C, PC, QC)(x); P(x) P*B(x) & P*C(x); y, z. QB(x, y) & QC(x, z) Q(x, y, z) RP: Corr(B(x: y) || C(x: z), P, Q) (x) P*B(x) PB(x) & m(x) < m(t) для рекурсивной B t – аргументы B Corr*(B, PB, QB)(x); z Corr*(C, PC, QC)(x, z); P(x) P*B(x); z, v. P(x) & QB(x, z, v) P*C(x, z); z, v, y. P(x) & QB(x, z, v) & QC(x, z, y) Q(x, v, y) RS: Corr(B(x: z, v); C(x, z: y), P, Q)(x) Corr*(B, PB, QB)(x); Corr*(C, PC, QC)(x); P(x) & E P*B(x); P(x) & E P*C(x); y. P(x) & E & QB(x, y) Q(x, y); y. P(x) & E & QC(x, y) Q(x, y) RC: Corr(if (E(x)) B(x: y) else C(x: y), P, Q)(x)

Пример 5. 1. Программа умножения через сложение. formula m(nat a: nat) = a; Умн(nat a, b: nat c) { if (a = 0) c = 0 else c = b + Умн(a – 1, b) } post c = a b measure m(a); Corr(B, P & E, Q)(x); Corr(C, P & E, Q)(x) QС: Corr(if (E) B(x: y) else C(x: y), P, Q) (x) Генерируются цели: formula Q(nat a, b, c) = c = a b; QC 1: Corr(c = 0, λa. a = 0, Q)(a); QC 2: Corr(c = b + Умн(a – 1, b), λa. a = 0, Q) (a) y. P(x) & L(S(x: y)) Q(x, y); P(x) y. L(S(x: y)) T 0: Corr(S, P, Q)(x) Генерируется лемма применением T 0. 1: QC 1: lemma not a = 0 & c = 0 implies Q(a, b, c);

Перепишем вторую цель в виде суперпозиции: QC 2: Corr(Умн, a, Умн(a – 1, b: t); c = b + t, λa. not a = 0, Q) (a) RS: Corr*(B, PB, QB)(x); z Corr*(C, PC, QC)(x, z); P(x) P*B(x); z, v. P(x) & QB(x, z, v) P*C(x, z); z, v, y. P(x) & QB(x, z, v) & QC(x, z, y) Q(x, v, y) Corr(B(x: z, v); C(x, z: y), P, Q)(x) Применяя RS. 3, RS. 4, RS. 5, получим: formula m(nat a: nat) = a; formula Q(nat a, b, c) = c = a b; QC 2_RS 3: lemma not a = 0 implies a – 1 >= 0 & m(a – 1) < m(a); QC 2_RS 5: lemma not a = 0 & Q(a – 1, b, t) & c = b + t implies Q(a , b, c);

Пример 5. 2. Программа D(a, b: c) вычисления наибольшего общего делителя (НОД) положительных a и b. x ― делитель a divisor(x, a) z ≥ 0. x z = a divisor 2(с, a, b) divisor(с, a) & divisor(с, b) НОД(c, a, b) divisor 2(с, a, b) & x. (divisor 2(x, a, b) x ≤ c) Свойства НОД: a = b НОД(a, a, b) (5. 21) a > b & НОД(c, a, b) НОД(c, a - b, b) (5. 22) НОД(c, a, b) НОД(c, b, a) (5. 23) formula НОД(nat c, a, b) = divisor 2(с, a, b) & forall nat x. divisor 2(x, a, b) implies x <= c;

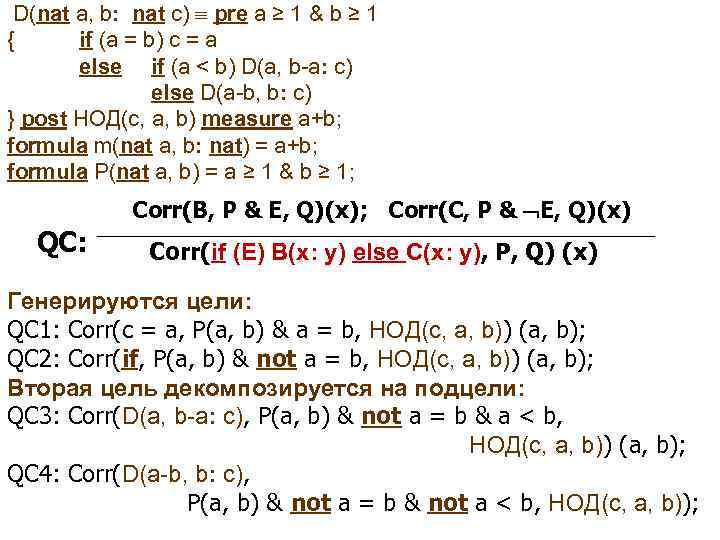D(nat a, b: nat c) pre a ≥ 1 & b ≥ 1 { if (a = b) c = a else if (a < b) D(a, b-a: c) else D(a-b, b: c) } post НОД(c, a, b) measure a+b; formula m(nat a, b: nat) = a+b; formula P(nat a, b) = a ≥ 1 & b ≥ 1; Corr(B, P & E, Q)(x); Corr(C, P & E, Q)(x) QС: Corr(if (E) B(x: y) else C(x: y), P, Q) (x) Генерируются цели: QC 1: Corr(c = a, P(a, b) & a = b, НОД(c, a, b)) (a, b); QC 2: Corr(if, P(a, b) & not a = b, НОД(c, a, b)) (a, b); Вторая цель декомпозируется на подцели: QC 3: Corr(D(a, b-a: c), P(a, b) & not a = b & a < b, НОД(c, a, b)) (a, b); QC 4: Corr(D(a-b, b: c), P(a, b) & not a = b & not a < b, НОД(c, a, b));

QC 1: Corr(c = a, P(a, b) & a = b, НОД(c, a, b)) (a, b); Генерируется лемма применением T 0. 2: QC 1: lemma P(a, b) & a = b & c = a implies НОД(c, a, b); Для целей: QC 3: Corr(D(a, b-a: c), P(a, b) & not a = b & a < b, НОД(c, a, b)) (a, b); QC 4: Corr(D(a-b, b: c), P(a, b) & not a = b & not a < b, НОД(c, a, b)); применяется правило: z Corr*(C, PC, QC)(z); SP(PB, B)(x) ; P(x) PB(x) & P*C(B(x)); y. P(x) & QC(B(x), y) Q(x, y) RB: Corr(C(B(x): y), P, Q)(x)

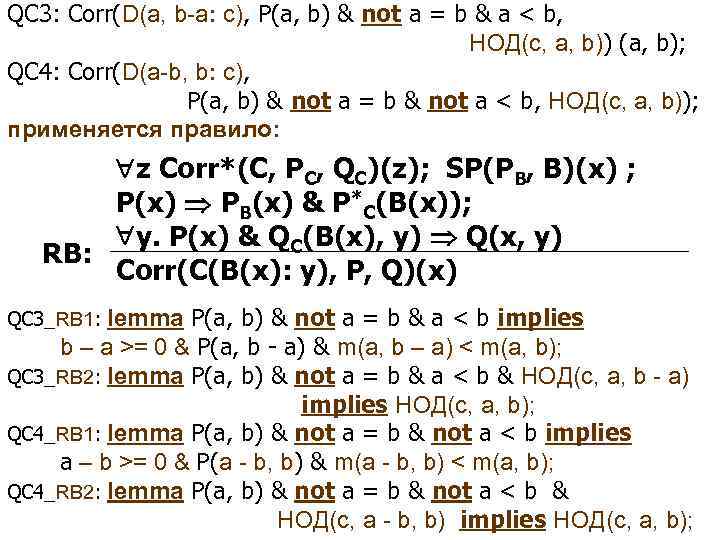QC 3: Corr(D(a, b-a: c), P(a, b) & not a = b & a < b, НОД(c, a, b)) (a, b); QC 4: Corr(D(a-b, b: c), P(a, b) & not a = b & not a < b, НОД(c, a, b)); применяется правило: z Corr*(C, PC, QC)(z); SP(PB, B)(x) ; P(x) PB(x) & P*C(B(x)); y. P(x) & QC(B(x), y) Q(x, y) RB: Corr(C(B(x): y), P, Q)(x) lemma P(a, b) & not a = b & a < b implies b – a >= 0 & P(a, b - a) & m(a, b – a) < m(a, b); QC 3_RB 2: lemma P(a, b) & not a = b & a < b & НОД(c, a, b - a) implies НОД(c, a, b); QC 4_RB 1: lemma P(a, b) & not a = b & not a < b implies a – b >= 0 & P(a - b, b) & m(a - b, b) < m(a, b); QC 4_RB 2: lemma P(a, b) & not a = b & not a < b & НОД(c, a - b, b) implies НОД(c, a, b); QC 3_RB 1:

6. Язык предикатного программирования

Лексемы ЛЕКСЕМА : : = ИДЕНТИФИКАТОР | КЛЮЧЕВОЕ-СЛОВО | КОНСТАНТА | ОПЕРАЦИЯ | РАЗДЕЛИТЕЛЬ| МЕТКА ИДЕНТИФИКАТОР : : = ( _ | [: alpha: ] ) (_ | [: alnum: ])* КЛЮЧЕВОЕ-СЛОВО : : = int | nat | real | inf | nan | char | string | bool | true | false | nil | type | in | subtype | enum | struct | union | array | | set | predicate | lambda | module | measure | import | if | else | for | switch | case | pre | post| or | xor ОПЕРАЦИЯ : : = + | - | * | / | % | ^ | ! | << | >> | ~ | & | | | ? | = | < | > | <= | >= | != | <- РАЗДЕЛИТЕЛЬ : : = ( | ) | [ | ] | { | } | , | ; | : |. |. . | [: blank: ] КОНСТАНТА : : = ЦЕЛАЯ-КОНСТАНТА | ВЕЩЕСТВЕННАЯ-КОНСТАНТА | СИМВОЛЬНАЯ-КОНСТАНТА | СТРОКОВАЯ-КОНСТАНТА | ЛОГИЧЕСКАЯ-КОНСТАНТА СТРОКОВАЯ-КОНСТАНТА : : = ” СИМВОЛ* ” ЛОГИЧЕСКАЯ-КОНСТАНТА : : = true | false

Определение предиката <имя предиката> (<описания аргументов> : <описания результатов>) [ pre <предусловие>] [ {<оператор>} ] [post <постусловие>; ] sign(real x: int s) { if (x>0) s = 1 else if (x = 0) s = 0 else s = -1 } post s = sign(x)

Операторы Оператор <переменная> = <выражение> присваивания Вызов <имя предиката>([<аргументы>]: <результаты> ) предиката <выражение>([<аргументы>]: <результаты> ) Параллельный <оператор1> ||…|| <оператор. N> оператор Условный if (<условие>) <оператор1> оператор else <оператор2> Оператор switch (<выр>) { выбора case выр1: <оператор1> ………………. case выр. N: <оператор. N> default : <оператор. N+1 > } <описание переменных> Оператор суперпозиции <оператор1> ; …; <оператор. N>

Выражения <выражение> : : = <первичное> | <выражение> <знак бинарной операции> <выражение> | <знак унарной операции> <выражение> | <условное выражение> <знак унарной операции> : : = + | - | ! | ~ <знак бинарной операции> : : = * | / | % | + | - | << | >> | in | > | <= | >= | != | & | ^ | or | xor <первичное>: : = <переменная> | <константа> | <агрегат> | <модификация> <вызов функции> | <имя предиката> | <имя типа> | <генератор предиката> | (<выражение>) | <элемент списка> | <определение массива> | <конструктор> | <распознаватель> | <поле объединения> a & b if (a) b else false a or b if (a) true else b

Описания переменных real pi = 3. 14, x, y, z; A(real x, y: nat n) { Complex φz; B(x, y: φz); C(φz: n) } A(real x, y: nat n) { B(x, y: Complex φz); C(φz: n) } A(real x, y: nat n) { Complex φz = B(x, y); C(φz: n) }

Структура предикатной программы module <имя модуля> [( <описания параметров модуля> ) ]; <список описаний> Модуль последовательность импорта, описаний типов, глобальных переменных и определений предикатов Области локализации

Определения типов type <имя типа> [(<параметры>)] = <изображение типа>; Базисные типы bool, nat, int, real, char Структурные типы struct (<тип поля 1> <пробел> <имя поля 1> , … ) <алгебраический тип> set (<тип конечного базового множества> ) array (<тип элемента>, <список типов индексов> ) predicate ( <типы аргументов> : <типы результатов> ) pre … post … type Complex = struct(real re, im ); type Diapason(nat n) = 1. . n+1; type Ar(nat n) = array(real, Diapason(n), 1. . 5);

Алгебраические типы union ( <описание конструкторов>) <описание конструктора>: : = <имя конструктора> [ ( <описание полей>) ] <конструктор>: : = <имя конструктора> [ ( <список выражений>) ] <распознаватель>: : = <имя конструктора>? [ ( <выражение>) ] <поле объединения>: : = <первичное выражение>. <имя поля>

Списки Seq(T) = NIL + (T Seq) type list (type T) = union ( nil, cons (T car, list(T) cdr) ); switch (s) { case nil: 0 case cons(h, t): 1 + length(t) }; list(T) x, y, z; T a; z = a z = x + y z = a + y z = x + y + a x. car x. cdr last(x) len(x) z. car = { Comp. Union(z: i, x, y) ; Comp. Struct(y: u, v); u }

Массивы type ar 1_5 = array (int, 1. . 5); ar 1_5 squ; squ = for (var i) i*i; ar 1_5 r = for (i) 100 - i; type Ar(nat k) = array (real, 1. . k); F (nat n, Ar(n) x: Ar(n+1) x') { x' = for (var j) { case 1. . n : x[j] + 1 case n + 1 : 0 } } type MATR(nat k) = array(real, 1. . k); perm_lines(nat n, MATR(n) a, nat k, m : MATR(n) a' ) pre 1 <= k < m <= n { a' = a with for (i, j) { case (k, 1. . n): a[m, j] case (m, 1. . n): a[k, j] } }

[<тип массива>] ( [<список выражений>] ) <выражение-массив> + <выражение-массив> <вырезка массива> : : = <выражение-массив>[<суженный тип индексов>] <суженный тип индексов> : : = <изображение типа>

Формулы ФОРМУЛА : : = ЛОГИЧЕСКОЕ-ВЫРАЖЕНИЕ | ( ФОРМУЛА ) | [КВАНТОРНАЯ-ЧАСТЬ] ФОРМУЛА | ! ФОРМУЛА | ФОРМУЛА & ФОРМУЛА | ФОРМУЛА or ФОРМУЛА | ФОРМУЛА -> ФОРМУЛА | ФОРМУЛА <-> ФОРМУЛА ЛОГИЧЕСКОЕ-ВЫРАЖЕНИЕ : : = ВЫРАЖЕНИЕ КВАНТОРНАЯ-ЧАСТЬ : : = ( КВАНТОР СПИСОК-ПОДКВАНТОРНЫХ-ПЕРЕМЕННЫХ ) [КВАНТОРНАЯ-ЧАСТЬ] КВАНТОР : : = ! | ? | forall | exists “!” - квантор всеобщности, а “? ” - квантор существования. СПИСОК-ПОДКВАНТОРНЫХ-ПЕРЕМЕННЫХ : : = [ИЗОБРАЖЕНИЕ-ТИПА [: blank: ]] ПОДКВАНТОРНАЯ-ПЕРЕМЕННАЯ (, ПОДКВАНТОРНАЯ-ПЕРЕМЕННАЯ)* ПОДКВАНТОРНАЯ-ПЕРЕМЕННАЯ : : = ИДЕНТИФИКАТОР

Императивное расширение операторы перехода и помеченные операторы Для предиката-функции допускается отсутствие результатов ОПЕРАТОР-ИМПЕРАТИВНОГО-РАСШИРЕНИЯ : : = ГРУППОВОЙ-ОПЕРАТОР-ПРИСВАИВАНИЯ | break | ОПЕРАТОР-FOR | ОПЕРАТОР-ЕСЛИ ГРУППОВОЙ-ОПЕРАТОР-ПРИСВАИВАНИЯ : : = | СПИСОК-ПЕРЕМЕННЫХ | = | СПИСОК-ВЫРАЖЕНИЙ | ОПЕРАТОР-FOR : : = for ( ЗАГОЛОВОК-ЦИКЛА ) { ОПЕРАТОР [; ОПЕРАТОР] } ЗАГОЛОВОК-ЦИКЛА : : = [[ИЗОБРАЖЕНИЕ-ТИПА] ПАРАМЕТР-ЦИКЛА = ВЫРАЖЕНИЕ] ; [УСЛОВИЕ-ЗАВЕРШЕНИЯ] ; [ПЕРЕСЧЕТ-ПАРАМЕТРА] ПАРАМЕТР-ЦИКЛА : : = ИДЕНТИФИКАТОР УСЛОВИЕ-ЗАВЕРШЕНИЯ : : = ВЫРАЖЕНИЕ ПЕРЕСЧЕТ-ПАРАМЕТРА : : = ОПЕРАТОР

Модифицируемые переменные A (int x: int x') { x' = x + 1 } Допускаются операторы вида: x = x + 1 и x++ A[i] = x является эквивалентом A’ = A with [i: x] B. f = x эквивалентен B’ = B with (f: x) G(…: A[i]) заменяется на G(…: X x); A’ = A with [i: x] Оператор вида x' = x можно опускать. Допустимы короткий условный и оператор выбора с пустыми ветвями при условии, что все результаты существующих ветвей являются модифицируемыми переменными