2008年学业考试复习(第一轮) 第四章 基本图形(一)
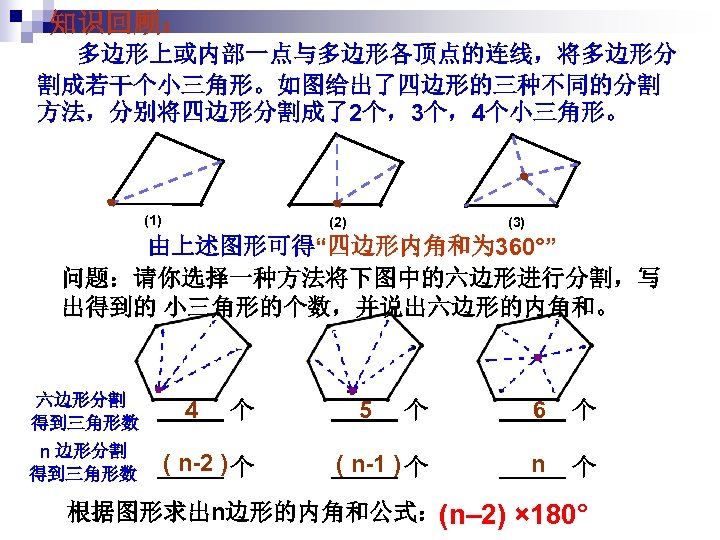
知识回顾： 多边形上或内部一点与多边形各顶点的连线，将多边形分 割成若干个小三角形。如图给出了四边形的三种不同的分割 方法，分别将四边形分割成了2个，3个，4个小三角形。 (1) (3) (2) 由上述图形可得“四边形内角和为 360°” 问题：请你选择一种方法将下图中的六边形进行分割，写 出得到的 小三角形的个数，并说出六边形的内角和。 六边形分割 得到三角形数 n 边形分割 得到三角形数 4 个 ( n-2 ) 个 5 个 6 个 ( n-1 ) 个 n 个 根据图形求出n边形的内角和公式：(n– 2) × 180°
n边形的内角和公式： (n– 2) × 180° n边形外角和： 360° (1)已知一个多边形的内角和是 1080°, 则它是 八 边形。 (n– 2) × 180°= 1080° (2) 正十边形的每个内角度数为 144° ；
操作：将△ABC绕AC的中点O逆时针旋转 180°得到△CDA, A E D 问题：(1)讨论四边形ABCD的形状; (2)图中有哪些线段相等; O F B C 平行四边形： 边 性 质 对角线 角 对边平行，对边相等 对角线互相平分 对角相等，邻角互补 “平行四边形是中心对称图形， 对角线的交点就是它的对称中心 ” (3)四边形ABCD的四个内角相 互之间有怎样的关系; (4)过点O作直线交AD, BC于 点E, F, 又得到哪些正确结论？ (5)连结BE, DF, 四边形BFDE 是平行四边形吗？ 1. 一组对边平行且相等 平行四边形 2. 两组对边分别平行 判定方法 3. 两组对边分别相等 4. 对角线互相平分
例1. 已知□ABCD中, 直线MN // AC, 分别交AB于P，BC 于Q, 交DA延长线于M, 交DC延长线于N. 求证：PM=QN M A D P B C Q N
例1. 已知□ABCD中, 直线MN // AC, 分别交AB于P，BC 于Q, 交DA延长线于M, 交DC延长线于N. 求证：PM=QN M A D P B C Q N
例2. 已知△ABC ，(1)求作以A, B, C为其中三个顶点的 平行四边形。 D 2 D 1 A C B D 3
(2) 建立如图的平面直角坐标系，请根据顶点A, B, C的坐 标，求出第四个顶点的坐标。 y D 2 (-1, 2) D 1 (5, 2) A(2, 2 ) (B) O M 夹在两条平行线 间的垂线段相等 N C(3, 0) x D 3 (1, -2) OM=CN = OC - ON =3 -2=1
(3)每个平行四边形四个顶点的横坐标之间有怎样的等量关系？ 其纵坐标之间的关系呢？ (4)猜想：图(4)中顶点C的坐标（用含a, b, c, d, e, f的代数式表示） y D 2 (-1, 2) D 1 (5, 2) A(2, 2 ) O (B) (0, 0) C(3, 0) D 3 (1, -2) x c+e-a , d+f-b
例3. 某公园有一块平行四边形的草坪(□ABCD )，现有三棵 古树位于点A、C、E处(E在CD上），园林局决定在这块草 坪上再栽种一棵，使得四棵树所在的位置恰好是平行四边形 的四个顶点。(要求三棵古树不能移动 ) D A C E B 请你找出符合要求的植树点， 画出示意图，并对你的设计作 适当的说明。(画图 具不限)
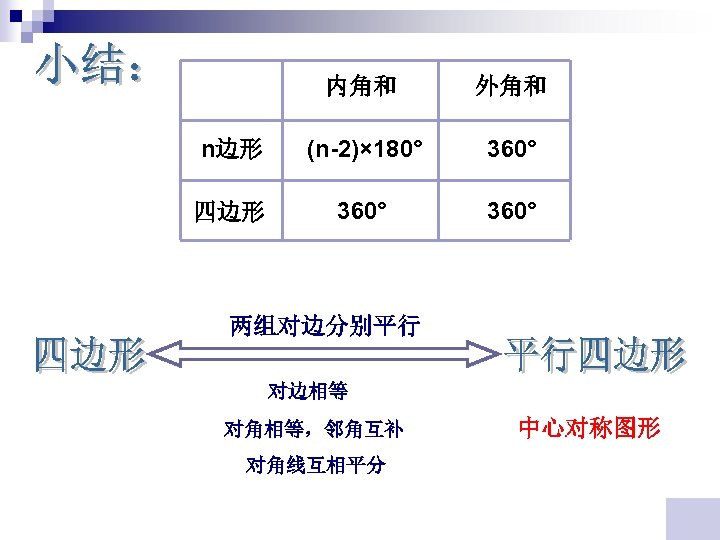
内角和 外角和 n边形 (n-2)× 180° 360° 四边形 360° 两组对边分别平行 对边相等 对角相等，邻角互补 对角线互相平分 中心对称图形
1. 如图，□ABCD的周长为 20 cm，对角线 AC, BD相交于点O，OE⊥BD交AD于点E， 则△ABE的周长为 cm; A E D O B 2. 如图，若将四根木条钉成的矩形木框挤 压变形为平行四边形ABCD的形状，若想 使其面积为矩形面积的一半，则这个平行 四边形最小内角的度数为 ； C D A C B
3. 如图，P为Rt△ABC所在平面内任意一点(不在直线AC上)， ∠ACB=90 °, M为AB边中点； 操作：以PA, PC为邻边作平行四边形PADA， 连结PM并延长至点E，使ME=PM，连结DE。 探究：请猜想与线段DE有关的三个结论，并 予以证明。 C P A M B
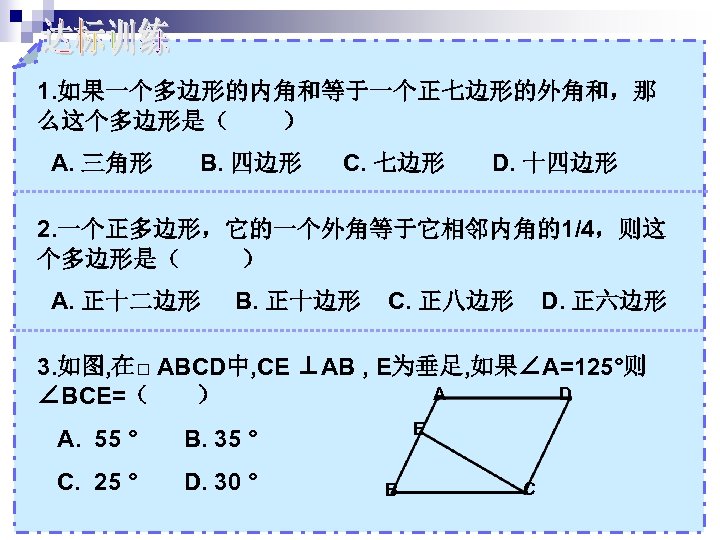
1. 如果一个多边形的内角和等于一个正七边形的外角和，那 么这个多边形是（ ） A. 三角形 B. 四边形 C. 七边形 D. 十四边形 2. 一个正多边形，它的一个外角等于它相邻内角的1/4，则这 个多边形是（ ） A. 正十二边形 B. 正十边形 C. 正八边形 D. 正六边形 3. 如图, 在□ ABCD中, CE ⊥AB , E为垂足, 如果∠A=125°则 A D ∠BCE=（ ） A. 55 ° C. 25 ° D. 30 ° E B. 35 ° B C
4. 如图所示，在□ ABCD中，对角线AC, BD交于点O，下 A D 列式子中一定成立的是（ ） A. AC ⊥BD B. OA=OC C. AC=BD D. AO=OD O B 5. 如图，在□ ABCD中，CE是∠DCB的平 分线，F是AB的中点，AB=6，BC=4，则 AE: EF: FB= ； C D A 6. 如图，直角梯形ABCD中，AD//BC，AB ⊥BC，AD=2，BC=3，∠BCD=45°，将腰 CD以点D为中心逆时针旋转 90°至ED，连 结AE, CE，则△ADE的面积为 ； C E B F E A B D C
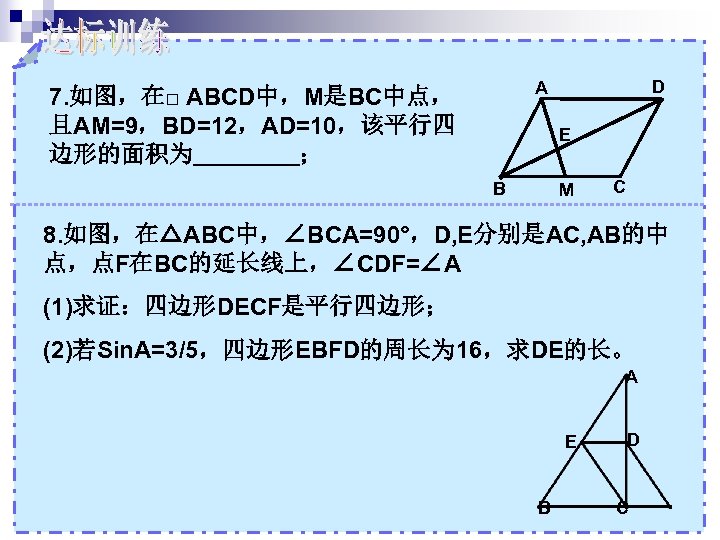
D A 7. 如图，在□ ABCD中，M是BC中点， 且AM=9，BD=12，AD=10，该平行四 边形的面积为 ； E B M C 8. 如图，在△ABC中，∠BCA=90°，D, E分别是AC, AB的中 点，点F在BC的延长线上，∠CDF=∠A (1)求证：四边形DECF是平行四边形； (2)若Sin. A=3/5，四边形EBFD的周长为 16，求DE的长。 A E B D C
9. 如图, 在□ ABCD内有一点满足DE⊥AD 于D，∠EBC=∠EDC，∠ECB=45°，请 找出与BE相等的一条线段，并予以证明。 A D E B C A P 10. 已知□ ABCD和点P，当点P在图(1)中位置时， 则有结论：S△PBC=S△PAB+S△PCD B D 图(1) E C 请你参考上述信息，当P分别在图(2), (3)中位置时，图中的三 角形又有怎样的数量关系？请写出你对这两种情况的猜想， 并选择其中一种情况的猜想给予证明。 A P D A D P B 图(2) C B 图(3) C
有三个角是直角 有一个内角是直角 对角线相等 四 边 形 矩形 有一组邻边相等 对角线互相垂直 平 行 四 边 形 正 方 形 有一组邻边相等 对角线互相垂直 四条边都相等 菱形 有一个内角是直角 对角线相等
二、知识概要(性质) 边 角 对角线
三、基本练习 (填空题) 1. 如图，根据四边形的不稳定性制作边长为 16 cm的可活 动的菱形衣架，若墙上钉子间的距离AB=BC=16 cm， 则∠ 1=_____度。 120 2. 已知，矩形ABCD的长AB=4，宽AD=3，按如图放置 在直线AP上，然后不滑动转动，当它转动一周时（ 6π A→A′），顶点A所经过的路线长等于____。
三、基本练习 (填空题) 30 3. 如图，已知正方形纸片ABCD，M，N分别是AD，BC 的中点，把BC向上翻折，使点C恰好落在MN上的P 点处，BQ为折痕，则∠PBQ=____度。
三、基本练习 (选择题) 1. 如图，已知正方形ABCD的边长为 2，如果将线段BD 绕着点B旋转后，点D落在CB的延长线上的D’处， B 那么tan∠BAD′等于（ ） (A) 1 (B) (C) (D) 2 2. 矩形ABCD的顶点A，B，C，D按照顺时针方向排列， 若在平面直角坐标系中，B，D两点对应的坐标分别 是（2，0），（0，0），且A，C两点关于x轴对称， 则C点对应的坐标是（ ） B (A)(1, 1) (B) (1, -1) (C) (1, -2) (D) ( , - )
三、基本练习 (选择题) 3. 如图，有一块矩形纸片ABCD，AB=10，AD=6， 将纸片折叠，使AD边落在AB边上，折痕为AE，再将 △AED以DE为折痕向右折叠，AE与BC交于点F，则 △CEF的面积为（ ） C (A) 4 (B)6 (C)8 (D)10
例1. 人师傅做铝合金窗框分下面三个步骤 进行: （1）先截出两对符合规格的铝合 金窗料，使AB=CD，EF=GH.
例1. 人师傅做铝合金窗框分下面三个步 骤进行: （2）摆成如图所示的四边形，则这时窗 框的形状是 平行四边形 ，根据的数学道 理： 两组对边分别相等的四边形是平行四边形 。
例1. 人师傅做铝合金窗框分下面三个步骤 进行: （3）将直角尺靠紧窗框的一个角，调整窗框的 边框，当直角尺的两条直角边与窗框无缝隙时， 说明窗框合格，这时窗框是 矩 形，根据的数学 道理是 有一个角是直角的平行四边形是矩形 。
想一想 还有什么方法可以说明这 个铝合金窗框是合格的? B A D ∠A= AC=BD ∠B= ∠C=90 ° A B C D C
若这个铝合金窗框ABCD两条对角线的夹 角∠ AOB为 60 ° ， △ AOB的周长为 3 m。 A （1）求窗框对角线AC长； B 60 o D C
若这个铝合金窗框ABCD两条对角线的夹 角∠ AOB为 60 ° ， △ AOB的周长为 3 m。 （2）求窗框ABCD的面积。 A B 60 o D C
例2. 如图，两张等宽的纸条交叉重叠在一 起，猜想重叠部分的四边形ABCD是什么形 状？说说你的理由。 F E
例3. 将一张矩形的纸对折再对折， 然后沿着图中的虚线剪下，打开，你会 发现这是一个菱形。你能解释其中的道 理吗？
若展开后的菱形纸片ABCD中，两条对 角线AC= ，BD= 4 。 （1）求菱形ABCD的面积； （2）求菱形ABCD的周长； （3） 求∠ADC的度数。
想一想 如果想得到一个正方形，该怎 么剪？并解释你这样做的道理。
例4. 已知正方形ABCD （1）若一条对角线BD长为 2 cm， 求这个正方形的周长、面积。 A D B C
例4. 已知正方形ABCD （2）若E为对角线上一点，连接EA、 EC。EA=EC吗？说说你的理由。 A D E B C
例4. 已知正方形ABCD （3）若AB=BE，求∠ AED的大小。 A D E B C
例5. 顺次连接任意四边形各边的中点，所构成 的四边形以下简称为“中点四边形”。试判断中点四 边形EFGH的形状，并说明理由。 （1）添加一个条件，使四边形 EFGH为菱形； AC=BD （2）添加一个条件，使四边形 EFGH为矩形； AC ⊥ BD （3）添加一个条件，使四边形 EFGH为正方形； AC=BD且AC ⊥ BD
那么，特殊平行四边形的“中点四 边形”会是怎样的图形呢？ 1. 矩形的“中点四边形”是 菱 形； 2. 菱形的“中点四边形”是 矩 形； 3. 正方形的“中点四边形”是 正方 形。
中考链接 1. （河北省2005）如图，在矩形ABCD中，E、F、G、 H分别是AB、BC、CD、DA的中点。若AB=2，AD=4， 则阴影部分的面积为 （ B. ） A. 3 B. 4 C. 6 D. D. 8
中考链接 2. （陕西省2005）如图，在一个由 4× 4个小正 方形组成的正方形网格中，阴影部分面积与正 方形ABCD的面积比是 （ B. ） A. 3： 4 B. 5： 8 C. 9： 16 D. D. 1： 2
3. 已知正方形ABCD， ME⊥ BD， MF⊥ AC，垂足分别为E、F （1） M是AD上的点，若对角线AC=12 cm， 求ME+MF的长。 （2）若M是AD上的一 个动点，ME+MF的长度 是否发生改变？ （3）当M点运动到何 处时，四边形MFOE的面 积最大？ M A D F E O B C
四、训练题 1. 如图，正方形MNPQ网格中，每个小方格的边长都相 等，正方形ABCD的顶点分别在正方形MNPQ的4条 边的小方格的顶点上。 （1）设正方形MNPQ网格中 每个小方格的边长为 1，求： ①△ABQ, △BCM, △CDN, △ADP的面积 ②正方形ABCD的面积 （2）设MB=a，BQ=b，利用这个图形中直角三 角形和正方形的面积关系，你能验证已学过 的哪一个数学公式或定理吗？相信你能给出 简明的推理过程。
2. 如图，在△ABC中，∠ACB=90°，BC的中垂线DE 交BC于点D, 交AB于点E，F在DE的延长线上，并 且AF=CE. （1）证明：四边形ACEF是平行四边形. （2）当∠B的大小满足什么条件时，四边形 ACEF是菱形？请回答并证明你的结论. （3）四边ACEF有可能是正方形吗？请证明 你的结论。
3. 探究下列问题： （1）如图①，在△ABC中，CP⊥AB于点P，求 证: AC 2 -BC 2=AP 2 -BP 2； （2）如图②，在四边形ABCD中，AC⊥BD, 垂足 为P，猜一猜AB, BC, CD, DA之间有何数量关系， 用式子表示出来（不必说明理由）； （3）如图③，在矩形ABCD中，P为内部任意一 点，请猜想出AP, BP, CP, DP之间的数量关系， 并证明之。
4. 如图，OABC是一张放在平面直角坐标系中的 矩形纸片，O为原点，点A在x轴上，点C在y 轴上，OA=10，OC=6。 （1）如图①，在OA上选取一点G，将 △COG沿CG翻折，使点O落在BC边上， 设为E，求折痕CG所在直线的解析式。
4. （2）如图②，在OC上任取一点D，将 △AOD沿AD翻折，使点O落在BC边上，记为 E’。 ①求折痕AD所在直线的解析式； ②再作E’F//AB，交AD于点F，若抛物线 过点F， 求此抛物线的解析式，并判断它与直线AD的 交点的个数。
4. （3）如图③，在OC，OA上选取适当的点D’， G’，使纸片沿D’G’翻折后，点O落在BC边上， 记为E’’。请你猜想：折痕D’G’所在直线与② 中的抛物线会用什么关系？用（1）中的情形 验证你的猜想。
5. 正方形通过剪切可以拼成三角形（如图①）。方 法如下： 仿上例用图示的方法，解答下列问题： 操作设计： （1）如图②，对直角三角形，设计一种 方案，将它分成若干块，再拼成一个 与原三角形等面积的矩形。 （2）如图③，对任意三角形，设计一种 方案，将它分成若干块，再拼成一个 与原三角形等面积的矩形。 （3）对于任意四边形，能否通过恰当的分割和重新组 合拼接，使其成为一个与四边形等面积的矩形。
课后作业 1. 完成《浙江中考》P 116练习. 2. 对特殊的平行四边形，矩形、 菱形、正方形的性质及判定方法 进行总结归纳。
Скачать презентацию 2008年学业考试复习 第一轮 第四章 基本图形 一 知识回顾 多边形上或内部一点与多边形各顶点的连线 将多边形分 割成若干个小三角形 如图给出了四边形的三种不同的分割 方法 分别将四边形分割成了2个 3个 4个小三角形
f19b677d9343cb484f110c2b37911c54.ppt