20 CHAPTER Elasticity of Demand Supply

20 CHAPTER Elasticity of Demand & Supply

From Ch. 3 make sure you know the following: • Define demand supply and state the laws of demand supply. • Determine equilibrium price and quantity from supply and demand graphs and schedules.

• From law of demand, a consumer will buy more when price declines, or P↓ → Qd ↑ • But how much more or less? • Will you buy more of 2 different goods as their P decline by 1 KD? • We use the concept of elasticity

• Elasticity of demand measures: how much the Qd changes with a given change in P of the good, change in consumers’ income (I), or change in price of related product, or: %∆Qd to %∆P, or %∆I, or %∆Pof related goods • Price elasticity is a concept that also relates to supply.

II. Price Elasticity of Demand - The degree of responsiveness or sensitivity of consumers to a change in price is measured by the concept of price elasticity of demand. 1. If consumers are relatively responsive to price changes, demand is said to be elastic

2. If consumers are relatively unresponsive to price changes, demand is said to be inelastic 3. Note that with both elastic and inelastic demand, consumers behave according to the law of demand: they are responsive to price changes.

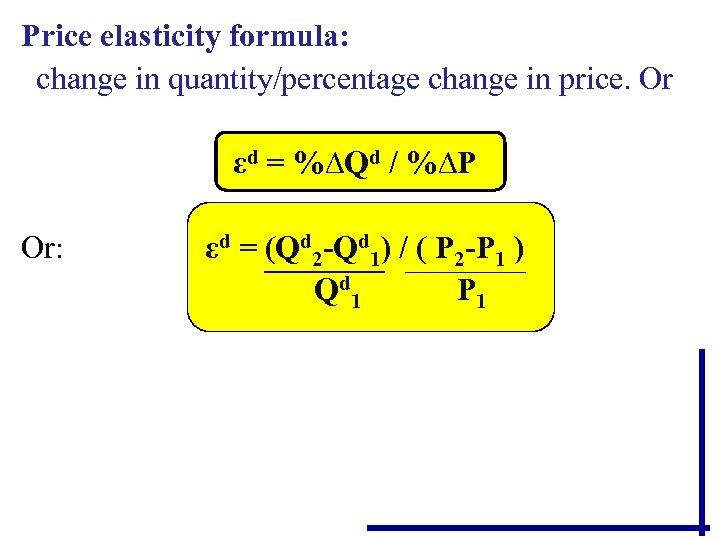Price elasticity formula: change in quantity/percentage change in price. Or εd = %∆Qd / %∆P Or: εd = (Qd 2 -Qd 1) / ( P 2 -P 1 ) Q d 1 P 1

• Using two price-quantity combinations of a demand schedule, calculate the percentage change in quantity by dividing the absolute change in quantity by one of the two original quantities. Then calculate the percentage change in price by dividing the absolute change in price by one of the two original prices.

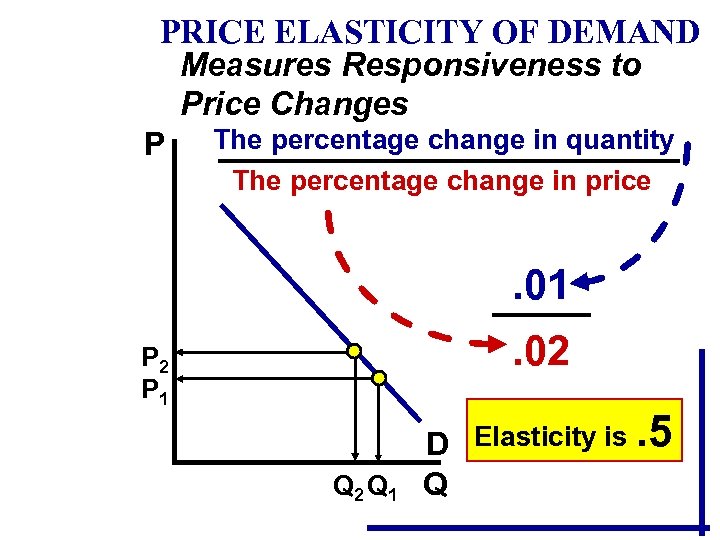PRICE ELASTICITY OF DEMAND Measures Responsiveness to Price Changes P The percentage change in quantity The percentage change in price . 01. 02 P 1 Q 2 Q 1 D Elasticity is. 5 Q

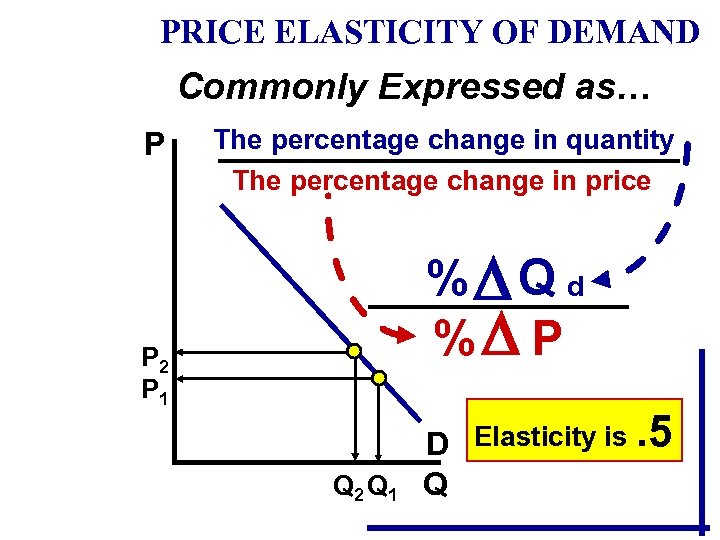PRICE ELASTICITY OF DEMAND Commonly Expressed as… P The percentage change in quantity The percentage change in price % Q d % P P 2 P 1 Q 2 Q 1 D Elasticity is. 5 Q

PRICE ELASTICITY OF DEMAND The Price-Elasticity Coefficient and Formula εd = Percentage change in quantity demanded of product X Percentage change in price of product X Or equivalently… εd = Percentage change in quantity demanded of X Original quantity demanded of X Change in price of X Original price of X Elimination of the Minus Sign

PRICE ELASTICITY OF DEMAND Interpretations of Ed Elastic Demand εd = . 04. 02 =2 . 01. 02 =. 5 Inelastic Demand εd = Unit Elasticity εd = . 02 =1

Percentages also make it possible to compare elasticities of demand for different products. Because of the inverse relationship between price and quantity demanded, the actual elasticity of demand will be a negative number. However, we ignore the minus sign and use the absolute value of both percentage changes.

• If the coefficient of elasticity of demand is > 1, we say demand is elastic; elastic • The quantity demanded is “relatively responsive” when εd is >1. • If the coefficient is < 1, demand is inelastic • Demand is “relatively unresponsive” when εd <1. • A special case is if εd = 1; this is called unit elasticity

Note: Inelastic demand does not mean that consumers are completely unresponsive. This extreme situation called perfectly inelastic demand would be very rare, and the demand curve would be vertical.

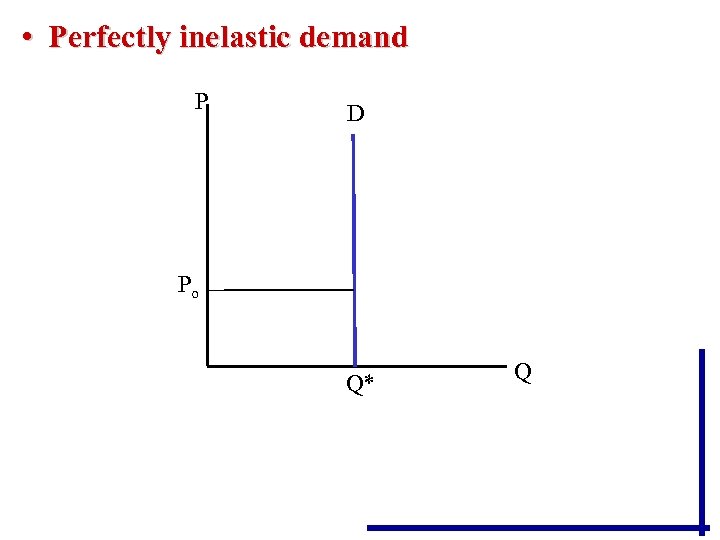• Perfectly inelastic demand P D Po Q* Q

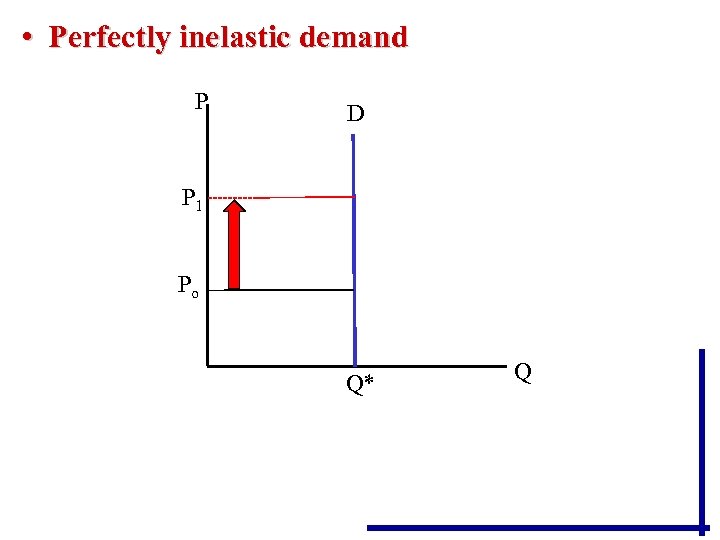• Perfectly inelastic demand P D P 1 Po Q* Q

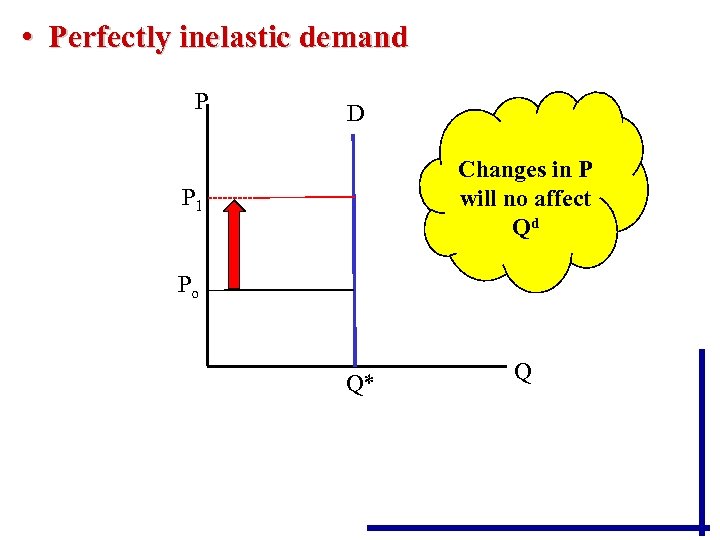• Perfectly inelastic demand P D Changes in P will no affect Qd P 1 Po Q* Q

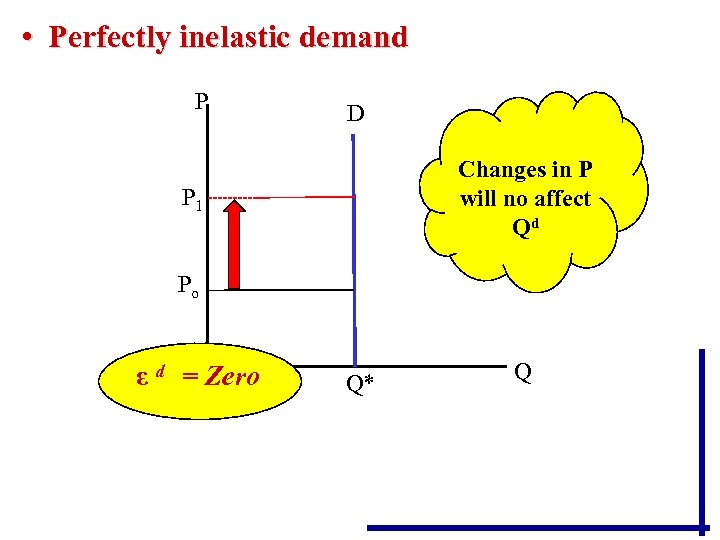• Perfectly inelastic demand P D Changes in P will no affect Qd P 1 Po ε d = Zero Q* Q

• Elastic demand does not mean consumers are completely responsive to a price change. This extreme situation, in which a small price reduction would cause buyers to increase their purchases from zero to all that it is possible to obtain, is perfectly elastic demand, and the demand curve would be horizontal.

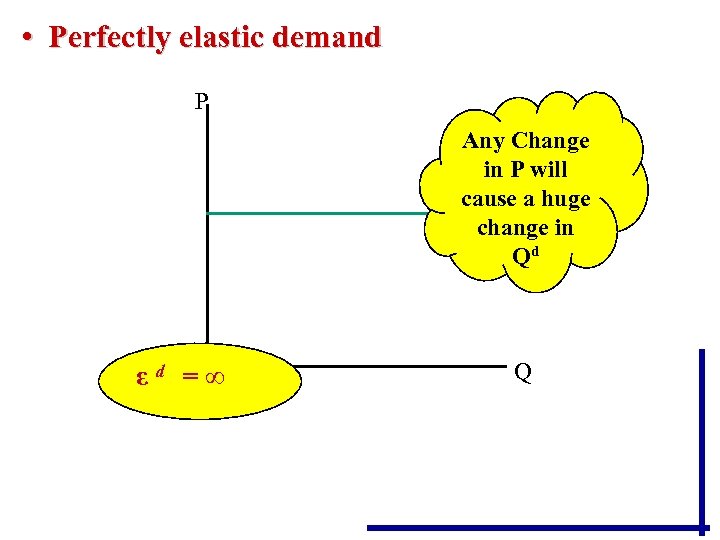• Perfectly elastic demand P Any Change in P will cause a huge change in Qd εd =∞ Q

• Consider the following example: Price Qd 5 4 4 5 To calculate elasticity, which price-quantity combination should we use as P 1 and Qd 1? Assumption 1: let P 1=5 and P 2=4, and Qd 1=4 while Qd 2=5, then: εd = [(5 -4)/4] / [(4 -5)/5] = 1/4 * (-5) (ignoring the minus) = |-5/4| or 1. 25 so demand is elastic

• Consider the following example: Price Qd 5 4 4 5 To calculate elasticity, which price-quantity combination should we use as P 1 and Qd 1? Assumption 2: let P 1=4 and P 2=5, and Qd 1=5 while Qd 2=4, then: εd = [(4 -5)/5] / [(5 -4)/4] = -1/5 * (4) (ignoring the minus) = |- 4/5| or 0. 8 so demand is inelastic

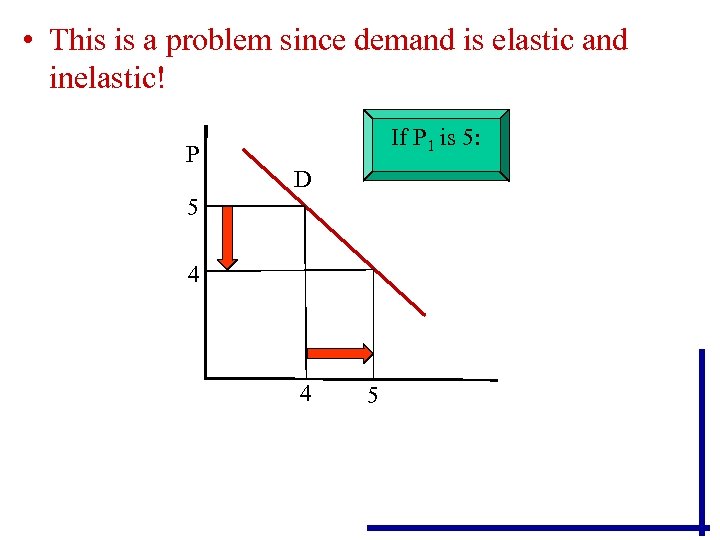• This is a problem since demand is elastic and inelastic! P If P 1 is 5: D 5 4 4 5

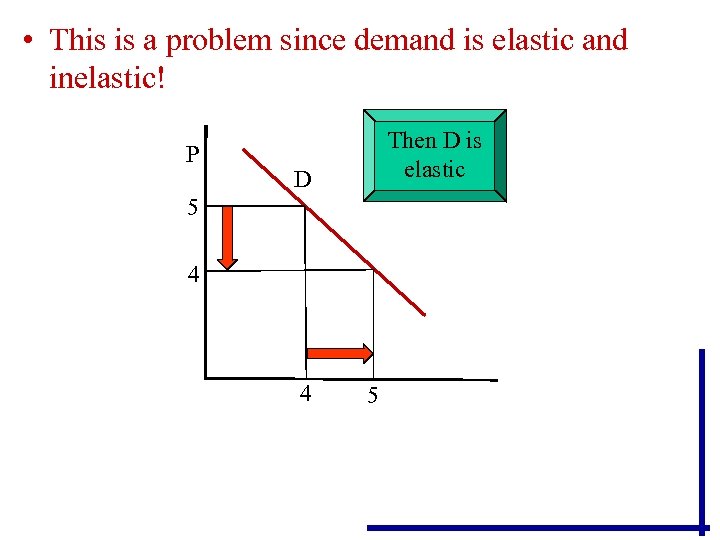• This is a problem since demand is elastic and inelastic! P Then D is elastic D 5 4 4 5

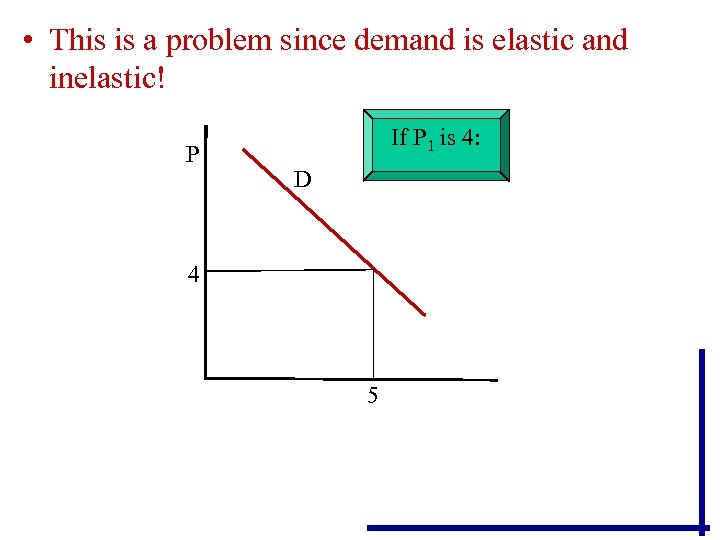• This is a problem since demand is elastic and inelastic! P If P 1 is 4: D 4 5

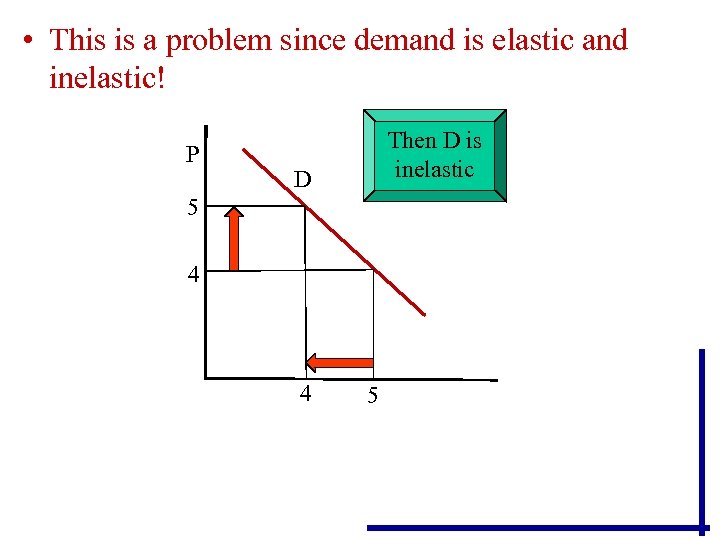• This is a problem since demand is elastic and inelastic! P Then D is inelastic D 5 4 4 5

• To solve this problem, we use the average, or “the midpoint formula” for elasticity: εd = (Qd 2 - Qd 1) ( P 2 -P 1 ) ÷ d + Qd )/2 (Q 2 ( P 2 -P 1 )/2 1

• To solve this problem, we use the average, or “the midpoint formula” for elasticity: εd = (Qd 2 - Qd 1) ( P 2 -P 1 ) ÷ d + Qd )/2 (Q 2 ( P 2+P 1 )/2 1 Applying to our example: εd = (5 -4)/(4. 5) ÷ (4 -5)/(4. 5) εd = |-1| = 1

• To solve this problem, we use the average, or “the midpoint formula” for elasticity: εd = (Qd 2 - Qd 1) ( P 2 -P 1 ) ÷ d + Qd )/2 (Q 2 ( P 2+P 1 )/2 1 Applying to our example: εd = (5 -4)/(4. 5) ÷ (4 -5)/(4. 5) εd = |-1| = 1 Demand is Unitary Elastic!

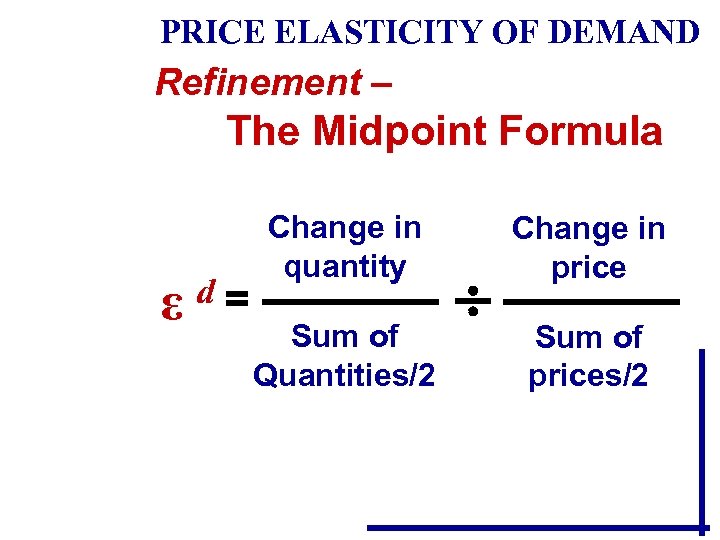PRICE ELASTICITY OF DEMAND Refinement – The Midpoint Formula ε d= Change in quantity Sum of Quantities/2 Change in price Sum of prices/2

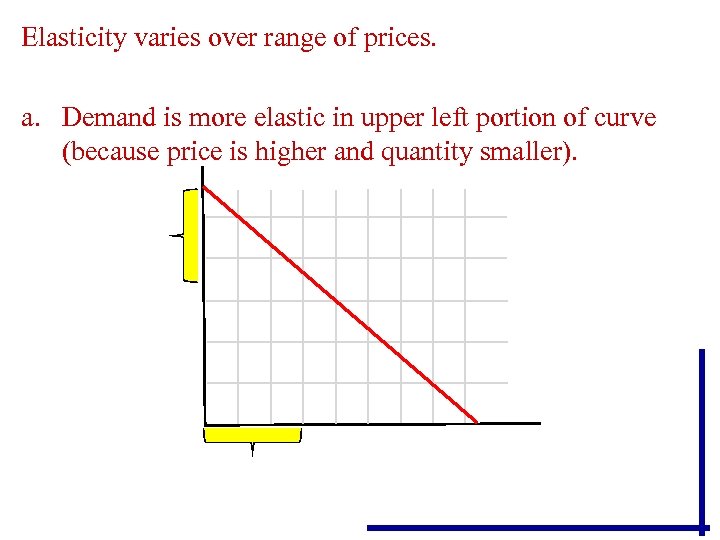Elasticity varies over range of prices. a. Demand is more elastic in upper left portion of curve (because price is higher and quantity smaller).

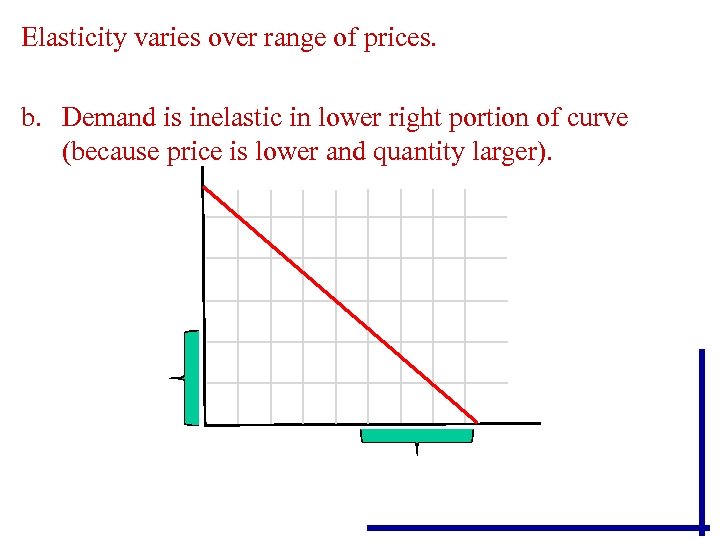Elasticity varies over range of prices. b. Demand is inelastic in lower right portion of curve (because price is lower and quantity larger).

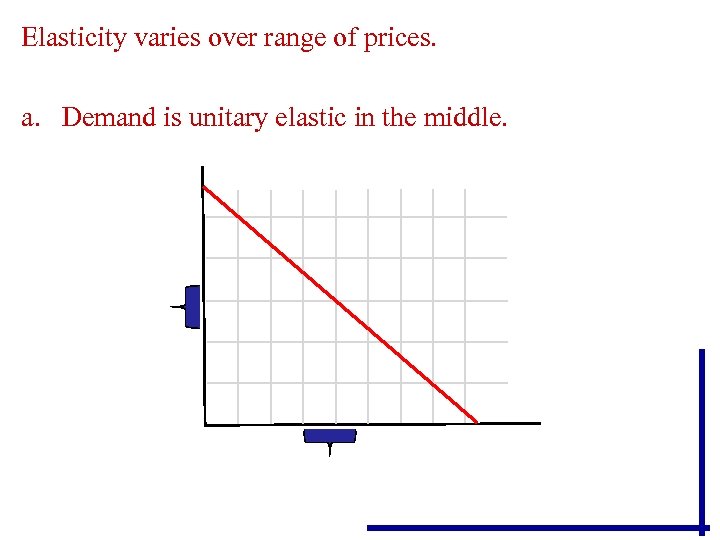Elasticity varies over range of prices. a. Demand is unitary elastic in the middle.

• It is impossible to judge elasticity of a single demand curve by its flatness or steepness, since demand elasticity can measure both as elastic and as inelastic at different points on the same demand curve.

Total Revenue Test • TR = Px. Q • A total-revenue test is the easiest way to judge whether demand is elastic or inelastic. • This test can be used in place of an elasticity formula, unless there is a need to determine the elasticity coefficient. • Elastic demand the total-revenue test: Demand is elastic if a decrease in price results in a rise in total revenue, or if an increase in price results in a decline in total revenue. (Price and revenue move in opposite directions).

• Elastic demand the total-revenue test: • Demand is elastic if a decrease in price results in a rise in total revenue, • or if an increase in price results in a decline in total revenue. • Price and revenue move in opposite directions.

• Inelastic demand the total-revenue test: • Demand is inelastic if a decrease in price results in a fall in total revenue, • or an increase in price results in a rise in total revenue. • (Price and revenue move in same direction).

• Unit elasticity and the total-revenue test: • Demand is unitary elastic if total revenue does not change when the price changes. • Table 20 -2 provides a summary of the rules and concepts related to elasticity of demand.

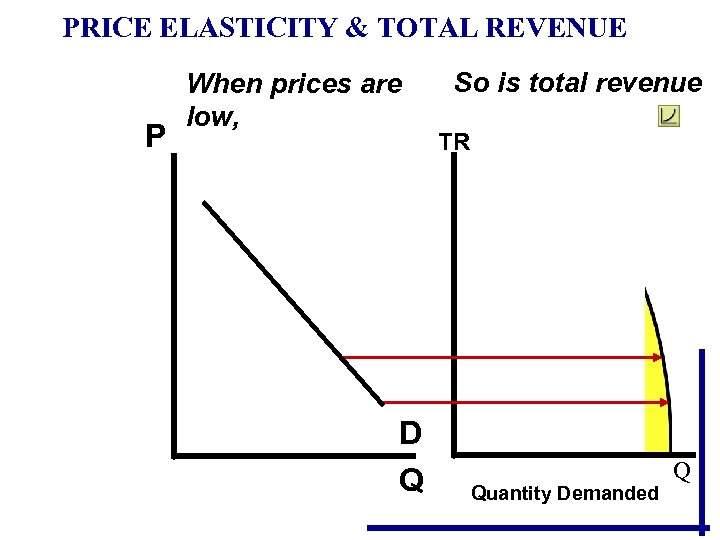PRICE ELASTICITY & TOTAL REVENUE P When prices are low, D Q So is total revenue TR Quantity Demanded Q

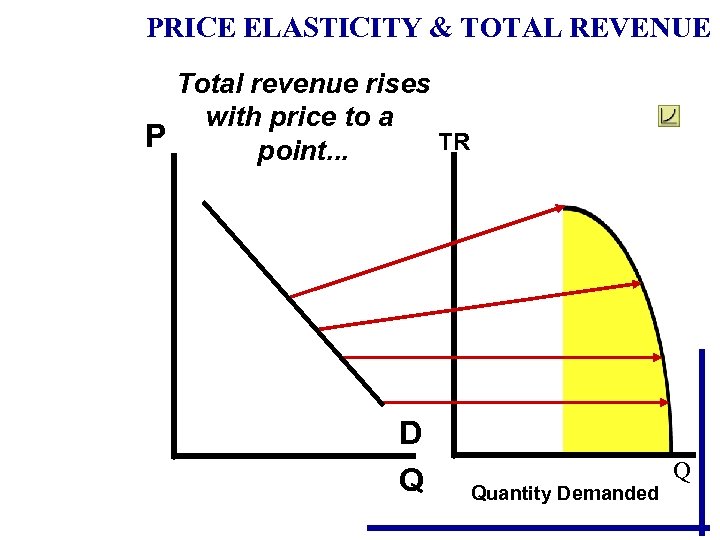PRICE ELASTICITY & TOTAL REVENUE Total revenue rises with price to a P TR point. . . D Q Quantity Demanded Q

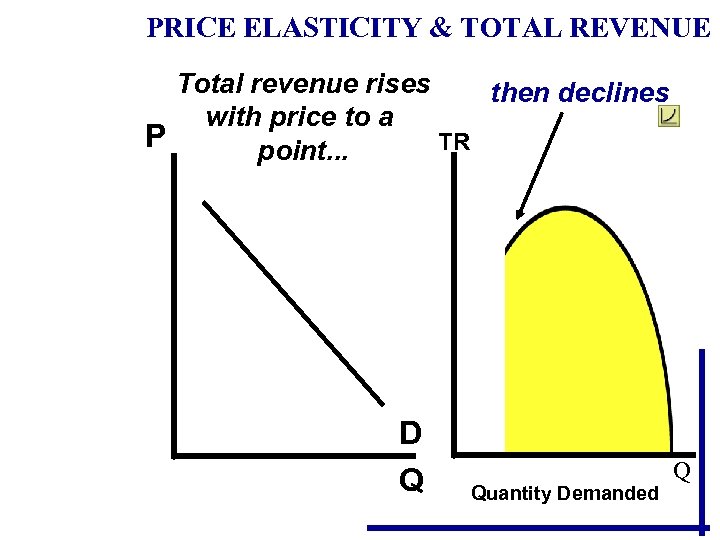PRICE ELASTICITY & TOTAL REVENUE Total revenue rises then declines with price to a P TR point. . . D Q Quantity Demanded Q

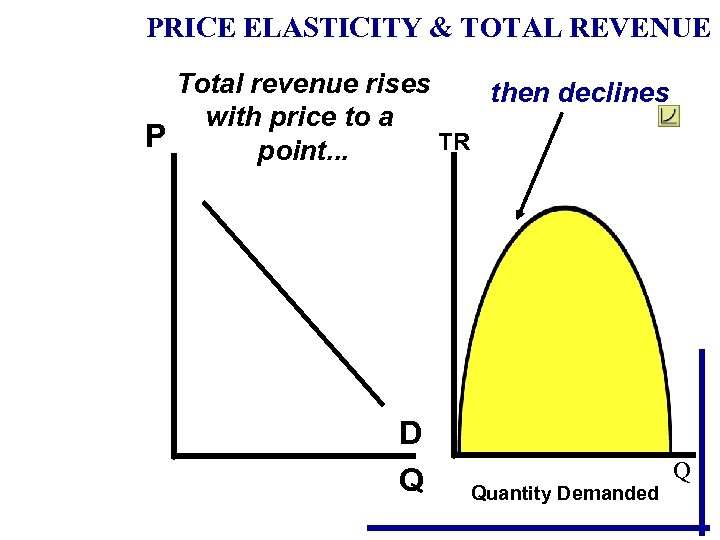PRICE ELASTICITY & TOTAL REVENUE Total revenue rises then declines with price to a P TR point. . . D Q Quantity Demanded Q

PRICE ELASTICITY & TOTAL REVENUE Total revenue rises then declines with price to a P TR point. . . Total Revenue Test D Q Quantity Demanded

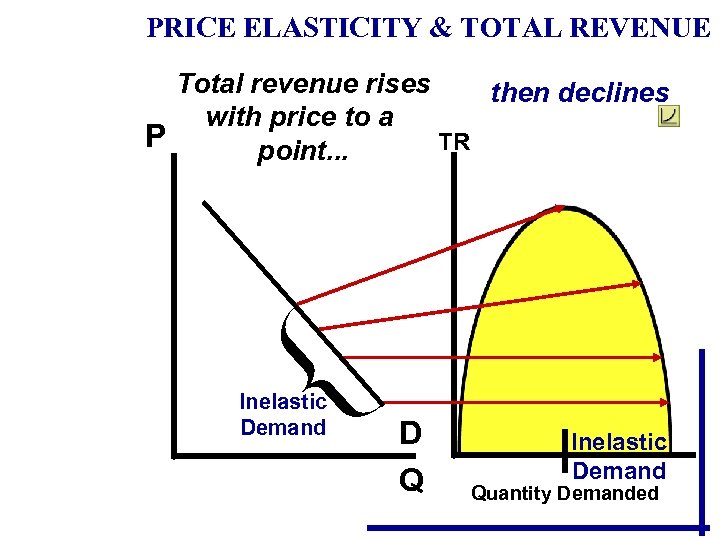PRICE ELASTICITY & TOTAL REVENUE Total revenue rises then declines with price to a P TR point. . . Inelastic Demand D Q Inelastic Demand Quantity Demanded

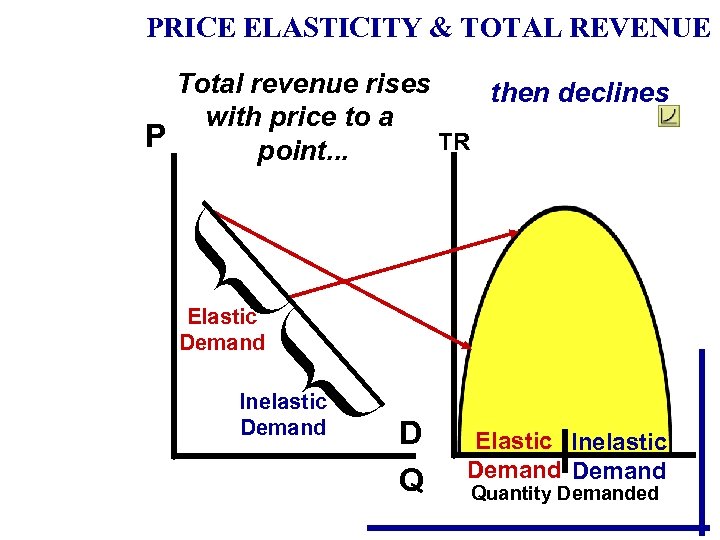PRICE ELASTICITY & TOTAL REVENUE Total revenue rises then declines with price to a P TR point. . . Elastic Demand Inelastic Demand D Q Elastic Inelastic Demand Quantity Demanded

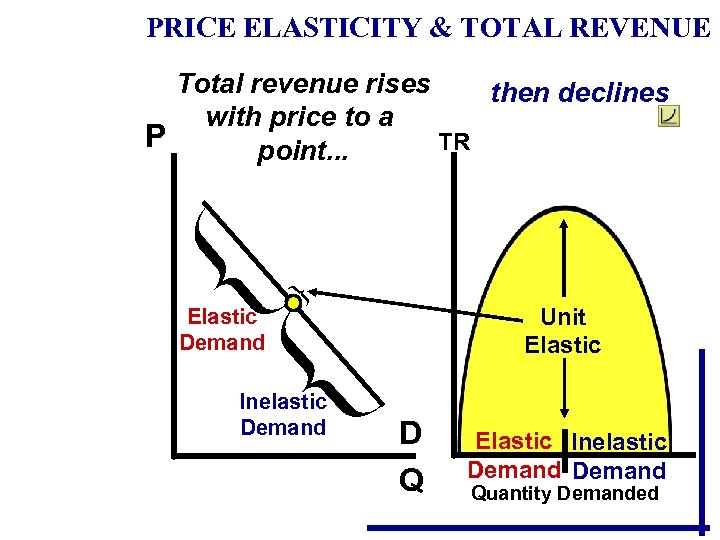PRICE ELASTICITY & TOTAL REVENUE Total revenue rises then declines with price to a P TR point. . . Unit Elastic Demand Inelastic Demand D Q Elastic Inelastic Demand Quantity Demanded

Determinants of Price Elasticity: There are several determinants of the price elasticity of demand. 1. Substitutes for the product: Generally, the more product substitutes, the more elastic the demand. 2. The proportion of price relative to income: Generally, income the larger the expenditure relative to one’s budget, the more elastic the demand, because buyers notice the change in price more. 3. luxury vs. Necessity products: Generally, the less products necessary the item, the more elastic the demand. 4. Time factor: Generally, the longer the time period factor involved, the more elastic the demand becomes.

practical applications: There are many practical applications of the price elasticity of demand. 1. Inelastic demand for agricultural products helps to explain why bumper crops depress the prices and total revenues for farmers. 2. Governments look at elasticity of demand when levying excise taxes. Excise taxes on products with inelastic demand will raise the most revenue and have the least impact on quantity demanded for those products. 3. Demand for cocaine is highly inelastic and presents problems for law enforcement. Stricter enforcement reduces supply, raises prices and revenues for sellers, and provides more incentives for sellers to remain in business. Crime may also increase as buyers have to find more money to buy their drugs.

Price Elasticity of Supply • The concept of price elasticity also applies to supply. The elasticity formula is the same as that for demand. εs = % ∆Qs / % ∆ P • As with price elasticity of demand, the midpoints formula is more accurate.

PRICE ELASTICITY OF SUPPLY ε s= Percentage change in quantity supplied of good X Percentage change in the price of good X Now, compare the immediate market period, the short-run, and long run. . .

• The ease of shifting resources between alternative uses is very important in price elasticity of supply because it will determine how much flexibility a producer has to adjust output to a change in the price. • The degree of flexibility, and therefore the time period, will be different industries. (Figure 20 -3)

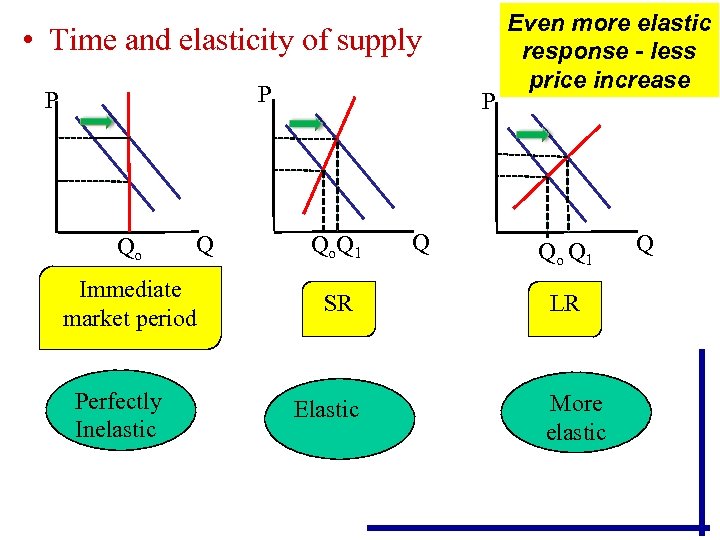• Time and elasticity of supply P P Qo Q Immediate market period Perfectly Inelastic P Qo. Q 1 SR Elastic Q Even more elastic response - less price increase Qo Q 1 LR More elastic Q

• The market period is so short that elasticity of supply is inelastic; it could be almost perfectly inelastic or vertical. In this situation, it is virtually impossible for producers to adjust their resources and change the quantity supplied. (Think of adjustments on a farm once the crop has been planted. )

• The short‑run supply elasticity is more elastic than the market period and will depend on the ability of producers to respond to price change. Industrial producers are able to make some output changes by having workers work overtime or by bringing on an extra shift. • The long‑run supply elasticity is the most elastic, because more adjustments can be made over time and quantity can be changed more relative to a small change in price, as in Figure 20 -3 c. The producer has time to build a new plant.

Applications of the price elasticity of supply. 1. Antiques and other non-reproducible commodities are inelastic in supply, sometimes the supply is perfectly inelastic. This makes their prices subject to fluctuations in demand. 2. Gold prices are volatile because the supply of gold is highly inelastic, and unstable demand resulting from speculation causes prices to fluctuate significantly.

Cross and income elasticity of demand: Cross elasticity of demand refers to the effect of a change in a product’s price on the quantity demanded for another product. Numerically, the formula is shown for products X and Y. εxy = %∆Qx / %∆Py 1. If εxy > 0, then X and Y are substitutes. 2. If εxy < 0, then X and Y are complements. 3. If εxy = 0, then X and Y are unrelated, independent products.

Income elasticity of demand The percentage change in quantity demanded that results from some percentage change in consumer incomes. εI = %∆Qx / %∆I 1. If εI >0, this is a normal good. 2. If εI >0, this is an inferior good.

LAST WORD: Elasticity and Pricing Power: Why Different Consumers Pay Different Prices A. Sellers often charge different prices for goods based on differences in price elasticity of demand. B. The ability to charge different prices depends on some market power; that is, some ability to control price (unlike the competitive model where all buyers and sellers exchange at exactly the same price).

• C. Customers are grouped according to elasticities: Business travelers have more inelastic demand for air travel, and can be charged a higher price than the more price elastic tourist.

Next: Chapter 21 Consumer Behavior and Utility Maximization