20 12 2012 Угол между скрещивающимися прямыми Урок

20. 12. 2012 Угол между скрещивающимися прямыми Урок стереометрии в 10 классе учитель математики МБОУ СОШ № 8 Рузаевского муниципального района Республики Мордовия Н. В. Перепелова

В математике есть своя красота, как в живописи и поэзии. Эта красота проявляется иногда в отчетливых, ярко очерченных идеях, где на виду всякая деталь умозаключений, а иногда поражает она нас в широких замыслах, скрывающих в себе кое-что недосказанное, но многообещающее. Н. Е. Жуковский

Вопросы для повторения • Взаимное расположение прямых в пространстве • Какой из четырех углов, полученных при пересечении двух прямых, мы называем углом между пересекающимися прямыми • Дайте определение угла между скрещивающимися прямыми

Повторение: Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимися. b n a m M a b

Повторение: При нахождении угла между пересекающимися прямыми используют формулу (теорема косинусов)

Устные упражнения

В кубе ABCDA 1 B 1 C 1 D 1 все ребра равны 1. Найдите угол между прямыми АВ и CB 1 D 1 A 1 C 1 B 1 D A C B Ответ: 9 0

В кубе ABCDA 1 B 1 C 1 D 1 все ребра равны 1. Найдите угол между прямыми А 1 В и CB 1 D 1 A 1 C 1 B 1 D A C B Ответ: 6 0

В кубе ABCDA 1 B 1 C 1 D 1 все ребра равны 1. Найдите угол между прямыми А 1 В и AC D 1 A 1 C 1 B 1 D A C B Ответ: 6 0

В кубе ABCDA 1 B 1 C 1 D 1 все ребра равны 1. Найдите угол между прямыми CА и BD 1 A 1 C 1 B 3 D A C 3 D B C C 2 B 2

В кубе ABCDA 1 B 1 C 1 D 1 все ребра равны 1. Найдите угол между прямыми CА и BD 1 A 1 D 1 C 1 B 1 C 3 B 3 D D C C 2 A B B B 2

В кубе ABCDA 1 B 1 C 1 D 1 все ребра равны 1. Найдите угол между прямыми CА и BD 1 C 2 B

В кубе ABCDA 1 B 1 C 1 D 1 все ребра равны 1. Найдите угол между прямыми CА и BD 1 A 1 D 1 B 1 D 5 C 1 A C 3 B 3 D C B C 2 B 2 3 2 B C 2 Ответ: 9 0

В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите угол между прямыми АВ и CС 1 E 1 D 1 F 1 C 1 A 1 E B 1 F D A C B Ответ: 9 0

В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите угол между прямыми АВ и DE 1 D 1 F 1 C 1 A 1 E B 1 F D A C B Ответ: 4 5

В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите угол между прямыми АВ и A 1 С 1 E 1 D 1 F 1 C 1 A 1 E B 1 F D A C B Ответ: 3 0

В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите угол между прямыми А 1 В и ED 1 E 1 D 1 F 1 C 1 A 1 E B 1 F D A C B Ответ: 4 5

Практикум

В правильной шестиугольной призме A … F 1, все ребра которой равны 1. Постройте сечение, проходящее через точку А 1 параллельное плоскости В 1 ВС 1 Е 1 D 1 О 1 F 1 А 1 1 В 1 Е А пересекаются 4. Плоскость АА 1 D 1 D параллельна плоскости D О F 1. АА 1 параллельно ВВ 1 С 1 2. А 1 D 1 параллельно В 1 С 1 3. АА 1 и A 1 D 1 1 С В 1 ВВ 1 С 1 С

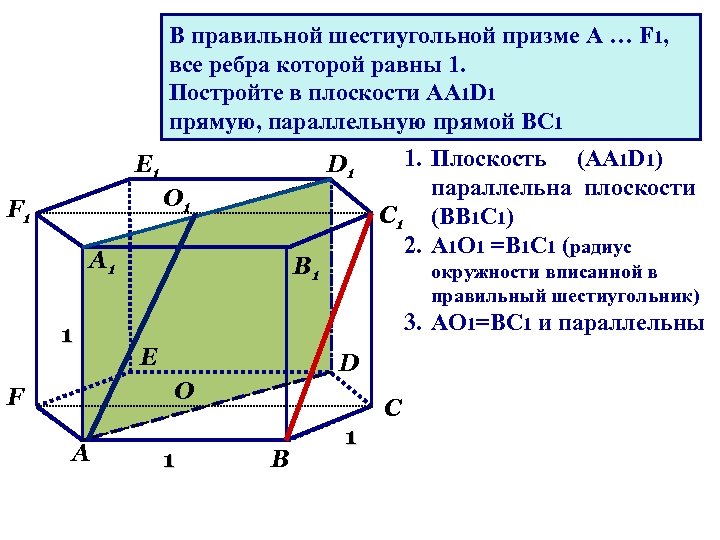В правильной шестиугольной призме A … F 1, все ребра которой равны 1. Постройте в плоскости АА 1 D 1 прямую, параллельную прямой ВС 1 Е 1 D 1 О 1 F 1 А 1 1 В 1 окружности вписанной в правильный шестиугольник) 3. АО 1=ВС 1 и параллельны Е D О F А 1. Плоскость (АА 1 D 1) параллельна плоскости С 1 (ВВ 1 С 1) 2. А 1 О 1 =В 1 С 1 (радиус 1 С В 1

Решите задачи В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, все ребра которой равны 1, найдите косинус угла между прямыми AB 1 и BC 1

В правильной шестиугольной призме A … F 1, все ребра которой равны 1, найдите косинус угла между прямыми AB 1 и BC 1 Е 1 D 1 О 1 F 1 С 1 А 1 1 В 1 Е D О F А 1 В 1 1) Построим плоскость АА 1 D 1 D параллельную плоскости ВВ 1 С 1 С. Тогда прямая AO 1 параллельна прямой BC 1, и искомый угол φ между прямыми AB 1 и BC 1 С равен B 1 AO 1.

В правильной шестиугольной призме A … F 1, все ребра которой равны 1, найдите косинус угла между прямыми AB 1 и BC 1 А 3) По теореме косинусов 2 2 2 AO 1 + AB 1 - B 1 O 1 Cos B 1 AO 1 = 2 AO 1 AB 1 Cos B 1 AO 1 =0, 75 В 1 1 Ответ: 0, 75

Самостоятельная работа

Критерии оценивания выполнения задания С 2 баллы Критерии оценивания 2 Правильный ход решения. Верно построен или описан искомый угол. Получен верный ответ 1 1) Правильный ход решения. Получен верный ответ, но имеется ошибка в построении и описании искомого угла, не повлиявшая на ход решения 2) Правильный ход решения. Верно построен и описан искомый угол, но имеется ошибка в одном из вычислений, допущенная из-за невнимательности, в результате чего получен неверный ответ 0 1) Ход решения правильный, но оно не доведено до конца, или решение отсутствует. Нет ответа 2) Ход решения правильный, но имеются существенные ошибки в вычислениях, приведшие к неправильному ответу 3) Неправильный ход решения, приведший к неверному ответу 4) Верный ответ получен случайно при неверном

Способы решения задачи на нахождение угла между скрещивающимися прямыми

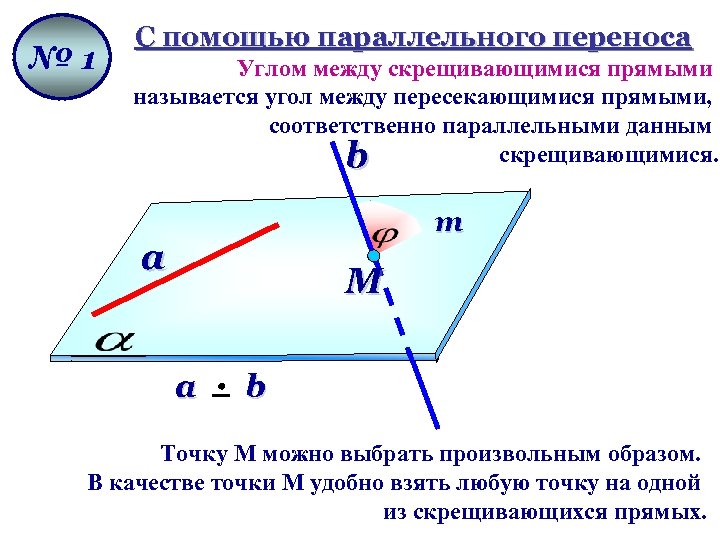№ 1 С помощью параллельного переноса Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимися. b m a M a b Точку М можно выбрать произвольным образом. В качестве точки М удобно взять любую точку на одной из скрещивающихся прямых.

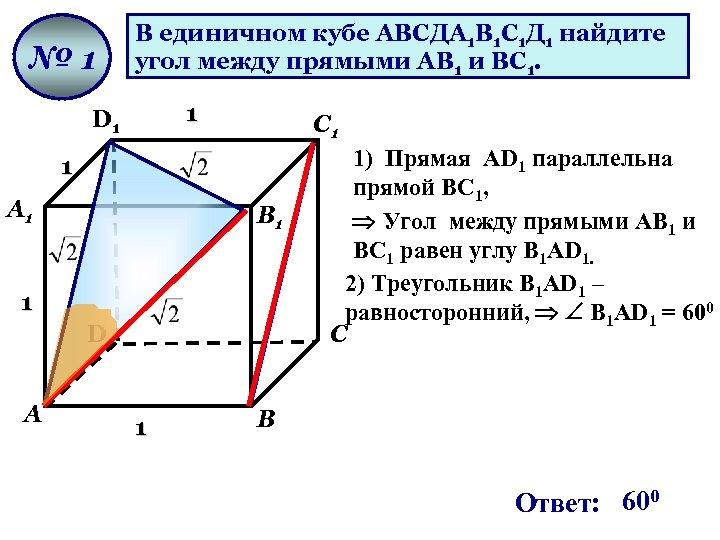№ 1 В единичном кубе АВСДА 1 В 1 С 1 Д 1 найдите угол между прямыми АВ 1 и ВС 1. 1 D 1 С 1 1 А 1 В 1 1 D А 1 1) Прямая AD 1 параллельна прямой ВС 1, Угол между прямыми АВ 1 и ВС 1 равен углу В 1 AD 1. 2) Треугольник В 1 AD 1 – равносторонний, В 1 AD 1 = 600 С В Ответ: 600

С помощью тетраэдра № 2 D В А С 2 2 (AC + BD )-(CD + AB ) Cos AD, CB = 2 AD CB

С помощью тетраэдра № 2 В единичном кубе АВСДА 1 В 1 С 1 Д 1 найдите угол между прямыми АВ 1 и ВС 1. D D 1 А А 1 С С 1 В 1. Построим тетраэдр с противоположными ребрами AB 1 и BC 1 2. Применяя формулу, получаем Cos AB 1, BC 1 =0. 5 AB 1, BC 1=60 В 1 2 2 (BB 1 + AC 1 )-(AB + B 1 C 1) Cos AB 1, BC 1= 2 AB 1 BC 1

Способ «в три косинуса» № 3 b a a b 1) Построим плоскость, которой принадлежит прямая а, прямая b ее пересекает b 1 проекцию прямой b на плоскость 3)Прямые a и b 1 пересекаются, прямые b и b 1 пересекаются Cos ab =Cos ab 1 Cos bb 1 2) Построим

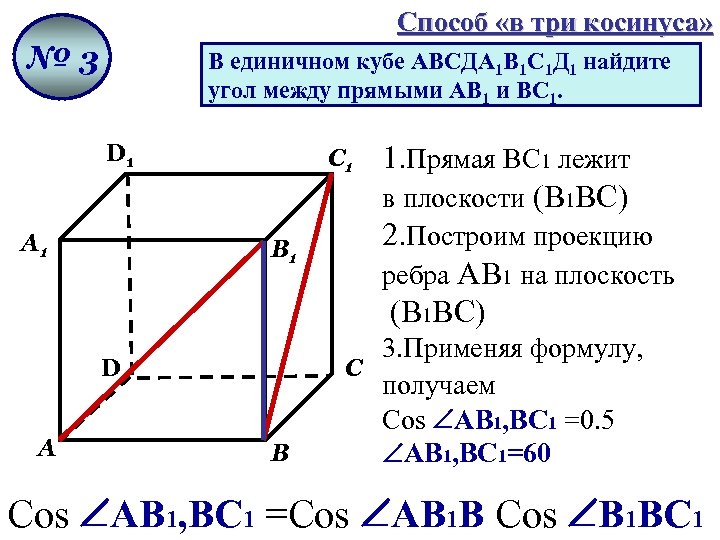Способ «в три косинуса» № 3 В единичном кубе АВСДА 1 В 1 С 1 Д 1 найдите угол между прямыми АВ 1 и ВС 1. D 1 А 1 С 1 В 1 D А В 1. Прямая BC 1 лежит в плоскости (B 1 BC) 2. Построим проекцию ребра АВ 1 на плоскость (B 1 BC) 3. Применяя формулу, С получаем Cos AB 1, BC 1 =0. 5 AB 1, BC 1=60 Cos AB 1, BC 1 =Cos AB 1 B Cos B 1 BC 1

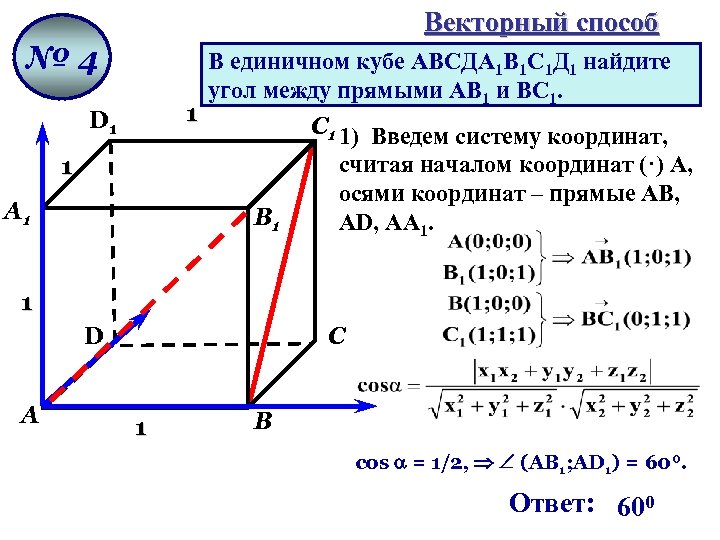Векторный способ № 4 1 D 1 В единичном кубе АВСДА 1 В 1 С 1 Д 1 найдите угол между прямыми АВ 1 и ВС 1. 1 А 1 В 1 С 1 1) Введем систему координат, считая началом координат (·) А, осями координат – прямые АВ, АD, АА 1. 1 D А С 1 В cos = 1/2, (АВ 1; AD 1) = 600. Ответ: 600

Жизнь не спросит, что ты учил. Жизнь спросит, что ты знаешь.

Домашнее задание • Презентация урока Электронный журнал https: //sc 8 ruz. eljur. ru • Статья В. И. Рыжика «Об углах между скрещивающимися прямыми и немного о прочих углах» Сайт учителя http: //perepelovanv. ucoz. ru/

Домашнее задание В кубе ABCDA 1 B 1 C 1 D 1 все ребра равны 1, найдите угол между прямыми : • • • CА и B 1 D C 1 B и CA 1 C 1 B и DB 1 CА 1 и DC 1 BD 1 и DC 1 BA 1 и AC 1 • • • BA 1 и DB 1 AD 1 и CA 1 AD 1 и DB 1 C 1 A 1 и BD 1

Домашнее задание В правильной четырехугольной пирамиде SАВСД, все ребра которой равны 1, точка Е – середина ребра SD. Найдите тангенс угла между прямыми АЕ и SВ.

Видео-лекции и уроки • Учитель высшей категории, лауреат премии Фонда Сороса Тер-Ованесян Геворк Левонович http: //uchu 24. ru/video/ugol-mezhdu-skreschivayuschimisja-prjamymi. html • Решение задач С 2 http: //www. youtube. com/watch? v=r. DFq. Nztv. OTg http: //ege-ok. ru/2012/03/26/ugol-mezhdu-skreshhivayushhimisyapryamyimi-zadanie-s 2/ http: //www. egetrener. ru/view_tema. php? tema=skre http: //www. cleverstudents. ru/angle_between_skew_lines. html

Литература • В. А. Смирнов Готовимся к ЕГЭ. Геометрия. Стереометрия. / – М. : МЦНМЩ, 2011 • В. А. Смирнов ЕГЭ 2011. Математика. Задача С 2. Геометрия. Стереометрия. / Под редакцией А. Л. Семенова и И. В. Ященко – М. : МЦНМЩ, 2011

Подведение итогов урока: • Сегодня на уроке я повторил … • Сегодня на уроке я научился … • Мне необходимо еще поработать над …

Проверка решения S В правильной четырехугольной пирамиде SАВСД, все ребра которой равны 1, точка Е – середина ребра SD. Найдите тангенс угла между прямыми АЕ и SВ. 1 1 Р Е К Д D М С К О А Р 1 М 1 В Ответ: 2

В правильной шестиугольной призме A … F 1, все ребра которой равны 1, найдите косинус угла между прямыми AB 1 и BC 1 Е 1 D 1 О 1 F 1 С 1 А 1 1 В 1 Е А 1 С В 1 AO 1 = (диагональ квадрата) AB 1 = (диагональ квадрата) D О F 2) Рассмотрим треугольник АВ 1 О 1. B 1 O 1= 1 (радиус описанной окружности)