2 х 3 х 2 sin

2– х 3 х + 2 = [sin x] Розв’яжемо це рівняння графічно, для цього побудуємо графік функції: у = х2 – 3 х + 2

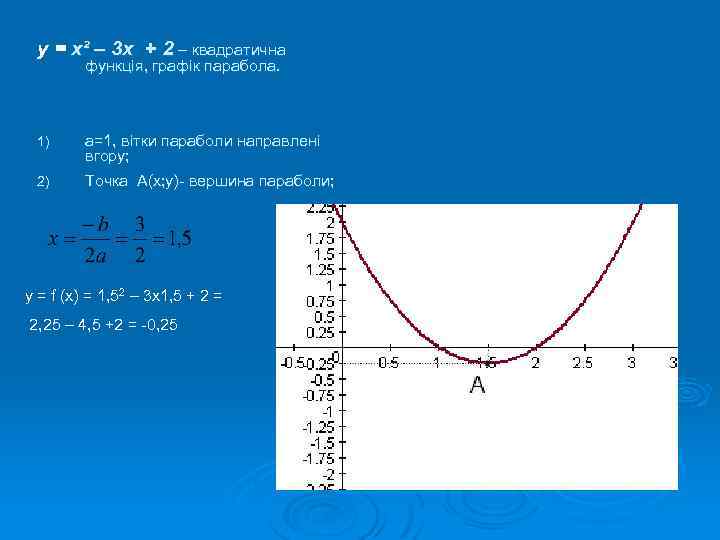у = х² – 3 х + 2 – квадратична функція, графік парабола. 1) а=1, вітки параболи направлені вгору; 2) Точка A(x; y)- вершина параболи; y = f (x) = 1, 52 – 3 х1, 5 + 2 = 2, 25 – 4, 5 +2 = -0, 25

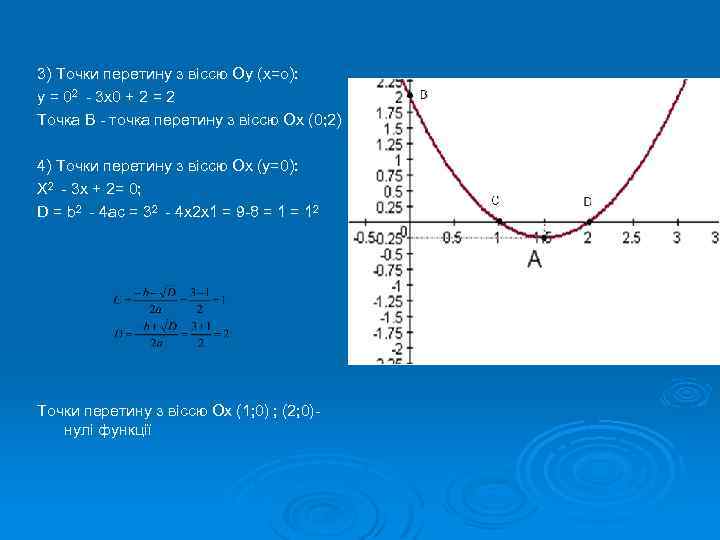3) Точки перетину з віссю Оу (х=о): у = 02 - 3 х0 + 2 = 2 Точка B - точка перетину з віссю Оx (0; 2) 4) Точки перетину з віссю Ох (у=0): Х 2 - 3 х + 2= 0; D = b 2 - 4 ac = 32 - 4 х2 х1 = 9 -8 = 12 Точки перетину з віссю Ох (1; 0) ; (2; 0)нулі функції

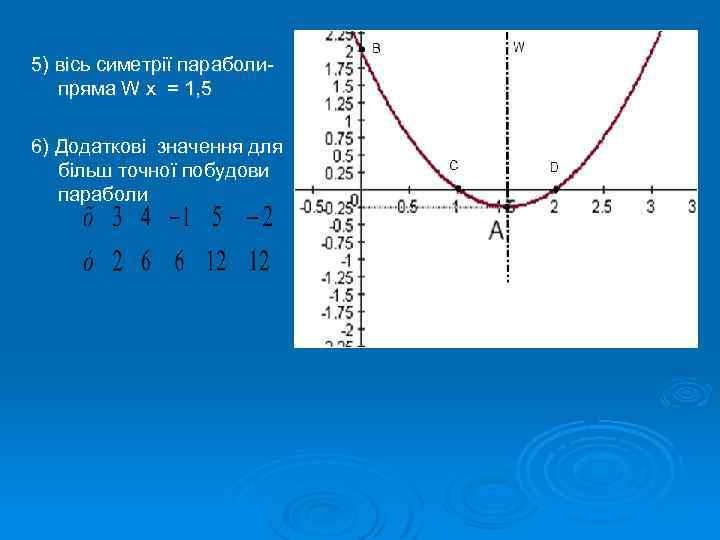5) вісь симетрії параболипряма W x = 1, 5 6) Додаткові значення для більш точної побудови параболи

Побудуємо у = [ sin x] З’ясуємо поняття цілої частини числа: [х] – ціла частина числа х. [х] – найбільше ціле число, що не перевищує х. Якщо х є [0; 1), то у = [х] = 0; Якщо х є [1; 2], то у = [х] = 1; Якщо х є [-1; 0], то у = [х] = -1.

Графік у = [ sin X] зображено на слайді: [ sin X] = 0, якщо X є [0;

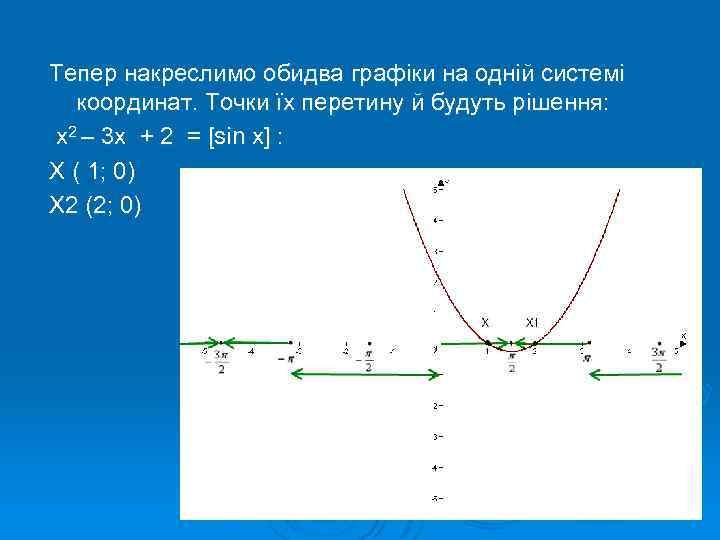Тепер накреслимо обидва графіки на одній системі координат. Точки їх перетину й будуть рішення: х2 – 3 х + 2 = [sin x] : X ( 1; 0) X 2 (2; 0)