2 ТЕОРІЯ МАСОВОГО ОБСЛУГОВУВАННЯ ТА ЇЇ ВИКОРИСТАННЯ В

2. ТЕОРІЯ МАСОВОГО ОБСЛУГОВУВАННЯ ТА ЇЇ ВИКОРИСТАННЯ В УПРАВЛІННІ ВИРОБНИЦТВОМ • при обслуговуванні технологічних ліній ремонтними бригадами, • при визначенні показників надійності роботи устаткування, • при визначенні можливості підвищення продуктивності виробництва

cмо Системи масового обслуговування (СМО) призначені для обслуговування потоку замовлень або вимог, що надходять у випадкові моменти часу. Кожна СМО складається з деякого числа каналів обслуговування (технологічні лінії, лінії зв’язку, робочі точки чи агрегати, під’їздні шляхи, ремонтні бригади, тощо). Виконання замовлення, що надходить у систему, тобто його обслуговування, продовжується деякий випадковий час, після чого канал звільняється і готовий прийняти наступне замовлення. ЕРЛАНГ

Потік замовлень Потік обслуговування μ λ Станція інтенсивність потоку замовлень - середня частота надходження замовлень у одиницю часу За 1 годину відбулося 15 замовлень, отже, в середньому, одне замовлення приходиться на інтервал у 60/15=4 хвилини. Інтенсивність потоку : = 1/4 = 0, 25. Час обслуговування замовлення є випадковим, але на виході створюється потік обслуговування з інтенсивністю , що визначається середнім часом обслуговування. Якщо середній час обслуговування одного замовлення складає 0. 5 хвилини, то інтенсивність потоку обслуговування = 1 / 0. 5 = 2. Потік, у якого =const, називається стаціонарним.

Два типи СМО • СМО з відмовами, у яких замовлення, що надійшло у той момент, коли усі канали зайняті, отримує відмову і не обслуговується; • СМО з очікуванням, у яких кожне замовлення, що надійшло у систему, коли немає вільних каналів, залишається у черзі і очікує, поки звільниться якийсь канал і візьме її на обслуговування.

Теорема Хінчина: число переходів із стану і у стан j (Si Sj), що здійснюється за одиницю часу дорівнює добутку кількості систем у стані Si та ймовірності переходу, що здійснюється за одиницю часу. Для стаціонарного процесу потоки виходів і входів для кожного із станів мають бути збалансованими. • В теорії потоків, коли швидкість переходу з одного стану в інший є великою, процес функціонування системи описується рівняннями Колмогорова: n і pі ( і+ i)=pm m+pn n , Sn Si i m Sm Де рi, рm, рn – ймовірності перебування системи у відповідних станах Si, Sm, Sn. і, i– інтенсивності переходів із стану Si, m, n - інтенсивності переходів у стан Si із станів Sm та Sn.

2. 1. СМО з відмовами 2. 1. 1. Одноканальна СМО • Одноканальна СМО може знаходитися лише в одному з двох станів: S 0 - канал вільний, S 1 – канал занятий. λ S 1 0 S μ р0 = р1 p 0+р1 = 1. р1=( p 0 ) / р0+( р0)/ =1 p 0=1/(1+ / )= /( ) (1) p = (2)

Основні показники СМО з відмовами • Відносна пропускна здатність Q визначається ймовірністю того, що в момент надходження замовлення є вільний канал і воно буде обслуговуватись. • Для одноканальної системи Q = p 0. Q = ( ) (3) • Абсолютна пропускна здатність А: А = Q (4) Для одноканальної системи: A = ( ) (5) Ймовірність того, що замовлення буде обслуженим, визначається р0, а ймовірність отримання відмови – р1. Pвідмови=p 1= ( ) (6)

2. 1. 2. Багатоканальні СМО Двоканальна СМО з відмовами S 0 λ μ S 1 λ 2μ S 2 Для стану S 0 баланс потоків: . (7) Для стану S 1 баланс потоків визначається: З урахуванням того, що р1 = р0 , отримуємо 2 р2 = р1, (8)

Оскільки р0+р1+р2=1 Для двоканальної СМО з відмовами: (9)

Для двоканальної СМО: Ймовірність обслуговування (відносна пропускна здатність): (10) Ймовірність відмови: (11)

Триканальна СМО з відмовами S 0 λ μ S 1 λ 2μ λ S 2 3μ S 3 Для стану S 2: р2 +2 р2 = р1 +3 р3 (12) (13)

n-КАНАЛЬНА СМО З ВІДМОВАМИ S 0 λ μ λ S 1 2μ S 2 λ 3μ S 3 λ 4μ λ nμ Sn (14) (15) Q = 1 - pn Cередня кількість зайнятих каналів: (16)

3. СМО з очікуванням S 0 3. 1. ОДНОКАНАЛЬНА СМО З ОЧІКУВАННЯМ λ λ λ S 3 μ S 1 μ S 2 μ μ μ Sk Для стану S 0: р0 = р1 р1=( / ) p 0 інтенсивність навантаження СМО = / (18) Якщо < , то < 1 Якщо > , то > 1 , черга буде зростати до нескінченності Ймовірність стану S 1: P 1= P 0 Для стану S 1: P 1+ P 1= P 0+ P 2 Оскільки P 0= P 1 то P 2= P 1 P 2=Р 1 = 2 Р 0

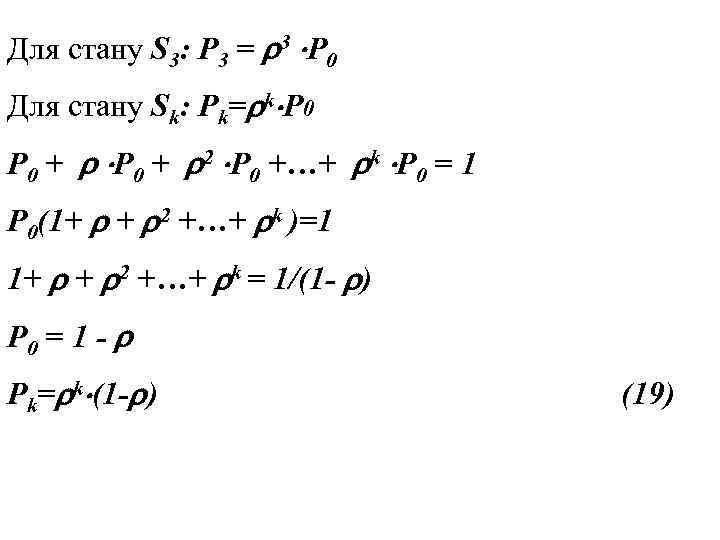
Для стану S 3: Р 3 = 3 Р 0 Для стану Sk: Рk= k Р 0 + 2 Р 0 +…+ k Р 0 = 1 Р 0(1+ + 2 +…+ k )=1 1+ + 2 +…+ k = 1/(1 - ) P 0 = 1 - Pk= k (1 - ) (19)

Характеристики СМО з очікуванням • Середня довжина черги Lср: Lср=1 p 2 +2 p 3 +…+(k-1)pk= 2 (1 - )(1+2 +3 2+…+k k-1) • Середня кількість замовлень в системі Ls Ls=0 p 0+1 p 1+2 p 2+…+ k pk • Середній час очікування замовлення в черзі Ws (22)

• Середня тривалість перебування замовлення у системі Ws (23) (час очікування у черзі + час обслуговування) • Ймовірність утворення черги р3 pчерг=1–p 0–p 1=1–(1 - )- (1 - ) = 2 (24)

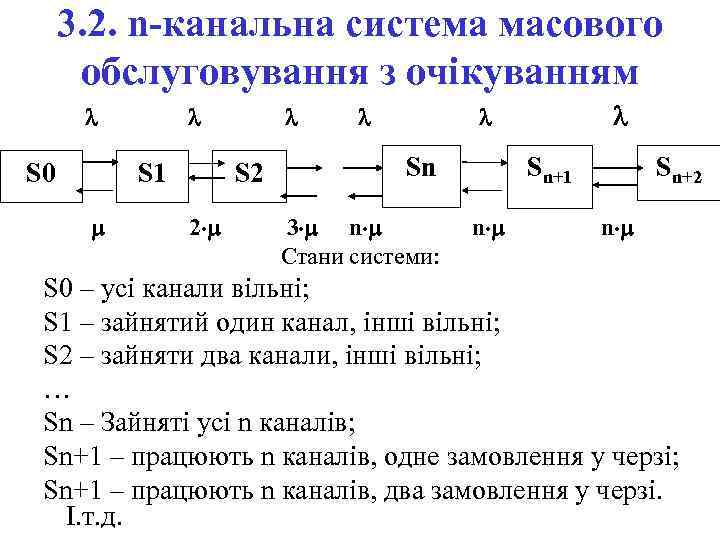
3. 2. n-канальна система масового обслуговування з очікуванням S 0 S 1 S 2 2 Sn 3 n Стани системи: Sn+1 Sn+2 n S 0 – усі канали вільні; S 1 – зайнятий один канал, інші вільні; S 2 – зайняти два канали, інші вільні; … Sn – Зайняті усі n каналів; Sn+1 – працюють n каналів, одне замовлення у черзі; Sn+1 – працюють n каналів, два замовлення у черзі. І. т. д.

Якщо ρ<1 – існують фінальні ймовірності: Ймовірність p 0: Cередня кількість замовлень у черзі: Середня кількість замовлень у системі

Середній час перебування замовлення у черзі: Середній час перебування замовлення у системі: