Сп_замены__НВ треуг.ppt
- Количество слайдов: 49

2. Способы преобразования прямоугольных проекций 2. 1. Введение
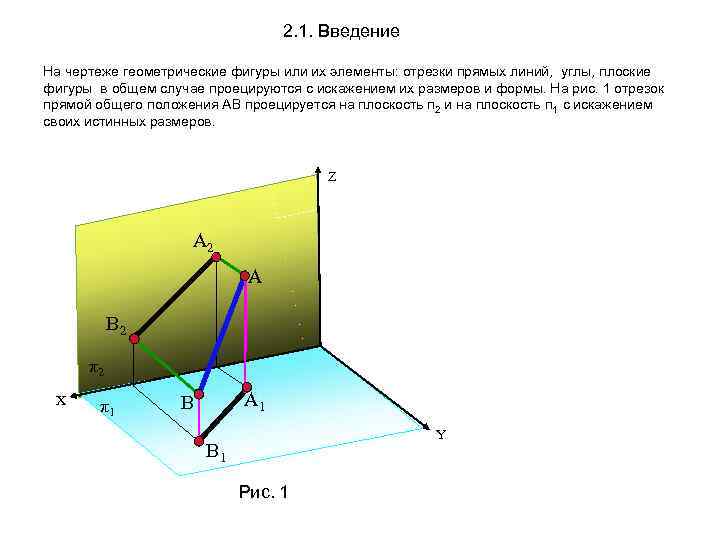
2. 1. Введение На чертеже геометрические фигуры или их элементы: отрезки прямых линий, углы, плоские фигуры в общем случае проецируются с искажением их размеров и формы. На рис. 1 отрезок прямой общего положения АВ проецируется на плоскость п 2 и на плоскость п 1 с искажением своих истинных размеров. Z А 2 А В 2 π2 Х π1 А 1 В Y В 1 Рис. 1
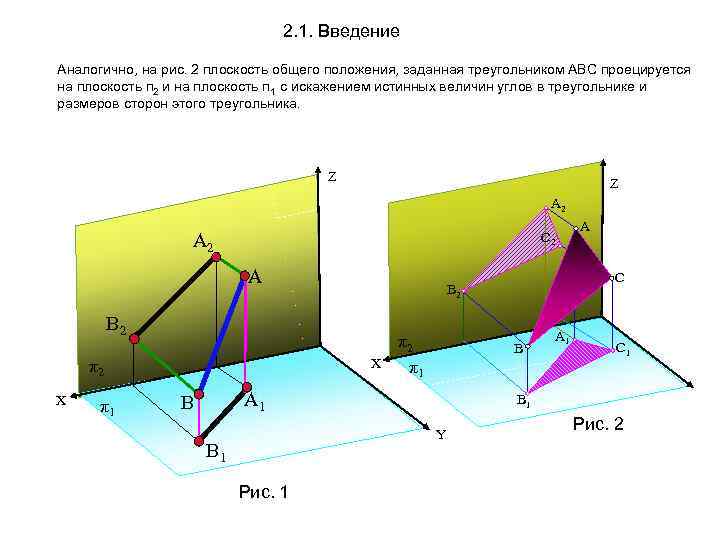
2. 1. Введение Аналогично, на рис. 2 плоскость общего положения, заданная треугольником АВС проецируется на плоскость п 2 и на плоскость п 1 с искажением истинных величин углов в треугольнике и размеров сторон этого треугольника. Z Z А 2 С 2 А X π2 Х π1 π2 π1 В А 1 В Рис. 1 А 1 С 1 В 1 Y В 1 С В 2 А Рис. 2
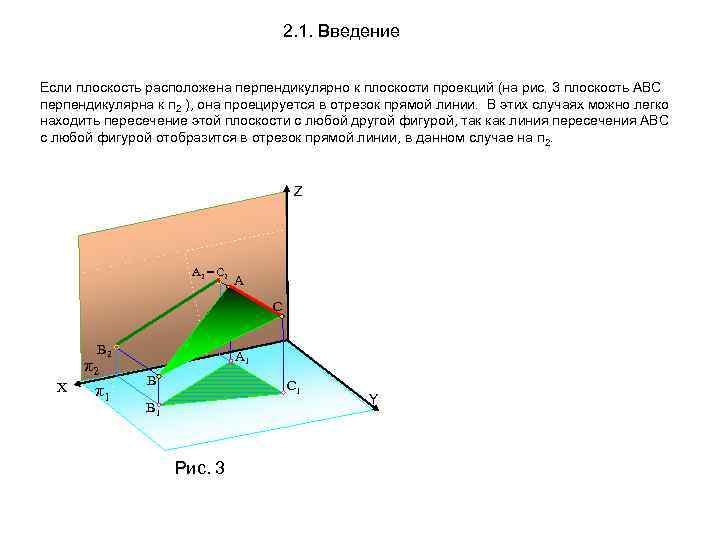
2. 1. Введение Если плоскость расположена перпендикулярно к плоскости проекций (на рис. 3 плоскость АВС перпендикулярна к п 2 ), она проецируется в отрезок прямой линии. В этих случаях можно легко находить пересечение этой плоскости с любой другой фигурой, так как линия пересечения АВС с любой фигурой отобразится в отрезок прямой линии, в данном случае на п 2. Z А 2 = С 2 А С В 2 X π2 π1 А 1 В С 1 В 1 Рис. 3 Y
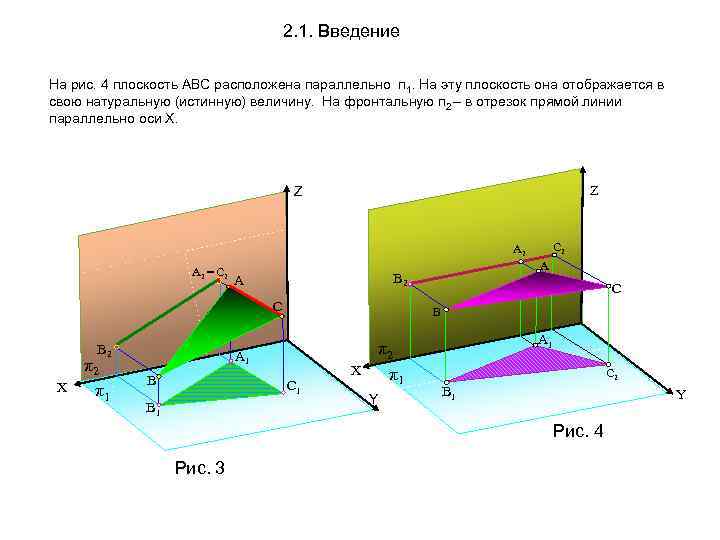
2. 1. Введение На рис. 4 плоскость АВС расположена параллельно п 1. На эту плоскость она отображается в свою натуральную (истинную) величину. На фронтальную п 2 – в отрезок прямой линии параллельно оси Х. Z Z С 2 А 2 = С 2 А С В 2 X π2 π1 С 1 В 1 С В А 1 В А В 2 X π2 π1 Y А 1 Н. В. С 2 В 1 Y Рис. 4 Рис. 3
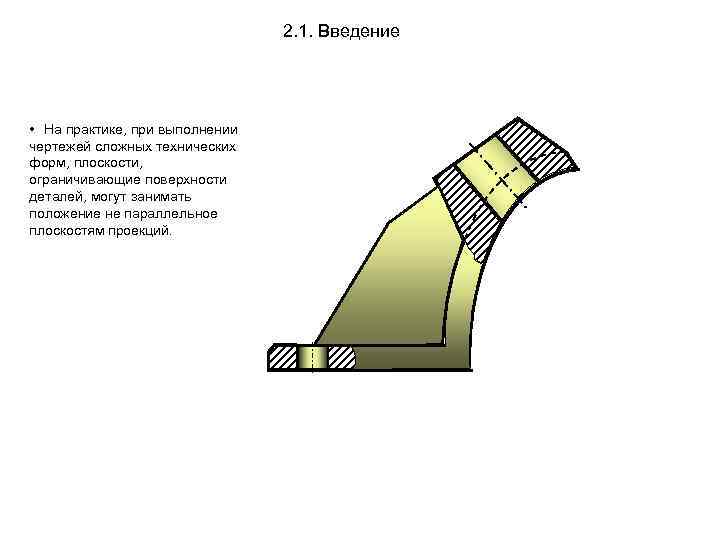
2. 1. Введение • На практике, при выполнении чертежей сложных технических форм, плоскости, ограничивающие поверхности деталей, могут занимать положение не параллельное плоскостям проекций.
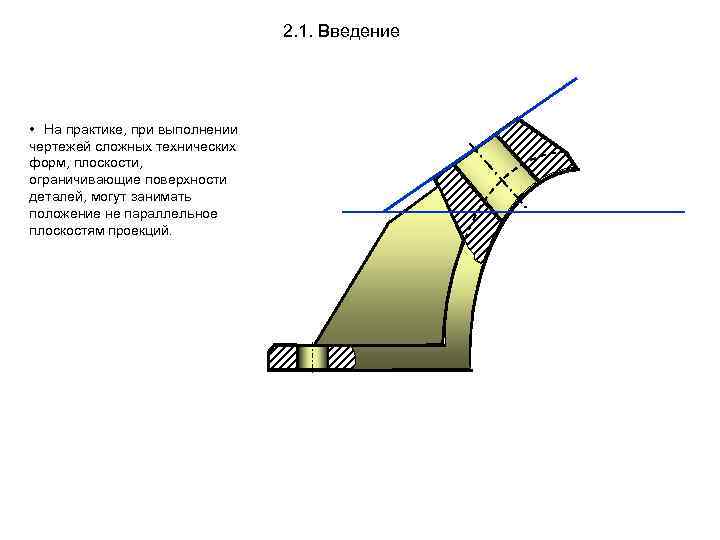
2. 1. Введение • На практике, при выполнении чертежей сложных технических форм, плоскости, ограничивающие поверхности деталей, могут занимать положение не параллельное плоскостям проекций.
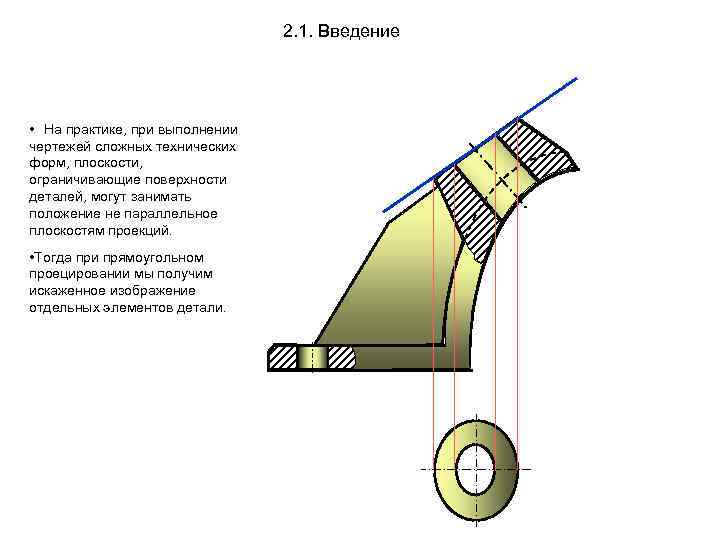
2. 1. Введение • На практике, при выполнении чертежей сложных технических форм, плоскости, ограничивающие поверхности деталей, могут занимать положение не параллельное плоскостям проекций. • Тогда при прямоугольном проецировании мы получим искаженное изображение отдельных элементов детали.
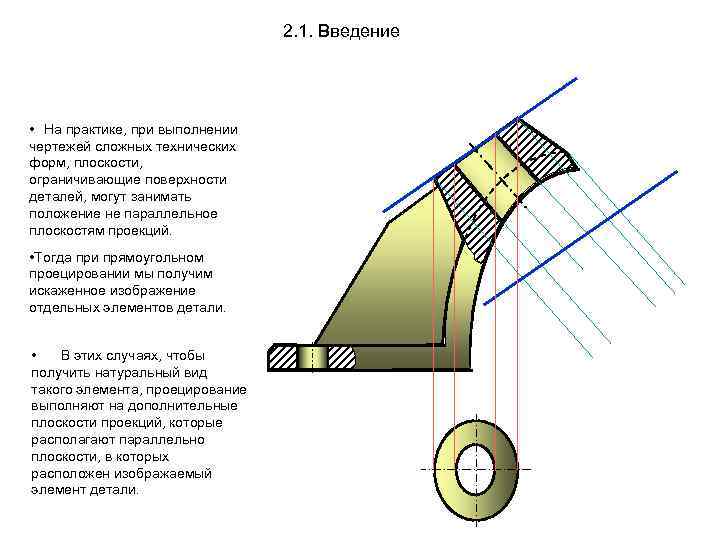
2. 1. Введение • На практике, при выполнении чертежей сложных технических форм, плоскости, ограничивающие поверхности деталей, могут занимать положение не параллельное плоскостям проекций. • Тогда при прямоугольном проецировании мы получим искаженное изображение отдельных элементов детали. • В этих случаях, чтобы получить натуральный вид такого элемента, проецирование выполняют на дополнительные плоскости проекций, которые располагают параллельно плоскости, в которых расположен изображаемый элемент детали.
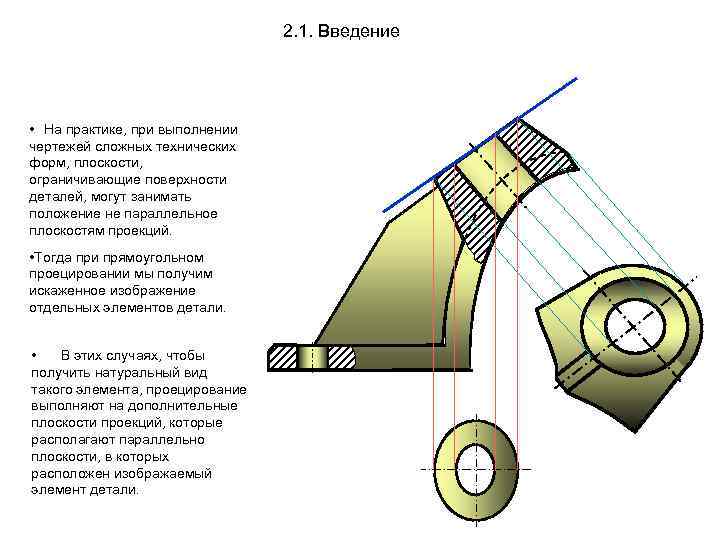
2. 1. Введение • На практике, при выполнении чертежей сложных технических форм, плоскости, ограничивающие поверхности деталей, могут занимать положение не параллельное плоскостям проекций. • Тогда при прямоугольном проецировании мы получим искаженное изображение отдельных элементов детали. • В этих случаях, чтобы получить натуральный вид такого элемента, проецирование выполняют на дополнительные плоскости проекций, которые располагают параллельно плоскости, в которых расположен изображаемый элемент детали.

• Для получения изображений на дополнительные плоскости разработаны способы преобразования прямоугольных проекций. • Из существующих способов можно выделить два основных: способ перемены (замены) плоскостей проекций и способ вращения. • Первый из них основан на том, что фигура не изменяет своего положения в пространстве, а плоскости проекций подстраиваются относительно фигуры таким образом, чтобы можно было получить желаемое изображение данной фигуры. • Второй основан на том, что плоскости проекций не изменяют своего положения в пространстве, а фигура, наоборот, изменяет свое положение путем вращения вокруг некоторой оси. • Другие способы основаны на комбинации перемещения и вращения.
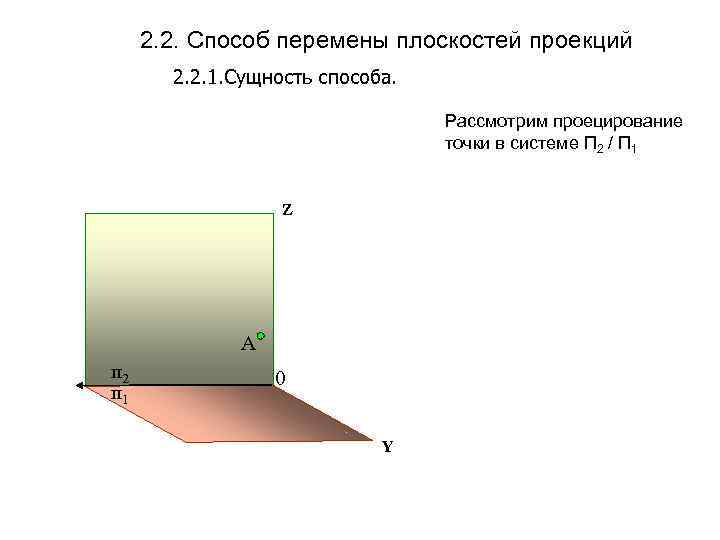
2. 2. Способ перемены плоскостей проекций 2. 2. 1. Сущность способа. Рассмотрим проецирование точки в системе П 2 / П 1 Z А п 2 п 1 0 Y
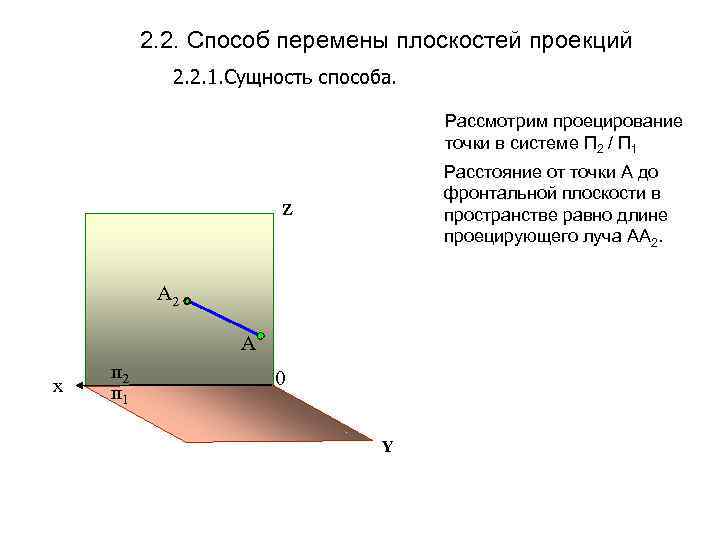
2. 2. Способ перемены плоскостей проекций 2. 2. 1. Сущность способа. Рассмотрим проецирование точки в системе П 2 / П 1 Расстояние от точки А до фронтальной плоскости в пространстве равно длине проецирующего луча АА 2. Z А 2 А х п 2 п 1 0 Y
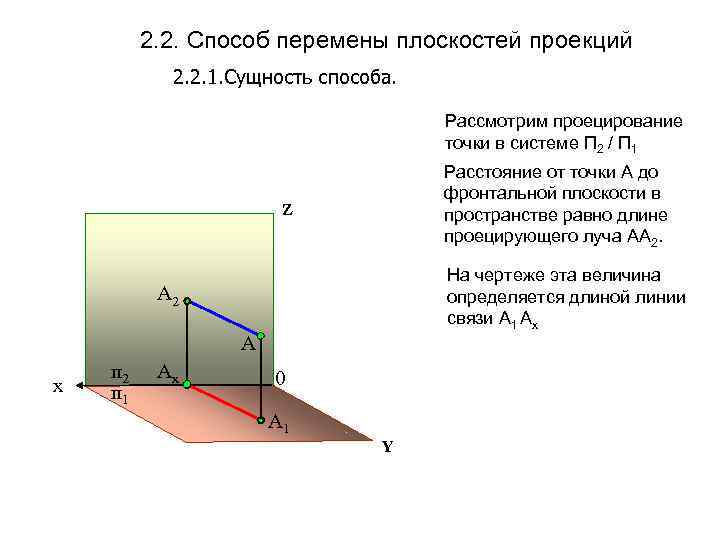
2. 2. Способ перемены плоскостей проекций 2. 2. 1. Сущность способа. Рассмотрим проецирование точки в системе П 2 / П 1 Расстояние от точки А до фронтальной плоскости в пространстве равно длине проецирующего луча АА 2. Z На чертеже эта величина определяется длиной линии связи А 1 Ах А 2 А х п 2 п 1 Аx 0 А 1 Y
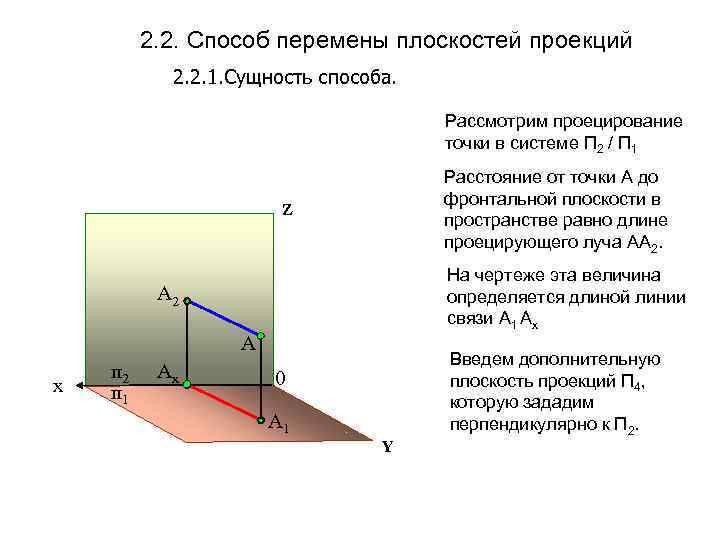
2. 2. Способ перемены плоскостей проекций 2. 2. 1. Сущность способа. Рассмотрим проецирование точки в системе П 2 / П 1 Расстояние от точки А до фронтальной плоскости в пространстве равно длине проецирующего луча АА 2. Z На чертеже эта величина определяется длиной линии связи А 1 Ах А 2 А х п 2 п 1 Аx Введем дополнительную плоскость проекций П 4, которую зададим перпендикулярно к П 2. 0 А 1 Y
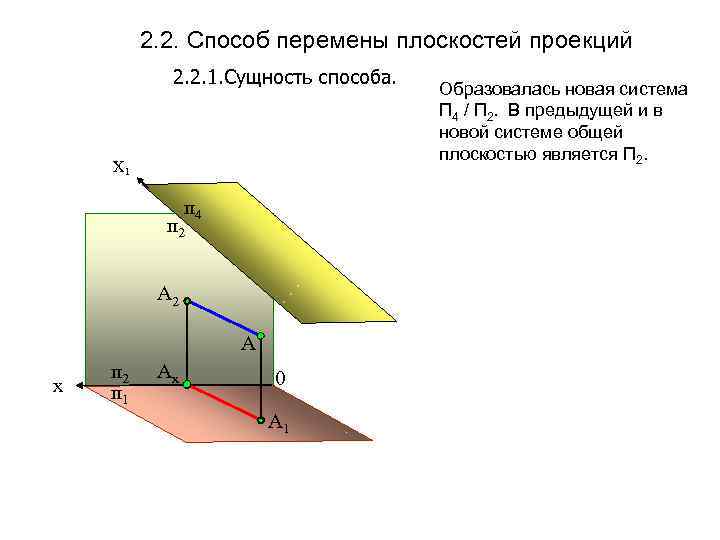
2. 2. Способ перемены плоскостей проекций 2. 2. 1. Сущность способа. Х 1 п 4 п 2 А х п 2 п 1 Аx 0 А 1 Образовалась новая система П 4 / П 2. В предыдущей и в новой системе общей плоскостью является П 2.
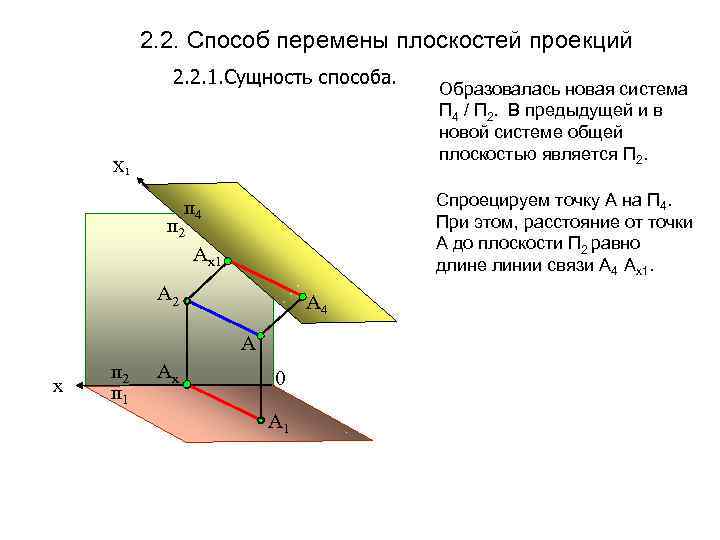
2. 2. Способ перемены плоскостей проекций 2. 2. 1. Сущность способа. Х 1 Спроецируем точку А на П 4. При этом, расстояние от точки А до плоскости П 2 равно длине линии связи А 4 Ах1. п 4 п 2 Аx 1 А 2 А 4 А х п 2 п 1 Аx Образовалась новая система П 4 / П 2. В предыдущей и в новой системе общей плоскостью является П 2. 0 А 1
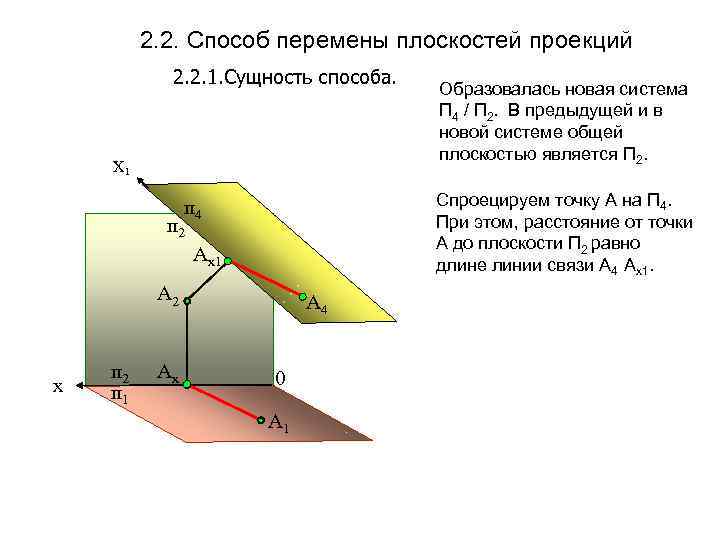
2. 2. Способ перемены плоскостей проекций 2. 2. 1. Сущность способа. Х 1 Спроецируем точку А на П 4. При этом, расстояние от точки А до плоскости П 2 равно длине линии связи А 4 Ах1. п 4 п 2 Аx 1 А 2 х п 2 п 1 Аx Образовалась новая система П 4 / П 2. В предыдущей и в новой системе общей плоскостью является П 2. А 4 0 А 1
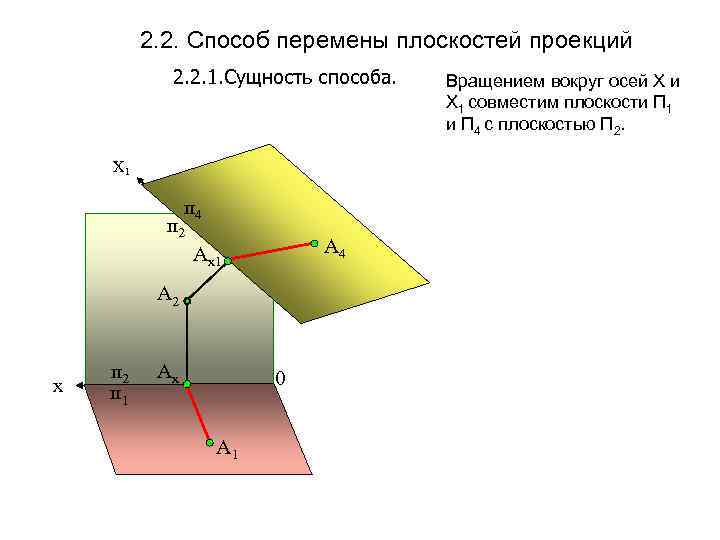
2. 2. Способ перемены плоскостей проекций 2. 2. 1. Сущность способа. Х 1 п 4 п 2 А 4 Аx 1 А 2 х п 2 п 1 А 4 Аx 0 А 1 Вращением вокруг осей Х и Х 1 совместим плоскости П 1 и П 4 с плоскостью П 2.
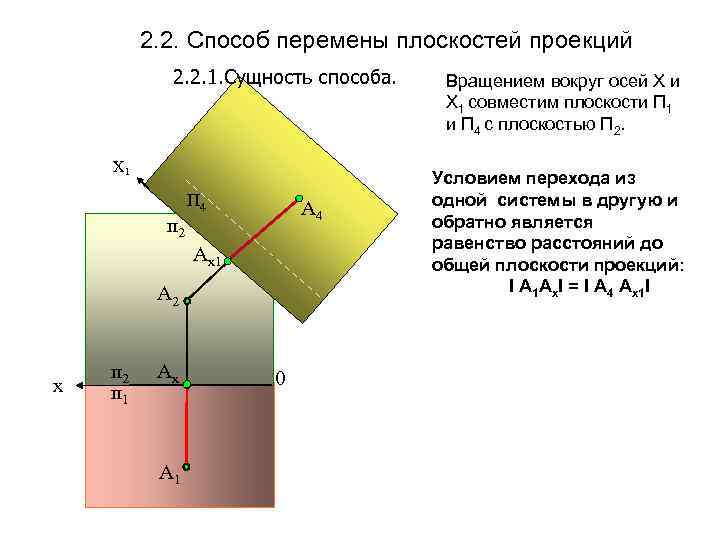
2. 2. Способ перемены плоскостей проекций 2. 2. 1. Сущность способа. Х 1 п 2 П 4 Аx 1 А 2 х п 2 п 1 Аx А 1 0 Вращением вокруг осей Х и Х 1 совместим плоскости П 1 и П 4 с плоскостью П 2. Условием перехода из одной системы в другую и обратно является равенство расстояний до общей плоскости проекций: I А 1 Ах. I = I А 4 Ах1 I
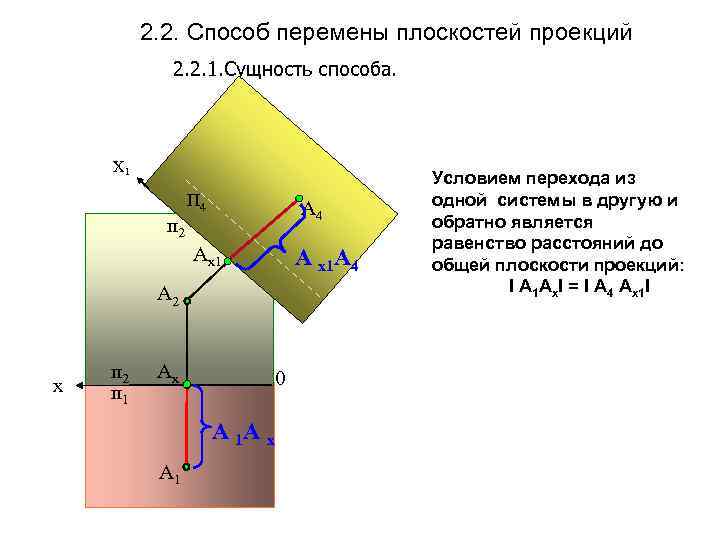
2. 2. Способ перемены плоскостей проекций 2. 2. 1. Сущность способа. Х 1 п 2 П 4 Аx 1 А х1 А 4 А 2 х п 2 п 1 Аx 0 А 1 А х А 1 Условием перехода из одной системы в другую и обратно является равенство расстояний до общей плоскости проекций: I А 1 Ах. I = I А 4 Ах1 I

2. 2. Способ перемены плоскостей проекций • В начертательной геометрии при решении задач с применением способа перемены плоскостей проекций чаще всего приходится решать следующие четыре: • Прямую ОП преобразовать в прямую уровня • Прямую ОП преобразовать в проецирующую • Плоскость ОП преобразовать в плоскость уровня
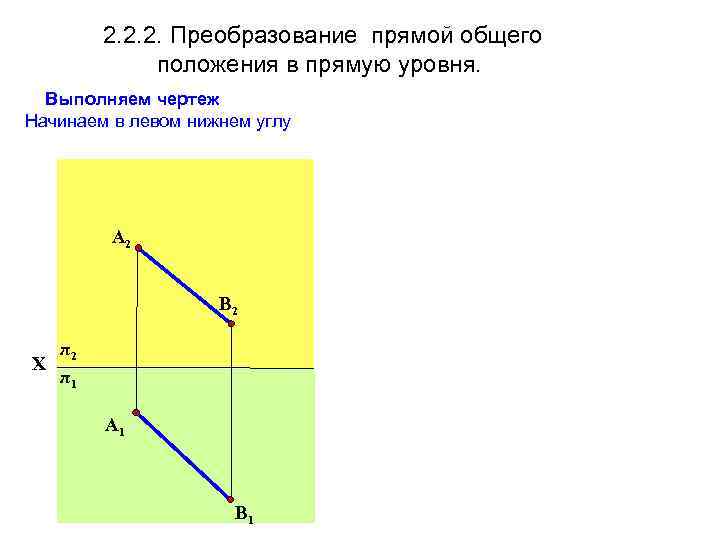
2. 2. 2. Преобразование прямой общего положения в прямую уровня. Выполняем чертеж Начинаем в левом нижнем углу A 2 В 2 π2 Х π1 A 1 В 1
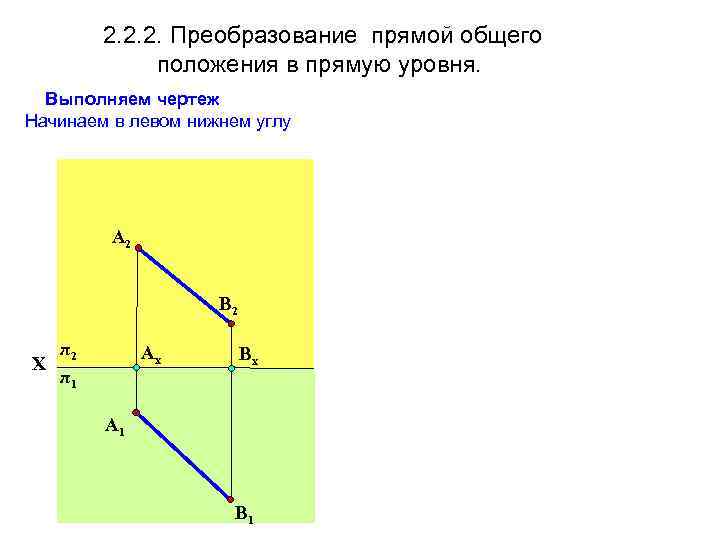
2. 2. 2. Преобразование прямой общего положения в прямую уровня. Выполняем чертеж Начинаем в левом нижнем углу A 2 В 2 π2 Х π1 Aх Вх A 1 В 1
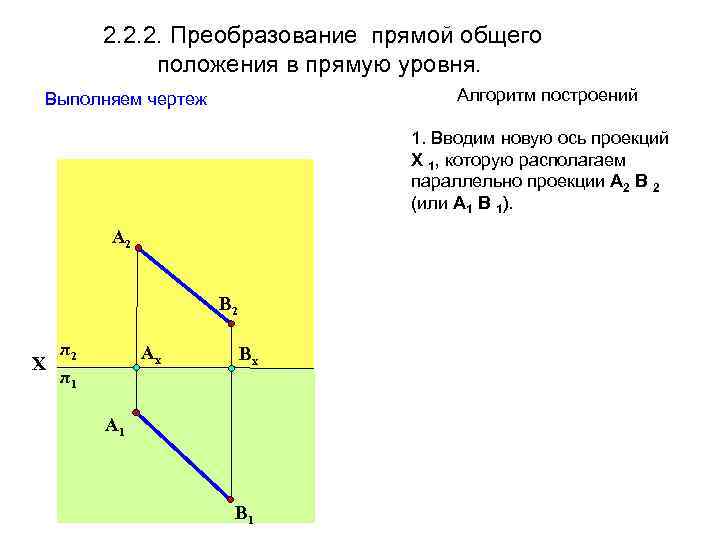
2. 2. 2. Преобразование прямой общего положения в прямую уровня. Алгоритм построений Выполняем чертеж 1. Вводим новую ось проекций Х 1, которую располагаем параллельно проекции А 2 В 2 (или А 1 В 1). A 2 В 2 π2 Х π1 Aх Вх A 1 В 1
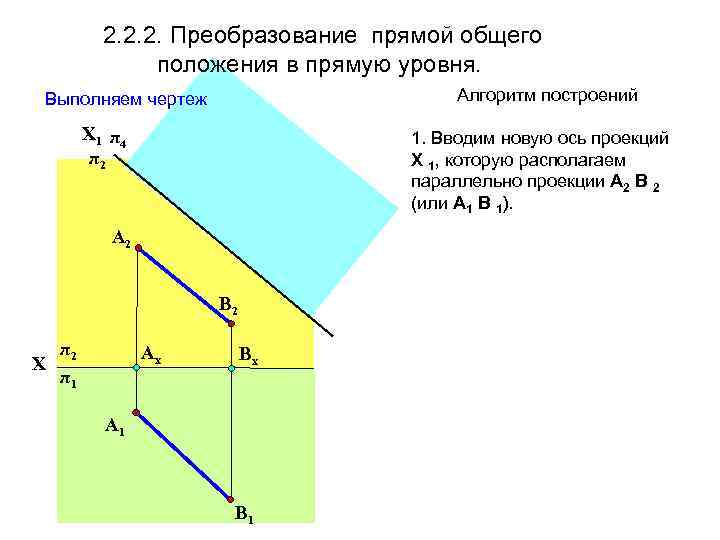
2. 2. 2. Преобразование прямой общего положения в прямую уровня. Алгоритм построений Выполняем чертеж Х 1 π 4 π2 1. Вводим новую ось проекций Х 1, которую располагаем параллельно проекции А 2 В 2 (или А 1 В 1). A 2 В 2 π2 Х π1 Aх Вх A 1 В 1
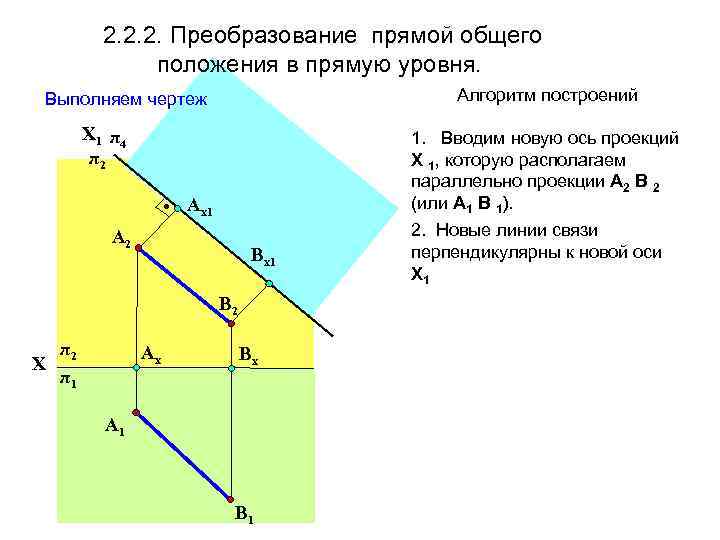
2. 2. 2. Преобразование прямой общего положения в прямую уровня. Алгоритм построений Выполняем чертеж Х 1 π 4 π2 1. Вводим новую ось проекций Х 1, которую располагаем параллельно проекции А 2 В 2 (или А 1 В 1). • Aх1 A 2 Вх1 В 2 π2 Х π1 Aх Вх A 1 В 1 2. Новые линии связи перпендикулярны к новой оси Х 1
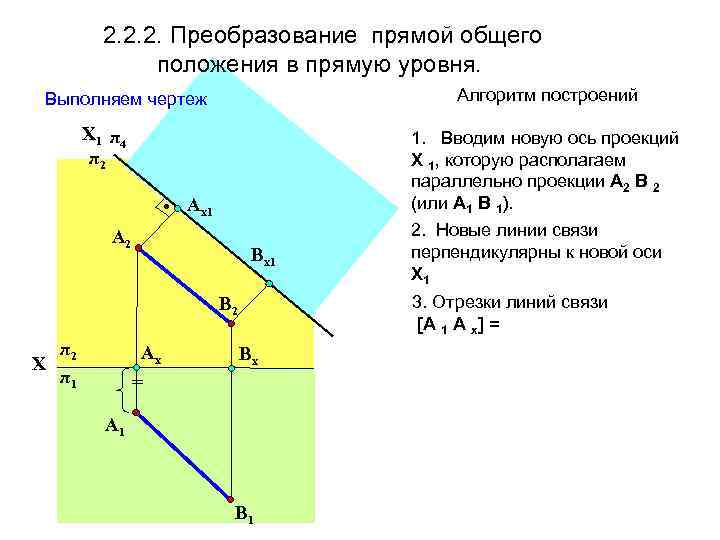
2. 2. 2. Преобразование прямой общего положения в прямую уровня. Алгоритм построений Выполняем чертеж Х 1 π 4 π2 1. Вводим новую ось проекций Х 1, которую располагаем параллельно проекции А 2 В 2 (или А 1 В 1). • Aх1 A 2 Вх1 3. Отрезки линий связи [А 1 А х] = В 2 π2 Х π1 Aх 2. Новые линии связи перпендикулярны к новой оси Х 1 Вх = A 1 В 1
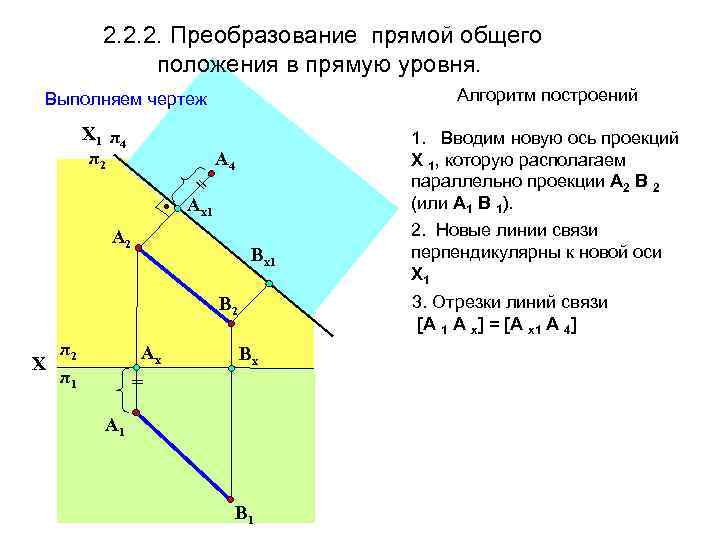
2. 2. 2. Преобразование прямой общего положения в прямую уровня. Алгоритм построений Выполняем чертеж Х 1 π 4 π2 = • Aх1 1. Вводим новую ось проекций Х 1, которую располагаем параллельно проекции А 2 В 2 (или А 1 В 1). A 4 A 2 Вх1 3. Отрезки линий связи [А 1 А х] = [А х1 А 4] В 2 π2 Х π1 Aх 2. Новые линии связи перпендикулярны к новой оси Х 1 Вх = A 1 В 1
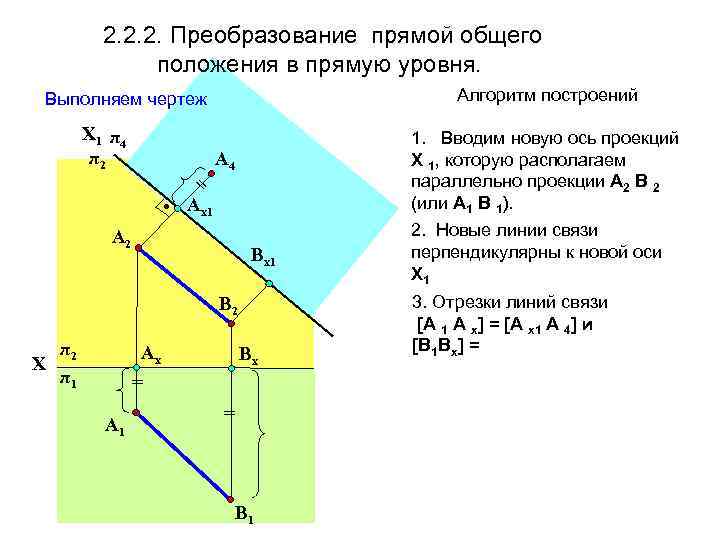
2. 2. 2. Преобразование прямой общего положения в прямую уровня. Алгоритм построений Выполняем чертеж Х 1 π 4 π2 = • Aх1 1. Вводим новую ось проекций Х 1, которую располагаем параллельно проекции А 2 В 2 (или А 1 В 1). A 4 A 2 Вх1 В 2 π2 Х π1 Aх Вх = A 1 = В 1 2. Новые линии связи перпендикулярны к новой оси Х 1 3. Отрезки линий связи [А 1 А х] = [А х1 А 4] и [В 1 Вх] =
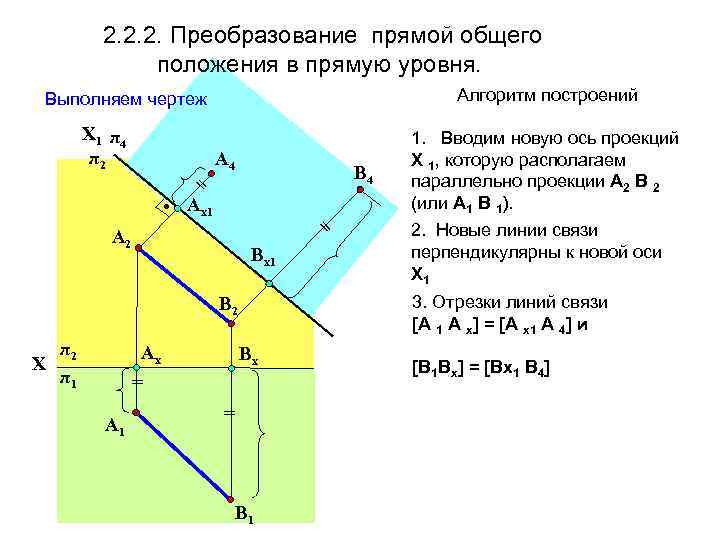
2. 2. 2. Преобразование прямой общего положения в прямую уровня. Алгоритм построений Выполняем чертеж Х 1 π 4 π2 = • Aх1 A 4 В 4 = A 2 Вх1 Aх Вх = A 1 2. Новые линии связи перпендикулярны к новой оси Х 1 3. Отрезки линий связи [А 1 А х] = [А х1 А 4] и В 2 π2 Х π1 1. Вводим новую ось проекций Х 1, которую располагаем параллельно проекции А 2 В 2 (или А 1 В 1). = В 1 [В 1 Вх] = [Вx 1 В 4]
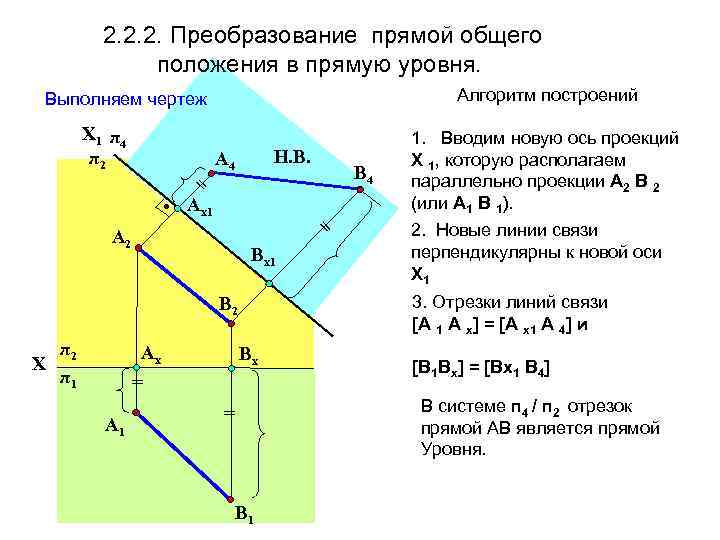
2. 2. 2. Преобразование прямой общего положения в прямую уровня. Алгоритм построений Выполняем чертеж Х 1 π 4 π2 = • Aх1 Н. В. A 4 = A 2 Вх1 Aх Вх = A 1 2. Новые линии связи перпендикулярны к новой оси Х 1 3. Отрезки линий связи [А 1 А х] = [А х1 А 4] и В 2 π2 Х π1 В 4 1. Вводим новую ось проекций Х 1, которую располагаем параллельно проекции А 2 В 2 (или А 1 В 1). [В 1 Вх] = [Вx 1 В 4] В системе п 4 / п 2 отрезок прямой АВ является прямой Уровня. = В 1
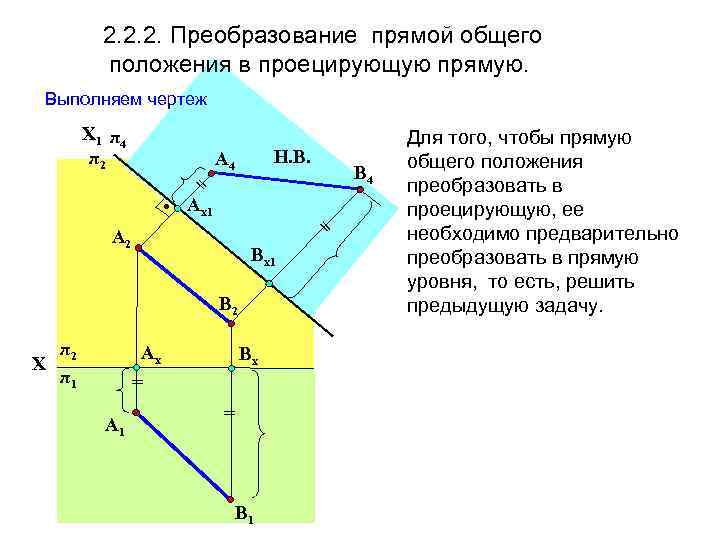
2. 2. 2. Преобразование прямой общего положения в проецирующую прямую. Выполняем чертеж Х 1 π 4 π2 = • Aх1 Н. В. A 4 = A 2 Вх1 В 2 π2 Х π1 Aх Вх = A 1 В 4 = В 1 Для того, чтобы прямую общего положения преобразовать в проецирующую, ее необходимо предварительно преобразовать в прямую уровня, то есть, решить предыдущую задачу.
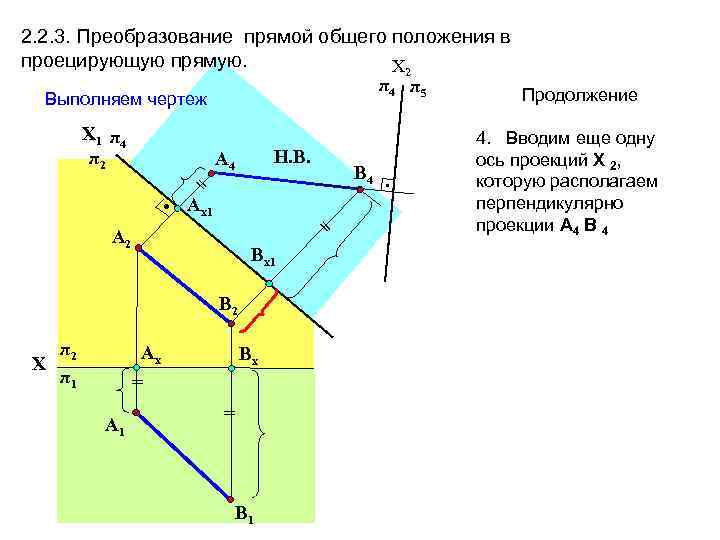
2. 2. 3. Преобразование прямой общего положения в проецирующую прямую. Х 2 π4 π5 Выполняем чертеж Х 1 π 4 π2 = • Aх1 Н. В. A 4 = A 2 Вх1 В 2 π2 Х π1 Aх Вх = A 1 В 4 = В 1 • Продолжение 4. Вводим еще одну ось проекций Х 2, которую располагаем перпендикулярно проекции А 4 В 4
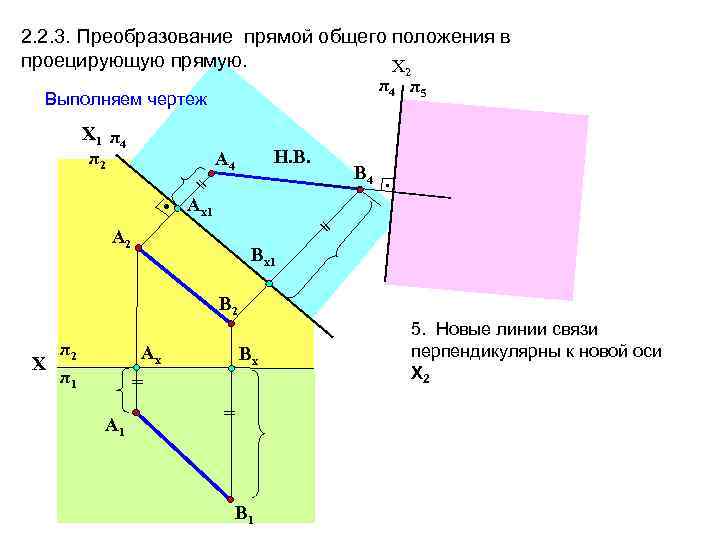
2. 2. 3. Преобразование прямой общего положения в проецирующую прямую. Х 2 π4 π5 Выполняем чертеж Х 1 π 4 π2 = • Aх1 Н. В. A 4 • = A 2 В 4 Вх1 В 2 π2 Х π1 Aх Вх = A 1 = В 1 5. Новые линии связи перпендикулярны к новой оси Х 2
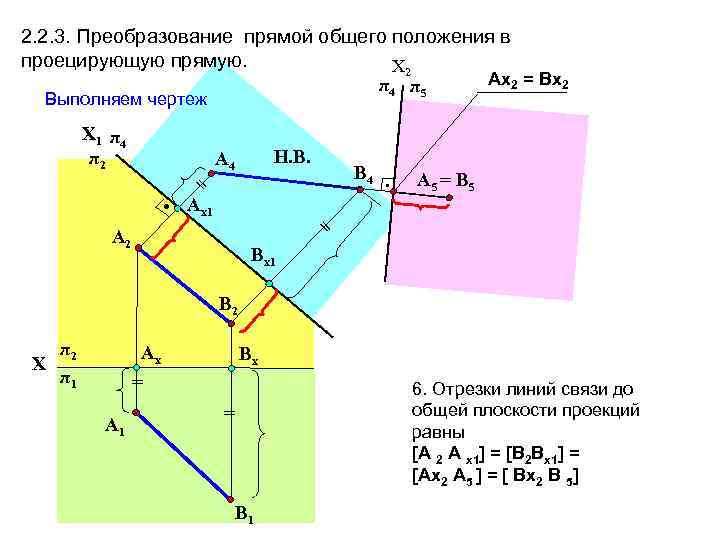
2. 2. 3. Преобразование прямой общего положения в проецирующую прямую. Х 2 π4 π5 Выполняем чертеж Х 1 π 4 π2 = • Aх1 Н. В. A 4 • А 5 = В 5 = A 2 В 4 Аx 2 = Вх2 Вх1 В 2 π2 Х π1 Aх Вх = A 1 6. Отрезки линий связи до общей плоскости проекций равны [А 2 А х1] = [В 2 Вх1] = [Аx 2 А 5 ] = [ Вх2 В 5] = В 1

2. 3. 2. 2. Определение натуральной длины отрезка и углов его наклона к плоскостям проекций способом прямоугольного треугольника Данный способ является разновидностью способа перемены плоскостей проекций, удобен для промежуточных построений при решении сложных задач. Будет нами использоваться при рассмотрении следующей темы.
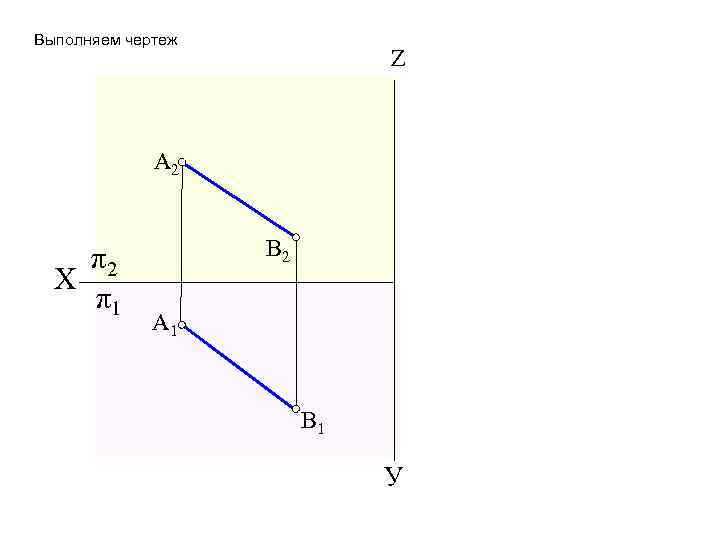
Выполняем чертеж Z A 2 π2 Х π1 В 2 A 1 В 1 У
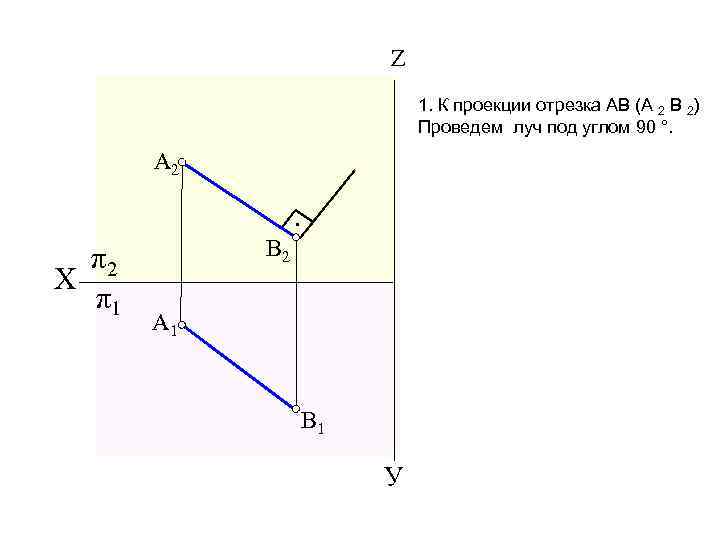
Z 1. К проекции отрезка АВ (А 2 В 2) Проведем луч под углом 90 °. A 2 • π2 Х π1 В 2 A 1 В 1 У
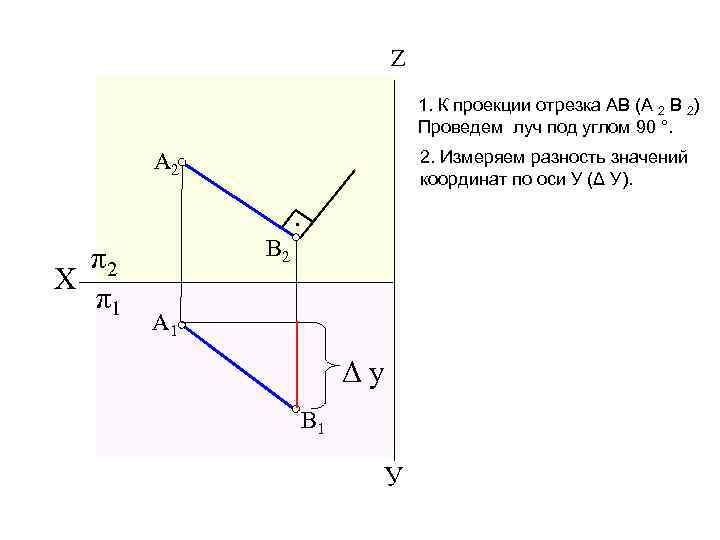
Z 1. К проекции отрезка АВ (А 2 В 2) Проведем луч под углом 90 °. 2. Измеряем разность значений координат по оси У (Δ У). A 2 • π2 Х π1 В 2 A 1 Δy В 1 У
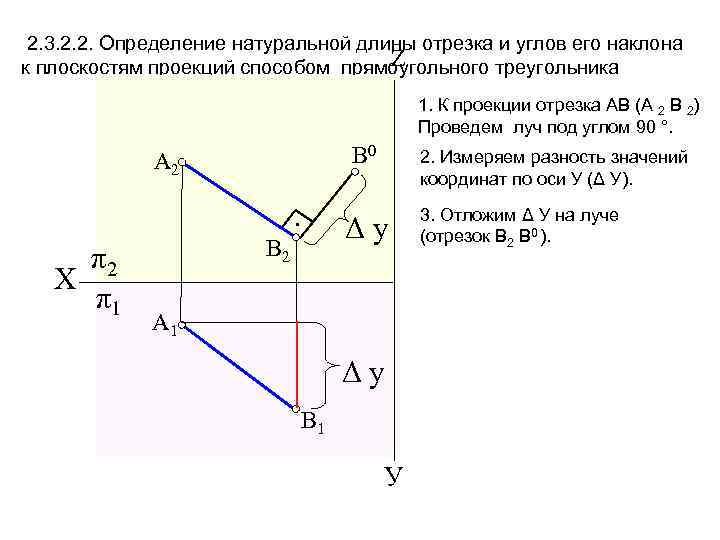
2. 3. 2. 2. Определение натуральной длины отрезка и углов его наклона Z к плоскостям проекций способом прямоугольного треугольника 1. К проекции отрезка АВ (А 2 В 2) Проведем луч под углом 90 °. В 0 A 2 Δy • π2 Х π1 2. Измеряем разность значений координат по оси У (Δ У). В 2 A 1 Δy В 1 У 3. Отложим Δ У на луче (отрезок В 2 В 0 ).

2. 3. 2. 2. Определение натуральной длины отрезка и углов его наклона Z к плоскостям проекций способом прямоугольного треугольника A 2 1. К проекции отрезка АВ (А 2 В 2) Проведем луч под углом 90 °. н. в. В 0 2. Измеряем разность значений координат по оси У (Δ У). 3. Отложим Δ У на луче (отрезок В 2 В 0 ). • π2 Х π1 В 2 4. Отрезок А 2 В 0 – является натуральной длиной АВ. A 1 Δy В 1 У
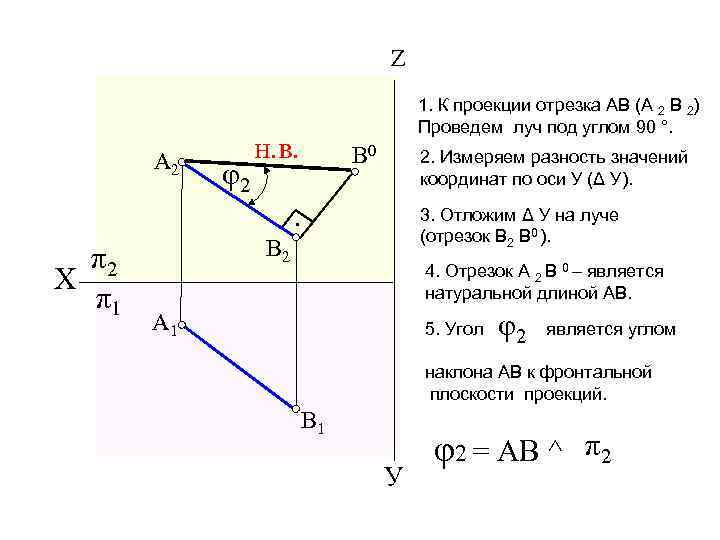
Z A 2 φ2 1. К проекции отрезка АВ (А 2 В 2) Проведем луч под углом 90 °. н. в. В 0 2. Измеряем разность значений координат по оси У (Δ У). 3. Отложим Δ У на луче (отрезок В 2 В 0 ). • π2 Х π1 В 2 4. Отрезок А 2 В 0 – является натуральной длиной АВ. A 1 5. Угол φ2 является углом наклона АВ к фронтальной плоскости проекций. В 1 У φ2 = АВ ^ π2
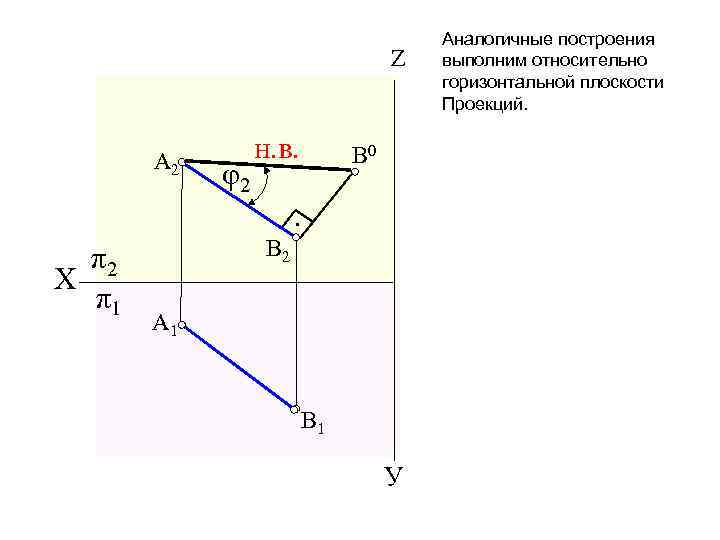
Z A 2 φ2 н. в. В 0 • π2 Х π1 В 2 A 1 В 1 У Аналогичные построения выполним относительно горизонтальной плоскости Проекций.
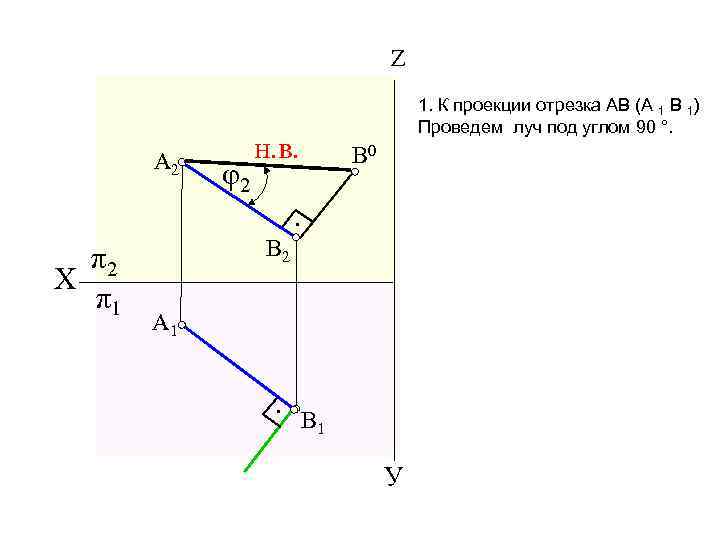
Z A 2 φ2 1. К проекции отрезка АВ (А 1 В 1) Проведем луч под углом 90 °. н. в. В 0 • A 1 • π2 Х π1 В 2 В 1 У
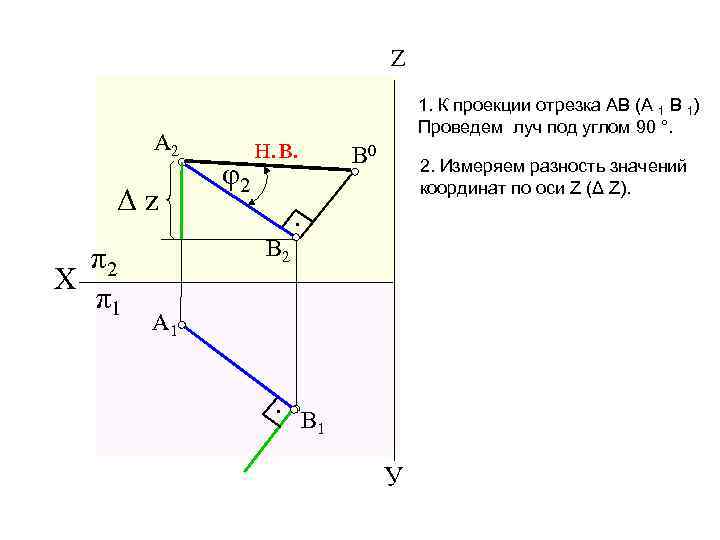
Z A 2 Δz φ2 1. К проекции отрезка АВ (А 1 В 1) Проведем луч под углом 90 °. н. в. В 0 2. Измеряем разность значений координат по оси Z (Δ Z). • A 1 • π2 Х π1 В 2 В 1 У
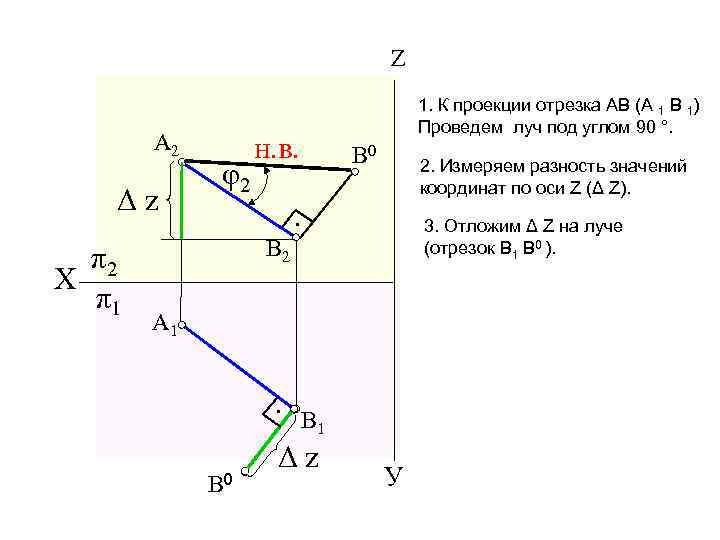
Z A 2 Δz φ2 1. К проекции отрезка АВ (А 1 В 1) Проведем луч под углом 90 °. н. в. В 0 2. Измеряем разность значений координат по оси Z (Δ Z). 3. Отложим Δ Z на луче (отрезок B 1 В 0 ). • A 1 • π2 Х π1 В 2 В 0 В 1 Δz У
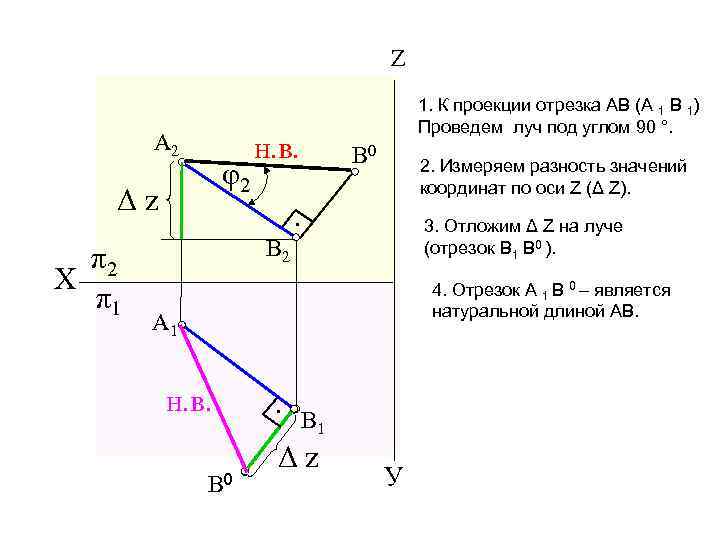
Z A 2 φ2 Δz 1. К проекции отрезка АВ (А 1 В 1) Проведем луч под углом 90 °. н. в. В 0 2. Измеряем разность значений координат по оси Z (Δ Z). 3. Отложим Δ Z на луче (отрезок B 1 В 0 ). • 4. Отрезок А 1 В 0 – является натуральной длиной АВ. A 1 н. в. В 0 • π2 Х π1 В 2 В 1 Δz У
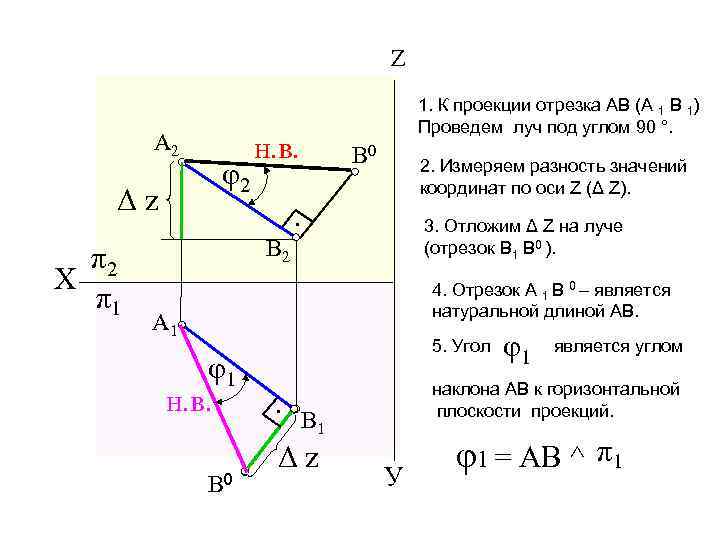
Z A 2 Δz φ2 1. К проекции отрезка АВ (А 1 В 1) Проведем луч под углом 90 °. н. в. В 0 2. Измеряем разность значений координат по оси Z (Δ Z). 3. Отложим Δ Z на луче (отрезок B 1 В 0 ). • 4. Отрезок А 1 В 0 – является натуральной длиной АВ. A 1 φ1 н. в. В 0 5. Угол • π2 Х π1 В 2 является углом наклона АВ к горизонтальной плоскости проекций. В 1 Δz φ1 У φ1 = АВ ^ π1
Сп_замены__НВ треуг.ppt