2 Случайная погрешность

• 2. Случайная погрешность

• Результат измерения является случайной величиной, так как содержит случайную погрешность • Дать количественные оценки результата измерения и его случайной погрешности позволяет теория вероятностей и математическая статистика

Случайная величина • Переменная, которая может принимать любое значение из заданного множества значений и с которой связано распределение вероятностей • Может принимать дискретные и непрерывные значения

• Случайную величину, которая может принимать только отдельные значения, называют дискретной • Случайную величину, которая может принимать любые значения из конечного или бесконечного интервала, называют непрерывной (измеренные значения физических величин и их случайные погрешности)

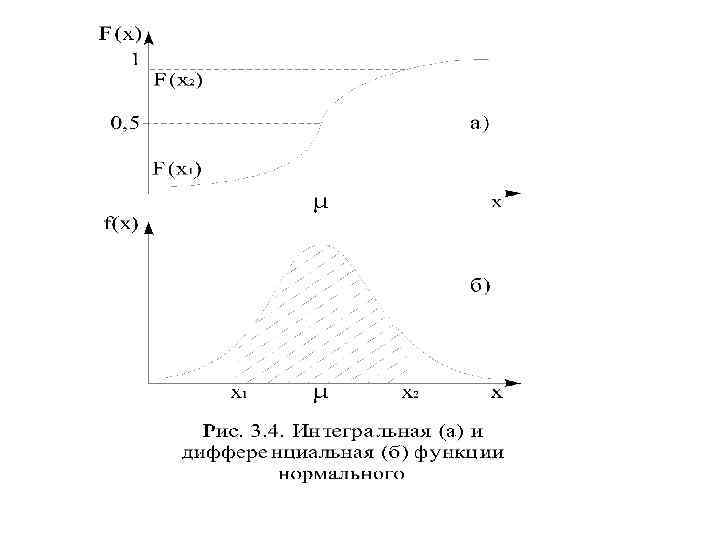
• Все случайные величины подчиняются определенным закономерностям, называемым законами распределения • Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями • Различают две формы закона: интегральную и дифференциальную

• Интегральная форма – функция распределения вероятностей – функция, задающая для любого значения х вероятность того, что случайная величина Х будет меньше или равна х:

Функция распределения вероятностей

Свойства функции распределения вероятностей

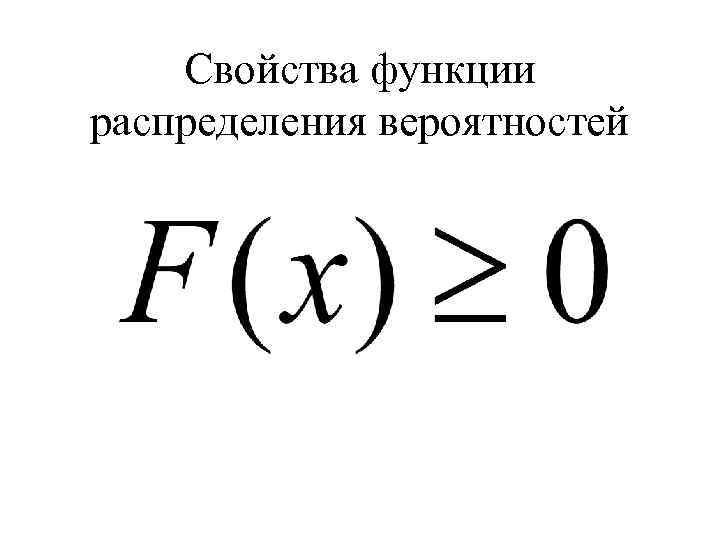Свойства функции распределения вероятностей • значения функции распределения принадлежат отрезку [0, 1] • – функция распределения неубывающая

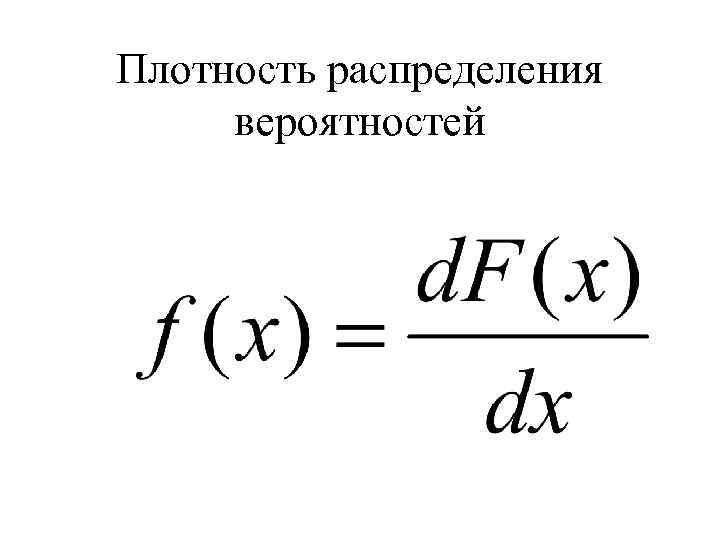Плотность распределения вероятностей

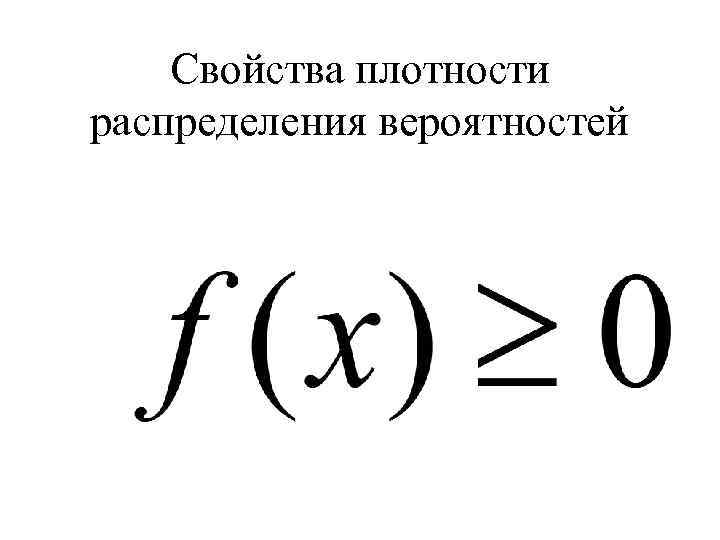Свойства плотности распределения вероятностей

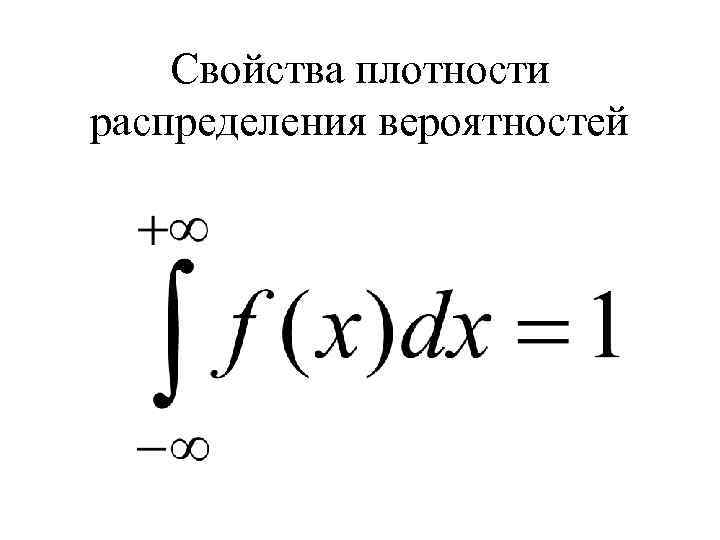Свойства плотности распределения вероятностей

– Для того, чтобы охарактеризовать случайную величину, часто достаточно определить положение центра и меру разброса значений – Для нахождения этих параметров могут быть использованы некоторые усредненные числовые величины – начальные и центральные моменты

– Начальные моменты - усредненные величины, отсчитываются от начала координат – Центральные моменты -усредненные величины отсчитываются от центра

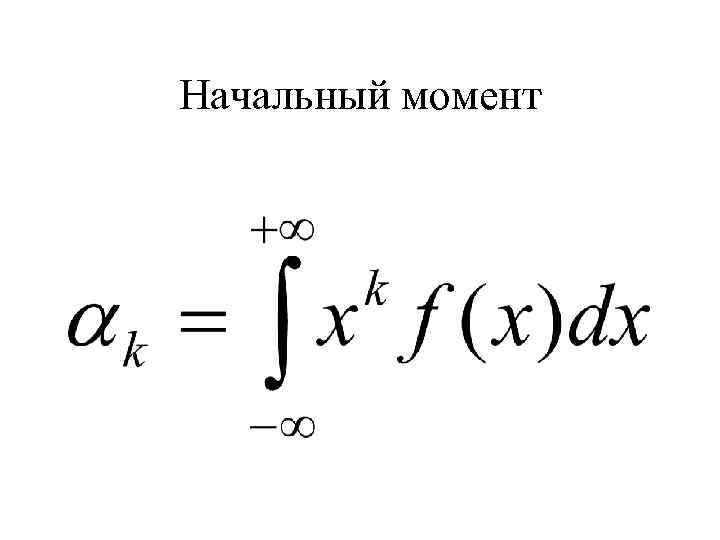Начальный момент

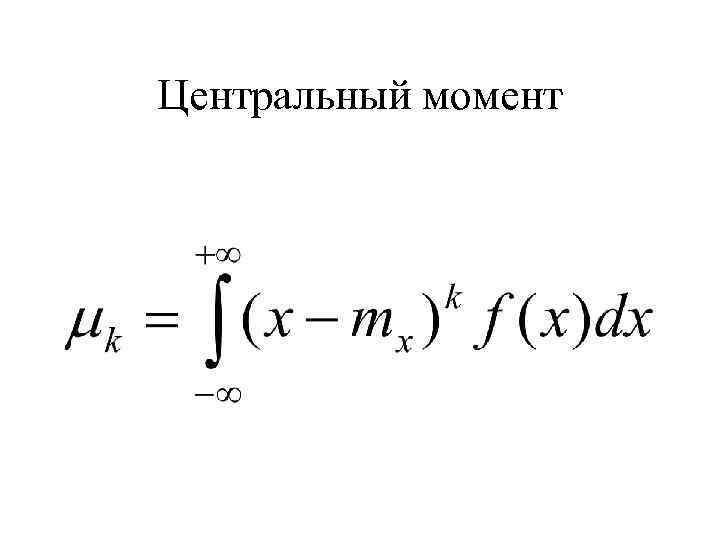Центральный момент

• Координата центра в зависимости от вида распределения (мера положения) может быть охарактеризована 2 медианой 2 математическим ожиданием 2 модой 2 центром размаха

Медиана (50% квантиль) - точка на оси Х, слева и справа от которой вероятность появления различных значений одинакова и равна 0, 5:

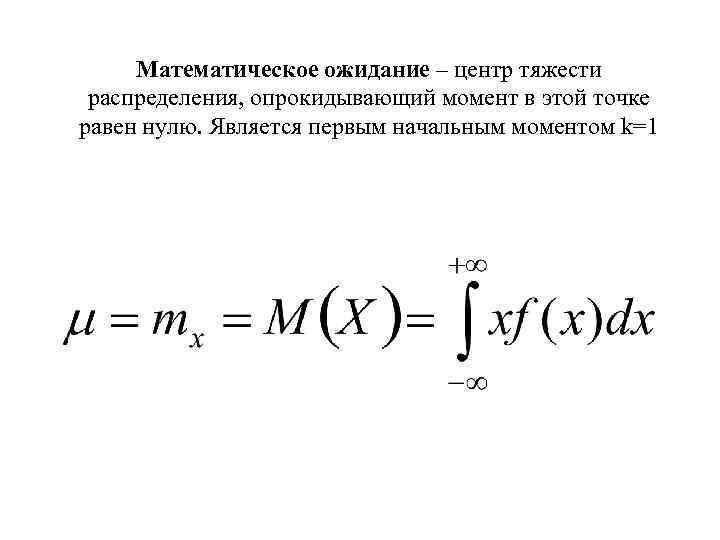Математическое ожидание – центр тяжести распределения, опрокидывающий момент в этой точке равен нулю. Является первым начальным моментом k=1

• Мода – это координата максимума распределения • Распределения с одним максимумом называются одномодальные, с двумя – двухмодальные

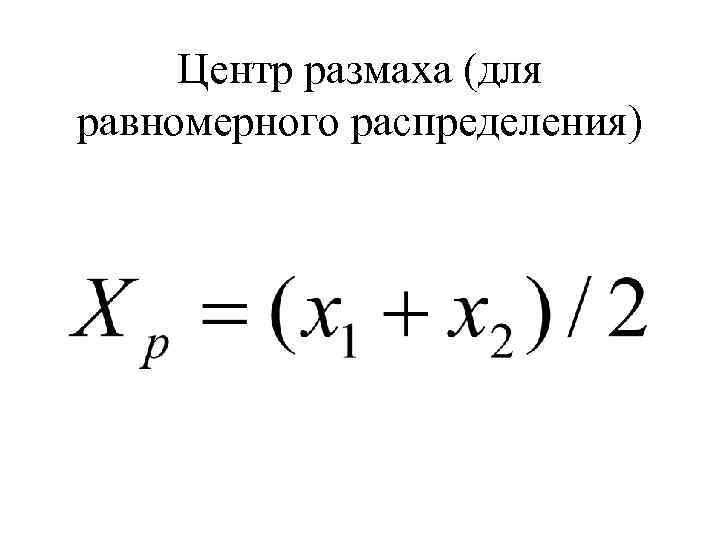Центр размаха (для равномерного распределения)

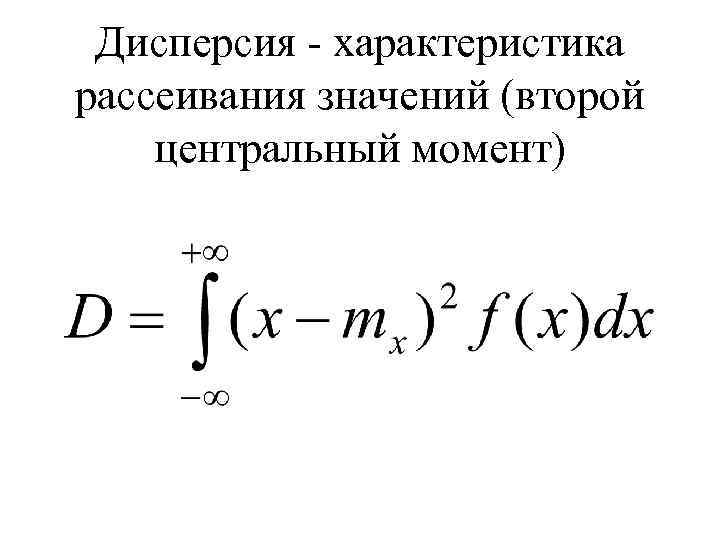Дисперсия - характеристика рассеивания значений (второй центральный момент)

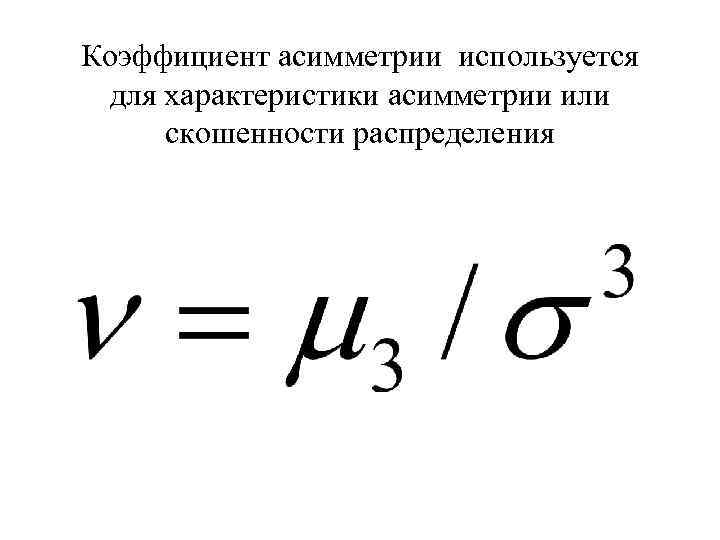Коэффициент асимметрии используется для характеристики асимметрии или скошенности распределения

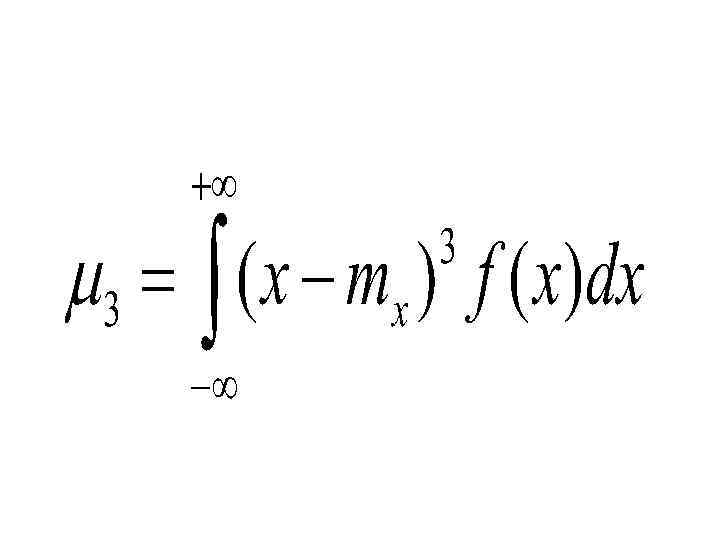
– Четвертый центральный момент используется для расчета эксцесса и характеристики плосковершинности распределения

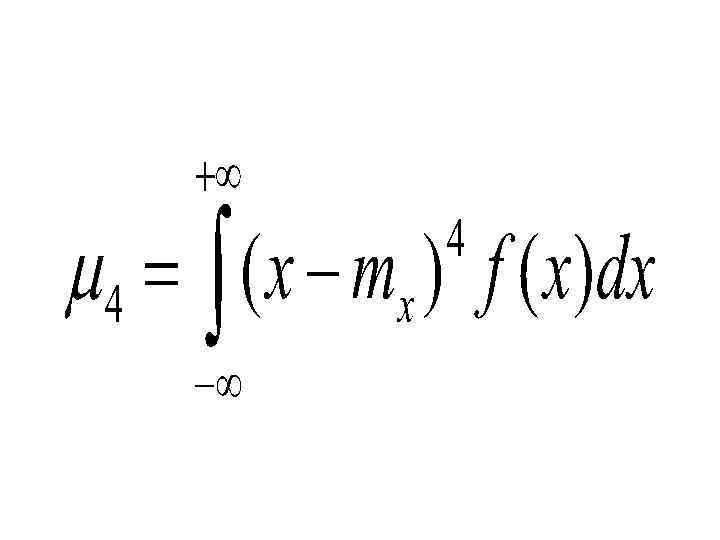
• Операция определения на основе выборочных данных числовых значений параметров распределения называется оцениванием • Оценкой является статистика, используемая для оценивания параметра распределения (генеральной совокупности)

• Оценка может быть: точечной интервальной • Точечная оценка выражается одним числом • Интервальная - интервалом

• Точечной оценкой математического ожидания результатов наблюдений является среднее арифметическое значение измеряемой величины

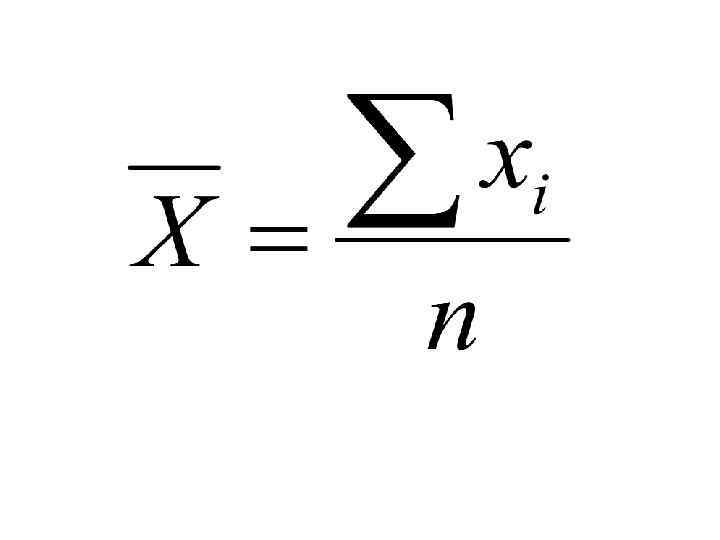
• Точечная оценка дисперсии представляет собой сумму квадратов отклонений результатов наблюдений от их среднего арифметического , деленную на число наблюдений минус единица

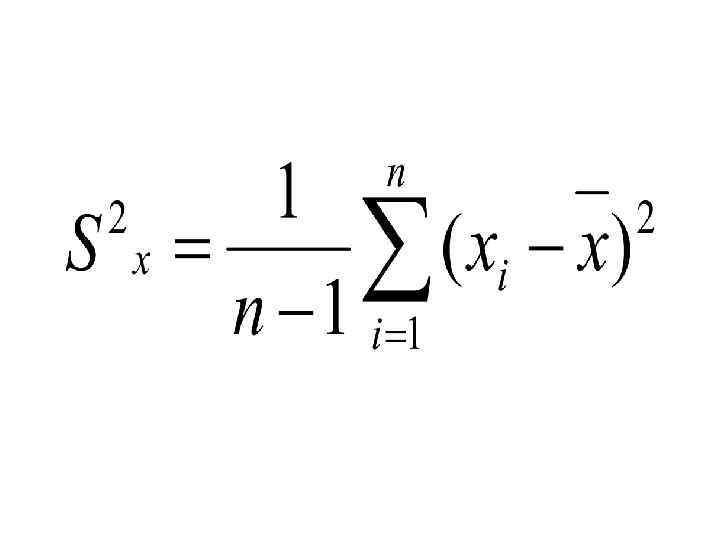
Стандартное отклонение результатов (СКО) наблюдений – положительный корень из дисперсии

СКО среднего арифметического значения (результата измерений) в корень из n раз меньше СКО результата отдельного наблюдения

Нормальное распределение (распределение Лапласа – Гаусса) • Распределение вероятностей непрерывной случайной величины Х такое, что плотность распределения вероятностей при < х < принимает действительное значение

Функция нормального закона распределения

Нормирование • Линейное преобразование нормально распределенной случайной переменной Х, после которого получается случайная переменная Z с математическим ожиданием 0 и дисперсией 1, называется нормированием:

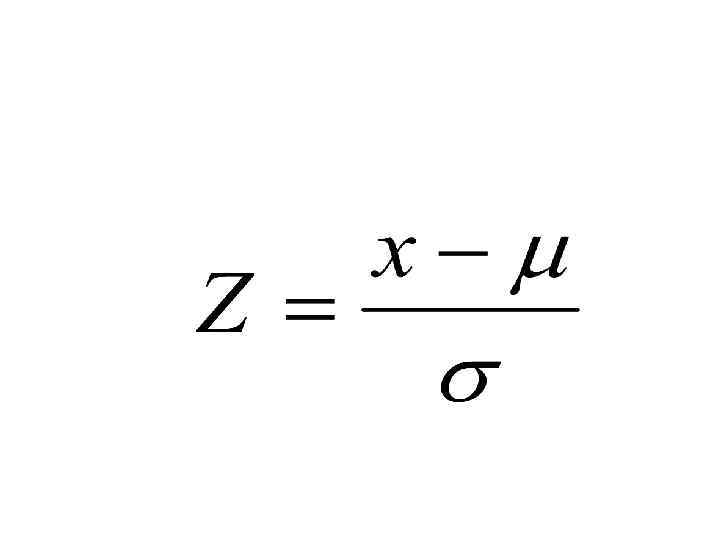
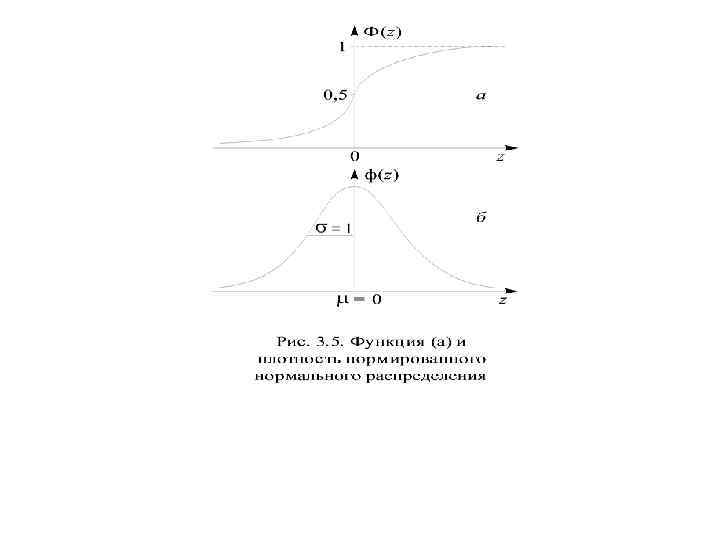
Стандартное нормальное распределение (стандартное распределение Лапласа – Гаусса, или нормированное нормальное распределение • Распределение вероятностей стандартизованной нормальной случайной величины Z, плотность распределения которой равна

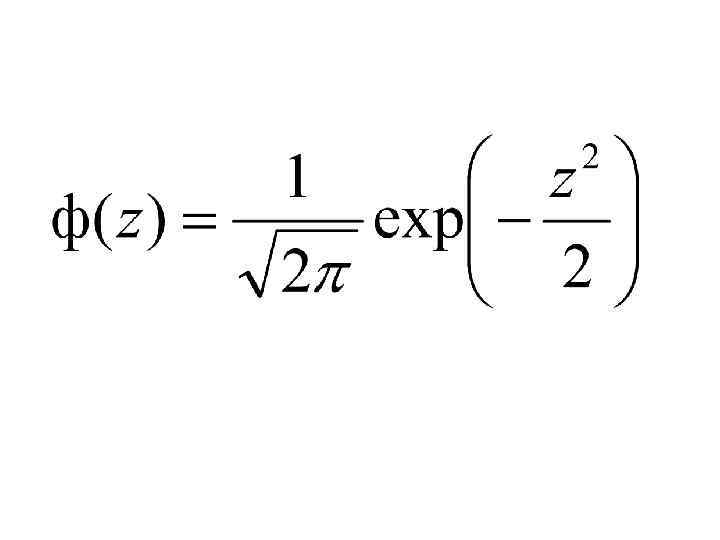
Значение функции нормированного нормального распределения

Нормирование • Нормирование позволяет все возможные варианты нормального распределения свести к одному случаю: = 0, = 1.

• Значения функции Ф(z) и плотности нормированного нормального распределения рассчитаны и сведены в таблицы (табулированы). Таблица составлена только для положительных значений z: • Ф(–z) = 1–Ф(z)

По таблицам можно найти значения функции с любым математическим ожиданием и средним квадратическим отклонением

Погрешность равна разности измеренного значения и истинного, оценкой которого является математическое ожидание

Нормальное распределение погрешностей

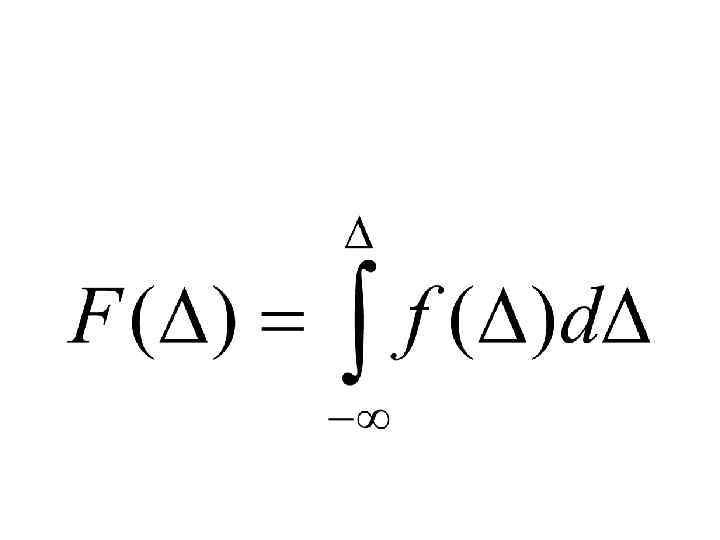
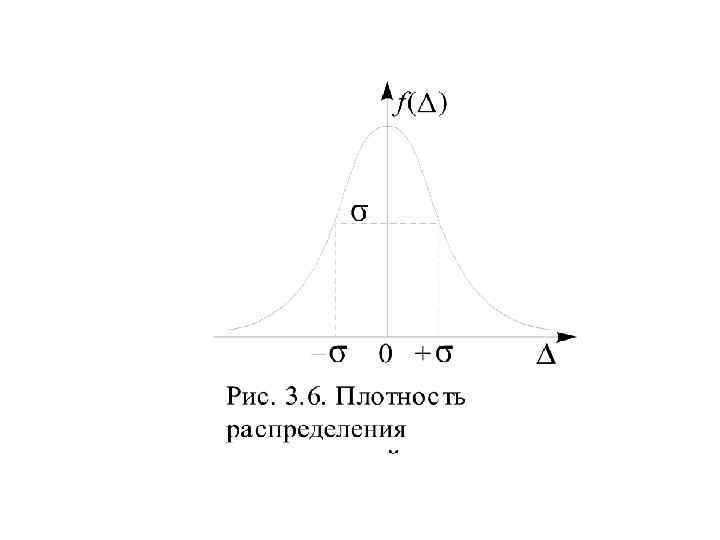
• Погрешности, одинаковые по величине, но противоположные по знаку, имеют одинаковую плотность распределения вероятностей, т. е. при большом числе наблюдений встречаются одинаково часто • Малые погрешности будут встречаться чаще, чем большие

Вероятность нахождения случайной в интервал от х1 до х2 можно определить по формуле

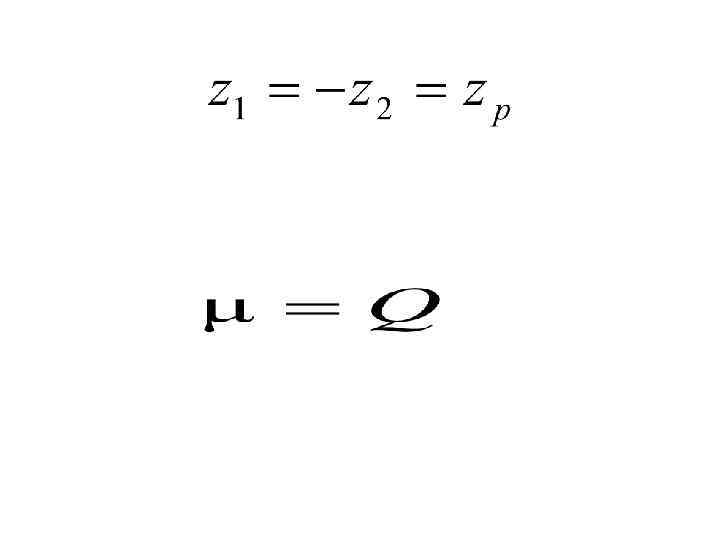
вероятность нахождения результата наблюдения в заданном интервале равна

zp аргумент (квантиль) функции нормированного нормального распределения, определенной на интервале от до :

Вероятность того, что истинное значение будет находиться в определенном интервале равна

вероятность нахождения в погрешности в определенном интервале соответственно равна

Если таблицы нормированного нормального распределения составлены для положительных значений аргумента от 0 до , то вероятность нахождения истинного значения и случайной погрешности в заданном интервале определяется

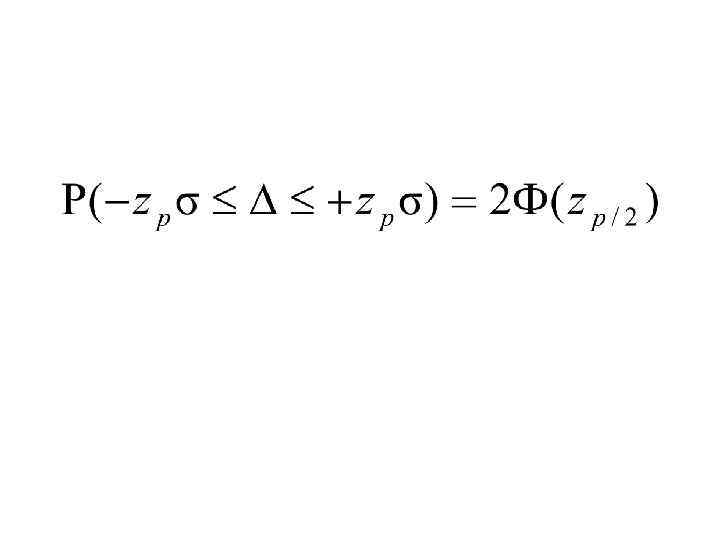
доверительный интервал, устанавливающий отклонения среднего арифметического от истинного значения определяется формулой

Он указывает, что с доверительной вероятностью равной Р истинное значение находится в интервале

Вероятность того, что истинное значение находится в пределах х k. При к=1

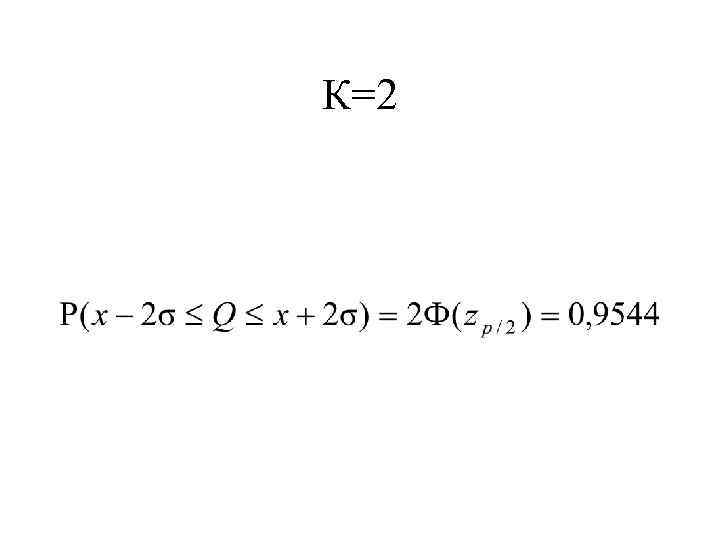К=2

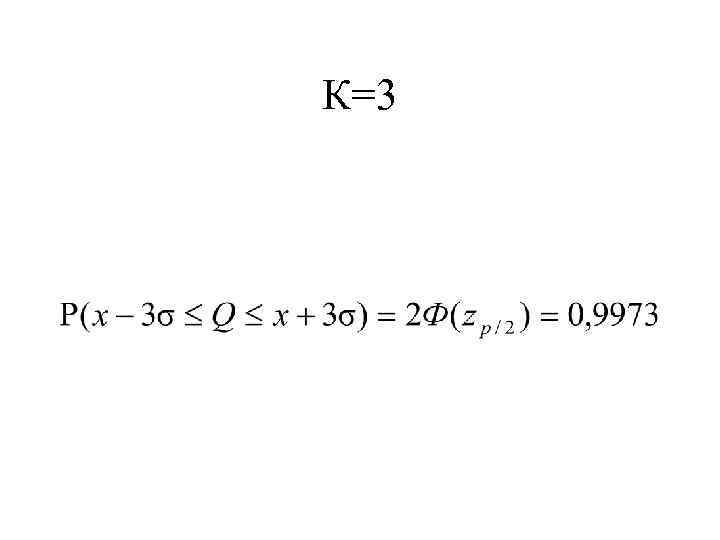К=3

Для определения доверительных границ, в пределах которых истинное значение находится с наперед заданной доверительной вероятностью необходимо • 1. Задаться доверительной вероятностью, которую чаще всего выбирают из следующего ряда 0, 9; 0, 95 или 0, 99. Для технических измерений обычно выбирают 0, 95;

2. Вычислить значение функции нормированного нормального распределения

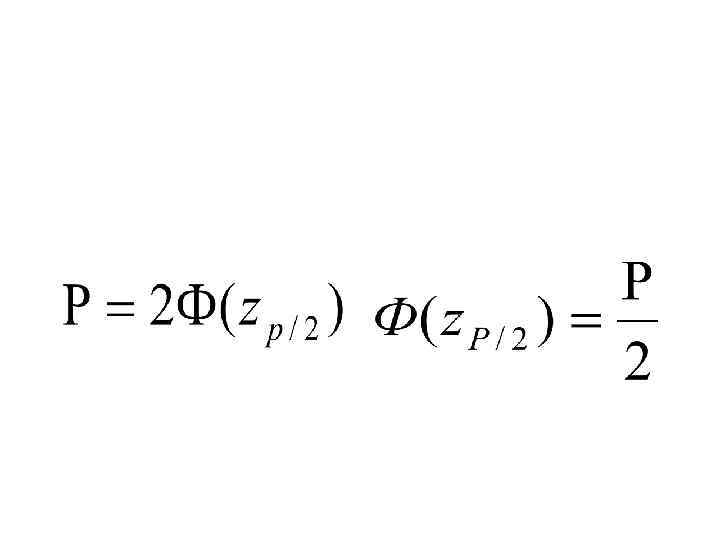
• 3. Определить квантили zp/2 из таблиц нормированного нормального распределения, при которых функция примет значение Ф(zp) или Ф(zp/2)

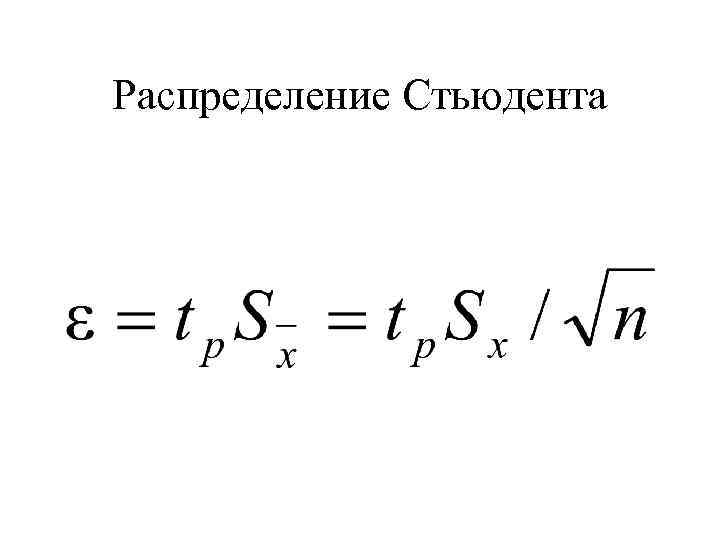Распределение Стьюдента

Прямоугольное (равномерное распределение)

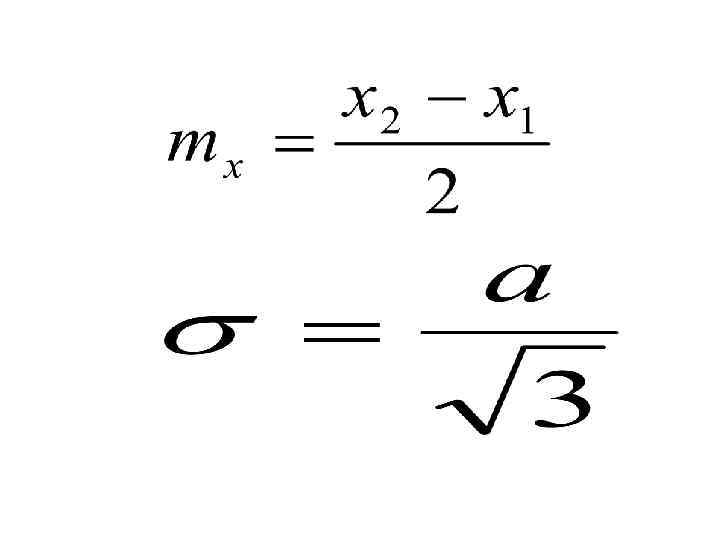
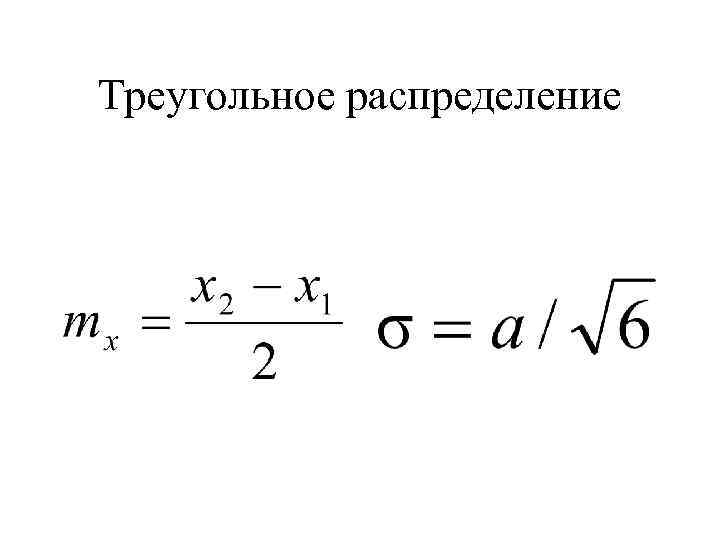Треугольное распределение