2 ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ

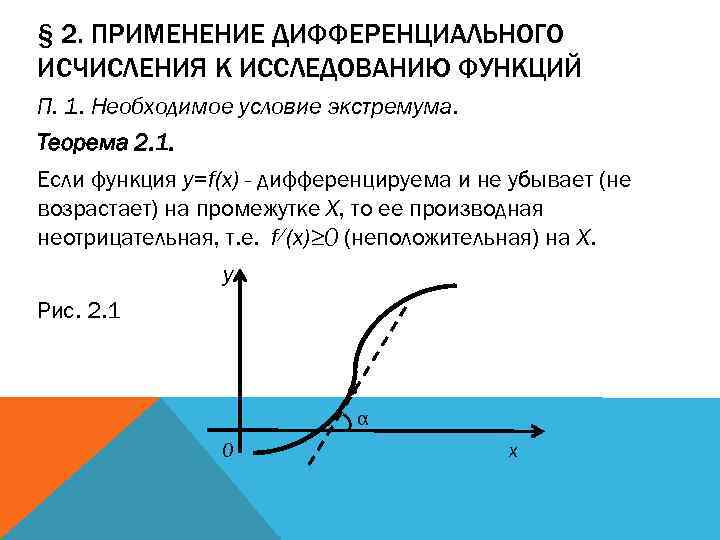§ 2. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ П. 1. Необходимое условие экстремума. Теорема 2. 1. Если функция y=f(x) - дифференцируема и не убывает (не возрастает) на промежутке X, то ее производная неотрицательная, т. е. f/(x)≥ 0 (неположительная) на X. y Рис. 2. 1 α 0 x

ОПР. 2. 1. Пусть функция y=f(x) определена в некоторой окрестности точки x 0 из множества X и непрерывна в этой точке. Если во всех точках этой окрестности выполняется условие f(x)≤f(x 0), то x 0 называется точкой локального максимума. Если во всех точках этой окрестности выполняется условие f(x)≥f(x 0), то называется точкой локального минимума. Точки максимума и минимума называют точками экстремума. Если рассмотреть касательные в точках экстремума, то можно заметить, что либо в этих точках они параллельны оси абсцисс, либо вовсе не существуют.

Лемма 2. 2. Пусть в некоторой окрестности точки x 0 производная функции отрицательна, т. е. f/(x 0)<0. Тогда найдется такая окрестность этой точки, в которой знак приращения функции противоположен знаку приращения ее аргумента, т. е. в указанной окрестности если ∆x>0, то и ∆f<0 и, если ∆x<0, то и ∆f>0. Теорема 2. 2. (теорема Ферма или необходимое условие экстремума) Пусть функция y=f(x) непрерывна в некоторой окрестности точки x 0 и имеет локальный экстремум в этой точке. Тогда производная функции в этой точке либо равна нулю, либо не существует. Док-во: Возможны 4 случая: 1) f/(x 0)>0; 2) f/(x 0)<0; 3) f/(x 0)=0; 4) f/(x 0)не существует. Рассмотрим каждый из случаев в отдельности.

1. Пусть f/(x 0)>0, тогда в силу леммы 2. 1. найдется такая окрестность точки , в которой знаки ∆x и ∆f совпадают. Поэтому в указанной окрестности ∆f может принимать как положительные, так и отрицательные значения. Согласно определению точек локального экстремума через приращение в случае, если x 0 - точка локального максимума, то в окрестности точки x 0 приращение функции должно быть только отрицательно, а в случае, если x 0 - точка минимума, то приращение функции должно быть только положительно, что противоречит лемме 2. 1. 2. Аналогично доказывается невозможность второго случая. Следовательно, если у функции в точке локальный экстремум, то производная функции в этой точке либо равна нулю, либо не существует. Теорема доказана.

П. 2. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ Теорема 2. 3. (теорема Ролля) Пусть функция y=f(x) удовлетворяет следующим условиям: 1) она непрерывна на отрезке [a, b]; 2) она дифференцируема в интервале (a, b); 3) на концах отрезка [a, b] она принимает одинаковые значения, т. е f(a)=f(b); Тогда внутри отрезка [a, b] существует, по крайней мере, одна точка c, в которой выполняется f/(c)=0. Геометрически теорема Ролля означает, что у графика непрерывной на отрезке [a, b] и дифференцируемой внутри его функции, принимающей на концах этого отрезка равные значения, существует точка внутри отрезка [a, b] , в которой касательная параллельна оси OX.

Теорема 2. 4. (теорема Лагранжа) Пусть функция y=f(x) удовлетворяет следующим условиям: 1) она непрерывна на отрезке [a, b]; 2) она дифференцируема в интервале (a, b); Тогда в интервале (a, b) найдется точка c, в которой выполняется равенство. Замечание 1. Геометрический смысл данной теоремы состоит в том, что если взять секущую, проведенную к графику функции y=f(x) , проходящую через точки (a, f(a)) и (b, f(b)), то величина является ее угловым коэффициентом. С другой стороны значение f/(c) является угловым коэффициентом касательной, проведенной к графику функции y=f(x) в точке (c, f(c)). Из теоремы Лагранжа следует, что на отрезке [a, b] существует такая точка c, что касательная в этой точке к графику функции параллельна секущей, проходящей через концы отрезка. Таких точек может быть несколько, но, по крайней мере, одна существует наверняка.

Замечание 2. Часто записывают вывод теоремы в следующем виде f(b)-f(a)= =f/(c)(b-a) и называют формулой конечных приращений или формулой Лагранжа. Замечание 3. Если положить a=x, b=x+∆x, тогда b-a=∆x и формула Лагранжа примет вид f(x+∆x)-f(x)=f/(x+θ∆x)∆x, где 0<θ<1. Теорема 2. 5. (теорема Коши) Пусть функции y=f(x) и y=g(x) удовлетворяют следующим соотношениям: 1) они непрерывны на отрезке [a, b]; 2) они дифференцируемы в интервале (a, b); 3) производная g/ (x) не обращается в нуль ни в одной точке интервала (a, b). Тогда существует такая точка c∈(a, b), в которой выполняется равенство. Эта формула называется обобщенной формулой конечных приращений или формулой Коши.

П. 3. ФОРМУЛА ТЕЙЛОРА Пусть дан многочлен с неизвестными коэффициентами. Постараемся выразить коэффициенты этого многочлена через функцию f(x). Пусть x=0, тогда f(0)=a 0. Поскольку f(x) - многочлен, то эта функция дифференцируема. Вычислим первую производную от него, получим. Полагая в этом равенстве x=0, получим f/(0)=a 1. Далее вычислим вторую производную и при x=0 получим f//(0)=2 a 2, откуда a 2=0, 5 f//(0). Продолжая этот процесс, мы получим коэффициенты. Теперь подставим эти значения в исходную формулу. Итак, если f(x) - многочлен n-ой степени, то имеет место равенство

Теорема 2. 6. (теорема Тейлора) Пусть функция y=f(x) имеет в точке a и некоторой ее окрестности производные порядка (n+1). Пусть x - любое значение аргумента из указанной окрестности, x≠a. Тогда между точками x и a найдется такая точка ξ, что справедлива следующая формула: Эта формула называется формулой Тейлора для произвольной функции, а последний член в ней – остаточным членом. При a=0 мы получаем разложение которое называется формулой Маклорена.

П. 4. ПРАВИЛО ЛОПИТАЛЯ Теорема 2. 7. (теорема Лопиталя) Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a. Пусть также и g/ (x)≠ 0 в указанной окрестности точки a. Тогда, если существует предел отношения производных (конечный или бесконечный), то существует и предел формула , причем справедлива

Следствие 1. Пусть функции f(x) и g(x) определены и дифференцируемы на луче (a, +∞). Пусть также и g/ (x)≠ 0. Тогда, если существует предел отношения производных (конечный или бесконечный), то существует и предел , причем справедлива формула Следствие 2. Если производные f/(x) и g/(x) удовлетворяют тем же условиям, что и сами функции f(x) и g(x), то правило Лопиталя можно применить повторно. При этом получаем

Следствие 3. Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a. Пусть также и в указанной окрестности точки g/ (x)≠ 0. Тогда, если существует предел отношения производных (конечный или бесконечный), то существует и предел , причем справедлива формула Следствие 4. Пусть функции f(x) и g(x) определены и дифференцируемы на луче (a, +∞). Пусть также и g/ (x)≠ 0. Тогда, если существует предел отношения производных (конечный или бесконечный), то существует и предел причем справедлива формула. ,