Diskretka_l2-2012.ppt
- Количество слайдов: 15

§ 2 Отображения. Элементарные тождества Пусть А и В непустые множества. Если каждому элементу х А ставится в соответствие единственный элемент y В, то говорят, что задано отображение F множества А в множество В. F: A B 1

Элемент y – образ элемента х, элемент х – прообраз элемента y. Отображение F : A B называется инъективным, если разным элементам из А ставятся в соответствие разные элементы из В. Отображение F : A B называется сюрьективным, если каждый элемент из В является образом некоторого элемента из А. 2

Отображение F : A B называется биективным, если оно одновременно инъективно и сюрьективно. Пусть N = {1, 2, …} – множество натуральных чисел и Nn = {1, 2, …, n} - его начальный отрезок из n элементов. Пусть дано множество А и пусть существует биективное отображение множества А в множество Nn. В этом случае говорим, что мощность множества А равна n. Два отображения F 1 : A 1 B 1 и F 2 : A 2 B 2 считаются равными, если A 1= A 2, B 1 = B 2 и 3

Если А = В, то отображение F : A B называется преобразованием множества А, биективное преобразование F множества А называется его подстановкой. Если |A| = n, то говорят, что подстановка множества А имеет степень n. Если А является n-множеством, причём А={x 1, …, xn}, то любое отображение F : A B может быть задано в виде двустрочной таблицы 4

Пусть А – конечное множество из n элементов и F – произвольное отображение множества А в себя. Теорема 1: Следующие утверждения равносильны: 1. Отображение F – инъективно. 2. Отображение F – биективно. 3. Отображение F – сюрьективно. Доказательство: Пусть F задано в виде двустрочной таблицы причём А={x 1, …, xn}. 5

Пусть L 0 – число элементов множества А, которые отсутствуют в нижней строке таблицы F, L 1 – число элементов множества А, которые в ней представлены точно 1 раз, L 2 – число элементов представленных точно 2 раза и т. д. Имеем следующие отношения: L 0 + L 1 + … + L n = n a) L 1 + 2 L 2 + … + n. Ln = n б) в а) просуммированы все элементы; в б) просуммировано число мест в нижней строке табличного задания F. 6

Пусть теперь F инъективно, тогда L 2 + … + Ln =0 и поэтому из а) и б) имеем: L 0 + L 1 = n Значит L 0 = 0 и F – сюрьективно. Отсюда получаем справедливость 1) 2) 3). В обратную сторону Пусть F – сюрьективно. Тогда L 0 = 0. Вычтем из б) соотношение а). Имеем: L 2 + 2 L 3 + … + (n-1)Ln = 0 7

Поскольку все Li 0, то отсюда имеем L 2 = L 3 = … = L n = 0 и, следовательно, L 1 = n, что означает, что F инъективно, т. е. справедливо 3) 1). 8

Элементарные тождества. 1. Правило равенства. Если А и В – конечные множества и существует биективное отображение F : A B , то |A| = |B|. 2. Правило суммы. Если А 1, … , Аn – конечные, попарно непересекающиеся множества, то 3. Правило произведения. Если А 1, … , Аn – конечные множества, то 9

Бинарные отношения. Пусть дано декартово произведение множеств A 1 … An. Подмножество R A 1 … An называется n – местным отношением на множествах A 1… An. Говорят, что элементы а 1, …, аn находятся в отношении R, если (а 1, …, аn ) R. 10

Бинарным отношением R между элементами множеств А и В называется подмножество декартова произведения А В. Если (a, b) R, то пишут a. Rb. Отношение «быть меньше» на множестве натуральных чисел: {(a, b) : a, b N и a < b} Бинарным отношением на множестве А называют подмножество декартова квадрата А А. 11

Способы задания бинарного отношения R на конечном множестве А: 1. Матричный Пусть n-множество А состоит из элементов а 1, …, аn. Тогда для бинарного отношения R на А определим матрицу DR = (rij), i, j = 1, …, n rij = 1, если ai. Raj Матрица бинарного отношения R A 2, где = {1, 2, 3} имеет вид 0, в. Апротивном случае 0 1 1 Dr = 0 0 1 1 0 0 12
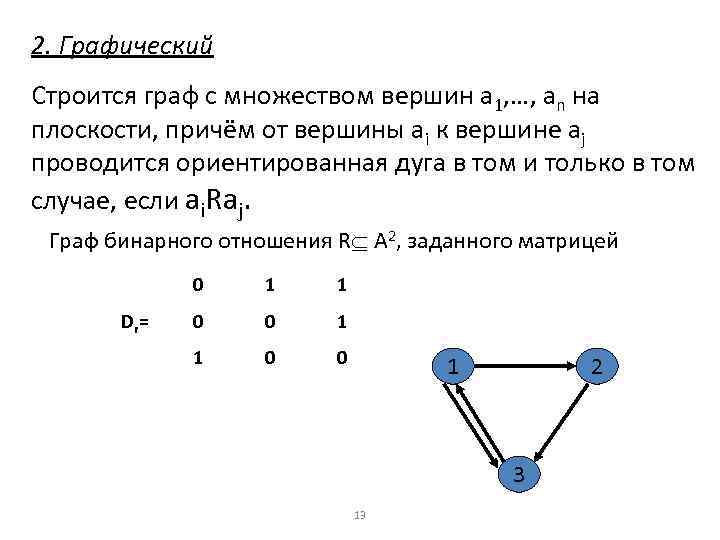
2. Графический Строится граф с множеством вершин а 1, …, аn на плоскости, причём от вершины аi к вершине аj проводится ориентированная дуга в том и только в том случае, если ai. Raj. Граф бинарного отношения R A 2, заданного матрицей 0 Dr = 1 1 0 0 1 2 3 13

Основные свойства матриц бинарных отношений – САМОСТОЯТЕЛЬНО! Бинарное отношение R на множестве А называется рефлексивным, если справедливо а. Rа, а А. Рефлексивные отношения представляются матрицами, у которых на главной диагонали стоят 1. Отношение R называется симметричным, если для любых а 1, а 2 А из а 1 R а 2 следует а 2 R а 1. Симметричные отношения представляются симметричными матрицами, т. е. матрицами с условием rij = rji , i, j = 1, …, n. 14

Отношение R называется транзитивным, если для любых а 1, а 2, а 3 А из а 1 R а 2 и а 2 R а 3 следует а 1 R а 3. ПРИМЕРЫ: 1. Отношения «=» и « » являются рефлексивными отношениями на множестве N, но отношение «<» таковым не является. 2. Отношение «=» является симметричным, а «<» и « » нет. 3. Отношения «<» , « » и «=» являются транзитивными, а отношение R = {(a, b): a, b N и a = b-1} – нет, так как 3 R 4 и 4 R 5, но не 3 R 5. 15
Diskretka_l2-2012.ppt