2. Основные понятия кинематики и динамики жидкости Течение

2. Основные понятия кинематики и динамики жидкости Течение называется установившимся, если характеристики течения не зависят от времени, т. е. могут изменяться лишь от точки к точке. Если в данной точке пространства характеристики течения изменяются со временем, то течение называется неустановившимся. = (x, y, z, t); p = p (x, у, z, t). Линией тока называется кривая, в каждой точке которой вектор скорости направлен по касательной к этой линии (рис. 2. 1). Совокупность линий тока, проходящих через замкнутый контур L, образует трубчатую поверхность — трубку тока (рис. 2. 2). Жидкость, находящаяся внутри трубки тока, образует струйку. Рис. 2. 1 Линия тока Рис. 2. 2 Трубка тока

Сечение струйки s, нормальное в каждой своей точке к линиям тока, называется живым сечением (рис. 2. 3). Гидравлический радиус Rг живого сечения определяется как отношение площади живого сечения s к смоченному периметру , т. е. Rг = s/. (2. 1) Под смоченным периметром (рис. 2. 4) понимается та часть геометрического живого сечения, по которой жидкость соприкасается с твердыми стенками. Рис. 2. 3. Живое сечение Рис. 2. 4. Смоченный периметр Если форма и площадь живого сечения по длине потока не изменяются, то поток называется равномерным. В противном случае поток называется неравномерным. В том случае, когда живое сечение плавно изменяется по длине, течение называется плавно изменяющимся.

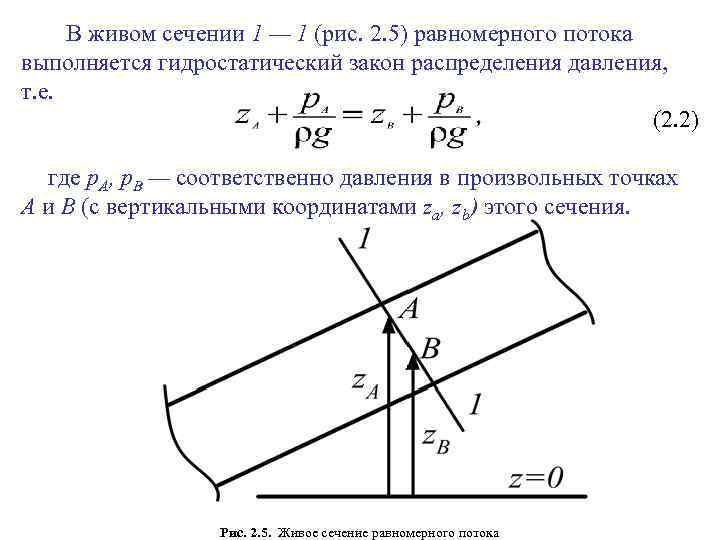В живом сечении 1 — 1 (рис. 2. 5) равномерного потока выполняется гидростатический закон распределения давления, т. е. (2. 2) где р. А, р. B — соответственно давления в произвольных точках А и В (с вертикальными координатами za, zb) этого сечения. Рис. 2. 5. Живое сечение равномерного потока

Расходом жидкости через поверхность s называется количество жидкости, протекающей через эту поверхность в единицу времени. Объемный расход Q, массовый расход QМ, весовой расход QG определяются по формулам: QМ = *Q, QG=q*QМ (2. 3) Средняя скорость определяется из равенства =Q/s. (2. 4) Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу (рис. 2. 6. ) с переменным живым сечением. Расход жидкости через трубу в любом ее сечении постоянен, т. е. Q 1 = Q 2 = const, откуда Q = 1 s 1 = 2 s 2= const, где 1, 2 — средние скорости в сечениях 1 - 1 и 2 - 2. Рис. 2. 6. Труба с переменным диаметром при постоянном расходе

Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис. 2. 7). Рис. 2. 7. Трубопровод переменного диаметра в случае идеальной жидкости

Уравнение Бернулли для идеальной жидкости при установившемся движении в поле силы тяжести (2. 5) где z 1, z 2 - расстояния от центров выбранных живых сечений 1 -1 и 2 -2 до некоторой произвольной горизонтальной плоскости z = 0 (рис. 2. 7); 1, 2 - скорости; P 1, P 2 -давления в этих сечениях. Уравнение Бернулли выражает собой закон сохранения механической энергии. Величина (2. 6) называется полным напором и представляет собой удельную (приходящуюся на единицу силы тяжести) механическую энергию жидкости в рассматриваемом сечении.

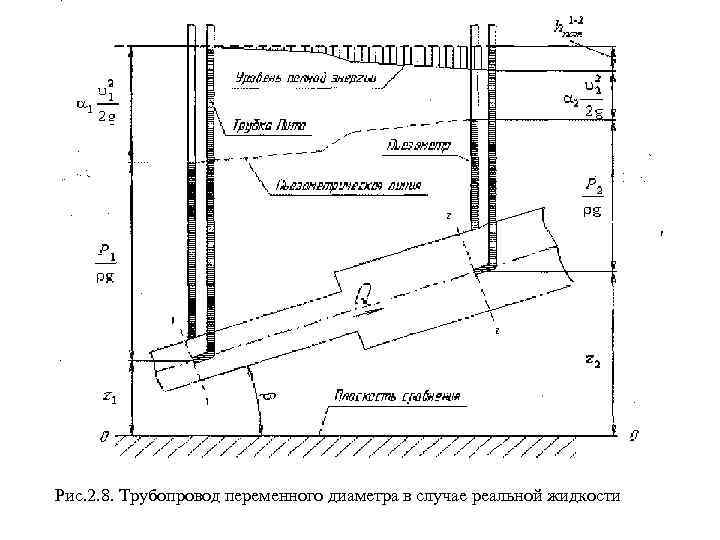Рис. 2. 8. Трубопровод переменного диаметра в случае реальной жидкости

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения 2. 5. Дело в том, что при движении реальной жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1 -1 будет больше, чем в сечении 2 -2 на величину потерянной энергии h 1 -2. (2. 6) где 1, 2 — коэффициенты Кориолиса, учитывающие неравномерность распределения скоростей частиц жидкости в сечениях; при течении по круглой цилиндрической трубке = 2 для ламинарного режима течения и 1, 1 - для турбулентного; при решении практических задач обычно принимается = 1. С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии: z - геометрический напор или удельная потенциальная энергия положения;

p/( g) - пьезометрический напор или удельная потенциальная энергия давления; 2/(2 g) - скоростной напор или удельная кинетическая энергия; h 1 -2 - потери напора, т. е. часть удельной механической энергии, израсходованной на работу сил трения на участке между сечениями 1 - 1 и 2 - 2 (см. рис. 2. 8). Потери напора h 1 -2 , отнесенные к единице длины трубопровода, называются гидравлическим уклонном: 7) В случае равномерного движения несжимаемой жидкости i = hl-2 / l, (2. 8) где l — расстояние между выбранными сечениями.

3. Режимы движения жидкости При ламинарном режиме движения частицы жидкости перемещаются по траекториям, направленным вдоль общего течения, в частности, вдоль оси трубы без поперечного перемешивания. При турбулентном режиме движения частицы жидкости перемещаются по случайным, неопределенно искривленным траекториям, имеющим пространственную конфигурацию. Движение имеет беспорядочный хаотический характер. Его особенность - наличие поперечных и продольных (относительно направления общего течения) пульсаций скорости и пульсаций давления, что существенно влияет на затраты энергии при перемещении жидкости. Re = d /v Если Re < 2320, то режим течения ламинарный. Если Re > 2320, режим турбулентный.

4. Гидравлические сопротивления Запас механической энергии жидкости, которым обладает каждая ее единица силы тяжести, называется напором Н. Из-за работы сил трения напор по ходу движения жидкости непрерывно уменьшается. Разность начального и конечного напоров между двумя какими-либо живыми сечениями потока называется потерями напора hпот. Эти потери напора представляют собой сумму потерь напора на трение по длине потока hдл и в местных сопротивлениях hм Hпот =hдл+hм. (4. 1) Потери напора по длине для труб постоянного диаметра определяются по формуле (4. 2) где - коэффициент гидравлического сопротивления (гидравлического трения); l - длина трубы; d - ее внутренний диаметр; - средняя скорость потока.

Т. о. в общем виде = (Re, /d). Численно определяется в зависимости от области сопротивления. При ламинарном режиме движения (Re < Reкр ), = (Re) =64/Re. (4. 3) В общем случае является функцией числа Рейнольдса (Re) и относительной шероховатости стенок трубы /d. Здесь - абсолютная эквивалентная шероховатость, т. е. такая высота равномерно-зернистой шероховатости, при которой в квадратичной зоне сопротивления потери напора равны потерям напора для данной естественной шероховатости трубы. При турбулентном режиме движения (Re > Reкр) различают три зоны сопротивления. 1. Зона гидравлически гладких труб (Reкp < Re 10 ; = (Re)): = 0, 3164/Re 0, 25 (4. 4) формула Блазиуса, используемая при Re 105 ; формула Конакова, используемая при Re < 3 • 106.

2. Зона шероховатых труб (10 d/ < Re 500 d/ ; = (Re, /d): (4. 5) формула Альтшуля. 3. Зона вполне шероховатых труб или квадратичная зона (Re>500 d/ ; = ( /d)): =0, 11 ( /d)0, 25 – (4. 6) формула Шифринсона. Местными сопротивлениями называются участки трубопровода, в которых происходит резкая деформация потока (к ним относятся, в частности, все виды арматуры трубопроводов - вентили, задвижки, тройники, колена и т. д. ). Потери напора в местных сопротивлениях h. М определяются по формуле (4. 7) где — коэффициент местного сопротивления, зависящий от его геометрической формы, состояния внутренней поверхности и Re.