2 ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ МАТЕРИАЛОВЕДЕНИЯ 2 1 Реальные материалы

2 ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ МАТЕРИАЛОВЕДЕНИЯ 2. 1 Реальные материалы, реальные процессы и их описание. 2. 2 Термодинамика поведения систем. 2. 3 Условия перехода системы из одного состояния в другое. 2. 4 Энергия системы и ее изменение. 1 -й закон термодинамики. 2. 5 Направление перехода системы из одного состояния в другое. 2. 5. 1 Энтропия и 2 -ой закон термодинамики. 2. 5. 2 Свободная энергия. 2. 6 Химический потенциал. 2. 7 Правило фаз Гиббса. 2. 8 Построение диаграмм состояний. 2. 8. 1 Эксперимент. 2. 8. 2 Теория. 1

2. 1 РЕАЛЬНЫЕ МАТЕРИАЛЫ, РЕАЛЬНЫЕ ПРОЦЕССЫ И ИХ ОПИСАНИЕ Человек живет в окружении реального мира и реально протекающих процессов. окружающий мир П Р И Р О Д А МАТЕРИАЛЫ 1 2 Почему камень твердый, но хрупкий? Почему железо твердое, но ковкое? Почему железо прочнее алюминия? Почему идет дождь? Как и когда зарождаются цунами? 3 2

Для познания окружающего мира и использования его для удовлетворения своих нужд человек придумал науку. Основная задача науки отвечать на вопросы: что такое (что это); как, почему; что будет, если…. Почему камень твердый? Почему железо прочнее алюминия? Почему идет дождь? Как сделать сталь более прочной? В науке есть два направления исследования: эксперимент (сбор данных, анализ, выводы, законы); теория (физическое, математическое описание, моделирование). 3

2. 2 ТЕРМОДИНАМИКА ПОВЕДЕНИЯ СИСТЕМ В физике твердого тела при изучении формирования различных структур и фазовых состояний и их последовательное превращение при изменении внешних условий применяются широкое применение нашли два подхода описания систем: статистическая теория и термодинамический метод описания систем. В материаловедении широкое применение нашел последний метод. С позиций термодинамики рассматриваются процессы перехода металла из жидкой фазы в твердую и наоборот, поведение дефектов кристаллической решетки, процессы образования новых фаз в твердом состоянии. Термодинамический метод позволяет теоретически (из «первых принципов» ) построить диаграмму состояний, определить, находится рассматривается система в равновесии или ее состояние будет изменяться , а если так, то в каком направлении и до какой степени. 4

Система В термодинамике под системой понимается выделенная совокупность частиц, взаимодействующих друг с другом и с внешними телами. Примеры систем …. ? 5

Система В термодинамике под системой понимается выделенная совокупность частиц, взаимодействующих друг с другом и с внешними телами. Примеры систем …. ? Газ в комнате (молекулы) Жидкость в сосуде (молекулы) Слиток металла (атомы металла) Слиток сплава (атомы разных металлов) Состояние системы характеризуется набором параметров. 6

Параметры системы – это ее характеристики, которые можно количественно однозначно определить (в виде числа). Параметры системы: масса, объем, плотность, ……………. . и другие характеристики известные нам из курса физической химии. Одним из главных параметров, определяющим состояние системы, является энергия. В общем случае при изменении хотя бы одного параметра система совершает переход из одного состояния в другое. С 1 С 2 С 3 7

2. 3 УСЛОВИЯ ПЕРЕХОДА СИСТЕМЫ ИЗ ОДНОГО СОСТОЯНИЯ В ДРУГОЕ Термодинамический метод описания систем позволяет определить, является ли состояние системы (С 2) равновесным при данных условиях или система самостоятельно перейдет в состояние С 1 или С 3 (до +) С 1 С 2 С 3 При этом термодинамический метод не может ответить на вопрос – каков механизм перехода, с какой скоростью происходит переход (недо - ) Главным критерием устойчивости или неустойчивости системы является условие минимального значения энергии системы в данных условиях. Значение энергии системы определяет такие важные характеристики как Виды состояния системы Виды перехода системы из одного состояния в другое 8

РАЗЛИЧНЫЕ СОСТОЯНИЯ СИСТЕМЫ Виды состояния системы и их характеристики Равновесное – в нем система может находиться сколь угодно долго (Е=Еmin) Неравновесное – при незначительном воздействии система уходит из этого состояния Устойчивое - при внешнем воздействии система возвращается в прежнее состояние Неустойчивое – в нем система находится не может Безразличное – Квазиравновесное - РАЗЛИЧНЫЕ ПЕРЕХОДЫ СИСТЕМЫ ИЗ ОДНОГО СОСТОЯНИЯ В ДРУГОЕ Виды перехода системы и условие перехода С 1 Самопроизвольное ∆ Е < 0 Вынужденное ∆ Е > 0 Без изменения энергетического состояния ∆ Е = 0 С 2 9

2. 4 ЭНЕРГИЯ СИСТЕМЫ И ЕЕ ИЗМЕНЕНИЕ, ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ • Энергия системы – характеристики: – Один из параметров системы – Неоднозначный параметр – Функция состояния системы – Универсальная функция, имеющая для различных процессов свой смысл, свое название (параметры системы – абсолютный характер) (энергия - относительный характер) ( Е = f (m, V, P, T, ……………. . ) ) (свободная энергия, энергия Гиббса) ∆E = ∆Q + W Энергию системы можно увеличить , передав ей некоторое количество теплоты и совершив над ней работу ∆E = ∆Q + W(внеш) ∆E = ∆Q - W(с) Закон сохранения энергии Универсальный закон природы , позволяющий определять состояние системы, возможность и направление перехода системы из одного состояния в другое. 10

Поведение и состояние системы с точки зрения 1 -го закона ТД E = Q + W ∆ ∆ ∆E = E 2 – E 1 , здесь E 2 - энергия конечного состояний, Е 1 - энергия начального состояния системы условия изменения состояния системы 1) ∆E < 0 . . . 2) ∆E = 0 Q = 0 W = 0 или Q = Wc 3) Система изолированная Q = 0 Wвнешн = 0 ∆E = 0 4) Система неизолированная Q ≠ 0 Wвнешн ≠ 0 ∆E = 0 ∆E ≠ 0 cостояние системы 1 cостояние системы 2 C 1 переход системы C 2 11

Рассмотрим некоторое количество вещества и назовем его системой С. Энергию С можно увеличить, если совершить над ней работу или если сообщить ей некоторое количество тепла. В общем случае эту ситуацию можно описать уравнением ∆ E = Q + W, где ∆ E = Е 2 – Е 1 Мы получили 1 -й закон термодинамики или закон сохранении энергии. Рассмотрим, как этот закон описывает реальные сложные системы. а) ∆ E = Q – W, система производит работу над внешней средой; б) ∆ E = - Q + W, система отдает тепло во внешнюю среду; в) Если Q = 0, W =0, то ∆ E = 0, данная система остается в прежнем состоянии (изолированная система); г) При Q ≠ 0, W ≠ 0 возможно ∆ E ≠ 0 и ∆ E = 0 (неизолированная система).

Особый характер параметра «энергия» Энергия системы является особым параметром в отличие от других параметров, однозначно количественно определяющих данную характеристику ( например, система имеет массу 2 кг, объем 1 м 3, …. . ). Энергия системы как параметр не является однозначной количественной характеристикой системы. Величина Е есть понятие относительное т. к. всегда можно выбрать нулевой уровень энергии Ео исходя из практической целесообразности. Пример: при Т=0, при Т=Тn …. . Энергия системы как параметр является универсальной характеристикой. Изменения энергии системы ∆ E не зависит от «маршрута» процесса, от цикличности процесса. Пример: кусок металла …. .

СПАСИБО ЗА ВНИМАНИЕ 14

ЗАКЛЮЧЕНИЕ Добрый совет студенту от опытного преподавателя

Реальность жизни: Студенты запоминают менее четверти того, что они слышат, и лишь половину из того, что они и видят и слышат. Отсюда вывод: Необходимо писать конспект, если хочешь получить зачет или сдать экзамен.

эмпатия • Интуитивное знание о чувствах, мыслях, внутреннем состоянии другого человека, • Сопереживание и переживание сходных эмоций с эмоциями собеседника, Умение принять чужую точку зрения, примерить на себя роль другого человека, активный поиск выход из сложной ситуации именно с позиции другого человека,

Контрольная работа № 1 Описать поведение и состояние системы с точки зрения 1 -го закона термодинамики ∆E = ∆Q + W, где ∆E = E 2 – E 1 Здесь ∆E ∆Q WСистема изолированная ∆E = ? (условие состояния системы) Система неизолированная ∆E = 0 (при каких условиях) ∆E ≠ 0 (при каких условиях) 18

19

20

2. 5 Направление перехода системы из одного состояния в другое 2. 5. 1 Энтропия и 2 -ой закон термодинамики • Из опыта известно, что теплота всегда переходит от более горячего тела к более холодному (и ни как наоборот) Т 1 T 2 Q 1 Q 2 Условие или состояние системы: T 1 > T 2 Q 1 = - Q 2 IQ 1 I = IQ 2 I Введем новый параметр системы: энтропия S = Q / T и изменение энтропии ∆S для тел 1 и 2 соответственно ∆S = (Q 1/ T 1) – (Q 2/ T 2)

Для практического использования второго закона термодинамики при изучении и описании поведения систем удобнее рассмотреть другую формулировку, предложенную Р. Клаузиусом (1865): для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния , называемая энтропией S, такая, что ее полный дифференциал для любых процессов можно записать d. S => d. Q / T где d. Q бесконечно малое количество тепла , переданное системе в обратимом процессе, отнесенное к абсолютной температуре Т.

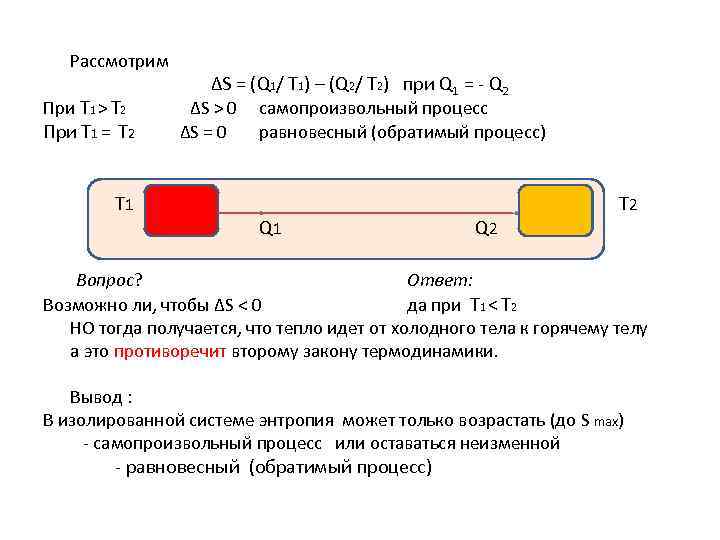Рассмотрим ∆S = (Q 1/ T 1) – (Q 2/ T 2) при Q 1 = - Q 2 При Т 1 > Т 2 ∆S > 0 При Т 1 = Т 2 ∆S = 0 Т 1 самопроизвольный процесс равновесный (обратимый процесс) Q 1 Вопрос? Q 2 T 2 Ответ: Возможно ли, чтобы ∆S < 0 да при Т 1 < Т 2 НО тогда получается, что тепло идет от холодного тела к горячему телу а это противоречит второму закону термодинамики. Вывод : В изолированной системе энтропия может только возрастать (до S max) - самопроизвольный процесс или оставаться неизменной - равновесный (обратимый процесс)

Пример Образец с Тоб и печь с Тп рассматриваем как изолированную единую систему для которой d. S => d. Q / T = 0 : 1) при Тоб < Тп имеем неизотермический процесс (нагрев образца) при этом ∆S > d. Q / T > 0 и S возрастает пока не достигнет значения Smax 2) при Тоб = Тп изотермический процесс (взаимный теплообмен) S = Smax ∆S = d. Q / T = 0

2. 5. 2 Свободная энергия Первое начало ТД ∆ E = Q + W (1) или ∆ E = Q – W (2) Второе начало ТД ∆ S => Q / T или T ∆ S => Q Первое и второе начала термодинамики в объединенной форме для случая, когда система сама производит работу W (2), имеют вид: ∆ E< = T ∆ S – W(2) преобразуем ∆ E – T ∆ S < = – W(2) Введем новую функцию F = E – TS тогда ∆F = ∆ E – T ∆ S < = – W(2) Теперь можно записать ∆F = < = – W(2) или W (2) < = – ∆F Здесь F – свободная энергия (энергия системы, которая может быть превращена в работу) Система произвела работу W (2) при этом ее собственная энергия уменьшилась на величину ∆F В общем случае полная энергия системы Е = Е внутр + F

Имеем ∆F < = - W (2), Здесь W (2) работа, которую совершает система. Пример. Образец и печь – единая общая система (замкнутая и W (2) = 0 ). В этом случае ∆F < = 0 : - если ∆F < 0, то это самопроизвольный процесс - идет нагрев образца, при этом свободная энергия уменьшается, пока не достигнет значения F min при Тоб = Тп ; - если ∆F = 0, значит наступило тепловое равновесие при Тоб = Тп и это теперь соответствует обратимому процессу внутри системы. По изменению свободной энергии системы можно предсказывать направление процесса.

ДВА ВЫВОДА 1. Энтропия замкнутой системы при любых происходящих в ней процессах не может убывать она увеличивается – самопроизвольный процесс Процесс идет до тех пор пока S = S max или остается неизменной (∆ S = 0) – равновесный процесс 2. Свободная энергия замкнутой системы при любых происходящих в ней процессах не может возрастать она убывает – самопроизвольный процесс. (∆F < 0) Процесс идет до тех пор пока F = F min или остается неизменной (∆F = 0) – равновесный (обратимый) процесс 27

РЕЗЮМЕ Состояние системы (устойчивое, неустойчивое, безразличное, …. ) определяет полная энергия системы Е. Направление процесса и предел, до которого длится процесс можно определить по изменению энтропии или изменению свободной энергии ∆S > = 0 ∆F < = 0 28

Основные понятия термодинамики Виды систем Изолированная система Замкнутая система Неизолированная Незамкнутая система Полная энергия системы 1) Образец с Тоб в термостате или 2) Образец с Тоб и печь с Тп как изолированная единая система Образец с Тоб как система и Печь с Тп как внешняя среда, находящаяся в контакте с системой Е = Е внутр + F Е внутр – внутренняя энергия, которая …… F – свободная энергия которая …… 29

30

31

ВСЕМИРНЫЙ ЗАКОН ПРИРОДЫ Если в системе протекают самопроизвольные процессы , то в ней А) возрастает энтропия, до максимального значения, после чего наступает равновесное состояние ; Б) уменьшается свободная энергия до минимального значения, после чего наступает равновесное состояние. На практике это означает с 1) самопроизвольный процесс перехода порядок – беспорядок. РАЗРУШЕНИЕ 1) самопроизвольный процесс выравнивания температуры (переход тепла от более нагретой области к менее нагретой). 32

ВСЕМИРНЫЙ ЗАКОН ПРИРОДЫ Если в системе протекают самопроизвольные процессы , то в ней А) возрастает энтропия, до максимального значения, после чего наступает равновесное состояние ; Б) уменьшается свободная энергия до минимального значения, после чего наступает равновесное состояние. На практике это означает с 1) самопроизвольный процесс перехода порядок – беспорядок. РАЗРУШЕНИЕ 1) самопроизвольный процесс выравнивания температуры (переход тепла от более нагретой области к менее нагретой). ТЕПЛОВАЯ СМЕРТЬ ВСЕЛЕННОЙ 33

ТЕПЛОВАЯ СМЕРТЬ ВСЕЛЕННОЙ 34

Тепловая смерть Вселенной - это теория, выдвинутая Р. Клаузиусом в 1865, согласно которой Вселенная рассматривается как замкнутая система, поэтому согласно второму началу термодинамики, энтропия Вселенной стремится к максимуму, в результате чего со временем в ней должны прекратиться все макроскопические процессы. 35

2. 6 ХИМИЧЕСКИЙ ПОТЕНЦИАЛ Химический потенциал это еще один из параметров системы, описывающий ее состояние. С(1) закрытая однородная система ∆ E = T ∆ S – W(2) Равновесное состояние: ∆ S = 0, W(2) = 0, ∆ E = 0 и S = S max C (2) к системе добавили ∆ n молей другого компонента ∆ E = T ∆ S – W(2) + µ ∆ n µ - химический потенциал при S = S max и Е = Е min новое равновесное состояние ∆ S = 0, W(2) = 0 µ = ∆ E / ∆ n Из этого уравнения можно определить физический смысл нового параметра: Изменение энергии системы при изменении ее состава (добавления к ней другого компонента или изменения ее количественного состава. C (3) закрытая неоднородная система (две фазы ж и тв, два компонента А и В Условие равновесия µ(ж, А) = µ(тв, А) и µ(тв, В) = µ(ж, В)

37

38

2. 7 ПРАВИЛО ФАЗ ГИББСА s = k – f + 2 s – число cтепеней свободы - число внешних и внутренних параметров, которые можно изменять без изменения числа фаз в системе. Система (1): вода – пар Система (2): чистый металл Система (3) : двойной сплав А - В